Skip to main content
SpringerLink
Log in

Uncertainty Intercomparison of Different Hydrological Models in Simulating Extreme Flows

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

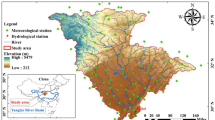
A growing number of investigations on uncertainty quantification for hydrological models have been widely reported in past years. However, limited studies are found on uncertainty assessment in simulating streamflow extremes so far. This article presents an intercomparison of uncertainty assessment of three different well-known hydrological models in simulating extreme streamflows using the approach of generalized likelihood uncertainty estimation (GLUE). Results indicate that: (1) The three modified hydrological models can reproduce daily streamflow series with acceptable accuracy. When the threshold value used to select behavioral parameter sets is 0.7, XAJ model generates the best GLUE estimates in simulating daily flows. However, the percentage of observations contained in the calculated 95 % confidence intervals (P-95CI) is low (<50 %) when simulating the high-flow index (Q10). (2) Decreasing average relative length (ARIL), P-95CI and increasing average asymmetry degree (AAD) are found, when the threshold value increases for both daily-flows and high-flows. However, there is a significant inconsistence between sensitivity of daily-flows and high-flows to various threshold values of the likelihood function. Uncertainty sources from parameter sets, model structure and inputs collectively accounts for above sensitivity. (3) The best hydrological model in simulating daily-flows is not identical under different threshold values. High P-95CIs of GLUE estimate for high-flows (Q10 and Q25) indicate that TOPMODEL generally performs best under different threshold values, while XAJ model produces the smallest ARIL under different threshold values. The results are expected to contribute toward knowledge improvement on uncertainty behaviors in simulating streamflow extremes by a variety of hydrological models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Abebe N, Ogden F, Pradhan N (2010) Sensitivity and uncertainty analysis of the conceptual HBV rainfall-runoff model: Implications for parameter estimation. Journal of Hydrology 389(3–4):301–310

    Article  Google Scholar 

  • Alvisi S, Franchini M (2011) Fuzzy neural networks for water level and discharge forecasting with uncertainty. Environmental Modelling and Software 26:523–537

    Article  Google Scholar 

  • Aronica G, Hankin B, Beven K (1998) Uncertainty and equifinality in calibrating distributed roughness coefficients in a flood propagation model with limited data. Advances in Water Resources 22(4):349–365

    Article  Google Scholar 

  • Arora VK (2002) The use of the aridity index to assess climate change effect on annual runoff. J Hydrol 265:164–177

    Article  Google Scholar 

  • Bahremand A, Smedt FD (2010) Predictive analysis and simulation uncertainty of a distributed hydrological model. Water Resour Manage 2010(24):2869–2880

    Article  Google Scholar 

  • Bates BC, Campbell EP (2001) A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall–runoff modeling. Water Resources Research 37:937–947

    Article  Google Scholar 

  • Benke KK, Lowell KE, Hamilton AJ (2007) Parameter uncertainty, sensitivity analysis and prediction error in a water-balance hydrological model. Mathematical and Computer Modeling 47(11–12):1134–1149

    Google Scholar 

  • Bergström S (1976) Development and application of a conceptual runoff model for Scandinavian catchments. Ph.D. Thesis. SMHI Reports RHO No. 7, Norrköping, Sweden

    Google Scholar 

  • Bergström S (1995) The HBV model. In: Singh VP (ed) Computer models of watershed hydrology. Water Resources Publications, Highlands Ranch, CO., pp 443–476

    Google Scholar 

  • Beven K (2001) How far can we go in distributed hydrological modeling? Hydrology and Earth System Sciences 5(1):1–12

    Article  Google Scholar 

  • Beven KJ, Binley A (1992) The future of distributed models, model calibration and uncertainty prediction. Hydrological Processes 6:279–298

    Article  Google Scholar 

  • Beven KJ (1993) Prophecy, reality and uncertainty in distributed hydrological modelling. Advances in Water Resources 16:41–51

    Article  Google Scholar 

  • Beven KJ, Freer J (2001a) A dynamic TOPMODEL. Hydrological Processes 15:1993–2011

    Article  Google Scholar 

  • Beven KJ, Freer J (2001b) Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. Journal of Hydrology 249:11–29

    Article  Google Scholar 

  • Beven KJ, Kirby MJ (1979) A physically based variable contributing area model of basin hydrology. Hydrological Science Bulletin 24:43–69

    Article  Google Scholar 

  • Beven KJ (1997) Distributed hydrological modelling: Applications of the TOPMODEL concept. John Wiley and Sons, Chichester

    Google Scholar 

  • Blazkova S, Beven K (2004) Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. Journal of Hydrology 292:153–172

    Article  Google Scholar 

  • Carpenter TM, Georgakakos KP (2004) Impacts of parametric and radar rainfall uncertainty on the ensemble streamflow simulations of a distributed hydrological model. Journal of Hydrology 298:202–221

    Article  Google Scholar 

  • Cameron D, Beven KJ, Tawn J, Blazkova S, Naden P (1999) Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty). Journal of Hydrology 219:169–187

    Article  Google Scholar 

  • Chowdhury S, Sharma A (2007) Mitigating parameter bias in hydrological modelling due to uncertainty in covariates. Journal of Hydrology 340:197–204

    Article  Google Scholar 

  • Davies A (1997) Monthly snowmelt modelling for large-scale climate change studies using the degree day approach. Ecological Modelling 101(2–3):303–323

    Article  Google Scholar 

  • Diaz-Ramirez JN, McAnally WH, Martin JL (2012) Sensitivity of simulating hydrologic processes to gauge and radar rainfall data in subtropical coastal catchments. Water Resour Manage 26:3515–3538

    Article  Google Scholar 

  • Engeland K, Xu C-Y, Gottschalk L (2005) Assessing uncertainties in a conceptual water balance model using Bayesian methodology. Hydrological Sciences Journal 50(1):45–63

    Article  Google Scholar 

  • Freer J, Beven K, Ambroise B (1996) Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach. Water Resources Research 32(7):2161–2173

    Article  Google Scholar 

  • Georgakakos KP, Seo DJ, Gupta H et al (2004) Towards the characterization of streamflow simulation uncertainty through multimodel ensembles. Journal of Hydrology 298:222–241

    Article  Google Scholar 

  • Huang B, Jiang B (2002) AVTOP: A full integration of TOPMODEL into GIS. Environmental Modelling and Software 17(3):261–268

    Article  Google Scholar 

  • Iorgulescu I, Beven KJ, Musy A (2005) Data-based modelling of runoff and chemical tracer concentrations in the haute-menthue (Switzerland) research catchment. Hydrological Processes 19:2557–2574

    Article  Google Scholar 

  • Jiang T, Chen Y, Xu C, Chen X, Singh V (2007) Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. Journal of Hydrology 336(3–4):316–333

    Article  Google Scholar 

  • `Jin X, Xu C, Zhang Q, Singh VP (2010) Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. Journal of Hydrology 383:147–155

    Article  Google Scholar 

  • Ju Q, Yu Z, Hao Z, Ou G, Zhao J, Liu D (2009) Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model. Neurocomputing 72(13–15):2873–2883

    Article  Google Scholar 

  • Kavetski D, Franks S, Kuczera G (2002) Confronting input uncertainty in environmental modelling. In: Gupta HV, Sorooshian S, Rousseau AN, Turcotte R (eds) Calibration of watershed models. AGU Water Science and Applications Series, Duan, pp 49–68

    Google Scholar 

  • Kavetski D, Kuczera G, Franks SW (2006a) Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory Water Resources Research 42:W03407

    Article  Google Scholar 

  • Kavetski D, Kuczera G, Franks SW (2006b) Bayesian analysis of input uncertainty in hydrological modeling: 2. Application Water Resources Research 42(581):W03408

    Article  Google Scholar 

  • Kuczera G, Parent E (1998) Monte Carlo assessment of parameter uncertainty in conceptual catchment models: The metropolis algorithm. Journal of Hydrology 211:69–85

    Article  Google Scholar 

  • Lamb R, Beven KJ, Myrabø S (1998) Use of spatially distributed water table observations to constrain uncertainty in a rainfallrunoff model. Advances in Water Resources 22(4):305–317

    Article  Google Scholar 

  • Li L, Xia J, Xu C-Y, Singh VP (2010) Evaluation of the subjective factors of the GLUE method and comparison with the formal Bayesian method in uncertainty assessment of hydrological models. Journal of Hydrology 390:210–221

    Article  Google Scholar 

  • Li L, Xu C-Y, Xia J, Engeland K, Reggiani P (2011) Uncertainty estimates by Bayesian method with likelihood of AR (1) &normal model and AR (1) &multi-normal model in different time-scales hydrological models. Journal of Hydrology 406:54–65

    Article  Google Scholar 

  • Lin K, Guo S, Zhang W, Liu P (2007) A new baseflow separation method based on analytical solutions of the Horton infiltration capacity curve. Hydrological Processes 21(13):1719–1736

    Article  Google Scholar 

  • Marshall L, Nott D, Sharma A (2007) Towards dynamic catchment modelling: A Bayesian hierarchical modelling framework. Hydrological Processes 21:847–861

    Article  Google Scholar 

  • Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models- Part 1-a. discussion of principles. Journal of Hydrology 10(3):282–290

    Article  Google Scholar 

  • Quinn P, Beven KJ, Lamb R (1995) The ln(α/tan β) index: how to calculate it and how to use it in the TOPMODEL framework. Hydrol Process 9:161–185

    Article  Google Scholar 

  • Rango A (1992) World-wide testing of the Snowmelt runoff model with applications for predicting the effects of climate change. Nordic Hydrology 23:155–172

    Google Scholar 

  • Refsgaard JC, Storm B (1996) Construction calibration and validation of hydrological models. In: Abbott MB, Refsgaard JC (eds) Distributed hydrological modelling, water science and technology library, vol 22, Kluwer Academic Publishers. Dordrecht, The Netherlands, pp 41–54

    Chapter  Google Scholar 

  • Seibert J (2003) Reliability of model predictions outside calibration conditions. Nordic Hydrology 34:477–492

    Google Scholar 

  • Stedinger JR, Vogel RM, Lee SU, Batchelder R (2008) Appraisal of the generalized likelihood uncertainty estimation (GLUE) method. Water Resources Research 44:W00B06. doi:10.1029/2008WR006822

    Article  Google Scholar 

  • Talebizadeh M, Morid S, Ayyoubzadeh SA et al (2010) Uncertainty analysis in sediment load modeling using ANN and SWAT model. Water Resour Manage 24:1747–1761

    Article  Google Scholar 

  • Thorndahl S, Beven KJ, Jensen JB (2008) Event based uncertainty assessment in urban drainage modeling, applying the GLUE methodology. Journal of Hydrology 357:421–437

    Article  Google Scholar 

  • Vazquez RF, Beven K, Feyen J (2009) GLUE based assessment on the overall predictions of a MIKE SHE application. Water Resour Manage 23:1325–1349

    Article  Google Scholar 

  • Wu S, Li J, Huang GH (2008) Characterization and evaluation of elevation data uncertainty in water resources modeling with GIS. Water Resour Manage 22:959–972

    Article  Google Scholar 

  • Xiong LH, Guo SL (2004) Effects of the catchment runoff coefficient on the performance of TOPMODEL in rainfall-runoff modeling. Hydrological Processes 18:1823–1836

    Article  Google Scholar 

  • Xiong LH, Wan M, Wei XJ (2009) Indices for assessing the prediction bounds of hydrological models and application by generalized likelihood uncertainty estimation. Hydrological Sciences Journal 54:852–871

    Article  Google Scholar 

  • Xu C-Y, Tunemar L, Chen YD, Singh VP (2006) Evaluation of seasonal and spatial variations of conceptual hydrological model sensitivity to precipitation data errors. Journal of Hydrology 324:80–93

    Article  Google Scholar 

  • Yang J, Reichert P, Abbaspour KC, Xia J, Yang H (2008) Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. Journal of Hydrology 358:1–23

    Article  Google Scholar 

  • Yang T, Shao Q, Hao Z, Chen X, Zhang Z, Xu C, Sun L (2010) Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in Pearl River Basin, Southern China. Journal of Hydrology 380(3–4):386–405

    Article  Google Scholar 

  • Zhao RJ, Zhuang YL, Fang LR, Liu XR, Zhang QS (1980) The Xinanjiang model. Hydrological Forecasting Proceedings Oxford Symposium, 129. IAHS publication, pp. 351–356.

Download references

Acknowledgements

The work was jointly supported by grants from the National Natural Science Foundation of China (40901016, 40830639, 40830640), a grant from the State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering (2009586612, 2009585512), grants of Special Public Sector Research Program of Ministry of Water Resources (201201025), and the Fundamental Research Funds for the Central Universities (2010B00714).

Author information

Authors and Affiliations

  1. State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, 818, Beijing Nanlu, Urumqi, Xinjiang, 830011, People’s Republic of China

    Xi Chen & Tao Yang

  2. State Key Laboratory of Hydrology-Water Resources and Hydraulics Engineering, Hohai University, Nanjing, 210098, China

    Tao Yang, Xiaoyan Wang & Zhongbo Yu

  3. Department of Geosciences, University of Oslo, P.O. Box 1047, Blindern, 0316, Oslo, Norway

    Chong-Yu Xu

  4. Department of Geoscience, University of Nevada Las Vegas, Las Vegas, NV, 89154-4010, USA

    Zhongbo Yu

Authors
  1. Xi Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tao Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaoyan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chong-Yu Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhongbo Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tao Yang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, X., Yang, T., Wang, X. et al. Uncertainty Intercomparison of Different Hydrological Models in Simulating Extreme Flows. Water Resour Manage 27, 1393–1409 (2013). https://doi.org/10.1007/s11269-012-0244-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-012-0244-5

Keywords

Search

Navigation