Developing an Efficient Pattern Discovery Method for CPU Utilizations of Computers

Abstract

Mining repeated patterns (often called motifs) in CPU utilization of computers (also called CPU host load) is of fundamental importance. Many recently emerging applications running on high performance computing systems rely on motif discovery for various purposes, including efficient task scheduling, energy saving, etc. In this paper, we propose an efficient motif discovery framework for CPU host load. The framework is elaborately designed to take into account the important properties in host load data. The framework benefits from its ability of on-line discovery and the adaptivity to work with massive data. The experiments are conducted in this paper and the experimental results show that the proposed method is effective and efficient.

1 Introduction

It is very useful to discover repeated patterns, which is often called motifs in the area of pattern discovery [30], in CPU host load of a cluster system. Essentially, the CPU host load is time series data [12]. Many applications rely on motifs discovery in time series data [4], including (1) the algorithms for mining association rules in time series data based on pattern discovery [5, 17], (2) classification algorithms that are based on building typical prototypes of each class [16, 25], (3) anomaly detection [6] and (4) finding periodic patterns [15].

Although motif discovery in CPU host load is desired in many applications, there is not much work on this specific topic. Existing work in literature mainly focuses on predicting host load [8, 9, 36]. However, in the field of mining time series data, few motif discovery methods can be found [4, 30, 32]. Many current mining methods rely on the known patterns [1, 3, 11, 19]. Although these methods have shown their effectiveness and efficiency in many data mining problems for time series, they do not perform well for motif discovery in CPU host load due to the following challenges and features in host load motif discovery.

The first and most difficult task is to find the motifs with unknown length and shape. In our earlier work, we show that the tremendous time and space complexity of discovering exact unknown motifs. This is because discovering unknown motifs from time series data requires to compare the similarity of all possible sub-sequences in the time series data. The whole process has the time complexity as high as $O(n^6)$.

For discovering motifs with arbitrary lengths, traditional distance measure methods are not capable of producing accurate results any more. The work in [13] points out that DTW distance and Euclidean distance have the problem of inconsistent similarity, which means that these measures tend to produce higher distance value for longer sub-sequences of time series data. The problem of inconsistent similarity is demonstrated by the experiments presented in Fig. 1.

Fig. 1

Example of inconsistent similarity. Top left similar time series of length 128. Top right similar time series of length 64. Bottom left similar time series of length 32. Bottom right Euclidean and DTW distances of the 3 time series

In Fig. 1, we consider a pair of similar time series. The lengths of the data are originally 128 (top left). We gradually reduce the data sampling rate to produce their shorter versions: the lengths of 64 (top right) and 32 (bottom left). We measure the distance between a pair of time series in each figure using two most widely used distance measure, Euclidean distance and Dynamic Time Warping (DTW) distance. Results show that although there is no obvious difference in similarity between these pairs, their distances are different. This property of traditional distance measurements make it almost impossible to mine the patterns with different lengths.

Existence of noise is another inherent property of CPU host load data. It is critical to effectively handle the noise. As shown in Fig. 4, although we human being can easily identify the trend of a CPU host load with noise, the noise makes it very difficult for the computers to perform the traditional similarity measurement [4]. In [4], the authors illustrate that the pulse noise greatly affects similarity measure and casts difficulties in time series data mining. For similar reasons, continuous noise will also reduce the effectiveness of classic similarity measure.

Fig. 2

Illustration of noise impact: a raw data, b raw data with noise, c Gaussian smoothed data

Fig. 3

The effect of noise on distance measure and effectiveness of Gaussian filter

We conducted experiments and compared two time series data using two most classic similarity measures, Euclidean distance and Dynamic Time Warping (aka. DTW) distance. These two distance measures are widely used in many time series data mining techniques. The two selected time series data are three periods of sine wave and its slightly shifted version. They have similar trends and therefore should be considered as similar patterns. Figure 2 illustrates the experiment. Figure 2a presents the two raw time series. Figure 2b is the noisy version of the time series in Fig. 2a. In Fig. 2c we can see that the original time series data are restored from the noisy data in Fig. 2b. The results of distance measure are shown in Fig. 3. By adding Gaussian noise with the variance of $\sigma ^2$, the effectiveness of both DTW distance and Euclidean distance measures are compromised severely. However, the Gaussian smoothed data have almost the same distance as the distance of raw data. These results indicate that when the noise is big enough, applying distance measure on untreated noisy data can no longer identify any similarity between two time series.

Another problem of discovering motifs for CPU host load is that the host load data do not obey the Gaussian distribution. This property of host load data weakens several effective indexing method used for time series data. In [28], Lin et al. proposes a promising symbolic indexing method for the time series data, which assumes that the time series data follow the Gaussian distribution. However, our observation shows that CPU host load do not obey Gaussian distribution. We compare the host load data with the Gaussian distribution in Fig. 6. It can be seen that more host load data points are at the lower end of the value range of the Gaussian distribution.

These above properties of CPU host load make the traditional motif discovery methods ineffective, which necessitate a new method specially designed for CPU host load. Our method reduces the noise of host load and improves the effectiveness of time series representation. Moreover, we reveal the problem of inconsistent similarity in finding motifs of arbitrary lengths and present our solution. In our method, we represents the host load in a space of reduced dimension and proposes a new distance measurement method. The motif discovery method presented in this work is able to find similar motifs accurately and efficiently.

The rest of this paper is organized as follows. Section 2 briefly reviews related work and introduces the background in time series data mining and host load analysis, which is related to CPU host load mining. Section 3 presents our noise reduction method. In Sect. 4, we first briefly overviews the existing SAX indexing method and then present our method to improve it. Section 5 introduces the problem of inconsistent similarity and our solution the problem. Our fast motif discovery algorithm is proposed in Sect. 6, along with a cascade model to accelerate the discovering process. The experiments are presented in Sect. 7 to show the effectiveness and efficiency of the proposed method. Section 8 finally concludes this paper.

2 Background and Related Work

2.1 Background

Definition 1

(Time series) A time series $T = t_1,\ldots ,t_m$ is an ordered set of m real-valued variables [30].

Definition 2

(CPU host load data) A CPU host load data is a time series data, $T = t_1,\ldots ,t_m$, where $t_i$ is the average CPU utilization in period i.

In this paper, all host load data come from the Google cluster trace which recorded the running data of a Google cluster with more than 12,000 machines in [35].

Definition 3

(Subsequence) Given a time series of length m, $T= t_1,\ldots ,t_m$, a subsequence of T is a time series in T, $S= t_i,\ldots ,t_j$, where $1\le i< j\le m$.

Essentially, a motif referred to in this work is a subsequence of CPU host load data.

Definition 4

(Time series indexing) Given a time series dataset D that contains a set of time series data and a querying time series data Q, a time series indexing method I is a method that returns such a subset N of D that for every time series data $N_i$ in N, $Distance(N_i, Q)\le R$, where R is a predefined distance.

A good indexing method can make the task of time series data mining more effective and efficient.

Definition 5

(Match) Given two time series P and Q with length of m and of n respectively, if P and Q match then $Distance(P,Q)\le R$, where Disntance(X, Y) is the similarity function between two time series data and R is a predefined similarity value.

With the definition of match, we can define the motif.

Definition 6

(Motif) A motif is a set of subsequences in a time series dataset which match to each other.

In the task of motif discovery, it is very useful to determine the length of the motif we are looking for. According to the definition of motif, a motif can theoretically be a set of short subsequences, i.e., a short span of, such as two, data points. In practice, however, longer motifs are much more valuable. Therefore, the task of motif discovery is defined as:

Definition 7

(Motif discovery) Given a time series dataset, the task of motif discovery is to find all motifs with the length l that is greater than a predefined length n.

A motif discovery algorithm typically runs on a single time series in order to find all repeated patterns on the time series data itself, or runs on multiple time series data to concurrently find all motifs across this batch of time series data. There are three possible approaches to find motifs in a batch of time series data. First, we first find the motifs in two time series data, and then repeat the above phase to find all motifs in a batch of time series data. Second, we develop an algorithm to process a batch of time series data in a single phase. Finally, if we can get rid of self-matching in the time series data, the problem of finding motifs in a batch of time series data can be reduced to the problem of finding motifs in a single time series data.

2.2 Related Work

Essentially, CPU host load data are time series data [12]. Many researchers have conducted work in finding motifs in time series data. In [30], Lin et al. developed a symbolic representation-based motif discovery algorithm to find the kth most similar motif. A probabilistic method for motif discovery is proposed in [4] to accelerate the process. In [34], a motif discovery method for multi-dimensional data is proposed. These methods consider finding motifs from generic raw data. [32] presented a method of discovering exact motifs (the length of the shape of the motif are known in advance). The method gives a possible way to find exact motifs from short time series in a reasonable time. However, the time complexity of the method is still very high, which makes it not practical to work with long time series.

In [25], the influence of noise on mining time series data is shown. Some noise resistant mining algorithms are proposed [29]. These algorithms are able to process the data with sudden noise. However, for extremely noisy data like host load, we find that the pre-processing of noise reduction can produce better performance.

Given that the scale of CPU host load data grows fast over time, especially in a cluster or Cloud system which may consist of tens of thousands of machines, an effective indexing method is the necessity for efficient mining from CPU host load data. In literature, many time series indexing methods have been proposed [20, 24, 25, 28]. In these indexing methods, one of the most promising research is the symbolic aggregate approximation (SAX) representation proposed by Lin et al. [28]. The method reduces the time series dimensions by applying Piecewise Aggregate Approximation (PAA), and then symbolises each PAA segment to obtain a discrete representation. The method greatly simplifies the raw time series data. However, we notice that some time series data do not obey the Gaussian distribution. Also, as suggested by [2], the SAX representation does not guarantee the equiprobability of symbol occurrences. This defect may further hamper the effectiveness of the representation method and any data mining algorithms that are based on it.

In [10], Dinda analysed several statistical properties of host load data. In [7], Di et al. also analysed some statistical properties of CPU host load data and demonstrated their probability distribution. Li et al. [27, 37], Guo et al. [14] proposed a tool for performance model optimising SpMv on GPU and CPU. [26] detailed a scheduling method for cluster.

3 Noise Reduction of CPU Host Load

As shown in Fig. 3 and also in [4], noise is a non-trivial problem in time series data mining. In [38], Zhang et al. found that CPU host load data present a frequent periodical peak pattern in short terms. Although the property casts a light on short-term prediction, noise can dominate the distance measure between two similar host loads for the long-term motif discovery, which will cause them to be deemed different based on the distance measure. As the process goes on, the noise may often be amplified and deteriorate the situation.

Fortunately the high frequency noise can be smoothed by applying several low-pass filters. Gaussian smoother is one of these filters. Gaussian filter has been used in image processing to remove high frequency noise of an image. As in [18], Gaussian filter has a direct relation with neurophysiological findings in animals and psychophysics in human, which supports our assumption that time series smoothed by Gaussian filter can maintain the major trend similar to human intuition. This finding provides the ideas of designing a method that can maintain intuitive pattern of time series data without losing important information.

For a single CPU, its host load can be considered as a function f(t), where t is time. Therefore, we can apply 1-dimension Gaussian filter defined as follows.

$$\begin{aligned} G(x)=\frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{x^2}{2\sigma ^2}} \end{aligned}$$

(1)

The effect of a Gaussian filter is a convolution of Gaussian function g(x) and signal f(t)

$$\begin{aligned} (f*g)(\tau )=\int {f(\tau )g(x-\tau )d\tau } \end{aligned}$$

(2)

The discrete implementation of Gaussian filter can be found in various literature. Theoretically a Gaussian smoother has infinite length. However, one can easily calculate that the elements within $3\sigma$ accounts for 99.73 % of all elements, where $\sigma$ is the standard deviation of the Gaussian function. For applicability and without sacrificing much accuracy, we only examine the elements within $3\sigma$.

Fig. 4

Illustration of Gaussian filter retaining the tread of raw data

Figure 3 shows the effectiveness of a Gaussian filter. The original distance of two time series data is restored excellently from the highly noisy versions of them. Figure 4 shows how the Gaussian filter removes pulse noise and high frequency noise intuitively. It is clear in the figure that the filter retains the intuitive trend of host load data.

4 CPU Host Load Indexing

Indexing time series data is an efficient way to reduce search space and accelerate motif discovery. In this section we briefly overview the SAX indexing method proposed in [28] and then present our improved method.

4.1 Overview of PAA

In Sect. 1 we have briefly discussed the importance of host load indexing. In [28], Lin et al. proposed a symbolic method named SAX which transforms time series into symbol series. The SAX indexing method is based on PAA [21]. We first introduce the PAA method.

A time series C of length n can be represented in a w-dimension space by a vector $\bar{C}=\bar{c_1},\ldots ,\bar{c_w}$. The ith element of $\bar{C}$ is

$$\begin{aligned} \bar{c_i}=\frac{w}{n}\sum ^{\frac{n}{w}i}_{j=\frac{n}{w}(i-1)+1}c_j \end{aligned}$$

(3)

That is, the PAA method segments time series into $\frac{n}{w}$ parts of equal length and represents each part with new value which averages over all old values in that part. Hence, the presented time series is reduced to $\frac{w}{n}$ dimension. Now we can have the definition of dimensional reduction rate:

Definition 8

(Dimensional reduction rate) Given a time series T with length n, if T is represented with length w in a indexing method I, then the dimensional reduction rate of I is $\frac{n}{w}$.

Figure 5 shows how the PAA representation works. In this case, a time series with the length of 128 data points is reduced to a PAA representation with 8 data points. In other words, PAA averages over every 16 consecutive points to generate a new value.

The benefits of PAA is that the method provides effective dimensional reduction with time complexity O(n). Meanwhile, PAA provides lower bounding which ensures that for two time series data P and Q, the distance between them in the representation space will be no more than that in the original space. Namely, the following equation holds.

Fig. 5

A time series data reduced dimensionally by PAA and then symbolised by SAX

$$\begin{aligned} Disntace_{RepresentationSpace}(P,Q)\le Distance(P,Q) \end{aligned}$$

(4)

Lower bounding ensures the real distance between two time series will not be underestimated. The benefits of this property is that for a given query time series data Q, one can find all the possible results in the representation space. More specifically for the motif discovery task, lower bounding enables one to find all possible motifs and reduce the time complexity by applying the techniques such as early abandon.

4.2 The Refined Symbolic Aggregate Approximation Indexing

After the dimension of a time series data has been reduced using PAA, we can then discretize the time series data symbolically. The basic idea of symbolizing time series data is proposed in [28]. However, it is based on the assumption that the normalized time series data follow the Gaussian distribution [31].

Symbolic Aggregate Approximation, also known as SAX, divides the value range of a time series dataset into a given number of equal sized area under the Gaussian curve. In the case shown in Fig. 5, the value range is divided into three, i.e., the area above the top dash line, the area between top and bottom dash line and the area below the bottom dash line. We assign a symbol to each area and then all the values which fall into an area in a time series data are represented by the symbol assigned to that area. Such a symbol assignment method ensures that all symbols are assigned in a equiprobable way. It is easy to know that given a limited number of symbols, the even symbol assignment across data points maximizes the representation effectiveness, since each symbol carries the same volume of information to avoid unnecessary information loss.

Fig. 6

Normal probability plot of host load data

However, as mentioned in Sect. 1, CPU host load data disobey the Gaussian distribution. We use a normal probability plot Fig. 6 to illustrate this. In the plot, the vertical axis is the probability of a data point to be less than the value shown in horizontal axis. Note that the values of vertical axis are plotted under the cumulative distribution function of values in horizontal axis rather than linearly. In this way, a dataset which obeys Gaussian distribution should be plotted along a straight line rather than a curve. In Fig. 6, data are plotted as a curve which far deviates from the red reference line. This indicates that the data do not follow the Gaussian distribution. Therefore, assuming that host load fluctuate following the Gaussian distribution will greatly harm the validity of the SAX indexing method. With the Gaussian distribution the number of symbols assigned to greater values are approximately the same as those to lower values. However, the data with lower values actually occur more frequently.

Moreover, as pointed out by [2], the PAA representation also compromises equiprobability. Since PAA uses the average over a certain number of consecutive raw data points, the raw data represented by PAA may embody a different probability distribution. The inequality in assigning symbols may waste the symbol resource by assigning more than enough symbols to those points that are rarely observed, while the parts of a time series that occur more frequently and therefore potentially contain the fundamental patterns are not represented with an adequate number of symbols.

Our strategy is simple but effective. We measure the actual distribution of a data set before the SAX indexing. A real-world dataset can be very large, especially in the “Big Data” era. However, we can always take a reasonable amount of data as our sampling data. The sampling methods have been used for long time in many different fields and its validity has been theoretically and practically verified.

Let us assume that m symbols are assigned to a time series at the dimension reduction rate n. We arbitrarily take a number of time series to form a sample set $S=\{T_1,\ldots ,T_n\}$. The number of values in the set, denoted by Q, is

$$\begin{aligned} Q = \sum _{i=0}^{n}Lengthof(T_i) \end{aligned}$$

(5)

The raw data are first represented by PAA. These PAA values are then sorted in the ascending order. Because of the limited size of the sample set, this process can be completed quickly. As we are assigning m symbols, we create a bucket with the volume of $V=\frac{Q}{m}$. Next, we sequentially put the sorted values into the bucket. When the bucket is full, we record the last value that was put, which represents the upper bound of the values that are put in this round. After this, the bucket is cleared and then refilled by the remaining data values. After all values are put, m values are recorded, each of which corresponds to the maximum value in each bucket. Compared to the sample dataset, the entire dataset always has a wider value range. To make sure every value in the whole dataset can be assigned with a symbol, we do not use the maximum value of the last bucket but use the previous $m-1$ values as the dividing points of m data intervals, which are used to determine which interval a raw data is located and therefore determine which symbol should be assigned to the data. This method may cause the first and last intervals to have slightly more values than other intervals. However, this will not compromise the statistical equality of each value interval because of the strong representativeness of the sample dataset. This way we transform the dimensionally reduced time series data into a string of symbols, based on which we can further apply discretization.

5 Distance Measure

In Sect. 1, we discussed that traditional similarity measure methods were no longer capable of discovering the motifs of arbitrary length. In this section, we show the existence of similarity inconsistency geometrically and propose our similarity-consistent measurement method. In order to facilitate the discussion, we first give the definition of Euclidean distance and dynamic time warping distance, further details of which can be found in [24].

Definition 9

(Euclidean distance) For two time series $T_1 = \{x_1, x_2, \ldots , x_n\}$ and $T_2 = \{y_1, y_2, \ldots , y_n\}$ with length n, the Euclidean distance between $T_1$ and $T_2$ is defined as:

$$\begin{aligned} d(T_1,T_2) =\sqrt{\sum _{i=1}^{n}{(x_i-y_i)^2}} \end{aligned}$$

(6)

Definition 10

(Dynamic time warping distance) Assume time series $T_1 = \{x_1, x_2, \ldots , x_m\}$ with length m and $T_2 = \{y_1, y_2, \ldots , y_n\}$ with length n. The warping path between between $T_1$ and $T_2$ is $W = \{w_1,w_2,\ldots w_K\}$. Then the dynamic time warping distance between $T_1$ and $T_2$ is:

$$\begin{aligned} d(T_1,T_2) =\sqrt{\sum _{k=1}^{n}{w_k}} \end{aligned}$$

(7)

5.1 Similarity Inconsistency

The problem of similarity inconsistency is introduced in Sect. 1. Similarity inconsistency leads to a difficult situation where for time series subsequences with varied lengths, it is impossible to decide whether two subsequences are similar with a given threshold. In the case we show in Fig. 1, if we set the similarity threshold to be 3 under the Euclidean distance or 2 under the DTW distance, the traditional method will not be able to find longer patterns such as the pair with 128 data points. On the contrary, the threshold could be too large for shorter time series such as the one with 32 data points, which can cause dissimilar subsequences to be regarded as motifs while long similar patterns are ignored.

Fig. 7

Demonstration of similarity bias. a 2 Data points time series. b 2 Data points time series in original space. c 3 Data points time series. d 3 Data points time series in original space

Let us begin with the simplest case. Assume 2 subsequences, $\textit{TS}1$ and $\textit{TS}2$, each with 2 data points, as shown in Fig. 7a. We plot these time series in points in a 2-dimension space in Fig. 7b since they have only two data points. According to the definition of Euclidean distance, Euclidean distance between time series $\textit{TS}1$ and $\textit{TS}2$ in Fig. 7a is the length between the two points $\textit{TS}1$ and $\textit{TS}2$ in Fig. 7b. Then we extend the time series $\textit{TS}1$ and $\textit{TS}2$ by one more data point respectively as in Fig. 7c. Similarly, the Euclidean distance between $\textit{TS}1^{\prime }$ and $\textit{TS}2^{\prime }$ is the length between the points $\textit{TS}1^{\prime }$ and $\textit{TS}2^{\prime }$ in Fig. 7d. Note that the projection of the points $\textit{TS}1^{\prime }$ and $\textit{TS}2^{\prime }$ in Fig. 7d on X-Y plane is $\textit{TS}1$ and $\textit{TS}2$ in the original space as in Fig. 7b. Thus, as we add a dimension to $\textit{TS}1$ and $\textit{TS}2$, the distance from $\textit{TS}1^{\prime }$ to $\textit{TS}2^{\prime }$ in Fig. 7d must be no less than that from $\textit{TS}1$ to $\textit{TS}2$ in Fig. 7b, since in Fig. 7d the line segment $\textit{TS}1-\textit{TS}2$ constructs the cathetus and the line segment $\textit{TS}1^{\prime }-\textit{TS}2^{\prime }$ constructs the hypotenuse. Although for both time series pairs in Fig. 7a, c, we can lift $\textit{TS}1$ and $\textit{TS}1^{\prime }$ by 0.2 to make them the same time series as $\textit{TS}2$ and $\textit{TS}2^{\prime }$ respectively, the similarity under the measure of Euclidean distance for the two pairs changes when the lengths of time series grow.

We can further extend the time series in a higher dimensional space and the same results can be derived. Namely, for any two pairs of time series with different lengths, the pair with longer time series data will always have greater Euclidean distance if the two pairs have the same level of similarity.

For the DTW distance we still have the same conclusion since the length warping path under DTW grows with the increase in the length of time series being measured.

5.2 Similarity-Consistent Distance Measure

From the definition of Euclidean distance, we can see that the reason for similarity inconsistency is because the number of terms under the radical sign increases as the length of time series increases. Similarly for the DTW distance, the number of terms is subject to the length of warping path, which depends on the length of time series in question. Therefore we adopt a simple but effective solution to tackle the problem of similarity inconsistency. In this work, the similarity-consistent Euclidean distance between two time series is calculated by:

$$\begin{aligned} d_{consistent}(T_1,T_2) =\sqrt{\frac{\sum _{i=1}^{n}{(x_i-y_i)^2}}{n}} \end{aligned}$$

(8)

In the above equation, the terms are averaged to eliminate the effect of distance accumulation. Similarly for the DTW distance, the number of terms is the length of warping path. The similarity consistent DTW distance can be calculated by:

$$\begin{aligned} \textit{DTW}_{consistent}(T_1,T_2) =\sqrt{\frac{\sum _{k=1}^{n}{w_k}}{K}} \end{aligned}$$

(9)

The effectiveness of the two similarity consistent distance measurements can be validated using the case study shown in Fig. 1. Table 1 shows the distance values of the 3 pairs of motifs shown in Fig. 1 under our proposed distance measure. It is clear that our similarity consistent distance measure is length-invariant.

Table 1 Distance of Fig. 1 case under our proposed consistent distance measure

After presenting the indexing method and the similarity consistent distance measure, we can extend the original distance measures of PAA indexing [21] and SAX indexing (the extension of PAA) [28].

We first introduce the original distance measure of SAX representation.

In the PAA representation, the distance between two original time series can be measured in the representation space using Eq. (10).

$$\begin{aligned} \textit{DR}(\bar{Q},\bar{C})=\sqrt{\frac{n}{w}}\sqrt{\sum _{i=1}^{w}(\bar{q_i}-\bar{c_i})^2} \end{aligned}$$

(10)

The distance measure given by [21] provides a detailed proof of lower bounding for PAA indexing.

As for the SAX indexing, a minimum distance is proposed as in Eq. (14) to provide lower bounding, where $\hat{Q}$ and $\hat{C}$ are two time series in the SAX representation.

$$\begin{aligned} \textit{MINDIST}(\hat{Q},\hat{C})=\sqrt{\frac{n}{w}}\sqrt{\sum _{i=1}^{w}dist((\hat{q_i}-\hat{c_i}))^2} \end{aligned}$$

(11)

In the SAX distance measure MINDIST, $dist(\hat{q_i}-\hat{c_i})$ is the minimum distance, which can be looked up from a distance table. The table is created following the following equation:

$$\begin{aligned} cell_{r,c}= {\left\{ \begin{array}{ll} 0 &{} if \mid r-c\mid \le 1\\ \beta _{max(r,c)-1}-\beta _{min(r,c)} &{} otherwise \end{array}\right. } \end{aligned}$$

(12)

We can easily derive the similarity consistent version of the two distance measures. We calculate the similarity consistent distance in PAA and SAX using Eqs. (13) and (14), respectively.

$$\begin{aligned} \textit{DR}_{consistent}(\bar{Q},\bar{C})= & {} \sqrt{\frac{1}{w}}\sqrt{\sum _{i=1}^{w}(\bar{q_i}-\bar{c_i})^2}\end{aligned}$$

(13)

$$\begin{aligned} \textit{MINDIST}_{consistent}(\hat{Q},\hat{C})= & {} \sqrt{\frac{1}{w}}\sqrt{\sum _{i=1}^{w}dist((\hat{q_i}-\hat{c_i}))^2} \end{aligned}$$

(14)

6 Efficient Motif Discovery

By applying SAX representation, we can reduce dimensionality and numerosity of a given series of CPU host load. Deploying pattern discovery algorithms on indexed CPU host load reduces search space greatly. In this section, we start from brute force algorithm, then present its improved algorithms as our pattern discovery algorithm.

6.1 Brute Force Motif Discovery

One of the motif discovery methods in the SAX representation is the brute force motif discovery algorithm. For two CPU host load data P and Q, a brute force algorithm finds all possible subsequences in P and try to match each subsequence to Q. The pseudo code of brute force algorithm is as Algorithm 1.

In this algorithm, finding all subsequences in a CPU host load is a very computational expensive task. The time complexity of each brute force subsequence is O(n!), which is unbearable in reality. Moreover, the algorithm finds all motifs without considering the length of them. In other words, most of the motifs found by this algorithm are very short (e.g., containing two data points), which are meaningless comparing to longer ones. In this work, an improved algorithm is proposed to find potentially long motifs.

6.2 Improved Motif Discovery Algorithm

Our improvement technique modifies the brute force to find longest possible motifs and does not require search all subsequences. The algorithm is outlined in Algorithm 2. This algorithm reduces the number of iterations greatly. However, in the worst case, the algorithm still has the time complexity of $O(nm^2)$.

Definition 11

(Trivial match) In a time series data, given a subsequence C beginning at position p, a matching subsequence M beginning at q and a distance R, we claim that M is a trivial match to C of order R, if either $p = q$ or there does not exist a subsequence $M^{\prime }$ beginning at $q^{\prime }$ such that $D(C,M^{\prime })> R$, and either $q< q^{\prime } < p$ or $p< q^{\prime } < q$.

Fig. 8

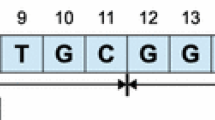
The illustration of trivial match [23]

As shown in Fig. 8, trivial matches are essentially same motifs which are slightly different. Lin et al. proposed that trivial matches occur more often in smooth time series [23]. Since the noise reduction method smoothed our host load data, many trivial matches can be found which slow down the motif discovery process. There is no solution yet to solve the trivial match problem completely, especially for an on-line motif discovery algorithm. A simple method is recording the increment of distance when searching a time series data. Typically when the distance between a motif series and a time series data reaches to a local minimum, the current match is possibly the best match. Certainly, this method will take more time. To balance the performance and matching quality, this work develops a simple but efficient algorithm, which is outlined in Algorithm 3.

When the algorithm finds a motif, it moves along the time series for half of the motif length to avoid trivial match. The algorithm speeds up the search process even further.

6.3 Cascade Pattern Discovery

To further accelerate pattern discovery process, it is necessary to index CPU host load using indexing method introduced in Sect. 4. The lower bounding property of indexing methods we uses allow us to skip most of dissimilar patterns which account for a very high proportion in search space. However, it is still inevitable to calculate the true distance of some pattern candidates, which reduces the efficiency of proposed pattern discovery framework.

For a pattern pair which considered to be similar, their distances under both raw data space and indexed space are sure to be at least lower than the threshold given, and we only know the pair are similar after we measured their distance under raw data space. But another case is, a pair of patterns are similar under indexed space, but not actually similar under raw data space. In this case, we waste time on measuring the true distance of a pair of dissimilar patterns. The latter case is what we stresses on, that is, to skip as much as dissimilar pairs as possible before they have to be calculated under raw data space.

In the field of mining known patterns in time series data, Rakthanmanon et al. [33] applied a cascading method to accelerate mining process. Similarly, we can transplant the idea to mining unknown patters.

Fig. 9

Cascade of different indexing technique for pattern discovery

Figure 9 shows how cascade indexed pattern discovery improves efficiency of the algorithm. Initially, two series of CPU host load data are indexed with SAX, under the same length of dimensional reduction rate. Meanwhile, we also have PAA indexed version of the two host load, as well as raw data. We apply our trivial match skip algorithm to find possible patterns. Since SAX indexing guarantees lower bounding, we can confidently say all unqualified pattern pair candidates are removed and the remaining host load subsequence pairs contains all possible patterns. Then, we retrieve PAA indexed version of qualified candidates under SAX representation and apply trivial match skip algorithm to the data. Again, PAA also lower bounds Euclidean distance, and all candidate pattern pairs measured greater distance than the given threshold are disposed. Since the tightness of PAA lower bounding is higher than that of SAX, now we have only a small part of remaining candidates compared to qualified candidates under SAX representation. For this small part of candidates, we will have to compare their real distance by retrieving raw data correspond to them. However, we have eliminated most of unqualified candidates by applying pattern discovery algorithm on reduced search space and avoided unnecessary calculation to the best we can.

7 Experimental Evaluation

We performed experimental evaluation of effectiveness of our proposed method. The experiments were conducted on a Intel Core i5 4-core 3.2-GHz machine with 16 GB memory. Our experiments aim to answer the following questions:

• 1. The effectiveness of our pattern discovery algorithm.

• 2. The efficiency of pattern discovery.

• 3. How PAA and SAX representation effects pattern discovery efficiency.

The experiments we conduct are based on Google cluster trace, which records the resource usage of 12,000 machines of a real world cluster, spanning 30 days. We reorganised the dataset to gather CPU host load of each machine. All the data are z-normalized to eliminate the negative effect of scaling and vertical shift.

7.1 Mining Patterns in Google Cluster Trace

To illustrate the effectiveness of our proposed pattern discovery method, we start with showing some discovered patterns in the whole dataset.

Fig. 10

Patterns discovered using host load a as reference

Figure 10 shows patterns found in the dataset for host load in Fig. 10. The five host load comes from five different machines, and our aim is to find all other machines which share similar subsequences as in host load a. In the dataset, host load b, c, d and e have similar patterns with host load a. This intuitive experiment shows that our method finds patterns effectively. The result also strongly suggests that host load which share same similar patterns are more likely to be the same type, which allows one using patterns discovered to classify CPU host load, as mentioned in Sect. 1. It is clear that host load b, c and d represent a periodical trend as host load a, giving the fact that in this dataset periodical CPU host load are relatively rare.

7.2 Efficiency of Indexing

Although the efficiency of indexing methods have been compared in various papers [28, 30], we still want to investigate whether the performance results follow the similar trend when they are applied for the motif discovery in the host load. As it has been shown in [22], different types of datasets can dramatically affect the efficiency of the indexing methods.

The efficiency of a indexing method can be defined as follows.

Definition 12

(Indexing efficiency) Given an indexing method I with the dimensional reduction rate R, the indexing efficiency of I is the time spent in indexing with the reduction rate R.

Fig. 11

Indexing efficiency of three indexing methods with dimensional reduce rate of 10

We conducted the experiments to compare the indexing efficiency among raw data indexing, PAA indexing and SAX indexing methods. We take 1, 10, 100 and 1000 MB of test dataset from the whole dataset. In each dataset, we take a host load series as our query. By linearly searching the test dataset, all host load within R from the query should be found according to the definition.

It can be seen from Fig. 11 that PAA and SAX reduce the time consumption greatly, and the SAX indexing is even faster than the PAA indexing. It is notable that the PAA indexing is approximately 10 times faster than the raw data indexing, which is expected as we use 1 PAA data point to represent 10 raw data points, namely the reduction rate is 10. As for the SAX indexing, since its distance measure comes from looking up a distance table, it is slightly faster than PAA.

As mentioned above, the reduction rate is an ultimate factor that affects the efficiency of indexing. Meanwhile, it also increases the probability of incorrect indexing.

Definition 13

(Wrong indexing result) Given an indexing method $S = I(Q)$, where S is the resulting data of a query data Q. a wrong indexing result is a time series $T_{wrong}$ in S where the distance between $T_{wrong}$ and Q under I is less than R, but the distance under raw data indexing is greater than R.

The solution of the wrong indexing problem is simple. We can deploy a hierarchical indexing method, in which the lower level of the indexing method returns a dataset of possible results, while the higher level identifies and throws away the wrong indexing results. The requirement for a hierarchical indexing method is that the lower level indexing should be fast and provide the lower bound of the real distance, while the higher level of indexing should returns the exact distance. If the lower level indexing is unable to determine the lower bound of the distance measure, it is possible that the indexing method misses a qualified result. Our carefully selected indexing method, namely SAX and PAA, provide lower bounding.

In [28], the authors give the notion of tightness of lower bounding to indicate how accurately the distance in the representation space can represent the real distance. Theoretically, the more dimensional reduction in the representation space, the less tightness the lower bounding is. Although higher dimensional reduction rate can accelerate the searching process, the later exact search may slow the whole process down. To show the numerical relation between indexing efficiency and dimensional reduction rate, we conducted the experiments and plot the results in Fig. 12.

Fig. 12

The proportional relation of efficiency between three indexing methods with different dimensional reduction rates. $A=\frac{t(Smoothed raw data)}{t(SAX)}$, $B=\frac{t(Smoothed raw data)}{t(PAA)}$, $C=\frac{t(PAA)}{t(SAX)}$, where t(X) is the time spent with the indexing method X

In the experiments, we used the three indexing methods on a 1000 MB dataset with different dimensional reduction rate, and recorded the average time of returning the result from a query. As shown in Fig. 12, the ratio of efficiency between raw data and SAX increase linearly with the dimensional reduction rate. The same trend is also observed for the PAA indexing. Therefore, we can conclude that the efficiency of each indexing method can be deduced from Eq. (15), where I is the PAA or SAX indexing method, $Raw\_data$ is raw data indexing and a is a constant coefficient.

$$\begin{aligned} Efficiency(I)=\frac{Efficiency(Raw\_data)}{Dimensinal\_reduction\_rate*a} \end{aligned}$$

(15)

According to the experimental results in Fig. 12, we can determine the coefficient a is 0.82 and 1.5 for the PAA indexing and the SAX indexing, respectively. Therefore, the PAA indexing is $0.82*dimensional\_reduction\_rate$ times faster than the raw data indexing, while the SAX indexing is $1.5*dimensional\_reduction\_rate$ times faster. We can also deduce that the SAX indexing is 1.8 times faster than the PAA indexing. This result strongly supports the hierarchy structure of our cascade discovery method, where the most efficient indexing method designed to be on the top and the most inefficient indexing method on the bottom.

7.3 Efficiency of Pattern Discovery

In Sect. 6, we presented three pattern discovery methods and a cascade discovery framework to further accelerate the process. Theoretically the brute force method is expected to be the slowest, while the trivial match skip method is the fastest and can produce the best result. We start with comparing how much trivial match skip algorithm improved efficiency of the other two algorithms, and then we evaluate the performance of cascade accelerating method.

Fig. 13

The time spent by the two algorithms with different data sizes; the dimensional reduction rate is 20

As shown in Fig. 13, as the dataset size increases, the time spent by the second algorithm (i.e., the method to discover the longest possible motif) increases very fast. By contrast our improved algorithm which skips the trivial matches can still finish in a reasonable time. The brute force algorithm is unable to produce any result in an acceptable time.

To evaluate the efficiency of pattern discovery under cascade framework under different set of parameters, we mine patterns hide in an arbitrarily selected host load in a 1.20 GB dataset contains more than 12,000 CPU host load come from different machines in a cluster of Google. The experiment is repeated for 30 times to acquire average value. For each selected host load, we mine patterns by set a variety of PAA dimensional reduction rate ranging from 5 to 50, and number of symbols used in SAX representation, ranging from 30 to 110. The result are shown in Fig. 14.

Fig. 14

Time spent of cascade mining method under different parameter set

As in Fig. 14, It is clear that number of symbols assigned to SAX representation greatly decides how fast the algorithm process. When more symbols are assigned to a host load, distance measure under SAX representation bounds more tightly to the true distance of the raw data, thus unqualified pattern pair candidates can be easier eliminated before proceed to retrieve PAA indexing. However, when the number of symbols assigned increase, the benefits the algorithm take is lessen. Assigning more symbols than enough, in this case, 30, will not result in notable improvements in efficiency.

Another factor influences time consumption of cascade pattern discovery method is dimensional reduction rate of PAA. When the rate is 1, PAA indexing simply degrade to raw data, which result in the absence of the middle level of our cascade method, and all unqualified candidates which are unable to be picked out by SAX indexing will be handed over directly to raw data pattern discovery, which is much less efficient. However, when the dimensional reduction rate is greater than a certain value, the efficiency of the cascade framework will also be reduced. The reason is given by [2]. When dimensional reduction rate increase, the PAA indexed time series are tend to be have less average value and standard deviation, result in poor tightness of lower bounding. In this case, the ability of identify unqualified pattern pair candidates of the middle level of our cascade model is weaken.

8 Conclusion

In this paper we propose an efficient motif discovery method for CPU host load data. We analysed the problems and challenges for discovering motifs in CPU host load, which are that: (1) it is difficult to discover the motifs with arbitrary length due to its high time complexity and the problem of similarity inconsistency; (2) it is necessary to reduce noise in CPU host load before applying any data mining algorithm; (3) the CPU host load data do not obey Gaussian distribution. Our proposed method can discover the motifs in host load efficiently. Indexing CPU host load allows us to eliminate impossible candidates and reduces time complexity. With cascade discovery method, we can mine patterns quickly and also accurately. The fact that our method is resist of noise and the increase number of host load. Experimental results strongly backs our method by demonstrating high efficiency of the trivial skip algorithm and the effectiveness of cascade pattern discovery approach. Experiments also investigated how to choose parameters to achieve best performance and why choosing parameters carelessly can result in violation of efficiency.