Volatility Spillovers and Contagion During Major Crises: An Early Warning Approach Based on a Deep Learning Model

Abstract

This paper contributes to the ongoing debate on the nature and characteristics of the volatility transmission channels of major crash events in international stock markets between 03 July 1997 and 09 March 2021. Using dynamic conditional correlations (DCC) for conditional correlations and volatility clustering, GARCH-BEKK for the direction of transmission of disturbances, and the Diebold-Yilmaz spillover index for the level of volatility contagion, the paper finds that the climbs in external shock transmissions have long-lasting impacts in domestic markets due to the contagion effect during crisis periods. The findings also reveal that the heavier magnitude of financial stress is transmitted between Asian countries via the Hong Kong stock market. Additionally, the degree of volatility spillovers between advanced and emerging equity markets is smaller compared to the pure spillovers between advanced markets or emerging markets, offering a window of opportunity for international market participants in terms of portfolio diversification and risk management applications. Furthermore, the study introduces a novel early warning system created by integrating DCC correlations with a state-of-the-art deep learning model to predict the global financial crisis and COVID-19 crisis. The experimental analysis of long short-term memory network finds evidence of contagion risk by verifying bursts in volatility spillovers and generating signals with high accuracy before the 12-month crisis period. This provides supplementary information that contributes to the decision-making process of practitioners, as well as offering indicative evidence that facilitates the assessment of market vulnerability for policymakers.

1 Introduction

Volatility is one of the fundamental indicators of risk measures in financial markets. Estimating volatility at the individual equity level, the broad market level or the worldwide level has substantial significance for market participants, financial organizations, and policymakers. One of the biggest challenges in generating accurate volatility prediction is the growing interconnectedness of financial markets in recent years, due to the globalization and advancements in information technology, which increases the contagion of shocks between countries and aggravates the impact of crises. Following the stock market crash of 1987, the debate has been heated among researchers and policymakers regarding the joint and dramatic turmoil among international financial markets which are located in different regions and have different characteristics. More specifically, starting from the early 1990s, the frequency of financial crises has increased and drastic movements of volatility are being observed, not only in the originator country but also in the regional and inter-regional markets. Although the early studies concerning volatility transmission date back to the aftermath of the 1997–1998 Asian financial crisis,¹ financial contagion and volatility spillovers across different types of stock markets have become a major area of interest in the last two decades (Corsetti et al., 2005; Forbes & Rigobon, 2002; Guo et al., 2011; Jin & An, 2016; Okorie & Lin, 2021).Historically, individual and institutional investors were willing to extend their investments into foreign emerging markets to take advantage of portfolio diversification and enhanced risk-return trade-off. The rationale behind this diversification was primarily the reduced interconnectedness between developed and emerging markets, as well as the protection aptitude of big drawdowns during any possible financial crisis (Bouslama & Ouda, 2014; Thomas et al., 2021). However, a series of financial crises with growing devastating impacts, such as the Asian crisis of 1997, the global financial crisis of 2008, and the COVID-19 recession of 2020, has shown that all these crises have a feature in common: the transmission of volatility across regional and global levels due to the cross-market connections. When these market connections remain steady, the shocks are transmitted through the linkages and the recovery can be achieved by the financial and economic activities within the country. However, if the market linkages are disrupted after the shocks, the crisis starts to feed itself and the country’s fundamental economic and financial dynamics would not be enough to contain the impact of the crisis. In that case, a wider rescue plan with international intervention would be needed. The latter form of crisis is known as “financial contagion”. Now that the phenomenon and impacts of financial contagion are broadly known, market participants’ risk appetite for emerging markets is diminished and growing interest has been observed among investors for developed markets (Akhtaruzzaman et al., 2021; Berger & Turtle, 2011; Mensi et al., 2017).

In the recent years, Machine Learning (ML) applications have emerged to deal with the nonlinear dynamic characteristics and the complex nature of financial markets. D’amato et al. (2022) showed that deep learning techniques provide more reliable results compared to the conventional methods by capturing complex data interactions. In a similar vein, Song et al. (2023) compared the deep learning with hybrid ML and traditional econometric forecasting model by using different frequencies and found that the forecasting accuracy of the deep learning is highest including in correlation analysis and feature importance ranking. Our study extends the above literature and contributes to the empirical literature of financial econometrics with volatility transmission channels during three different major crisis events in the last few decades as well as developing an early warning system (EWS) by using one of the most sophisticated deep learning algorithms to predict crisis events based on the obtained transmission channels. Specifically, the novel contributions of the present paper are as follows:

• In most studies, EWS systems are developed based on return series, while only a few studies considered the volatility spillover effects between markets. To the best of our knowledge, the long short-term memory (LSTM) model has not been covered in the literature to develop EWS-based correlations and transmission channels among developed and emerging stock markets. Moreover, the dynamic conditional correlation (DCC) method is integrated with an advanced deep learning algorithm for the first time to examine the impact of foreign information in a domestic market during the global financial crisis (GFC) and COVID-19 crises.

• In this study, daily data, which tend to be more responsive compared to lower frequency data, is obtained from eleven different emerging and developed markets. The existing literature mainly focuses on Eurozone markets or developed economies rather than emerging markets. Thus, by covering and analysing the emerging markets of Asia, we are able to see the progress of changes in terms of vulnerability of foreign shocks and channels of contagion between emerging and developed markets during major events.

• As the impact of COVID-19 crisis is still ongoing for many markets, and the source of crises and the major hubs for transmission channels are different in different crisis events, the present study contributes to the literature by providing a comparison of interdependencies and the changing intensity of contagion channels between markets for different periods.

The remainder of the paper is organized as follows. Section 2 presents the literature review. Section 3 covers the methodological framework, including the machine learning algorithms and contagion specification, while Sect. 4 provides the data and preliminary analysis. Section 5 discusses the empirical results of the study. Finally, Sect. 6 draws the conclusion and suggests directions for future studies.

2 Literature Review

Financial crises have received great attention and become a global phenomenon due to the increasing turbulences in emerging and developed markets in the recent years. The characteristics of financial crises tend to reveal themselves in diverse forms and relying on a single definition may lead to a biased results, therefore each crisis should be studied separately. Laeven and Valencia (2020) identified 151 banking crises, 236 currency crises and 79 sovereign debt crises during the period from 1970 to 2017, excluding the recent novel COVID-19 crisis which had a devastating impact on economies and resulted in a global economic recession. Furthermore, political events, such as the Russia-Ukraine war, create exogenous shocks across different asset classes and lead heterogenous impacts on global stock markets (Aliu et al., 2023; Boubaker et al., 2022; Yarovaya & Mirza, 2022). To date, a broad range of studies have focused on revealing causes, timing, and impacts of financial crises that break out in different parts of the world. Baig and Goldfajn (1999) studied contagion effects between five countries of Asia during the crisis period, and their findings imply that the correlations in exchange rates and sovereign risk spreads jump during crisis periods as investors tend to react similarly during turbulent times. Yet, the contagion effects among equity markets were found to be more tentative. The study of Jang and Sul (2002) adopted the Granger-causality test and revealed that the contagion effect is more severe between those Asian countries that are more economically connected. On the other hand, Sander and Kleimeier (2003) investigated the patterns of Asian crisis using the Granger-causality methodology and found that the Asian crisis changed contagion patterns between Asia and other related countries from the pre-crisis to post-crisis period. They concluded that there is no detectable systematic pattern that favours cointegration of the countries, which contracts with the results of Jang and Sul (2002). Meanwhile, Fry et al. (2010) proposed a new model to identify contagion effects via transmission channels of the subprime crisis using the alterations in high order distribution of returns. The findings of the study revealed that the correlation-based tests are not able to detect the new channels of contagion during the crisis periods, unlike proposed co-skewness tests. Idier (2008) supported the idea of probability of new contagion channels during the subprime crisis period by adopting Markov switching multifractal model between CAC, DAX, FTSE and NYSE indices using daily return series. In contrast, Horvath and Petrovski (2013) examined co-movements in the European stock markets by using multivariate GARCH models, and stated that there are no empirical findings to support any changes in the degree of stock market integrations caused by the GFC among selected groups of countries. Furthermore, Aloui et al. (2011) show that strong evidence of time-varying dependence and high level of contagion effects exist between BRIC countries and the US during the global financial crisis. In a separate study, Min and Hwang (2012) analysed the process of contagion effects by using the dynamic conditional correlations (DCC) model for the OECD countries and the US from 2006 to 2010. They found strong evidence of increasing contagion during the US financial crisis for the UK, Australia and Switzerland stock markets, while limited volatility and return contagion in the Japanese Stock Market.

More recently, Akhtaruzzaman et al. (2021) analysed contagion effects between China and the G7 countries by focusing on financial and nonfinancial firms. They used DCC models to estimate financial transmission channels and the results indicated that China and Japan have been the main transmitters of spillovers during the COVID-19 crisis period. He et al. (2020) investigated the contagion effects of COVID-19 on stock markets by applying conventional t-tests and non-parametric Mann–Whitney tests. They used daily return data from the stock markets of eight countries, and the findings revealed bidirectional contagion effects among Asian, European and American stock markets, and that COVID-19 did not have a negative effect on the selected stock markets. On the other hand, the study of Wang et al. (2022) rejects the idea that COVID-19 had no impact on stock markets, as the empirical results of their study show that the pandemic has led to massive shocks in international financial markets. They also provided evidence of directional spillover channels between selected markets, where Chinese and Japanese financial markets were detected as net spillover recipients, while British and American stock markets functioned as main spillover transmitters during the pandemic, in contrast to the results of Akhtaruzzaman et al. (2021).

In addition, Baker et al. (2020) and Ramelli and Wagner (2020) examined the reaction of stock prices to COVID-19, while Bouri et al. (2021) explored extreme return connectedness between different asset classes during the pandemic. Abuzayed et al. (2021) focused on systemic distress risk spillover by using conditional value at risk (CoVaR) and dynamic conditional correlation (DCC) methods. Their results indicated that the developed markets in North America and Europe were exposed to a more marginal risk compared to Asian stock markets during the COVID-19 period.

Deep learning methods have been also increasingly used in the financial market analysis due to their data-driven and self-adaptive nature. Gunduz et al. (2017) studied the hourly movements of 100 stocks from the Istanbul Stock Exchange using a convolutional neural network (CNN) model. A number of technical indicators and temporal features had been used to train the model, and the experimental results showed that the proposed algorithm improves the prediction of stock returns compared to the baseline logistic regression. Maqsood et al. (2020) extended the dataset by adding the US, Hong Kong, Turkey, and Pakistan stock exchanges as well as employing the sentiment analysis from the Twitter dataset. 11.42 million tweets were analysed and used as an input for the DL CNN model, which shows that major events do have impacts on the stocks of selected markets, and deep learning (DL) models are able to evaluate large datasets and provide significant improvements to predict patterns of stock movements. Likewise, Kim and Kang (2019) examined KOSPI 200 index using LSTM, CNN and MLP. The experimental results of the study show that LSTM provides improved forecasting performance compared to CNN and ML, as it works better with sequential data compared to others. Similar results have been obtained by Kim and Won (2018) and Sanboon et al. (2019) when using DL models on various datasets. A growing number of studies are being conducted in the financial literature using deep learning models, covering a wide range of fields including exchange rate prediction (Dautel et al., 2020; Fisichella & Garolla, 2021; Ni et al., 2019), stock market forecasting (Gao et al., 2022; Hiransha et al., 2018; Vargas et al., 2017), cryptocurrency analysis (Awoke et al., 2021; Jamshed & Dixit, 2022; McNally et al., 2018), and the energy market (Assaad & Fayek, 2021; Fan et al., 2019; Wang et al., 2019; Zhao et al., 2017).

In view of this summary of the existing literature, the present state of research shows that there are ambiguities in the volatility spillover analysis, and the role of machine learning methods in the asymmetric shock transmissions remains controversial compared to the classical time series approaches. As discussed in Thakkar and Chaudhari (2021) and Chopra and Sharma (2021), artificial intelligence models possess superior capabilities and require further research to improve the accuracy volatility forecasts. As far as we are aware, there is no application in the finance literature that combines the DCC model with an advanced deep learning algorithm to develop an EWS system for the purpose of crash prediction. In contrast to previous studies, this paper adopts and builds an advanced LSTM architecture for each selected period with improved learning rules and optimized hyperparameters, which may help to the deficiency in internationally accepted standard performance parameters. Finally, our study offers a timely set of empirical outcomes that are missing from the previous literature.

3 Methodology

3.1 The Dynamic Conditional Correlation Method

The dynamic conditional correlation (DCC) model, introduced by Engle (2002), is the generalized version of Bollerslev’s (1990) constant conditional correlation (CCC) model and is used to estimate volatility spillover and dependencies among different time series. The DCC model allows us to examine time-dependent conditional correlations as well as large correlation matrices. Since the model’s coefficients are independent from the number of correlated series, it provides more flexibility compared to the earlier models. The methodology can be built on a two-step procedure. In the first step, the univariate GARCH (1,1) procedure is followed to obtain the conditional variance of each parameter, while in the second step, the conditional correlation estimates are conducted by using the standardized residuals acquired in the first step. Considering this, the mean equations are given as follows:

$$ \begin{aligned} R_{ft} & = \mu_{f} + \mathop \sum \limits_{l = 1}^{n} \alpha_{fl} R_{ft - l} + \mathop \sum \limits_{l = 1}^{n} \beta_{fl} R_{st - l} + \varepsilon_{ft} \\ R_{st} & = \mu_{s} + \mathop \sum \limits_{l = 1}^{n} \alpha_{sl} R_{st - l} + \mathop \sum \limits_{l = 1}^{n} \beta_{sl} R_{ft - l} + \varepsilon_{st} \\ \end{aligned} $$

(1)

where $f$ denotes the first country and $s$ indicates the second country. The mean equations above are used to obtain residual series, which then will be applied to derive the variance equations as shown:

$$ \begin{aligned} \sigma_{ft}^{2} & = \alpha_{f0} + \alpha_{f1} \varepsilon_{ft - 1}^{2} + \beta_{f1} \sigma_{ft - 1}^{2} \\ \sigma_{st}^{2} & = \alpha_{s0} + \alpha_{s1} \varepsilon_{st - 1}^{2} + \beta_{s1} \sigma_{st - 1}^{2} \\ \end{aligned} $$

(2)

where ${\sigma }_{t}^{2}$ denotes conditional variance, ${\alpha }_{1}$ and ${\beta }_{1}$ indicate ARCH and GARCH terms. The standardized residuals are denoted by $\varepsilon$ and ${\alpha }_{0}$ refers the constant term.

Following the data generating process of Engle (2002), the dynamic conditional correlation procedure can be defined as follows:

$$ Q_{t} = \left( {1 - \alpha - \beta } \right)P + \alpha \varepsilon_{t - 1} \varepsilon^{\prime}_{t - 1} + \beta Q_{t - 1} $$

(3)

where ${Q}_{t}$ represents the covariance matrix with ${Q}_{t}=({q}_{fs,t})$, $P = E\left[ {\varepsilon_{t} \varepsilon^{\prime}_{t} } \right]$ and $\alpha +\beta <1$. A significant ARCH term ($\alpha )$ indicates that the correlations vary appreciably over time, henceforth the spillovers exist among the selected markets. The GARCH parameter ($\beta )$ indicates the persistence of the shock to the correlation, therefore the shock at time $t-1$ effects the correlation at time $t$. Although the correlation is mean reverting as $\alpha +\beta <1$, it is possible to have a $\alpha +\beta =1$, which means the conditional correlation is integrated to the order 1. For further details, see Engle and Sheppard (2001), and Hafner and Franses (2009).

3.2 The GARCH-BEKK Model

Another approach adopted by the present paper is named by Baba–Engle–Kraft–Kroner as BEKK model and initially was introduced by Baba et al. (1990) and Engle and Kroner (1995). The GARCH-BEKK specification with single lag is defined as follows:

$$ H_{t} = C^{\circ\prime}C^\circ + D^{\prime}\varepsilon_{t - 1} \varepsilon^{\prime}_{t - 1} D + G^{\prime}H_{t - 1} G $$

(4)

where ${H}_{t}$ is the variance–covariance matrix, $D$ and $G$ are the $k\times k$ parameter matrices, ${C}^{\circ }$ is the constant matrix with lower triangular vector, and ${\varepsilon }_{t-1}$ is the lagged residual term. The restriction applies to constant matrix ${C}^{\circ }$ to be the lower triangular, while the parameter matrices have no restrictions. As the present study focuses on potential spillover effects between each selected markets, the key point is to obtain estimated parameters of $D$ and $G$ matrices. Specifically, we would like to see the linkages among variances of selected markets which is demonstrated by the off-diagonal coefficients of matrix $G$. Moreover, the coefficients estimated by the matrix $D$ provides innovations on volatility. In other words, the off-diagonal elements of D and G matrices deliver details about “news effect” and “spillover effect”, respectively (Kim et al., 2015). In this regard, the significance of D and G can be used to assess the degree of shocks and spillovers between selected markets (Li & Majerowska, 2008). Thus, the BEKK model with the bivariate system is utilized, and the equation is given as follows:

$$ \begin{aligned} {H}_{t} &={C}^{{^\circ }^{^{\prime}}}{C}^{^\circ }+\left(\begin{array}{cc}{d}_{11}& {d}_{21}\\ {d}_{12}& {d}_{22}\end{array}\right)\left(\begin{array}{cc}{\varepsilon }_{1,t-1}^{2}& {\varepsilon }_{1,t-1}{\varepsilon }_{2,t-1}\\ {\varepsilon }_{2,t-1}{\varepsilon }_{1,t-1}& {\varepsilon }_{2,t-1}^{2}\end{array}\right)\left(\begin{array}{cc}{d}_{11}& {d}_{12}\\ {d}_{21}& {d}_{22}\end{array}\right)\\ & \quad+\left(\begin{array}{cc}{g}_{11}& {g}_{21}\\ {g}_{12}& {g}_{22}\end{array}\right){H}_{t-1}\left(\begin{array}{cc}{g}_{11}& {g}_{12}\\ {g}_{21}& {g}_{22}\end{array}\right) \end{aligned}$$

(5)

More specifically, the expanded form of the conditional variance elements can be written as:

$$ \begin{aligned} {h}_{11,t} &={d}_{11}^{2}{\varepsilon }_{1,t-1}^{2}+{d}_{21}^{2}{\varepsilon }_{2,t-1}^{2}+2{d}_{11}{d}_{21}{\varepsilon }_{1,t-1}{\varepsilon }_{2,t-1}+{g}_{11}^{2}{h}_{11,t-1}^{2}+{g}_{21}^{2}{h}_{22,t-1}^{2} \\ & \quad +2{g}_{11}{g}_{22}{h}_{12,t-1} \\ {h}_{22,t} &={d}_{12}^{2}{\varepsilon }_{1,t-1}^{2}+{d}_{22}^{2}{\varepsilon }_{2,t-1}^{2}+2{d}_{12}{d}_{22}{\varepsilon }_{1,t-1}{\varepsilon }_{2,t-1}+{g}_{12}^{2}{h}_{11,t-1}^{2}+{g}_{22}^{2}{h}_{22,t-1}^{2} \\ &\quad +2{g}_{11}{g}_{22}{h}_{21,t-1} \end{aligned} $$

(6)

where ${h}_{ij,t}$ indicates ${(i,j)}^{th}$ element of ${H}_{t}$ which is the conditional variance, ${\varepsilon }_{i,t}$ refers to the ${(i)}^{th}$ element of error term ${\varepsilon }_{t}$. In the first equation ${d}_{12}$ and ${g}_{21}$, and in the second equation ${d}_{21}$ and ${g}_{12}$, are in the focus in terms of their significance, as they provide the information about spillover effects between markets. It should also be noted that the signs of the estimated coefficients here are not important, as the conditional variance is determined by their squared value. The BEKK model is estimated by maximising the quasi-likelihood method under the assumption of conditional normality.

3.3 The Diebold and Yilmaz Spillover Index

The Diebold and Yilmaz (2009) methodological framework is one of the most common and popular spillover models in the current literature. By adopting forecast error variance decompositions from the VAR model, it allows assessing news and shocks across different markets by enabling bidirectional connections among parameters in a single spillover index. However, one of the main issues in the Diebold and Yilmaz (2009) model is the structure which is built on the Cholesky decomposition due to the highly sensitive variable ordering. To overcome of this deficiency, Diebold and Yilmaz (2012) improved the model to make the forecast error variance decompositions invariant to the ordering of the variables by adopting the generalized impulse response approach of Koop et al. (1996) and Pesaran and Shin (1998). Therefore, the revised version of Diebold and Yilmaz (2012) framework is adopted in this study to examine volatility spillovers between markets.

Consider a covariance stationary $p$-th order, $N$-variable VAR:

$${R}_{t}={\mu }_{0}+\sum_{p=1}^{p}{\varnothing }_{p}{R}_{t-p}+{\varepsilon }_{t}$$

(7)

where ${R}_{t}$ is a vector of $N$-variables, implying the volatilities of returns from stock markets at time t, ${\varnothing }_{p}$ indicates N × N coefficient matrix, and ${\varepsilon }_{t}$ is an $N\hspace{0.17em}\times \hspace{0.17em}1$ independent and identically distributed vector of disturbances with covariance matrix $\Sigma$.

One of the fundamental part of the method is the moving average representation of the VAR which is given by:

$${R}_{t}={\mu }_{0}+\sum_{i=0}^{\infty }{K}_{i}{\varepsilon }_{t-i}$$

(8)

where the N × N coefficient matrix of ${K}_{i}$, which is defined by:

$${K}_{i}={\varnothing }_{1}{K}_{i-1}+ {\varnothing }_{2}{K}_{i-2}+\dots +{\varnothing }_{p}{K}_{i-p}$$

(9)

where ${K}_{0}$ represents the identity matrix of N × N with ${K}_{i}=0 \quad \text{for}\, i<0.$

The given framework of Diebold and Yilmaz (2012) with the generalized VAR specification of Koop et al. (1996) and Pesaran and Shin (1998) enables to produce variance decompositions without relying on the ordering of the variables. According to the method, the H-step ahead error variance for $H=\mathrm{1,2},\dots ,\infty$ obtained from forecasting the $i$ th parameter that are due to innovations from the $j$th parameter for $i,j=1,\dots N;and i\ne j$, is defined as:

$${\Psi }_{ij}\left(H\right)=\frac{{{\sigma }_{jj}^{-1}\sum_{h=0}^{H-1}({d}_{i}^{^{\prime}}{K}_{h}\delta {d}_{j})}^{2}}{\sum_{h=0}^{H-1}({d}_{i}^{^{\prime}}{K}_{h}\delta {{K}_{h}^{^{\prime}}d}_{i})}$$

(10)

where $\delta$ is the estimated variance matrix of the vector $\varepsilon$, ${\sigma }_{jj}$ is the estimated standard deviation of the error term $\varepsilon$ for the $j$th element, and ${d}_{i}$ is the the selection vector with the $i$th element unity and zero otherwise. Under the generalized decomposition, the sums of forecast error variance contributions are not equal to 1: $\sum_{j=1}^{N}{\Psi }_{ij}(H)\ne 1.$ Therefore, each entry of the variance decomposition matrix needs to be normalized by its row sum as follow:

$${\widetilde{\Psi }}_{ij}\left(H\right)=\frac{{\Psi }_{ij}\left(H\right)}{\sum_{j=1}^{N}{\Psi }_{ij}\left(H\right)}$$

(11)

with $\sum_{j=1}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)=1$ and $\sum_{i,j=1}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)=N$ by construction where it allows normalizing the contributions of spillover from shocks. We can then calculate the total volatility spillover index as follow:

$$TS\left(H\right)=\frac{\sum_{i,j=1,i\ne j}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}{\sum_{i,j=1}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}\times 100=\frac{\sum_{i,j=1,i\ne j}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}{N}\times 100$$

(12)

which allows to measure average contribution of spillover from volatility shocks to other variables. In other words, the total spillover index states the degree of shocks to volatility spillover between the markets. On the other hand, this method is very adjustable as the variance decompositions are invariant to the ordering of the parameters. Therefore, Diebold and Yilmaz (2012) further introduced the directional spillover concept by using the normalized factors of the generalized variance decomposition matrix. The size of the directional spillover received by market $i$ from other markets $j$ can be measured using the Eq. 13, as follow:

$${DS}_{i\leftarrow j}\left(H\right)=\frac{\sum_{j=1,i\ne j}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}{\sum_{j=1}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}\times 100=\frac{\sum_{j=1,i\ne j}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}{N}\times 100$$

(13)

Conversely, the size of the directional spillover transmitted by market $i$ to all other markets $j$ is given in the Eq. 14, as follow:

$${DS}_{i\to j}\left(H\right)=\frac{\sum_{j=1,i\ne j}^{N}{\widetilde{\Psi }}_{ji}\left(H\right)}{\sum_{j=1}^{N}{\widetilde{\Psi }}_{ij}\left(H\right)}\times 100=\frac{\sum_{j=1,i\ne j}^{N}{\widetilde{\Psi }}_{ji}\left(H\right)}{N}\times 100$$

(14)

The difference between the aggregate volatility shocks transmitted to market $i$, and those gross volatility shocks received by all other markets indicates the net volatility spillover which can be computed as follows:

$${NS}_{i}\left(H\right)={DS}_{i\to j}\left(H\right)-{DS}_{i\leftarrow j}\left(H\right)$$

(15)

In other words, the above equation reflects whether a market (country) is a receiver or transmitter of volatility shocks. Furthermore, the net pairwise volatility spillover can be calculated as follows:

$${NPS}_{ij}\left(H\right)=\left(\frac{{\widetilde{\Psi }}_{ji}\left(H\right)}{\sum_{i,z=1}^{N}{\widetilde{\Psi }}_{iz}\left(H\right)}-\frac{{\widetilde{\Psi }}_{ij}\left(H\right)}{\sum_{j,z=1}^{N}{\widetilde{\Psi }}_{jz}\left(H\right)}\right)\times 100=\frac{{\widetilde{\Psi }}_{ji}\left(H\right)-{\widetilde{\Psi }}_{ij}\left(H\right)}{N}\times 100$$

(16)

which is basically the difference between total volatility shocks sent by market $i$ to market $j$ and those received by market $i$ from market $j$.

We implement the total spillover index in this study to examine interdependence and spillover activity across selected markets for different crisis and non-crisis periods as well as presenting the degree of contributions from each market to all remaining markets.

3.4 Early Warning System Via Long Short-Term Memory Model

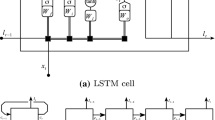
LSTMs are a specialized category of Recurrent Neural Network (RNN)-based deep learning models. The LSTM algorithm has a unique ability to learn the order dependence among sequenced elements, which provides a significant advantage in time series analysis (Tong & Yin, 2021).² The model was first introduced by Hochreiter and Schmidhuber (1997), and was later improved by Graves (2013) to overcome of the long-term dependence problems. A LSTM network consists of a memory cell, which enables to store information over time, and a special gating units, namely, input gates, forget gates, and output gates, to control the flow of data. These gates allow LSTM cells to learn the important parts of a sequence and forget the less important ones. Therefore, it can identify complexities and non-linearities in times series data, which offers a key advantage especially during the turbulent times in stock markets. The structure of a memory cell in an LSTM unit is shown in Fig. 1.

Fig. 1

The structure of a memory cell in LSTM unit

In Fig. 1, ${x}_{t}$ refers to the input data at time $t$, ${c}_{t}$ is the vector of the memory cell and ${h}_{t}$ denotes the output vector of the LSTM cell. The estimation procedure of LSTM network is defined as follows:

Step 1: Estimation of the candidate memory cell

In this step, the value of the memory cell ${\widetilde{C}}_{t}$ is predicted with

$${\widetilde{C}}_{t}=\mathrm{tanh}\left[{W}_{c} \left({h}_{t-1},{x}_{t}\right)+{b}_{c}\right]$$

(17)

where ${W}_{c}$ is the weight matrix, ${h}_{t-1}$ is the output vector of the LSTM cell at the previous time, and ${b}_{c}$ is the bias vector.

Step 2: Estimation of the input gate

The vector of the input gate ${i}_{t}$ is determined at this stage where it controls the new information in the current state of the network. It is represented as:

$${i}_{t}=\upsigma \left[{W}_{i} \left({h}_{t-1},{x}_{t}\right)+{b}_{i}\right]$$

(18)

where $\upsigma$ is the sigmoid activation function, ${W}_{i}$ is the weight matrix, and ${b}_{i}$ is the bias vector.

Step 3: Estimation of the forget gate

In step three, the value of the forget gate ${f}_{t}$ is computed where it evaluates the relevancy of past information and remembers only the relevant information at the current slot while discarding (temporarily) irrelevant data. It is written as:

$${f}_{t}=\upsigma \left[{W}_{f} \left({h}_{t-1},{x}_{t}\right)+{b}_{f}\right]$$

(19)

where ${W}_{f}$ is the weight matrix and ${b}_{f}$ is the bias vector.

Step 4: Estimation of the current state of the memory cell

Given the values of the input gate, the forget gate and the candidate memory cell in the previous steps, we can now compute the current value of the memory cell ${c}_{t}$:

$${c}_{t}={f}_{t}*{c}_{t-1}+{i}_{t}*{\widetilde{C}}_{t}$$

(20)

where ${c}_{t-1}$ is the previous state of memory cell and “$*"$ refers the dot product which indicates the operation of the artificial neural network.

Step 5: Estimation of the output gate

In this stage, the value of the output gate ${o}_{t}$ is calculated where it produces the output from the network at the current slot. It is represented by:

$${o}_{t}=\upsigma \left[{W}_{o} \left({h}_{t-1},{x}_{t}\right)+{b}_{o}\right]$$

(21)

where ${W}_{o}$ is the weight matrix, and ${b}_{o}$ is the bias vector.

Step 6: Estimation of the output of the LSTM unit

In the final stage, the predicted output of the LSTM unit ${h}_{t}$ is produced.

$${h}_{t}= {o}_{t}*\mathrm{tanh}({c}_{t})$$

(22)

The internal process of a neuron is performed using the three control gates and a memory cell which allows the LSTM model to efficiently store, read and update long period of data.

3.5 Model Construction

In this stage, the optimal LSTM model is constructed for the present study. First, the data have been split into two periods from 03 July 1997 to 30 July 2009 and from 31 July 2009 to 09 March 2021. Engle’s (2002) dynamic conditional correlation (DCC) model is conducted for each selected period on a bivariate basis to extract the correlations. Then obtained correlations are transferred to the LSTM model for training and testing with the proportion of 80:20 setting. To build the model, one input layer, two hidden layers consisting of LSTM blocks with sufficient neurons, and a single output layer are chosen. The sigmoid activation function is adopted for the calculation of the input and output doors, while tangent activation function is used for the vector creating in cell state. For the hyperparameter process, the initial learning rate is set to 0.01 and 1000 epochs are chosen for training the data, but early stopping is applied if there is no improvement after 100 epochs to prevent an overfitting problem (Prechelt, 1998). The reproduction phase of the model has been performed based on batch weighting, which accumulates changes in the weight matrix over an entire presentation of the training data set. The weights are updated by the ADM optimization algorithm. Then in the final stage, based on the results received during the trials, the early warning system is created using the sigma method of Sevim et al. (2014).³ The signals are triggered in various sigma levels, and in case of false alarms, the given signals are verified using the evaluation metrics of root mean square error (RMSE) and mean squared error (MSE) by applying the following equations:

$$RMSE=\sqrt{\frac{1}{n}\sum_{t=1}^{n}{\left({\sigma }_{t}^{2}-{\widehat{\sigma }}_{t}^{2}\right)}^{2}}$$

(23)

$$MSE=\frac{1}{n}\sum_{t=1}^{n}{\left({\sigma }_{t}^{2}-{\widehat{\sigma }}_{t}^{2}\right)}^{2}$$

(24)

where n denotes the rank of forecasted data, ${\sigma }_{t}^{2}$ is the actual series which is obtained by the DCC model and ${\widehat{\sigma }}_{t}^{2}$ is the predicted correlations at time $t$ acquired by using the LSTM model.

4 Data and Preliminary Analysis

The data for the present paper are retrieved from Bloomberg database and cover closing prices of widely accepted indices from ten Asian stock markets, i.e., the Nikkei 225 Index (NIKKEI) from Japan, the Hang Seng Index (HSI) from Hong Kong, the Korea Composite Stock Market Index (KOSPI) from South Korea, the Taiwan Capitalization Weighted Stock Index (TAIEX) from Taiwan, the Straits Times Index (STI) from Singapore, the SSE Composite Index (SSE) from China, the PSE Composite Index (PSE) from the Philippines, the Stock Exchange of Thailand Index (SET) from Thailand, the Kuala Lumpur Composite Index (KLCI) from Malaysia, and the Jakarta Stock Exchange Composite Index (JCI) from Indonesia. Moreover, the S&P 500 Composite Index (SP500) from the US is also considered to give a broader perspective during different crisis periods, as the source for the GFC in 2007–2009 is believed to have been the US (Chan et al., 2019). In order to satisfy stationarity, closing price series have been converted to return series by taking the first difference of the log-transformed series using the below formula:

$${R}_{t}=\mathrm{log}({P}_{t}/{P}_{t-1})*100$$

(25)

where ${R}_{t}$ denotes the logarithmic return at time $t$. ${P}_{t}$ and ${P}_{t-1}$ are the closing price of the index at time $t$ and $t-1$ respectively.

The full sample period of the study consists of 4726 return data in total, starting from 03 July 1997 to 09 March 2021. Specifically, the data is split into five different sub-periods coving both pre-crisis and crisis periods. The Asian crisis period spans from 03 July 1997 to 29 December 1998 with 315 observations. Pre-GFC period covers data between 06 January 1999 and 26 June 2007 with 1675 observations, and the GFC period takes place between 05 July 2007 and 30 July 2009 with 410 return series. Following, pre-COVID-19 crisis period extends from 31 July 2009 to 10 March 2020 with 2030 observations, and finally COVID-19 crisis period covers the dates between 11 March 2020 and 09 March 2021 with 283 counts. During the data cleansing, one of the major challenges is non-synchronous holidays in different markets, which leads to computation difficulties and negatively affects the output of the models. To deal with this issue, the return series on these days are taken as zero, as zero return indicates the actual return on non-trading days (Yarovaya et al., 2016a). In terms of the selection of the different sub-periods, there is still no consensus in the financial literature regarding the dating of a specific crisis period (Kose, 2011). Furthermore, the dating is also not consistent across papers that study different financial market crises, such as Chiang et al. (2007), Valencia and Laeven (2008), Baur and Fry (2009), Syllignakis and Kouretas (2011), Kenourgios and Padhi (2012), and Arghyrou and Kontonikas (2012). Therefore, to identify breaking points, this paper considers the structural break tests of Bai and Perron (1998, 2003) and Lee and Strazicich (2013). The structural break tests are applied multiple times to the full period, and as expected, presence of multiple breaks are identified which differ from one market to another. Therefore, the identified multiple breaking points are compared with sharp movements in closing prices for each index to capture the common patterns. Finally, the chosen dates are divided to pre-crisis and crisis periods and used as an input for the selected models. Table 18 presents the descriptive statistics of the daily stock market returns for six different periods. Based on the result of the Jarque–Bera test statistic, the normality assumption of null hypotheses is rejected in all selected markets, confirming the non-normal distribution in all series. These results are expected, as returns of equities do not follow normal distribution (Beedles & Simkowitz, 1978). Thus, return distribution is not symmetrical and the series have either positive or negative skewness. Positive skewness appears when the median has a smaller value than the mean, while negative skewness occurs when the median has a greater value than the mean. Eastman and Lucey (2008) suggest that in the event of negative skewness, most returns will be higher than the average, and therefore market participants would prefer to invest in negatively skewed equities.

According to the table, majority of the markets present negative skewness during the full period, with the only exception of KLCI and SET indices, which indicate positive skewness. The Asian and COVID-19 crisis periods exhibit positive skewness in seven out of eleven markets (63.6%), while the GFC period and pre-COVID-19 crisis period indicate negatively skewed returns in all markets. Similar to the concept of skewness, kurtosis indicates sharp events and can be interpreted as a gauge of greatest point in both directions. The kurtosis in a normal distribution is three. A positive kurtosis refers to leptokurtosis, while negative kurtosis demonstrates platykurtosis. Emenike and Aleke (2012) suggest that high kurtosis values indicate large shocks in the time series with either type of sign. As is clear from the tables, the values of kurtosis are only positive in all selected return series which demonstrate leptokurtosis, and range between 0.654 (NIKKEI during COVID-19 crisis period) and 40.749 (KLCI during the full sample period). The KLCI has the highest maximum value with 8.799, while the SET has the lowest minimum value with − 6.976 in daily return series. Malaysia’s KLCI Index has the greatest gap between maximum and minimum values with 8.799 and, − 6.185 during the Asian crisis period which is also justified by the standard deviation and sample variance. The value of standard deviation is 1.456% in Malaysia’s KLCI Index which is the highest among others in all periods. Japan’s NIKKEI and Hong Kong’s HSI Indices have the smallest gap between minimum and maximum values during the COVID-19 crisis period and pre-COVID-19 crisis periods, with − 1.766% and 1.333%, and − 1.761% and 1.443% respectively. This is also supported by the standard deviation which is 0.514% for the NIKKEI and 0.247% for the HSI. These results indicate the lowest volatility compared to others. To sum up: as expected, the stock markets show lower volatility during the pre-crisis periods, while volatility rises during the crisis periods.

4.1 Correlation Coefficient Test

One of the most traditional approaches to assessment of stock market dependences is the estimation of the unconditional correlation coefficient matrix, which is also known as Pearson’s r. The Pearson product-moment correlation coefficient is a measure of the strength of a linear association between two variables. The coefficient number ranges between − 1.0 and 1.0, where a value of 0 indicates that there is no association between the two markets. A value greater than 0 indicates a positive association: that is, as the value of stock index A increases, so does the value of the stock index B. A value less than 0 indicates a negative association: that is, as the value of stock index A increases, the value of the stock index B decreases. This method is often applied by market participants to manage risk exposure, but it is important to note that the method does not provide any information regarding causation (Kim et al., 2020).

The Pearson’s correlation coefficient between any two stock markets $i$ and $j$ is calculated as follows:

$${P}_{ij,t}=\frac{{E}_{t-1}\left\{\left({R}_{i,t}{R}_{j,t}\right)-{(R}_{i,t})({R}_{j,t})\right\}}{\sqrt{{E}_{t-1}\left\{\left({R}_{i,t}^{2}\right)-{({R}_{i,t})}^{2}\right\}}\sqrt{{E}_{t-1}\left\{\left({R}_{j,t}^{2}\right)-{({R}_{j,t})}^{2}\right\}}}$$

(26)

where ${R}_{i}$ and ${R}_{j}$ are vectors of return series of stock markets $i$ and $j$ respectively, and $P$ is the Pearson’s correlation coefficient.

Table 19 reports the cross-correlation matrices for each selected periods. According to the results, there is a notable increases in cross-country correlations during the turbulent periods compared to pre-crises periods. In most cases, Asian markets are more correlated with each other, compared to the correlation with the US stock market which is not surprising due to the regional dynamics. On the other hand, the majority of market pairs are positively correlated except for the SET index, which can be considered for diversification by international investors to minimise portfolio risk. The top three market pairs in terms of the magnitude of correlations are STI-HSI (Pearson’s r of 0.806), STI-KOSPI (Pearson’s r of 0.768) during the GFC period, and SSE-SP500 (Pearson’s r of 0.759) during the pre-COVID-19 crisis period which indicate high degree of linear dependence and possibility of potential contagion. The lowest correlation coefficient is observed between the SSE and the KOSPI during the Asian Crisis period which is reported as 0.001. It should also be noted that the cross-market correlations are higher in the recent years compared to the earlier periods, which is perhaps due to the globalization and increasing financial market integration (Sirimevan et al., 2019; Wu, 2020). In addition, the full sample period provides broader perspective regarding correlations and indicates some differences compared to the sub-periods. One of the most notable changes is observed in the NIKKEI, which shows very weak correlations in crises periods compared to pre-crises periods. Specifically, its estimated correlations with the US market is virtually non-existent, suggesting a potential for portfolio diversification and the existence of risk management strategies between US and Japanese equity markets in the long-run. Similarly, Thailand’s SET index continues to be a good hedge in the region by negatively cointegrating with the major equity markets. The highest degree of correlation is found between STI and HSI (Pearson’s r of 0.656) during the full period, confirming the study of Hui (2005). A higher level of long-term correlation between markets increases contagion risks and limits the diversification window for international investors. Therefore, examining short-run correlation coefficients among equity markets is important, since diversification benefits and risk exposure significantly change during different sub-periods within the region.

4.2 Unit Root Test

In order to test stationarity of the return series, the Augmented Dickey–Fuller (ADF) test proposed by Dickey and Fuller (1981) and the Phillips–Perron (PP) test proposed by Phillips and Perron (1988) were conducted. The following equation shows the testing procedure for the ADF test regression:

$$\Delta {Y}_{t}={a}_{0}+\beta {Y}_{t-1}+{a}_{1}\Delta {Y}_{t-1}+{a}_{2}\Delta {Y}_{t-2}+\dots +{a}_{p}\Delta {Y}_{t-p}+{\varepsilon }_{t}$$

(27)

where $Y$ is the dependent variable, ${a}_{0}$ is the constant and $p$ is the lag order of the autoregressive process. Lag length is determined by minimizing the Schwarz information criterion (SIC) until the last lag is statistically significant. The null hypothesis refers ${Y}_{t}$ series have unit root, which signifies the data is nonstationary if it is accepted.

The PP method provides a non-parametric approach compared to ADF test by considering unspecified autocorrelation and heteroscedasticity in addition to the unit root test. It addresses the issue of serial correlation by modifying the t-test statistic in the non-augmented DF regression so the asymptotic properties of the regression will not be impacted. The test equation is given as follows:

$$\Delta {Y}_{t}= \mu +{a}_{t}+(p-1)\Delta {Y}_{t-1}+{\varepsilon }_{t}$$

(28)

Table 20 reports the stationarity results of index returns for selected time frames. According to the results on the table, the test statistic is smaller than the critical values which allows rejecting the null hypothesis of unit root (nonstationary) in both ADF and PP tests at all levels of significance for each series.

5 Empirical Results

This section presents the empirical implementation of the selected methodologies. First, the paper investigates transmission mechanisms in tranquil times and compares two pre-crisis periods, which are the Pre-GFC and Pre-CC (COVID-19 crisis) periods. Next, the three major crisis—namely; the Asian crisis in 1997–1998, the GFC in 2007–2008 and the COVID-19 crisis in 2020—are compared as the main focus of this study. Furthermore, we extend the analysis of financial crises by developing an Early Warning System (EWS) based on a deep learning LSTM model and predict the dynamic correlation patterns between markets, which is one of the main contribution of the paper. Finally, we assess the identified correlations, determine thresholds for “excessive spillover” by using the sigma model and test the given contagion risk by following the MSE and RMSE loss functions.

5.1 Subsample Analysis: Comparison of Pre-Crisis Periods

Table 1 presents the estimated results of the dynamic conditional correlation (DCC) method for each pre-crisis periods. In the DCC method, the estimated parameter alpha1 indicates the ARCH term, which shows the impact of news from previous periods on the current conditional correlation. Similarly, the coefficient beta1 refers to the GARCH term, which represents the long-run magnitude of persistence in the conditional correlation.

Table 1 Comparison of DCC estimates

According to the results, the obtained conditional correlations are positive in almost all markets for each period, except for the US and Japan stock markets during the Pre-GFC, and Malaysia during the Pre-CC period. The estimates of alpha1 and beta1 reports significance at 1% level in most cases, which reveals the time-varying variance and covariance process, thus confirming the non-constant conditional correlations. The joint DCC parameters of a1 and b1 are summed to 0.8862 for Pre-GFC, and 0.9228 for Pre-CC period which are close to one in both cases suggesting the correlation structure is considerably persistent. The persistence of correlations is higher in Pre-CC period compared to Pre-GFC, where similar results are obtained in individual cases as well. The sum of the alpha1 and beta1 parameters are lower than unity in all selected markets, which indicates mean reverting correlation process. In other words, if the conditional correlations between two equity markets increase following a negative event in one of the countries, it will again return to the long-run unconditional correlation path. Overall, this is an expected outcome as two tranquil periods are compared which also confirms that the DCC model is accurately defined and able to capture correlation structure among the markets for selected periods.

To further assess the time variation of the volatility spillover across selected markets, the bivariate GARCH-BEKK method is employed. The Tables 2, 3, 4, and 5 report the estimation results of GARCH-BEKK models for each tranquil period. The estimated coefficient ${\alpha }_{ij}$ represents the ARCH term, indicating “news surprises” among equity markets. Furthermore, the estimated GARCH term parameter, ${\beta }_{ij}$, depicts the persistence of innovations between markets (Kim et al., 2015). These two coefficients indicate the volatility spillovers among the equity markets as well as highlighting the persistence of shocks between each other. Both the “news effect” and “volatility spillover” helps us to analyse possible transmission mechanisms either within the region of Asia or with the US. In all given tables below, the p-values are indicated in parentheses under each one of the estimated parameters, while the significance level is denoted with asterisks. Finally, it should be noted that, the correct readings of tables are from rows to columns. For example, the news effects of SP500 to the remaining equity markets can be followed in the first row. In other words, the markets in the rows indicate the “source” of spillover, while the recipients of the shocks are reported in the columns. According to the empirical results, similar characteristics of financial stress have been evidenced during both pre-crisis periods. Specifically, the role of the US and Hong Kong is strong in terms of the volatility transmission channels, where they both contribute to the volatility of remaining stock markets with a great extent. However, the emerging markets of Asia are somehow more immune to these news shocks and volatility spillover effects such as Thailand and China. Statistical significance of coefficients is limited in both periods, mostly in 10% level. A two way relationship between selected equity markets is also observed in both periods where China and Korea are leading in terms of interdependencies with the rest of the countries. Past news about shocks in the equity markets of Japan and Hong Kong positively affect the current conditional volatility of the remaining markets, while previous news for Singapore and Taiwan have a negative impact on the current volatility on the rest of the markets. Besides, the current conditional volatility of one market depends not only on its own past volatility but also past volatility of the other market, confirming interdependencies among each other.

Table 2 GARCH-BEKK results for ${\alpha }_{ij}$: Pre-GFC period

Table 3 GARCH-BEKK results for ${\beta }_{ij}$: Pre-GFC period

Table 4 GARCH-BEKK results for ${\alpha }_{ij}$: Pre-CC period

Table 5 GARCH-BEKK results for ${\beta }_{ij}$: Pre-CC period

The in-depth analysis of volatility transmission channels and contagion effects across stock indices is conducted by applying the Diebold and Yilmaz (2012) framework in Tables 6 and 7. According to the empirical results in the given tables, the estimated Total Spillover Index is 19.033% during Pre-GFC period, while the magnitude of the total volatility spillovers during Pre-CC period is slightly higher with 22.025% which supports the earlier findings of DCC model. In terms of the contribution to others (spillovers), the Hong Kong Stock Market is the most influential during the Pre-GFC period with 2.736% which corroborates the earlier findings of Chow (2017). It is an expected outcome since Hong Kong is considered as international financial hub of Asia with significantly larger equity market capitalization to GDP ratio compared to other Asian countries. On the other hand, the US records the highest outward volatility spillover with 9.894% during the Pre-CC period which is in line with the study of Rapach et al. (2013). Taiwan is surprisingly one of the major contributors of spillover among Asian markets during the Pre-CC period which is consistent with the findings of Yarovaya et al. (2016b). The outward spillover contribution from Thailand has the lowest degree for both selected periods which indicates it is the least influential among all.

Table 6 Comparison of DY framework across markets: pre-GFC period

Table 7 Comparison of DY framework across markets: Pre-CC period

The contribution from others column presents the sensitivity degree of external shocks for each market. Based on the outcome of Tables 6 and 7, Hong Kong and Singapore have the highest sensitivity to inward volatility spillover during the Pre-GFC period with 4.410% and 3.796% respectively. Similarly, the impact of volatility spillovers from all foreign markets to a domestic market have the largest reported values for China and Singapore during the Pre-CC period with 3.822% and 3.928% respectively. It should be noted that China was one of the least sensitive countries to external shocks during the Pre-GFC period, while it has become one of the most sensitive during the Pre-CC. One of the reasons behind this dramatic change is that the Chinese market was shielded by restrictions for international market participants in early stages, while it became more accessible for foreign investors in recent years as revealed by Fernández et al.’s (2016) de-jure measure of equity market liberalizations. On the other hand, Thailand is one of the least vulnerable countries to external news in both periods with Korea during the Pre-GFC period and Malaysia during the Pre-CC period.

Turning to cross-country spillovers, the obtained record in tables indicate that the US is one of the leading volatility transmitters in both periods followed by Hong Kong in first pre-crisis period and Taiwan in second pre-crisis period. Furthermore, the volatility spillover amongst mature markets is positive and larger which indicates stronger cross-market interdependence and financial linkages amid these markets. Nevertheless, the cross-market volatility spillovers between emerging markets of Asia are trivial in most cases or even virtually non-existent. These findings are in line with the work of IMF (2016) that developed financial markets are more prone to high level of integrations with each other compared to emerging markets.

Overall, the Asian markets tend to receive volatility transfer from the intra-regional and inter-regional level prior to crises. The reported values of pairwise volatility spillovers also indicate growing interconnectedness between markets which increase the exposure of portfolio risk for market participants. However, the degree of volatility spillovers among advanced and emerging equity markets is less compared to the sole spillovers between advanced market or emerging markets, offering a window of opportunity for international market participants in terms of portfolio diversification and risk management.

5.2 Subsample Analysis: Comparison of Crisis periods

One of the major contributions of the present paper to the empirical finance literature is the analysis of volatility transmission channels across equity markets during the different crisis periods. In examining this phenomenon, the Asian crisis, the GFC, and the COVID-19 crisis periods are separately covered in this section and in-depth investigation of information transfer channels is conducted and compared in intra- and inter-regional levels as well as in cross-market context. As the interpretation of the rows and columns within the tables are provided and explained in the previous section, the same logical perspective applies when interpreting given tables in the present section.

Results in Table 8 reports the correlation dynamics based on the DCC model. Based on the obtained empirical values, the conditional correlation relationship is positive in most of the selected markets for each period. However, there are some exceptions such as Malaysia during the Asian crisis period; the US, Japan, Singapore, and Thailand during the GFC period; and the Philippines, Singapore, and Thailand during the COVID-19 crisis period. Moreover, the coefficients of alpha1 and beta1 report significance in 10% level in most cases which reveal the time-varying variance and covariance process, thereby confirming the non-constant conditional correlations. The joint DCC parameters of a1 and b1 are summed to 0.9140 for the Asian crisis period, 0.8762 for the GFC period, and 0.5506 during the COVID-19 crisis period suggesting the correlation structure is considerably persistent. On the other hand, the ARCH parameter is the strongest during the COVID-19 crisis period (0.0284), while it is the weakest during the Asian crisis period (0.0021) which indicates shocks are remarkably stronger in the recent periods compared to earlier crises. However, there is a different story for individual cases as the magnitude of crisis impacts and exposure to shocks vary for each market. Furthermore, the GARCH parameter is significantly lower during the COVID-19 crisis period compared to earlier crises which exhibits the degree of reduced volatility. The sum of the alpha1 and beta1 parameters are lower than unity in all selected markets, which implies the existence of dynamic conditional correlations. In other words, if the conditional correlations between two equity markets increase following a negative event in one of the countries, it will again return to the long-run unconditional correlation path. Overall, the empirical DCC findings of present study are in line with Gupta and Guidi (2012) where they analyse the time varying co-movements of Asian markets and we can confirm the existence of correlations over time and the presence of contagion effect during different crisis periods among selected markets.

Table 8 Comparison of DCC estimates

Tables 9, 10, 11, 12, 13, and 14 present the results from bivariate GARCH-BEKK model for pairs of each stock market. The news surprises based on ${\alpha }_{ij}$ coefficient is presented in Tables 9, 11, and 13. Additionally, volatility transmission channels are represented by coefficient ${\beta }_{ij}$ in Tables 10, 12, and 14 for each crisis period.

Table 9 GARCH-BEKK results for ${\alpha }_{ij}$: Asian Crisis period

Table 10 GARCH-BEKK results for ${\beta }_{ij}$: Asian Crisis period

Table 11 GARCH-BEKK results for ${\alpha }_{ij}$: GFC period

Table 12 GARCH-BEKK results for ${\beta }_{ij}$: GFC period

Table 13 GARCH-BEKK results for ${\alpha }_{ij}$: COVID-19 Crisis period

Table 14 GARCH-BEKK results for ${\beta }_{ij}$: COVID-19 Crisis period

The behaviour of volatility spillovers during the Asian financial crisis can be seen in Tables 9 and 10. According to the estimated results, the presence of strong volatility spillover channels was identified. Countries that transmit increased spillovers during the Asian financial crisis are also the most severely impacted ones. Specifically, Indonesia and Hong Kong indicate sizeable news and volatility spillover effects to the rest of the region. It is also interesting to notice that Indonesia and Hong Kong are main recipients of volatility shocks during this period as well as the Philippines. On the other hand, Japan and the US seem to be very immune to the external shocks together with China. However, the case of China is different due to the restrictions on foreign capital movements as mentioned in the earlier section. Moreover, there is significant bi-directional volatility spillover among some cross-market pairs, such as Japan and Malaysia, Singapore and Thailand as well as China and Hong Kong. The impact of USA on the continent of Asia is rather limited in terms of shock and volatility spillovers, indicating minimal financial risk propagation during the crisis. Finally, most of the parameters are significant in various levels, suggesting long lasting financial distress among pairs. It should also be mentioned that the financial linkages are stronger between the equity markets of Southeast Asia compared to the stock markets of Far East Asia.

Next, we investigate the cross-market linkages during the GFC period which is considered one of the most significant financial shocks in the post-war period (Edey, 2009). The picture during the GFC period is different compared to the Asian crisis, since the epicentre of the crisis is the US which is the biggest economy and main financial hub of the world. According to Tables 11 and 12, the US is the biggest contributor of the financial distress as expected, and the most affected countries are the emerging markets of Asia, especially Malaysia, the Philippines and Singapore. Similar vulnerability is also detected in Taiwan, yet with a lower magnitude compared to the aforementioned markets. It is very interesting to note that Japan, Hong Kong and China are the least impacted ones. Two-way volatility spillover effect is found between some markets, including the US and Taiwan, Korea and Indonesia, and Singapore and Hong Kong. Moreover, co-movements between Singapore and Indonesia are rather weak, signifying reduced risk for international portfolio managers. The findings of the GFC period are mostly in line with the study of Hesse and Frank (2009) in terms of interdependencies within the region.

Finally, the recent COVID-19 crisis period is investigated in Tables 13 and 14. The estimated results are mixed compared to the earlier crisis periods. The main transmitter of news shocks and volatility spillovers is Hong Kong, while the role of China on other markets continue to be limited. The magnitude of financial distress is severely increased for some countries such as Japan and Taiwan which is most probably due to the strict lockdown measures and government policies in these countries (Zehri, 2021). Notably, China is neither net transmitter nor net recipient of shocks and spillovers during the crisis period, which is very surprising as the crisis started in China. The effect of financial market of China seems to be minimal which contradicts with the findings of Fu et al. (2021), yet it is in line with the study of Zehri (2021) as the heavier magnitude of financial stress transmits via Hong Kong. Less parameters are statistically significant compared to the earlier crises, which indicate there will be no long-lasting effects. Bi-directional relationships exist between Japan and the US, and Singapore and Thailand, while two-way volatility spillover effect is found between most of the markets such as Korea and Indonesia, Taiwan and China, as well as Malaysia and the Philippines. It should also be mentioned that, the financial interlinkages and spillover channels are stronger within the markets of Far East Asia compared to the Southeast Asian economies, implying different crisis characteristics than the Asian crisis period or the GFC period. In general terms, the equity markets of Asia as well as the US are profoundly succumbed to strong volatility spillovers, from both peripheral and core stock markets. The news shocks turn into important and enduring stress transmission, so that it can be said that the financial sector is one of the most volatile and susceptible to increasing financial distress and episode of financial catastrophes.

In order to provide a better understanding of the direction and intensity of volatility spillovers across selected markets, Diebold and Yilmaz (2012) methodology based on generalized VAR specification is employed. The detail analysis of volatility transmission mechanisms between markets is depicted in Tables 15, 16, and 17 for each selected subperiod. The reported total volatility spillover index is lowest during the Asian financial crisis with 19.033%, while it is the highest during the COVID-19 crisis period with 39.671%. The index is equal to 28.582% during the GFC crisis period, suggesting some co-movements between markets, yet larger percentage of external shocks between markets is explained by idiosyncratic shocks. When it comes to the magnitude of Contribution to Others, Hong Kong is the source of the largest volatility transmission in the region, especially during the GFC period, confirming the earlier results by GARCH-BEKK model. The US has the highest values for Asian and COVID-19 crisis periods, while the contribution of Thailand is lowest among all, supporting the earlier findings of Wang and Liu (2016). Consequently, the strength of regional spillovers is higher than the intensity of international volatility spillovers.

Table 15 Comparison of DY framework across markets: Asian Crisis period

Table 16 Comparison of DY framework across markets: GFC period

Table 17 Comparison of DY framework across markets: COVID-19 Crisis period

Based on the obtained results, it can be said that the greater number of markets react to their own shocks, such as, Japan during the GFC period with 8.930%, and Thailand during the Asian and COVID-19 crisis periods with 8.643% and 8.797% respectively, making them the least dependent markets in the sample. On the other hand, Singapore is the least independent among all with less than 3.0% forecast error variance in GFC and COVID-19 crisis periods, indicating the lowest reaction to domestic shocks. The column Contribution from Others reports notable results in terms of sensitivity to foreign news shocks. According to the tables, Singapore is one of the highest spillover recipients in each crisis period, followed by Hong Kong during the Asian crisis period, the Philippines during the GFC period, and Korea in the COVID-19 crisis period. Japan and USA are the two immune countries regarding external financial distress with the lowest sensitivity level. In terms of pairwise spillover channels, Hong Kong and USA are net contributors of volatility shock propagations, while China, Thailand, Taiwan and the Philippines are the net recipients of cross-country shocks. As a result, these findings display important implications in terms of portfolio diversification opportunities especially in the developed equity markets of Asia since the impact of external shocks are limited compared to the emerging economies. However, the lower dependency to foreign shocks reduces the chances of estimating volatility of these markets based on external news transmission. Therefore, developed markets might be considered in terms of risk management perspective, but risk averse investors should be more careful when investing in emerging markets of Asia as external shocks might create larger declines due to the phenomenon of meteor shower effect proposed by Engle et al. (1990).

5.3 LSTM Based Early Warning System: Experimental Evaluation

In the final section, a comprehensive experimental evaluation is conducted by applying the LSTM based early warning system during the GFC and COVID-19 crisis periods separately. In order to understand the precision and robustness of the proposed model with empirical evidence, we evaluate the LSTM model based on two stages. In the first stage, the early warning signals are identified based on the varying sigma levels in accordance with Sevim et al. (2013) and Sevim et al. (2014), and in the second stage the accuracy of the signals are tested with RMSE and MSE error criteria. Two different LSTM model is created to improve the prediction capability for two distinct phases and to avoid the model learning from dissimilar paths. Therefore, the training process of the model covers two different periods for each crisis. The data from 03 July 1997 to 29 August 2006 is used for training to estimate the GFC period, while the period of 31 July 2009 and 10 March 2017 is used in the training process to predict COVID-19 crisis period. However, as we want to reveal potential spillovers effect before the actual crisis begins, our testing period starts before each crisis to identify potential transmission channels. Lastly, since the main focus of the study is the Asian markets, the early warning detection analysis is conducted based on Hong Kong stock market as it is identified as the centre of shock transmissions during the crisis periods based on the empirical results in the previous section.

Figure 2 depicts the graphical representation of EWS analysis for each pair of market with the Hong Kong’s Hang Seng index during the GFC period. The red line shows the real correlation paths based on Dynamic Conditional Correlation method, while the blue line indicates the correlations based on LSTM predictions. The absolute value of sigma parameter ranges between 1.5 and 3 according to the empirical finance literature (Tarantino & Cernauskas, 2009) where it represents a heuristic value to improve the signal performance. The threshold values are based on the various sigma levels where absolute values of higher sigma levels indicate expected persistence of potential volatility spillovers. Based on obtained results, the proposed model is able to generate signals well before the actual contagion began, except for the Hong Kong and Japan case where the first signal was detected only a few months ago. The prediction capability of the LSTM for information transmission channels is also strong and close to the actual path in most cases, except for the later stages in Singapore and China. In some cases, such as the US and Japan, the model signals several times within the 12-month period before the crisis occurs which is highlighting the potential risk of financial contagion between markets.

Fig. 2

Prediction of correlations based on LSTM network for the GFC period

The picture is slightly different during the COVID-19 crisis period as presented in the Fig. 3. The test results of the model are stronger compared to the GFC period, thus making the risk contagion predictions highly accurate. As we can see in the blue lines, the LSTM model predicted most of the significant correlations and triggered alert well before the crisis occurs. Although, we focus on the COVID-19 crisis, one thing that should also be mentioned here is the trade war between China and the US in 2018 which caused a rapid decline in major stock market indices all around the world in early 2018. Specifically, in February 2018, the S&P 500 wiped out $2.8 trillion, while global indices had lost more than $5 trillion. The huge jumps in risk contagion during that time can be seen in the figure below, especially in the correlations with China, Taiwan, Malaysia and Indonesia. The models were able to predict the unexpected shock transmission in advance and signalled potential contagion effect. In some cases, multiple signals were detected such as Hong Kong and Japan, and Hong Kong and Taiwan cases. When it comes to the COVID-19 crisis period, the proposed model identified financial distress among market pairs and signalled for the potential crisis event. However, the EWS system did not signal within the last 12-month period before the crisis occurred, which might be due to the unidirectional volatility spillovers from China to Hong Kong as revealed by Ahmed et al. (2021). Apart from that, we obtain strong evidence supporting the high degree of efficacy and generalization capacity of the proposed deep learning system.

Fig. 3

Prediction of correlations based on LSTM network for the COVID-19 Crisis period

Finally, the predictions are tested by using the RMSE and MSE criteria for each crisis period as shown in Table 21. Based on the given empirical results, it can be clearly said that the proposed model provides extreme accuracy regarding volatility contagion effects between selected pairs. Specifically, the estimated correlations with Korea and the Philippines stock markets have smallest values for MSE criterion during the GFC period, followed by Malaysia with 0.7%. On the other hand, the prediction results are more superior for China and Korea during the COVID-19 crisis period based on the MSE loss function. Moreover, the highest error rate among all selected markets is found in the correlation series with Taiwan Stock Market based on MSE in both periods. Although the general failure rate is slightly higher in RMSE series, similar results are found. When two crisis periods are compared in terms of model accuracy, the results draw a more complicated framework as it is hard to evaluate the clear superiority. It should be noted that the accuracy of the predictions is highly dependent on the architecture of the deep learning model and training process. According to the train scores, there are no distinct differences for the predicted series except for Indonesia during the GFC period and Taiwan during the COVID-19 crisis period. In these two series, the model provides the largest error rates which may lead a bias for the testing period. Yet, the test scores are less affected, confirming the predictive accuracy of the proposed model.

6 Conclusion

Increased incidence of financial crises in the last few decades has reignited interest in the role of financial linkages and crisis prediction models. Moreover, the pace of globalisation in the international financial markets has raised the question of whether interconnectedness between markets, a source for volatility transmission and possible contagion risk, can provide an early warning signal for crises. This paper examines volatility transmission channels across ten Asian markets and the US market for three different crisis periods and two calm periods by applying DCC, GARCH-BEKK, and Diebold-Yilmaz spillover index. In addition, we developed an early warning system to predict financial crises using the LSTM algorithm based on deep learning approach.

The empirical results indicate that the climb in external shock transmissions has long lasting impacts in domestic markets due to the contagion effect during the crisis periods, leading a more permanent surge in volatility spillovers across markets. Compared to the calm periods, all selected equity markets exposed intensified volatility spillovers during the crisis periods, confirming the findings of Suleman et al. (2017). However, it is revealed that the degree of volatility spillovers among advanced and emerging equity markets is less compared to the pure spillovers between advanced markets or emerging markets, offering a window of opportunity for international market participants in terms of portfolio diversification and risk management. Thus, the outcome of the present study is not only relevant to academics, but also to a wide range of investors. On the other hand, the proposed EWS system identified intensifying volatility transfers and generated signals within the last 12-month period before crises occur, suggesting important implications for policy makers since they need to take economic decisions during the crises times to prevent irreversible impacts on the broad economy due to the financial contagion. Of equal importance are the implications for risk and asset management practitioners, due to the fact that diversification advantages may continue to exist in turbulent periods.

The contribution of this paper to the field of empirical finance and existing literature is three-fold. First and foremost, this study explores all key relevant crises periods in the last three decades, including the recent COVID-19 crisis where there are still huge gaps due to the ongoing impacts. Therefore, the present study contributes to the literature by providing comparison of interdependencies and changing intensity of contagion channels between markets for different periods. Second, the magnitudes and directions of volatility spillovers are verified for each selected calm and turbulent episodes, which offer key information for investors and financial regulators in terms of diversification benefits and macroeconomic stability. Third, instead of following earlier studies, we developed a novel EWS system and successfully predicted correlations and transmission channels with high accuracy, providing supplementary information that contributes the decision-making process of practitioners, as well as offering indicative evidences that facilitate the assessment of market vulnerability to policy-makers. Finally, the effectiveness and reliability of the LSTM model is confirmed with two different loss function to avoid false signals.

In a nutshell, the framework introduced here improves our ability to empirically evaluate as well as quantify volatility spillover and contagion channels in terms of financial market perspective. Furthermore, the proposed deep learning method in the present paper, allows us to identify and predict financial contagion risk across selected countries. Consequently, the model provides significant implications, not only for government related institutions, but also for market participants in terms of possible contagion risks between selected markets. Thus, through the provided analysis in this study, policymakers can concentrate volatility transmission channels and make use of the model to maintain the financial stability, while market participants can benefit for managing their portfolio allocations and limit their risk exposure. Although the present study adopts wide range of Asian markets with a large dataset, the methodology here can be applied to EMEA region or different financial instruments; such as energy, bonds, currencies or cryptos after appropriate modifications. The main limitation of the study was accessing older data specifically for the emerging markets of Asia, and non-synchronous holidays in different markets which required special attention. Therefore, a further direction can be drawn by extending the data and parameters to propose an adaptive or coactive network based hybrid models. The value of such novel developments remains to be examined in future research endeavours.

Appendix

See Tables 18, 19, 20 and 21.

Table 18 Descriptive statistics of selected stock markets for each period

Table 19 Pearson correlation coefficient matrix of stock indices for each period

Table 20 ADF and PP stationary tests for selected periods

Table 21 Comparison of accuracy for prediction results