Introduction

The fundamental role of deadwood—often referred to as coarse woody debris (CWD) and generally defined to be above or equal to 10 cm in diameter (IPCC 2006; Riedel et al. 2020)—in forest ecosystems has been widely recognized. It is particularly relevant for biodiversity, i.e. as a habitat and food source of animals (e.g. Siitonen 2001; Müller and Bütler 2010; Stokland et al. 2012), and for the ecosystem carbon (C) balance (e.g. Harmon et al. 1986; Turner et al. 1995; Pregitzer and Euskirchen 2004). About 8% of the world’s forest total C stock in 2007 was stored in deadwood (Pan et al. 2011). In relation to the C stock in the living biomass, the C stock in deadwood amounted to even 20% (Pan et al. 2011). In contrast, German forests retain currently about 1.23 billion tons of C in living biomass and 33.6 million tons of C (2.7%) in deadwood (Riedel et al. 2019). However, between 2012 and 2017, 0.08 t C ha−1 yr−1 or 7.3% in relation to the living biomass have been stored in deadwood (Riedel et al. 2019).

Since 1994, Germany (as a Contracting State) has been required to prepare national emission inventories of greenhouse gases under the United Nations Framework Convention on Climate Change and, since 2005, within the scope of the Kyoto Protocol (UNFCCC 1998). The latter was replaced by the Paris agreement after 2020. Greenhouse gas (GHG) emissions from forests are reported in the sectors land use, land-use change, and forestry. Carbon stock changes in forests are reported for five different pools, including the deadwood pool. The deadwood pool includes standing and downed dead wood, stumps and dead roots in the soil (IPCC 2006). The GHG reporting for German forests is mainly based on the German National Forest Inventory (NFI), which is repeated every ten years (Riedel et al. 2017), on the German Carbon Inventory taking place also every ten years in the midpoint between two consecutive NFIs (Schwitzgebel and Riedel 2019), and on the German National Forest Soil Survey (Höhle et al. 2018).

As part of an inventory, deadwood (i.e. CWD) is usually assessed in terms of volume, i.e. diameter and length, and decay class (DC). The DC reflects the decay or decomposition stage i.e. the degree of decomposition of CWD along a gradient between undecomposed and fully decomposed and is usually assessed according to visual criteria (Russell et al. 2015). The number of the DCs used varies dependent on country and/or purpose of the particular monitoring (see also Herrmann 2017).

Currently, there are some shortcomings in the reporting of deadwood regarding the completeness and the level of detail. In order to convert deadwood volumes assessed in the field into biomass and further into carbon, country-specific data for different deadwood densities (DD) and carbon concentrations (CC) per DC can be used for a Tier 2 approach according to the Intergovernmental Panel on Climate Change (IPCC) guidelines (IPCC 2006). Up to now there are very few country-specific measurements of DD and CC for the main tree species in Germany. The data basis of DD and CC per DC for above-ground deadwood is therefore still insufficient.

Values from literature provide a first approximation for national-level estimates. Therefore, we compiled existing DD and CC data per DC for the economically most important German or Central European tree species European beech (Fagus sylvatica L.), Norway spruce (Picea abies L. Karst.), Scots pine (Pinus sylvestris L.) and common and/or sessile oak (Quercus robur L. and/or -petraea (Matt.) Liebl.). However, because different decay classification systems (DCS) often allocate pieces of CWD to different classes, the application of DD and CC values of other countries and studies is hindered (see also Sandström et al. 2007). Therefore, we developed a conversion method for the harmonization of these data with the German four-class system—independently from the duration of the decay phases, in the first step. Based on this, we conducted a meta-analysis to calculate mean DD and CC values per tree species and DC and to identify their main drivers.

Materials and methods

Greenhouse gas reporting and deadwood assessment in the German National Forest Inventory

In the German NFI CWD is measured within a radius of 5 m around each sample point (Riedel et al. 2020). Standing and downed CWD is currently assessed based on a diameter threshold of 10 cm at breast height in the former case and, at the thicker end in the latter case. In addition, for the latter case the minimum length is also 10 cm. Stumps are assessed with a diameter threshold of 20 cm at the cut surface and a minimum height of 10 cm. For each CWD object the decomposition stage is classified according to a DCS with four DCs, based on Albrecht (1990) (Riedel et al. 2020, Table 1) and the corresponding volume is calculated based on length (or height) and diameter (see Riedel et al. (2020) for further details). All tree species are subdivided into three groups: conifers, deciduous trees (except for oaks) and oaks (Riedel et al. 2020). As part of the GHG reporting, the deadwood C stock is calculated based on deadwood volume and, according to DD and CC for each DC and tree-species group (UBA 2018). However, until now, DD has been based on only one single study for each group and with oaks and all other deciduous trees pooled into one group. DD values for the latter were determined on a single experimental site in an old-growth beech stand in the Solling in the centre of Germany (Müller-Using and Bartsch 2009). In addition, DD values for conifers are based on a North(east) American study that combined four main North American softwood species (Abies balsamea, Picea rubens, Thuja occidentalis, Tsuga canadensis) (Fraver et al. 2002). For each tree species and DC, the C content is further calculated according to the IPCC default value of 50% (IPCC 2006; UBA 2018).

Table 1 Deadwood classification system used within the German national forest inventory
Full size table

Data selection

We searched for published studies, project reports and data sets on DD and CC per DC in different DCS’ for European beech, common and/or sessile oak, Norway spruce and Scots pine and compiled them into a new database. The literature search was done via Web of Science and Google Scholar. In addition, the bibliographies of the identified articles were used. Unpublished material was not considered in the database. We included only studies for which essential background information, i.e. assessment method, drying time and climatic region, was clearly documented. If available, additional information, e.g. diameter and forest management, was considered and added to our database. We restricted our literature search to studies conducted within the natural range of the four tree species, i.e. Central Europe as well as Scandinavia and Northwest-Russia in the case of spruce and pine. As the main purpose of our analysis was to derive country-specific estimates for DDs and CCs for Germany, we tested for a significant difference in the derived DD values of spruce and pine between Central Europe and Northwest Russia. As no significant difference was detected, those values were also included in our database and subsequent analysis.

Data analysis

Calculation method for harmonization

To calculate the deadwood density for each decay class, an equal distribution of the DCs—by characteristics, not time(!)—is assumed in the first step (Fig. 1a); since we have no information on the specific distribution of the DCs for the majority of studies. This reflects a full decomposition gradient between undecomposed and fully decomposed, corresponding to a degree of decomposition of 100% undecomposed (at the beginning of DC one) and 0% undecomposed (i.e. 100% decomposed, at the end of DC four). The equal distribution of the DCs is obtained by dividing the value of undecomposed deadwood (100%) by the number of DCs within the DCS. This corresponds to the class width (%). In the case of the German reference DCS with four DCs (Table 1), each DC comprises 25% (Fig. 1a). In comparison with a DCS with three and eight DCs, i.e. the smallest and largest DCS’ in the present study (Přivětivỳ et al. 2017; Teodosiu et al. 2012), each class comprises 33.3% (100% / 3 = 33.3%) or 12.5% (100% / 8 = 12.5%). The same procedure was applied for each individual DCS.

Fig. 1
figure 1

Procedure of the conversion method (DC = decay class, DD = deadwood density, DCS = deadwood classification system). a Percentage distribution of deadwood decomposition for each DC, b arithmetic mean for each DC is calculated and, c combined with the corresponding DD value of the specific study, d inserting DD values of the respective DCS into a function, e calculating the DD values of the respective DC of the reference DCS

Full size image

As there is also no information on the distribution of the deadwood density within the particular classes, an equal distribution of the DD values within the DCs is further assumed. Thus, the arithmetic mean of the degree of decomposition of each DC in the respective DCS is calculated in the next step. Here, it should be noted that the arithmetic means correspond to the DD values of the respective DCs in the different studies. The arithmetic mean of the density estimate in a particular DC was attributed to the midpoint of this class. For the German four-class system, these are 87.5%, 62.5%, 37.5% and 12.5% for DC 1, 2, 3 and 4, respectively (Fig. 1b). In the case of the smallest DCS with three DCs, the arithmetic means and the corresponding density values are 83.3% and 0.392 g cm−3 (DC 1), 50% and 0.236 g cm−3 (DC 2) and 16.6% and 0.149 g cm−3 (DC 3) (Přivětivỳ et al. 2017) (Fig. 1c). The same procedure was applied for the eight-class system (Teodosiu et al. 2012; Merganičová and Merganič 2010) and all other classification systems. Afterwards, the DD values of each individual DCS of the different studies, which should be harmonized with our four-class reference system, were inserted into a function that best described the relationship between DD values and the degree of decomposition. In the case of the three- and eight-class system, for example, a linear (Fig. 1d) and a polynominal regression (not shown) of the second degree were used.

Finally, the decay class means of the reference system (87.5% (DC 1), 62.5% (DC 2), 37.5% (DC 3) and 12.5% (DC 4)) were inserted into the function of the DCS to be harmonized. With this, the DD values of the individual DCs of the reference system were obtained (Fig. 1e). The same procedure was also applied to derive the carbon concentrations for each individual DC of the reference system.

We are aware that the assumption of an equal distribution of the DCs based on equidistance by characteristics, not time may be an oversimplification of the complex decomposition process [see also (Herrmann 2017)]. The approach presented here is purely mathematical and based on logical combinations between the different DCS’. The decomposition or residence time in each individual DC and DCS is not considered here. Although an individual piece of wood will move from one DC to the next over time, in this analysis time is not an issue. The calculation of C stocks as targeted here is done at a single inventory, and the fate of the individual pieces of wood is of no regard. Thus, the length of a DC, i.e. the time a piece of decaying wood would be considered to be in this class, does not influence the analysis and the assumption of equal distribution is justified.

Conversion of dry density to basic density

Dry density (= dry weight / dry volume) – if measured in one of the different studies—was converted to basic density (= dry weight / fresh volume) according to

$$ {\text{Bd}} = {\text{Dd}} \times \frac{100 - \beta v}{{100}}\,\,({\text{Niemz}}\,{\text{ and}}\,{\text{ Sonderegger}}\,{2}0{17}) $$
(1)

where Bd = basic density, Dd = dry density and βv = % of volume swelling or shrinkage (17.9, 11.9 and 12.1 for beech, spruce and pine, respectively).

Here it should be noted that this conversion was developed for intact wood. With increasing decomposition and depending on rot type and tree species (and corresponding decomposition of cell wall components) this should be viewed as an approximation.

Statistical analysis

For harmonization of the DD and CC values of the different studies with the DCS of the German NFI, the function that best described the original data according to plausibility and goodness of fit (R2) was used. If two models were equivalent in terms of R2, the simpler model (e.g. linear instead of polynomial) was used.

Statistical and model analyses were conducted using R 3.5.1 (R Core Team 2018). All significance testing was performed using an alpha level of 0.05. The assumption of normality was assessed graphically using residual QQ-plots and scatter plots of residuals vs. fitted values, as well as via parametric tests (the Kolmogorov–Smirnov test and, for sample sizes below 50 (Brosius 2011), the Shapiro–Wilk test (Dormann 2012)).

To test for significant differences in DD and CC between the different DCs at the species level, adjusted (i.e. estimated marginal) means were calculated and compared with the Tukey HSD test. In addition, the 95% confidence interval and the root mean square error (RMSE%; = standard error in relation to mean DD value) were calculated as well.

A one-way ANOVA followed by Tukey HSD test was conducted to analyse possible differences between the three species overall, as well as for each DC.

To analyse the influence of substrate specific, climatic and environmental variables (as shown in Table 2 and 3) on DD and CC, linear mixed-effects (lme) models were used. To decide if lme or simple linear model should be applied, the standardized residuals of the independent variable reference (i.e. author and data set) as a possible random factor were plotted against the zero-intercept line in the first step (Fig. S1). Reference was chosen in order to control for possible dependencies in the individual data sets. The dependent variable was square root transformed if the residuals were not normally distributed. Backward selection, starting with the full model (i.e. the ‘beyond optimal model’ (Zuur et al. 2009)), was used to identify the best model. To decide if a model is better than a previous model, we used the explained variation (r2) and the AIC as 1st and 2nd criteria. Eta squared was used as an effect size measure. Since there was only one study for oak, it was not included in the above analysis and treated separately for comparative description.

Table 2 Wood density per decay class as well as corresponding standard deviation (SD; if specified) for coarse woody debris (CWD) of Fagus sylvatica, Picea abies, Pinus sylvestris and Quercus sp
Full size table
Table 3 Carbon concentration per decay class as well as corresponding standard deviation (SD; if specified) for coarse woody debris (CWD) of Fagus sylvatica, Picea abies, Pinus sylvestris and Quercus sp
Full size table

Results

General description of the data base

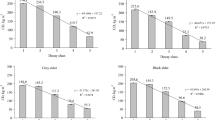
In total, 41 different data sets from 14 European countries were compiled for DD (Table 2). The majority of these data sets, 23, were assembled for spruce; 9 for pine; 8 for beech and one for oak. The number of DCs varied between three and eight. For CC, 20 data sets from 8 different European countries were found; 8 for spruce, 5 for pine; 6 for beech and one for oak (Table 3). Based on these data sets, the mean DDs and CCs per DC were calculated (Fig. 2, Table 4 and 5).

Fig. 2
figure 2

Derived basic densities in CWD of Fagus sylvatica, Picea abies and Pinus sylvestris; boxplots display median, lower and upper quartile, minimum and maximum values; points outside boxplots represent outliers; different letters indicate significant differences between group means (p < 0.05; Tukey HSD method)

Full size image
Table 4 Estimated marginal means (emmean) and corresponding confidence limits (CL; from lowest to highest) for deadwood basic density per decay class of Picea abies, Pinus sylvestris and Fagus sylvatica. Different letters indicate significant differences between group means (p < 0.05; Tukey HSD method)
Full size table
Table 5 Estimated marginal means (emmean) and corresponding confidence limits (CL; from lowest to highest) for carbon concentration per decay class of Picea abies, Pinus sylvestris and Fagus sylvatica. Different letters indicate significant differences between group means (p < 0.05; Tukey HSD method)
Full size table

Deadwood density

With increasing DC, significantly lower mean basic densities were observed for all tree species, except for beech between DC 3 and 4 (Fig. 2, Table 4). The decrease in density was linear for spruce and pine, with a decrease in DC 4 to about 42% of the density in DC 1 in spruce and to 44% in pine. In CWD of beech an exponential decrease to about 40% in DC 4 (the highest decrease of all species) was observed (Fig. 2, Table 4). According to the interquartile range in Fig. 2, the density variation was lowest in DC 4 for spruce and beech, but highest for pine. Overall, the mean basic density of CWD of beech was significantly different from the one of spruce and pine, which were not different to each other (p < 0.05, Tukey HSD). When comparing individual DCs between species, the mean basic density of beech CWD was significantly different from that of spruce and pine for DC 1 (p < 0.001 each, Tukey HSD) and, in the case of beech and pine, also for DC 2 (p < 0.05, Tukey HSD). There was no significant difference between the DD of any of the three tree species for DC 3 and 4 (see also Table S2). The DDs derived for oak were 0.495 g cm−3 DC 1, 0.430 g cm−3 DC 2, 0.305 g cm−3 DC 3 and 0.130 g cm−3 in DC 4, which suggests an inverse exponential decrease—with the highest density reduction between DC 3 and 4—to about 26% of the DD in DC 1. The DD values reported for oak CWD were in the range of those of beech for DC 1, but were approx. 20% higher thereafter (DC 2 and 3) and 33% lower than DD of beech in DC 4.

Carbon concentration

Carbon concentration significantly increased from about 49% in DC 1 to about 52% in DC 4 for spruce and pine, while no significant change in CC could be detected for CWD of beech. CC of beech CWD remained stable at about 47% (Table 5). Similar to DD, the overall mean CC of CWD of beech was significantly different from the one of spruce and pine, which were not different to each other (p < 0.001, Tukey HSD). In detail, the mean CC of beech CWD was significantly lower than that of pine for all DCs (1: p < 0.05, 2 and 3: p < 0.001, 4: p < 0.01, Tukey HSD) and from the mean CC of spruce for DC 2, 3 and 4 (p < 0.01, Tukey HSD; Table S3). For oak the following CC values were derived: 47.8% DC 1, 48.8% DC 2, 49.7% DC 3 and 50.6% DC 4. CC values for oak were about one per cent lower than those of spruce in DC 1 and 4 and, similar to spruce and pine, showed a linear increase with increasing DC.

Influencing factors

Deadwood density

Up to 92% of the variation in DD values could be explained with a linear mixed effects model, mainly by the variables decay class—with the biggest share (70.7%) -, CWD type and tree species and their interactive effects as well as reference as a random factor (6.3%), whereas total annual precipitation explained below 1% (Table 6). If we subtract the random factor, which cannot be predicted, 86% of the variation in DD values may be predicted for the tree species investigated here.

Table 6 Linear mixed effects model (sqrt-transformed; ANOVA table) to predict the deadwood basic density of Fagus sylvatica, Picea abies and Pinus sylvestris: Basic density ∼ Decay class + Tree species + CWD type + Total annual precipitation + Decay class × tree species + Decay class × CWD type + (1 | Reference)
Full size table

Based on a reduced model that consisted of decay class and tree species and their interactive effects, about 87% of the variation in DD values—76% without the random factor—could already be explained (Table S1). However, with only DC as an explanatory variable, about 84%, 71% without the random factor, of the variance could be accounted for (Table S1).

Carbon concentration

About 86% of the variation in CC—52% without the random factor—can be explained by a lme model with decay class (22%), tree species (21%) and their interactive effect (9%) as predictors (Table 7).

Table 7 Linear mixed effects model to predict the deadwood carbon concentration of Fagus sylvatica, Picea abies and Pinus Sylvestris: Carbon concentration ∼ Decay class + Tree species + Decay class × tree species + (1 | Reference)
Full size table

Discussion

To our knowledge, this is the first study that synthesized existing data on deadwood densities and carbon concentrations for the most important Central European tree species across different decay classification systems and countries, i.e. over a wide area. While this study presents the big advantage of producing more stable estimates across different sites and for a larger area (i.e. Europe), by balancing the influence of individual studies and including a large number of samples in different data sets as well as a wide range of climatic conditions and decomposer communities, it may also introduce potential errors if applied on the small scale, i.e. local areas. However, until now, the opposite (i.e. scaling up from local values) has usually been performed (Di Cosmo et al. 2013). Recently, Harmon et al. (2020) compiled and examined estimates of CWD decomposition rates on a global level to assess the C release from CWD more reliably. Based on our study, CWD C stocks can be estimated more reliably across larger areas, i.e. Europe.

Calculation method for harmonization

Since we have no information on the specific distribution of the DCs for the majority of studies, unequal weighting (as another possible option for harmonization) would not be possible. Another possibility would be to use the description of the characteristics of each individual class and possibly combine or reduce classes depending on the number of classes in each DCS. However, taking into account the many different DCS that exist, with classes between three and eight and the often subjective interpretation of the description along with a lack of sharpness of the boarders, this would also be impractical. As a consequence, according to our evaluation, no other method than the used logical approach seems to be feasible.

Deadwood density

Estimating the density of dead wood in advanced stages of decay is challenging (see Rock (2005) for a review). The stages of decay may be different along a piece of wood, the estimation of volume is less straightforward and the estimation of wood mass is more complicated as with sound, solid, undecayed e.g. logs, Especially in advanced stages of decay, when fragmentation, un-even distribution of destructive agents, and loss of cell-wall stability influence form and distribution of mass in a given volume, determination of volumes, sampling of material for mass determination and thus estimation of density is difficult. The different studies we used here followed different field sampling and laboratory protocols. The variability of the given densities caused by this was not considered, as not all studies contained sufficient information to allow for an assessment. Since the focus of this article is on conversion factors for decay classes, which are to be used in consecutive field inventories, this would contribute to a systematic error and bias, and should cancel out when differences between inventories are calculated.

With increasing DC a significant decrease in DD was observed in our study for all three species, except for beech between DC 3 and 4, as has been found by others (e.g. Müller-Using and Bartsch 2009; Herrmann et al. 2015; Köster et al. 2015). The significantly higher DD values of CWD of beech compared to spruce and pine in DC 1 and compared to pine in DC 2 in our study are consistent with the mainly higher wood density in angiosperms when compared to gymnosperms (Cornwell et al. 2009; Thomas and Martin 2012). Similar to Herrmann et al. (2015) and Yatskov et al. (2003), we found no significant difference between the densities of the three species in DC 3 and 4. Further, we observed the lowest variation of our derived DD values—based on the interquartile range in Fig. 2—in DC 4 for beech and spruce, but the highest in the same DC for pine. In contrast, an increase in density variation with increasing DC, with the highest variation in the most advanced DC, was sometimes detected (Teodosiu and Bouriaud 2012; Di Cosmo et al. 2013). However, in the case study from the Eastern Carpathians (Teodosiu and Bouriaud 2012), the density variation in the most advanced decay class (DC 8) was reduced again. The higher density variation observed for pine in DC 4 in our study might be due to the higher density of the more decay resistant heartwood (see also Herrmann et al. 2015).

Similar to our lme model, where DC contributed the biggest share (70.7%) of the total explained variation in DD (92%), DC explained the biggest part of the variation in density (68%)—followed by (tree) species (6.1%) and their interaction (7.1%)—also in the study by Yatskov et al. (2003). In contrast to Yatskov et al. (2003), CWD type (or position) had a bigger influence on the variation in DD than tree species in our study. However, eight species—instead of three in our study—were examined in that study. In total, about 81% of the variation in density could be explained in that study (Yatskov et al. 2003). Similar, 86% of the total variation in density, with DC comprising 81%, was explained for downed woody debris with the same factors in a study in the boreal forest of Canada (Seedre et al. 2013). For comparison, 84% of the variation in DD could already be explained with DC as the only factor in our study. Further, DC turned out to be a good indicator for DD also in a modelling approach from a Norway spruce old-growth forest in the Eastern Carpathians (Teodosiu and Bouriaud 2012).

In comparison with the mean DD values for deciduous trees, i.e. beech, currently implemented in the national inventory report (NIR) (UBA 2018), mean DDs for beech calculated here are considerably lower in all DCs—up to 25% at the maximum in DC 4—except for DC 3 where DD for beech in our study is about 20% higher. In addition, the RMSE for beech calculated in our study is about sixfold or 84% lower at the maximum in DC 2 when compared to the current NIR value; which is most likely the effect of eight data sets included in our study instead of one in the current NIR (UBA 2018). This difference is even more pronounced for spruce and pine, where the RMSE based on our study is about ninefold or 90% lower for spruce and 85% lower for pine in DC 2 and 3. Our mean DD values for spruce and pine are up to 70% higher in DC 3 and about 30% higher in DC 4, while almost no difference was observed for DC 1 and 2. Compared to our results, the biomass-expansion factors currently implemented in the NIR would thus substantially over- or underestimate—depending on tree species and DC—the real value. Furthermore, the mean DD values currently used within the NIR are based on dry density, which is generally higher than basic density and would lead to an overestimation of the real field-based biomass.

Carbon concentration

We observed a significant increase in CC by more than 2.5% between DC 1 and DC 4 for CWD of spruce and pine and no change with significantly lower CCs for CWD of beech; similar to Herrmann and Bauhus (2018). Lower CC for angiosperms when compared to gymnosperms were also found in a global literature review of CC in live trees (Thomas and Martin 2012) as well as in a review of CCs in woody detritus from the Northern Hemisphere (Harmon et al. 2013). The general pattern of CC per DC observed in Harmon et al. 2013 was the same that we detected for our tree species. Increasing CC with increasing DC for CWD of pine and spruce were also found in other studies (e.g. Köster et al. 2015; Bütler et al. 2007).

Based on our lme model, about 86% of the total variation in CC (including the random factor) could be explained based on decay class (22%), tree species (21%) and their interactive effect (9%). For comparison, about 62% of the variation in CC in CWD of the same tree species could be explained by tree species (35%), decomposition time (12%), diameter (2.5%) and a random factor (13%) in a study across different sites in Central Europe, i.e. Germany (Herrmann and Bauhus 2018).

Our study showed, that based on the calculated confidence limits in Table 5 the application of the IPCC default value for carbon concentration in CWD of 50% (UNFCCC 1998) might under- and/or overestimate the real value depending on DC up to a maximum of about 2.5% (under- and overestimate) for spruce, 3.4% (under-) and 1.6% (overestimate) for pine and 4.2% (overestimate) for beech. Based on our mean values, these figures would be 1.5 (under-) and 1.3% (overestimate) for spruce, 2.2 (under-) and 0.5% (overestimate) for pine and, 2.9% (overestimate; at the maximum) for beech.

Conclusions

Based on the current study, reliable estimates, i.e. mean values as well as confidence limits for DD and, based on a more restricted data base also for CC for the tree species investigated here, were obtained for the whole of Germany and/or (Central) Europe.

DD was mainly dependent on decay class and can be predicted based on DC, CWD type and tree species with high precision. In comparison to the values currently used in the GHG reporting, our DD values are mostly higher, up to a maximum of about 70%, while the RMSE is almost tenfold lower at the maximum.

Based on the CC confidence limits calculated here, the IPCC default value of 50% CC might under- and overestimate the real carbon concentration of spruce, pine and beech by about 4% at the maximum.

Our calculated mean DD and CC values for the whole of Germany can be used to convert deadwood volumes assessed in the field into biomass and further into carbon. Based on these values, the accuracy of C stock assessment in deadwood as part of the GHG reporting for Germany can be substantially improved.

The presented approach may also be used for the assessment of CWD C stocks in other European countries.