Wrong Way Risk corrections to CVA in CIR reduced-form models

Abstract

In this paper we provide an efficient methodology to compute the credit value adjustment of a European contingent claim subject to some default event concerning the issuer solvability, when the underlying and the default event are correlated. In particular, in a Black and Scholes market/CIR intensity-default model, we consider a second order expansion around the origin of a vulnerable call option with respect to a correlation parameter $\rho$, which may be used to describe the wrong way risk of the contract, measuring the dependence between the underlying asset price and the option’s issuer default intensity. Numerical implementations of this approach are compared with the benchmark Monte Carlo simulations.

1 Introduction

As a consequence of the exponential growth of the over-the-counter (OTC) financial market, the valuation of contingent claims subject to possible counterparty default, named counterparty credit risk (CCR), has gained interest in the last decade, after the past global financial crisis, both from the practitioner and the academic perspective. Indeed, according to the Basel III Accord (2010), to compensate for those risks a financial institution must charge a premium, generally known as credit value adjustment (CVA), defined as the (positive) difference between the default-free contract value and its value under default risks, or equivalently as the risk-neutral expectation of the residual discounted net present contract value (or expected exposure) at time of default (see e.g. Brigo et al. 2013; Gregory 2012). When speaking of options, these are called defaultable (or vulnerable), and if the default-free option value can be evaluated in closed or semi-closed form, an efficient option evaluation is tantamount to efficiently determining the contract’s CVA.

The two main approaches to CCR are the structural and the reduced-form ones which both use the time of default to represent the default event.

Johnson and Stulz (1987) firstly used the structural approach to price a vulnerable option, and this was later extended by Klein (1996) to more general liability structures. In these papers, default could happen only at maturity. More recently, Ballotta et al. (2019) proposed a more complex structural approach, based on correlated Lèvy processes.

In the structural approach, the default time is typically a stopping time with respect to the observable market filtration $\mathcal {F}$. On the contrary, in the reduced-form (or intensity) approach, it is not measurable with respect to $\mathcal {F}$, to incorporate also risk factors exogenous to the market. It is assumed that its distribution conditioned to the market filtration is represented by a regular hazard process with stochastic intensity. As a general reference on the topic, we quote the extensive work by Bielecki and Rutkowski (2002) and Bielecki et al. (2011) just to mention some. This is the framework we are going to use in the present paper.

Although the representation of CVA in terms of a risk-neutral expectation enables to employ many derivatives valuation techniques (from Monte Carlo to PDE based and/or hybrid techniques, see e.g. Goudenège et al. 2020), the actual CVA computation can be challenging when dependence is allowed in the underlying stochastic model. This problem is particularly relevant where statistical correlation between the counterparty default event and the investor exposure is possible; that is when wrong way risk (WWR) might occur, which means that a decrease in the counterparty’s credit quality produces a higher exposure for the derivative’s holder. A classic example of WWR (see Zhu and Pykhtin 2007) comes up when a bank (the investor I) enters into a swap with an oil producer (the counterparty C), receiving the fixed and paying the floating, hence lower oil prices have the double effect of worsening the counterparty credit quality, even though increasing the swap value for the bank. Another example of WWR is as follows: investor I buys a put option from bank C (the counterparty), written on another bank B, whose investment portfolio may be highly and negatively affected by defaulting of C (for example, both banks belong to the same financial system). Hence the higher the investor’s exposure, the greater the probability of failure.

Of course, the opposite effect, known as right way risk (RWR), can also occur when exposure is likely to be reduced if the counterparty defaults. Both effects are essential from a risk management point of view; neglecting such dependencies between counterparty default and investor exposure leads to overestimation or underestimation of the risk and mis-pricing.

Spurred by these considerations, a wide literature to include RWR/WWR in derivative evaluation developed. An extensive presentation of the correlation issues concerning Credit Risk can be found in Brigo et al. (2013), Glasserman and Yang (2016) discussed bounds on WWR using linear programming techniques. Resampling methods, proposed in Pykthin and Rosen (2011), applied again in Rosen and Saunders (2012) and Cherubini (2013), are based on the use of a copula function to impose a dependence between exposure and credit, leaving fixed the marginal distributions, a method that proved to be particularly appealing to practitioners, for its simplicity and computational efficiency. When using the reduced-form approach, the hazard (or the intensity) process is typically taken as correlated to the option’s underlying, see e.g. Alòs et al. (2021), Antonelli et al. (2021), Baviera et al. (2016), Brigo and Vrins (2018), Brigo et al. (2018), Feng and Osterlee (2017) and Hull and White (2012).

Following those ideas, we consider a vulnerable European plain vanilla option (or equivalently its unilateral CVA) in a Black and Scholes market model and a default intensity represented by a Cox–Ingersoll–Ross (CIR) diffusion, with correlated driving processes. Even in this very classical model, the presence of WWR makes the problem much more complex from a computational point of view. We derive a handy approximation formula based on a second-order expansion of the price representation formula with respect to the correlation coefficient, as an alternative to the benchmark Monte Carlo approach. Monte-Carlo methods (MC) are most commonly used in this setting (see e.g. Hull and White 2012; Rosen and Saunders 2012). Our method (stemmed from the works Antonelli and Scarlatti 2009; Antonelli et al. 2021 and extending those results), being analytical, leads to a faster methodology than MC simulations, nevertheless exhibiting comparable accuracy. In particular, the correlation expansion presented in Antonelli et al. (2021) involves a representation of the coefficients as solutions of a chain of parabolic PDE problems, whose solutions are characterized by the Feynman Kaĉ formulas. The procedure implies evaluating multiple integrals whose dimension grows with the order of approximation. In the current work, we succeed in simplifying the coefficients representation, using intermediate analytic derivative price formulas, obtained by conditioning and change-of-measure techniques.

Recently, a similar methodology has been applied to deal with CVA in stochastic volatility market models (see Alòs et al. 2021, 2022). Along the years, other value adjustments have been introduced and an evaluation theory developed, an extension of the current method to that context is to be found in Antonelli et al. (2022). We remark that this methodology not only provides representation formulas with handy approximations (due to expansion coefficients written at correlation zero), but it is also easily extendable to include multiple risk factors in the model, as shown in the quoted papers. In general, we refer the interested reader to the volume (Glau et al. 2016) for an updated overview on the topic.

The paper is organized as follows. Section 2 introduces the pricing problem for a vulnerable option and the related CVA using the intensity-based approach to write a general representation formula. In Sect. 3, we present the market/stochastic intensity model and we specialize the representation formula to this case. In Sect. 4, we introduce a second-order approximation for the price of the vulnerable option and its CVA and we propose a method to compute the expansion coefficients. Finally we test the efficiency and accuracy of our approximation procedure, comparing the results with those obtained by implementing enhanced Monte-Carlo simulations.

2 CVA: the intensity-based approach

In this section, we briefly recall the main setting and definition of the intensity approach to vulnerable options.

We consider a finite time interval [0, T] and a complete probability space $(\Omega , {\mathcal {F}}, Q)$, endowed with a filtration ${\mathbb {F}}=\{{\mathcal {F}}_t\}_{t\in [0,T]}$, augmented with the Q-null sets and made right continuous. We assume that all processes have a cádlág version.

The market is described by the money market account denoted by $D^{-1}(t,s)= \textrm{e}^{r(s-t)}$, r being the constant risk-free rate, and by a process $\{X_t\}_{t\in [0,T]}$ representing an asset log-price (whose dynamics will be specified later). We assume to be in absence of arbitrage and that the given probability Q is a risk neutral measure, already selected by some criterion. In this market, a defaultable European option paying $\Phi (X_T) \ge 0$ at maturity, is traded. We denote by $\tau$ the default time of the issuer of the claim and by $\{Z_t\}_{t\in [0,T]}$ a bounded ${\mathcal {F}}_t$-adapted recovery process. We model $\tau$ by means of the canonical construction of the default time as in Bielecki et al. (2011) section 3.2.2, therefore we assume there exists a differentiable adapted ${\mathbb {F}}$-hazard process

$$\begin{aligned} \Gamma _t = \int _0^t \lambda _u du \end{aligned}$$

for some non negative ${\mathbb {F}}$-adapted intensity process $\{\lambda _t\}_{t\in [0,T]}$, and we define

$$\begin{aligned} {\tau =\inf \{t>0: \textrm{e}^{-\Gamma _t}\le U\},} \qquad \Gamma _0=0 \end{aligned}$$

for some uniform random variable U independent of ${\mathbb {F}}$.

To properly evaluate this type of derivative, we need to include the information generated by the default time. Let us define the process

$$\begin{aligned} H_t = {\textbf{1}}_{\{\tau \le t\}}, \quad t\in [0,T]\quad \text { (here }{\textbf{1}}_A \text { denotes the indicator function of a set } A), \end{aligned}$$

and let ${\mathbb {H}}=\{{\mathcal {H}}_t\}_{t\in [0,T]}$ be the filtration it generates. For $t\in [0,T]$, we set the progressively enlarged filtration ${\mathcal {G}}_t={\mathcal {F}}_t\vee {\mathcal {H}}_t$, which is the smallest filtration making $\tau$ a stopping time. We uniquely extend the risk neutral probability to ${\mathbb {G}}$ and we keep denoting it by Q.

Following the canonical construction, the so-called H-hypothesis (see e.g. Bielecki and Rutkowski 2002; Bielecki et al. 2011) is automatically satisfied (Bielecki et al. 2011-Remark 3.2.1) and every ${\mathbb {F}}$-martingale remains a ${\mathbb {G}}$-martingale under Q, which implies that $D(t,s)\textrm{e}^{X_s}$, for $s\ge t$, remains a ${\mathbb {G}}$-martingale.

In ${\mathbb {G}}$, for any given time $t\in [0,T]$, the price of a defaultable call is given by no arbitrage pricing by

$$\begin{aligned} {c^{d,{\mathbb {G}}}(t,T) }= \mathbb {E}^Q\big [D(t,T)\Phi (X_T) 1_{\{\tau > T\}} + D(t,\tau ) Z_{\tau } 1_{\{t < \tau \le T \}} \big \vert {\mathcal {G}}_t\big ], \end{aligned}$$

(1)

while the corresponding default-free value is

$$\begin{aligned} c(t,T) = \mathbb {E}^Q[D(t,T)\Phi (X_T) \vert {\mathcal {F}}_t]. \end{aligned}$$

(2)

Correspondingly the CVA is given by

$$\begin{aligned} {CVA^{{\mathbb {G}}}(t,T)} =1_{\{\tau > t\}} [c(t,T) - c^{d, {\mathbb {G}}}(t,T)]. \end{aligned}$$

(3)

The two prices are adapted with respect to two different filtrations, where the smaller one represents the market information and it is therefore important to understand the price dynamics in ${\mathbb {F}}$, for instance for hedging purposes. To derive this dynamics, we exploit the Key-Lemma (as employed in Antonelli et al. 2021 or in the standard references Bielecki et al. 2014; Bielecki and Rutkowski 2002 or Bielecki et al. 2011), which implies that for any ${\mathbb {G}}$-adapted process $\{Y^{{\mathbb {G}}}_t\}_t$ there exists an ${\mathbb {F}}$-adapted process $\{Y^{{\mathbb {F}}}_t\}_t$, such that

$$\begin{aligned} Y^{{\mathbb {G}}}_t{\textbf{1}}_{\{\tau>t\}}=Y^{{\mathbb {F}}}_t{\textbf{1}}_{\{\tau >t\}}, \qquad \forall t. \end{aligned}$$

We apply this result and we denote by $c^{d}(t,T)$ the ${\mathbb {F}}$-adapted projection of $c^{d,{\mathbb {G}}}(t,T)$.

Consequently we have an ${\mathbb {F}}$-adapted CVA projection given by

$$\begin{aligned} CVA(t,T) := c(t,T) - c^{d}(t,T), \end{aligned}$$

(4)

coinciding with $CVA^{{\mathbb {G}}}(t,T)$ on $\{\tau >t\}$.

By using the canonical construction, we obtain a more treatable expression of $c^d(t,T)$ and of CVA(t, T). Indeed, let us introduce

$$\begin{aligned} F_t=Q(\tau \le t \vert {\mathcal {F}}_t), \qquad \forall \, t\ge 0, \end{aligned}$$

(5)

the conditional distribution of the default time $\tau$ given ${\mathcal {F}}_t$. Then $F_t(\omega )<1$ a.s. for all $t>0$ and we have

$$\begin{aligned} F_t= 1 - \textrm{e}^{-\Gamma _t}. \end{aligned}$$

(6)

By the consequences of the Key-Lemma (see again Antonelli et al. 2021), we may rewrite (1) on $\{\tau >t\}$ as

$$\begin{aligned} \begin{aligned} c^d(t,T) =&\mathbb {E}^Q\left[ \textrm{e}^{-\int _t^T (r+\lambda _s) ds}\Phi (X_T) + \int _t^T Z_{s} \lambda _s \textrm{e}^{-\int _t^s (r+\lambda _u) du} ds \Big \vert {\mathcal {F}}_t\right] , \end{aligned} \end{aligned}$$

(7)

recovering formulas (3.1) and (3.3) in Lando (1998). For the sake of exposition we shall assume the recovery process to be identically null, leading to the simpler expression

$$\begin{aligned} c^d(t,T) =\textrm{e}^{-r(T-t)}\mathbb {E}^{ Q}\left[ \textrm{e}^{-\int _t^T\lambda _s ds}\Phi (X_T)\Big \vert {\mathcal {F}}_t\right] , \end{aligned}$$

(8)

and consequently (4) becomes

$$\begin{aligned} CVA(t,T) = \textrm{e}^{-r(T-t)} \mathbb {E}^Q\left[ \Big (1-\textrm{e}^{-\int _t^T\lambda _s ds}\Big )\Phi (X_T)\Big \vert {\mathcal {F}}_t\right] . \end{aligned}$$

(9)

From now on, we will be working in ${\mathbb {F}}$, keeping in mind that all equalities are meant on the set $\{\tau >t\}$.

Remark 1

In case of non zero recovery, the process $\{Z_t\}_{t\in [0,T]}$ in (7) should be specified. The two most common choices are either $Z_t=Rc(t,T)$ (risk-free close-out hypothesis) or $Z_t=Rc^d(t,T)$ (replacement close-out hypothesis) for a constant $0 \le R \le 1$. When characterizing the price by means of a Backward Stochastic Differential Equation (BSDE), the first choice leads to the expression (see e.g. Antonelli et al. 2021)

$$\begin{aligned} c^d(t,T)= Rc(t,T)+ (1-R)\textrm{e}^{-r(T-t)} \mathbb {E}^Q\Big [\textrm{e}^{-\int _t^T \lambda _s ds}\Phi (X_T)\big \vert \mathcal {F}_t\Big ], \end{aligned}$$

while the second, solving the equation, gives

$$\begin{aligned} c^d(t,T) = \textrm{e}^{-r(T-t)} \mathbb {E}^Q\Big [\textrm{e}^{- (1-R) \int _t^T \lambda _s ds} \Phi (X_T)\big \vert \mathcal {F}_t \Big ], \end{aligned}$$

implying

$$\begin{aligned} CVA(t,T) = (1-R) \textrm{e}^{-r(T-t)} \mathbb {E}^Q\left[ \Big (1-\textrm{e}^{-\int _t^T\lambda _s ds}\Big )\Phi (X_T)\Big \vert {\mathcal {F}}_t\right] \end{aligned}$$

or

$$\begin{aligned} CVA(t,T) = \textrm{e}^{-r(T-t)} \mathbb {E}^Q\left[ \Big (1-\textrm{e}^{-(1-R)\int _t^T\lambda _s ds}\Big )\Phi (X_T)\Big \vert {\mathcal {F}}_t\right] , \end{aligned}$$

respectively. Indeed, both cases are straightforward extensions of (8), so considering $R=0$ is not restrictive.

Remark 2

We recall that introducing the survival process

$$\begin{aligned} S_t:=1-F_t, \quad t\in [0,T] \end{aligned}$$

and the (deterministic) survival function $J(t) = P(\tau> t) = \mathbb {E}[1_{\{\tau > t\}}]=\textrm{e}^{-\int _0^t \psi (s) ds}$, for some non-negative function $\psi$, we have $\mathbb {E}[S_t]=J(t)$,

$$\begin{aligned} dS_t = - \lambda _t S_t dt=\frac{\lambda _t S_t}{\psi _t J(t)} dJ(t) =: \zeta _t dJ(t) \end{aligned}$$

and it is possible to rewrite

$$\begin{aligned} CVA(t,T) = - (1-R)\frac{1}{S_t} \int _t^T\mathbb {E}\left[ D(t,u) c(u,T) \zeta _u \vert {\mathcal {F}}_t\right] dJ(u), \end{aligned}$$

(10)

(for details, see Brigo and Vrins 2018). If the intensity process is independent of the underlying, the expectation in the CVA factorizes, with $\mathbb {E}[\zeta _t] = 1$, so we simply get

$$\begin{aligned} CVA^{ind}(t,T) = - (1-R) \frac{1}{S_t} \int _t^T\mathbb {E}[ D(t,u) c(u,T) \vert {\mathcal {F}}_t] dJ(u), \end{aligned}$$

which is the basic representation of the (unilateral) CVA on which the regulatory adjustment formula (see Basel III) is built (see Gregory 2010). As a matter of fact, when the interest rates follow a deterministic process, by taking $t=0$ (hence $S_0=1$) and defining $EE(u) = \mathbb {E}[c(u,T) \vert \mathcal {F}_0]$, we have

$$\begin{aligned} CVA^{ind}(0,T) = - (1-R)\int _0^T D(0,u) EE(u) dJ(u), \end{aligned}$$

(11)

(having chosen the risk-free close-out hypothesis). Banks with an internal model method must compute the CVA according to the following formula

$$\begin{aligned} CVA^{Basel}=\, & LGD_{MKT} \sum _{k=1}^N \max \left( 0, \textrm{e}^{-s_{k-1} t_{k-1} /LGD_{MKT}}-\textrm{e}^{-s_{k} t_{k} /LGD_{MKT}} \right) \nonumber \\{} & {} \times \frac{1}{2} \left( EE(t_{k-1}) D(0,t_{k-1}) + EE(t_{k}) D(0,t_{k}) \right) , \end{aligned}$$

(12)

where $0=t_0< t_1< \cdots < t_N = T$ is a given time grid, the $s_k$’s are the corresponding counterparty credit spreads, and $LGD_{MKT}$ is the market loss-given-default of the counterparty, assumed equal to $1-R$.

Since $\int _0^{t_k} h(u) du \approx \frac{s_k t_k}{LGD}$ (see Hull 2012), it is immediately seen that the expression in (12) is essentially the trapezoidal quadrature rule approximation of the Riemann–Stieltjes integral (11), and, as such, it converges there when $\max _k(t_k-t_{k-1}) \rightarrow 0$ (see e.g. Dragomir 2011). According to the Basel Commitee requirements, WWR is taken into account by simply multiplying the previous formula by a factor $\alpha > 1.2$.

3 A representation formula under correlation

In this section, we introduce a representation formula for the price of a vulnerable plain vanilla call option, and the related CVA, in the case of correlated risk factors, assuming without loss of generality (see Remark 1) $R \equiv 0$.

The setting here is the same as in Antonelli et al. (2021), but we are going to use a different approach to evaluate the expansion coefficients in a handier and more efficient way, which allows pushing the expansion up to the second order in a quite straightforward manner.

We write our market model, in flow notation, for $x\in {\mathbb {R}}$ and $y>0$ to be

$$\begin{aligned} \begin{aligned} X^{t,x}_s(\rho )&= x + \left( r- \frac{\sigma ^2}{2}\right) (s-t)+ \sigma \left[ \rho \left( B_s^1-B^1_t\right) +\sqrt{1-\rho ^2}\left( B^2_s-B_t^2\right) \right] , \\ \lambda ^{t,y}_s&= y + \int _t^s \gamma (\theta - \lambda _u) du +\eta \int _t^s \sqrt{\lambda _u }dB^1_u, \end{aligned} \end{aligned}$$

(13)

where $(B^1, B^2)$ is a two dimensional standard Brownian motion and the constants $\sigma , \gamma , \theta , \eta \in (0, +\infty )$. We also assume the Feller condition $2\gamma \theta > \eta ^2$ to be satisfied, so $\lambda _s>0,\, \forall s\in [0,T]$, Q-almost surely. The pair defining the market is jointly Markovian, thus, from (8), the price of a defaultable call option with maturity T and strike price $\textrm{e}^\kappa$ can be rewritten as a deterministic function of the state variables at time t, on the event $\{\tau >t\}$, as

$$\begin{aligned} c^{d}(x,y,t,T;\rho )= \textrm{e}^{-r(T-t)}\mathbb {E}^Q\left[ \textrm{e}^{-\int _t^T\lambda ^{t,y}_s ds}\left( \textrm{e}^{X^{t,x}_T}-\textrm{e}^\kappa \right) ^+\right] , \end{aligned}$$

(14)

for $X^{t,x}_t=x$ and $\lambda _{t,y}^t=y$. The intensity is a Markov process also individually and since it is an affine process (see e.g. Alfonsi 2015 for an overview on affine processes), bond pricing theory implies that the expected survival process, given by $\displaystyle P(y,t,T):=\mathbb {E}^Q(\textrm{e}^{-\int _t^T\lambda ^{t,y}_s ds})$ can be written as

$$\begin{aligned} P(y,t,T)= & {} a(t,T)\textrm{e}^{-y b(t,T)}, \end{aligned}$$

(15)

$$\begin{aligned} { a(t,T) }= & {} \left( \frac{2 \delta \textrm{e}^{(\gamma +\delta )(T-t)/2}}{2\delta +(\delta +\gamma )(\textrm{e}^{\delta (T- t)}-1)} \right) ^{2 \gamma \theta /\eta ^2} \end{aligned}$$

(16)

$$\begin{aligned} {b(t,T)}= & {} \frac{2(\textrm{e}^{\delta (T- t)}-1)}{2\delta +(\delta +\gamma )(\textrm{e}^{\delta (T- t)}-1)},\quad \delta =\sqrt{\gamma ^2+2\eta ^2}, \end{aligned}$$

(17)

the latter being a continuous positive function.

Correlation in the dynamical model (13) induces a dependence between the derivative contract’s value and the counterparty default probability. Indeed, for a call option, a growth of the underlying asset price increases the contract value. When correlation is positive, the corresponding increase in the intensity $\lambda _t$ raises the probability of default.

Employing a CIR process meets the desirable requirement that the intensity be positive, but it makes quite impossible to compute $c^d(x,y,t,T;\rho )$ in closed form, when $\rho \ne 0$. Therefore, we aim at developing a handy representation to construct an approximation formula of polynomial order by power series expansion in $\rho$ around 0, if enough regularity is achieved.

Without loss of generality, for ease of exposition, we set $t=0$, $r=0$ and we simplify the notation of $\lambda ^{0,y}_s$, P(y, 0, T) and $c^d(x,y,0,T;\rho )$ to $\lambda _s$, P(0, T) and $c^d(x,y,T;\rho )$.

Conditioning internally with respect to $\mathcal {F}^1_T=\sigma (\{B^1_u:0\le u\le T\})$, we have

$$\begin{aligned} \begin{aligned} c^d(x,y,T;\rho )&= \mathbb {E}^Q\left[ \textrm{e}^{-\int _0^T\lambda _s ds}\left( \textrm{e}^{X_T(\rho )}-\textrm{e}^\kappa \right) ^+\right] \\&= \mathbb {E}^Q\left[ \textrm{e}^{-\int _0^T\lambda _s ds}\mathbb {E}\left[ \left( \textrm{e}^{X_T(\rho )}-\textrm{e}^\kappa \right) ^+\big \vert \mathcal {F}^1_T\right] \right] \end{aligned} \end{aligned}$$

(18)

But $X_T(\rho )\vert \mathcal {F}^1_T\sim \mathcal {N}\left( x-\frac{\sigma ^2}{2}T+\sigma \rho B_T^1, (1-\rho ^2)\sigma ^2 T\right)$, where $\mathcal {N}$ denotes the Gaussian distribution, so the inner expectation gives a conditioned Black & Scholes formula

$$\begin{aligned} \mathbb {E}^Q\left[ \left( \textrm{e}^{X_T(\rho )}-\textrm{e}^\kappa \right) ^+\vert \mathcal {F}^1_T\right] =\textrm{e}^{x+\sigma \rho B_T^1-\frac{(\sigma \rho )^2T}{2}}N(D_1(x,T,\rho ))-\textrm{e}^{\kappa }N(D_2(x,T,\rho )), \end{aligned}$$

(19)

$N(\cdot )$ being the standard normal distribution function, where for $i=1,2$, we have denoted the random variables

$$\begin{aligned} \begin{aligned} D_i(x,T,\rho )&=\beta (T,\rho )B_T^1+\alpha _i(x,T,\rho )\sim \mathcal {N}\left( \alpha _i(x,T,\rho ),\frac{\rho ^2}{1-\rho ^2}\right) , \\ \beta (T,\rho )&=\frac{\rho }{(1-\rho ^2)^{1/2}\sqrt{T}}, \\ \alpha _i(x,T,\rho )&=\frac{x-\kappa -\frac{\sigma ^2}{2}T+\sigma ^2(2- i)(1-\rho ^2)T}{\sigma (1-\rho ^2)^{1/2}\sqrt{T}}. \end{aligned} \end{aligned}$$

(20)

Hence, from (19), we obtain

$$\begin{aligned} c^d(x,y,T;\rho ) = \textrm{e}^{x} \textrm{e}^{-\frac{\sigma ^2\rho ^2T}{2}}F(\rho )-\textrm{e}^{\kappa }G(\rho ) , \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{aligned} F(\rho )&= \mathbb {E}^Q \left[ \textrm{e}^{-\int _0^T\lambda _s ds}\textrm{e}^{\sigma \rho B_T^1}N(D_1(x,T,\rho )) \right] , \\ G(\rho )&= \mathbb {E}^Q \left[ \textrm{e}^{-\int _0^T\lambda _s ds}N(D_2(x,T,\rho )) \right] . \end{aligned} \end{aligned}$$

(22)

The above representation can be made a little more explicit by an appropriate change of Numéraire. Introducing the $\mathcal {F}$-adapted Q-martingale

$$\begin{aligned} L_u:=\frac{\mathbb {E}^Q\left[ \textrm{e}^{-\int _0^T\lambda _s ds}\big \vert \mathcal {F}_u\right] }{P(0,T)}, \quad u\in [0,T], \end{aligned}$$

to define the T-forward measure $Q^T(A):=\mathbb {E}^Q[L_T1_A]$ (see Bjork 2009 for the method), we have

$$\begin{aligned} \begin{aligned} F(\rho )&= P(0,T)\mathbb {E}^{Q^T}\left[ \textrm{e}^{\sigma \rho B_T^1}N\big ( D_1 (x,T,\rho )\big )\right] \\ G(\rho )&= P(0,T)\mathbb {E}^{Q^T}\left[ N\big (D_2(x,T,\rho )\big )\right] . \end{aligned} \end{aligned}$$

(23)

We notice here that the martingale which defines the new measure is different from the one proposed in Brigo and Vrins (2018), allowing a factorization of each expectation in (22) different from the factorization in Brigo and Vrins (2018) (see Sect. 5 for more details).

By Girsanov theorem, we know that the process

$$\begin{aligned} {\bar{B}}^1_s=B^1_s+\eta \xi _s, \qquad \xi _s=\int _0^s\sqrt{\lambda _u}b(u,T)du \end{aligned}$$

(24)

is a $Q^T$-Brownian motion, and consequently we rewrite the representation formula for the price of the vulnerable option under the T-forward measure

$$\begin{aligned} \begin{aligned} c^d(x,y,T;\rho )&=P(0,T)\Big [\textrm{e}^{x}\textrm{e}^{-\frac{\sigma ^2\rho ^2T}{2}}F^T(\rho )-\textrm{e}^{\kappa }G^T(\rho )\Big ],\\ F^T(\rho )&= \mathbb {E}^{Q^T} \left[ \textrm{e}^{\sigma \rho ({\bar{B}}_T^1-\eta \xi _T)}N( {\bar{D}}_1(x,T,\rho )) \right] ,\\ G^T(\rho )&= \mathbb {E}^{Q^T} \left[ N({\bar{D}}_2(x,T,\rho ))\right] \\ {\bar{D}}_i(x,T,\rho )&= \alpha _i(x,T,\rho ) +\beta (T,\rho )\big ({\bar{B}}_T^1-\eta \xi _T\big ) ,\quad i=1,2. \end{aligned} \end{aligned}$$

(25)

We remark that for $\rho =0$, the above formulas simplify and setting

$$\begin{aligned} {\bar{D}}_{1,2}(x,T,0)= D_{1,2}(x,T,0)=:{ d_{1,2}(x) }=\frac{x-\kappa \pm \frac{\sigma ^2}{2}T}{\sigma \sqrt{T}}, \end{aligned}$$

(26)

we have $F^T(0) = P(0,T) N(d_1 ), G^T(0)= P(0,T) N(d_2)$, hence

$$\begin{aligned} c^d(x,y,T;0) = P(0,T) c^{BS}(x,T), \end{aligned}$$

where $c^{BS}(x,T)$ denotes the Call option Black and Scholes pricing function.

4 The second order approximation

In this section, we compute a second order approximation for (25) and later we compare its accuracy with a benchmark Monte Carlo estimates of the prices given by (14). The first order expansion was already considered in Antonelli et al. (2021), where the change-of-numéraire technique was not employed. As shown before, this allows to isolate a bond-like expression coming from the default intensity and consequently a simpler handling of each term.

First, we remark that (25) shows that $c^d$ is a regular function in $\rho$ and we may approximate it by a Taylor polynomial around 0 of any order and estimate, at least numerically, the error. As we are going to see, the coefficients computations are a bit involved, hence we focus on a second-order approximation formula, which gives very satisfying results in terms of efficiency and accuracy. This represents an improvement with respect to the first order approximation obtained in Antonelli et al. (2021), as it catches better the price behavior with respect to the correlation parameter $\rho$, as we will comment later in the numerical section. Also, this extension keeps the advantage of being rather simple to implement and computationally fast compared to any Monte Carlo approach.

Thus, for $k\ge 1$, we set

$$\begin{aligned} g_{1,k}(x,y,T):=\frac{\partial ^k \textrm{e}^{-\frac{\sigma ^2\rho ^2T}{2}}F^T(\rho )}{\partial \rho ^k}\vert _{\rho =0},\;\;g_{2,k}(x,y,T):=\frac{\partial ^k G^T(\rho )}{\partial \rho ^k}\vert _{\rho =0}, \end{aligned}$$

and, by recalling that $c^{BS}(x,T)= \textrm{e}^x F^T(0) - \textrm{e}^{\kappa }G^T(0)$, we aim at computing the following second order approximation of the vulnerable option price

$$\begin{aligned} \begin{aligned} c^{d,(2)}(x,y,T;\rho )&= P(0,T)\Big [c^{BS}(x,T) + \rho \left[ \textrm{e}^x g_{1,1}(x,y,T) - \textrm{e}^{\kappa }g_{2,1}(x,y,T)\right] \\&\quad + \frac{\rho ^2}{2} \left[ \textrm{e}^x g_{1,2}(x,y,T) - \textrm{e}^{\kappa } g_{2,2}(x,y,T)\right] \Big ]. \end{aligned} \end{aligned}$$

(27)

Correspondingly, we have the second order expansion for the CVA (see (3)):

$$\begin{aligned} \begin{aligned} CVA^{(2)}(0,T;\rho )&= c^{BS}(x,T)\big [1- P(0,T)\big ]\\&\quad -\rho P(0,T) \big [\textrm{e}^x g_{1,1} (x,y,T)- \textrm{e}^{\kappa }g_{2,1}(x,y,T)\big ] \\&\quad - \frac{\rho ^2}{2}P(0,T) \big [\textrm{e}^x g_{1,2}(x,y,T) - \textrm{e}^{\kappa } g_{2,2}(x,y,T)\big ]. \end{aligned} \end{aligned}$$

(28)

In (28), we immediately recognize that the first contribution $c^{BS}(x,T)(1- P(0,T))$ corresponds to the CVA under independence. The remaining terms are therefore the correction due to RWR/WWR.

By differentiating and taking $\rho =0$, after some lengthy calculations (see “Appendix 1”), we arrive at (by virtue of (26))

$$\begin{aligned}{} & {} g_{1,1}(x,y,T)=-\eta \left[ \sigma N(d_1(x))+ \frac{1}{\sqrt{T}}N'( d_1(x))\right] m(T,y) \end{aligned}$$

(29)

$$\begin{aligned}{} & {} g_{2,1}(x,y,T)=-\eta \frac{1}{\sqrt{T}}N'( d_2(x))m(T,y) \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \begin{aligned}g_{1,2}(x,y,T)&=\Big [\Big ( \sigma ^2 N(d_1(x)) + 2\sigma \frac{ N'(d_1(x))}{\sqrt{T}} + \frac{N''(d_1(x))}{T}\Big )s^2(T,y) \\&\quad + d''_1(x)N'(d_1(x)) - \sigma ^2T N(d_1(x)) \Big ] \end{aligned} \end{aligned}$$

(31)

$$\begin{aligned}{} & {} g_{2,2}(x,y,T) = d''_2(x) N'(d_2(x)) + \frac{1}{T} N''(d_2(x)) s^2(T,y), \end{aligned}$$

(32)

where

$$\begin{aligned} \begin{aligned} m(T,y)&=\mathbb {E}^{Q^T}[\xi _T]= \int _0^T\mathbb {E}^{Q^T}\big [\sqrt{\lambda _u}\big ]b(u,T)du,\\ s^2(T,y)&=\mathbb {E}^{Q^T}\left[ \big ({\bar{B}}^1_T+\eta \xi _T\big )^2\right] = T + 2 \eta \mathbb {E}^{Q^T}\left[ {\bar{B}}^1_T \xi _T\right] + \eta ^2 \mathbb {E}^{Q^T}\left[ \xi _T^2\right] . \end{aligned} \end{aligned}$$

To make the previous approximation implementable, it remains to compute m(T, y) and $s^2(T,y)$.

Approximation of m(T, y). In Grzelak and Oosterlee (2011), it is given the following efficient approximation for the standard CIR model:

$$\begin{aligned} \begin{aligned}&\mathbb {E}^Q\left[ \sqrt{\lambda _t}\right] \approx C_1 + C_2 \textrm{e}^{-C_3 t}:={\tilde{\Lambda }}(t),\\&C_1=\sqrt{\theta -\frac{\eta ^2}{8 \gamma }}, \ \ C_2=\sqrt{\lambda }-C_1, \ \ C_3 = -\log \left( \frac{\Lambda -C_1}{C_2}\right) , \end{aligned} \end{aligned}$$

(33)

with $\displaystyle \Lambda =\sqrt{\lambda \textrm{e}^{-\gamma }+ \theta (1- \textrm{e}^{-\gamma })+\frac{\theta (1- \textrm{e}^{-\gamma })}{2[\lambda \textrm{e}^{-\gamma }+\theta (1- \textrm{e}^{-\gamma })]}- \frac{\eta ^2}{4\gamma }( 1-\textrm{e}^{-\gamma }) }.$

Since the dynamic of the process $\lambda _s$ under the new measure $Q^T$ is

$$\begin{aligned} d{\lambda _s} = \gamma (\theta - \lambda _s h(s)) ds + \eta \sqrt{\lambda _s} d {\bar{B}}^1_s, \end{aligned}$$

(34)

where $h(s) = 1+\frac{\eta ^2}{\gamma }b(s,T)$, we consider the approximation (33) with modified parameters: $\gamma \leadsto {\tilde{\gamma }}:= \gamma (1+\frac{\eta ^2}{\gamma }\bar{b})$ and $\theta \leadsto {\tilde{\theta }}:= \theta / (1+ \frac{\eta ^2}{\gamma }\bar{b})$, where $\bar{b}=\frac{1}{T}\int _0^T b(s,T)ds$. Consequently

$$\begin{aligned} m(T,y) \approx \int _0^T {\tilde{\Lambda }}(t) b(t,T) dt := {\hat{m}}(T,y). \end{aligned}$$

(35)

We tested the quality of the approximation (35) by comparing it with the direct application of $\Delta$-method and the Monte Carlo estimation, for several parameter choices. Results are reported in “Appendix 2”.

Approximation of $s^2(T,y)$. By Itô’s integration by parts ($\xi$ is a continuous, square integrable, finite variation process), we have

$$\begin{aligned} {\bar{B}}^1_T \xi _T = \int _0^T {\bar{B}}^1_t \sqrt{\lambda _t} b(t,T) dt+\int _0^T \xi _t d{\bar{B}}^1_t \Rightarrow \mathbb {E}^{Q^T} \left[ {\bar{B}}^1_T \xi _T \right] = \int _0^T \mathbb {E}^{Q^T}\left[ {\bar{B}}^1_t \sqrt{\lambda _t}\right] b(t,T) dt. \end{aligned}$$

Since $\displaystyle d (\sqrt{\lambda _s}) = \frac{4 \gamma [\theta - \lambda _s h(s)]-\eta ^2}{8 \sqrt{\lambda _s}} ds + \frac{\eta }{2} d {\bar{B}}^1_s,$ (under the Feller’s condition the drift term is well-defined), again by Itô’s integration by parts we get

$$\begin{aligned} {\bar{B}}^1_t \sqrt{\lambda _t} = \int _0^t {\bar{B}}^1_s \frac{4 \gamma (\theta - \lambda _s h(s))-\eta ^2}{8 \sqrt{\lambda _s}} ds + \frac{\eta }{2} \int _0^t {\bar{B}}^1_s d {\bar{B}}^1_s + \int _0^t \sqrt{\lambda _s} d{\bar{B}}^1_s + \frac{\eta }{2} t. \end{aligned}$$

Thus,

$$\begin{aligned} \mathbb {E}^{Q^T}\left[ {\bar{B}}^1_t \sqrt{\lambda _t}\right] = \frac{\eta }{2} t + \int _0^t \mathbb {E}^{Q^T}\left[ {\bar{B}}^1_s \frac{4 \gamma (\theta - \lambda _s h(s))-\eta ^2}{8 \sqrt{\lambda _s}} \right] ds, \end{aligned}$$

and by approximating the process $\lambda _s$ by its expectation, $\mathbb {E}^{Q^T}[\lambda _s]$, the second term gives zero contribution and we obtain the approximation

$$\begin{aligned} \mathbb {E}^{Q^T}\left[ {\bar{B}}^1_t \sqrt{\lambda _t}\right] \approx \frac{\eta }{2} t, \quad \text {which implies }\quad \mathbb {E}^{Q^T}\left[ {\bar{B}}^1_T \xi _T\right] \approx \frac{\eta }{2} \int _0^T t b(t,T) dt. \end{aligned}$$

Finally, we approximate $\mathbb {E}^{Q^T}[(\xi _T)^2] \approx m(T,y)^2$, and we conclude

$$\begin{aligned} s^2(T,y) \approx T + \eta ^2 \int _0^T t b(t,T) dt + \eta ^2 \hat m(T,y)^2 := {\hat{s}}^2(T,y). \end{aligned}$$

(36)

We tested the quality of the approximations (35) and (36) on a randomly chosen sets of CIR model parameters: results are reported in “Appendix 2”.

Remark 3

A theoretical estimation of the error made by stopping the Taylor expansion at the second order can be done by taking the third derivative of (25) with respect to $\rho$ and trying to bound it uniformly in [0, 1).

This is not possible since that derivative will contain terms of the type $\displaystyle \frac{\rho ^n}{ (1-\rho ^2)^{\frac{2m+1}{2}} }$, for $n,m=0,1,2, \dots$, which can be bounded uniformly only in an interval $[0,\rho _0]$ for some $\rho _0<1$.

If such an interval is fixed, then exploiting that a CIR process has bounded moments of any order, that the process $\xi$ is positive and so is $\eta$, the moment generating function of the Gaussian random variable ${\bar{B}}^1_T$ and the derivatives of the Gaussian density, one may prove that

$$\begin{aligned} \left| c^{d}(x,y,T;\rho ) -c^{d,(2)}(x,y,T;\rho ) \right| \le \frac{C}{ (1- \rho _0)^{\frac{7}{2}} }\rho ^3 \end{aligned}$$

Remark 4

Once the representation (25) is obtained, it is reasonable trying to determine a hedging strategy, which is not straightforward since we are in an incomplete market. As discussed in Antonelli et al. (2022), if the market is rich enough, a hedging strategy might be devised by investing on the underlying (delta hedging) and on a bond that has $\lambda$ as its rate of return, by taking derivatives of the approximation formula with respect to those two assets. Nevertheless, this hedging will not be perfect, leaving out a component in the price represented by a martingale orthogonal to the space generated by the two assets (underlying and bond). This martingale will depend on the risk neutral probability determining the price, which is not unique and that needs being selected by some criterion. What criterion to use (minimal martingale measure, minimal variance, etc.) is a delicate issue and it deserves a careful analysis that goes beyond the aim of the present paper and that we hope to address in future work.

5 The Brigo–Vrins approach

In a recent paper, Brigo and Vrins (2018) consider a general methodology based on a change of measures to address the problem of computing CVA under WWR in a stochastic-intensity default setup. Their starting point is formula (10) applied to a general portfolio price process $V_t$. In such a framework, the EPE (expected positive exposure) under WWR is the function (see Remark 2 for notation)

$$\begin{aligned} EPE(t) = \mathbb {E}[D(0,t) V_t^+ \zeta _t]. \end{aligned}$$

and Girsanov theorem is used to factorize the EPE. Indeed, they define an equivalent martingale measure $Q^{C^{\mathcal {F},t}} \sim Q$ according to

$$\begin{aligned} Z_s^t:= \frac{dQ^{C^{\mathcal {F},t}}}{dQ} = \frac{M^t_s}{M^t_0}, \ \ \ M_s^t = \mathbb {E}[D(0,t) \lambda _t S_t \vert \mathcal {F}_s], \ s \in [0,t], \end{aligned}$$

from which they prove that

$$\begin{aligned} \mathbb {E}[D(0,t) V_t^+ \zeta _t] = \mathbb {E}^{C^{\mathcal {F},t}}[V_t^+] \mathbb {E}[ D(0,t) \zeta _t ]. \end{aligned}$$

(37)

The so defined measure $Q^{C^{\mathcal {F},t}}$ is called wrong-way measure and it is associated with the numéraire $C^{\mathcal {F},t}_{\cdot } = D(0,\cdot ) M_{\cdot }^t$.

Hence, the dynamics of $V_t$ under the measure $Q^{C^{\mathcal {F},t}}$ has to be obtained to compute the previous expression. Assuming $V_t$ to be a diffusion under Q, the change of measure results in a drift adjustment (see Brigo and Vrins 2018 for the full details).

In Brigo et al. (2018), this result was applied to compute CVA for a call option under WWR in the market model described by (13). Since the risk free rate is assumed to be constant, we have $\mathbb {E}[D(0,t)\zeta _t]=-\textrm{e}^{-rt}$. Moreover, the explicit expression of the new drift is

$$\begin{aligned} \theta _t^s \equiv \theta _t^s(\lambda _t) = \rho \eta \sqrt{\lambda _t} \left( \frac{a(s,t) \partial _t b(s,t)}{a(s,t) \partial _tb(s,t) \lambda _t - \partial _ta(s,t)} - b(s,t) \right) , \end{aligned}$$

(38)

with the functions $a(\cdot , \cdot )$ and $b(\cdot ,\cdot )$ given respectively by (16) and (17). To compute the expectations in (37), it is necessary to replace the process $\{\lambda _t\}_{\{t\in [0,T]\}}$ with a deterministic proxy $\{\lambda (t)\}_{\{t\in [0,T]\}}$ in (38), so that (37) can be evaluated analytically leading to the approximation (see Brigo et al. 2018):

$$\begin{aligned} \textrm{e}^{x_0+\sigma \Theta (t)} N\left( \frac{{\hat{\alpha }}(t)+\beta (t) \sigma \sqrt{t}}{\sqrt{1+\beta ^2(t)}} \right) - \textrm{e}^{\kappa -rT} N\left( \frac{{\hat{\alpha }}(t) - \sigma \sqrt{T-t}}{\sqrt{1+\beta ^2(t)}} \right) , \end{aligned}$$

(39)

where

$$\begin{aligned} \Theta (t)= & {} \int _0^t \theta (u,t)du, \ \ \theta (u,t)=\theta ^t_u(\lambda (u)), \ \ {\hat{\alpha }}(t) = \alpha (t) + \frac{\Theta (t)}{\sqrt{T-t}}\\ \alpha (t)= & {} \frac{1}{\sigma \sqrt{T-t}} \left( x_0-\kappa + \left( r+ \frac{\sigma ^2}{2} \right) T - \sigma ^2 t\right) , \ \ \beta (t) = \sqrt{\frac{t}{T-t}}. \end{aligned}$$

Two proxies are considered for $\lambda (t)$, $\mathbb {E}[\lambda _t]$ and $\mathbb {E}^{C^{\mathcal {F},t}}[\lambda _t]$: while the first is analytically known, the second requires a further approximation step (see Brigo et al. 2018). CVA under WWR is then obtained through a numerical integration procedure by inserting (39) in (10), specialized for the CIR intensity process, that is by taking $J(t) = P(y,0,t)$ (see (15)).

6 Numerical results

In this section, we aim at assessing the performance of the second-order approximation obtained by inserting the approximations (35) and (36) in (28), that we finally denote with

$$\begin{aligned} \widehat{CVA}^{(2)} (T,\rho )= c^{BS}(x,T)\big [1- P(0,T)\big ] - \rho h_1(T) - \frac{\rho ^2}{2} h_2(T), \end{aligned}$$

(40)

where

$$\begin{aligned} h_1(T):=P(0,T) \big [\textrm{e}^x {\hat{g}}_{1,1} (x,y,T)- \textrm{e}^{\kappa } {\hat{g}}_{2,1}(x,y,T)\big ] \end{aligned}$$

and

$$\begin{aligned} h_2(T):=P(0,T) \big [\textrm{e}^x {\hat{g}}_{1,2}(x,y,T) - \textrm{e}^{\kappa } {\hat{g}}_{2,2}(x,y,T)\big ], \end{aligned}$$

${\hat{g}}_{i,j}$ being the coefficients evaluated with ${\hat{m}}$, ${\hat{s}}^2$. Furthermore, we intend to size the contribution to CVA due to the correlation $\rho$. We recall that Wrong Way Risk corresponds to $\rho >0$: the asset value and the probability of default move in the same direction.

We choose the intensity process parameters (Table 1) as in Brigo et al. (2018), Brigo and Alfonsi (2005): in particular, Set a was exogeneously given and it corresponds to the scenario with the highest (1 year) default probability; Set b and Set c come from a calibration process on CDS market quotes. In the first set of experiments, the strike price was fixed to $K=\textrm{e}^{\kappa }=100$ and we considered three maturities, $T=0.5$, $T = 1$ and $T=5$: the underlying volatility was $\sigma =10\%$ and without loss of generality we also set the risk-free rate $r = 0$ and $t = 0$. The log-asset was set to 4.6052. All the algorithms were implemented in MatLab$^{\copyright }$ (R2019b), and ran on an Intel Core i7 2.40 GHZ with 8 GB RAM.

Table 1 Parameter sets for the CIR default intensity

The benchmark Monte Carlo method was implemented by using the Euler discretization scheme with full truncation for the intensity process $\{\lambda _t\}_{\{t\in [0,T]\}}$ (see Lord et al. 2010) and the exact simulation of the Brownian motion for the underlying $\{X_t\}_{\{t\in [0,T]\}}$. In order to reduce the variance of the estimator, a control variates technique was considered, by using the default-free price as control: in the considered cases, this reduced the length of the confidence interval by at least one order of magnitude. In our numerical experiments we generated $M=10^6$ sample paths with a time step discretization equal to 1.0e−03 for all the maturities. The length of the $95\%$ confidence interval varies between 1.0e−03 and 1.0e−04. The implemented algorithm took about 52 s for the computation of each CVA value, $\widehat{CVA}^{(MC)}(T,\rho )$.

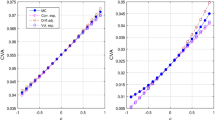
The results of the numerical implementation are reported in Figs. 1, 2 and 3 and they show the quality of the proposed second order approximation. We also observed that the use of the different approximations of m(T, y), as reported in “Appendix 2”, does not particularly significantly impact the quality of the estimator (40). A comparison with the first order approximation, i.e.

$$\begin{aligned} \widehat{CVA}^{(1)}(T,\rho ) = c^{BS}(x,T)\big [1- P(0,T)\big ] - \rho h_1(T), \end{aligned}$$

and the Brigo-Vrins (BV) method are also displayed (see Sect. 5). In particular, the latter required to evaluate numerically the integral (10) and the integral defining the function $\Theta (t)$ for the computation of EPE(t), $0 < t \le T$. Both integrations were implemented by using a trapezoidal routine: notice that the function $\Theta (t)$ must be computed for every value of the correlation parameter $\rho$. The implemented procedure takes approximately 4.5e−02 s to calculate each CVA value, $\widehat{CVA}^{(BV)}(T,\rho )$.

As it can be seen from Tables 2, 3 and 4, the absolute relative error with respect to the benchmark Monte Carlo estimation as a function of the correlation parameter $\rho$, $\vert \frac{\widehat{CVA}^{(\cdot )}(T,\rho )-\widehat{CVA}^{(MC)}(T,\rho )}{\widehat{CVA}^{(MC)}(T,\rho )}\vert$, worsens for increasing maturity. The first and second-order approximations behave similarly for small $\rho$, while for larger values, the second order is constantly better, especially in the most extended maturity scenario. We observe that the first-order approximation and the BV method produce in many instances similar relative error patterns, except for the parameter Set b, where the BV method seems to get worse for small T, as correlation decreases, although the error remains in the order of 1.0e−03. In contrast, the second-order approximation is systematically better at the cost of a minimal increase in computational complexity. As a matter of fact, we stress that it is sufficient to calculate the (approximated) coefficients ${\hat{g}}_{i,j}$ only once to obtain an entire CVA curve as a function of $\rho$, unlike the Monte Carlo and the BV methods, which require a new run of simulations and computations for each choice of the correlation parameter. The computation of the first and second order coefficients $h_1$ and $h_2$ in our implementation took about 5.0e−04 and 4.0e−03 s, respectively: the overall evaluation of the our second order approximation formula took approximately 2.0e−03 s. The quality of $\widehat{CVA}^{(2)}$ is particularly appreciable in the case of Set b, where the convexity of the CVA figure seems most evident (see Fig. 2).

We further remark that the first-order approximation $\widehat{CVA}^{(1)}$ yields results comparable to that proposed in Antonelli et al. (2021). The coefficient of this approximation in the Taylor expansion is, in fact, the same but it has a more explicit representation in the present paper.

Fig. 1

CVA approximations for the Set a: blue circles are MC estimates, magenta diamonds and red stars are the first and second order approximations, respectively, and green squares are the results of the BV method (color figure online)

Fig. 2

CVA approximations for the Set b: blue circles are MC estimates, magenta diamonds and red stars are the first and second order approximations, respectively, and green squares are the results of the BV method (color figure online)

Fig. 3

CVA approximations for the Set c: blue circles are MC estimates, magenta diamonds and red stars are the first and second order approximations, respectively, and green squares are the results of the BV method (color figure online)

Table 2 Set a: the absolute relative error with respect to the Monte Carlo estimate

Table 3 Set b: the absolute relative error with respect to the Monte Carlo estimate

Table 4 Set c: the absolute relative error with respect to the Monte Carlo estimate

In the second set of experiments, we report the values of the (approximated) coefficients of the second-order expansion, i.e. the credit value adjustment under independence, $CVA^{ind}:= c^{BS}(x,T)\big [1- P(0,T)\big ]$, and the terms $h_1$ and $h_2$ (see (40)), in Tables 5, 6 and 7 referring to Set a, Set b and Set c, respectively.

The coefficients $h_i, i=1,2$ in formula (40) are found to be negative. This result is widely expected since it can be supposed that the Credit Value Adjustment (CVA) would increase when the parameter $\rho$ is positive. This is because, with a positive $\rho$, the probability of the counterparty defaulting increases as the value of the contract increases. As a result, a higher credit adjustment is required to account for this risk.

Moreover, $h_2$ is found to be typically one or two times smaller than $h_1$, except in Set b, where it is often comparable (or even larger) in magnitude to $h_1$. This finding is consistent with the first onset of experiments (see Fig. 2) where it is observed that the dependence of the CVA on the parameter $\rho$ exhibits non-negligible convexity, which is reflected in the magnitude of the corresponding coefficient. Consequently, the coefficient introduces a non-negligible correction term, and it highlights the importance of considering the impact of parameter dependencies on CVA calculations.

Overall, these findings emphasize the significance of the parameter $\rho$ involved in CVA calculations to account for WWR/RWR, and they suggest the need for a comprehensive analysis of their impact on the resulting derivative values.

Table 5 The values of the coefficients of the second-order approximation for the CVA, for different time-to-maturity TtM and strike prices K, Set a

Table 6 The values of the coefficients of the second-order approximation for the CVA, for different time-to-maturity TtM and strike prices K, Set b

Table 7 The values of the coefficients of the second-order approximation for the CVA, for different time-to-maturity TtM and strike prices K, Set c

7 Conclusions

This paper addresses the issue of estimating CVA within the framework of intensity models, while accounting for wrong-way risk (WWR), which refers to the presence of a correlation between the derivative contract’s value and the counterparty’s default probability. We propose a technique based on approximating the CVA value as a function of the correlation parameter using first or second-order Taylor polynomials. The coefficients of this approximation are obtained using a change-of-numeraire approach. We demonstrate the effectiveness of our method in approximating the coefficient of the Taylor polynomials for a plain vanilla call option, where the underlying follows a GBM dynamic and the intensity of default is a correlated CIR process. Our approach proves to be both accurate and efficient, as shown by a series of numerical experiments compared with the results obtained by Monte Carlo estimations and the method in Brigo et al. (2018). Additionally, our technique enucleates the WWR contribution of negative correlation providing a quantitative measure for the impact of such a risk.

The approach in the present paper opens to further research in several directions. Firstly, it could be extended to consider other risk drivers, such as stochastic interest rates, which can significantly affect CVA estimates. Secondly, the method could be applied to other types of underlying/intensity models, including those with jumps or mean-reverting features. Lastly, it could be worth trying to apply it on other types of derivatives, such as forward starting options or path-dependent products, which are more complex and can pose greater challenges for CVA estimation. These extensions could help to further validate the proposed method and broaden its applicability in practical settings.

Appendices

Appendix 1: The approximation coefficients

In this section, we justify the calculations that lead to formulas (29), (30),(31) and (32). We start by recalling that

$$\begin{aligned} \begin{aligned} F^T(\rho )&=\mathbb {E}^{Q^T} \left[ \textrm{e}^{\sigma \rho ({\bar{B}}_T^1-\eta \xi _T)}N( {\bar{D}}_1(x,T,\rho ) \right] ,\\ G^T(\rho )&= \mathbb {E}^{Q^T} \left[ N({\bar{D}}_2(x,T,\rho ))\right] \\ {\bar{D}}_i(x,T,\rho )&= \alpha _i(x,T,\rho ) +\beta (T,\rho )\big ({\bar{B}}_T^1-\eta \xi _T\big ) ,\quad i=1,2, \end{aligned} \end{aligned}$$

(41)

where

$$\begin{aligned} \begin{aligned} \beta (T,\rho )&=\frac{\rho }{(1-\rho ^2)^{1/2}\sqrt{T}}, \\ \alpha _i(x,T,\rho )&=\frac{x-\kappa -\frac{\sigma ^2}{2}T+\sigma ^2(2- i)(1-\rho ^2)T}{\sigma (1-\rho ^2)^{1/2}\sqrt{T}}, \end{aligned} \end{aligned}$$

(42)

and that, for $k\ge 1$, we set

$$\begin{aligned} g_{1,k}(x,y,T):=\frac{\partial ^k \textrm{e}^{-\frac{\sigma ^2\rho ^2T}{2}}F^T(\rho )}{\partial \rho ^k}\Big \vert _{\rho =0},\;\;g_{2,k}(x,y,T):=\frac{\partial ^k G^T(\rho )}{\partial \rho ^k}\Big \vert _{\rho =0}. \end{aligned}$$

By setting $k=1$, we have

$$\begin{aligned} g_{2,1}(x,y,T) = \mathbb {E}^{Q^{T}}\biggr [\frac{\partial }{\partial \rho }\Big (N({\bar{D}}_2(x,T,\rho ))\Big )\Big \vert _{\rho =0}\biggr ]= N'(d_2(x))\mathbb {E}^{Q^T}\biggl [\frac{\partial {\bar{D}}_2(x,T,\rho )}{\partial \rho }\Big \vert _{\rho =0}\biggr ], \end{aligned}$$

having denoted $d_i(x):= {\bar{D}}_i(x,T,0), i=1,2$. From (42) we get $\beta '(T,0)=\frac{1}{\sqrt{T}}$ and $\alpha '_2(x,T,0)=0$, therefore we obtain

$$\begin{aligned} \frac{\partial {\bar{D}}_2(x,T,\rho )}{\partial \rho }\vert _{\rho =0}=\frac{\eta }{\sqrt{T}} \xi _T+\frac{{\bar{B}}_T^1}{\sqrt{T}}. \end{aligned}$$

Hence for $g_{2,1}(x,y,T)$ we have the simple formula:

$$\begin{aligned} g_{2,1}(x,y,T)=N'( d_2(x)) \frac{\eta }{\sqrt{T}}\; m(T,y), \end{aligned}$$

with $m(T,y)=\mathbb {E}^{Q^T}[\xi _T]= \int _0^T\mathbb {E}^{Q^T}[\sqrt{\lambda _u}]b(u,T)du$. The computation of $g_{1,1}(x,y,T)$ requires the same steps. Indeed we have

$$\begin{aligned} \begin{aligned} g_{1,1}(x,y,T)&=\mathbb {E}^{Q^{T}}\biggr [\frac{\partial }{\partial \rho }\Big (\textrm{e}^{\sigma \rho B_T^1} N({\bar{D}}_1(x,T,\rho ))\Big )\Big \vert _{\rho =0}\biggr ]\\&=\mathbb {E}^{Q^{T}}\biggr [(\sigma \eta \xi _T+ \sigma {\bar{B}}_T^1) N(d_1(x))+\frac{\partial {\bar{D}}_1(x,T,\rho )}{\partial \rho }\Big \vert _{\rho =0}\; N'(d_1(x))\biggr ]\\&= \sigma \eta \; m(T,y)N(d_1(x))+N'(d_1(x)) \mathbb {E}^{Q^{T}}\left[ \frac{\partial {\bar{D}}_1(x,T,\rho )}{\partial \rho }\Big \vert _{\rho =0}\right] , \end{aligned} \end{aligned}$$

but $\frac{\partial {\bar{D}}_1(x,T,\rho )}{\partial \rho }\Big \vert _{\rho =0}=\frac{\partial {\bar{D}}_2(x,T,\rho )}{\partial \rho }\Big \vert _{\rho =0}$, whence

$$\begin{aligned} g_{1,1}(x,y,T)=\sigma \eta \;m(T,y)N(d_1(x))+N'(d_1(x)) \frac{\eta }{\sqrt{T}}\; m(T,y). \end{aligned}$$

We now proceed to compute the second derivatives,

$$\begin{aligned} g_{1,2}(x,y,T) = \mathbb {E}^{Q^{T}}\biggr [\frac{\partial ^2}{\partial \rho ^2}\Big (N({\bar{D}}_2(x,T,\rho ))\Big )\Big \vert _{\rho =0}\biggr ] \end{aligned}$$

and

$$\begin{aligned} g_{2,2}(x,y,T) = \mathbb {E}^{Q^{T}}\biggr [\frac{\partial ^2}{\partial \rho ^2}\Big (\textrm{e}^{\sigma \rho B_T^1} N({\bar{D}}_1(x,T,\rho ))\Big )\Big \vert _{\rho =0}\biggr ]; \end{aligned}$$

straightforward calculations give

$$\begin{aligned} \begin{aligned} g_{1,2}(x,y,T)&= \mathbb {E}^{Q^T}\big [({\bar{B}}^1_T+\eta \xi _T)^2\big ] \Big (\sigma ^2 N(d_1(x)) +2 \frac{\sigma N'(d_1(x))}{\sqrt{T}} + \frac{N''(d_1(x))}{T}\Big ) \\&\quad - \sigma ^2 T N(d_1(x)) + N'(d_1(x)) d''_1(x) \\ g_{2,2}(x,y,T) =&N'(d_2(x)) d''_2(x)+ \mathbb {E}^{Q^T}[({\bar{B}}^1_T+\eta \xi _T)^2] \frac{N''(d_2(x))}{T}, \end{aligned} \end{aligned}$$

(43)

where $d''_1(x) = (x-\kappa -3 \sigma ^2 T /2)/(\sigma \sqrt{T})$ and $d''_2(x) = (x-\kappa - \sigma ^2 T /2)/(\sigma \sqrt{T})$.

Appendix 2: $\Delta$-method: results

Assuming that a function $\phi (\cdot )$ is sufficiently smooth, from the first-order Taylor expansion we get $\phi (X) \approx \phi (\mathbb {E}[X]) + \phi '(\mathbb {E}[X]) (X-\mathbb {E}[X])$, from which

$$\begin{aligned} var(\phi (X)) \approx \left( \phi '(\mathbb {E}[X]) \right) ^2 var(X). \end{aligned}$$

(44)

By applying the approximation to the function $\phi (x) = \sqrt{x}$, evaluated in the process $\lambda _t$, and recalling that $var(\sqrt{X}) = \mathbb {E}[X]-\mathbb {E}[\sqrt{X}]^2$, we get

$$\begin{aligned} \mathbb {E}^{Q^T}[\sqrt{\lambda _t}] = \sqrt{\mathbb {E}^{Q^T}[\lambda _t] - var^{Q^T}(\sqrt{\lambda _t})} \approx \sqrt{\mathbb {E}^{Q^T}[\lambda _t] - \frac{var^{Q^T}(\lambda _t)}{4 \mathbb {E}^{Q^T}[\lambda _t]}} : = \Lambda (t) \end{aligned}$$

(45)

(see Grzelak and Oosterlee 2011). The error of this approximation is entirely due to the approximation (44). In particular, we assume that the first-order terms in the Taylor expansion around the expectation give an accurate representation. Further remarks on the conditions for the $\Delta$-method to perform well can be found in Oehlert (1992).

In our framework the dynamic of the intensity default process under the $Q^T$ measure is given by

$$\begin{aligned} d{\lambda _s} = \gamma (\theta - \lambda _s h(s)) ds + \eta \sqrt{\lambda _s} d {\bar{B}}^1_s \end{aligned}$$

(46)

where $h(s) = 1+\frac{\eta ^2}{\gamma }b(s,T)$. By setting ${K(t) }:= \int _0^t h(s) ds$, we have that

$$\begin{aligned} \lambda _t = \lambda _0 \textrm{e}^{-\theta K(t)} + \gamma \theta \textrm{e}^{-\theta K(t)} \int _0^t \textrm{e}^{-\theta K(s)} ds + \eta \textrm{e}^{-\theta K(t)} \int _0^t \textrm{e}^{-\theta K(s)} \sqrt{\lambda _s} d {\bar{B}}^1_s, \end{aligned}$$

(47)

from which we get

$$\begin{aligned} \mathbb {E}^{Q^T}[\lambda _t] = \lambda _0 \textrm{e}^{-\theta K(t)} + \gamma \theta \textrm{e}^{-\theta K(t)} \int _0^t \textrm{e}^{-\theta K(s)} ds, \end{aligned}$$

(48)

and, by Itô isometry,

$$\begin{aligned} \begin{aligned} var^{Q^T}(\lambda _t)&= \mathbb {E}^{Q^T}[\lambda _t^2]-\left( \mathbb {E}^{Q^T}[\lambda _t]\right) ^2 = \eta ^2 \textrm{e}^{-2 \theta K(t)} \int _0^t \textrm{e}^{-2 \theta K(s)} \mathbb {E}^{Q^T}[\lambda _s] ds\\&= \lambda _0 \eta ^2 \textrm{e}^{-2 \theta K(t)}\int _0^t \textrm{e}^{-2 \theta K(s)} ds + \eta ^2 \gamma \theta \textrm{e}^{-2 \theta K(t)} \int _0^t \textrm{e}^{-\theta K(s)} \int _0^s \textrm{e}^{-\theta K(r)} dr ds. \end{aligned} \end{aligned}$$

From the definition of the function $\displaystyle {b(t,T)=\frac{2(\textrm{e}^{\delta (T- t)}-1)}{2\delta +(\delta +\gamma )(\textrm{e}^{\delta (T- t)}-1)}}$, where $\delta =\sqrt{\gamma ^2+2\eta ^2}$, we have

$$\begin{aligned} \int \left( 1{ +}\frac{\eta ^2}{\gamma } b(t,T)\right) dt = t {-} \frac{\eta ^2}{\gamma }\left( \frac{2 t}{\delta -\gamma }+\frac{4 \ln \left( \delta -\gamma +\delta \textrm{e}^{\delta (T-t)}+\gamma \textrm{e}^{\delta (T-t)}\right) }{\delta ^2-\gamma ^2} \right) + C. \end{aligned}$$

Hence, $\mathbb {E}^{Q^T}[\lambda _t]$ and $var^{Q^T}(\lambda _t)$ can be easily computed to get $\Lambda (t)$, and therefore

$$\begin{aligned} m(T,y) \approx \int _0^T \Lambda (t) b(t,T) dt, \end{aligned}$$

by using numerical integration routines.

Besides approximation (45), in Grzelak and Oosterlee (2011) Grzelak and Oosterlee proposed to use, for the CIR model, the following function

$$\begin{aligned} \mathbb {E}^Q[\sqrt{\lambda _t}] \approx C_1 + C_2 \textrm{e}^{-C_3 t}:={\tilde{\Lambda }}(t) \end{aligned}$$

(49)

where the coefficients $C_1,C_2$ and $C_3$ are set to fit as much as possible to the function $\Lambda (t)$ (see Sect. 4). We tested the quality of the $\Delta$-method approximation of $\mathbb {E}^{Q^T}[\sqrt{\lambda _t}]$ (45) and its functional approximation (49) for a set of parameters $\gamma , \theta , \eta$ and $\lambda _0$: some results are displayed in Fig. 4, where they are compared with a Monte Carlo approximation, obtained from simulation of the process (46) through the Euler discretization scheme with full truncation, with time step 1.0e−03, and 1.0e+05 trajectories (Fig. 5).

Fig. 4

Approximation of $\mathbb {E}^{Q^T}[\sqrt{\lambda _t}]$. The dotted lines represent the Monte Carlo estimation, the squared dash-dotted and the star dash-dotted are the $\Delta$ and its functional approximation, respectively

Fig. 5

Approximation errors with respect to Monte Carlo of $s^2(T,y)$