Skip to main content
SpringerLink
Log in

Three-dimensional Modeling of Cracking with Thermo-hydromechanical Process by Considering Rock Heterogeneity

  • Original Paper
  • Published:
Rock Mechanics and Rock Engineering Aims and scope Submit manuscript

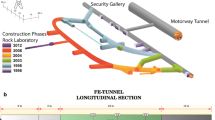
Abstract

This study is part of numerical simulations performed on an in-situ heating test conducted by the French National Radioactive Waste Management Agency (Andra) at the Meuse/Haute-Marne Underground Research Laboratory (URL) to study the thermo-hydromechanical behavior of the host Callovo-Oxfordian COx claystone in quasi real conditions, through the international research project DECOVALEX. We present a numerical study of damage and cracking process in saturated claystone subjected to thermo-hydromechanical coupling by considering material heterogeneity distribution. For this purpose, a macroscopic elastic model is first determined by using two steps of homogenization by taking into account the effects of porosity and mineral inclusions. This model is implemented into a finite element code devoted to solving thermo-hydromechanical coupling problems. The nucleation and propagation of cracks are described by using an extended phase-field method, considering the effects of temperature and fluid pressure on the evolution of phase-field. The proposed model is applied to the numerical analysis of cracking process due to excavation and heating around a group of boreholes (CRQ). The numerical results of the 3D simulation are compared with in-situ measurements of temperature and pore pressure distribution. The excavation damage zone and heating fracture is reproduced and analysed according to the structure of the heating position and the heterogeneity of the rock.

Highlights

  • A phase-field model is developed with thermo-hydromechanical processes;

  • Both tensile and shear cracks are taken into account;

  • Crack nucleation is emphasized by spatial heterogeneity of material properties;

  • Cracking processes due to thermal-hydraulic interaction are analyzed in three-dimensional conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Abbreviations

\(\alpha _b\) :

Scalar of thermal dilation coefficient in drained condition for isotropic material

\(\alpha _f\) :

Thermal dilation coefficient of fluid

\(\alpha _m\) :

Differential thermal dilation of saturated porous medium

\(\varvec{\sigma }\) :

Stress tensor

\(\varvec{I}\) :

Second order unit tensor

\(\epsilon ^e\) :

Elastic strain tensor

\(\Gamma\) :

Set of cracks

\(\gamma\) :

Crack density

\(\phi\) :

Porosity

\(\rho ^0_f\) :

Volumetric density of fluid

\(\theta\) :

Variation of temperature

\(A_{\Gamma }\) :

Crack surface

b :

Biot coefficient for isotropic material

\(C_\sigma ^b\) :

Volumetric specific heat for constant stress under drained condition

\(d^s\) :

Damage variable of shear crack

\(d^t\) :

Damage variable of tensile crack

E :

Total energy

\(E_c\) :

Fracture surface energy

\(E_e\) :

Elastic strain energy of damaged material

\(K_b\) :

Bulk modulus of drained material

\(K_f\) :

Bulk modulus of fluid

\(K_m\) :

Bulk modulus of solid matrix

\(K_{reuss}\) :

Reuss equivalent bulk modulus

M :

Scalar coefficient of Biot modulus

m :

Fluid mass change per unit initial volume

p :

Fluid pressure or pore pressure

s :

Entropy

T :

Temperature

\(w_c\) :

Energy density per unit volume requested to create crack

\(w_e\) :

Elastic strain energy of cracked material

\(\beta _i\) :

Mean value of random variable for mineral inclusions volumetric fraction

\(\beta _p\) :

Mean value of random variable for porosity

\(\mathbb {C}^{hom}\) :

Macroscopic elastic tensor of heterogeneous rocks

\(\mathbb {C}^{in}\) :

Elastic tensor of inclusions

\(\mathbb {C}^{mp}\) :

Effective elastic tensor of porous matrix

\(\mathbb {C}^{m}\) :

Elastic tensor of solid matrix

\(\mathbb {I}\) :

Fourth order unit tensor

\(\mathbb {P}^i\) :

Fourth order Hill tensor for spherical inclusions

\(\mathbb {P}^p\) :

Fourth order Hill tensor for ellipsoidal pores

\(\mathbb {P}^{\pm }_\sigma\) :

Operators for spectral decomposition of stress tensor

\(\Omega _i\) :

Volume of inclusions

\(\Omega _m\) :

Volume of solid clay matrix

\(\Omega _p\) :

Volume of pores

\(\sigma ^t_1\) :

Major Terzaghi effective principal stress

\(\sigma ^t_3\) :

Minor Terzaghi effective principal stress

\(\sigma _t\) :

Average value of uniaxial tensile strength

\(\varphi\) :

Friction angle

\(\xi _i\) :

Probability density for inclusions

\(\xi _p\) :

Probability density for pores

c :

Cohesion

\(f_i\) :

Random distribution of mineral inclusions volumetric fraction

\(f_p\) :

Random distribution of porosity

G :

Shear modulus

\(g_c^s\) :

Toughness parameter for shear crack

\(g_c^t\) :

Toughness parameter for tensile crack

\(h_s\) :

Degradation variable for shear crack

\(h_t\) :

Degradation variable for tensile crack

k :

Small positive value to avoid calculating error

\(l_d\) :

Length scale parameter for width of smeared cracks

\(m_i\) :

Homogeneity index for mineral inclusions

\(m_p\) :

Homogeneity index for pores

References

  • Armand G, Leveau F, Nussbaum C, deLaVaissiere R, Noiret A, Jaeggi D, Landrein P, Righini C (2014) Geometry and properties of the excavation induced fractures at the meuse-haute-marne url drifts. Rock Mech Rock Eng 47:21–41

    Article  Google Scholar 

  • Armand G, Bumbieler F, Conil N, delaVaissiere R, Bosgiraud JM, Vu MN (2017) Main outcomes from in situ thermo-hydro-mechanical experiments programme to demonstrate feasibility of radioactive high-level waste disposal in the Callovo-Oxfordian claystone. J Rock Mech Geotech Eng 9:415–427

    Article  Google Scholar 

  • Armand G, Conil N, Talandier J, Seyedi DM (2017) Fundamental aspects of the hydromechanical behaviour of Callovo-Oxfordian claystone: from experimental studies to model calibration and validation. Comput Geotech 85:277–286

    Article  Google Scholar 

  • Bernard PE, Moes N, Chevaugeon N (2012) Damage growth modeling using the thick level set (TLS) approach: efficient discretization for quasi-static loadings. Comput Methods Appl Mech Eng 233–236:11–27

    Article  Google Scholar 

  • Birkholzer JT, Bond AE, Hudson JA, Jing L, Tsang CF, Shao H, Kolditz O (2018) Decovalex-2015: an international collaboration for advancing the understanding and modeling of coupled thermo-hydro-mechanical-chemical (thmc) processes in geological systems

  • Birkholzer JT, Tsang CF, Bond AE, Hudson JA, Jing L, Stephansson O (2019) 25 years of Decovalex-scientific advances and lessons learned from an international research collaboration in coupled subsurface processes. Int J Rock Mech Min Sci 122:103995

    Article  Google Scholar 

  • Borden MJ, Verhoosel CV, Scott MA, Hughes TJ, Landis CM (2012) A phase-field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217:77–95

    Article  Google Scholar 

  • Bourdin B, Francfort GA, Marigo JJ (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48:797–826

    Article  Google Scholar 

  • Bourdin B, Francfort GA, Marigo JJ (2008) The variational approach to fracture. J Elast 91:5–148

    Article  Google Scholar 

  • Braun P (2019) Thermo-hydro-mechanical behavior of the Callovo-Oxfordian claystone: Effects of stress paths and temperature changes. Ph.D. thesis. Université Paris-Est

  • Bryant EC, Sun W (2018) A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics. Comput Methods Appl Mech Eng 342:561–584

    Article  Google Scholar 

  • Cheng AHD (2016) Poroelasticity, vol 27. Springer, Heidelberg

    Google Scholar 

  • Choo J, Sun W (2018) Coupled phase-field and plasticity modeling of geological materials: from brittle fracture to ductile flow. Comput Methods Appl Mech Eng 330:1–32

    Article  Google Scholar 

  • Conil N, Manon V, Plua C, Vu NM, Seyedi D, Armand G (2020) In situ investigation of the THM behavior of the Callovo-Oxfordian claystone. Rock Mech Rock Eng 53:2747–2769

    Article  Google Scholar 

  • Coussy O (2004) Poromechanics. Wiley, Hoboken

    Google Scholar 

  • DeBuhan P, Dormieux L (1996) On the validity of the effective stress concept for assessing the strength of saturated porous materials: a homogenization approach. J Mech Phys Solids 44:1649–1677

    Article  Google Scholar 

  • de La Vaissiere R, Armand G, Talandier J (2015) Gas and water flow in an excavation-induced fracture network around an underground drift: a case study for a radioactive waste repository in clay rock. J Hydrol 521:141–156

    Article  Google Scholar 

  • Evans B, Fredrich JT, Wong TF (1990) The brittle-ductile transition in rocks: recent experimental and theoretical progress. The Brittle-Ductile Transition in rocks. Geophys Monogr Ser 56:1–20

    Google Scholar 

  • Fang J, Wu C, Li J, Liu Q, Wu C, Sun G, Qing L (2019) Phase field fracture in elasto-plastic solids: variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int J Mech Sci 156:382–396

    Article  Google Scholar 

  • Farhat F, Shen W, Shao J (2017) A micro-mechanics based viscoplastic model for clayey rocks. Comput Geotech 89:92–102

    Article  Google Scholar 

  • Fei F, Choo J (2020) A phase-field method for modeling cracks with frictional contact. Int J Numer Methods Eng 121:740–762

    Article  Google Scholar 

  • Fei F, Choo J (2020) A phase-field model of frictional shear fracture in geologic materials. Comput Methods Appl Mech Eng 369:113265

    Article  Google Scholar 

  • Fei F, Choo J (2021) Double-phase-field formulation for mixed-mode fracture in rocks. Comput Methods Appl Mech Eng 376:113655

    Article  Google Scholar 

  • Francfort GA, Marigo JJ (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46:1319–1342

    Article  Google Scholar 

  • Giraud A, Huynh Q, Hoxha D, Kondo D (2007) Application of results on Eshelby tensor to the determination of effective poroelastic properties of anisotropic rocks-like composites. Int J Solids Struct 44:3756–3772

    Article  Google Scholar 

  • Kim J, Tchelepi H, Juanes R (2011) Stability and convergence of sequential methods for coupled flow and geomechanics: fixed-stress and fixed-strain splits. Comput Methods Appl Mech Eng 200:1591–1606

    Article  Google Scholar 

  • Lubarda V, Krajcinovic D, Mastilovic S (1994) Damage model for brittle elastic solids with unequal tensile and compressive strengths. Eng Fract Mech 49:681–697

    Article  Google Scholar 

  • Lydzba D, Shao JF (2002) Stress equivalence principle for saturated porous media. Comptes Rendus Mec 330:297–303

    Article  Google Scholar 

  • Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199:2765–2778

    Article  Google Scholar 

  • Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field fe implementations. Int J Numer Methods Eng 83:1273–1311

    Article  Google Scholar 

  • Miehe C, Hofacker M, Schänzel LM, Aldakheel F (2015) Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic-plastic solids. Comput Methods Appl Mech Eng 294:486–522

    Article  Google Scholar 

  • Moes N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Methods Eng 46:131–150

    Article  Google Scholar 

  • Moes N, Stolz C, Chevaugeon N, Bernard PE (2010) A level set based model for damage growth: the thick level set approach. Int J Numer Methods Eng 86:358–380

    Article  Google Scholar 

  • Mori T, Tanaka K (1973) Averages stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall 21:571–574

    Article  Google Scholar 

  • Murakami S (2012) Continuum damage mechanics: a continuum mechanics approach to the analysis of damage and fracture, vol 185. Springer Science & Business Media, Heidelberg

    Google Scholar 

  • Oliver J (1996) Modelling strong discontinuities in solid mechanics via strain softening constitutive equations, part 1: fundamentales. Int J Numer Methods Eng 39:3575–3600

    Article  Google Scholar 

  • Robinet JC, Sardini P, Coelho D, Parneix JC, Pret D, Sammartino S, Boller E, Altmann S (2012) Effects of mineral distribution at mesoscopic scale on solute diffusion in a clay-rich rock: example of the Callovo-Oxfordian mudstone (Bure, France). Water Resour Res 48:W05554

    Article  Google Scholar 

  • Seyedi D et al (2021) Upscaling THM modelling from small-scale to full-scale in-situ experiment in the Callovo-Oxfordian claystone. Int J Rock Mech Min Sci 144:1365–1609

    Article  Google Scholar 

  • Seyedi D, Armand G, Conil N, Vitel M, Vu MN (2017) On the thermo-hydro-mechanical pressurization in Callovo-Oxfordian claystone under thermal loading. Poromechanics VI 2017:754–761

    Article  Google Scholar 

  • Seyedi DM, Armand G, Noiret A (2017) transverse action-a model benchmark exercise for numerical analysis of the Callovo-Oxfordian claystone hydromechanical response to excavation operations. Comput Geotech 85:287–305

    Article  Google Scholar 

  • Tsang CF, Stephansson O, Jing L, Kautsky F (2009) Decovalex project: from 1992 to 2007. Environ Geol 57:1221–1237

    Article  Google Scholar 

  • Ulloa J, Wambacq J, Alessi R, Samaniego E, Degrande G, François S (2022) A micromechanics-based variational phase-field model for fracture in geomaterials with brittle-tensile and compressive-ductile behavior. J Mech Phys Solids 159:104684

    Article  Google Scholar 

  • Wong Tf, Baud P (2012) The brittle-ductile transition in porous rock: a review. J Struct Geol 44:25–53

    Article  Google Scholar 

  • Wu JY (2017) A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J Mech Phys Solids 103:72–99

    Article  Google Scholar 

  • Wu JY, Nguyen VP, Thanh Nguyen C, Sutula D, Bordas S, Sinaie S (2019) Phase field modelling of fracture. Adv Appl Mech 53:1–183

    Google Scholar 

  • You T, Waisman H, Zhu QZ (2021) Brittle-ductile failure transition in geomaterials modeled by a modified phase-field method with a varying damage-driving energy coefficient. Int J Plast 136:102836

    Article  Google Scholar 

  • Yu Z, Shao J, Duveau G, Vu MN, Armand G (2021) Numerical modeling of deformation and damage around underground excavation by phase-field method with hydromechanical coupling. Comput Geotech 138:104369

    Article  Google Scholar 

  • Yu Z, Shao JF, Vu MN, Armand G (2021) Numerical study of thermo-hydro-mechanical responses of in situ heating test with phase-field model. Int J Rock Mech Min Sci 138:104542

    Article  Google Scholar 

  • Yu Z, Shao J, Sun Y, Wang M, ngoc Vu M, Plua C (2023) Numerical analysis of hydro-thermal fracturing in saturated rocks by considering material anisotropy and micro-structural heterogeneity. Int J Rock Mech Min Sci 170:105457

    Article  Google Scholar 

  • Yu Z, Sun Y, Vu MN, Shao JF (2023) Modeling of mixed cracks in rock-like brittle materials under compressive stresses by a double-phase-field method. Rock Mech Rock Eng 56:2779–2792

    Article  Google Scholar 

  • Zhang X, Sloan SW, Vignes C, Sheng D (2017) A modification of the phase-field model for mixed mode crack propagation in rock-like materials. Comput Methods Appl Mech Eng 322:123–136

    Article  Google Scholar 

  • Zhao JJ, Shen WQ, Shao JF, anc Liu ZB, Vu MN (2022) A constitutive model for anisotropic clay-rich rocks considering micro-structural composition. Int J Rock Mech Min Sci 151:105029

    Article  Google Scholar 

Download references

Acknowledgements

This work is jointly supported by the French National Agency for radioactive waste management (ANDRA), the DECOVALEX project, the National Natural Science Foundation of China (No. 12202099) and the China Postdoctoral Science Foundation funded project (No. 2023M730525). DECOVALEX is an international research project comprising participants from industry, government and academia, focusing on development of understanding, models and codes in complex coupled problems in sub-surface geological and engineering applications. The authors appreciate and thank the DECOVALEX-2023 Funding Organizations for their financial and technical support of the work described in this paper. The statements made in the paper are, however, solely those of the authors and do not necessarily reflect those of the Funding Organizations.

Author information

Authors and Affiliations

  1. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, College of Resources and Civil Engineering, Northeastern University, Shenyang, 110819, China

    Zhan Yu

  2. University of Lille, CNRS, EC Lille, LaMcube, UMR9013, 59000, Lille, France

    Zhan Yu, Jianfu Shao & Yue Sun

  3. Institut Universitaire de France (IUF), Paris, France

    Jianfu Shao

  4. Andra, Chatenay Malabry, France

    Minh-ngoc Vu, Carlos Plua & Gilles Armand

Authors
  1. Zhan Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianfu Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yue Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Minh-ngoc Vu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Carlos Plua
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Gilles Armand
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianfu Shao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Positions of Sensors and Dates of the Heater Boreholes Drilling

Appendix: Positions of Sensors and Dates of the Heater Boreholes Drilling

In order to identify the coordinates of the sensor points, the origin (0,0,0) of the model domain is located at the mid-distance between the heads of borehole CRQ1720 and CRQ1721 (See Tables 5 and 6). In this way, the studied 3D domain of cube with a side length of 50 m vary between x=\(-\) 2.6 m to 47.4 m (parallel to the heater boreholes); y=\(-\) 25.0 m to 25.0 m (parallel to the GCS gallery) and z = – 25 m to 25 m (perpendicular to the heater boreholes and the GCS gallery). In this defined coordinate system, the position of sensor points are shown as follows:

Table 5 The position of sensor points used in simulation of CRQ test
Full size table

The detail date of the main operations during CRQ test is:

  • The drift of GCS gallery: \(15{th}\) September 2010

  • The drift of heater boreholes: between \(20{th}\) and \(30^{30}\) October 2017 (see Table)

  • The first heating phase: between \(3{rd}\) June and \(31{st}\) July 2019

  • The second heating phase: between \(13{th}\) January and \(14{th}\) February 2020

Table 6 Dates of the heater boreholes drilling for CRQ test
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, Z., Shao, J., Sun, Y. et al. Three-dimensional Modeling of Cracking with Thermo-hydromechanical Process by Considering Rock Heterogeneity. Rock Mech Rock Eng (2023). https://doi.org/10.1007/s00603-023-03536-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00603-023-03536-4

Keywords

Search

Navigation