DPWSS: differentially private working set selection for training support vector machines

Support vector machines

The SVM is an efficient classification method in machine learning that originates from structural risk minimization (Vapnik & Vapnik, 1998). It finds an optimal separating hyperplane with the maximal margin to train a classification model. Given training instances x_i $\in$ Rⁿ and labels y_i $\in${1,−1}, the main task for training a SVM is to solve the QP optimization problem as follows (Fan, Chen & Lin, 2005):

(1) $$\begin{array}{c}\underset{\alpha }{min}f(\alpha )={\displaystyle \frac{1}{2}{\alpha }^{T}Q\alpha -e^T\alpha }\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}0\le {\alpha }_i\le C,i=1,\dots ,l\\ y^T\alpha =0\end{array}$$where Q is a symmetric matrix with Q_ij = y_iy_jK(x_i,x_j), and K is the kernel function, e is a vector with all 1’s, C is the upper bound of vector α.

Working set selection

Generally, the QP problem is hard to solve in the training process of the SVMs. When the optimization methods handle the large matrix Q, the whole vector α will be updated repeatedly in the iterative process. Nevertheless, the decomposition methods only update a subset of vector α in every iteration to solve the challenge and change from one iteration to another. The subset is called the working set. The method for determining the working set is called WSS, which originally derives from the optimality conditions of Karush-Kuhn-Tucker (KKT). Furthermore, SMO-type decomposition methods restrict the working set to only two elements (Platt, 1999). A pair of elements that violate the KKT optimality conditions are called “violating pair” (Keerthi, Shevade & Bhattacharyya, 2001).

Definition 1 (Violating pair (Keerthi, Shevade & Bhattacharyya, 2001; Fan, Chen & Lin, 2005)). Under the following restrictions:

(2) $$I_{up}(\alpha )\equiv \left\{t\right|\alpha t<C,yt=1or\alpha t>0,yt=-1\},$$

(3) $$I_{low}(\alpha )\equiv \left\{t\right|\alpha t<C,yt=-1or\alpha t>0,yt=1\}.$$

For the k^th iteration, if $i\in Iup({\alpha }^k)$, $j\in Ilow({\alpha }^k)$, and $-yi\mathrm{\nabla }f({\alpha }^k)i>-yj\mathrm{\nabla }f({\alpha }^k)j$, then {i, j} is a “violating pair”.

Violating pairs are important in WSS. If working set B is a violating pair, the function value in SMO-type decomposition methods strictly decreases (Hush & Scovel, 2003). Under the definition of violating pair, a natural choice of the working set B is the “maximal violating pair”, which most violates the KKT optimality condition.

WSS 1 (WSS via the “maximal violating pair” (Keerthi, Shevade & Bhattacharyya, 2001; Fan, Chen & Lin, 2005; Chen, Fan & Lin, 2006)). Under the same restrictions (2) and (3) in Definition 1,

1. Select

   (4) $$i\in \arg \underset{t}{max}\{-yt\mathrm{\nabla }f({\alpha }^k)t|t\in Iup({\alpha }^k)\},$$

   (5) $$j\in \arg \underset{t}{min}\{-yt\mathrm{\nabla }f({\alpha }^k)t|t\in Ilow({\alpha }^k)\},$$or (6) $$j\in \arg \underset{t}{max}\{yt\mathrm{\nabla }f({\alpha }^k)t|t\in Ilow({\alpha }^k)\}.$$

2. Return B = {i, j}.

Keerthi, Shevade & Bhattacharyya (2001) first proposed the maximal violating pair, which has become a popular way in WSS. Fan, Chen & Lin (2005) pointed out that it was concerned with the first order approximation of f(α) in (1) and gave a detailed explanation. Meanwhile, they proposed a new WSS algorithm by using more accurate second order information.

WSS 2 (WSS using second order information (Fan, Chen & Lin, 2005; Chen, Fan & Lin, 2006)).

1. Define a_it and b_it,

(7) $$a_{it}\equiv K_{ii}+K_{tt}-2K_{it},$$

(8) $$b_{it}\equiv -y_i\mathrm{\nabla }f({\alpha }^k)i+yt\mathrm{\nabla }f({\alpha }^k)t>0,$$

(9) $${\overline{a}}_{it}\equiv \{\begin{array}{cc}{a}_{it}& if{a}_{it}>0,\\ \tau & otherwise.\end{array}$$

2. Select

(10) $$i\in \arg \underset{t}{max}\{-y_t\mathrm{\nabla }f({\alpha }^k{)}_t|t\in I_{up}({\alpha }^k)\},$$

(11) $$j\in \arg \underset{t}{min}\{-{\displaystyle \frac{b_{it}^2}{{\overline{a}}_{it}}}|t\in I_{low}({\alpha }^k),-y_t\mathrm{\nabla }f({\alpha }^k)t<-y_i\mathrm{\nabla }f({\alpha }^k{)}_i\}.$$

3. Return B = {i, j}.

WSS 2 uses second order information and checks only O(l) possible working sets to select j through using the same i as in WSS 1. The WSS 2 algorithm achieves faster convergence than existing selection methods using first order information. It has been used in the software LIBSVM (Chang & Lin, 2007) (since version 2.8) and is valid for all symmetric kernel matrices K, including the non-positive definite kernel.

Lin (2001, 2002) pointed out the maximal violating pair was important to SMO-type methods. When the working set B is the maximal violating pair, SMO-type methods converge to a stationary point. Otherwise, it is uncertain whether the convergence will be established. Chen, Fan & Lin (2006) proposed a general WSS method via the “constant-factor violating pair”. Under a fixed constant-factor σ specified by the user, the selected violating pair is linked to the maximal violating pair. The “constant-factor violating pair” is considered to be a “sufficiently violated” pair. And they prove the convergence of the WSS method.

WSS 3 (WSS via the “constant-factor violating pair” (Fan, Chen & Lin, 2005; Chen, Fan & Lin, 2006)).

1. Given a fixed 0 < σ ≤ 1 in all iterations.

2. Compute

(12) $$m({\alpha }^k)=\underset{t}{max}\{-y_t\mathrm{\nabla }f({\alpha }^k{)}_t|t\in I_{up}({\alpha }^k)\},$$

(13) $$M({\alpha }^k)=\underset{t}{min}\{-y_t\mathrm{\nabla }f({\alpha }^k{)}_t|t\in I_{low}({\alpha }^k)\}.$$

3. Select i, j satisfying

(14) $$i\in I_{up}({\alpha }^k),j\in I_{low}({\alpha }^k),$$

(15) $$-yi\mathrm{\nabla }f({\alpha }^k{)}_i+y_j\mathrm{\nabla }f({\alpha }^k{)}_j\ge \sigma (m({\alpha }^k)-M({\alpha }^k))>0.$$

4. Return B = {i, j}.

Clearly (15) guarantees the quality of the working set B if it is related to the maximal violating pair. Fan, Chen & Lin (2005) explained that WSS 2 was a special case of WSS 3 under the special value of σ.

Furthermore, Zhao et al. (2007) employed algorithm WSS 2 to test the datasets by LIBSVM. They find two interesting phenomena. One is that some α are not updated in the entire training process. Another is that some α are updated again and again. Therefore, they propose a new method WSS-WR and a certain α are selected only once to improve the efficiency of WSS, especially the reduction of the training time.

Differential privacy

Recently, with the advent of the digital age, huge amounts of personal information have been collected by web services and mobile devices. Although data sharing and mining large-scale personal information can help improve the functionality of these services, it also raises privacy concerns for data contributors. DP provides a mathematically rigorous definition of privacy and has become a new accepted standard for private data analysis. It ensures that any possible outcome of an analysis is almost equal regardless of an individual’s presence or absence in the dataset, and the output difference is controlled by a relatively small privacy budget. The smaller the budget, the higher the privacy. Therefore, the adversary cannot distinguish whether an individual’s in the dataset (Liu, Li & Li, 2017). Furthermore, DP is compatible with various kinds of data sources, data mining algorithms, and data release models.

In dataset D, each row corresponds to one individual, and each column represents an attribute value. If two datasets D and D’ only differ on one element, they are defined as neighboring datasets. DP aims to mask the different results of the query function f in neighboring datasets. The maximal difference of the query results is defined as the sensitivity Δf. DP is generally achieved by a randomized mechanism $M:D\to R^d$, which returns a random vector from a probability distribution. A mechanism M satisfies DP if the effect of the outcome probability by adding or removing a single element is controlled within a small multiplicative factor (Lee, 2014). The formal definition is given as follows.

Definition 2 (ε-differential privacy (Dwork, 2006)). A randomized mechanism M gives ε-DP if for all datasets D and D’ differing on at most one element, and for all subsets of possible outcomes S $\subseteq$ Range (M),

(16) $$Pr[M(D)\in S]\le \exp (\epsilon )\times Pr[M(D^{\prime })\in S].$$

Sensitivity is a vital concept in DP that represents the largest effect of the query function output made by a single element. Meanwhile, sensitivity determines the requirements of how much perturbation by a particular query function (Zhu et al., 2017).

Definition 3 (Sensitivity (Dwork, 2006)). For a given query function $f:D\to R^d$, and neighboring datasets D and D’, the sensitivity of f is defined as

(17) $$\mathrm{\Delta }f=\underset{D,D^{\prime }}{max}{\Vert f(D)-f(D^{\prime })\Vert }_1.$$

The sensitivity $\mathrm{\Delta }f$ depends only on the query function f, and not on the instances in datasets.

Any mechanism that meets Definition 2 is considered as satisfying DP (Lee, 2014). Currently, two principal mechanisms have been used for realizing DP: the Laplace mechanism (Dwork et al., 2006) and the exponential mechanism (McSherry & Talwar, 2007).

Definition 4 (Laplace mechanism (Dwork et al., 2006)). For a numeric function $f:D\to R^d$ on a dataset D, the mechanism M in Eq. (18) provides ε-DP.

(18) $$M(D)=f(D)+Lap{\left(\frac{\mathrm{\Delta }f}{\epsilon }\right)}^d.$$

The Laplace mechanism gets the real results from the numerical query and then perturbs it by adding independent random noise. Let Lap(b) represent the random noise sampled from a Laplace distribution according to sensitivity. The Laplace mechanism is usually used for numerical data, while for the non-numerical queries, DP uses the exponential mechanism to randomize results.

Definition 5 (Exponential mechanism (McSherry & Talwar, 2007)). Let $q(D,r)$ be a scoring function on a dataset D that measures the quality of output $r\in R$, $\mathrm{\Delta }q$ represents the sensitivity. The mechanism M satisfies ε-DP if

(19) $$M(D)=\left(returnr\propto \exp \left({\displaystyle \frac{\epsilon q(D,r)}{2\mathrm{\Delta }q}}\right)\right).$$

The exponential mechanism is useful to select a discrete output in a differentially private manner, which employs a scoring function q to evaluate the quality of an output r with a nonzero probability.

An improved WSS method

In the process of training SVMs, WSS is an important step in SMO-type decomposition methods. Meanwhile, the special properties of the selection process in WSS are perfectly combined with the exponential mechanism of DP. WSS 3 algorithm is a more general algorithm to select a working set by checking nearly $O(l^2)$ possible B’s to decide j, although under the restricted condition of parameter σ. By using the same $i\in \arg m(a^k)$ as in WSS 2, which checks only $O(l)$ possible B’s, we propose WSS 4 to select a working set based on WSS 3 as below. To make the algorithm easy to understand, we replace $M(a^k)$ with $M^{\prime }(a^k)$.

WSS 4 (An improved WSS via the “constant-factor violating pair”)

1. Given a fixed 0 < σ ≤ 1 in all iterations.

2. Compute

(20) $$m({\alpha }^k)=\underset{t}{max}\{-y_t\mathrm{\nabla }f({\alpha }^k{)}_t|t\in I_{up}({\alpha }^k)\},$$

(21) $$M^{\prime }({\alpha }^k)=\underset{t}{max}\{y_t\mathrm{\nabla }f({\alpha }^k{)}_t|t\in I_{low}({\alpha }^k)\}.$$

3. Select i, j satisfying

(22) $$i\in \arg m({\alpha }^k),j\in I_{low}({\alpha }^k),$$

(23) $$m({\alpha }^k)+y_j\mathrm{\nabla }f({\alpha }^k{)}_j\ge \sigma (m({\alpha }^k)+M\mathrm{\prime }({\alpha }^k))>0.$$

4. Return B = {i, j}.

The scoring function and sensitivity in the exponential mechanism

In the exponential mechanism, the scoring function is an important guarantee for achieving DP. The rationality of scoring function design is directly related to the execution efficiency of mechanism M. For one output r, the greater the value of the scoring function, the greater the probability that r will be selected. Based on the definition of the “maximal violating pair”, it is obvious that

(24) $$m({\alpha }^k)+M^{\prime }({\alpha }^k)\ge m({\alpha }^k)+y_j\mathrm{\nabla }f({\alpha }^k{)}_j.$$

From Eqs. (23) and (24), we conclude that

(25) $$m({\alpha }^k)+M\mathrm{\prime }({\alpha }^k)\ge m({\alpha }^k)+y_j\mathrm{\nabla }f({\alpha }^k{)}_j\ge \sigma (m({\alpha }^k)+M^{\prime }({\alpha }^k))>0.$$

We design a simple scoring function q(D, r) for the DPWSS algorithm based on WSS 4 and Eq. (25) as follows

(26) $$1\ge q(D,r)={\displaystyle \frac{m({\alpha }^k)+y_j\mathrm{\nabla }f({\alpha }^k{)}_j}{m({\alpha }^k)+M^{\prime }({\alpha }^k)}\ge \sigma ,}$$where r denotes the working set B, which contains violating pair i and j. The larger the value of scoring function q(D, r), the closer the selected violation pair is to the maximal violation pair. The sensitivity of scoring function q(D, r) is

(27) $$\mathrm{\Delta }q=1-\sigma ,$$and the value of $\mathrm{\Delta }q$ is a small number, less than 1.

In the exponential mechanism, the output r is selected randomly with probability

(28) $$\mathrm{P}\mathrm{r}(r)=\exp \left(\frac{\epsilon q(D,r)}{2\mathrm{\Delta }q}\right)/\sum _{r\mathrm{\prime }\in R}\exp \left(\frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}\right).$$

Privacy budget

Privacy budget is a vital parameter in DP, which controls the privacy level in a randomized mechanism M. The smaller the privacy budget, the higher the privacy level. When the allocated privacy budget runs out, mechanism M will lose privacy protection, especially for the iteration process. To improve the utilization of the privacy budget, every pair of working sets is selected only once during the entire training process as in Zhao et al. (2007). Meanwhile, in DPWSS every iteration is based on the result of the last iteration, but not based on the entire original dataset. Therefore, there is no need to split the privacy budget for every iteration.

Description of DPWSS algorithm

In the DPWSS algorithm, DP is achieved by privately selecting the working set with the exponential mechanism in every iteration. We first present an overview of the DPWSS algorithm and then elaborate on the key steps. Finally, we describe an SMO-type decomposition method using the DPWSS algorithm in detail.

The description of the DPWSS Algorithm 1 is shown below.

The DPWSS algorithm selects multiple violating pairs that meet the constraints based on WSS 4, and then randomly selects one with a certain probability by the exponential mechanism to satisfy DP. Firstly, the DPWSS algorithm computes m(α) and M’(α) for the scoring function q from Line 1 to Line 4 and determines i as one element of the violating pair. Secondly, it computes the scoring function q from Line 5 to Line 12. The constraints in Line 6 represent that the violating pair {i, j} has not been previously selected, meanwhile the value range of the other element j and the violating pair are valid for the changes of gradient G. The constraints in Line 8 represent that the scoring function value is effective under constant-factor σ. Line 14 and Line 15 are key steps in the exponential mechanism, which randomly select a violating pair with the chosen probability of the scoring function q. Lastly, the DPWSS algorithm outputs the violating pair {i, j} as the working set B in Line 15. The time and memory complexity of DPWSS algorithm is O(l).

In summary, a SMO method using the DPWSS algorithm is shown below.

Algorithm 2 is an iterative process, which first selects working set B by DPWSS, then updates dual vector α and gradient G in every iteration. After the iterative process, the algorithm outputs the final α. There are three ways to get out of the iterative process. One is that α is a stationary point, another is that all violating pairs have been selected, and the last one is that the number of iterations exceeds the maximum value. Using Algorithm 2, we privately release the classification model of SVMs with dual vector α while satisfying the requirement of DP.

Privacy analysis

In the DPWSS algorithm, randomness is introduced by randomly selecting working sets with the exponential mechanism. By using the exponential mechanism, a violating pair is selected randomly with a certain probability. The greater the probability, the closer the selected violating pair is to the maximal violating pair. For every iteration, the violating pair in the outputs of the DPWSS algorithm is uncertain. The uncertainty masks the impact of individual record change on the algorithm results, thus protecting the data privacy.

According to the definition of DP mentioned in Section 3, we proved that the DPWSS algorithm satisfies DP strictly by theorem 1 as shown below.

Theorem 1 DPWSS algorithm satisfies DP.

Proof Let M(D, q) be to select the output r of the violating pair in one iteration, and ε be the allocated privacy budget in the DPWSS algorithm. Based on Eq. (28), we randomly select violating pair r as a working set with the following probability by the exponential mechanism. To accord with the standard form of the exponential mechanism, we use q to denote q’ in the DPWSS algorithm.

${\displaystyle \frac{Pr(M(D,q)=r)}{Pr(M(D\mathrm{\prime },q)=r)}={\displaystyle \frac{\exp \left({\displaystyle \frac{\epsilon q(D,r)}{2\mathrm{\Delta }q}}\right)/\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}{\exp \left({\displaystyle \frac{\epsilon q(D\mathrm{\prime },r)}{2\mathrm{\Delta }q}}\right)/\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D\mathrm{\prime },r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}}}$

$=\exp \left({\displaystyle \frac{\epsilon (q(D,r)-q(D\mathrm{\prime },r))}{2\mathrm{\Delta }q}}\right)\times {\displaystyle \frac{\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D\mathrm{\prime },r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}{\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}}$

$\le \exp \left({\displaystyle \frac{\epsilon }{2}}\right)\times {\displaystyle \frac{\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon }{2}}\right)\exp \left({\displaystyle \frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}{\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}}$

$$=\exp \left({\displaystyle \frac{\epsilon }{2}}\right)\times \exp \left({\displaystyle \frac{\epsilon }{2}}\right)\times {\displaystyle \frac{\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}{\sum _{r\mathrm{\prime }\in O}\exp \left({\displaystyle \frac{\epsilon q(D,r\mathrm{\prime })}{2\mathrm{\Delta }q}}\right)}=\exp (\epsilon )}$$

According to Definition 2, we prove that

$$Pr(M(D,q)=r)\le \exp (\epsilon )\times Pr(M(D\mathrm{\prime },q)=r).$$

Therefore, the DPWSS algorithm satisfies DP.

Algorithm 2 is an iterative process, in which DPWSS is a vital step to privately select a working set. As the DPWSS algorithm satisfies DP, we perform the steps of updating dual vector α and gradient G in every iteration without accessing private data. To improve the utilization of the privacy budget, every pair of working sets is selected only once during the entire training process. Meanwhile, in Algorithm 2 every iteration is based on the result of the last iteration, but not based on the original datasets. Therefore, Algorithm 2 satisfies DP.

Datasets and experimental environment

The datasets are partly selected for the experiments as Zhang, Hao & Wang (2019), Fan, Chen & Lin (2005) and Zhao et al. (2007). All datasets are for binary classification, and available at http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/. The basic information of the datasets includes dataset size, value range, number of features, and imbalance ratio, which is shown in Table 2 below. To make the figures look neater in the experiments, we use breast to denote the breast-cancer dataset and German to denote the german.number dataset.

To carry out the contrast experiments efficiently, we use LIBSVM (version 3.24) as an implementation of the DPWSS algorithm in C++ language and GNU Octave (version 5.2). All parameters are set to default values.

An example of a private classification model

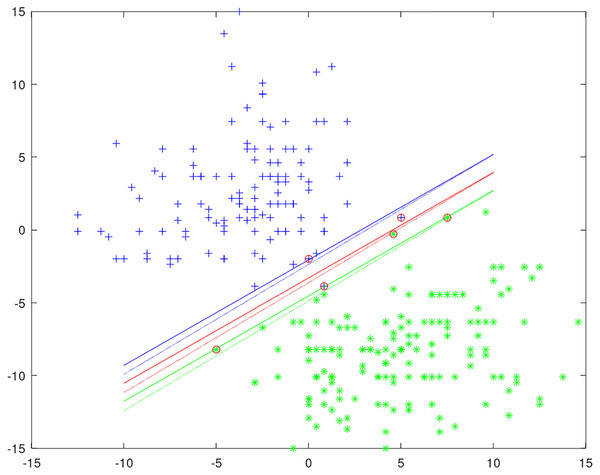
Unlike other privacy SVMs, which introduce randomness into the objective function or classification result by the Laplace mechanism, in our method the randomness is introduced into the training process of SVM. It is achieved by privately selecting the working set with the exponential mechanism in every iteration. We give an example of a private classification model to show how privacy is protected in Fig. 1. The data uses two columns of the heart dataset and moves the positive and negative instances to each end for easier classification. The solid lines represent the original non-private classification model and circles represent support vectors. The dotted lines represent a private classification model by training SVM with the DPWSS algorithm. It is observed that the differences between the private and non-private classification models are very small, and achieves similar accuracy of classification. All the classification models generated are different from each other to protect the training data privacy.

Algorithm performance experiments

In this section, we evaluated the performance of the DPWSS algorithm vs WSS 2 by experiments for the entire training process. The metrics of performance include classification capability, algorithm stability, and execution efficiency under different constant-factor σ and privacy budget ε.

The classification capability is measured by AUC, Accuracy, Precision, Recall, F1, and Mcc.

(29) $$AUC={\displaystyle \frac{{\sum }_{i\in positiveClass}ran{k}_i-{\displaystyle \frac{M(1+M)}{2}}}{M\times N}}$$

The rank_i denotes the serial number of instance i after sorting by the probability, M is the number of positive instances and N is the number of negative instances. The higher the AUC, the better the usability of the algorithm. Other metrics are calculated as shown below, and they are all based on confusion matrix.

(30) $$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(31) $$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(32) $$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(33) $$F1={\displaystyle \frac{2TP}{2TP+FP+FN}}$$

(34) $$Mcc={\displaystyle \frac{TP\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}}$$

The algorithm stability is measured by the error of optimized objective value between DPWSS algorithm and WSS 2, named objError.

(35) $$objError=\left|ob{j}_{DPWSS}-ob{j}_{WSS2}\right|$$

The smaller the objError, the better the stability of the algorithm.

The execution efficiency of the algorithm is measured by the ratio of iteration between the two algorithms, named iterationRatio.

(36) $$iterationRatio={\displaystyle \frac{\mathrm{\#}iterationwithDPWSS}{\mathrm{\#}iterationwithWSS2}}$$

The smaller the iterationRatio, the better the execution efficiency of the algorithm. We do not compare the training time between the two algorithms as it is a millisecond class for the entire training process to most of the datasets.

To evaluate the influence of different constant-factor σ and privacy budget ε to the three metrics for algorithm performance, we set σ at 0.1, 0.3, 0.5 and 0.7 under ε fixed at 1 and set ε at 0.1, 0.5 and 1 under σ fixed at 0.7. We do not set σ at 0.9, because under the circumstances, most of the violating pairs will be filtered out that the algorithm fails to reach the final objective value.

Firstly, we measure the classification capability of the DPWSS algorithm vs WSS 2. The experiments for the DPWSS algorithm were repeated five times under different σ and ε, and the averages of the experimental results are shown in Table 3. Observed from the results, the DPWSS algorithm achieves almost the same classification capability as WSS 2 on all datasets. The maximum error between them is no more than 3%. Due to the repeated execution of the iterative process, the DPWSS algorithm obtains a well private classification model. The classification capability is not affected by the randomness of DP and the filtering effect of parameter σ on violating pairs. The DPWSS algorithm introduces randomness into the training process of SVMs, not into the objective function or classification result. There are no requirements of the differentiability of the objective function and the complex sensitivity analysis, and the less influence of high-dimensional data on noise. Therefore, the DPWSS algorithm achieves the target extremum through the optimization process under the current condition. Meanwhile, the imbalance of dataset has little effect on the classification capability of the DPWSS algorithm.

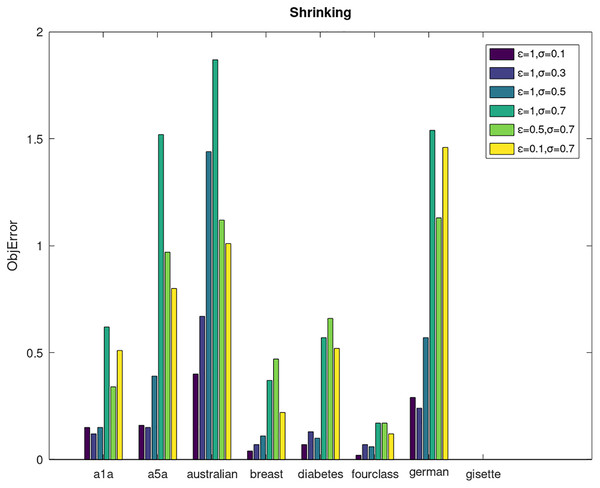
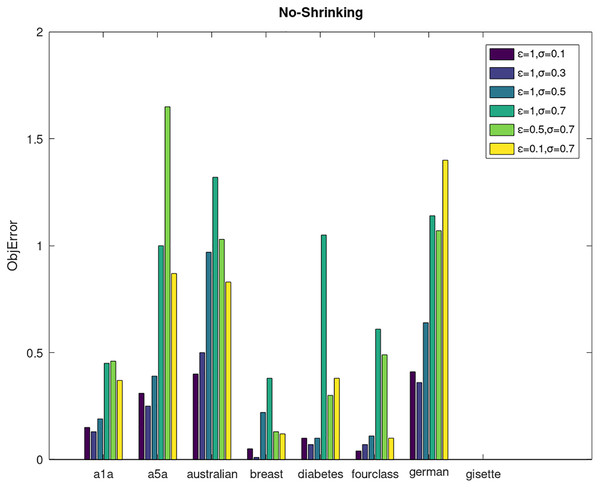
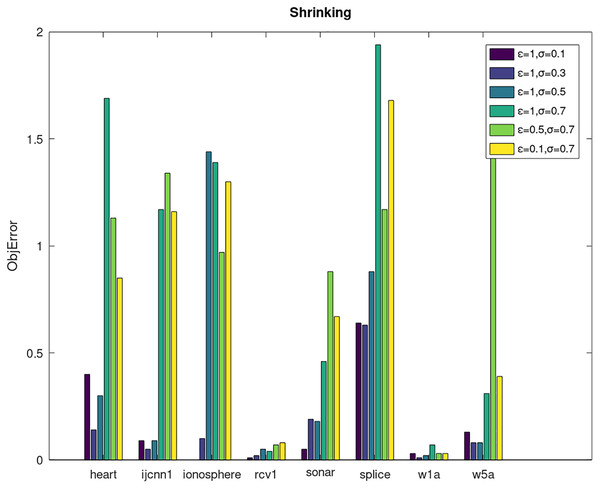
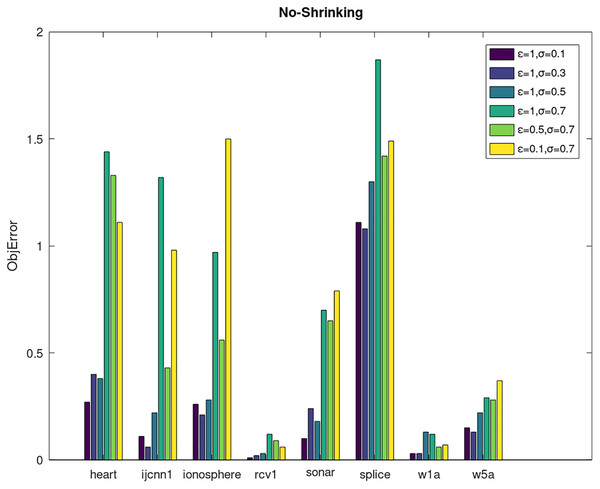
Secondly, we compare the optimized objective values and measure the algorithm stability by objError between the DPWSS algorithm and WSS 2. The experimental results are shown in Figs. 2–5. Observed from the results, the DPWSS algorithm achieves similar optimized objective values with WSS 2 on all datasets under different σ and ε. The errors between the DPWSS algorithm and WSS 2 are very small (nearly within two). Due to the repeated execution of the iterative process, the DPWSS algorithm converges stably to optimized objective values and is not affected by the randomness of DP and the filtering effect of parameter σ on violating pairs. With the increase of σ, the errors also tends to increase.

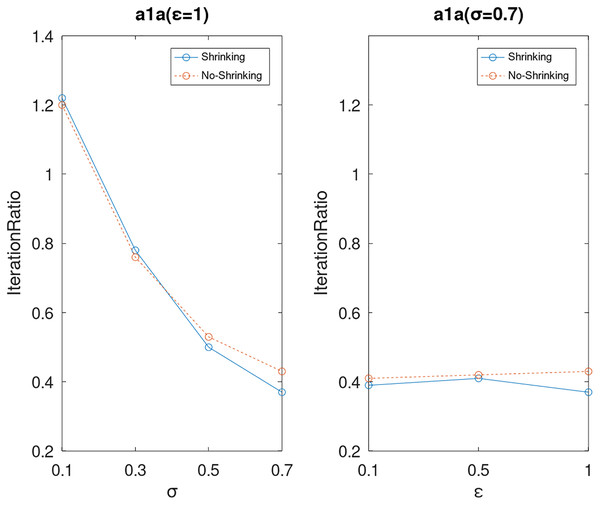
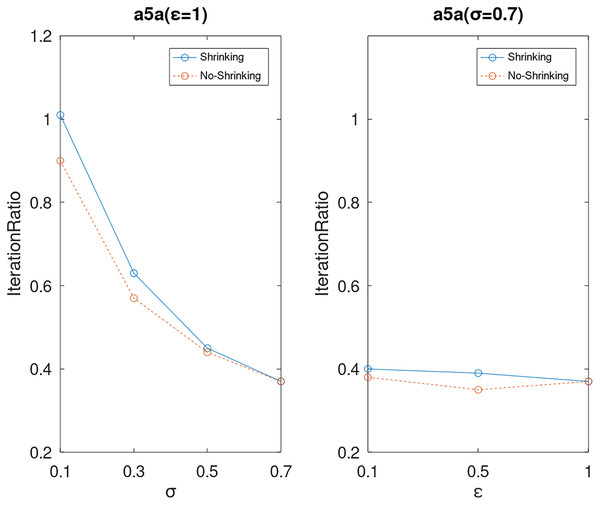
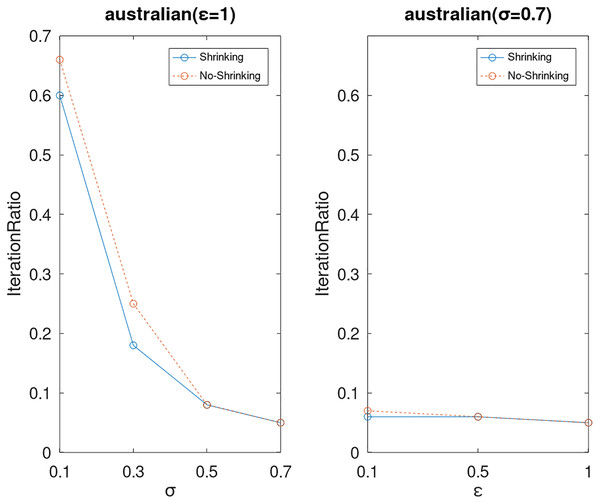
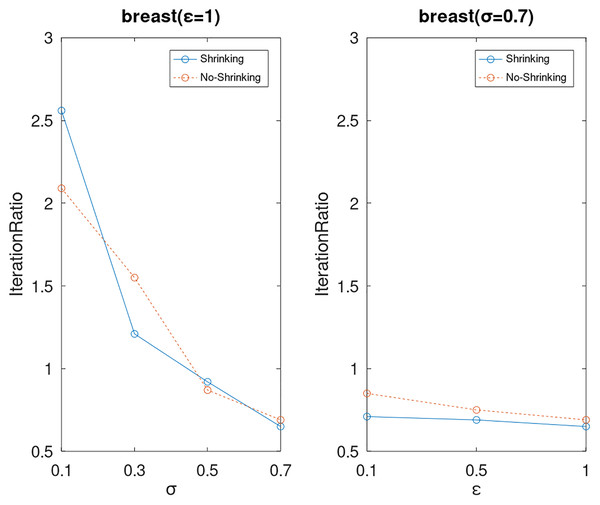
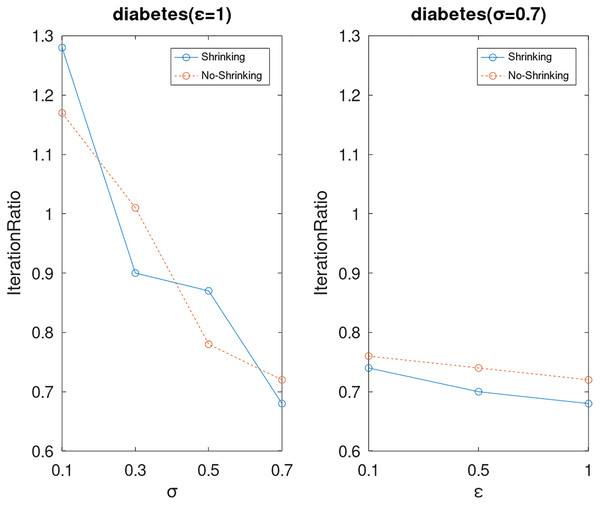
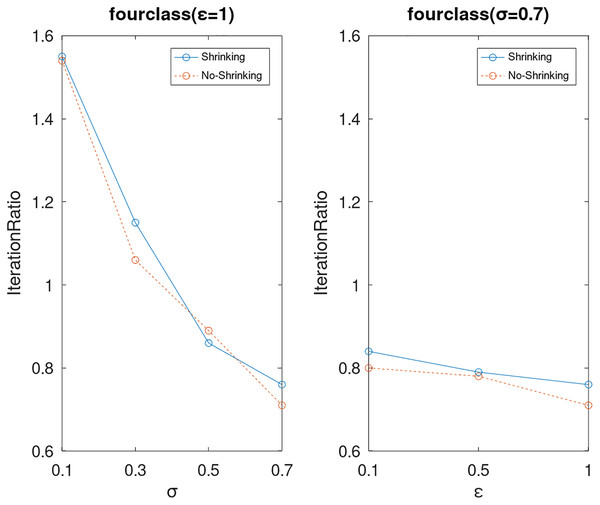
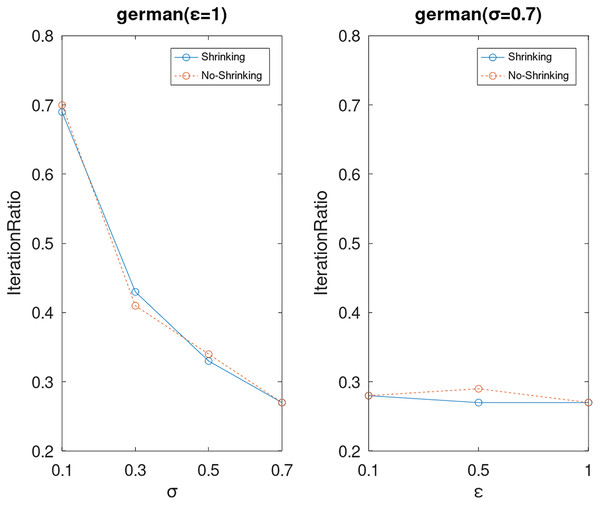
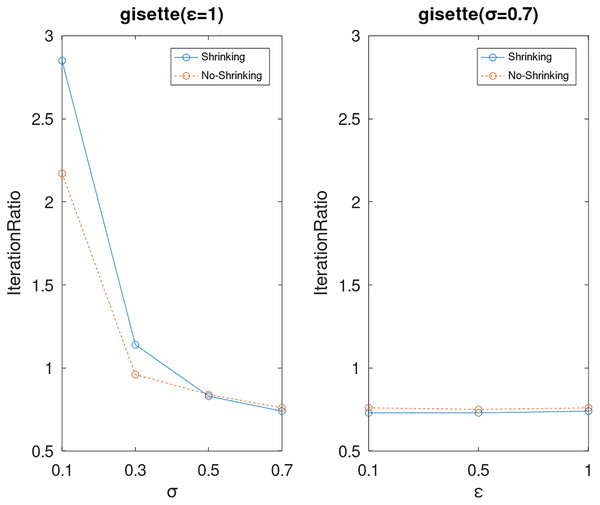
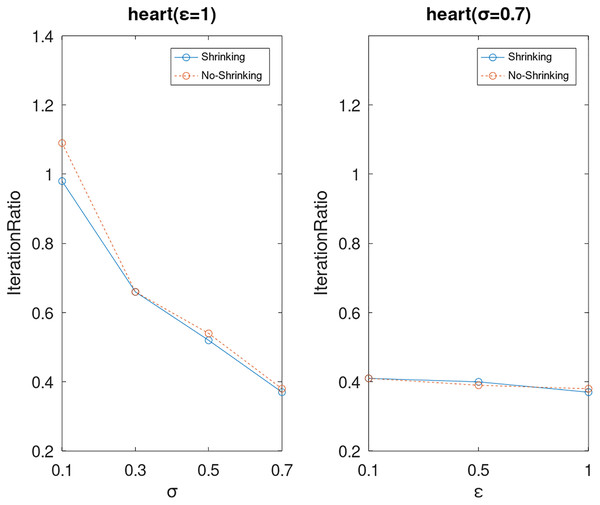
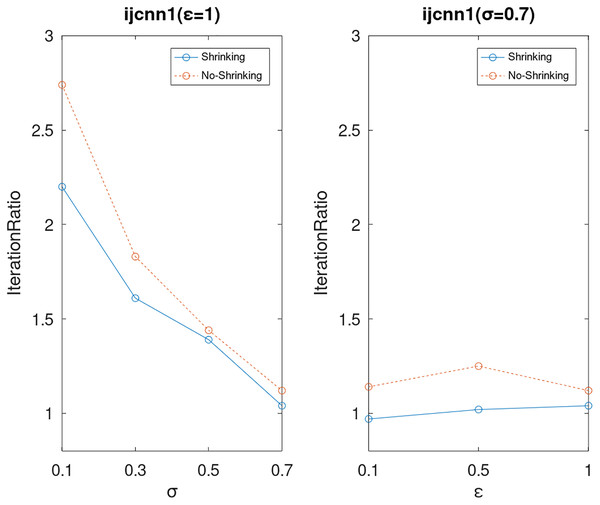
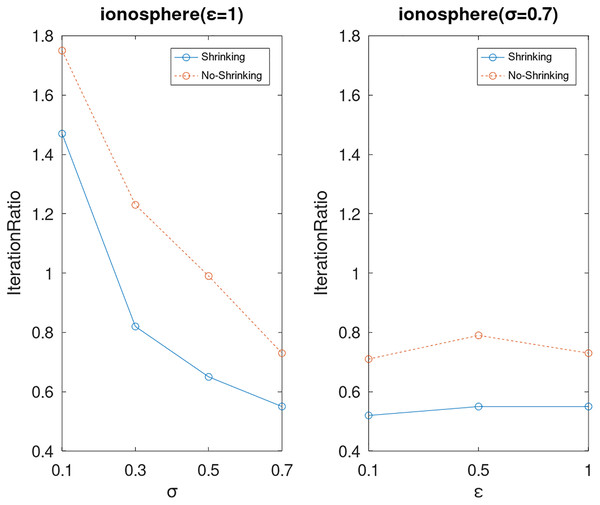
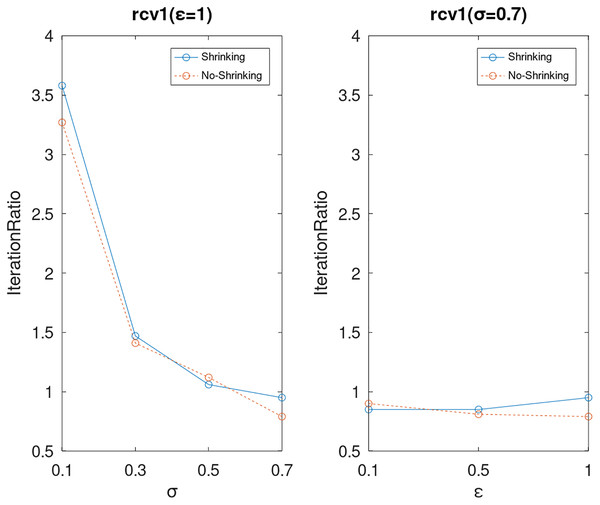
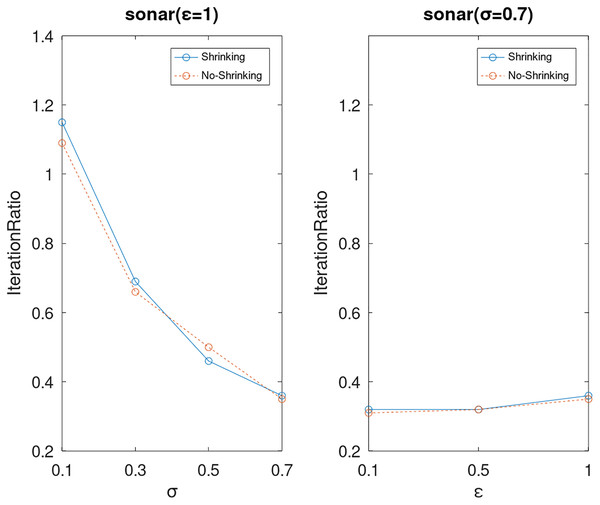
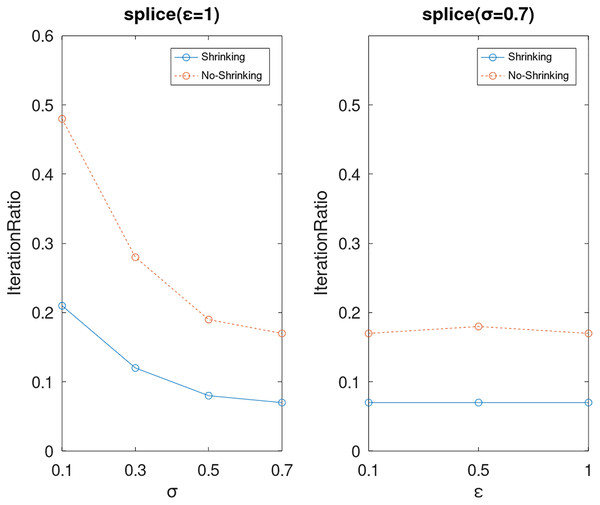
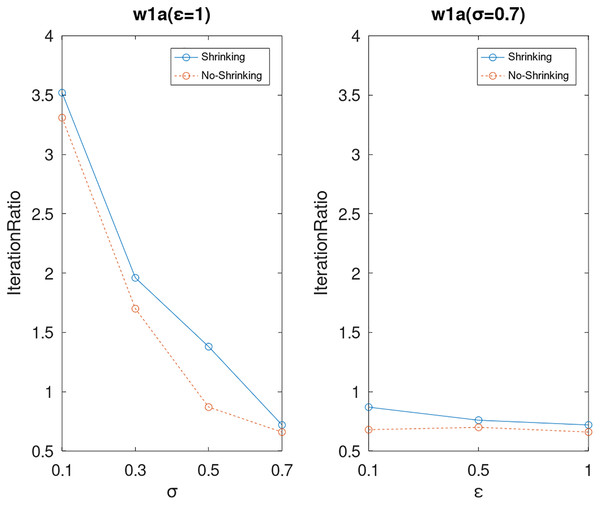
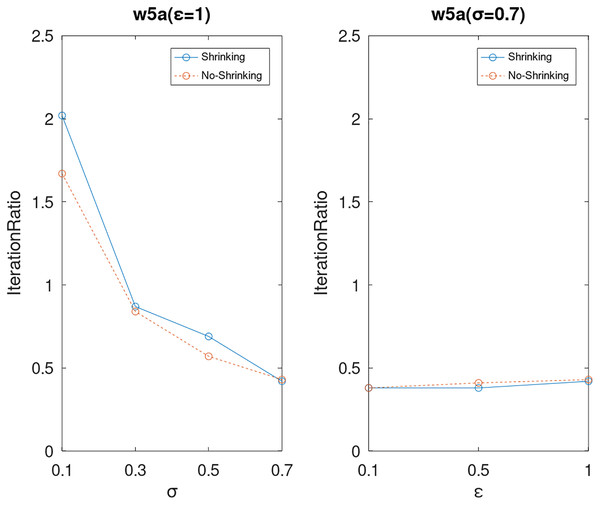
Lastly, we compare the iterations and measure the execution efficiency by iterationRatio between the two algorithms. The experimental results are shown in Figs. 6–21. Observed from the results, the DPWSS algorithm achieves higher execution efficiency with fewer iterations vs WSS 2 on all datasets under different σ and ε. Because the DPWSS algorithm introduces randomness into the WSS process, the iterations will increase more or less. However, with the increase of constant-factor σ, the iterations are affected by the filtering effect of it on violating pairs larger and larger. When σ increases to 0.3, the execution efficiency of the DPWSS algorithm is already higher than WSS 2 for most datasets. When σ increases to 0.7, the iterations of the DPWSS algorithm are far less than WSS2 for all datasets except ijcnn1. Therefore, our method should set larger σ for big datasets. While the privacy budget ε has little effect on iterations under a fixed constant-factor σ.

In the above experiments, we compared the average results of five times running of the DPWSS algorithm with the WSS 2 algorithm. It can be seen from the experimental results that the two algorithms have similar classification capability and optimized objective value under different parameter combinations. Under the same set of parameters, the experimental results of DPWSS algorithm differ little each time, and the main difference lies in the iterations. These slight differences show that the DPWSS algorithm has good usability while satisfying DP. Due to the limitations of the paper, we have not listed each running result in the experiments.