Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-03T05:03:12.324Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum Multiple Construction of Subfactors

Published online by Cambridge University Press:  20 November 2018

Marta Asaeda
Marta Asaeda*
Affiliation:
Department of Mathematics, University of California, Riverside, Riverside, CA 92521, U.S.A.. e-mail: marta@math.ucr.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct the quantum $s$-tuple subfactors for an AFD 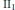$\text{I}{{\text{I}}_{1}}$ subfactor with finite index and depth, for an arbitrary natural number $s$. This is a generalization of the quantum multiple subfactors by Erlijman and Wenzl, which in turn generalized the quantum double construction of a subfactor for the case that the original subfactor gives rise to a braided tensor category. In this paper we give a multiple construction for a subfactor with a weaker condition than braidedness of the bimodule system.

Keywords

46L3781T05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 3 , 01 September 2008 , pp. 321 - 333
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Erlijman, J., New subfactors from braid group representations. Trans. Amer. Math. Soc. 350(1998), no. 1, 185–211.Google Scholar
[2] Erlijman, J., Two-sided braid groups and asymptotic inclusions. Pacific J. Math 193(2000), no. 1, 57–78.Google Scholar
[3] Erlijman, J., Multi-sided braid type subfactors. Canad. J. Math. 53(2001), no. 3, 546–564.Google Scholar
[4] Erlijman, J., Multi-sided braid type subfactors. II. Canadian Mathematical Bulletin, 46(2003), no. 1, 80–94.Google Scholar
[5] Erlijman, J. and Wenzl, H., Subfactors from braided C* tensor categories. To appear in Pacific J. Math. Preprint http://www.math.ucsd.edu/∼wenzl/cat.pdf.Google Scholar
[6] Evans, D. E. and Kawahigashi, Y., Quantum Symmetries on Operator Algebras. Oxford University Press, New York, 1998.Google Scholar
[7] Kawahigashi, Y., Classification of paragroup actions in subfactors. Publ. Res. Inst.Math. Sci. 31(1995), no. 3, 481–517.Google Scholar
[8] Kawahigashi, Y., Longo, R., and Müger, M., Multi-interval subfactors and modularity of representations in conformal field theory. Comm. Math. Phys. 219(2001), no. 3, 631–669.Google Scholar
[9] Lickorish, W. B. R., An Introduction to Knot Theory. Graduate Texts in Mathematics 175, Springer-Verlag, New York, 1997.Google Scholar
[10] Ocneanu, A., Quantized groups, string algebras and Galois theory for algebras. In: Operator Algebras and Applications, Vol. 2. London Math. Soc. Lecture Note Ser. 136, Cambridge University Press, cambridge, 1988, pp. 119–172.Google Scholar
[11] Ocneanu, A., Quantum symmetry, differential geometry of finite graphs and classification of subfactors. University of Tokyo Seminary Notes 45, 1991. (Notes recorded by Kawahigashi, Y..)Google Scholar
[12] Popa, S., Symmetric enveloping algebras, amenability and AFD properties for subfactors. Math. Res. Lett. 1(1994), no. 4, 409–425.Google Scholar
[13] Xu, F., Orbifold construction in subfactors. Comm. Math. Phy. 166(1994), no. 2, 237–254.Google Scholar