Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T08:05:06.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Large Sieve Inequalities via Subharmonic Methods and the Mahler Measure of the Fekete Polynomials

Published online by Cambridge University Press:  20 November 2018

T. Erdélyi  and
D. S. Lubinsky
T. Erdélyi
Affiliation:
Department of Mathematics, Texas A&M University, College Station TX 77843, U.S.A. email: terdelyi@math.tamu.edu
D. S. Lubinsky
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332-0160, U.S.A. email: lubinsky@math.gatech.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate large sieve inequalities such as

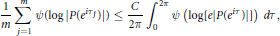$$\frac{1}{m}\underset{j=1}{\overset{m}{\mathop{\sum }}}\,\,\psi \left( \log \,|P({{e}^{i\tau j}})| \right)\,\le \,\frac{C}{2\pi }\,\int_{0}^{2\pi }{\psi }\,\left( \log [e\,|P({{e}^{i\tau }})|] \right)\,d\tau ,$$

where 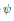$\psi$ is convex and increasing, 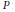$P$ is a polynomial or an exponential of a potential, and the constant 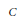$C$ depends on the degree of 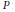$P$, and the distribution of the points 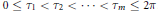$0\,\le \,{{\tau }_{1}}\,<\,{{\tau }_{2}}\,<\,\cdots \,<\,{{\tau }_{m}}\,\le \,2\pi$. The method allows greater generality and is in some ways simpler than earlier ones. We apply our results to estimate the Mahler measure of Fekete polynomials.

Keywords

41A17
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 4 , 01 August 2007 , pp. 730 - 741
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Beller, E. and Newman, D. J., An extremal problem for the geometric mean of polynomials. Proc. Amer. Math. Soc. 39(1973), 313–317.Google Scholar
[2] Borwein, P., Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics 10, Springer-Verlag, New York, 2002.Google Scholar
[3] Borwein, P. and Erdélyi, T., Polynomials and Polynomial Inequalities. Graduate Texts in Mathematics 161, Springer-Verlag, New York, 1995.Google Scholar
[4] Borwein, P. and Erdélyi, T., On the zeros of polynomials with restricted coefficients. Illinois J. Math. 41(1997), no. 4, 667–675.Google Scholar
[5] Boyd, D., On a problem of Byrnes concerning polynomials with restricted coefficients. Math. Comput. 66(1997), no. 220, 1697–1703.Google Scholar
[6] Davis, P. J. and Rabinowitz, P., Methods of Numerical Integration. 2nd edition. Academic Press, Orlando, FL, 1984.Google Scholar
[7] Erdélyi, T., Li, X., and Saff, E. B., Remez- and Nikolskii-type inequalities for logarithmic potentials. SIAM J. Math. Anal. 25(1994), 365–383.Google Scholar
[8] Golinskii, L., Lubinsky, D. S., and Nevai, P., Large sieve estimates on arcs of a circle. J. Number Theory 91(2001), no. 2, 206–229.Google Scholar
[9] Kobindarajah, C. K. and Lubinsky, D. S., Marcinkiewicz-Zygmund inequalities for all arcs of the circle. In: Advances in Constructive Approximation, Nashboro Press, Brentwood, TN, 2004, pp. 255–264.Google Scholar
[10] Littlewood, J. E., The real zeros and value distributions of real trigonometric polynomials. J. London Math. Soc. 41(1966), 336–342.Google Scholar
[11] Lubinsky, D. S., Marcinkiewicz-Zygmund inequalities: methods and results. In: Recent Progress in Inequalities, Math. Appl. 430, Kluwer Academic Publishers, Dordrecht, 1998, pp. 213–240.Google Scholar
[12] Lubinsky, D. S., Mate, A., and Nevai, P., Quadrature sums involving pth powers of polynomials. SIAM J. Math. Anal. 18(1987), no. 2, 531–544.Google Scholar
[13] Mastroianni, G. and Russo, M. G., Weighted Marcinkiewicz inequalities and boundedness of the Lagrange operator. In: Mathematical Analysis and Applications, Hadronic Press, Palm Harbor, FL, 2000, pp. 149–182.Google Scholar
[14] Montgomery, H. L., The analytic principle of the large sieve. Bull. Amer. Math. Soc. 84(1978), no. 4, 547–567.Google Scholar
[15] Ransford, T., Potential Theory in the Complex Plane. London Mathematical Society Student Texts 28, Cambridge University Press, Cambridge, 1995.Google Scholar
[16] Zhong, L. and Zhu, L. Y., The Marcinkiewicz-Zygmund inequality on a smooth simple arc. J. Approx. Theory 83(1995), no. 1, 65–83.Google Scholar