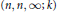Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kamiya, Shigeyasu
2013.
Note on non-discrete complex hyperbolic triangle groups of type $(n,n,\infty;k)$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 89,
Issue. 8,
Sun, Li-Jie
2017.
Notes on complex hyperbolic triangle groups of type (m, n, ∞).
Advances in Geometry,
Vol. 17,
Issue. 2,
p.
191.
Паркер, Джон Р.
and
Сан, Лі-Джі
2017.
Complex hyperbolic triangle groups with 2-fold symmetry.
Proceedings of the International Geometry Center,
Vol. 10,
Issue. 1,
Hattori, Toshiaki
2018.
Shimizu's lemma for classical groups.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 6,
p.
1281.