Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T11:07:39.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On Isomorphisms of Lattices of Closed Subspaces

Published online by Cambridge University Press:  20 November 2018

P. A. Fillmore  and
W. E. Longstaff
P. A. Fillmore
Affiliation:
Dalhousie University, Halifax, Nova Scotia
W. E. Longstaff
Affiliation:
University of Western Australia, Nedlands, Western Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

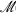By a projectivityof vector spaces Xand Yover fields F and G is meant an isomorphism Ψ:(X) → 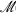(Y) of their lattices of subspaces. A basic theorem of projective geomtry [2, p. 44] asserts that, for spaces of dimension at least 3, any such projectivity is of the form Ψ(M) = SM for a bijection S:X → Y which is semi-linear in the sense that S is an additive mapping for which there exists an isomorphism σ:F→ G such that

S(λx) = σ(λ)Sx for all λ ∈ Fand all x∈ X.

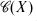In [12] Mackey obtained a continuous version of this result: for real normed linear spaces Xand Y, the lattices and 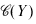of closed subspaces are isomorphic if and only if X and Yare isomorphic (i.e., via a bicontinuous linear bijection).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 5 , 01 October 1984 , pp. 820 - 829
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Arnold, B. H., Rings of operators on vector spaces, Ann. Math. 45 (1944), 24–49.Google Scholar
2. Baer, R., Linear algebra and projective geometry, monographs in Pure and Applied Mathematics Vol. II (Academic Press, New York, 1952).Google Scholar
3. Bandelt, H. -J., Tight residuated mappings and d-extensions, Universal Algebra (Proc. Colloq on Universal Algebra, Esztergom, 1977), Colloq, Math. Soc. J. Bolyai, North-Holland.Google Scholar
4. Eidelheit, M., On isomorphisms of rings of linear operators, Studia Math. 9 (1940), 97–105.Google Scholar
5. Hadwin, D. W., An addendum to Limsups of lats, Indiana Univ. Math. J. 29 (1980), 313–319.Google Scholar
6. Halmos, P. R., Ten problems in Hilbert space, Bull. Amer. Math. Soc. 76 (1970), 887–933.Google Scholar
7. Halmos, P. R., Limsups oflats, Indiana Univ. Math. J. 29 (1980), 293–311.Google Scholar
8. Hewitt, E. and Stromberg, K., Real and abstract analysis (Springer-Verlag, New York, 1965).Google Scholar
9. Kakutani, S. and Mackey, G. W., Ring and lattice characterizations of complex Hilbert space, Bull. Amer. Math. Soc. 52 (1946), 727–733.Google Scholar
10. Longstaff, W. E., A note on transforms of subspaces of Hilbert space, Proc. Amer. Math. Soc 76 (1979), 268–270.Google Scholar
11. Longstaff, W. E., Subspace maps of operators on Hilbert space, Proc. Amer. Math. Soc. 84 (1982), 195–201.Google Scholar
12. Mackey, G. W., Isomorphisms of normed linear spaces, Ann. Math. 43 (1942), 244–260.Google Scholar
13. McAsey, M. J. and Muhly, P. S., On projective equivalence of invariant subspace lattices, Lin. Alg. Appl. 43 (1982), 167–179.Google Scholar
14. Radjavi, H., Isomorphisms of transitive operator algebras, Duke Math. J. 41 (1974), 555–564.Google Scholar