Abstract
Lightning has been directly observed or inferred on all giant planets, generally accepted to be occurring in their water clouds. However, much as Earth has both cloud–cloud and cloud–ground lightning, this does not mean all flashes occur in a narrow altitude range: on Jupiter, the Galileo spacecraft detected lightning flashes apparently below the cloud base, explicable as lightning due to precipitation, and the Juno SRU detected small flashes far above it, at pressures of only 1–2 bars. We use a computationally light 1D entraining plume model, incorporating particle growth and noninductive charging, which predicts this wide range of Jovian lightning provides freezing point depressions caused by ammonia, and modify it to use a van der Waals equation of state instead of an ideal gas, as well as integrating the evaporation of rain; this allows modeling of planets colder than Jupiter, where clouds and lightning occur at greater pressures. For Saturn, the uppermost lightning is predicted at 3–4 bars; unlike on Jupiter, ammonia is not required to match the Cassini observations. For Uranus and Neptune, depending on their convective structures, very high rates of lightning are possible in the deep water clouds; while deeper than on Jupiter or Saturn, lightning is predicted likely to peak above the water cloud base, at pressures around 100 bars. Voyager 2's radio observations of Uranian and Neptunian sferics may thus be either due to attenuation of deep water lightning of this type, or due to lightning in the shallow ammonia clouds; future observations are required to resolve this dichotomy.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Lightning has been observed on all four giant planets, although it appears to be most common on Jupiter. On Saturn, radio detection of lightning sferics at radio wavelengths, known as "Saturn electrostatic discharges" because their source was initially controversial, was achieved by Voyagers 1 & 2 and later Cassini. Optical detection of lightning is complicated by ring shine, but was achieved in 2009 during equinox (Dyudina et al. 2010) when ring shine was minimal, and again in 2010–11 (Dyudina et al. 2013) with short-exposure images during Saturn's great storms. Saturnian lightning depths are consistent with its occurring either in ammonium hydrosulfide clouds or in water clouds as on Jupiter. With Saturn's colder temperatures, the water clouds are expected to be deeper than on Jupiter, with a cloud base at 10–20 bar pressure (Atreya et al. 2019). While Saturnian lightning flashes seem to have comparable energy to Jovian ones, they are observed much less frequently, with no more than two storms observed on the planet at any given time (Dyudina et al. 2013).
Lightning sferics were also detected on Uranus, and less conclusively on Neptune, by Voyager 2, which remains the only spacecraft to have visited the ice giants. These planets' atmospheric structures are substantially different from Jupiter and Saturn, with a much higher abundance of heavy elements and thus much thicker and deeper cloud decks; the water cloud base may occur at atmospheric pressures greater than 1000 bars, and even ammonia clouds extend below ∼5 bars (Atreya et al. 2020). Surprisingly, the lightning sferics detected on Uranus were much more energetic and more common than on Neptune (Zarka et al. 2004; Aplin et al. 2020), despite the apparent visual quiescence associated with lesser vertical mixing of the former's atmosphere as observed by Voyager 2 (Herbert et al. 1987) and the Infrared Space Observatory (ISO; Encrenaz et al. 1998) and the otherwise similar nature of the two.
Given that our knowledge of the composition, temperature profiles, and the kinematics of 3D atmospheric convection at relevant depths in these bodies is lacking, a parameterized study using a 1D entraining plume model, similar to the one of Aglyamov et al. (2021) for Jupiter, is appropriate and has the potential to be useful for predicting the unknown lightning distributions of these planets, connecting them to atmospheric properties, and suggesting future observations that might be done with an orbiter and probe (NAS 2022). In this study, we build such a model for the water clouds of Saturn, Uranus, and Neptune, with added complications relative to Earth and Jovian conditions: a nonideal gas equation is used to account for the high-pressure conditions, and the evaporation of rain below the cloud base is accounted for fully in the generation of lightning.
A Uranus orbiter and probe has been named as the highest-priority new Flagship mission for the 2022–2032 decade by the US National Academy of Sciences (NAS 2022), and could permit observations of lightning with far greater sensitivity and coverage than Voyager 2 achieved. As was shown for Jupiter using the Juno Stellar Reference Unit (Becker et al. 2020), depth determination via optical measurements is possible. Such observations would allow some constraints on the depth of the observed lightning with additional information coming from sferics. If Uranian lightning does originate in water clouds, the latter would offer a rare source of information, potentially including constraints on local water abundance, about a deep atmospheric level otherwise largely inaccessible: because of their high water fraction, Uranus's and Neptune's water cloud bases are expected to be far deeper than Jupiter's, hundreds of kilometers below the visible cloud layers.
2. Numerical Model
The 1D of lightning generation presented here is an improvement on that in Aglyamov et al. (2021), and a full description of that model minus the nonideal equation of state and subcloud precipitation can be found in that paper. It is built in turn directly on the work of Gibbard (1996), and indirectly on Stoker (1986), Yair et al. (1992), and Yair et al. (1995). The model generates a depth distribution of lightning energies from one cylindrically symmetric updraft within a storm system, which is assumed to be stable in time. A brief recapitulation of this model follows, with a full description in the Appendix.
The convective model begins at a given pressure and temperature at the model bottom, and proceeds with pressure steps upward, calculating the values of state variables for both a moist parcel within the entraining plume and a dry parcel outside it. First, a parcel of moist air is raised from the model bottom, following a dry adiabat below the cloud base and a moist adiabat above it, while the surrounding downdrafts are assumed to follow a dry adiabat throughout and have zero water content. Since water has a higher molecular weight than hydrogen, the parcel will initially be negatively buoyant; if it is lifted, however, condensation will release latent heat and substantially raise the parcel temperature, increasing buoyancy. The condensed vapor is converted to cloud particles in the smallest particle size bin, which at this point immediately precipitate out (being noted as precipitation originating at this pressure level for later calculations). When the parcel becomes buoyant (the level of free convection), with its density being less than that of a dry parcel at the same pressure level, it acquires a positive upward velocity that initially increases. However, it also begins to entrain the surrounding dry gas of the downdraft, at a rate that increases with velocity, which drives its temperature closer to that of the surrounding material, and also reduces in moisture content and cloud density in proportion to the fraction of newly entrained material. Advected cloud material also increases the rising parcel's density and decreases its buoyancy. Eventually, the plume loses buoyancy and its upward velocity again begins to decrease, and finally drops to zero. While condensed particles are removed from the parcel below the level of free convection, above it sufficiently small particles—whose terminal velocity is smaller than the upward velocity of the plume—are advected with it, and grow by collision, until they precipitate out (by growing too large to be suspended and/or being carried to the upper atmosphere where the plume slows down).
Once this is complete, the electrical calculation is run: at every pressure level, the locally suspended particles are added to particles that precipitated higher up in the atmosphere with the latter being weighted by the ratio of the fall velocity they precipitated at to their local fall velocity. The total particle size distribution is then assumed to undergo collisional noninductive charging (as per Keith & Saunders 1989), producing a positive or negative charging rate in time for every particle size bin. While the total net charging rate is zero, smaller particles acquire positive charge and larger particles acquire negative charge, and larger particles have a faster terminal velocity. This forms an electric current, and creates an increasing electric field. Once the field reaches its breakdown value, a lightning flash occurs, with all energy stored in the electric field released; dividing this by the time-to-lightning gives a lightning power per unit area, which is calculated in this way for individual pressure steps and can be summed throughout the column.
Several changes are made in the current version of the model to adapt it to Saturn, Uranus, and Neptune conditions. First, the higher pressures involved in the water clouds of these planets, especially for Uranus and Neptune, make the ideal gas equation of state used by Gibbard (1996) and Aglyamov et al. (2021) a poor approximation. The upper portion of the water cloud in these bodies may be at roughly 100 bar pressure and room temperature. There the mean free path is of order a nanometer, only a few times the collision diameter for hydrogen molecules. Therefore, the gas can no longer be considered to be composed of point particles, and a correction must be made for the finite molecular volumes. To do so we use the van der Waals-based equation of state of Hemmes et al. (1986). This equation was chosen because it is relatively computationally inexpensive, accurate for the moderate temperatures and pressures (less than 1000 K and 1000 bar) involved, and has a closed form that allows differentiation:
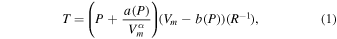
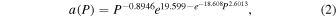
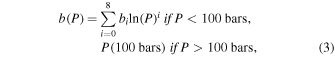
where P is the pressure in bars, Vm is the molar volume in cm–3, R is the gas constant, α = 2.846, b0 = 20.285, b1 = −7.44171, b2 = 7.318565, b3 = −3.463717, b4 = 0.87372903, b5 = −0.12385414, b6 = 0.0098570583, b7 = −0.00041153723, and b8 = 0.00000702499.
Since this equation and its derivatives give the temperature as a function of pressure and molar volume, the variable tracked with the ascending plume is now molar volume instead of temperature, and the temperature is calculated when needed directly from the pressure and molar volume.
The van der Waals equation above was derived for hydrogen, and does not address secondary constituents such as helium and water vapor. To prevent complexities related to mixing, we assume they follow the same per-mole equation of state, with the only difference being molecular weight; as such, the gas at a given temperature and pressure will have a set molar volume regardless of composition, and the total density scales linearly with molar mass.
Second, multiple changes were made to prevent the arbitrary pressure level of the model base from affecting the results if all convective and lightning activity happens above. The temperature of the moist parcel is now taken to be equal to the surrounding air at the cloud base and all points below, only diverging above the cloud base. Additionally, the evaporation of precipitation below the cloud base is now included.
Evaporation is assumed to proceed according to Knudsen's equation (Equation (5) below) and the evaporation coefficient of Kessler (1969). Evaporation proceeds when the vapor pressure of the water is lower than the saturation vapor pressure by a deficit pressure P x . Evaporation due to a vapor pressure deficit should proceed at the same rate as condensation due to a vapor pressure excess; such condensation has a theoretical maximum where every excess vapor molecule that impacts the droplet sticks to it. These impacts are generated by both random thermal motion and the falling velocity of the droplet, with the velocities of the two being randomly oriented relative to one another and therefore adding as a root sum of squares:

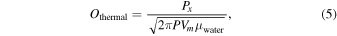

where O is the impact rate (m−2 s−1), Othermal and Ofall are its thermal and mechanical components, respectively, P is the overall pressure (Pa), P x is the deficit vapor pressure (Pa), Vm is the molar volume (m3), vfall is the droplet fall velocity (m s−1), and μwater is the molar mass of water (kg).
Experimentally, the growth and evaporation of water droplets is substantially slower than Knudsen's equation would directly predict, due to a number of microphysical processes (i.e., evaporating cooling of the droplet surface). This requires an evaporation coefficient ε < 1; we use the Kessler (1969) evaporation coefficient:
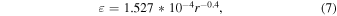
which depends on droplet radius (in m). Specifically, the coefficient for each particle size bin is calculated from the droplet radius r0 that is the arithmetic mean of the bin boundaries.
This can be used to calculate the rate of mass loss for a given droplet per unit surface area, and thereby the rate at which droplet radius decreases:
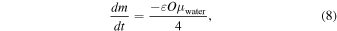

where ρ is the density of water.
As in the model's previous version, the particle size distribution in each bin is assumed to be linear in radius:
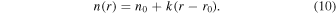
There are two direct effects of droplet evaporation on the particle size distribution: droplets at the bottom end of a larger bin moving into a smaller bin, and the shrinkage of particles that stay within a given bin. For the former effect, the instantaneous change in droplet number depends on the number of droplets at the bottom end of the larger bin (radius rmin):
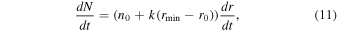
and the change in mass by:
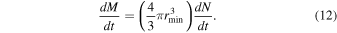
This is an increase in the particle number and mass for the smaller bin, and a decrease for the larger bin. The same equation is used for the smallest size bin for the overall evaporation of particles.
For the latter effect, the droplet number per bin remains constant, but the bin mass decreases for an integral of all droplets in the bin:
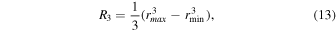
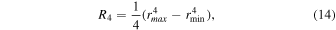
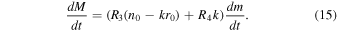
This is then applied to the precipitation falling from the cloud base, using the terminal velocity of droplets to convert from a time derivative to a space derivative.
Once the particle size distribution is known at every pressure level, the electric field can be calculated. Here, however, the steady-state assumption of the previous version of the model must be abandoned in favor of a more realistic procedure. Previously, the model assumed that particle charges would grow linearly in time with collisional noninductive charge transfer as per Keith & Saunders (1989), leading to quadratic growth of the electric field in time at a given pressure level. This is a valid approximation if the time a droplet takes to fall through the atmospheric column is much longer than the time to generate a breakdown electric field. Within the cloud, this is generally true for conditions in the giant planets. However, most of this charging is due to collisions of large precipitating particles with smaller cloud particles, and below the cloud base, where the smallest particles evaporate very quickly, charging is therefore extremely slow. Electric field growth is nonetheless still expected, as the droplets in question formed significantly higher up in the ascending plume and have already acquired a charge by the time they precipitate.
As such, we use two separate models of electric field growth. Above the cloud base, the electric field is quadratic in time, as in the previous version of the model; below the cloud base, however, particle charge is calculated for a given particle as it falls from its point of precipitation. At a given pressure level, charge is therefore constant in time and the electric field grows linearly with time. This difference leads to a visible discontinuity in graphs of the flash rate at the cloud base, but not one so large as to be unacceptable.
An additional complication for Uranus and Neptune is electromagnetic levitation: unlike for Jupiter and Saturn, breakdown fields in the water cloud region are high enough that, before such fields are reached, the electrostatic force on falling particles from the field affects particle velocities. Eventually, in a 1D model, this leads to a field that is constant in time, which Gibbard (1996) argues will prevent lightning in ice giant water clouds.
There are, however, reasons lightning may nonetheless be possible. First, while it is true that the electric field becomes stable in time for a 1D model, this does not mean all particles are falling with the same velocity, but rather that the relative velocities and charges cancel out. This, however, is within the context of a constant particle size distribution in distinct bins; particle growth over time and precipitation from above and below would prevent an equilibrium. A full analysis of these effects would require a 2D model of the plume to account for time evolution. Second, real storms are not axisymmetric, and horizontal winds are substantial. Within the context of significant moving charges, this implies electromagnetic as well as electrostatic effects, along with turbulence effects.
Since electric field growth for Uranus and Neptune's water clouds is fast compared to the fall times, it seems unlikely for a stable electric field to keep charged particles suspended for a full storm lifetime. Nevertheless, the effects of electrostatic levitation are likely to decrease electric field growth.
To address this issue, we further modify electric field growth. Electric field growth proceeds as above until reaching a value El where levitation becomes significant. Between El and the breakdown field (if the breakdown field is larger than El), by contrast, the electric field grows as the square root of time either above or below the cloud base. As such, electrical potential energy is built up linearly in time, with a constant power, from this point until the breakdown field is reached and lightning discharges.
3. Choice of Parameters
The model includes a number of parameters, such as molar masses, which are somewhat reliably known for Saturn but not for Uranus and Neptune. Additionally, several constants are retained from Aglyamov et al. (2021): the drag coefficient is 0.5, colliding water droplets will stick together 80% of the time and transfer charge the remaining 20%, and colliding ice particles will never stick together and always transfer charge. These parameter values were set in Aglyamov et al. (2021) as matching terrestrial thunderstorm lightning rates and altitudes when the model is applied to Earth's atmosphere; the changes made in this version of the model have minimal relevance for Earth conditions (the pressures are low enough to use the ideal gas equation of state, while rain evaporation is limited by the presence of a solid surface), and the calibration therefore retains its relevance for this work.
The plume radius is set to 5 km, as for Jupiter. The stratospheric temperature profiles for Saturn, Uranus, and Neptune of Lindal (1992) are used at pressures of less than 0.25 bars. The remaining free parameters are water abundance and temperature at the model base, along with the choice of the pressure level at which to set the said base, and the water freezing point, which is depressed relative to 273 K due to supercooling and dissolved ammonia; Earth calibration is best fit by a freezing point depression of 10–20 K, due to supercooled liquids. Breakdown field is, as in Aglyamov et al. (2021), assumed to be proportional to pressure, using the formula from Gibbard (1996):

Unlike Jupiter and Saturn, Uranus and Neptune have sufficient enrichment of methane to affect the molar weight of the dry atmosphere substantially. The methane enrichment is known only approximately from observation (Atreya et al. 2020); we use the composition of the nonwater atmosphere of Wiktorowicz & Ingersoll (2007), with a molar weight of 5.685 g mol–1.
The maximum pressure level was set at a depth so that the bulk of the precipitation evaporates before reaching it. At Saturn, 30 bars was chosen; for all water abundances considered, no precipitation reached further than 28 bars. For Uranus and Neptune, the situation is more difficult: there is substantial uncertainty in their deep atmospheric composition, and due to the high water abundance, the cloud base is deep. This not only strains the limits of the Van der Waals equation of state, but it also requires a large pressure step size, decreasing the accuracy. Furthermore, for particularly cold and high water temperature profiles, there may be no conventional cloud base, but rather an "ocean surface" below which the single phase is continuous with condensed water rather than hydrogen gas, although this is unlikely (Wiktorowicz & Ingersoll 2007). We set the model base for both ice giants at 2000 bars, which for most choices of the water abundance is well below the cloud base, and do not consider temperature–composition combinations with a deeper cloud base. Evaporating precipitation can fall well below the cloud base, at most roughly 100 bars, but compared to the total depths and uncertainties involved here this is small, and for the combinations we consider, all precipitation evaporates before reaching the model bottom.
For the oxygen abundance of Saturn, we use the constraint of Visscher & Fegley (2005) of 1.9–6.1 times solar abundance and extend the uncertainty intervals, considering oxygen abundances of 1.5 × solar, 2.5 × solar, 4.5 × solar, and 7.5 × solar. The last of these values is in line with the observed Saturnian carbon abundance from methane. For Uranus and Neptune, uncertainties are much higher; from their densities they may be composed primarily of ices, but ices can be replaced with a mixture of rock and hydrogen without a change in density. In reality, Uranus and Neptune are expected to have all three, but the proportions are unclear. For both, we consider abundances of 32 × solar, 60 × solar, 80 × solar, 100 × solar, and 128 × solar, in terms of mass fraction (corresponding to enrichments of approximately 70 × solar, 160 × solar, 240 × solar, 340 × solar, and 560 × solar if expressed in terms of O:H ratio). This corresponds to water mass fractions (out of hydrogen, helium, and water) of 20%, 37.5%, 50%, 62.5%, and 80%, covering the range of estimates; for comparison, Wiktorowicz & Ingersoll (2007) reach an estimate of 53.8% water by mass, while Moses et al. (2020) estimate an O:H ratio that is <45 × solar for Uranus and 250 × solar for Neptune.
The freezing point of water is set in 20 K intervals between 273 K (the freezing point of pure water) and 153 K (the ammonia–water eutectic is at 177 K, with this temperature adding supercooling on the upper edge of the best fit for Earth, to capture the widest range of plausible freezing points).
Temperature choices were based on Leconte et al. (2017), for conditions without a stable radiative layer (because such a layer is not present in the model). For Saturn, temperatures of 360 and 380 K at 30 bars were considered; the latter more closely matched observed upper tropospheric temperatures. For Uranus and Neptune, temperatures were selected so that the upper atmosphere would match observations and Leconte et al. (2017); this led to temperatures at 2000 bars of 960 K for Uranus and 940 K for Neptune.
The electric field El at which electrostatic levitation becomes significant is set based on a charging model that includes levitation, run for the particle distributions at 40 bars, 100 bars, 250 bars, and the cloud base for various water abundances. For both Uranus and Neptune, the electric field stabilized between 5 × 106 N C–1 and 1.5 × 107 N C–1 in most cases, so El was set to 107 N C–1 for both.
The model's sensitivity to the oxygen abundance and water freezing point (that is, physically, ammonia content) is described below and shown in the figures; oxygen abundance has the biggest effect on the flash rate, and both it and freezing point can lead to sharp changes in the flash rate and flash rate profile. The primary effect of changing the base temperature is to raise or lower the cloud base, and thus compress or stretch the entire flash rate profile, but these changes are generally smooth. Changing the percentage of time that water and/or ice particles stick together upon collision, as opposed to transferring charge, can have a substantial effect on the model predictions, the liquid coefficients especially. The most likely source of error is plume radius: it controls the entrainment of dry air and therefore the overall vigor of convection, and is not set by calibration with Earth. However, while changing the plume radius has a substantial effect on the flash rate, it achieves this primarily by altering the strength of convection, and constraints are thus given by observations (the plume must be large enough to cause convection, but not so large as to escape into space; in reality, an oversized plume would break up).
4. Results
We tested the model by running it for Jupiter and comparing with Aglyamov et al. (2021). While the altered equation of state does not produce substantively different flash rates for Jupiter, the addition of evaporation does produce a substantial effect. As seen in Table 1 and Figure 1, the flash rates rapidly decrease below the cloud base. For water abundances up to 3 × solar, the precipitation evaporates fully before reaching the 10 bar pressure level. These depth distributions are comparable to earlier results for 3 × solar and 10 × solar water, but for 1 × solar or subsolar water they imply substantially less deep lightning than for Aglyamov et al. (2021) due to evaporation below the cloud base.
Figure 1. Modeled flash rates for Jupiter, for the water abundances given in the left column.
Download figure:
Standard image High-resolution imageTable 1. Depth Distribution of Jovian Flash Rates for 330K Temperature at 10 bars
| Water Abundance | Deepest Possible Flashes | Fraction Lightning Power at 0–4 bars (Freezing Point 233 K) | Fraction Lightning Power at 0–4 bars (Freezing Point 173 K) |
|---|---|---|---|
| 0.1 × solar | 3 bars | NA | 100% |
| 0.3 × solar | 4.5 bars | 100% | 99% |
| 1 × solar | 6.5 bars | 93% | 71% |
| 3 × solar | 9 bars | 56% | 38% |
| 10 × solar | >10 bars | 19% | 11% |
Download table as: ASCIITypeset image
A single point where all liquid instantaneously freezes is of course a simplification; several Jupiter model runs were performed with a gradual phase transition, with a linear change in density and charging efficiency over a range of temperatures. The results showed behavior similar to that at a single freezing point, intermediate between the center and cold end point of the temperature range. For instance, at 1 × solar water abundance and gradual freezing between 273 K and 193 K, the total flash rates are 374 W m−2, close to the 388 W m−2 for sharp freezing at 233 K, and similar behavior is observed for higher water abundances. At 0.1 × and 0.3 × solar water, however, the gradual phase transition enables higher lightning rates than a sharp transition at 233 K (though still less than a sharp transition at 193 K) by enabling some liquid to persist into the upper atmosphere where convection is occurring and thus allowing substantial particle growth.
Entraining plumes form on Saturn as well as Jupiter, but have notably lower velocities for the same water abundance. For 1 × solar water, a plume on Jupiter acquires a maximum velocity of 20–27 m s−1, and for 3 × solar water this reaches 35–42 m s−1, while for 0.3 × solar water it is reduced to 10–14 m s−1. A plume on Saturn for 1.5 × solar water reaches a maximum velocity of 10–14 m s−1, and for 7.5 × solar water 24–28 m s−1. That is, the convection on Jupiter is as vigorous (as measured by upwelling velocity) as the equivalent would be on Saturn with five to seven times higher water abundance. Nevertheless, lightning is generated on Saturn at rates that equal or surpass those on Jupiter for similar water abundances. Saturnian flash rates are shown in Table 2 and Figure 2; a flash rate is output in units of W m–2, where the area in the denominator represents the area of the strongest updraft, which is less than half of the area of the strongest convection in a storm system. The overall planetary flash rate is lower still. For a 233 K freezing point, this power output goes from 5000 W m−2 for 1.5 × solar water to 43,000 W m−2 for 7.5 × solar water. This is greater than the predicted flash rates for the same water abundance on Jupiter, especially for lower water abundances. Furthermore, as shown in Table 3, when compared to similar water abundances for Jupiter, less freezing point depression is required to generate lightning. This is because, while Saturn's atmosphere is overall colder than Jupiter's, the cloud base is defined by the point where the saturation vapor pressure curve intersects a scaled adiabat (representing the atmospheric water vapor pressure), with the former being steeper as a function of pressure; shifting the adiabat to lower temperatures moves the intersection to both higher temperatures and pressures. Thus, for a given water mass fraction, Saturn's cloud base and convection occur at higher temperatures than on Jupiter, allowing substantial particle growth even at near-solar water abundance. Nevertheless, for a 273 K freezing point without any freezing point depression or supercooling, no lightning occurs for 1.5 × solar water and only limited lightning (190 W m−2) at 2.5 × solar water, while other parameter combinations generate from 2500 to 43,000 W m−2.
Figure 2. Saturn model results for the (left) plume velocity and (right) flash rate, for the water abundances stated in the left column.
Download figure:
Standard image High-resolution imageTable 2. Saturn Flash Rates (W m−2) for 253 K Freezing Point
| 1.5 × solar water | 2.5 × solar water | 4.5 × solar water | 7.5 × solar water | |
|---|---|---|---|---|
| 0–3 bars | 22 | 27 | 16 | 51 |
| 3–6 bars | 490 | 1159 | 2147 | 2519 |
| 6–9 bars | 970 | 1832 | 4364 | 6603 |
| 9–12 bars | 1988 | 4629 | 2275 | 8543 |
| 12–15 bars | 0 | 2893 | 1582 | 3012 |
| 15–18 bars | 0 | 0 | 190 | 5419 |
| 18–21 bars | 0 | 0 | 0 | 626 |
| 21–24 bars | 0 | 0 | 0 | 0 |
Download table as: ASCIITypeset image
Table 3. Comparison of the Total Flash Rate (W m−2) for the Same Water Abundance, Jupiter vs. Saturn
| Water Freezing Point and Abundance | Jupiter | Saturn |
|---|---|---|
| 273 K, 1 × solar | 0 | 0 |
| 253 K, 1 × solar | 0 | 569 |
| 213 K, 1 × solar | 594 | 2338 |
| 153 K, 1 × solar | 725 | 1379 |
| 273 K, 3 × solar | 0 | 1137 |
| 253 K, 3 × solar | 2780 | 14,566 |
| 213 K, 3 × solar | 4442 | 7200 |
| 153 K, 3 × solar | 5184 | 7174 |
Download table as: ASCIITypeset image
For 1.5 × solar water, Saturn's lightning power is concentrated at pressure levels of 3 to 12 bars. As seen in Table 2, a higher water abundance deepens the cloud base, and therefore also the deep end of this distribution; for 7.5 × solar water, substantial lightning extends down to 20–21 bars. On the shallow end of this distribution, the lightning power at 0–3 bars is a small fraction of the total lightning power for any water abundance and freezing point, with a maximum of 66 W m−2 for 7.5 × solar water and a 233 K freezing point. Lightning power at 3–6 bars, however, is substantial; outside of the two scenarios with minimal lightning mentioned above, it ranges from 280 to 2700 W m−2. In both of these ranges, the lightning power changes nonmonotonically and relatively little with water abundance. Meanwhile, this "relatively shallow" lightning power decreases with increasing ammonia fraction (decreasing freezing point). This effect is not prominent on Jupiter because a freezing point depression is required for substantial particle growth, but on Saturn the cloud base is deep enough that particle growth occurs regardless. Two effects then favor decreased lightning for the high ammonia content on Saturn. First, ice has a higher charging coefficient than water, leading to more lightning for the same particle size distribution. Second, because upwelling velocities on Saturn are lower than on Jupiter, particle growth enabled by freezing point depression largely leads to particles large enough to precipitate; as such, a greater freezing point depression decreases the total cloud particle content in the shallow atmosphere.
On Uranus and Neptune, unlike Jupiter and Saturn, the freezing point depression has only a limited effect because the bulk of both the convection and lightning happens well below the pressure level corresponding to 273 K. As such, only the end-member freezing points of 273 K (pure water) and 153 K (ammonia–water eutectic with supercooling) were considered, since any other ammonia–water mixture would have a freezing point between those bounds. The resulting convection behavior is shown in Figure 3: a large water content leads to buoyancy being achieved only a large distance above the cloud base, but potentially very strong convection where it does occur, with upwelling speeds of more than 250 m s−1 in the extreme case, although this assumes that a temperature contrast is built up all the way from the cloud base rather than evolving as multiple vertical cells. Even for 32 × solar water, this leads to extreme flash rates—for Neptunian gravity and a 940 K base temperature, the total lightning power is approximately 2.5 MW m–2, and this increases with water abundance. As shown in Table 4 and Figure 4, much of this is generated at depths of over 100 bars, but substantial lightning is generated at shallower depths as well. Hundreds of kilowatts in lightning power per square meter can be released at pressures of 0–30 bars, much more than on Jupiter or Saturn. Since lightning power cannot exceed overall power from convection, such strongly convective regions would be rare.
Figure 3. Model results for Uranus and Neptune for the (left) plume velocity, (center) mass fraction cloud suspended in the plume, and (right) vapor mass fraction, for the water abundances and planet stated in the column.
Download figure:
Standard image High-resolution imageFigure 4. Modeled flash rates for (left) Uranus and (right) Neptune, for the water abundances stated in the left column.
Download figure:
Standard image High-resolution imageTable 4. Uranus and Neptune Flash Rates (W m−2) for 273 K Freezing Point
| Planet & water abundance | 0–30 bars | 30–100 bars | 100–200 bars | 200 bars and below |
|---|---|---|---|---|
| Uranus, 32 × solar | 205,395 | 981,721 | 585,355 | 174,457 |
| Uranus, 60 × solar | 395,191 | 2,081,595 | 539,638 | 462,742 |
| Uranus, 80 × solar | 471,238 | 2,770,892 | 98,373 | 267,172 |
| Uranus, 100 × solar | 658,631 | 2,840,410 | 93,699 | 551,845 |
| Uranus, 128 × solar | 1,499,758 | 3,707,309 | 4,659,038 | 112,433,514 |
| Neptune, 32 × solar | 272,712 | 1,104,474 | 907,497 | 207,545 |
| Neptune, 60 × solar | 536,232 | 2,263,682 | 1,039,991 | 575,677 |
| Neptune, 80 × solar | 689,999 | 3,176,756 | 330,609 | 407,906 |
| Neptune, 100 × solar | 511,446 | 3,506,926 | 28,046 | 131,839 |
| Neptune, 128 × solar | 1,669,778 | 2,455,844 | 2,959,815 | 54,575,369 |
Download table as: ASCIITypeset image
5. Discussion
Galileo detected deep lightning flashes on Jupiter to at least the 8 bar pressure level (Little et al. 1999; Dyudina et al. 2002), which would imply at least a 3 × solar water abundance at these locations. While this provides tenuous evidence for 3 × solar or higher water abundance in Jovian storms, it is consistent with lower abundances elsewhere on the planet, since "wetter" regions will have more convective activity and lightning. For comparison, observations with the Juno microwave radiometer have produced 1–5 × solar water in a narrow equatorial region of Jupiter (Li et al. 2020), with work to derive a "global" water abundance continuing.
It must, however, be noted that this model does not consider hail, formed by precipitation being caught in repeated updrafts and continuing to grow. Similarly, "mushballs" (Guillot et al. 2020) are not incorporated into the model. It is certain that hailstones larger than those produced in the model will occur on Jupiter; for them to cause deeper lightning, however, they must make up a significant fraction of Jupiter's total precipitation flux. The model also does not consider collisional ice splintering, which may significantly affect the ice particle size distribution (Sullivan et al. 2018; Qu et al. 2020); this process would lead to a greater amount of smaller particles, and therefore to faster evaporation.
An additional caveat is provided by the fact that only one of the flashes Galileo detected was confirmed by Dyudina et al. (2002) to be at a depth of 8+ bars; the other five flashes are consistent with pressures of 2–6 bars, although they may also be deeper. Lightning within this pressure range is predicted even for solar water abundance. As such, it is possible that the deepest flash was generated by some other process, or alternatively that it occurred in conditions where the cloud tops were elevated unusually far into the stratosphere and thereby caused a higher observed depth from the topmost scattering layer rather than actually being unusually deep. It is also possible that the deepest flash was actually a combination of several nearby flashes over the 6.4 s exposure time.
Unlike on Jupiter, lightning on Saturn was not observed optically until Cassini, and even then with difficulty (Dyudina et al. 2010). Radio emissions from lightning have been observed before and since, but they too indicate less frequent lightning than on Jupiter. Our numerical model predicts similar lightning power on Saturn as on Jupiter, if the atmosphere is convecting. Observations of Saturn, however, are consistent with intermittent convection, with large storms sweeping through every several decades but otherwise a less feature-dense atmosphere than Jupiter. Furthermore, atmospheric modeling also supports intermittent convection (Li & Ingersoll 2015), and lightning observations show that, at any given time, there is usually only one location on Saturn—one storm—that exhibits lightning flashes (Fischer et al. 2011). As such, it is entirely consistent with observations that when lightning occurs on Saturn, it does so with equal or greater intensity to Jupiter. Indeed, during the 2011 giant storm, Dyudina et al. (2013) detected flash rates 20× greater than Little et al. (1999) found for Jupiter storms, although a comparison per unit area is difficult to make because of the different structures of these storms.
The optical flash observations of Dyudina et al. (2010) and Dyudina et al. (2013) mostly occurred at similar depths, somewhere between 125 to 250 km below the cloud tops, with model-based uncertainties. If the cloud top estimate from Dyudina et al. (2013) of 1.2 bars is used, this corresponds to a pressure somewhere between 6 and 20 bars, in line with model predictions. Cassini was unable to detect lightning flashes with optical energy less than 2 × 108 J on the nightside or 1 × 109 J on the dayside, and found that the frequency of flashes increased with decreasing energy up to this detection limit, implying additional small flashes below the detection limit; since the breakdown field increases with density, this may be a shallower population of flashes. The flash with the lowest energy observed also had a very sharp brightness distribution, with a corresponding depth of 62–125 km below the cloud tops, 3–6 bars; Dyudina et al. (2013) note this observation as questionable, as it could have been a gamma-ray strike, but if real it provides evidence toward such a shallow lower-energy lightning population. The direction of this difference would parallel the Juno observations on Jupiter. Unlike Jupiter, however, we predict that this distribution does not continue further to lightning at the 1–2 bar level.
Ammonia or other antifreeze is not required to cause lightning on Saturn; its presence is consistent with observations, but unlike Jupiter, lightning is not evidence that Saturn's water clouds have an ammonia admixture. For Uranus and Neptune, an ammonia admixture has an even smaller influence, but does decrease the flash rate at shallow levels at temperatures below 273 K, due to ice being substantially more effective than water at charging.
The massive flash rates predicted for Uranus and Neptune rely on an assumption of simple convection that may break down for the massive depths involved in these planets' water clouds. Additionally, electrification of dense molecular hydrogen may not follow the low-pressure trend of a linearly increasing breakdown field. If massive plumes spanning the entire water cloud do exist, they may be expected to be stable over a fairly long span of time given the distances involved; as such, while the time it takes to generate lightning is longer for these higher pressures, lightning should eventually occur. An additional assumption is that the background temperature profile is a dry adiabat; a subadiabatic profile is possible if there is additional mixing, and a superadiabatic profile has also been suggested (Guillot 1995).
Voyager 2 detected radio evidence of lightning at both Uranus and Neptune, although fewer and weaker signals than for Saturn, but no optical signal (Aplin et al. 2020). Lightning sufficiently deep in the water cloud would not be optically detectable. The maximum depth to which lightning can be detected optically is unclear, but Dyudina et al. (2013) suggest a 1:1 correspondence of optical and radio detections on Saturn that is consistent with observations, implying that all lightning on Saturn is shallow enough for optical detection (given suitable observing conditions). In that case, Uranian and Neptunian lightning down to at least 12–20 bars should be optically detectable. For sufficiently vigorous convection, substantial flash rates are predicted. However, the weak radio signals are inconsistent with such a flash profile, which would effectively be a distribution similar to Saturn but with 10× higher flash rate. The weakness of the signals implies that either the flashes are happening at a very shallow pressure level (in the ammonia clouds), they are of small horizontal extent for unclear reasons, or their depth is sufficient to attenuate the radio signal. Additionally, Voyager 2 had clearer detection of lightning on Uranus than on Neptune. For the same temperature and composition, Uranus's lower gravity tends to lead to lower lightning rates than Neptune in the 0–200 bar region and similar lightning rates below. Uranus is also believed to have a somewhat warmer deep atmosphere than Neptune; this effect raises the cloud base and intensifies convection, leading to higher "shallow" (in this case 0–200 bar) flash rates but substantially lower deep flash rates, and lower flash rates overall.
These distributions suggest two possible origins of ice giant lightning, which could be distinguished by optical observation. If the sferics detected by Voyager 2 came from the shallow or middle atmosphere, even at the 20 bar pressure level, a future Uranus orbiter may be able to detect optical lightning. The convective systems causing this lightning would be those of the ammonia cloud, though there may be ice and ammonia–water particles involved in electric field generation. If, by contrast, they came from the deep atmosphere and the water cloud, it is likely that the observed signal strength is detected after substantial attenuation. In this case, Neptune's few observed sferics are more attenuated because of Neptune's colder temperature profile and a deeper water cloud, whereas Uranian lightning is easier to observe because it is shallower. Nevertheless, both ice giants would be exhibiting lightning in an extreme high-pressure regime quite unlike anything seen on Earth, Jupiter, or Saturn.
The plausibility of such attenuation depends on the absorptivity of ice giant atmospheres, which is not well understood. The sferics on Uranus and Neptune were detected mostly in the HF band, at frequencies of 0.9–40 MHz for Uranus and 20–30 MHz for Neptune. Uranian discharges were measured as being approximately 10× (10 dB) weaker than Saturnian, and Neptunian 45× (16 dB) weaker than Uranian (Zarka & Pedersen 1986; Aplin et al. 2020). The absorptivity of a giant planet atmosphere in this radio wavelength range is expected to be dominated by water and ammonia, both in vapor and in cloud form. The absorption behavior of water under these high-pressure conditions is not directly known, although in general, in the low-frequency limit, water absorption should be proportional to the square of the frequency. Segelstein (1981) estimates an absorption coefficient of liquid water, at 30 MHz, of 0.0087 m−1, corresponding to a 10× decline in intensity (10 dB signal loss) over 265 m. For ice, absorption at radio wavelengths is strongly dependent on temperature, but signal loss in the Antarctic (at ∼10 MHz) is approximately 10 dB in 400–500 m (MacGregor et al. 2007), with estimates for colder Europa ice centering around 10 dB loss in 1000–3000 m (Moore 2000). These can be converted to water pressure for an equivalent mass of vapor, with absorption of 10 dB in 250–500 m water equating to 25–50 bar water, which for a 50% water (by mass) atmosphere is 50–100 bars of total pressure, comparable to the depths and depth contrasts predicted for Uranus and Neptune.
For water vapor, one must extrapolate from higher-frequency data. For example, the equation for water vapor self-interaction of Rosenkranz (1998) predicts very high attenuation; for 10% (by mass) water vapor at 100 bars pressure and 400 K, for example, the projected attenuation is approximately 900 dB m–1 gas, effectively totally opaque. More recent experiments predict greater transparency, but there remains substantial uncertainty about its degree, as the experimental data are at lower pressures and water contents than the Uranian and Neptunian clouds and therefore require extrapolation. The equations of Karpowicz & Steffes (2011) can be extrapolated to 10 dB absorption over 47 km under the above conditions, substantial but not total, while the follow-up modeling by Bellotti et al. (2016), despite mostly using the same data set, yields only 10 dB absorption over 2600 km, functionally transparent at the 100 bar level. Janssen et al. (2017) predict even less absorption, with water and ammonia becoming near-transparent in the radio at pressures above 100 bars, and estimate that the Juno MWR's channel 1 (600 MHz) should see down to depths in the thousands of bars. Further complicating affairs, lightning emissions are absorbed and/or scattered by cloud particles as well as by gas; at optical wavelengths, this is used to quantify lightning on Earth (Goodman et al. 2013; Peterson 2019) and on the giant planets (Little et al. 1999; Dyudina et al. 2010, 2013; Becker et al. 2020). Radio waves are not as strongly absorbed, but Earth-based radio observations at 20 MHz can be substantially impeded by rain, despite its small size compared to the wavelengths involved (Mondal & Bhattacharya 2015), showing that cloud absorption is also likely to be significant for Uranus and Neptune. As such, the possibility that Voyager 2 detected strongly attenuated deep lightning at the ice giants remains plausible, but uncertain. A future lightning campaign at Uranus with simultaneous optical and microwave/radio observations could address this ambiguity.
6. Conclusions
While lightning on Jupiter can be expected for even substantially subsolar water abundances, so long as ammonia antifreeze is available, as concluded in Aglyamov et al. (2021), evaporation below the cloud base leads to a bottom cutoff for the lightning that is dependent on water abundance. To fit Galileo's detection of a lightning flash at ∼8 bars, a water abundance of 3 × solar or more is required. This may be taken as weak evidence for water enrichment on Jupiter. The ammonia requirement does not hold for the other solar system giant planets.
Lightning on Saturn is predicted, and its depth is shown to fit Cassini observations. As for Jupiter, a distribution of shallow to deep lightning throughout the water cloud is predicted, but as with the whole water cloud it is deeper than on Jupiter; the upper edge of this distribution is at 3–4 bars, and at shallower altitudes no lightning is predicted. Saturn is only intermittently convective, and thunderstorms are rare, but in the presence of convective activity its local lightning power is predicted to at least match and likely exceed Jupiter's.
Uranus and Neptune are predicted to not have substantial lightning in the uppermost part of their water ice clouds, excluding cases inconsistent with Voyager 2 observations (although the possibility that Uranian convection and lightning varies greatly with the seasons, and Voyager 2's observations are thus not representative, cannot be excluded). Deep lightning in their liquid water clouds is possible; such a regime would involve extremely high cloud densities and electric fields and potentially very energetic flashes, which due to their depth would be largely hidden from even radio observations, particularly in Neptune's colder atmosphere. The situation is somewhat better for observations of Uranus, and radio detection of lightning should be part of the observational capability of a future Uranus Orbiter and Probe.
Acknowledgments
This work was performed under a Juno subcontract to Cornell University from the Southwest Research Institute; at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration; and at SETI Institute by the NASA Juno Participating Scientist Program. The theoretical models are available at https://zenodo.org/record/4039312 (Aglyamov 2022). Data sources in the published literature include Little et al. (1999), Dyudina et al. (2010), Dyudina et al. (2013), Becker et al. (2020), and Zarka & Pedersen (1986), as cited in the References section below.
Appendix A: The Jovian Entraining Plume Model
The following is a detailed description of the Aglyamov et al. (2021) model of electrification in an entraining plume, on which the model described here is based.
We begin with a parcel of moist air, surrounded by dry air of the appropriate composition for each body. So long as the moist air is no more buoyant than the dry air around it, both are assumed to follow an adiabatic profile, a dry adiabat except in the case when the moist air has a partial pressure of water exceeding the saturation vapor pressure calculated as per Lowe (1977), in which case water condenses, releasing its latent heat, and the temperature changes with pressure as per a moist adiabat. In calculating the heat capacity of Jovian air, only hydrogen and helium in the observed Jovian ratio (von Zahn et al. 1998) and water vapor (if any) are considered, as the contribution of other Jovian gases is negligible.
Once the moist parcel is buoyant, convection is initiated, and the parcel gains a positive upward velocity that initially increases, as well as being able to keep in suspension particles whose terminal velocity is lower than the parcel's upward vertical velocity, allowing condensate to accumulate and particles to grow. The parcel temperature is assumed to change adiabatically, and the faster the plume rises, the faster it will incorporate dry air from the surrounding, downwelling region. A larger entrainment rate is mathematically equivalent to a smaller plume radius, and leads to more dry air from the surrounding environment introduced into the column. The entrained air follows the environmental temperature profile. In the buoyant region it will be denser than the plume despite having a lower molecular weight, making buoyant convection more difficult. Further, positive buoyancy is required to accelerate initially stationary dry air to the plume's upward velocity. The condensate mass decreases buoyancy so long as it remains suspended in the plume, but this is a smaller effect.
Table 5 lists the symbols used. Like Gibbard (1996), we use an entrainment rate of:
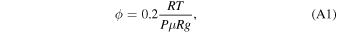
as the fraction of mass added per unit pressure. As such:
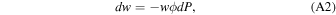
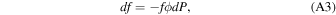
and the concentration of cloud particles in each size bin is likewise decreased; the plume radius increases, but is capped to be no more than a factor of √2 greater than the initial radius to leave room for downdrafts. That is, for a dry adiabat with entrainment we take:
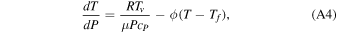
and for a moist adiabat with entrainment:
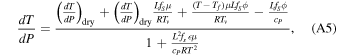
where Tv is the virtual temperature defined as:
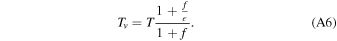
For an adiabat outside the plume, either below the level of free convection or in the regions of descending dry air, which are assumed to surround the plume, the terms with entrainment rate are zero. Note that, while it is possible that the external environment might not be characterized by a dry adiabat, what we care about is the temperature contrast created by the different temperature profiles within and outside the plume, which affect the buoyancy. Given that the entrainment is determined by the cross-sectional size of the plume, the distribution of which is not known for Jupiter, introducing a temperature profile different from a dry adiabatic would simply add another parameter that is at the moment poorly constrained. We felt it simpler to make the most idealized assumption for the tropospheric environmental temperature gradient. However, inclusion of a stratosphere is important as the reversal of the environmental temperature gradient at the tropopause strongly brakes the ascent of buoyant plumes. As the stratospheric temperature profile does not approximate an adiabat, the Jovian stratospheric environmental temperature profile at pressures less than 0.25 bars is assumed to be equal to that found by the Galileo probe, as per Seiff et al. (1998), and the Earth stratosphere to the ISA Standard Atmosphere.
Table 5. Definition of Appendix Symbols
| Units | ||
|---|---|---|
| b | radius of a given cloud particle | m |
| b0 | approximate radius of particles in a given bin = arithmetic mean of its bounds | m |
| C | aerodynamic drag coefficient of a particle, assumed constant | ⋯ |
| cP | specific heat capacity of dry air, taken as 14.5 kJ K−1 kg−1 for Jupiter | kJ K−1 kg−1 |
| E | electric field at a given pressure level | N C−1 |
| Ei | collision efficiency = probability that two colliding cloud particles will merge | ⋯ |
| Eq | charging efficiency = probability that two colliding particles will transfer charge | ⋯ |
| f | mass fraction of condensate vapor in air, 0.00625 for solar water abundance on Jupiter | ⋯ |
| fS | mass fraction of condensate vapor in the air that corresponds to the saturation vapor pressure | ⋯ |
| g | gravitational acceleration, assumed constant, 24.79 m s−2 for Jupiter | m s−2 |
| J | vertical current density at a given pressure level | C s−1 m−2 |
| k | slope of the particle density distribution as a function of radius | m−5 |
| L | latent heat of vaporization of the condensate (water), assumed constant at 2.257 MJ kg−1 | MJ kg−1 |
| M | total mass density of cloud particles within the size range of a bin | kg m−3 |
| N | total number density of cloud particles within the size range of a bin | m−3 |
| n0 | particle density distribution as a function of radius at the center of a bin | m−4 |
| P | pressure level under consideration | Pa |
| R | universal gas constant 8.314 J K−1 mol−1 | J K−1mol−1 |
| r | radius of the entraining plume | m |
| T | temperature of the ascending air parcel | K |
| Tf | temperature of the dry air surrounding the plume | K |
| tL | time since the last lightning discharge | s |
| w | upward velocity of the entraining plume at a given point | m s−1 |
| wi | terminal velocity for a particle of a given size relative to its surroundings | m s−1 |
| wrel | average relative velocity of particles in two size bins | m s−1 |
| ε | ratio of the molar mass of the condensate (water) to that of dry air, 8.2 for Jupiter. | ⋯ |
| μ | molar mass of dry air, assumed constant, 0.0022 kg mol−1 for Jupiter | kg mol−1 |
| φ | fraction of the entraining plume replaced with dry air per unit pressure rise | ⋯ |
Download table as: ASCIITypeset image
Particles are assumed to reach their terminal velocity immediately, given by:
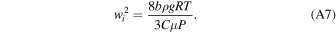
Particles in bins whose terminal velocity exceeds the upward velocity of the plume are precipitated immediately and removed from the plume, and any remaining particles left over in the plume if it reaches the top of the atmosphere are precipitated out at that point. The quantity and size distribution of these precipitating particles is recorded at each pressure level, to be included into the electrification model for deeper levels.
From the velocity and the hydrostatic pressure gradient, the time it takes the parcel to ascend through the pressure step of 10 Pa can be calculated and used for particle growth calculation. Both liquid water droplets and ice particles in the cloud are treated as being spherical with a constant density of 1000 kg m−3 for liquid and 400 kg m−3 for ice (graupel). They are divided into 31 bins according to their liquid-equivalent radius (from which their actual radius, mass, and volume immediately follow), with each bin's upper boundary being a radius √2 times its lower boundary. The smallest bin stretches from a radius of 10 μm to a radius of 14.1 μm, with the largest bin's upper bound being a radius of approximately 46.3 cm (not reached in practice, but estimated to be near the maximum size of Jovian hail). Particles initially condense with a flat distribution of radii in the smallest bin; changing the radius of this bin by a factor of two in either direction changes the flash rates by less than 10%, demonstrating stability with respect to the choice of size bin. The arithmetic mean of these upper and lower bounds, b0, is used as an approximate radius of particles within the bin in some of the calculations to follow. We describe the size distribution of particles by a piecewise linear function F(b) such that the number density of particles with radius between b1 and b2 in a region is:
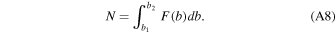
As such, F(b) has values with dimension m−4. In a given size bin, it is assumed that F(b) is linear except if this would cause it to be negative:
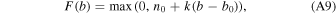
defined by two parameters per bin, n0 (with units m−4) and k (with units m−5); for empty bins n0 = k = 0. In the largest nonempty size bin, we thus tend to have F(b) be piecewise linear within the bin, with a negative slope until F(b) = 0 and constantly zero thereafter. It is assumed that all particles within a bin precipitate together, using the terminal velocity of a particle of radius b0. The total volume (and from it the total mass M) of particles in a given bin can thus be found by integrating:
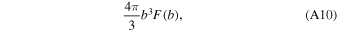
from the lower bound of the bin to either its upper bound or the x-intercept of F(b); the average mass can be found by dividing M by the integral of F(b) over that range, which is the number density N.
It is assumed that, whenever two cloud particles collide, they will stick together to form a single particle with probability equal to Ei . Calculating the frequency of such collisions requires knowing the typical relative velocities of cloud particles. It is assumed that the velocity is predominantly vertical, with the relative velocity of the cloud particles being the difference between the terminal velocity at the upper bound of the larger bin and the lower bound of the smaller bin. This ensures that particles from the same bin have a nonzero relative velocity and can merge with one another. As such, the number of collisions ncoll(i, j) between a particle from bin i and a particle from bin j, i ≥ j, per unit time and per unit volume is:

Multiplying by the time step gives a number of collisions per unit volume.
Collisions are assumed to remove a number of particles from the smaller bin equal to the number of collisions, with the average mass equal to the average mass of the smaller bin. This mass is in its entirety transferred to the larger bin. However, this increase will cause some of the particles in the larger bin to be transferred from bin i to bin i + 1. For this calculation, it is necessary to make simplifying assumptions. We define the radius b x as the radius of a particle that, when colliding with a particle of radius b0(j), would produce a particle with radius equal to the upper bound of bin i. Then, it is assumed that exactly the particles with a radius greater than bx are transferred to bin i + 1 upon collision, so that their total mass and number are transferred up a bin, along with the proportionate amount of mass initially from bin j. In this fashion, the total mass and number density are updated for each bin. Following this, n0 and k are rederived from M and N, with the formula dependent on whether or not F(b) has an x-intercept within the bin, and particle growth is iterated for the duration of the ascent through the pressure step.
In an actual storm, there would be a gradient between fully liquid and fully frozen particles. Here, to make the calculation tenable, we assume that all particles at a given altitude are either liquid water or ice; the boundary between them is set at a specific temperature, as the freezing point of water does not change significantly with pressure in this pressure range. This freezing point is set at 273 K or lower, the latter to simulate the possible supercooling of water—a complex phenomenon involving multiple microphysical effects—down to 233 K (e.g., Pruppacher & Klett 1997), or a more important depression (possible down to 173 K) due to the dilution of ammonia into water (Guillot et al. 2020). The difference between liquid water and ice lies in the values of Ei and Eq, the charging efficiencies. These efficiencies hold different values for liquid and ice: that is, Ei (liquid) + Eq(liquid) = 1, and Ei (solid) + Eq(solid) = 1. Since ice is assumed to satisfy Ei = 0 and thus Eq = 1, as Eq(liquid) decreases, charging and lightning will increasingly be dominated by that occurring at temperatures below freezing and therefore shift upward. However this also implies that Ei (liquid)—a variable parameter—increases, allowing for faster growth of particle size contrast and more lightning overall.
In this fashion, at each pressure level, a particle size distribution is calculated, as well as the sum of the size distribution of precipitation coming from above. The rest of the computations to determine electric field buildup do not alter this distribution; hence, electrostatic levitation (which might serve to increase the mean particle size at which fallout occurs) is not included. Furthermore, particle evaporation (virga) at altitudes above the 10 bar level and particle relofting (hail) are not considered. The following calculations are performed at each pressure level, but using a step size of 1 kPa.
First, the precipitation coming from above is weighted by the fraction of time it spends within the range of the pressure step. The height of this step is calculated as before, and the particle fall velocity as terminal velocity minus plume velocity. Any precipitating particles with a terminal velocity slower than the plume velocity are considered uninvolved in lightning production (in practice they would either be relifted or precipitate outside the plume area), while the upward-moving plume particles are added later. For a set particle radius, the time spent in a certain height range would be equal to height over velocity, but this leads to infinite values for particles just large enough to have a terminal velocity equal to the plume velocity. As such, each contributing particle radius within the bin is also weighted by the difference between its terminal velocity and the updraft velocity. The natural (asymptotic) weighting is:
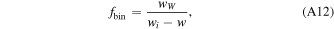
where wW is the updraft velocity at the point where the particle was dropped by the plume. Instead, we perform the calculation for particles slightly larger than the critical radius by treating the bin as if its lower bound was at the critical radius and taking an average velocity for this shrunken bin, leading to the weighting:
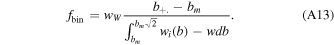
This yields:
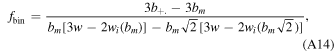
where wW is the plume velocity at the altitude of the precipitation's origin, w is the plume velocity at the altitude of the electric field growth, b+ is the bin's upper bound, and bm is the greater of the bin's lower bound and the critical levitating radius. The factor of √2 is the factor between the bin boundaries, as near the singularities bm approaches b+ and we wish to lower the weight of such bins to reflect that most particles in them are being lofted in these conditions.
This creates a weighted precipitation size distribution. Because n0 and k do not in general add linearly, we convert from n0 and k to M and N, add the weighted precipitation size distribution to the suspended cloud particle size distribution, and generate an overall particle size distribution that is then converted back to n0 and k. We assume this population is stable in time; in reality particles fall down and similar particles, which may have a charging history involving different conditions, fall from above.
Noninductive charge transfer is assumed, with the empirically observed formula for the amount of charge transferred between colliding ice particles of Keith & Saunders (1989). It is assumed that a collision between two particles will lead to charge transfer with probability:
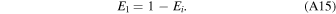
As a result, particles of equal size colliding will have no net effect. As such, wrel(i, j) is calculated simply as the difference between the terminal velocities wi (b0(i)) and wi (b0(j)), the arithmetic means of the bin bounds, and collision probability is calculated as with particle growth. In this fashion, a rate of charge accumulation per particle is calculated for each bin; under the assumptions being made, this rate is constant in time. Since particles are therefore charged linearly, the electric current caused by faster fall velocities of larger particles also increases linearly in time, and therefore the electric field is quadratic in time:

The current density is linear in time:
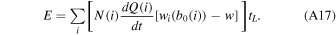
When the electric field reaches its breakdown value, a lightning discharge occurs. This breakdown value is taken as linear with pressure, with coefficient 5 m2 C−1 Pa−1 for hydrogen on Jupiter and 3 m2 C−1 Pa−1 for nitrogen/oxygen on Earth from Gibbard (1996), based on a combination of theoretical modeling and observational data. The energy released per unit volume is equal to this breakdown field, times the total charge transferred per unit area. When lightning thus occurs, the charge is assumed to reset to zero at that location and begins building up as before. Thus, dividing the energy per volume by the time-to-discharge yields a rate of the time-averaged energy production per unit volume. Integrating over pressure leads to a power per unit area. The calculated power is a rate per unit area of updraft; that is, it does not include downwelling regions of the storm, and it does not include sections of the atmosphere that do not contain a thunderstorm at a given time.







