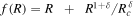Abstract
We investigate the formation of the large-scale structures in the present accelerated era in the f(R) gravity background. This is done by considering the linear growth of matter perturbations at low redshift z < 1. The effect of f(R) alters the behavior of the matter density perturbations from the matter-dominated universe to the late-time accelerated universe, which is encoded in the Newtonian gravitational constant as G → Geff. The modified gravitational constant (Geff) depends on the form of f(R). The late-time accelerated expansion affects the formation of large-scale structures by slowing down the growth of matter density. On the other hand, f(R) increases the growth rate of the matter density perturbations. We have found that the source term in the f(R) background, GeffΩm, overcomes the accelerated expansion and the effect of accelerated expansion suppresses the formation of the large-scale structures in the asymptotic future.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Today we live in the phase of accelerated expansion (Perlmutter et al. 1997; Riess et al. 1998) of the universe, which has the dynamical effect similar to inflation in the very beginning. We require the matter that has sufficient negative pressure to explain accelerated expansion of the universe but the known matter does not have such negative pressure. We can handle this problem by adding exotic matter in the gravitational Lagrangian density. These models are known as dark energy (DE) models (Sahni & Starobinsky 2000; Padmanabhan 2003; Copeland et al. 2006; Sahni 2008; Verma 2010). We can also consider the modification in the Lagrangian density of the gravitational part of Einstein's theory of general relativity to explain the accelerated expansion of the universe, broadly called the modified theory of gravity (MG).
In the present work, we consider the f(R) theory of gravity as an effective theory and study the large-scale structure formation. Of course, in the f(R) theory of gravity, we replace Ricci scalar R with a general function of R in the Einstein–Hilbert action (Capozziello 2002) and f(R) reduced to the general relativity (GR) in the 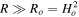 regime.
regime.
The astrophysical structures existing today in the universe had started evolving before the inflation in the very early universe. The motherland of initial seeds of the large-scale structures is inflation and was created due to quantum fluctuation in the inflation field in this period. These seeds started growing after decoupling of the matter from the radiation but in different ways in the radiation-dominated (RD), matter-dominated (MD) and the late-time cosmic acceleration phases. If we use DE models and f(R) models to explain accelerated expansion, they provide the same results after tuning the free parameters but the growth of matter perturbations is different in both approaches (Starobinsky 1998). Matter density perturbations are used as a tool to distinguish the DE models in GR background Λ cold dark matter (ΛCDM) from f(R) gravity models (Starobinsky 1998; Gannouji et al. 2009; Narikawa & Yamamoto 2010). The matter density perturbations depend on the models of f(R) gravity; therefore, their behavior varies with the parameters of the models.
One of the most popular models in f(R) gravity (Amendola et al. 2007; Appleby & Battye 2007; Hu & Sawicki 2007; Percival et al. 2007; Starobinsky 2007; Tsujikawa 2008) is the Dvali–Gabadadze–Porrati (DGP) brane-world model (Dvali et al. 2000), beyond the ΛCDM model. In this paper we have used the power-law models (Capozziello et al. 2003; Carloni et al. 2005; Jaime 2013; Motohashi 2015; Sharma & Verma 2022a, 2022b; Sharma et al. 2020, 2021; Yadav & Verma 2019), the Starobinsky model (Starobinsky 1998), and the ΛCDM model (Sahni & Starobinsky 2000; Padmanabhan 2003) to study the matter density perturbations and compare their results with observations (Cole et al. 2005) in the linear regime.
This paper is organized in five sections. In Section 2 we give the basic introduction of the modified theory of gravity and its dynamical equations. We discuss the cosmological perturbations in the linear regime and matter density perturbations in Section 3. In Section 4, we investigate the behavior of the growth index and modified gravitational constant. We also discuss the nature of matter density perturbations in the asymptotic future. At the end, in Section 5 we give a summary of the results of our work.
(Throughout the paper, we have used c = 1 and κ2 = 8π G).
2. Modified f(R) Background
A simple way to modify the gravity is to replace the Ricci curvature R with a function of R in the Einstein–Hilbert action (Amendola & Tsujikawa 2010; De Felice & Tsujikawa 2010; Sotiriou & Faraoni 2010; Tsujikawa 2018). Thus, the action in f(R) gravity is given as

where 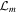 is the matter field Lagrangian density minimally coupled with curvature. Taking the variation of Equation (1) with respect to metric tensor gμ
ν
, we obtain the gravitational field equations as
is the matter field Lagrangian density minimally coupled with curvature. Taking the variation of Equation (1) with respect to metric tensor gμ
ν
, we obtain the gravitational field equations as
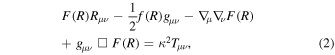
where □ ≡ gμ
ν
∇μ
∇ν
is the covariant d'Alembertian operator, F(R) = ∂f/∂R, ∇μ
is the covariant derivative, and Tμ
ν
is the energy-momentum tensor of matter filed and it should satisfy the energy-momentum conservation equation 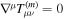 of the matter field. The trace of Equation (2) is
of the matter field. The trace of Equation (2) is
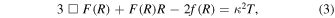
where  and the suffix m denotes pressureless matter (including dark matter). The Ricci scalar in the flat FLRW background metric is
and the suffix m denotes pressureless matter (including dark matter). The Ricci scalar in the flat FLRW background metric is 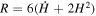 . The first derivative of the f(R) gives a new scalar degree of freedom that denotes the deviation from GR. If we consider the de Sitter universe, then the Hubble expansion rate is constant
. The first derivative of the f(R) gives a new scalar degree of freedom that denotes the deviation from GR. If we consider the de Sitter universe, then the Hubble expansion rate is constant 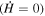 . Therefore, the Ricci scalar becomes constant and □F = 0 at the de Sitter point. We can rewrite Equation (3) for the de Sitter point as
. Therefore, the Ricci scalar becomes constant and □F = 0 at the de Sitter point. We can rewrite Equation (3) for the de Sitter point as
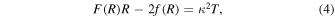
and the solution of the above Equation (4) becomes
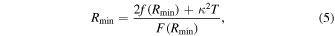
where Rmin is the value of the Ricci scalar at de Sitter point.
Equation (2) can also be written as
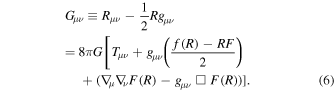
We can, in a straightforward way, compare the above Equation (6) with Einstein's equation Rμ
ν
− (1/2)Rgμ
ν
= κ2
Tμ
ν
in GR. We have modified the energy-momentum tensor as  .
.
We obtain Friedmann equations in the f(R) gravity as (Huang 2014)
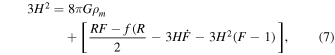
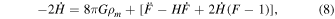
where 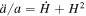 and
and  . Some extra terms appear in the Friedmann Equations (7) and (8) due to f(R) gravity, which act as pressure and energy density due to f(R) gravity. We have an effective equation of state in the f(R) gravity given as
. Some extra terms appear in the Friedmann Equations (7) and (8) due to f(R) gravity, which act as pressure and energy density due to f(R) gravity. We have an effective equation of state in the f(R) gravity given as
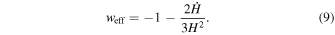
We obtain the effect of acceleration in the f(R) gravity without introducing an exotic form of matter as a DE component. The equation of state to explain the effect of the late-time acceleration is w = −1.03±0.03 in Aghanim et al. (2020). The expression of weff (Sharma & Verma 2022a) for model 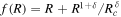 is
is
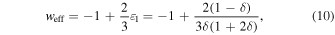
where ε1 ≃ (1 − δ)/[3δ(1 + 2δ)] and δ is a model parameter.
The value of weff ≃ −0.998 at δ = 0.98, which is consistent with Planck 2018 data (Aghanim et al. 2020). Figure 1 clearly shows that the value of weff never goes below −1.02 at δ = 2.2247. This value is inside the present observational limits. We can recover the ΛCDM model weff = −1 at δ = 1. The quantitative behavior of the model parameter δ for acceleration and inflation has been discussed in detail in our previous work (Sharma & Verma 2022a). We obtained the range of δ, which is 0.366 < δ < 1 for acceleration and for inflation (i.e., for a quasi–de Sitter universe) δ ≈ 0.98. Therefore, we restrict to this limit and use δ = 0.98 for late-time cosmic acceleration as well.
Figure 1. Plot between the weff and model parameter δ. We have found that weff gains both positive and negative values at different δ. There is a boundary line at δ ≃ 0.3.
Download figure:
Standard image High-resolution image3. Matter Density Perturbations in f(R) Gravity
Now, we study matter density perturbations in the linear regime, which enables us to distinguish DE models in f(R) gravity from the other theories of DE in GR. We can also distinguish the ΛCDM model from f(R) theories. We take a metric perturbation about the flat FLRW background (De Felice & Tsujikawa 2010):
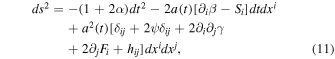
where α, β, γ, and ψ are scalar perturbations, Si and Fi are vector perturbations, and hij is the tensor perturbation. In this paper we focus on the scalar perturbations only. After using the longitudinal gauge, the line element without vector and tensor perturbations is given (De Felice & Tsujikawa 2010) as
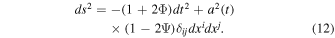
We include perturbations in the nonrelativistic matter with negligible pressure, pm = 0, in the f(R) background (De Felice & Tsujikawa 2010):
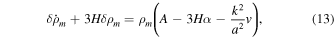
where 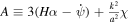 ,
, 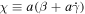 . After taking the longitudinal gauge α = Φ, ψ = Ψ and considering quasi-static approximation in the f(R) background (Boisseau et al. 2000; Copeland et al. 2006; Tsujikawa 2007; Tsujikawa et al. 2008), when the wavenumber k keeps deep inside the Hubble radius (k ≫ aH):
. After taking the longitudinal gauge α = Φ, ψ = Ψ and considering quasi-static approximation in the f(R) background (Boisseau et al. 2000; Copeland et al. 2006; Tsujikawa 2007; Tsujikawa et al. 2008), when the wavenumber k keeps deep inside the Hubble radius (k ≫ aH):

and
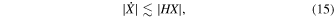
where 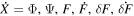 . Thus the equation for matter density perturbations becomes (De Felice & Tsujikawa 2010)
. Thus the equation for matter density perturbations becomes (De Felice & Tsujikawa 2010)
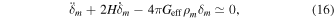
where δm = δ ρm /ρm and Geff is the effective gravitational coupling given in Tsujikawa (2007) and Tsujikawa et al. (2008) as
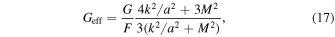
where M2 is the mass of the new degree of freedom given as
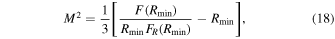
with FR
≡ ∂2
f(R)/∂R2. In Equation (16), the second term has the Hubble parameter. It carries the information of expansion of the universe and Geff contains the information about the modification of the gravity through f(R). In the high-density region (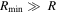 ) Equation (18) becomes M2 ≃ 1/3FR
(Tsujikawa et al. 2008). For viable f(R) gravity models, we have assumed ∣F(R)∣ ≪ 1 and ∣FR
∣ ≪ 1. Then Geff/G can be further written in the (Gannouji et al. 2009; Narikawa & Yamamoto 2010) simplified way as
) Equation (18) becomes M2 ≃ 1/3FR
(Tsujikawa et al. 2008). For viable f(R) gravity models, we have assumed ∣F(R)∣ ≪ 1 and ∣FR
∣ ≪ 1. Then Geff/G can be further written in the (Gannouji et al. 2009; Narikawa & Yamamoto 2010) simplified way as
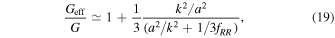
where fRR ≡ ∂2 f(R)/∂R2. Above relation shows that the Geff depends on the wavenumber k and on the f(R) model parameter. In the regime where k/a ≪ M the effective gravitational constant becomes Geff ≃ G, and mimics GR. In the scalar-tensor regime k/a ≫ M, Geff becomes ≃ 4G/3, from Equation (19). The transition from GR to scalar-tensor regime occurs during the MD phase at k/a = M.
Now, Equation (16), after changing the 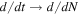 and a growth parameter
and a growth parameter 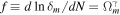 (where γ is the growth index) becomes
(where γ is the growth index) becomes
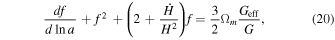
where 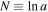 and Ωm
= 8π
G
ρm
/(3H2). We have found the constant growing mode of the matter density perturbation deep inside the MD universe from Equation (20) if f = p (Gannouji & Polarski 2008; Gannouji et al. 2009):
and Ωm
= 8π
G
ρm
/(3H2). We have found the constant growing mode of the matter density perturbation deep inside the MD universe from Equation (20) if f = p (Gannouji & Polarski 2008; Gannouji et al. 2009):
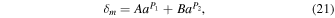
where 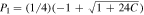 ,
, 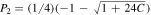 , and C ≡ (Geff/G)Ωm
= constant. This solution is also valid for z < 1. In the regime where k/a ≪ M we have C ≈ 1 and C ≈ (4/3) for k/a ≫ M. We get δm
in Starobinsky (2007) as
, and C ≡ (Geff/G)Ωm
= constant. This solution is also valid for z < 1. In the regime where k/a ≪ M we have C ≈ 1 and C ≈ (4/3) for k/a ≫ M. We get δm
in Starobinsky (2007) as
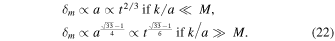
If we consider the growth index γ, as a function of redshift z, Equation (20) can be expressed in terms of Ωm
, wDE, γ, and 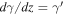 , using
, using 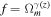 as
as
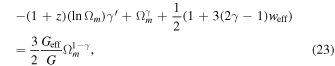
and 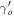 at redshift z = 0 is
at redshift z = 0 is
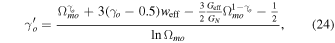
where Ωm is the matter density parameter and o indicates the present values of the parameters. Geff/G = 1 in the ΛCDM model in GR background and the above expression becomes
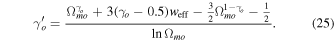
We have found the constraint on the growth index as 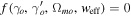 and the growth index in the DE models in GR given in Wang & Steinhardt (1998) and Nesseris & Perivolaropoulos (2008) as
and the growth index in the DE models in GR given in Wang & Steinhardt (1998) and Nesseris & Perivolaropoulos (2008) as
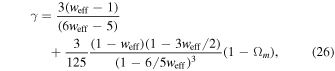
where γ takes constant value ∼0.56. However, we considered the dependence of γ on the redshift z beyond the GR. Therefore we can expand it around z as 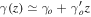 for 0 ≤ z ≤ 0.5 in Polarski & Gannouji (2008).
for 0 ≤ z ≤ 0.5 in Polarski & Gannouji (2008).
The growth of the matter perturbation changes after entering into the scalar-tensor regime until the time tacc, which is the epoch at which universe enters the late-time accelerated phase.
4. Model Dependence on the Growth of Matter Perturbations
We can distinguish the DE models in GR background and beyond the GR on the basis of the power spectrum of the growth of matter perturbations Δns , growth index γ, growth factor f, and Geff.
4.1. ΛCDM Model
In the ΛCDM model, the Λ term is used to explain the late-time cosmic acceleration with cold dark matter. In this model, the equation of state is constant wΛ = −1 and Geff = GN because df/dR = 1. We have Δns = 0 here, and the nonzero Δns indicates a theory beyond the GR.
In previous works (Peebles 1984; Lahav et al. 1991), several authors obtained approximately constant growth index γ with negligible dependence on the Ωm . Some papers (Wang & Steinhardt 1998; Gannouji & Polarski 2008; Gannouji et al. 2009) show γo = 6/11 ≈ 0.5454.
However, some authors realized that the growth index might be a function of redshift and therefore, the deviation from constant γ provides a new constraint on the theories beyond GR. This information is stored in the 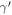 . For ΛCDM, (Gannouji & Polarski 2008) the growth index and its derivative are 0.554 ≤ γo
≤ 0.558 and
. For ΛCDM, (Gannouji & Polarski 2008) the growth index and its derivative are 0.554 ≤ γo
≤ 0.558 and 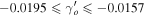 for 0.2 ≤ Ωmo
≤ 0.35. Many other models in the GR background (Gannouji & Polarski 2008) have
for 0.2 ≤ Ωmo
≤ 0.35. Many other models in the GR background (Gannouji & Polarski 2008) have 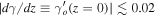 with slight dependence on Ωmo
. But for slowly varying wDE, and Ωm
= 0.3 the growth index is slightly higher γo
= 0.555 in Gannouji et al. (2009). A higher and positive value of the
with slight dependence on Ωmo
. But for slowly varying wDE, and Ωm
= 0.3 the growth index is slightly higher γo
= 0.555 in Gannouji et al. (2009). A higher and positive value of the 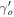 is a clear signal of the departure from the ΛCDM model. Authors have found the bound on the Δns
conservatively in Gannouji et al. (2009) as
is a clear signal of the departure from the ΛCDM model. Authors have found the bound on the Δns
conservatively in Gannouji et al. (2009) as
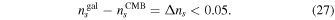
However, the observations (Tegmark et al. 2006) do not allow for any significant difference in between the slopes of the two power spectra.
4.2. Starobinsky Model
In this part of the paper, we have used the Starobinsky model in the f(R) gravity beyond the GR background, gives as
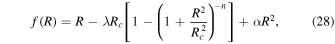
where λ, n > 0 and β Rc ≃ 2Λ(∞) (Gannouji et al. 2009). In the above model, the second term is used to explain the late-time cosmic acceleration and the third term for inflation (very early acceleration).
In the Starobinsky model, one finds (Gannouji et al. 2009) a distinction from the ΛCDM model on basis of the evolution of matter perturbations. There appears to be a difference in the spectral index ns
CMB of the primordial power spectrum 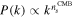 and spectral index ns
gal, calculated from the galaxy power spectrum
and spectral index ns
gal, calculated from the galaxy power spectrum 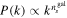 . We obtained Δns
in Starobinsky (2007) after dropping the α
R2 from the model given by Equation (28). In the MD era at k/a ≪ M
. We obtained Δns
in Starobinsky (2007) after dropping the α
R2 from the model given by Equation (28). In the MD era at k/a ≪ M
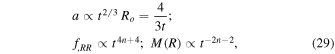
and δm
grows as t2/3 and it changes after k = aM(R) as 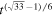 and to tacc, the end of the MD epoch (Starobinsky 2007; De Felice & Tsujikawa 2010). Thus,
and to tacc, the end of the MD epoch (Starobinsky 2007; De Felice & Tsujikawa 2010). Thus,
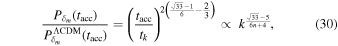
where time t = tacc corresponds to the end of the MD phase and at that epoch the universe enters into the later-time acceleration phase. Now, we have Δns (Starobinsky 2007; De Felice & Tsujikawa 2010):
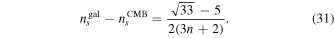
The above expression depends on the model parameter n. If n increases then Δns shifts toward the (Tegmark et al. 2006) bound given by Equation (27). Therefore, the constraint on n is n ≥ 2. For n = 1, Δns = 0.074, and for n = 2, Δns = 0.047 at k = 3000ao Ho , zacc = 0.7 and zk (tk ) = 2.5.
In this model, the growth index γo
(z = 0) ≃ 0.41 is smaller than the ΛCDM model in the GR background. We have also found out that γo
≃ 0.4, 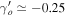 for Ωmo
= 0.32 and γo
≃ 0.43,
for Ωmo
= 0.32 and γo
≃ 0.43, 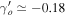 for Ωmo
= 0.23 in Gannouji & Polarski (2008) and Gannouji et al. (2009). The matter density of the universe is lower when γo
and the value of
for Ωmo
= 0.23 in Gannouji & Polarski (2008) and Gannouji et al. (2009). The matter density of the universe is lower when γo
and the value of 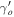 move closer to the predicted value even though it still remains far from it.
move closer to the predicted value even though it still remains far from it.
We have found the significant effect of the f(R) model on the source term as

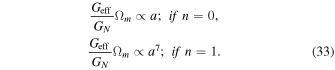
We have used different values of n at which we consider the de Sitter type background expansion, i.e., w = −1 and 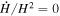 .
.
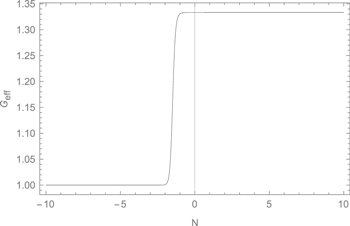
We have found that the source terms always dominates over the expansion term. Thus, Geff/GN remains 4/3 in the asymptotic future and the growth of the matter perturbations never ends. We can also see it from Figure 2 where growth in matter density is large at the present epoch but far back in the MD phase, and the growth rate was smaller than the present rate.
Figure 2. This is the plot between Geff and the number of e-foldings N in the Starobinsky model. We take the value of model parameters as n = 1 and λ = 1. It is seen that the growth never ends in this model in the asymptotic future.
Download figure:
Standard image High-resolution image4.3.
 Model
Model
We aim to study the evolution of the matter density perturbations in our model given by Equation (34) and compare it with the ΛCDM model in the GR background and the Starobinsky model in the f(R) background. Certainly, the evolution of the matter density perturbations δm or scalar perturbations begins at the preinflationary universe and further enters into the radiation and MD eras. Indeed, at the end, these perturbations enter into the late-time comic acceleration phase. These perturbations got frozen during inflation and started growing after reentering the Hubble horizon. Growth of the matter density perturbation far inside the MD era is δm ∝ t2/3 and after the transition from GR to the scalar-tensor regime at k = aH = M(R)a, δm evolves differently, which depends on the model parameters. Our f(R) model is given as
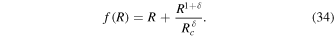
Now we calculate scale factor a, f(R),RR , and M2 from Equation (34) as
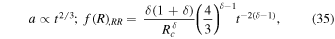
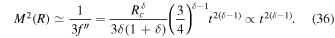
Further using Equation (36) to obtain the ratio 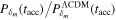 we have
we have
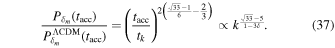
Thus, we can obtain the Δns
from Equation (37) by using the definition 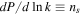 (Amendola & Tsujikawa 2010) as
(Amendola & Tsujikawa 2010) as
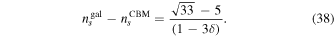
Equation (38) depends only on the model parameter δ. Figure 3 shows that when δ ≤ 1 then Δns
< 0, meaning  and if 1 < 3δ, or 1/3 < δ then Δns
> 0. The value of Δns
≃ −0.383795 at δ = 0.98, which is much larger than the lower bounds (Tegmark et al. 2006) given by Equation (27).
and if 1 < 3δ, or 1/3 < δ then Δns
> 0. The value of Δns
≃ −0.383795 at δ = 0.98, which is much larger than the lower bounds (Tegmark et al. 2006) given by Equation (27).
Figure 3. Plot in the left panel shows the behavior of Δns for 1 − 3δ > 0 and in the right panel for 1 − 3δ > 0. For accelerated expansion we have 0.336 < δ < 1. This means Δns is a negative value, but as δ → 0, then Δns also tends to zero. That is consistent with the current observations.
Download figure:
Standard image High-resolution imageWe have found a discrepancy between the spectral index obtained from the galaxy survey ns gal, and the primordial power spectrum from the Cosmic Microwave Background (CMB), ns CMB , beyond the GR background.
We have used the growth parameter f, the growth index γ, and the variation of the γ with redshift (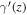 ) to distinguish f(R) models from the ΛCDM model. Information about the modification in GR is stored in the Geff and equation of state weff in Equations (18) and (9), respectively. At a large redshift Geff → G/F ≃ 1 and at a low redshift Geff → 4G/3F ≃ 1.33. Geff in the model given by Equation (34) is
) to distinguish f(R) models from the ΛCDM model. Information about the modification in GR is stored in the Geff and equation of state weff in Equations (18) and (9), respectively. At a large redshift Geff → G/F ≃ 1 and at a low redshift Geff → 4G/3F ≃ 1.33. Geff in the model given by Equation (34) is
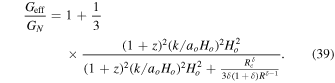
Now, we use  and
and ![$R\simeq 3{H}_{o}^{2}[{{\rm{\Omega }}}_{{mo}}{a}^{-3}+(1-3{w}_{\mathrm{eff}}){{\rm{\Omega }}}_{{DEo}}{a}^{-3(1+{w}_{\mathrm{eff}})}]$](https://content.cld.iop.org/journals/0004-637X/934/1/13/revision1/apjac7b8eieqn42.gif) in the above equation to obtain
in the above equation to obtain
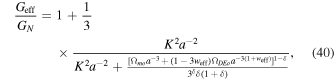
where K ≡ k/(ao Ho ) and 1 + z = 1/a.
The value of Geff does not seem to reach unity in the large redshift (during the MD era) regime. This means that the Newtonian gravitational constant is always modified in this model.
Further, we focus on the source term (last term) and expansion term (third term) or growth parameter at present and in the asymptotic future. We have obtained the modified gravitational constant from Equation (40) and the matter density parameter, Geff/GN
∝ a3(1−δ)−2 and 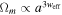 (Linder & Polarski 2019), respectively. Therefore, the combined expression becomes
(Linder & Polarski 2019), respectively. Therefore, the combined expression becomes

The value weff in Equation (34) are ∼−0.988 and ∼−1.02 (Sharma & Verma 2022a). Thus, we consider the equation of state for background accelerated expansion to be weff = − 1 in Equation (41) leading to
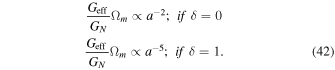
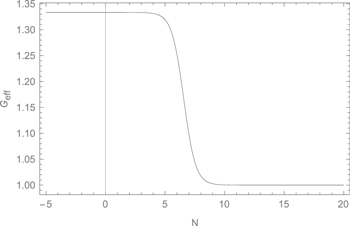
Here we notice that (Geff/GN )Ωm decreases in the asymptotic future and the expansion term dominates over it and the growth rate of the matter perturbation ends after ∼5e folds. However, at the present accelerated epoch, the source term dominates over the expansion term. We can see it from Figure 6.
We have γ in the f(R) gravity (Narikawa & Yamamoto 2010) as
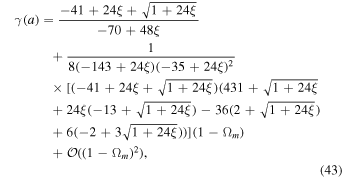
where Geff/G = ξ. Now we use Ωmo ≃ 0.32 and weff from Equation (10) for calculating the γo at z = 0 from Equation (43). This is given as

Hence, we can say that our results are very close to the ΛCDM model. After putting the value of the Geff/GN
from Equation (40) in Equation (24) to calculate the value of 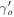 for the model
for the model 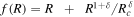 , we obtain
, we obtain

The large value of the 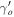 shows clear distinction from the DE in the GR background and from the ΛCDM model. The parameter
shows clear distinction from the DE in the GR background and from the ΛCDM model. The parameter 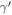 increases the transparency in the different types of DE models. The variation of
increases the transparency in the different types of DE models. The variation of 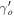 at different values of matter density Ωmo
with δ in Figure 4 shows
at different values of matter density Ωmo
with δ in Figure 4 shows 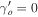 if δ is around 0.3. This means that we find the signature of the f(R) in this model for δ > 0.3. This gives a large range of the model parameter δ in large-scale structure formation and Figure 5 also shows the large value of
if δ is around 0.3. This means that we find the signature of the f(R) in this model for δ > 0.3. This gives a large range of the model parameter δ in large-scale structure formation and Figure 5 also shows the large value of 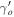 .
.
Figure 4. Plot of 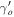 with respect to the model parameter δ for different Ωmo
. It shows the small dependence on the Ωmo
. It also provides a wide range of δ for matter density perturbations in the linear regime.
with respect to the model parameter δ for different Ωmo
. It shows the small dependence on the Ωmo
. It also provides a wide range of δ for matter density perturbations in the linear regime.
Download figure:
Standard image High-resolution imageFigure 5. Plot between 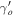 and γo
for different values of Ωmo
. This plot shows the small dependence of Ωmo
on the
and γo
for different values of Ωmo
. This plot shows the small dependence of Ωmo
on the 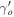 .
.
Download figure:
Standard image High-resolution image5. Conclusion
In this study we conclude that the growth rate is influenced due to the modified gravity models and it also depends on the f(R) form in the models. We find the value of γo
for the model given by Equation (34) with δ = 0.98 and Ωmo
= 0.32 to be 0.547. This value is in very close agreement with the ΛCDM model. But the value of 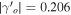 , which is larger than the ΛCDM value, where
, which is larger than the ΛCDM value, where  in the GR background. This allows us to distinguish this model from the ΛCDM model. We notice a the small dependence of
in the GR background. This allows us to distinguish this model from the ΛCDM model. We notice a the small dependence of 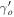 on the value of Ωmo
and also on the model parameter δ from Figure 4. In Figure 5, we show that our model gives the value of γo
within the range of observational values from the Dark Energy Survey/Planck/Joint Lightcurve Analysis/Baryon Acoustic Oscillations (Abbott et al. 2018) is γo
= 0.640 ± 0.076 and from the Planck/TT+TE+EE+Low+lensing (Aghanim et al. 2020) is γo
= 0.68 ± 0.089.
on the value of Ωmo
and also on the model parameter δ from Figure 4. In Figure 5, we show that our model gives the value of γo
within the range of observational values from the Dark Energy Survey/Planck/Joint Lightcurve Analysis/Baryon Acoustic Oscillations (Abbott et al. 2018) is γo
= 0.640 ± 0.076 and from the Planck/TT+TE+EE+Low+lensing (Aghanim et al. 2020) is γo
= 0.68 ± 0.089.
There is an another quantity, the Newtonian gravitational constant, which is potentially modified due to the f(R) model given by Equation (34). Its modification alters the behavior of the matter density perturbations.
We obtained the w ≃ −0.998 in our previous paper (Sharma & Verma 2022a). Thus, we assumed the de Sitter type background expansion and so the Hubble friction term of Equation (20) remains almost constant. Growth in the asymptotic future in our model, which is given by Equation (34), will end because Geff/GN
Ωm
∝ a−5 at δ = 1 decreases faster than the expansion term. On the other hand, the Starobinsky model shows the continuous growth in the matter density in the asymptotic future. At the present accelerated epoch, our model and the Starobinsky model both show an enhanced growth of the matter density at a low redshift i.e., z < 1 because Geff/GN
Ωm
is dominating over the expansion term 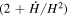 . We can see that Geff is higher than unity from Figures 2 and 6. Our model also supports the results (Linder & Polarski 2019) where the cosmic growth ends in the asymptotic future in the f(R) gravity and also in the ΛCDM model in GR. Therefore, our model and the ΛCDM model have the identical behavior of the growth of the matter density perturbations. Indeed, the real information about the model beyond GR is encoded in the form of Geff,
. We can see that Geff is higher than unity from Figures 2 and 6. Our model also supports the results (Linder & Polarski 2019) where the cosmic growth ends in the asymptotic future in the f(R) gravity and also in the ΛCDM model in GR. Therefore, our model and the ΛCDM model have the identical behavior of the growth of the matter density perturbations. Indeed, the real information about the model beyond GR is encoded in the form of Geff, 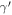 and the evolution of the cosmic growth.
and the evolution of the cosmic growth.
Figure 6. Plot between Geff and the number of e-foldings N in the model given by Equation (34).
Download figure:
Standard image High-resolution imageThe authors are thankful to IUCAA, Pune for support under the associateship program where most of the work was done. A.K.S. is also thankful to Vipin Sharma, Bal Krishna Yadav, and Vaishakh Prasad for the useful discussions on various aspects of matter density perturbations in the modified theory of gravity.