Abstract
We discuss dynamical friction in an N-body system in the presence of tidal interactions caused by a distant external source. Using the distant tide approximation, we develop a perturbation scheme for the calculation of dynamical friction that takes tidal effects into account in linear order. In this initial analytic approach to the problem, we neglect the influence of tides on the distribution function of stars in the background stellar system. Our result for the dynamical friction force in the appropriate limit is in agreement with Chandrasekhar's formula in the absence of tides. We provide preliminary estimates for the tidal contributions to the dynamical friction force. The astrophysical implications of our results are briefly discussed.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
When a body of mass M moves with velocity v M through an infinite homogeneous medium of stars with average stellar mass m, m ≪ M, it slows down due to the gravitational drag of the stars. The resulting dynamical friction force was first calculated by Chandrasekhar (Chandrasekhar 1943; Binney & Tremaine 2008) and is given by
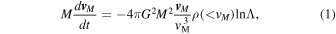
where vM
= ∣
v
M
∣, ρ( < vM
) is the density of stars with speeds less than vM
and 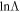 is the so-called Coulomb logarithm. In fact,
is the so-called Coulomb logarithm. In fact, 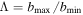 , where b is the scattering impact parameter,
, where b is the scattering impact parameter, 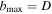 is the diameter of the smallest sphere that completely surrounds the whole system and
is the diameter of the smallest sphere that completely surrounds the whole system and 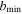 is the maximum of the size of the incident mass M and
is the maximum of the size of the incident mass M and  . For the background material and comprehensive treatment of Chandrasekhar's formula (1) and its limitations, see Binney & Tremaine (2008). Equation (1) can be interpreted in terms of gravitational wake, namely, the disturbance caused by the motion of M through the medium produces a density enhancement in the incident body's wake. This overdensity decelerates M via gravitational attraction; see Tremaine & Weinberg (1984) and the references cited therein.
. For the background material and comprehensive treatment of Chandrasekhar's formula (1) and its limitations, see Binney & Tremaine (2008). Equation (1) can be interpreted in terms of gravitational wake, namely, the disturbance caused by the motion of M through the medium produces a density enhancement in the incident body's wake. This overdensity decelerates M via gravitational attraction; see Tremaine & Weinberg (1984) and the references cited therein.
Chandrasekhar's formula (1) is a consequence of two-body Newtonian scattering of M from each of the stars in the medium; indeed, it is an approximate result that ignores the attractive gravitational interaction of the stars. In the scattering of M from a star of mass m, the final (t = ∞ ) deflected momentum of M has a component along the initial (t = −∞ ) direction of its incident momentum M v M that is invariant to linear order in the Newtonian constant G, but decreases to order G2 and beyond in accordance with (Binney & Tremaine 2008)
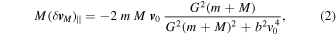
where
v
0 =
v
(t = −∞ ),
v
=
v
M
−
v
m
is the relative velocity, v0 = ∣
v
0∣ and b is, as before, the impact parameter. Here, 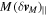 is the net change in the momentum of M along its initial direction of incidence as a consequence of gravitational scattering from m. The net loss of momentum of M along its initial direction of motion is the source of the dynamical friction force.
is the net change in the momentum of M along its initial direction of incidence as a consequence of gravitational scattering from m. The net loss of momentum of M along its initial direction of motion is the source of the dynamical friction force.
While numerous studies have verified that Chandrasekhar's formula (1) gives a rather accurate description in many different systems (e.g., van den Bosch et al. 1999; Boylan-Kolchin et al. 2008), the derivation of formula (1) is based on the assumption of an infinite homogeneous background medium and furthermore neglects the self-gravity of the background stars. In the meantime, the calculation of dynamical friction has been extended to inhomogeneous media. In spherically symmetric environments, for example, the phenomenon of "core stalling" has been found, where dynamical friction disappears within the central constant-density cores of massive halos (Read et al. 2006; Banik & van den Bosch 2021a). It has also been shown that a body orbiting outside a self-gravitating system experiences orbital decay and loses angular momentum (Lin & Tremaine 1983). Moreover, the influence of gravitational interaction of the background stars on dynamical friction has been considered in several analytical and numerical studies (see Tremaine & Weinberg 1984; Banik & van den Bosch 2021a, and the references cited therein).
In connection with tides, theoretical studies of dynamical friction in the presence of tidal interactions have generally used the impulse approximation for the sake of simplicity and have thus been restricted to the tidal shocking method (e.g., Spitzer 1958; Colpi & Pallavicini 1998; Gnedin et al. 1999; Binney & Tremaine 2008; Banik & van den Bosch 2021b). The impulse approximation was originally used by Fermi in quantum scattering calculations (Fermi 1936). In reference to tidal interaction, it signifies the change in the velocities of stars as a result of a brief tidal encounter of a galaxy. The time integral of tidal force is the impulse that results in the change of momentum. Within this approximation, the timescale of the encounter between the system and the external tidal source is much shorter than the dynamical timescale associated with the internal dynamics of the system. Naturally, this approximation is restrictive and cannot be applied to arbitrary astrophysical systems. Therefore, dynamical friction studies that deal with ordinary tidal interactions have been mostly based on N-body simulations (e.g., Muñoz et al. 2005; Renaud et al. 2011; Battaglia et al. 2015; Wang et al. 2017; Iorio et al. 2019). Indeed, various N-body simulations of Milky Way (MW) satellites have reported that the stellar components of these dwarf spheroidal (dSph) galaxies are not directly affected by the tidal field of the MW (e.g., Battaglia et al. 2015; Wang et al. 2017, 2019; Iorio et al. 2019); that is, the influence of tidal effects on the stellar kinematics must be rather small.
The main purpose of the present work is to extend Equation (2) in the presence of tidal interactions. Specifically, we study the two-body Newtonian scattering of M from a star of mass m within a stellar system that is under the tidal influence of a distant mass. To simplify matters, we expand the solution of the equation of relative motion of the binary in powers of the Newtonian gravitational constant and work to second order in G, since dynamical friction first appears at this order in accordance with Equation (2). In Section 2, we derive the equation of relative motion in the presence of the tides. To solve this equation, we present a perturbation scheme in powers of G in Section 3 and estimate the influence of tides on dynamical friction. The astrophysical implications of our results are briefly treated in Section 4. Finally, we discuss the limitations of our approach in Section 5.
2. Tidal Perturbation of the Gravitational Two-body System
Imagine a Newtonian two-body system with masses m1 and m2 within a stellar medium (of extent D) that is tidally perturbed by a distant galactic mass  ,
,  . We focus attention on the two-body system and neglect the gravitational interaction of the two bodies with the stars of the background medium. The external source
. We focus attention on the two-body system and neglect the gravitational interaction of the two bodies with the stars of the background medium. The external source  generates a gravitational potential Φ at the location of the two-body system. The equations of motion of m1 and m2 are given in a local Cartesian coordinate system by
generates a gravitational potential Φ at the location of the two-body system. The equations of motion of m1 and m2 are given in a local Cartesian coordinate system by
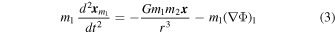
and
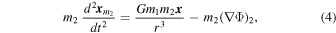
where
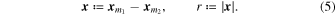
We assume that 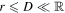 , where
, where 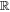 is the distance of the binary system to
is the distance of the binary system to 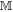 . We expand the gravitational force of
. We expand the gravitational force of 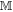 on the two-body system about its center of mass
on the two-body system about its center of mass
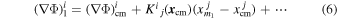
and
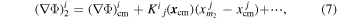
where Kij = ∇i ∇j Φ is the symmetric and traceless tidal matrix evaluated at the center of mass of the binary system
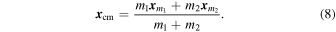
We assume that  is negligibly small compared to unity; therefore, we henceforth neglect terms of second and higher orders in Equations (6) and (7). Then, the equations of motion imply
is negligibly small compared to unity; therefore, we henceforth neglect terms of second and higher orders in Equations (6) and (7). Then, the equations of motion imply
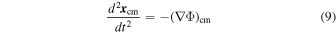
and
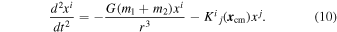
Appendix A contains the natural extension of the two-body approach developed here to an N-body system. However, it is not known how to derive the dynamical friction force within this scheme; therefore, in conformity with Chandrasekhar's approach, we hereafter ignore the gravitational interaction between the background stars.
To interpret Equations (9) and (10), we note that our dynamical system has a slow motion given by Equation (9) and a fast motion given by Equation (10). The slow motion involves the Keplerian revolution of the whole binary system about 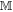 . The fast motion involves the internal scattering orbit of the tidally perturbed gravitational two-body system. We assume that during the fast motion, the slow motion can be considered to be essentially uniform. That is, the deviation of the Keplerian orbit of the center of mass of the binary from a straight line with constant velocity can be neglected during the fast motion of the binary. This approximation scheme can be naturally extended to include the background stellar medium in order to facilitate the calculation of dynamical friction. Moreover, in Equation (10), we neglect the temporal dependence of the tidal matrix Ki
j
(
x
cm) in our approach. In general, the temporal variation of the tidal field can lead to the possibility of resonance with the internal pulsation of the system; in fact, such a resonant orbital coupling has been investigated in Kuhn & Miller (1989) and Fleck & Kuhn (2003).
. The fast motion involves the internal scattering orbit of the tidally perturbed gravitational two-body system. We assume that during the fast motion, the slow motion can be considered to be essentially uniform. That is, the deviation of the Keplerian orbit of the center of mass of the binary from a straight line with constant velocity can be neglected during the fast motion of the binary. This approximation scheme can be naturally extended to include the background stellar medium in order to facilitate the calculation of dynamical friction. Moreover, in Equation (10), we neglect the temporal dependence of the tidal matrix Ki
j
(
x
cm) in our approach. In general, the temporal variation of the tidal field can lead to the possibility of resonance with the internal pulsation of the system; in fact, such a resonant orbital coupling has been investigated in Kuhn & Miller (1989) and Fleck & Kuhn (2003).
In the inertial reference frame that moves with the constant velocity of the center of mass, mass m1 with state 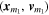 interacts gravitationally with mass m2 with state
interacts gravitationally with mass m2 with state  and the relative motion is given by Equation (10). The solution of this equation and the scattering process will be described in detail in the next section. However, it is simple to conclude from the uniform motion of the center of mass and the definition of relative motion that the net change in the velocities of m1 and m2 are given by
and the relative motion is given by Equation (10). The solution of this equation and the scattering process will be described in detail in the next section. However, it is simple to conclude from the uniform motion of the center of mass and the definition of relative motion that the net change in the velocities of m1 and m2 are given by 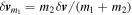 and
and 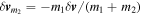 , where
, where  is the relative velocity.
is the relative velocity.
It remains to evaluate the external force acting on the center of mass in Equation (9) and the tidal matrix in Equation (10). Let 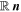 be the vector that connects
be the vector that connects 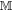 to the center of mass of the binary system and
n
be the corresponding unit vector. Then,
to the center of mass of the binary system and
n
be the corresponding unit vector. Then,
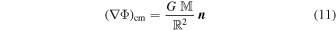
and
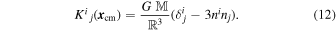
In the local Cartesian coordinate system x = (x, y, z) established in the inertial frame that moves with a constant velocity of the center of mass of the binary, we can choose the unit vector n to point in the z direction with no loss in generality. The equation for relative motion of the binary (10) now takes the form
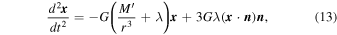
where we have introduced
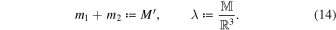
Inspection of the equation of relative motion of the binary (13) reveals that the external tidal force becomes comparable to the internal Newtonian inverse-square force at r ≈ R0, where R0 is the tidal radius given by
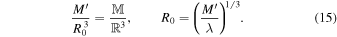
Indeed, for r > R0 the tidal force is dominant, while for r < R0 the Newtonian attractive force between m1 and m2 is dominant. The main purpose of the present paper is to determine how the tidal interaction modifies the dynamical friction force that is a consequence of gravitational drag as m1 scatters from m2. Therefore, we must limit our considerations to regions within a sphere of radius R0. In such regions, the tidal force is smaller than the internal Newtonian force of attraction and can be treated as a linear perturbation on the binary. This approach is consistent with the limiting situation in which the exterior tidal force disappears; that is, for λ → 0, we find R0 → ∞ and our treatment of dynamical friction reduces to the standard method (Chandrasekhar 1943; Tremaine & Weinberg 1984; Binney & Tremaine 2008). We treat the influence of tides as a first-order perturbation; therefore, we expect that the external tidal interaction will have a generally small effect on the internal dynamical friction force. The main purpose of this work is to determine the extent to which dynamical friction is modified by external tides.
3. Dynamical Friction in the Presence of Tides
To calculate the dynamical friction force in the presence of tides, we seek a perturbative solution of the equation of relative motion (13) within the domain bounded by the tidal radius R0. Let us first observe that Equation (13) is invariant under a constant temporal translation as well as a constant rotation in the (x, y) plane. We use these symmetries below.
3.1. Initial Motion in the (x, y) Plane
Let us first assume for the sake of simplicity that the unperturbed uniform relative motion occurs in the (x, y) plane. We can therefore rotate the Cartesian coordinate system about the z-axis such that the unperturbed relative motion occurs along the x-axis from (−x0, y0, z0) to (x0, y0, z0). Here, x0 = v0 t0, y0, and z0 are constants that characterize the unperturbed motion. That is,
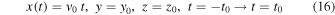
such that
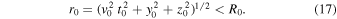
Let us note here that we have used the invariance under time translation to set x(t = 0) = 0. Henceforth, we will express the unperturbed motion in the background (x, y, z) coordinate system in the form
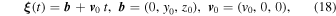
where b · v 0 = 0 and ∣ b ∣ = b is the impact parameter.
Let us recall here that dynamical friction is a phenomenon that first appears at order G2 in the standard treatment (Chandrasekhar 1943; Binney & Tremaine 2008). We therefore solve Equation (13) perturbatively to second order in the gravitational constant G and to linear order in the tidal parameter λ. Specifically, we assume a solution of the form
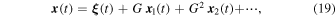
where we have treated G as the expansion parameter. Similarly, we write
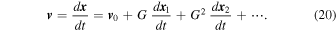
Henceforth, we drop terms of order G3 and higher. To proceed, it is useful to introduce the quantities
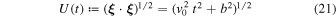
and
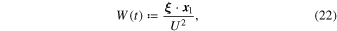
in terms of which we can write
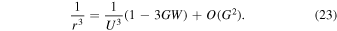
Plugging these expressions in Equation (13), we find to first order in G
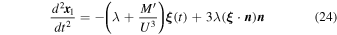
and to second order in G
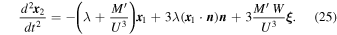
We must now solve these equations with the boundary conditions that initially at t = −t0, we have
x
1 = 0,
x
2 = 0, 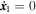 and
and 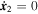 . Here,
. Here,  , etc.
, etc.
Using standard integrals, given for convenience in Appendix B, we find
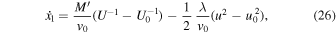
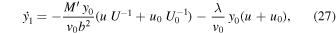
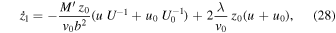
where, for the sake of convenience, we have introduced

Let us note from Equation (26) that  and hence
and hence 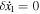 , which is the expected result at linear order in G from the standard treatment of dynamical friction. In general, the situation is different in the presence of tides, as will be demonstrated in the last part of this section; however, the tidal contribution does vanish in certain special cases that include initial motions along the x and z axes.
, which is the expected result at linear order in G from the standard treatment of dynamical friction. In general, the situation is different in the presence of tides, as will be demonstrated in the last part of this section; however, the tidal contribution does vanish in certain special cases that include initial motions along the x and z axes.
Integration of Equations (26)–(28) with the appropriate initial conditions results in
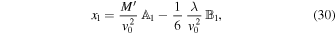
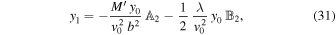
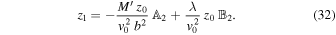
Here, we have introduced, for the sake of convenience, the functions
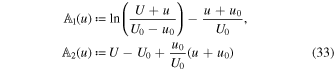
and

To go further, we can integrate the second-order perturbation equations for (x2, y2, z2). On the other hand, for the purpose of calculating dynamical friction, we only need the equation for x2; that is, we must integrate the first component of Equation (25) from t = − t0 to t = t0. More precisely, we need to calculate
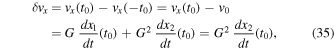
since we already know that  , i.e., the term linear in G vanishes in this case. We treat the tidal parameter λ to first order in our perturbation analysis; therefore, after some algebra we find
, i.e., the term linear in G vanishes in this case. We treat the tidal parameter λ to first order in our perturbation analysis; therefore, after some algebra we find
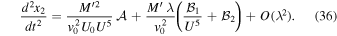
Here,
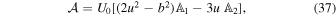
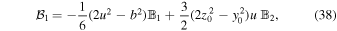
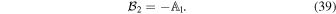
Next, we integrate Equation (36) from t = − t0 to t = t0 with the boundary condition that 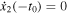 . The result is
. The result is
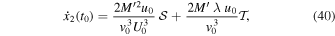
where
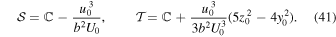
Here, 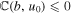 is given by
is given by
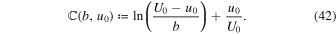
We can now derive the modification of Equation (2) in the presence of tides to second order in G. Suppose that m1 = M, m2 = m and  . Furthermore, our perturbative approach implies
. Furthermore, our perturbative approach implies
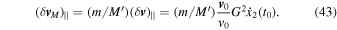
Using Equation (40), we find
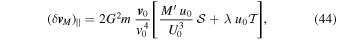
which is the analog of Equation (2) in the presence of tides. We note here the remarkable fact that  is negative; more specifically,
is negative; more specifically,  as a function of u0/b starts out from zero at u0/b = 0 with vanishing slope and then monotonically decreases to −∞ as u0/b → ∞. Moreover, let us note that in the presence of tides t0 > 0 is finite and is limited by Equation (17); however, in the absence of tides λ = 0 and we can let t0 → ∞ as in the standard treatment (Binney & Tremaine 2008). Therefore, in the absence of tides, t0 → ∞ , u0 = v0
t0 → ∞ and
as a function of u0/b starts out from zero at u0/b = 0 with vanishing slope and then monotonically decreases to −∞ as u0/b → ∞. Moreover, let us note that in the presence of tides t0 > 0 is finite and is limited by Equation (17); however, in the absence of tides λ = 0 and we can let t0 → ∞ as in the standard treatment (Binney & Tremaine 2008). Therefore, in the absence of tides, t0 → ∞ , u0 = v0
t0 → ∞ and  . Then, Equation (44) reduces to
. Then, Equation (44) reduces to
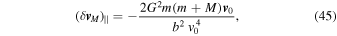
in agreement with Equation (2) to second order in G.
A comment is in order here regarding the fact that t0 = u0/v0 is essentially a free parameter in Equation (44). Indeed, in the application of Chandrasekhar's formula (1) to actual astrophysical systems, the scattering of M from each star of mass m in the system does involve a different finite t0 that we simply ignore. Instead, in each such case, we employ the result obtained from the ideal case with t0 = ∞ . This approximation does not ordinarily encounter any obstacles. However, the presence of a finite tidal radius R0 in the case under consideration implies that t0 is a free parameter subject to the restriction contained in the inequality 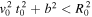 .
.
To find the analog of Chandrasekhar's formula (1) in the present case, we need to extend Equation (44) for an arbitrary star m to the background stars by taking the flux of the stars into account and integrating over the appropriate state space of the background stars. Let f( x m , v m , t) be the state-space number density of background stars. In the idealized infinite homogeneous background medium employed in the original derivation of Equation (1), the distribution function f reduces to f0, which is independent of temporal and spatial variables and is an isotropic function of v m ; however, in the presence of tides, the situation is quite different. Starting from an initial distribution function, it is possible to take the time dependence of tides into account and then basically integrate the tidal force (per unit mass of a star) over a certain interval of time and in this way come up with the change in the velocity of the star due to the corresponding tidal impulse. In principle, the evolution of the distribution function due to the presence of tides can thereby be determined (Spitzer 1958; Gnedin et al. 1999; Binney & Tremaine 2008; Banik & van den Bosch 2021b). The determination of the appropriate distribution function in the case under consideration requires a separate investigation and is beyond the scope of the present work.
To get a rough estimate of the influence of tides on dynamical friction, we henceforth ignore the difference between f( x m , v m , t) and f0(vm ). The net rate of change of momentum M v M per unit time is then given by
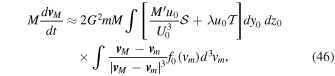
where v 0 has been replaced by v M − v m , as in the standard procedure (Binney & Tremaine 2008). For an isotropic function f0 = f0(vm ), Newton's shell theorem implies (Binney & Tremaine 2008)
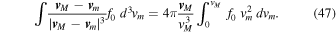
Using
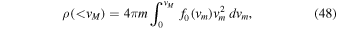
we finally arrive at
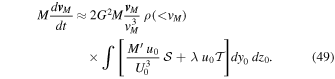
Let us proceed with the integration over dy0 ∧ dz0. Introducing the azimuthal angle φ, we have
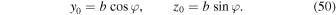
Then, dy0 ∧ dz0 = b db ∧ d φ and one can show that
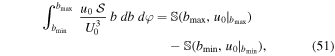
where
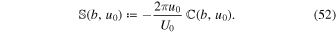
Let us observe that 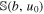 vanishes for u0 = 0, while for u0 > 0,
vanishes for u0 = 0, while for u0 > 0, 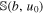 is a positive function of b/u0 that monotonically decreases from ∞ at b/u0 = 0 and tends to zero as b/u0 → ∞ .
is a positive function of b/u0 that monotonically decreases from ∞ at b/u0 = 0 and tends to zero as b/u0 → ∞ .
In the absence of tides, λ = 0, u0 → ∞ and 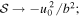 then, as expected, we recover
then, as expected, we recover 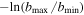 from Equation (51). However, in the presence of tides
from Equation (51). However, in the presence of tides 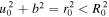 according to Equation (17); therefore, in Equation (51),
according to Equation (17); therefore, in Equation (51),  vanishes, since
vanishes, since 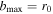 and hence
and hence 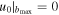 . To interpret this result physically, let us first note that u0 = v0
t0 vanishes when either v0 = 0 or t0 = 0. It is clear from Equation (2) that if v0 = 0, there is no scattering and dynamical friction force vanishes. On the other hand, if t0 vanishes, there is no time for interaction and hence no change in momentum is possible. Thus, for the nontidal part of the integral in Equation (49), we find
. To interpret this result physically, let us first note that u0 = v0
t0 vanishes when either v0 = 0 or t0 = 0. It is clear from Equation (2) that if v0 = 0, there is no scattering and dynamical friction force vanishes. On the other hand, if t0 vanishes, there is no time for interaction and hence no change in momentum is possible. Thus, for the nontidal part of the integral in Equation (49), we find
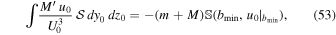
where
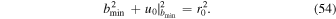
In our case, the nontidal part is thus − (m + M) times the analog of the Coulomb logarithm. As in the standard treatment of dynamical friction (Binney & Tremaine 2008), we assume 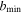 is the maximum of the size of the incident mass M and
is the maximum of the size of the incident mass M and  , while
, while 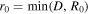 , where D is the diameter of the galactic system. In the absence of tides, the tidal radius R0 goes to infinity and, consequently, we have r0 = D.
, where D is the diameter of the galactic system. In the absence of tides, the tidal radius R0 goes to infinity and, consequently, we have r0 = D.
Let us next consider the tidal part of Equation (49), namely, the integral of 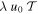 that turns out to be
that turns out to be
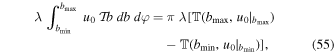
where 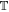 is proportional to u0 and is given by
is proportional to u0 and is given by
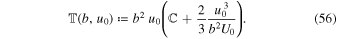
As illustrated in Figure 1, the function 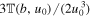 versus b/u0 starts from unity with zero slope at b/u0 = 0 and monotonically decreases to zero as b/u0 → ∞. As noted before,
versus b/u0 starts from unity with zero slope at b/u0 = 0 and monotonically decreases to zero as b/u0 → ∞. As noted before, 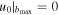 implies that
implies that 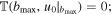 therefore,
therefore,

Figure 1. Plot of the tidal contribution to dynamical friction for motion along the x-axis.
Download figure:
Standard image High-resolution imageFinally, to determine the relative strength of the tidal part compared to the nontidal part in the calculation of dynamical friction force in the case of motion along the x-axis, we must calculate Ψx ,

once we ignore the influence of tides on the distribution function of the stars. In Section 4, we estimate Ψx for the case of the Fornax dSph galaxy tidally perturbed by the Galaxy (MW).
3.2. Initial Motion Along the z-axis
Let us assume that the unperturbed motion is given by
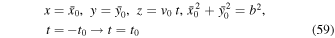
such that 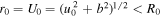 as before. That is,
as before. That is,
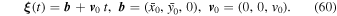
Let us note here that we have used the invariance under time translation to set z(t = 0) = 0.
Following the same procedures as in the previous subsection, we can obtain x 1 and x 2 for the perturbed motion. In the case of the linear deviation x 1, an inspection of Equation (13) reveals that we can find the results in this case from Equations (30)–(32) for motion along the x direction by simply letting λ → − 2 λ. Indeed,
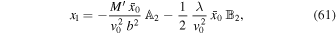
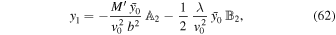
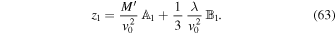
We are interested in the third component of Equation (25) in the present case. After some straightforward calculations, we find
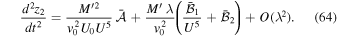
Here, the nontidal part is the same as in the case of motion along the x direction by the spherical symmetry of the Newtonian gravitational potential of a point mass; that is,

while changes occur in the tidal part. Indeed,
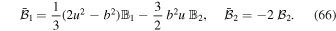
It follows that in this case
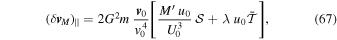
where
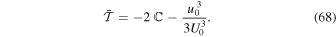
Following essentially the same arguments as before leads to the next step which involves
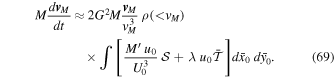
With 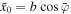 ,
,  , and
, and 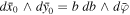 , we find
, we find
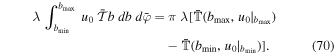
Here, 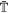 turns out to be
turns out to be
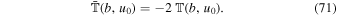
The negative sign in Equation (71) means that the tidal stretching along the z direction is clearly an antifriction force that opposes the dynamical friction force.
Finally, the relative strength of the tidal part compared to the nontidal part for motion along the z direction is given by Ψz = − 2Ψx , which we will estimate for the tidal perturbation of the Fornax dSph galaxy by the MW in Section 4.
3.3. General Treatment
In the general case, the initial fixed relative velocity vector is arbitrary; however, the freedom in a constant rotation about the z-axis may be employed to render v 0 in the (x, z) plane with no loss in generality. As before, we can write the unperturbed motion in the form

where
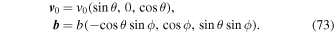
That is, 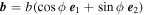 , where
e
1 = (0, 1, 0) is the unit vector in the y direction and
, where
e
1 = (0, 1, 0) is the unit vector in the y direction and 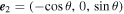 is the unit vector in the (x, z) plane normal to
v
0. Here, θ: 0 → π is the fixed polar angle of the initial relative velocity vector, while the azimuthal angle ϕ: 0 → 2π indicates the range of the possible directions of the impact parameter. As before, the motion takes place from t = − t0 → t = t0 and the freedom in time translation has been employed such that the midpoint of the unperturbed motion is at t = 0. Let us note that we work within the region bounded by the tidal radius R0, namely,
is the unit vector in the (x, z) plane normal to
v
0. Here, θ: 0 → π is the fixed polar angle of the initial relative velocity vector, while the azimuthal angle ϕ: 0 → 2π indicates the range of the possible directions of the impact parameter. As before, the motion takes place from t = − t0 → t = t0 and the freedom in time translation has been employed such that the midpoint of the unperturbed motion is at t = 0. Let us note that we work within the region bounded by the tidal radius R0, namely,
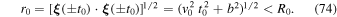
The general case considered here simply reduces to the two previous cases when (θ, ϕ) are chosen appropriately. Indeed, for θ = π/2 and ϕ = φ the unperturbed motion is along the x direction with 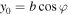 and
and 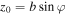 , while for θ = 0 and
, while for θ = 0 and 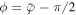 we recover the unperturbed motion along the z-axis with
we recover the unperturbed motion along the z-axis with 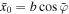 and
and 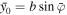 .
.
We now use the general Equations (19)–(25) and the results of Appendix B to integrate the perturbation equations. We find
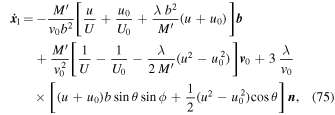
where
n
= (0, 0, 1) is the unit vector along the z-axis defined in Equation (11). Let us note that 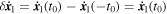 can be simply calculated from Equation (75) and is such that
can be simply calculated from Equation (75) and is such that
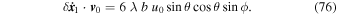
This quantity is in general nonzero in the presence of tides. It does vanish, however, for some special cases including θ = 0, i.e., for motion along the z-axis, and θ = π/2, i.e., for motion along the x-axis.
Integration of Equation (75) with the appropriate initial conditions gives
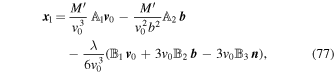
where 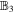 is given by
is given by
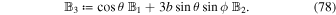
The net change in relative velocity is given by  . We are interested in
. We are interested in
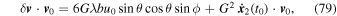
where the linear term in G is given by Equation (76). To find the equation for x 2, we must substitute Equation (77) into Equation (25). After some algebra, the result that we need is given by
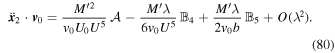
Here, 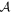 is given by Equation (37) and
is given by Equation (37) and
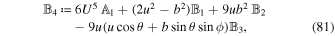
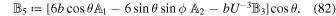
Next, we integrate Equation (80) from t = − t0 to t = t0 and keep only the linear terms in λ. The result is
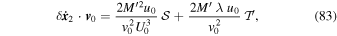
where 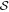 is given by Equation (41) and
is given by Equation (41) and 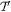 can be expressed as
can be expressed as

Here, P2(x) is the Legendre polynomial of the second degree (Abramowitz & Stegun 1964)

In Equation (84),  reduces to
reduces to 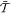 for motion along the z-axis (θ = 0) and to
for motion along the z-axis (θ = 0) and to 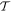 for motion along the x-axis (θ = π/2).
for motion along the x-axis (θ = π/2).
Let us recall that 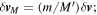 therefore,
therefore,
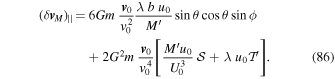
Next, we need to sum the contribution of all of the stars of the background medium. As before, we neglect the influence of tides on the distribution function. In summing over the flux of stars, the spatial integration is over b
db ∧ d
ϕ, as before. When we integrate over the azimuthal angle ϕ, terms proportional to 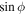 and
and 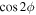 in Equations (84) and (86) vanish. As in the special cases we have considered above, we find
in Equations (84) and (86) vanish. As in the special cases we have considered above, we find
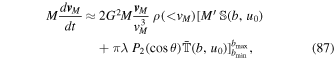
or, finally,
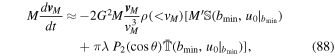
which reduces to our previous results for θ = π/2 and θ = 0. It is interesting to note that the tidal contribution to dynamical friction in our calculation vanishes for 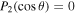 , which occurs for
, which occurs for 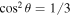 , i.e., when the polar angle of the initial velocity is θ = θ0 or θ = π − θ0, where θ0 ≈ 54.7°.
, i.e., when the polar angle of the initial velocity is θ = θ0 or θ = π − θ0, where θ0 ≈ 54.7°.
In principle, the dynamical friction force can be used to distinguish between Newtonian gravitation with particle dark matter and the Newtonian limit of nonlocal gravity theory, where the nonlocal aspect of the gravitational interaction simulates dark matter. Consequently, within the context of nonlocal gravity, there is no particle dark matter halo around galaxies. On the other hand, in the standard dark matter picture, the main contribution to dynamical friction experienced by the galactic bars comes from the dark matter halo. Therefore, it is natural to expect different amounts of dynamical friction within the galactic systems modeled in the particle dark matter scenario or nonlocal gravity. Appendix C contains a brief discussion of how Equation (88) can be extended to the Newtonian regime of nonlocal gravity.
4. Astrophysical Implications
As an application of our approach, we consider the Fornax dSph galaxy, which is one the most luminous and widely studied dSph galaxies of the Local Group. It is generally assumed that the tidal forces of the MW have not had much impact on the stellar kinematics of Fornax; however, see Hammer et al. (2019, 2020). In any case, there is no direct observational evidence for a tidal disturbance of the stellar component of Fornax (Wang et al. 2017). However, tidal stripping can still significantly affect the more extended dark matter component of Fornax. It is necessary to mention that the dark matter content of Fornax inferred from its stellar kinematics is unexpectedly low, by a factor of ∼3, compared to corresponding galaxies in cosmological simulations (Read et al. 2019). Therefore, tidal stripping of its dark matter halo has been proposed as a solution to this discrepancy (Peñarrubia et al. 2008; Genina et al. 2020).
Another important feature of Fornax that is relevant to our discussion is the puzzling spatial distribution of its globular clusters (GCs). The dark matter content of Fornax is enough to induce strong dynamical friction in the motion of GCs and the timescale of orbital decay is shorter than the age of GCs. However, there are several GCs within Fornax that are far from its center.
We can provide certain estimates for the influence of MW tides on the dynamical friction experienced by the GCs. To do so, it is first necessary to check the validity of our general approximation scheme. Our method works if the dynamical timescale within Fornax is much shorter than its orbital timescale about MW. Fornax's distance from MW is 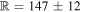 kpc, its total luminosity is L = (1.4 ± 0.4) × 107
L⊙ and its half-light radius is rhalf = 668 ± 34 pc (Walker et al. 2009, 2010). On the other hand, the stellar mass-to-light ratio of Fornax is ϒ* ≃ 4.6 ϒ⊙ (Peñarrubia et al. 2008). The baryonic matter density of Fornax is well fitted by a Plummer sphere (Walker et al. 2009, 2010), namely,
kpc, its total luminosity is L = (1.4 ± 0.4) × 107
L⊙ and its half-light radius is rhalf = 668 ± 34 pc (Walker et al. 2009, 2010). On the other hand, the stellar mass-to-light ratio of Fornax is ϒ* ≃ 4.6 ϒ⊙ (Peñarrubia et al. 2008). The baryonic matter density of Fornax is well fitted by a Plummer sphere (Walker et al. 2009, 2010), namely,
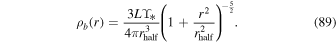
Finally, the dark matter content of Fornax can be described by universal two-parameter mass profiles presented in Walker et al. (2009, 2010) for dSphs. There are two different halo models for Fornax, a cuspy NFW halo and a cored one; for the present purpose, it does not matter which one is used. We employ the NFW dark matter halo:
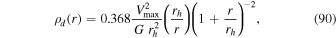
where rh
is the halo lengthscale and  is the maximum circular velocity associated with this halo. In the case of Fornax, these parameters are given by
is the maximum circular velocity associated with this halo. In the case of Fornax, these parameters are given by 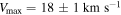 and rh
= 795 pc (Walker et al. 2009, 2010). Both densities (89) and (90) can be integrated to find the corresponding masses, i.e., Mb
(r) and Md
(r), enclosed within radius r. Let us define the baryonic mean density as
and rh
= 795 pc (Walker et al. 2009, 2010). Both densities (89) and (90) can be integrated to find the corresponding masses, i.e., Mb
(r) and Md
(r), enclosed within radius r. Let us define the baryonic mean density as 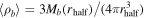 . Using the above-mentioned quantities we find 〈ρb
〉 ≃ 1.8 × 10−2
M⊙ pc−3 and we can hence calculate the internal Fornax dynamical timescale, namely,
. Using the above-mentioned quantities we find 〈ρb
〉 ≃ 1.8 × 10−2
M⊙ pc−3 and we can hence calculate the internal Fornax dynamical timescale, namely,
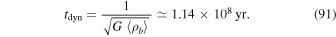
This is consistent with the estimate reported in Hammer et al. (2018a, 2018b) using a different method. On the other hand, the Keplerian period of Fornax in orbit about the MW is given by
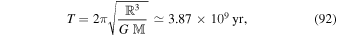
where we have used 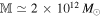 for the mass of the MW. Consequently, we have T/tdyn ≃ 33.8. Notice that by taking into account the dark matter density in Equation (91), the ratio T/tdyn gets even larger. There are other possible methods to estimate T, such as using the Fornax orbital parameters from Gaia DR2 data (Gaia Collaboration et al. 2018, 2020a, 2020b). However, all these estimates indicate that T/tdyn ≫ 1 and hence our approximation scheme is reasonably valid in this case.
for the mass of the MW. Consequently, we have T/tdyn ≃ 33.8. Notice that by taking into account the dark matter density in Equation (91), the ratio T/tdyn gets even larger. There are other possible methods to estimate T, such as using the Fornax orbital parameters from Gaia DR2 data (Gaia Collaboration et al. 2018, 2020a, 2020b). However, all these estimates indicate that T/tdyn ≫ 1 and hence our approximation scheme is reasonably valid in this case.
We are now in a position to estimate the tidal influence of the MW on the dynamical friction within Fornax. More specifically, we compute
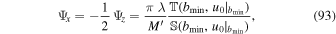
on the basis of Equations (58) and (71). To do so, we take the mean value of the King model core radii of Fornax GCs as representative of 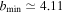 pc (Boldrini et al. 2019). Similarly, we use the mean mass of the GCs for
pc (Boldrini et al. 2019). Similarly, we use the mean mass of the GCs for 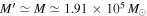 . Let us recall here that the tidal radius R0 is independent of the size of the binary system and is purely determined by the net two-body mass and the characteristics of the external source. For all interactions between a GC and the stars of the background medium, we get essentially the same tidal radius R0. That is,
. Let us recall here that the tidal radius R0 is independent of the size of the binary system and is purely determined by the net two-body mass and the characteristics of the external source. For all interactions between a GC and the stars of the background medium, we get essentially the same tidal radius R0. That is,
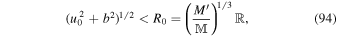
where for Fornax, R0 = 0.672 kpc. On the other hand, the characteristic size of the Fornax galaxy is given by D = 2 r200, where r200 is the radius at which ρb
+ ρd
= 200 ρcrit. Here, 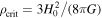 is the cosmic critical density and H0 is the Hubble constant, which we assume is given by H0 = 70 km s−1 Mpc−1. Using Equations (89) and (90), one can numerically determine r200; hence, we find D ≈ 18 kpc. Therefore, D > R0 and we find from Equation (93) that
is the cosmic critical density and H0 is the Hubble constant, which we assume is given by H0 = 70 km s−1 Mpc−1. Using Equations (89) and (90), one can numerically determine r200; hence, we find D ≈ 18 kpc. Therefore, D > R0 and we find from Equation (93) that 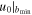 is at most ≈0.672 kpc. The determination of dynamical friction force in Fornax is not a simple task without implementing an appropriate distribution function. On the other hand, the ratios Ψx
and Ψz
are helpful in estimating the significance of tides in our problem. Given all the parameters discussed above, these ratios are Ψx
≈ 0.07 and Ψz
≈ −0.14. Therefore, for motion in the (x, y) plane the tidal effects enhance dynamical friction, while for motion along the z-axis tidal stretching diminishes dynamical friction. For motion along an arbitrary direction with polar angle θ, the corresponding ratio is given by
is at most ≈0.672 kpc. The determination of dynamical friction force in Fornax is not a simple task without implementing an appropriate distribution function. On the other hand, the ratios Ψx
and Ψz
are helpful in estimating the significance of tides in our problem. Given all the parameters discussed above, these ratios are Ψx
≈ 0.07 and Ψz
≈ −0.14. Therefore, for motion in the (x, y) plane the tidal effects enhance dynamical friction, while for motion along the z-axis tidal stretching diminishes dynamical friction. For motion along an arbitrary direction with polar angle θ, the corresponding ratio is given by  . Thus far, our preliminary analysis for Fornax implies that tidal effects would affect dynamical friction by a factor of around 10%; however, an appropriate distribution function is required to reach firm conclusions. Nonetheless, this conclusion is consistent with the observations where no sign of tidal disturbances is found in the stellar component within Fornax (Wang et al. 2017, 2019). Furthermore, our result is consistent with the N-body simulations claiming that the internal kinematics of Fornax is only mildly influenced by the tidal effects of MW (Battaglia et al. 2015).
. Thus far, our preliminary analysis for Fornax implies that tidal effects would affect dynamical friction by a factor of around 10%; however, an appropriate distribution function is required to reach firm conclusions. Nonetheless, this conclusion is consistent with the observations where no sign of tidal disturbances is found in the stellar component within Fornax (Wang et al. 2017, 2019). Furthermore, our result is consistent with the N-body simulations claiming that the internal kinematics of Fornax is only mildly influenced by the tidal effects of MW (Battaglia et al. 2015).
5. Discussion
We have presented an approximation scheme based on expansion in powers of the gravitational constant G to study the Chandrasekhar dynamical friction force in the presence of tides. The tidal interaction is considered within the distant tide linear perturbation approach. To extend our results to a system of stars, we need to determine the distribution function of the stars when tides are present. However, in this initial analytic study of dynamical friction in the presence of tides, we neglect the influence of tides on the phase space distribution of stars. The self-gravity of the stellar system is neglected as well. Depending on circumstances, tidal forces can strengthen or weaken the dynamical friction force. In connection with possible astrophysical applications of our results, we consider the influence of the Milky Way on the Fornax dwarf galaxy. In this case, preliminary estimates suggest that the effect of Galactic tides on dynamical friction within the Fornax dSph galaxy could be around 10%.
M.R. is grateful to Elena Asencio and Indranil Banik for sharing their unpublished research on the tidal stability of Fornax cluster dwarf galaxies. The work of M.R. has been supported by the Ferdowsi University of Mashhad.
Appendix A: Influence of Tides on a Gravitational N-body System
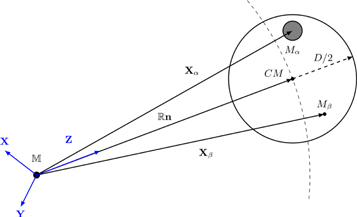
We consider a Newtonian astronomical system of N bodies with inertial masses Mα , α = 1, 2,...,N, in a background Cartesian coordinate system X = (X, Y, Z) as in Figure 2. The Newtonian gravitational force on Mα due to Mβ is
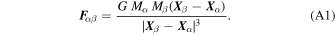
The N-body system is placed in the exterior gravitational field of an external source with potential Φ( X ) so that ∇2Φ = 0 at the N-body system. The equation of motion for Mα is
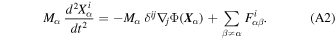
We define the center of mass of the N-body system in the standard manner, namely,
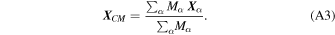
Figure 2. Schematic illustration of the tidal interaction under consideration in this paper: A stellar system with characteristic size D is tidally influenced by a distant mass  .
.
Download figure:
Standard image High-resolution imageLet us now introduce the approximation that the linear size of the N-body system D is much smaller than  , the distance to the source; that is
, the distance to the source; that is  . Therefore, we make a first-order tidal approximation
. Therefore, we make a first-order tidal approximation

It is useful to define the symmetric and traceless tidal matrix Kij ,
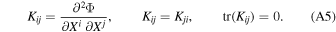
Moreover, we define
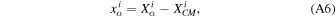
so that Equation (A2) now takes the form
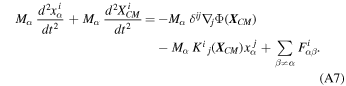
If we now sum this equation over α and use ∑α Mα x α = 0, we find to first order in the tides
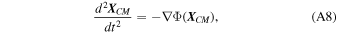
which describes the motion of the center of mass of the system about the source as though the tides never existed. This is, of course, true at the linear order in tidal perturbation. We note that
X
CM
is a function of time t, since the center of mass of the system orbits about the distant mass  . Combining Equations (A7) and (A8), we find the important result that
. Combining Equations (A7) and (A8), we find the important result that
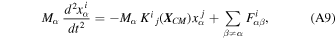
where in  , we have
X
β
−
X
α
=
x
β
−
x
α
.
, we have
X
β
−
X
α
=
x
β
−
x
α
.
Let us now derive the energy equation for the internal motions of the N-body system. To this end, we introduce v α = d x α /dt in Equation (A9) in the standard manner and obtain
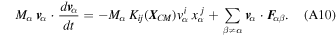
The total internal energy 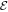 is the sum of internal kinetic and potential energies,
is the sum of internal kinetic and potential energies,
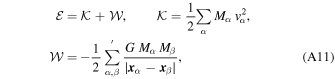
where a prime over the summation sign indicates that α ≠ β in the sum. Then, Equation (A10) implies
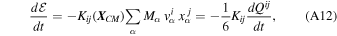
where Qij is the symmetric and traceless internal quadrupole tensor of the system given by
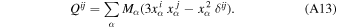
Let us note that we can write
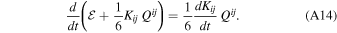
The temporal dependence of Kij has to do with the motion of the center of mass of the system, which is typically very slow compared to motions within the N-body system. During the fast internal motions of the system, the slow motion of the center of mass may be considered to be approximately uniform; that is, it may be a reasonable approximation in some cases to neglect the temporal dependence of the slow motion. Then, Equation (A14) implies that we have a tidally disturbed N-body system in the first order of tidal perturbation that is approximately conservative; that is, the sum total of kinetic plus potential plus tidal energies remains constant in time.
Similarly, the internal angular momentum of the system can be defined via
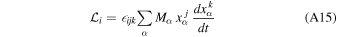
and equation of motion (A9) then implies
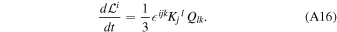
For astrophysical applications, this approach can be extended to include the virial theorem (Binney & Tremaine 2008) as follows. Let us define the quantities related to the moment of inertia of the system, namely,
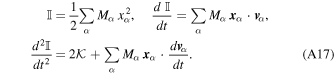
Then, from Equation (A9) we get
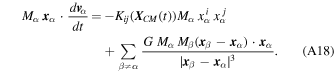
We sum this equation over α and write the sum again with α and β exchanged. Adding the resulting equations we finally get in the standard manner
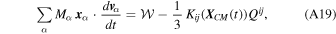
which is equal to 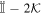 by Equation (A17). Finally, assuming the "fast" system relaxes over timescales short compared to the timescale of the "slow" center-of-mass motion, we can average our result over time. Assuming that the average of
by Equation (A17). Finally, assuming the "fast" system relaxes over timescales short compared to the timescale of the "slow" center-of-mass motion, we can average our result over time. Assuming that the average of 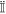 over time vanishes (Landau & Lifshitz 1988), we finally have the result
over time vanishes (Landau & Lifshitz 1988), we finally have the result
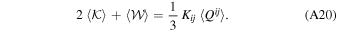
Appendix B: Useful Integrals
The integration of equations of motion in Section 3 is simplified using the indefinite integrals given below. Let us assume 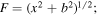 then,
then,
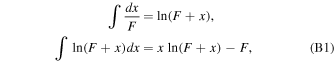
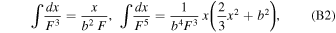
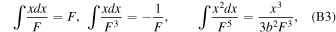
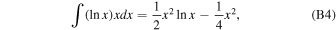
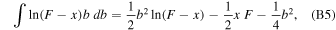
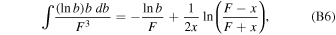
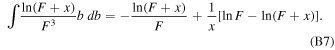
We also need to evaluate the definite integral
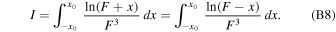
From  , we conclude
, we conclude
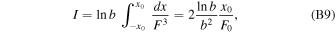
where F0 = F(x0, b). Similarly,
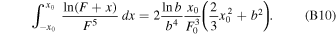
The corresponding definite integrals can be easily evaluated via integration by parts using Equation (B2).
Appendix C: Dynamical Friction and Tidal Interactions in Nonlocal Gravity
In a previous paper (Roshan & Mashhoon 2021), we extended Chandrasekhar's formula for dynamical friction to the Newtonian regime of nonlocal gravity theory and briefly studied its implications for barred spiral galaxies. Nonlocal gravity (NLG) is a classical nonlocal generalization of Einstein's theory of gravitation that takes the past history of the gravitational field into account. The gravitational field in NLG is local but satisfies partial integro-differential field equations. Moreover, NLG has been constructed in close analogy with the nonlocal electrodynamics of media. It turns out that such a classical nonlocal aspect of the gravitational interaction simulates dark matter. A detailed description of NLG is contained in Mashhoon (2017). It seems worthwhile to indicate briefly how the formal results of the present work can carry over to NLG. To this end, we must first describe the analog of the Newtonian inverse-square law in NLG.
In the Newtonian limit, NLG in effect involves the standard nonrelativistic gravitational force
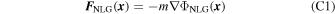
on a test particle of inertial mass m in the gravitational potential ΦNLG( x ), which satisfies the nonlocal Poisson equation that can be expressed in the form
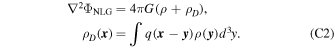
Here, ρ is the density of matter and ρD is the density of effective dark matter in NLG. In this theory, what appears as dark matter in astrophysics and cosmology is in reality the nonlocal aspect of gravity itself and its density is given by the convolution of a certain reciprocal kernel q with the density of matter ρ. The field equations of nonlocal gravity in the Newtonian regime of the theory reduce to the nonlocal Poisson equation (C2) provided the functions involved be smooth and satisfy certain reasonable mathematical properties (Mashhoon 2017). Moreover, the reciprocal kernel q must be determined on the basis of observational data.
To simplify matters, let us assume that q( x − y ) is spherically symmetric; then, for q(r), r = ∣ x − y ∣, two possible forms have been discussed in detail. These are (Mashhoon 2017)
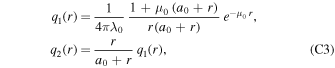
which contain three constant parameters. The basic NLG lengthscale is determined by λ0, since nonlocality disappears when λ0 tends to infinity; moreover, a0 moderates the short distance behavior of the kernel and μ0 is the "Yukawa" parameter. It proves useful to define a dimensionless parameter α0 = 2/(λ0 μ0). Solar system data provide a lower bound for a0, namely, a0 > 1014 cm (Chicone & Mashhoon 2016). With a0 = 0, q1 = q2 and the rotation curves of nearby spiral galaxies can be used to find μ0 and λ0. Indeed, observational data regarding nearby spiral galaxies and clusters of galaxies are consistent with (Rahvar & Mashhoon 2014)
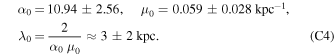
It is straightforward to calculate the force of gravity according to NLG on a point mass m due to another point mass 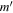 at position
r
. The result is a modification of Newton's law of universal gravitational attraction given by
at position
r
. The result is a modification of Newton's law of universal gravitational attraction given by

A detailed physical interpretation of this result is contained in Roshan & Mashhoon (2021). In Equation (C5), the net contribution of the effective dark matter is contained in Δ(r) ≥ 0. The function Δ(r) starts from zero at r = 0, increases monotonically with increasing r and approaches α0 w asymptotically as r → ∞. Here, w is a positive constant such that w = 1 for a0 = 0 and for a0 > 0, w depends upon whether the reciprocal kernel is chosen to be q1 or q2; however, for reasonable values of a0 less than a few parsecs, w is very close to unity. Henceforth, we ignore the deviation of w from unity. That is, NLG in the Newtonian regime is such that the magnitude of the force of gravity asymptotically approaches Newtonian gravity except that now the effective constant of gravitation is about an order of magnitude larger than the standard Newtonian constant of gravitation G.
With these introductory remarks about
F
NLG, we are now in a position to indicate how our Newtonian approach in this paper is affected by the presence of Δ(r). In Equations (3)–(4) and (10)–(12), the internal forces get multiplied by [1 + Δ(r)], while the external forces get multiplied by ![$[1+{\rm{\Delta }}({\mathbb{R}})]$](https://content.cld.iop.org/journals/0004-637X/926/1/44/revision1/apjac4241ieqn99.gif) . In the distant tide approximation, if
. In the distant tide approximation, if 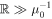 , then
, then 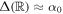 . In this case, the tidal radius is smaller than the Newtonian R0 given by Equation (15). Extending these considerations to dynamical friction, it has been shown in Roshan & Mashhoon (2021) that the nontidal "Chandrasekhar" dynamical friction force gets multiplied by
. In this case, the tidal radius is smaller than the Newtonian R0 given by Equation (15). Extending these considerations to dynamical friction, it has been shown in Roshan & Mashhoon (2021) that the nontidal "Chandrasekhar" dynamical friction force gets multiplied by 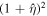 , where
, where 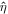 ,
, 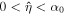 , is a constant that depends on the parameters of the stellar system and has been discussed in detail in Section 4.1 of Roshan & Mashhoon (2021). In the present case, we find that in Equation (88) the nontidal dynamical friction force gets multiplied by
, is a constant that depends on the parameters of the stellar system and has been discussed in detail in Section 4.1 of Roshan & Mashhoon (2021). In the present case, we find that in Equation (88) the nontidal dynamical friction force gets multiplied by 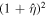 as before, while the tidal part of dynamical friction force gets multiplied by
as before, while the tidal part of dynamical friction force gets multiplied by 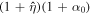 . Finally, the matter density in Equation (88) for dynamical friction would then simply refer to the baryonic density in this case, as there is no actual dark matter in NLG.
. Finally, the matter density in Equation (88) for dynamical friction would then simply refer to the baryonic density in this case, as there is no actual dark matter in NLG.