Abstract
The theoretical analysis of Allan & Cook on the mechanisms of orbital plane precession for medium-high circular orbits is briefly reviewed, and the fact that there are two types of possible precession mechanisms (not only the classical Laplace precession) for the long-term evolution of the orbital plane of medium-high near-circular orbits is especially emphasized. Based on two types of possible precession mechanisms, the analytical formulae of the quantitative variation ranges of orbital inclination derived by Zhao et al. are revised, and the complete analytical formulae for medium-high near-circular orbits are obtained. The qualitative characteristic formula for the variation of orbital inclination-longitude of the ascending node of geostationary orbits in Zhao et al. is generalized to medium-high near-circular orbits, and the more general analytical formulae are obtained. Taking the near-circular orbits with the altitudes as the geosynchronous and medium orbits of the BeiDou navigation satellites as examples, the theoretically quantitative and qualitative results from orbital plane precession are verified by the first-order semianalytical calculations with simplified models and numerical calculations with precise models to a certain extent. Moreover, the specific quantitative and qualitative results for medium-high near-circular orbits with the given initial inclinations and different initial longitudes of the ascending node are particularly presented, from which some conclusions are summarized. Due to the high similarity of orbital plane precession for natural satellites to that of artificial satellites, the results and methodology in this paper can be directly extended to the long-term evolution of the orbital plane for natural satellites and help to understand and explain some orbit dynamic phenomena of natural satellites.
Export citation and abstract BibTeX RIS
1. Introduction
Orbital plane precession is one of the significant dynamic phenomena in the long-term evolution of medium-high near-circular orbits. The study of orbital plane precession can be traced back to the 1960s. Sekiguchi (1961) first pointed out that there are three pairs of (six) equilibrium positions for the pole of the orbital plane of circular orbits with geosynchronous altitude under the secular effects of the Earth's oblateness perturbation and the lunisolar perturbations and presented the stabilities of libration of the pole of the orbital plane around these equilibrium positions, as well as the minimum periods of libration. The equilibrium positions for the pole of the orbital plane in Sekiguchi (1961) are just the poles of the Laplace planes illustrated in Tremaine et al. (2009) and Rosengren & Scheeres (2014a). The libration of the pole of the orbital plane around the equilibrium positions and the minimum periods of libration studied in Sekiguchi (1961) just correspond to the Laplace precession of the orbital plane and the minimum periods of precession discussed in Allan & Cook (1964), respectively.
Based on the simplified and approximate model, Allan & Cook (1964) revealed the mechanisms of orbital plane precession for medium-high circular orbits through ingenious theoretical analysis, in which the classical Laplace precession of the orbital plane and the Laplace plane have attracted more attention. Schildknecht (2007) stressed that the classical Laplace precession of the orbital plane is one basic characteristic of geostationary orbits. Tremaine et al. (2009) analyzed the properties of the Laplace planes in depth and clarified the stabilities of circular and elliptical orbits in the classical, orthogonal, and polar Laplace planes clearly. In view of its stability, Rosengren et al. (2014) proposed that the classical Laplace plane can be adopted as a graveyard disposal orbit for geosynchronous satellites to guarantee the long-term robustness.
On the basis of Allan & Cook (1964), Ulivieri et al. (2013) and Circi et al. (2016) investigated the influence of the practical motion of the lunar pole on the Laplace planes emphatically. Ulivieri et al. (2013) also presented a series of specific results of the variations of inclination and the periods of orbital plane precession for medium-high near-circular orbits through numerical calculations of their proposed models. Zhu et al. (2017) improved the simplified and approximate model in Allan & Cook (1964) and derived a doubly averaged model considering the regression of the lunar node for long-term evolution of the orbital plane of medium-high circular orbits, as well as the approximate analytical solutions of the evolution of the orbital plane near the classical Laplace plane.
Allan & Cook (1967), Rosengren et al. (2014), and Rosengren & Scheeres (2014a) took solar radiation pressure into consideration in the simplified and approximate model and modified the Laplace planes. Allan & Cook (1967) obtained the specific results of the inclination of the modified Laplace plane relative to the ecliptic and the periods of orbital plane precession of circular and near-circular orbits in the classical Laplace plane. Rosengren et al. (2014) deduced the condition formula of the modified Laplace planes, calculated the specific results of the inclinations of the classical Laplace planes with respect to the equator for Earth-orbital space objects with different area-to-mass ratios (A/m), and examined the evolution of the orbital plane of high-A/m space objects in the supersynchronous disposal orbits and classical Laplace plane, respectively, by numerical calculations of the simplified model. Rosengren & Scheeres (2014a) revealed the remarkable influence of solar radiation pressure on the Laplace planes and the stabilities of circular orbits in the classical, orthogonal, and polar Laplace planes after modification.
Based on the classical Laplace precession of the orbital plane, Zhang et al. (2015a) and Zhao et al. (2015) established a linkage between the orbital elements, the initial orbital values, and the classical Laplace precession mechanism and derived the analytical formulae of quantitative variation ranges of orbital inclination determined directly from the initial orbital values for near-circular geosynchronous orbits and 12 hr satellite orbits in the state of the classical Laplace precession in theory. Zhao et al. (2016) further derived the qualitative characteristic formula for the variation of orbital inclination-longitude of the ascending node of geostationary orbits governed by the classical Laplace precession of the orbital plane in theory. According to the orbital elements at the epoch MJD 57,219.210, Zhang et al. (2015b) presented the theoretical calculation results of the variation ranges of orbital inclination, the variation period of orbital inclination (or the period of orbital plane evolution), and the qualitative variation characteristic of orbital inclination-longitude of the ascending node for the BeiDou-M1 satellite in the state of the classical Laplace precession directly; pointed out that its variation ranges of orbital inclination can effectively evade the conditions of lunisolar resonances dependent only on inclination (Hughes 1980) so that its initial near-circular orbital characteristic can be maintained in the long-term evolution; and further verified these theoretical analyses through numerical calculations. According to the amendments of the classical Laplace plane and the classical Laplace precession mechanism arising from solar radiation pressure in Rosengren et al. (2014) and Rosengren & Scheeres (2014a), Zhang et al. (2014) ignored the Earth shadow and reported the quantitative variation ranges of orbital inclination for high-A/m space debris in geostationary orbits under the premise of initial near-circular orbit maintenance, as well as the qualitative variation characteristics of orbital inclination-longitude of the ascending node.
Nevertheless, the theoretically quantitative and qualitative results from orbital plane precession of medium-high near-circular orbits in Zhao et al. (2015, 2016) and Zhang et al. (2015a) were restricted to the case of the classical Laplace precession, and the actual and real polar Laplace precession was neglected. In this paper, we revise and generalize the theoretically quantitative and qualitative results in Zhao et al. (2015, 2016) and Zhang et al. (2015a), based on the classical and polar Laplace precession mechanisms of the orbital plane for medium-high near-circular orbits, to acquire the complete analytical formulae of the quantitative variation ranges of orbital inclination and the more general analytical formulae of qualitative variation characteristic of orbital inclination-longitude of the ascending node. We also verify the proposed theoretical results through semianalytical and numerical calculations.
2. Two Types of Possible Precession Mechanisms
Allan & Cook (1964) took into account the second-order zonal harmonic J2 of the Earth's gravitational field and the lunisolar perturbation terms up to the second-order Legendre polynomial  and derived the equation of evolution of the orbital plane of medium-high circular orbits based on the first-order averaged perturbation equations of Milankovitch orbital elements (Milankovitch 1939; Allan & Ward 1963; Rosengren & Scheeres 2014b) by neglecting the effect of the practical motion of the lunar pole and averaging the perturbation functions to eliminate the short-period terms. Then they further ingeniously obtained the equations of evolution of the orbital plane in the coordinate system O − 123, defined by the principal axes, by analogizing the fixed-axis rotation of the rigid body (see Figure 1); revealed two types of possible mechanisms of orbital plane precession for long-term evolution of medium-high circular orbits; and presented the calculation expressions of the period of orbital plane evolution.
and derived the equation of evolution of the orbital plane of medium-high circular orbits based on the first-order averaged perturbation equations of Milankovitch orbital elements (Milankovitch 1939; Allan & Ward 1963; Rosengren & Scheeres 2014b) by neglecting the effect of the practical motion of the lunar pole and averaging the perturbation functions to eliminate the short-period terms. Then they further ingeniously obtained the equations of evolution of the orbital plane in the coordinate system O − 123, defined by the principal axes, by analogizing the fixed-axis rotation of the rigid body (see Figure 1); revealed two types of possible mechanisms of orbital plane precession for long-term evolution of medium-high circular orbits; and presented the calculation expressions of the period of orbital plane evolution.
Figure 1. Two types of possible mechanisms of orbital plane precession for medium-high circular orbits: the classical and polar Laplace precessions (similar to Zhao et al. 2015). Here O − XYZ is the geocentric equatorial inertial coordination system; O − 123 is a coordinate system composed by the principal axes defined in Allan & Cook (1964); ϒ is the vernal equinox;  is the normal vector of the orbital plane at the initial time;
is the normal vector of the orbital plane at the initial time;  is the normal vector of the classical Laplace plane; α is the inclination of the classical Laplace plane relative to the equator; i0 refers to the initial orbital inclination; i* and
is the normal vector of the classical Laplace plane; α is the inclination of the classical Laplace plane relative to the equator; i0 refers to the initial orbital inclination; i* and  refer to the orbital inclinations when the longitude of the ascending node Ω = 0° and 90°, respectively (i.e.,
refer to the orbital inclinations when the longitude of the ascending node Ω = 0° and 90°, respectively (i.e.,  and
and  ); and
); and  and
and  are the normal vectors of the orbital plane with the inclinations i* and
are the normal vectors of the orbital plane with the inclinations i* and  , respectively. Note that the definitions of
, respectively. Note that the definitions of  and
and  here do not mean that when the initial longitude of the ascending node Ω0 = 90°, the precession mechanism of the orbital plane is exactly the polar Laplace precession (or the precession axis is exactly the O1 one or the X one), as seen in Figure 2 below.
here do not mean that when the initial longitude of the ascending node Ω0 = 90°, the precession mechanism of the orbital plane is exactly the polar Laplace precession (or the precession axis is exactly the O1 one or the X one), as seen in Figure 2 below.
Download figure:
Standard image High-resolution imageThe types of precession mechanisms of the long-term evolution of the orbital plane depend on the initial orbital state (or the initial orbital values). When λ2 < λ0 ≤ λ3, the normal vector of the orbital plane rotates around the principal axis O3 (see Figure 1). That is, the orbital plane precesses along the classical Laplace plane (the inclination of the classical Laplace plane relative to the Earth's equator is α, and its node line coincides with the direction of the vernal equinox). When λ1 ≤ λ0 < λ2, the normal vector of the orbital plane rotates around the principal axis O1 or the X-axis of the geocentric equatorial inertial coordination system O − XYZ (see Figure 1). That is, the orbital plane precesses along the polar Laplace plane (the coordinate plane O23) stated in Tremaine et al. (2009). Refer to Allan & Cook (1964) for the detailed calculation formulae of λ0, λ1, λ2, λ3, and α. We also present these calculation formulae in the Appendix for reference. For a given orbit, the quantities λ0, λ1, λ2, λ3, and α are constants determined by the initial state or values if the assumption that the lunar orbital plane coincides with the ecliptic is considered as in Allan & Cook (1964). It should be pointed out that the initial longitude of the ascending node Ω0 = 90° is not enough to make the orbital pole precess around the O1-axis or the X-axis in Figure 1. Namely, when Ω0 = 90°, the precession mechanism of the orbital plane is not always the polar Laplace precession, as seen in Figure 2. Accordingly, the definitions of  and
and  in Figure 1 do not mean that when
in Figure 1 do not mean that when  , the precession mechanism of the orbital plane is exactly the polar Laplace precession (or the precession axis is exactly the O1 one or the X one).
, the precession mechanism of the orbital plane is exactly the polar Laplace precession (or the precession axis is exactly the O1 one or the X one).
Figure 2. Initial values of orbital inclination and longitude of the ascending node corresponding to two types of possible precession mechanisms: (a) for near-circular geosynchronous orbits with an altitude H = 35,786 km and (b) for near-circular medium orbits with an altitude H = 21,528 km as the BeiDou-M navigation satellites (China Satellite Navigation Office 2013). The initial inclination i0 is set at intervals of 1° in the range of ![$\left[0^\circ ,90^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn15.gif) , and the initial longitude of the ascending node Ω0 is set at intervals of 4° in the range of
, and the initial longitude of the ascending node Ω0 is set at intervals of 4° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn16.gif) . The blue and red symbols correspond to the classical and polar Laplace precessions of the orbital plane, respectively. Note that these results are obtained under the assumption that the lunar orbital plane coincides with the ecliptic.
. The blue and red symbols correspond to the classical and polar Laplace precessions of the orbital plane, respectively. Note that these results are obtained under the assumption that the lunar orbital plane coincides with the ecliptic.
Download figure:
Standard image High-resolution imageNowadays, the classical Laplace precession is generally deemed to be the dynamical mechanism of the long-term evolution of the orbital plane of medium-high near-circular orbits, especially for the geosynchronous orbits. However, it should be stressed in particular that, theoretically, these two types of possible precession mechanisms (the classical and polar Laplace precessions) revealed by Allan & Cook (1964) both exist for near-circular geosynchronous orbits with an altitude H = 35,786 km. The initial values of orbital inclination and longitude of the ascending node corresponding to these two types of possible precession mechanisms are presented in Figure 2(a), under the assumption that the lunar orbital plane coincides with the ecliptic. It shows that the second type of mechanism that the orbital plane precesses along the polar Laplace plane occurs for high-inclination orbits. The understanding of geosynchronous orbits in the past was generally restricted to the low-inclination orbits, and the precession mechanism of the long-term evolution of the orbital plane of low-inclination geosynchronous orbits is indeed the classical Laplace precession. Nevertheless, the high-inclination cases were neglected in the past. For the near-circular medium orbits with an altitude H = 21,528 km, as the BeiDou-M navigation satellites (China Satellite Navigation Office 2013), theoretically, there are also two types of possible precession mechanisms for the long-term evolution of the orbital plane, and the corresponding initial values of orbital inclination and longitude of the ascending node are presented in Figure 2(b), under the assumption that the lunar orbital plane coincides with the ecliptic.
Satellite dynamics, are used to describe an orbit with the classical Keplerian elements. By integrating the theoretical analysis of Allan & Cook (1964) with the classical Keplerian elements, it can be more intuitive to reflect the quantitative and qualitative results governed by the dynamical mechanisms of the long-term evolution of the orbital plane of medium-high near-circular orbits.
3. Quantitative Results of Long-term Evolution of the Orbital Plane
3.1. Complete Analytical Formulae of Quantitative Variation Ranges of Orbital Inclination
According to the transformation relation between the geocentric equatorial inertial coordination system O − XYZ and the coordinate system O − 123 composed by the principal axes in Figure 1 and the theoretical analysis in Allan & Cook (1964), Zhao et al. (2015) merely established the linkage between the orbital elements and the mechanism of classical Laplace precession of the orbital plane by using Equation (3) in Zhao et al. (2015) and Equation (26a) in Allan & Cook (1964) and further derived the analytical formulae of the quantitative variation ranges of orbital inclination for near-circular geosynchronous orbits in theory. Equation (3) in Zhao et al. (2015) and Equation (26a) in Allan & Cook (1964), mentioned here, and Equations (22), (26b), (27a), and (27b) in Allan & Cook (1964), used below, are presented in the Appendix for reference.
However, as stated in Section 2, there are two types of possible mechanisms of orbital plane precession for medium-high near-circular orbits (not just the classical Laplace precession); hence, the analytical formulae of the quantitative variation ranges of orbital inclination obtained in Zhao et al. (2015) are theoretically incomplete.
For this reason, we examine these two types of possible precession mechanisms (the classical and polar Laplace precessions) of the orbital plane for medium-high near-circular orbits as a whole in this section, and we revise the analytical formulae of the quantitative variation ranges of orbital inclination derived in Zhao et al. (2015) by using a similar methodology. First, using Equation (3) in Zhao et al. (2015) and Equation (22) in Allan & Cook (1964), we establish the linkage between the orbital elements and the nontrivial integral λ0 of the long-term evolution of the orbital plane, from which the long-term evolution of the orbital plane governed by the classical Laplace precession mechanism or the polar Laplace precession mechanism, depending on the initial orbital values, can be determined directly. Then, we introduce two parameters,  and
and  (i.e., i* and
(i.e., i* and  are the orbital inclinations when the longitude of the ascending node Ω = 0° and 90°, respectively), and present their specific expressions by using Equations (26a) and (26b) in Allan & Cook (1964). Ultimately, based on the classical and polar Laplace precession mechanisms of the orbital plane, we derive the complete analytical formulae of the quantitative variation ranges of orbital inclination for medium-high near-circular orbits as follows:
are the orbital inclinations when the longitude of the ascending node Ω = 0° and 90°, respectively), and present their specific expressions by using Equations (26a) and (26b) in Allan & Cook (1964). Ultimately, based on the classical and polar Laplace precession mechanisms of the orbital plane, we derive the complete analytical formulae of the quantitative variation ranges of orbital inclination for medium-high near-circular orbits as follows:
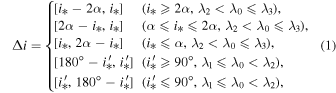
where
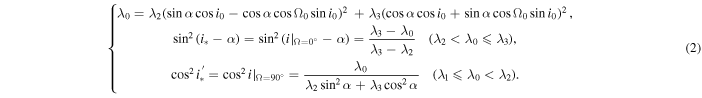
It should be specifically pointed out that the above complete analytical formulae of the quantitative variation ranges of orbital inclination for medium-high orbits are derived on the precondition of near-circular orbit. In other words, Equations (1) and (2) are valid only if the initial near-circular orbital characteristic is maintained in the long-term evolution of medium-high orbits. The above amendments of the analytical formulae of the quantitative variation ranges of orbital inclination in Zhao et al. (2015) not only have particular regard for the polar Laplace precession mechanism of the orbital plane but also present adaptable replacements of the original expressions, Equations (2) and (4) in Zhao et al. (2015), of the quantities i* and λ0.
For near-circular geosynchronous orbits with a nominal altitude H = 35,786 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 in the BeiDou navigation satellite system (China Satellite Navigation Office 2013), it is seen that the orbital plane precession mechanism is the classical Laplace precession from Figure 2. Likewise, the orbital plane precession mechanism is also the classical Laplace precession for the near-circular medium orbits with a nominal altitude H = 21,528 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 in the BeiDou navigation satellite system (China Satellite Navigation Office 2013). From Equations (1) and (2), we obtain a series of specific theoretical results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn20.gif) in the long-term evolution of these orbits for different initial longitudes of the ascending node Ω0 at intervals of 1° in the range of
in the long-term evolution of these orbits for different initial longitudes of the ascending node Ω0 at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn21.gif) , upon the precondition that the initial near-circular orbital characteristic is maintained; see the blue symbols in Figures 3(a) and (b). It is observed that the quantitative variation amplitudes of orbital inclination imax − imin in the long-term orbital evolution are all 2α for given initial inclination i0 = 55° and different initial longitude of the ascending node Ω0; when Ω0 = 0° and 360°, imin and imax have the minimum values, while when Ω0 = 180°, imin and imax have the maximum values from Figures 3(a) and (b). These are the marked features of the classical Laplace precession of the orbital plane for medium-high near-circular orbits revealed through the analytical formulae of Equations (1) and (2).
, upon the precondition that the initial near-circular orbital characteristic is maintained; see the blue symbols in Figures 3(a) and (b). It is observed that the quantitative variation amplitudes of orbital inclination imax − imin in the long-term orbital evolution are all 2α for given initial inclination i0 = 55° and different initial longitude of the ascending node Ω0; when Ω0 = 0° and 360°, imin and imax have the minimum values, while when Ω0 = 180°, imin and imax have the maximum values from Figures 3(a) and (b). These are the marked features of the classical Laplace precession of the orbital plane for medium-high near-circular orbits revealed through the analytical formulae of Equations (1) and (2).
Figure 3. Quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn22.gif) , periods of orbital plane evolution P, and maximum eccentricities emax in the long-term evolution of initial near-circular geosynchronous orbits with a nominal altitude H = 35,786 km and initial near-circular medium orbits with a nominal altitude H = 21,528 km in the BeiDou navigation satellite system (China Satellite Navigation Office 2013). Panel (a) shows the theoretical and first-order semianalytical results of
, periods of orbital plane evolution P, and maximum eccentricities emax in the long-term evolution of initial near-circular geosynchronous orbits with a nominal altitude H = 35,786 km and initial near-circular medium orbits with a nominal altitude H = 21,528 km in the BeiDou navigation satellite system (China Satellite Navigation Office 2013). Panel (a) shows the theoretical and first-order semianalytical results of ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn23.gif) for geosynchronous orbits; panel (b) shows the theoretical and first-order semianalytical results of
for geosynchronous orbits; panel (b) shows the theoretical and first-order semianalytical results of ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn24.gif) for medium orbits; panel (c) shows the theoretical results of P for geosynchronous orbits; panel (d) shows the theoretical results of P for medium orbits; panel (e) shows the first-order semianalytical results of emax for geosynchronous orbits; and panel (f) shows the first-order semianalytical results of emax for medium orbits. The initial inclination i0 = 55°, and the initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of
for medium orbits; panel (c) shows the theoretical results of P for geosynchronous orbits; panel (d) shows the theoretical results of P for medium orbits; panel (e) shows the first-order semianalytical results of emax for geosynchronous orbits; and panel (f) shows the first-order semianalytical results of emax for medium orbits. The initial inclination i0 = 55°, and the initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn25.gif) . The blue symbols corresponds to the theoretical results from the classical Laplace precession of the orbital plane, the cyan symbols correspond to the first-order semianalytical results based on the simplified models without the practical motion of the lunar pole, and the magenta symbols correspond to the first-order semianalytical results based on the simplified models with the practical motion of the lunar pole.
. The blue symbols corresponds to the theoretical results from the classical Laplace precession of the orbital plane, the cyan symbols correspond to the first-order semianalytical results based on the simplified models without the practical motion of the lunar pole, and the magenta symbols correspond to the first-order semianalytical results based on the simplified models with the practical motion of the lunar pole.
Download figure:
Standard image High-resolution imageHowever, from Figure 2, it is seen that the classical and polar Laplace precession mechanisms both exist in the long-term evolution of the orbital plane for near-circular geosynchronous orbits with an altitude H = 35,786 km and initial inclination i0 = 83° when the initial longitude of the ascending node Ω0 takes different values. The same phenomenon can also be observed for near-circular medium orbits with an altitude H = 21,528 km and initial inclination i0 = 87° when the initial longitude of the ascending node Ω0 takes different values. Likewise, from Equations (1) and (2), we obtain a series of specific theoretical results of quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn26.gif) in the long-term evolution of these orbits for different initial longitudes of the ascending node Ω0 at intervals of 1° in the range of
in the long-term evolution of these orbits for different initial longitudes of the ascending node Ω0 at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn27.gif) , upon the precondition that the initial near-circular orbital characteristic is maintained; see the blue and red symbols in Figures 4(a) and 5(a), respectively. The blue symbols correspond to the theoretical results from the classical Laplace precession of the orbital plane, while the red symbols correspond to the theoretical results from the polar Laplace precession of the orbital plane. It is observed that the quantitative variation amplitudes of orbital inclination imax − imin determined by the polar Laplace precession of the orbital plane are not a fixed value any longer as that determined by the classical Laplace precession of the orbital plane. It is a marked feature of the polar Laplace precession of the orbital plane for medium-high near-circular orbits revealed through the analytical formulae of Equations (1) and (2).
, upon the precondition that the initial near-circular orbital characteristic is maintained; see the blue and red symbols in Figures 4(a) and 5(a), respectively. The blue symbols correspond to the theoretical results from the classical Laplace precession of the orbital plane, while the red symbols correspond to the theoretical results from the polar Laplace precession of the orbital plane. It is observed that the quantitative variation amplitudes of orbital inclination imax − imin determined by the polar Laplace precession of the orbital plane are not a fixed value any longer as that determined by the classical Laplace precession of the orbital plane. It is a marked feature of the polar Laplace precession of the orbital plane for medium-high near-circular orbits revealed through the analytical formulae of Equations (1) and (2).
Figure 4. Quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn28.gif) , periods of orbital plane evolution P, and maximum eccentricities emax in the long-term evolution of initial near-circular geosynchronous orbits with an altitude H = 35,786 km and initial inclination i0 = 83°. Panel (a) shows the theoretical results of
, periods of orbital plane evolution P, and maximum eccentricities emax in the long-term evolution of initial near-circular geosynchronous orbits with an altitude H = 35,786 km and initial inclination i0 = 83°. Panel (a) shows the theoretical results of ![$\left[{i}_{\min },{i}_{\max }\right];$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn29.gif) panel (b) shows the theoretical results of P; panel (c) shows the first-order semianalytical results of
panel (b) shows the theoretical results of P; panel (c) shows the first-order semianalytical results of ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn30.gif) with and without the practical motion of the lunar pole; and panel (d) shows the first-order semianalytical results of emax with and without the practical motion of the lunar pole. The initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of
with and without the practical motion of the lunar pole; and panel (d) shows the first-order semianalytical results of emax with and without the practical motion of the lunar pole. The initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn31.gif) . The symbols with different colors have the same meaning as in Figure 3. In addition, the red symbols correspond to the theoretical results from the polar Laplace precession of the orbital plane.
. The symbols with different colors have the same meaning as in Figure 3. In addition, the red symbols correspond to the theoretical results from the polar Laplace precession of the orbital plane.
Download figure:
Standard image High-resolution image3.2. Periods of Orbital Plane Evolution
Using the expression of λ0 in Equation (2) above and Equations (27a) and (27b) in Allan & Cook (1964), the periods of orbital plane evolution (or the variation periods of orbital inclination) for medium-high near-circular orbits can also be calculated. For medium-high near-circular orbits with initial values as set in Figures 3(a) and (b), 4(a), and 5(a), we present a series of specific theoretical results of the periods of orbital plane evolution P upon the precondition that the initial near-circular orbital characteristic is maintained; see Figures 3(c) and (d), 4(b), and 5(b), respectively. The blue symbols in the figures correspond to the theoretical results from the classical Laplace precession of the orbital plane, while the red symbols correspond to the polar Laplace precession.
From Figures 3(c) and (d), it is seen that for the medium-high near-circular orbits with the given initial inclination i0 and different initial longitude of the ascending node Ω0, the period of orbital plane evolution P reaches the minimum when Ω0 = 0° and 360° and the maximum when Ω0 = 180°. It is another marked feature determined by the classical Laplace precession of the orbital plane for medium-high near-circular orbits.
3.3. Results of the First-order Semianalytical Calculations
To verify the above theoretical calculation results of quantitative variation ranges of orbital inclination based on the simplified and approximate model and to obtain information on the long-term evolution of orbital eccentricity, the first-order semianalytical calculations with simplified models are performed. Meanwhile, parallel calculations based on the simplified models with and without the practical motion of the lunar pole are conducted to reveal its influence on the long-term evolution of orbital inclination and eccentricity.
The second-order zonal harmonic J2 of the Earth's gravitational field and the lunisolar perturbation terms up to the second-order Legendre polynomial  are still taken into account in the simplified models. The first-order solutions take the complete first-order perturbation terms and the second-order secular terms of the perturbation factors of the simplified models. Thus, the first- and second-order secular terms, the first-order long-period terms, and the first-order short-period terms are involved in the first-order solutions (Liu 2000; Liu & Tang 2015).
are still taken into account in the simplified models. The first-order solutions take the complete first-order perturbation terms and the second-order secular terms of the perturbation factors of the simplified models. Thus, the first- and second-order secular terms, the first-order long-period terms, and the first-order short-period terms are involved in the first-order solutions (Liu 2000; Liu & Tang 2015).
In the first-order semianalytical calculations, the nonsingular elements applied to arbitrary eccentricity (0 ≤ e < 1),  , are adopted as the basic variables, where a, e, i, Ω, ω, and M are the classical Keplerian elements. The considered perturbation models are averaged over the fast variable λ or M up to the terms of
, are adopted as the basic variables, where a, e, i, Ω, ω, and M are the classical Keplerian elements. The considered perturbation models are averaged over the fast variable λ or M up to the terms of  , and then the averaged perturbation models are numerically integrated by the Runge–Kutta–Fehlberg 7(8) method to acquire the first- and second-order secular terms and the first-order long-period terms. Meantime, the first-order short-period terms at the corresponding times are calculated by using the analytical formulae in Liu et al. (2005), and then the first-order solutions are ultimately obtained. The minimum and maximum inclinations imin and imax and the maximum eccentricity emax in the long-term orbital evolution are directly obtained through successive comparisons in the process of the first-order semianalytical calculations. In addition, the JPL DE430 precise ephemeris3
is directly invoked to get the required lunisolar position coordinates in the first-order semianalytical calculations.
, and then the averaged perturbation models are numerically integrated by the Runge–Kutta–Fehlberg 7(8) method to acquire the first- and second-order secular terms and the first-order long-period terms. Meantime, the first-order short-period terms at the corresponding times are calculated by using the analytical formulae in Liu et al. (2005), and then the first-order solutions are ultimately obtained. The minimum and maximum inclinations imin and imax and the maximum eccentricity emax in the long-term orbital evolution are directly obtained through successive comparisons in the process of the first-order semianalytical calculations. In addition, the JPL DE430 precise ephemeris3
is directly invoked to get the required lunisolar position coordinates in the first-order semianalytical calculations.
For the medium-high near-circular orbits with altitudes  and
and  , given initial inclinations i0, and different initial longitudes of the ascending node Ω0 discussed in Section 3.1, the first-order semianalytical calculation results of the quantitative variation ranges of inclination
, given initial inclinations i0, and different initial longitudes of the ascending node Ω0 discussed in Section 3.1, the first-order semianalytical calculation results of the quantitative variation ranges of inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn37.gif) and maximum eccentricity emax, based on the simplified models with and without the practical motion of the lunar pole in the long-term orbital evolution, are presented in Figures 3(a), (b), (e), and (f); 4(c) and (d); and 5(c) and (d), respectively, by using different colored symbols. The cyan symbols in the figures correspond to the results without the practical motion of the lunar pole, while the magenta symbols correspond to the results with the practical motion of the lunar pole. The corresponding initial orbital values in these first-order semianalytical calculations are set as follows: the initial epoch is 00:00:00 UTC on 2019 May 5, the initial semimajor axis a0 = 42,164.1363 or 27,906.1363 km, the initial eccentricity e0 = 0.0001, the initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of
and maximum eccentricity emax, based on the simplified models with and without the practical motion of the lunar pole in the long-term orbital evolution, are presented in Figures 3(a), (b), (e), and (f); 4(c) and (d); and 5(c) and (d), respectively, by using different colored symbols. The cyan symbols in the figures correspond to the results without the practical motion of the lunar pole, while the magenta symbols correspond to the results with the practical motion of the lunar pole. The corresponding initial orbital values in these first-order semianalytical calculations are set as follows: the initial epoch is 00:00:00 UTC on 2019 May 5, the initial semimajor axis a0 = 42,164.1363 or 27,906.1363 km, the initial eccentricity e0 = 0.0001, the initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn38.gif) , the initial argument of perigee ω0 = 0°, and the initial mean anomaly M0 = 0°. To make the time spans of the first-order semianalytical calculations cover a variation period of orbital inclination, we take the theoretical values of the periods of orbital plane evolution P as references and set the time spans of the first-order semianalytical calculations as 120 yr for Figures 3(a) and (e), 40 yr for Figures 3(b) and (f), and 500 yr for Figures 5(c) and (d). Further considering the time span that the JPL DE430 precise ephemeris covers, we set the time spans of the first-order semianalytical calculations in Figures 4(c) and (d) as 600 yr. In addition, if the orbital perigee altitude is below 80 km in the first-order semianalytical calculation, we assume that orbital decay occurs, and then the calculation will be aborted.
, the initial argument of perigee ω0 = 0°, and the initial mean anomaly M0 = 0°. To make the time spans of the first-order semianalytical calculations cover a variation period of orbital inclination, we take the theoretical values of the periods of orbital plane evolution P as references and set the time spans of the first-order semianalytical calculations as 120 yr for Figures 3(a) and (e), 40 yr for Figures 3(b) and (f), and 500 yr for Figures 5(c) and (d). Further considering the time span that the JPL DE430 precise ephemeris covers, we set the time spans of the first-order semianalytical calculations in Figures 4(c) and (d) as 600 yr. In addition, if the orbital perigee altitude is below 80 km in the first-order semianalytical calculation, we assume that orbital decay occurs, and then the calculation will be aborted.
Figure 5. Quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn39.gif) , periods of orbital plane evolution P, and maximum eccentricities emax in the long-term evolution of initial near-circular medium orbits with an altitude H = 21,528 km and initial inclination i0 = 87°. Panel (a) shows the theoretical results of
, periods of orbital plane evolution P, and maximum eccentricities emax in the long-term evolution of initial near-circular medium orbits with an altitude H = 21,528 km and initial inclination i0 = 87°. Panel (a) shows the theoretical results of ![$\left[{i}_{\min },{i}_{\max }\right];$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn40.gif) panel (b) shows the theoretical results of P; panel (c) shows the first-order semianalytical results of
panel (b) shows the theoretical results of P; panel (c) shows the first-order semianalytical results of ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn41.gif) with and without the practical motion of the lunar pole; and panel (d) shows the first-order semianalytical results of emax with and without the practical motion of the lunar pole. The initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of
with and without the practical motion of the lunar pole; and panel (d) shows the first-order semianalytical results of emax with and without the practical motion of the lunar pole. The initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn42.gif) . The symbols with different colors have the same meaning as in Figures 3 and 4.
. The symbols with different colors have the same meaning as in Figures 3 and 4.
Download figure:
Standard image High-resolution imageFrom Figures 3(a) and (e), it can be seen that for certain initial longitudes of the ascending node Ω0, the maximum eccentricities emax in the long-term evolution up to 120 yr for the initial near-circular geosynchronous orbits with a nominal altitude H = 35,786 km and initial inclination i0 = 55° in the BeiDou navigation satellite system can even exceed 0.5 due to lunisolar resonances (Cook 1962; Hughes 1980, 1981; Zhao et al. 2015), but the theoretical results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn43.gif) accord well with the results of the first-order semianalytical calculations. Meanwhile, the first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination
accord well with the results of the first-order semianalytical calculations. Meanwhile, the first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn44.gif) and the maximum eccentricities emax with and without the practical motion of the lunar pole are consistent on the whole.
and the maximum eccentricities emax with and without the practical motion of the lunar pole are consistent on the whole.
From Figures 3(b) and (f), it can be seen that the long-term evolution of eccentricities up to 40 yr for the initial near-circular medium orbits with a nominal altitude  and initial inclination i0 = 55° in the BeiDou navigation satellite system can maintain their initial near-circular characteristic; the theoretical results of the quantitative variation ranges of orbital inclination
and initial inclination i0 = 55° in the BeiDou navigation satellite system can maintain their initial near-circular characteristic; the theoretical results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn46.gif) accord well with the results of the first-order semianalytical calculations without the practical motion of the lunar pole but roughly with the results with the practical motion of the lunar pole, and there are relatively obvious differences. Meanwhile, the first-order semianalytical calculation results of the maximum eccentricities emax with and without the practical motion of the lunar pole are consistent on the whole.
accord well with the results of the first-order semianalytical calculations without the practical motion of the lunar pole but roughly with the results with the practical motion of the lunar pole, and there are relatively obvious differences. Meanwhile, the first-order semianalytical calculation results of the maximum eccentricities emax with and without the practical motion of the lunar pole are consistent on the whole.
From Figures 4(c) and (d), it can be seen that all of the maximum eccentricities emax in the long-term evolution up to 600 yr for the initial near-circular orbits with a geosynchronous altitude H = 35,786 km, initial inclination i0 = 83°, and different initial longitude of the ascending node Ω0 can exceed 0.6 due to lunisolar resonances (Cook 1962; Hughes 1980, 1981; Zhao et al. 2015), and the theoretical results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn47.gif) , upon the precondition that the initial near-circular orbital characteristic is maintained, have obvious differences from the first-order semianalytical calculations. However, to a certain extent, the first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination
, upon the precondition that the initial near-circular orbital characteristic is maintained, have obvious differences from the first-order semianalytical calculations. However, to a certain extent, the first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn48.gif) reflect that both the classical and polar Laplace precession mechanisms of the orbital plane exist for the initial near-circular orbits with a geosynchronous altitude H = 35,786 km and initial inclination i0 = 83°. The first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination
reflect that both the classical and polar Laplace precession mechanisms of the orbital plane exist for the initial near-circular orbits with a geosynchronous altitude H = 35,786 km and initial inclination i0 = 83°. The first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn49.gif) and the maximum eccentricities emax with and without the practical motion of the lunar pole are also consistent on the whole.
and the maximum eccentricities emax with and without the practical motion of the lunar pole are also consistent on the whole.
From Figures 5(c) and (d), it can be seen that the long-term evolution of eccentricities up to 500 yr for the initial near-circular medium orbits with an altitude H = 21,528 km, initial inclination i0 = 87°, and different initial longitude of the ascending node Ω0 can maintain their initial near-circular characteristic. The theoretical results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn50.gif) accord well with the results of the first-order semianalytical calculations with and without the practical motion of the lunar pole on the whole, but there are obvious differences, in particular in the case of the classical Laplace precession of the orbital plane. The first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination
accord well with the results of the first-order semianalytical calculations with and without the practical motion of the lunar pole on the whole, but there are obvious differences, in particular in the case of the classical Laplace precession of the orbital plane. The first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn51.gif) with and without the practical motion of the lunar pole are consistent on the whole, and there are few differences for the maximum eccentricities emax.
with and without the practical motion of the lunar pole are consistent on the whole, and there are few differences for the maximum eccentricities emax.
To better compare the theoretical results and the first-order semianalytical calculation results of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn52.gif) for the long-term evolution of initial near-circular medium orbits with an altitude H = 21,528 km, initial inclination i0 = 87°, and different initial longitude of the ascending node Ω0, we replot these results in Figure 6. From Figure 6, it can be seen that in the case of the polar Laplace precession of the orbital plane, the theoretical results are well consistent with the first-order semianalytical calculation results. Then, it is verified that the polar Laplace precession mechanism of the orbital plane does exist through the first-order semianalytical calculations. The obvious differences in the case of the classical Laplace precession of the orbital plane lie in the inconsistent results of imin derived by the theoretical analysis and the first-order semianalytical calculations.
for the long-term evolution of initial near-circular medium orbits with an altitude H = 21,528 km, initial inclination i0 = 87°, and different initial longitude of the ascending node Ω0, we replot these results in Figure 6. From Figure 6, it can be seen that in the case of the polar Laplace precession of the orbital plane, the theoretical results are well consistent with the first-order semianalytical calculation results. Then, it is verified that the polar Laplace precession mechanism of the orbital plane does exist through the first-order semianalytical calculations. The obvious differences in the case of the classical Laplace precession of the orbital plane lie in the inconsistent results of imin derived by the theoretical analysis and the first-order semianalytical calculations.
Figure 6. Results of the theoretical and first-order semianalytical calculations of the quantitative variation ranges of orbital inclination ![$\left[{i}_{\min },{i}_{\max }\right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn53.gif) in the long-term evolution of initial near-circular medium orbits with an altitude H = 21,528 km and initial inclination i0 = 87°. The initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of
in the long-term evolution of initial near-circular medium orbits with an altitude H = 21,528 km and initial inclination i0 = 87°. The initial longitude of the ascending node Ω0 is set at intervals of 1° in the range of ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn54.gif) . The symbols with different colors have the same meaning as in Figures 3–5.
. The symbols with different colors have the same meaning as in Figures 3–5.
Download figure:
Standard image High-resolution imageWe further present the specific results of the long-term evolution of inclination and eccentricity for the initial near-circular orbits with altitudes H = 35,786 and 21,528 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300° in Figures 7 and 8, respectively, by the first-order semianalytical calculations based on the simplified models with and without the practical motion of the lunar pole. Similarly, when the initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°, the specific results for the initial near-circular orbits with an altitude H = 35,786 km and initial inclination i0 = 83° and those with an altitude H = 21,528 km and initial inclination i0 = 87° are presented in Figures 9 and 10, respectively. The cyan curves in Figures 7–10 correspond to the results without the practical motion of the lunar pole, while the magenta curves correspond to the results with the practical motion of the lunar pole. The influence of the practical motion of the lunar pole on the long-term evolution of orbital inclination and eccentricity can be further observed from Figures 7–10.
Figure 7. Long-term evolution of inclination and eccentricity up to 120 yr for the initial near-circular orbits with an altitude H = 35,786 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The cyan curves correspond to the results of the first-order semianalytical calculations based on the simplified models without the practical motion of the lunar pole, the magenta curves correspond to the results of the first-order semianalytical calculations based on the simplified models with the practical motion of the lunar pole, and the black curves correspond to the results of numerical calculations based on the precise models.
Download figure:
Standard image High-resolution imageFigure 8. Long-term evolution of inclination and eccentricity up to 40 yr for the initial near-circular orbits with an altitude H = 21,528 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The curves with different colors have the same meaning as in Figure 7.
Download figure:
Standard image High-resolution imageFigure 9. Long-term evolution of inclination and eccentricity up to 600 yr for the initial near-circular orbits with an altitude H = 35,786 km, initial inclination i0 = 83°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The curves with different colors have the same meaning as in Figures 7 and 8.
Download figure:
Standard image High-resolution imageFigure 10. Long-term evolution of inclination and eccentricity up to 500 yr for the initial near-circular orbits with an altitude H = 21,528 km, initial inclination i0 = 87°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The curves with different colors have the same meaning as in Figures 7–9.
Download figure:
Standard image High-resolution imageThe periods of orbital plane evolution observed from the long-term evolution of orbital inclination in Figures 7, 8 and 10 are in accord with the corresponding theoretical results in Figures 3(c) and (d) and 5(b) on the whole. This verifies the theoretical calculation of the period of orbital plane evolution by the first-order semianalytical calculations based on the simplified models to a certain extent.
In addition, it seems that the curves of the long-term evolution of inclination and eccentricity are broken for the cases Ω0 = 0°, 60°, 180°, and 300° in Figure 9 derived by the first-order semianalytical calculations based on the simplified models without the practical motion of the lunar pole, as well as for the case Ω0 = 0° in Figure 9 derived by the first-order semianalytical calculation based on the simplified models with the practical motion of the lunar pole. The specific reason for this phenomenon is as follows. Due to lunisolar resonances (Cook 1962; Hughes 1980, 1981; Zhao et al. 2015), the orbital eccentricities e can evolve to high enough, and the related orbital perigee altitudes can evolve to low enough (below 80 km). As stated above, when the orbital perigee altitude is below 80 km in the first-order semianalytical calculations, orbital decay is supposed to occur, and then the calculations are aborted, which makes these curves seem to be broken.
It should also be pointed out that there are model error accumulations in the first-order semianalytical calculations through numerical integrations of the averaged perturbation models, which cause the differences between the results with and without the practical motion of the lunar pole. Especially, from Figure 9, it is seen that there is a good coincidence between the curves of the long-term evolution of inclination and eccentricity, derived by the first-order semianalytical calculations with and without the practical motion of the lunar pole, within the first several decades from the initial epoch in the long-term calculations. Then, with the increase of the model error accumulations, the relatively obvious differences can be observed. This is the reason that orbital decays occur for the cases Ω0 = 60°, 180°, and 300° in Figure 9 in the first-order semianalytical calculations without the practical motion of the lunar pole, while orbital decays do not occur for these cases in the first-order semianalytical calculations with the practical motion of the lunar pole.
3.4. Verification of Numerical Calculations
To compare the first-order semianalytical calculation results based on the simplified models and further verify the theoretical results based on the simplified and approximate model, we perform numerical calculations based on the precise models for the long-term evolution of initial near-circular orbits with altitudes H = 35,786 and 21,528 km; initial inclinations i0 = 55°, 83°, and 87°; and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°, respectively, as in Section 3.3. The corresponding long-term evolution of inclinations and eccentricities for these orbits obtained by numerical calculations is presented in Figures 7–10 with black curves.
The Earth's gravitational field up to 20 × 20 order and degree, lunisolar perturbations, solar radiation pressure, and atmospheric drag perturbation (when the orbital altitude is less than 1000 km) are taken into account in the precise models. The JGM3 model is used to get the coefficients of the Earth's gravitational field. The JPL DE430 precise ephemeris is directly invoked to get the required lunisolar position coordinates, and the U.S. Standard Atmosphere 1976 model is used to get the atmospheric mass densities in the numerical calculations. The solar radiation pressure coefficient is set as 1.2, and the A/m value of the object in orbits is set as  . The initial orbital values of the numerical calculations are the same as the first-order semianalytical calculations. Likewise, if the orbital perigee altitude is below 80 km in the numerical calculation, we assume that orbital decay occurs, and then the calculation will be aborted.
. The initial orbital values of the numerical calculations are the same as the first-order semianalytical calculations. Likewise, if the orbital perigee altitude is below 80 km in the numerical calculation, we assume that orbital decay occurs, and then the calculation will be aborted.
From Figures 7–10, it is shown that although the long-term evolution of eccentricities obtained by numerical calculations with the precise models has relatively obvious differences from the first-order semianalytical calculations with the simplified models, the dynamical tendencies whether the initial near-circular characteristic can be maintained in the long-term evolution, revealed from the first-order semianalytical calculations and numerical calculations, are consistent. Meanwhile, when the initial near-circular orbital characteristic is maintained, most of the long-term evolution of inclinations obtained by numerical calculations accord with the first-order semianalytical calculations on the whole. This suggests the reliability of the first-order semianalytical calculations and further verifies the theoretical results based on the simplified and approximate model. In other words, the complete analytical formulae of the quantitative variation ranges of orbital inclination in Equations (1) and (2), upon the precondition that the initial near-circular orbital characteristic is maintained, are verified to be correct.
The orbital decay also occurs in the numerical calculation for the case Ω0 = 0° in Figure 9, mainly due to lunisolar resonances (Cook 1962; Hughes 1980, 1981; Zhao et al. 2015), and then the numerical calculation is aborted, which makes the curves of the long-term evolution of inclination and eccentricity seem to be broken. Meanwhile, the atmospheric drag perturbation is taken into account in the numerical calculation when the orbital altitude is below 1000 km, which accelerates the orbital decay. The differences between the results derived by the first-order semianalytical and numerical calculations mainly arise from the model errors and their accumulations.
4. Qualitative Results of Long-term Evolution of the Orbital Plane
4.1. Generalized Qualitative Characteristic Formulae of the Variation of Orbital Inclination-longitude of the Ascending Node
Similar to the qualitative characteristic formula for the variation of orbital inclination-longitude of the ascending node of geostationary orbits in Zhao et al. (2016), we use Equation (3) in Zhao et al. (2015), Equations (26a) and (26b) in Allan & Cook (1964), and the above parameters  and
and  defined in Equation (2) and derive the generalized qualitative characteristic formulae of the variation of orbital inclination-longitude of the ascending node for medium-high near-circular orbits
defined in Equation (2) and derive the generalized qualitative characteristic formulae of the variation of orbital inclination-longitude of the ascending node for medium-high near-circular orbits
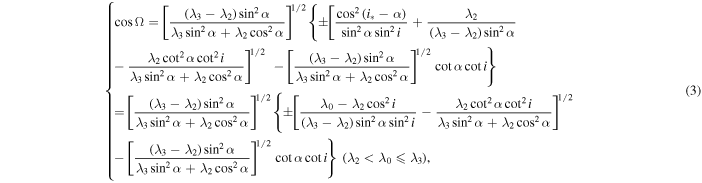
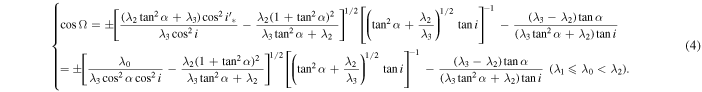
Equation (3) applies to the classical Laplace precession of the orbital plane. For the mathematical symbol "±" in Equation (3), the plus sign corresponds to the case ![${\left[\tfrac{{\lambda }_{3}{\sin }^{2}\alpha +{\lambda }_{2}{\cos }^{2}\alpha }{({\lambda }_{3}-{\lambda }_{2}){\sin }^{2}\alpha }\right]}^{1/2}\cos {\rm{\Omega }}\,+\,{\left[\tfrac{({\lambda }_{3}-{\lambda }_{2}){\sin }^{2}\alpha }{{\lambda }_{3}{\sin }^{2}\alpha +{\lambda }_{2}{\cos }^{2}\alpha }\right]}^{1/2}\cot \alpha \cot i\geqslant 0$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn58.gif) , while the minus sign corresponds to the case
, while the minus sign corresponds to the case ![${\left[\tfrac{{\lambda }_{3}{\sin }^{2}\alpha +{\lambda }_{2}{\cos }^{2}\alpha }{({\lambda }_{3}-{\lambda }_{2}){\sin }^{2}\alpha }\right]}^{1/2}\cos {\rm{\Omega }}\,+\,{\left[\tfrac{({\lambda }_{3}-{\lambda }_{2}){\sin }^{2}\alpha }{{\lambda }_{3}{\sin }^{2}\alpha +{\lambda }_{2}{\cos }^{2}\alpha }\right]}^{1/2}\cot \alpha \cot i\lt 0$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn59.gif) . Equation (4) applies to the polar Laplace precession of the orbital plane. For the mathematical symbol "±" in Equation (4), the plus sign corresponds to the case
. Equation (4) applies to the polar Laplace precession of the orbital plane. For the mathematical symbol "±" in Equation (4), the plus sign corresponds to the case  , while the minus sign corresponds to the case
, while the minus sign corresponds to the case  . As stated above, the quantities λ0, λ1, λ2, λ3, and α are constants determined by the initial state or values of the given near-circular orbit, if the assumption that the lunar orbital plane coincides with the ecliptic is considered as in Allan & Cook (1964). Then, from the initial orbital values, the qualitative characteristic of the variation of orbital inclination-longitude of the ascending node for an arbitrary medium-high near-circular orbit can be presented by Equations (3) and (4). This shows the generality of the qualitative characteristic formulae of Equations (3) and (4).
. As stated above, the quantities λ0, λ1, λ2, λ3, and α are constants determined by the initial state or values of the given near-circular orbit, if the assumption that the lunar orbital plane coincides with the ecliptic is considered as in Allan & Cook (1964). Then, from the initial orbital values, the qualitative characteristic of the variation of orbital inclination-longitude of the ascending node for an arbitrary medium-high near-circular orbit can be presented by Equations (3) and (4). This shows the generality of the qualitative characteristic formulae of Equations (3) and (4).
The qualitative characteristics of the variation of orbital inclination-longitude of the ascending node, derived by the theoretical formulae of Equations (3) and (4) for these initial near-circular orbits discussed in Figures 7–10, are presented in Figures 11–14 with the blue and red curves, respectively. The blue curves correspond to the classical Laplace precession of the orbital plane, while the red curves correspond to the polar Laplace precession of the orbital plane. It is worth pointing out that the qualitative characteristic curves of the variation of orbital inclination-longitude of the ascending node governed by the above theoretical formulae are in pairs. In general cases, according to the initial orbital values, the specific and single variation curve of orbital inclination-longitude of the ascending node for the long-term evolution of the initial near-circular orbits can be determined from the paired curves. Using the initial orbital values, we directly present the specific and single qualitative characteristic curves of the variation of orbital inclination-longitude of the ascending node for the long-term evolution of the corresponding orbits in Figures 11, 12 and 14, as well as the cases Ω0 = 120° and 240° in Figure 13 for the polar Laplace precession of the orbital plane. For the cases Ω0 = 0°, 60°, 180°, and 300° in Figure 13 in the state of classical Laplace precession of the orbital plane, we present the paired qualitative characteristic curves of the variation of orbital inclination-longitude of the ascending node. Moreover, the paired qualitative characteristic curves of the variation of orbital inclination-longitude of the ascending node for the case Ω0 = 180° are interwoven. When the paired qualitative characteristic curves of the variation of orbital inclination-longitude of the ascending node are close to each other or interwoven, predictably, some special dynamical phenomena may occur.
Figure 11. Qualitative characteristics of the variation of orbital inclination-longitude of the ascending node for the long-term evolution of the initial near-circular orbits with an altitude H = 35,786 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The blue curves correspond to the theoretical calculation results with Equation (3). The cyan curves correspond to the results of the first-order semianalytical calculations up to 120 yr based on the simplified models without the practical motion of the lunar pole, the magenta curves correspond to the results of the first-order semianalytical calculations up to 120 yr based on the simplified models with the practical motion of the lunar pole, and the black curves correspond to the results of numerical calculations up to 120 yr based on the precise models. The green curves correspond to the theoretical calculation results with Equation (5).
Download figure:
Standard image High-resolution imageFigure 12. Qualitative characteristics of the variation of orbital inclination-longitude of the ascending node for the long-term evolution of the initial near-circular orbits with an altitude H = 21,528 km, initial inclination i0 = 55°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The curves with different colors have the same meaning as in Figure 11. The time span of the first-order semianalytical and numerical calculations is 40 yr.
Download figure:
Standard image High-resolution imageFigure 13. Qualitative characteristics of the variation of orbital inclination-longitude of the ascending node for the long-term evolution of the initial near-circular orbits with an altitude H = 35,786 km, initial inclination i0 = 83°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The curves with different colors have the same meaning as in Figures 11 and 12. In addition, the red curves correspond to the theoretical calculation results with Equation (4). The time span of the first-order semianalytical and numerical calculations is 600 yr.
Download figure:
Standard image High-resolution imageFrom Figures 11–14, it can be seen that the qualitative characteristics of the variation of orbital inclination-longitude of the ascending node in cases of classical and polar Laplace precessions of the orbital plane are markedly different. For the classical Laplace precession of the orbital plane, the long-term evolution of the orbital plane for these orbits is in a state of circulation; i.e., the variation range of the longitude of the ascending node is ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn62.gif) . For the polar Laplace precession of the orbital plane, the long-term evolution of the orbital plane for these orbits is in a state of libration; i.e., the longitude of the ascending node varies merely in a certain range, and the transition between prograde and retrograde motion for these near-circular orbits occurs. In addition, it should be noted that for geostationary orbits in the mechanism of the classical Laplace precession of the orbital plane, the variation range of the longitude of the ascending node is
. For the polar Laplace precession of the orbital plane, the long-term evolution of the orbital plane for these orbits is in a state of libration; i.e., the longitude of the ascending node varies merely in a certain range, and the transition between prograde and retrograde motion for these near-circular orbits occurs. In addition, it should be noted that for geostationary orbits in the mechanism of the classical Laplace precession of the orbital plane, the variation range of the longitude of the ascending node is ![$\left[-90^\circ ,90^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn63.gif) (Zhao et al. 2016), which is different from the near-circular orbits with high inclinations discussed in this paper. The features of the long-term evolution of the orbital plane in a state of libration and the transition between prograde and retrograde motion for the polar Laplace precession of the orbital plane might offer a reference for the orbit design to meet the particular mission requirement.
(Zhao et al. 2016), which is different from the near-circular orbits with high inclinations discussed in this paper. The features of the long-term evolution of the orbital plane in a state of libration and the transition between prograde and retrograde motion for the polar Laplace precession of the orbital plane might offer a reference for the orbit design to meet the particular mission requirement.
4.2. Results of the First-order Semianalytical and Numerical Calculations
To verify the theoretical results of the qualitative characteristics of the variation of orbital inclination-longitude of the ascending node given by the analytical formulae of Equations (3) and (4), the results from the first-order semianalytical calculations based on the simplified models with and without the practical motion of the lunar pole and from the numerical calculations based on the precise models are also presented in Figures 11–14 with the cyan, magenta, and black curves respectively.
From Figures 11 and 12, it can be seen that the theoretical results of the qualitative characteristics of the variation of orbital inclination-longitude of the ascending node given by the analytical formula of Equation (3) from the classical Laplace precession of the orbital plane are in accord with the results of the first-order semianalytical and numerical calculations on the whole.
Although the initial near-circular orbital characteristic is no longer maintained in the long-term evolution as seen in Figure 9, from Figure 13, the theoretical results of the qualitative characteristics of the variation of orbital inclination-longitude of the ascending node for these orbits with the initial longitude of the ascending node Ω0 = 120° and 240°, given by the analytical formula of Equation (4) from the polar Laplace precession of the orbital plane, are in accord with the results of the first-order semianalytical and numerical calculations on the whole. For the cases Ω0 = 0°, 60°, 180°, and 300° in Figure 13 in the state of the classical Laplace precession of the orbital plane, the overall trend of the one certain characteristic curve for these orbits given by the analytical formula of Equation (3) is consistent with the results of the first-order semianalytical and numerical calculations in the initial stage of long-term evolution. The results of the first-order semianalytical calculations are also in accord with the results of numerical calculations in the initial stage of long-term evolution on the whole, and then the obvious differences are gradually revealed with time. In particular, for the case Ω0 = 60° in Figure 13, the variation of orbital inclination-longitude of the ascending node in the long-term evolution given by numerical calculation presents the transition between the paired qualitative characteristic curves determined by the analytical formula of Equation (3). It shows that special dynamical phenomena might occur when the paired qualitative characteristic curves of the variation of orbital inclination-longitude of the ascending node determined by the theoretial formula are close to each other.
From Figure 14, it can be seen that the theoretical results for these orbits with the initial longitude of the ascending node Ω0 = 60°, 120°, 240°, and 300° from the polar Laplace precession of the orbital plane are also consistent with the results of the first-order semianalytical and numerical calculations on the whole. The theoretical results for these orbits with the initial longitude of the ascending node Ω0 = 0° and 180° from the classical Laplace precession of the orbital plane are well consistent with the results of the first-order semianalytical calculations. Moreover, in the initial stage of long-term evolution of the orbital plane, the theoretical results for the cases Ω0 = 0° and 180° are well consistent with the results of the numerical calculations, and they are also well consistent between the results of the first-order semianalytical and numerical calculations; but the relatively obvious differences are gradually revealed with the increase of the timescale of long-term orbital evolution due to model errors.
Figure 14. Qualitative characteristics of the variation of orbital inclination-longitude of the ascending node for the long-term evolution of the initial near-circular orbits with an altitude H = 21,528 km, initial inclination i0 = 87°, and different initial longitude of the ascending node Ω0 = 0°, 60°, 120°, 180°, 240°, and 300°. The curves with different colors have the same meaning as in Figures 11–13. The time span of the first-order semianalytical and numerical calculations is 500 yr.
Download figure:
Standard image High-resolution imageTo a certain extent, the generalized qualitative characteristic formulae of Equations (3) and (4) of the variation of orbital inclination-longitude of the ascending node for medium-high near-circular orbits, derived on the basis of the simplified and approximate model, are verified by the first-order semianalytical calculations based on the simplified models and the numerical calculations based on the precise models.
5. Discussions
The trajectory of the orbital plane precession along the classical Laplace plane is an ellipse for medium-high near-circular orbits. Approximately, it is assumed that λ2 ≪ λ3 for medium-high near-circular orbits (Allan & Cook 1964); then the trajectory of the orbital plane precession along the classical Laplace plane can be regarded as a circle. Accordingly, the generalized qualitative characteristic formula of Equation (3) of the variation of orbital inclination-longitude of the ascending node from the classical Laplace precession of the orbital plane can be reduced to
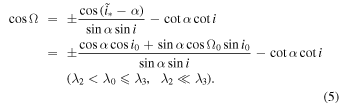
For the mathematical symbol "±" in Equation (5), the plus sign corresponds to the case  , while the minus sign corresponds to the case
, while the minus sign corresponds to the case  . The quantity
. The quantity  is the value of
is the value of  when λ2 ≪ λ3.
when λ2 ≪ λ3.
The theoretical results of the qualitative variation characteristics of orbital inclination-longitude of the ascending node from the classical Laplace precession of the orbital plane, derived by the reduced formula of Equation (5) for the long-term evolution of the corresponding near-circular orbits, are presented in Figures 11–14 with the green curves. From Figures 11 and 12, it is seen that the theoretical results given by Equation (5) are in accord with the results of the first-order semianalytical and numerical results on the whole, which reflects that the approximation is reasonable to a certain extent, but there are obvious differences for the results in Figures 13 and 14. In addition, according to the orbital elements at the epoch MJD 57,219.210, the qualitative variation characteristic of orbital inclination-longitude of the ascending node for the BeiDou-M1 satellite in the state of the classical Laplace precession presented directly in Zhang et al. (2015b) is just governed by Equation (5), and this equation is not explicitly presented in Zhang et al. (2015b). It should be pointed out that the generalized qualitative characteristic formula of Equation (4) of the variation of orbital inclination-longitude of the ascending node from the polar Laplace precession of the orbital plane cannot use the approximation as that for the classical Laplace precession. This is due to a feature of the trajectory (Equation (26b)) in Allan & Cook (1964) of the orbital plane precession along the polar Laplace plane.
For geostationary orbits, their initial inclination i0 = 0°, they are in the state of the classical Laplace precession of the orbital plane, and  . Then, from Equation (5), the qualitative characteristic formula
. Then, from Equation (5), the qualitative characteristic formula  in Zhao et al. (2016) can be obtained. This fully demonstrates the generality of the analytical formulae of Equations (3) and (4), which can be applied to all medium-high near-circular orbits with arbitrary initial values in the states of two types of possible precession mechanisms of the orbital plane.
in Zhao et al. (2016) can be obtained. This fully demonstrates the generality of the analytical formulae of Equations (3) and (4), which can be applied to all medium-high near-circular orbits with arbitrary initial values in the states of two types of possible precession mechanisms of the orbital plane.
Taking the direct solar radiation pressure into consideration in the simplified and approximate model in Allan & Cook (1964) and ignoring the Earth shadow, the form of the analytical formulae of the quantitative and qualitative results from the orbital plane precession for high-A/m space debris in medium-high near-circular orbits under the premise of initial near-circular orbit maintenance is the same as the ones derived in this paper, and only the amendment of the calculation of the quantity α arising from the solar radiation pressure is required, based on the analysis in Rosengren et al. (2014) and Rosengren & Scheeres (2014a). For different high-A/m space debris in geostationary orbits in the mechanism of the classical Laplace precession of the orbital plane under the premise of initial near-circular orbit maintenance, the quantitative variation ranges of orbital inclination reported in Zhang et al. (2014) are just derived by the corresponding analytical formula in Equation (1), and the qualitative variation characteristics of orbital inclination-longitude of the ascending node are just derived by the analytical formula  .
.
6. Conclusions
Based on two types of possible precession mechanisms, the complete analytical formulae of Equations (1) and (2) of the quantitative variation ranges of orbital inclination and the generalized qualitative characteristic formulae of Equations (3) and (4) of the variation of orbital inclination-longitude of the ascending node for medium-high near-circular orbits are derived in this paper. The completeness of the analytical formulae of Equations (1) and (2) mainly lies in the ideas that the polar Laplace precession of the orbital plane is particularly considered and the analytical formulae in Zhao et al. (2015) only applicable to the classical Laplace precession of the orbital plane are revised to cover these two types of possible precession mechanisms. Moreover, the calculation expressions of the quantities i* and λ0 in Zhao et al. (2015) are adaptably replaced. The generality of the analytical formulae of Equations (3) and (4) mainly lies in the ideas that the qualitative characteristic formula for geostationary orbits in Zhao et al. (2016) is generalized to arbitrary medium-high near-circular orbits and Equations (3) and (4) are applicable to two types of possible precession mechanisms. Moreover, the approximation λ2 ≪ λ3 is not used in Equation (3), and the trajectory of the orbital plane precession along the classical Laplace plane is closer to the actual motion. Taking the near-circular orbits with the altitudes as the geosynchronous and medium orbits of BeiDou navigation satellites as examples, the quantitative and qualitative results from orbital plane precession are verified by the first-order semianalytical calculations with simplified models and numerical calculations with precise models to a certain extent.
The theoretical results of the quantitative variation ranges of orbital inclination and qualitative variation characteristics of orbital inclination-longitude of the ascending node for medium-high near-circular orbits with given initial inclinations i0 and different initial longitudes of the ascending node Ω0 are particularly presented in this paper, as well as the corresponding first-order semianalytical and numerical calculation results, from which some conclusions can be summarized as follows.
Under the premise of initial near-circular orbit maintenance, it is found that for the classical Laplace precession of the orbital plane, the quantitative variation amplitudes of orbital inclination  in the long-term orbital evolution are all 2α; when Ω0 = 0° and 360°, imin and imax have the minimum values, and when Ω0 = 180°, imin and imax have the maximum values. For the polar Laplace precession of the orbital plane, the quantitative variation amplitudes of orbital inclination
in the long-term orbital evolution are all 2α; when Ω0 = 0° and 360°, imin and imax have the minimum values, and when Ω0 = 180°, imin and imax have the maximum values. For the polar Laplace precession of the orbital plane, the quantitative variation amplitudes of orbital inclination  are not a fixed value any longer as that arising from the classical Laplace precession of the orbital plane.
are not a fixed value any longer as that arising from the classical Laplace precession of the orbital plane.
For the classical Laplace precession of the orbital plane of medium-high near-circular orbits with high inclinations, the long-term evolution of the orbital plane is in a state of circulation; i.e., the variation range of longitude of the ascending node is ![$\left[0^\circ ,360^\circ \right]$](https://content.cld.iop.org/journals/1538-3881/159/4/162/revision1/ajab7009ieqn73.gif) . For the polar Laplace precession of the orbital plane, the long-term evolution of the orbital plane is in a state of libration; i.e., the longitude of the ascending node varies merely in a certain range, and the transition between prograde and retrograde motion occurs for these near-circular orbits with high inclinations, which might offer a reference for the orbit design to meet the particular mission requirement.
. For the polar Laplace precession of the orbital plane, the long-term evolution of the orbital plane is in a state of libration; i.e., the longitude of the ascending node varies merely in a certain range, and the transition between prograde and retrograde motion occurs for these near-circular orbits with high inclinations, which might offer a reference for the orbit design to meet the particular mission requirement.
Due to the high similarity of orbital plane precession of natural satellites to that of artificial satellites, the results and methodology in this paper can be directly extended to the long-term evolution of the orbital plane for natural satellites, such as Saturn's satellite Iapetus, discussed in Rosengren & Scheeres (2014a), and help to understand and explain some dynamic phenomena in the long-term orbital evolution of natural satellites.
This work is supported by the National Natural Science Foundation of China (grant Nos. 11873096 and 11533010) and the Youth Innovation Promotion Association CAS (grant No. 2017367).
Appendix: The Important Equations Used in Allan & Cook (1964) and Zhao et al. (2015)
The important equations used in Allan & Cook (1964) and Zhao et al. (2015) are presented here for reference.
The calculation formulae of the quantities λ0, λ1, λ2, λ3, and α are
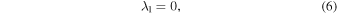
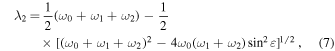
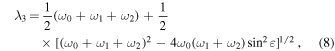
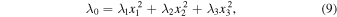
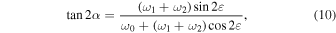
where ε is the obliquity of the ecliptic; x1, x2, and x3 are the components of the unit normal vector  of the orbital plane of the space object orbiting the Earth in the coordinate system O − 123 (see Figure 1) composed of the principal axes defined in Allan & Cook (1964); and
of the orbital plane of the space object orbiting the Earth in the coordinate system O − 123 (see Figure 1) composed of the principal axes defined in Allan & Cook (1964); and
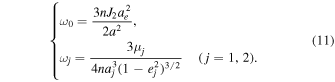
In Equation (11), n is the orbital mean motion of the space object orbiting the Earth, J2 is the second-order zonal harmonic of the Earth's gravitational field, ae is the mean equatorial radius of the Earth, a is the orbital semimajor axis of the space object orbiting the Earth, μj = Gmj (j = 1 for Sun, j = 2 for Moon), G is the gravitational constant, mj is the mass of the Sun or Moon, and aj and ej are, respectively, the orbital semimajor axis and eccentricity of the Sun or Moon. Equation (9) above is Equation (22) in Allan & Cook (1964).
The expression of the unit normal vector  of the orbital plane of the space object orbiting the Earth in the coordinate system O − 123, i.e., Equation (3) in Zhao et al. (2015), is
of the orbital plane of the space object orbiting the Earth in the coordinate system O − 123, i.e., Equation (3) in Zhao et al. (2015), is
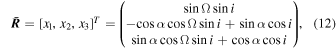
where i and Ω are the orbital inclination and longitude of the ascending node of the space object orbiting the Earth, respectively.
The expressions of the trajectories of the unit normal vector  of the orbital plane of the space object orbiting the Earth corresponding to two types of precession mechanisms projected on the coordinate planes of O − 123, i.e., Equations (26a) and (26b) in Allan & Cook (1964), are
of the orbital plane of the space object orbiting the Earth corresponding to two types of precession mechanisms projected on the coordinate planes of O − 123, i.e., Equations (26a) and (26b) in Allan & Cook (1964), are
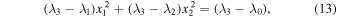
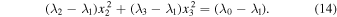
The calculation formulae of the periods of orbital plane evolution, i.e., Equations (27a) and (27b) in Allan & Cook (1964), are
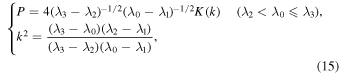
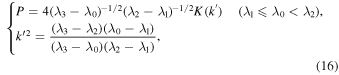
where  refers to the complete elliptic integral of the first kind.
refers to the complete elliptic integral of the first kind.

















