Universal Scaling Laws for Solar and Stellar Atmospheric Heating

Observations suggest that cool stars of spectral classes later than F5, including the Sun, with outer convection envelopes, possess hot outer atmospheres: the corona (${\rm{log}}(T/{\rm{K}})\gt 6$), the transition region (log(T/K) = 4–6), and the chromosphere (${\rm{log}}(T/{\rm{K}})\sim 4$) (Güdel 2004). The temperature of the corona is up to two orders of magnitude greater than that of the surface layer, the photosphere. However, two fundamental issues regarding the formation of hot atmospheres remain unsolved. First, it is a mystery how such high temperatures are achieved and maintained despite radiative and conductive cooling (Withbroe & Noyes 1977; Klimchuk 2006). Although it is widely argued that the surface magnetic field is crucial for supplying energy and momentum to the upper layers, the mechanisms of response of the atmospheres to the surface magnetic field have not been clarified yet. Second, young solar-type stars are known to exhibit far hotter coronae than their older siblings, including our Sun (Güdel 2004). However, it is not confirmed whether the heating mechanisms are common.

Ionizing radiation in the form of X-ray and extreme UV (XUV) from planet-hosting stars has a significant impact on close-in exoplanets. In the Sun, strong concentrations of magnetic field, the active regions, are the primary source of XUV emission and the arena of catastrophic outbursts called flares and coronal mass ejections, which may directly disturb the terrestrial environment (Benz & Güdel 2010; Fletcher et al. 2011; Shibata & Magara 2011; Toriumi & Wang 2019). The planet's atmosphere helps protect surface life from harmful radiation, but strong XUV radiation from active regions and flares may drive ionization and the subsequent escape of the atmospheres, threatening the habitability (Linsky 2019; Airapetian et al. 2020). On the other hand, it has been indicated that XUV may have triggered the birth of life by forming biologically relevant molecules in lower planetary atmospheres (Airapetian et al. 2016, 2017). Therefore, understanding how stellar atmospheric radiation responds to the surface magnetic field is critical for not only revealing the atmospheric heating but also searching for habitable exoplanets in our neighborhood.

Previous studies have shown that on a wide range of scales from solar active regions to the entire Sun and even late-type (F, G, K, and M) stars, the X-ray radiation power F has a uniform scaling relationship with a power-law index α slightly above unity with respect to the amount of magnetic flux on the stellar surface Φ, F ∝ Φ^α (α = 1.1–1.8) (Fisher et al. 1998; Pevtsov et al. 2003; Vidotto et al. 2014). The fact that the same power-law relationship continues over the scales suggests a common physical mechanism for the solar/stellar coronal heating. Specifically, the surface magnetic field is the ultimate source of the heating in both regimes, driven by photospheric convection at various scales. If the heating is caused by energy transport from the surface via magnetohydrodynamic waves and dissipation by small-scale turbulence, its intermittent dynamics develops eddies that cascade down to smaller scales, eventually dissipate, and form power-law (i.e., scale-free) spectra with common indices of 1.5–2.4 (Kolmogorov 1941; Boffetta et al. 1999; Aschwanden et al. 2016). Therefore, the scaling law of X-ray flux, F ∝ Φ^α , represents one of the most fundamental relationships in astrophysics and has provided the basis for investigating the coronal heating of the Sun and stars.

In this paper, we report on an analysis of the scaling laws between irradiances over a range of wavelength (i.e., of atmospheres of different temperatures) and photospheric magnetic flux, which sets the ground for understanding the universal atmospheric heating mechanism. Previous attempts to derive the scaling laws were based on limited temperature domains (e.g., Skumanich et al. 1975; Schrijver et al. 1989; Fisher et al. 1998; Pevtsov et al. 2003; Vidotto et al. 2014), unlike the present novel study wherein a wide range of temperatures is considered, or the temperature dependence of scaling laws was examined only with regard to indirect magnetic proxies such as the Ca ii K intensity (Rutten et al. 1991). More recent studies, such as Loukitcheva et al. (2009) and Barczynski et al. (2018), performed multiwavelength analysis using solar chromospheric and transition-region lines and continuum and found that the power-law index α increases with the formation temperature. Our study expands these studies and builds a bridge to the stellar regime.

The results presented here are based on the analysis of "Sun-as-a-star" synoptic data over 10 years (almost one solar activity cycle), which represents the global behavior of the Sun as a whole (spatially integrated over the disk), and a comparison of the obtained solar power-law relations with currently available stellar data.

2.1. Total Unsigned Magnetic Flux of the Sun

2.2. Spectral Irradiances of the Sun

To elucidate the atmospheric responses to the variation of magnetic flux, we analyzed the spectral irradiance data in X-ray, UV, visible, and radio bands, highlighting the atmospheric layers of the corresponding temperatures from ${\rm{log}}(T/{\rm{K}})=4$ to 7. The spectral lines analyzed in this study, formation temperatures, and data sources are summarized in Table 1. All obtained fluxes were converted to energy per unit area and per unit time at 1 au from the Sun.

Table 1. Summary of the Observables

Feature	${\rm{log}}(T/{\rm{K}})$	Wavelength (Å)	Basal	Minimum	Maximum	Unit	Source
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Total unsigned magnetic flux	3.8	6173.3	1.18 × 1023	1.16 × 1023	3.35 × 1023	Mx	SDO/HMI
X-rays 1–8 Å	6–7	1–8	0	1.00 × 10−9	4.81 × 10−5	W m−2	GOES/XRS
X-rays 5.2–124 Å	6–7	5.2–124	2.11 × 10−4	1.85 × 10−4	1.01 × 10−3	W m−2	SORCE/XPS
Fe xv 284 Å	6.4	284.15 ± 1.50	9.36 × 10−6	5.68 × 10−6	1.27 × 10−4	W m−2	SORCE/XPS
Fe xiv 211 Å	6.3	211.32 ± 1.50	1.20 × 10−5	9.88 × 10−6	6.75 × 10−5	W m−2	SORCE/XPS
Fe xii 193 + 195 Å	6.2	193.50 ± 2.50	6.16 × 10−5	5.66 × 10−5	1.72 × 10−4	W m−2	SORCE/XPS
F10.7 cm radio	∼6	10.7 × 108	68.83	63.67	466.57	sfu	DRAO
He ii 256 Å + blends	4.9	256.30 ± 3.00	5.53 × 10−5	5.20 × 10−5	1.21 × 10−4	W m−2	SORCE/XPS
Si iv 1393 Å	4.9	1393.85 ± 1.30	4.45 × 10−5	4.27 × 10−5	7.66 × 10−5	W m−2	SORCE/SOLSTICE
Si iv 1402 Å	4.9	1402.85 ± 0.85	2.32 × 10−5	2.25 × 10−5	3.91 × 10−5	W m−2	SORCE/SOLSTICE
C ii 1335 Å	4.3	1335.25 ± 1.90	1.57 × 10−4	1.52 × 10−4	2.46 × 10−4	W m−2	SORCE/SOLSTICE
H i 1216 Å (Lyα)	4.3	1215.70 ± 2.00	5.73 × 10−3	5.60 × 10−3	8.94 × 10−3	W m−2	SORCE/SOLSTICE
Mg ii k 2796 Å	(3.9)	2796.38 ± 0.78	0.0136	0.0135	0.0180	W m−2	SORCE/SOLSTICE
Mg ii h 2803 Å	(3.9)	2803.48 ± 0.65	0.0097	0.0096	0.0126	W m−2	SORCE/SOLSTICE
Ca ii K 3934 Å	(3.8)	3933.66 ± 0.50	0.0114	0.0111	0.0130	W m−2	SORCE/SIM and SOLIS/ISS
Ca ii H 3968 Å	(3.8)	3968.47 ± 0.50	0.0139	0.0139	0.0155	W m−2	SORCE/SIM and SOLIS/ISS
H i 6563 Å (Hα)	(3.8)	6562.80 ± 0.50	0.0369	0.0360	0.0448	W m−2	SORCE/SIM and SOLIS/ISS

Note. The first column shows the features, i.e., the total unsigned radial magnetic flux and the spectral lines. The second and third columns provide the formation temperature and wavelength range, respectively, for the measurement of irradiance. The temperatures are obtained from the CHIANTI database, except for the optically thick chromospheric lines, which are given in parentheses. The central wavelengths for Fe xv 284 Å and Fe xiv 211 Å and central wavelengths and windows for Si iv 1393 Å, Si iv 1402 Å, C ii 1335 Å, H i 1216 Å (Lyα), Mg ii k 2796 Å, and Mg ii h 2803 Å are adopted from Ayres (2021). Columns 4, 5, 6, and 7 show the basal flux, minimum and maximum values, and their physical units. 1 sfu = 10⁻²² W m⁻² Hz⁻¹. Column 8 provides the data source.

Download table as:  ASCIITypeset image

For the soft X-ray data, the 1–8 Å band data obtained by the X-ray Sensor (XRS) on board the Geostationary Operational Environmental Satellite (GOES) were used. The "science quality" level 2 data from the GOES-15 satellite (daily average) for the period of 2010 May to 2020 February were obtained to generate the 1–8 Å daily X-ray light curve. ⁵ For the stability and calibration, see the User's Guide available at the corresponding webpage. Also, we referred to Simões et al. (2015) for the noise level estimation (≲3 × 10⁻⁹ W m⁻² at 10⁻⁵ W m⁻² or less).

To measure the X-ray and extreme UV fluxes, we used the spectral irradiance data obtained by the XUV Photometer System (XPS; Woods & Rottman 2005) and the Solar Stellar Irradiance Comparison Experiment (SOLSTICE; McClintock et al. 2005) on board the Solar Radiation and Climate Experiment (SORCE) satellite from 2010 May through 2020 February. ⁶ Since its launch in 2003, the spacecraft and the instruments were overall stable and well calibrated, but the degradation of the battery capacity caused some gaps in observation (Woods et al. 2021). The daily spectral irradiance data of SORCE/XPS (level 4, version 12), which covers the wavelengths from 1 to 400 Å with a spectral resolution of 1 Å, were used to measure the fluxes of X-ray 5.2–124 Å (the ROSAT heritage band; Truemper 1982; Güdel 2007), Fe xv 284 Å, Fe xiv 211 Å, Fe xii 193 + 195 Å (combined), and He ii 256 Å. Note that the spectral models in the CHIANTI atomic database were used to construct the XPS level 4 spectra. Therefore, we limited the target spectra to the representative spectra listed above to minimize the possibility that the scaling relationships between the magnetic flux and irradiances are affected by the spectral models adopted in CHIANTI. For each spectral line, the noise level was estimated using the irradiance uncertainty provided in the data set. The central wavelength and wavelength range used to measure the irradiances are shown in Table 1. For the fluxes of Si iv 1393 Å, Si iv 1402 Å, C ii 1335 Å (combination of 1334.5 and 1335.7 Å), H i 1216 Å (Lyα), Mg ii k 2796 Å, and Mg ii h 2803 Å, the daily spectral irradiance data of SORCE/SOLSITCE (level 3, version 18), covering the wavelengths from 1150 to 3100 Å with a spectral resolution of 1 Å, were used. In this version, the geocoronal correction is applied to the Lyα data. The central wavelength and spectral windows are similarly presented in Table 1.

Chromospheric lines in the visible wavelengths (${\rm{log}}(T/{\rm{K}})\sim 4$) are used to diagnose the magnetic activity of the Sun and stars (e.g., Skumanich 1972; Wilson 1978; Baliunas et al. 1995). The spectral data of Ca ii K 3934 Å, Ca ii H 3968 Å, and H i 6563 Å (Hα) acquired by the Integrated Sunlight Spectrometer (ISS; Bertello et al. 2011) of the Synoptic Optical Long-term Investigations of the Sun (SOLIS) have been used to diagnose the chromospheric activities (e.g., Livingston et al. 2007). Because these spectra are provided as relative intensities with regard to the nearby continuum levels, the daily spectral irradiance data of the SORCE's Spectral Irradiance Monitor (SIM; Harder et al. 2005) (level 3, version 27), covering the spectral range from 2400 to 24200 Å with a 10–340 Å spectral resolution, were used to determine the absolute intensities. The spectral windows are shown in Table 1.

Note that in Table 1 the lines with different formation mechanisms are listed. For instance, the Si iv lines are an emission line with a single peak; the Mg ii and Ca ii lines are a self-reversal (i.e., double-peaked) line; and the Hα line is usually in absorption on the solar disk (e.g., Leenaarts et al. 2012, 2013). However, the formation of optically thick chromospheric lines is in general highly complicated due to radiative transfer processes such as multiple scattering, which may reflect different temperature regions. Although the spectral window is selected to extract the core of each line, it is difficult to narrow down the formation temperature to a single value. Therefore, the temperatures in Table 1, given in parentheses, should be considered as a reference. Also, Hα, usually in absorption on the disk, is included in the analysis to examine whether this well-observed line shows any correlations with other proxies.

For the Sun's radio emission, the F10.7 cm flux data (Tapping 2013) provided by the Dominion Radio Astrophysical Observatory (DRAO) were used. ⁷ We used the "adjusted" daily flux, which is measured at local noon and corrected for the modulation of the Sun–Earth distance, given in solar flux units (1 sfu = 10⁻²² W m⁻² Hz⁻¹). When no strong flare occurs, the radio flux is composed of steady thermal bremsstrahlung from the chromosphere (${\rm{log}}(T/{\rm{K}})\sim 4$), gyroresonance emission from a strong magnetic field above active regions, and coronal bremsstrahlung (Gary & Hurford 1994). Because we focused on the variable component of radio flux (see below), which likely originates from the active-region corona, we assumed that the formation temperature of the F10.7 cm radio flux is ${\rm{log}}(T/{\rm{K}})\sim 6$. Although the uncertainty is not provided in the F10.7 cm data, Tapping & Charrois (1994) suggested that the average error in the flux determinations is not more than 0.5%, and we used this value for estimating the noise levels in this study.

2.3. Derivation of Power-law Indices

2.4. Stellar Data in the Literature

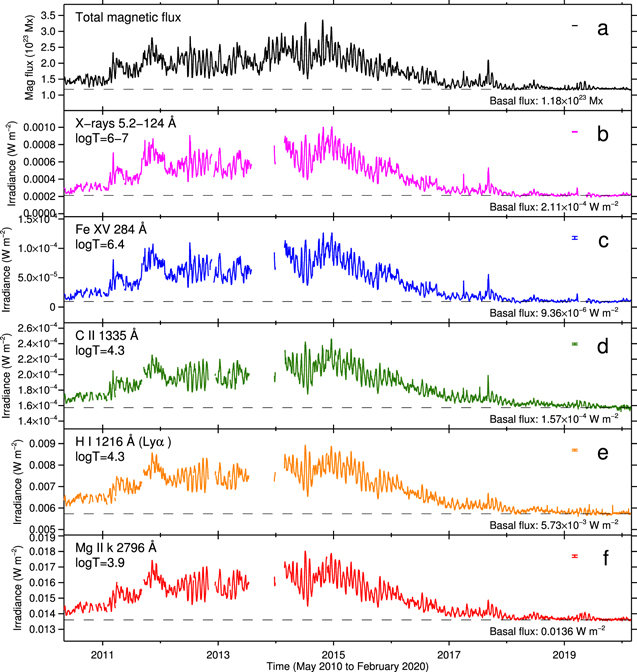
The resultant time series of daily total magnetic flux and the light curves in the 5.2–124 Å band and Fe xv 284 Å, Fe xii 195 Å, C ii 1335 Å, and Mg ii k 2796 Å spectral lines are shown in Figure 1 (see Figure 5 in the Appendix for all spectral lines). These plots demonstrate that the long-term variation of solar magnetic activity peaked in 2014 with a minimum around 2019. Each spike corresponds to the transit of active regions over the solar disk. The striking correspondence between the spikes of magnetic flux and those of irradiances demonstrates that different layers of solar atmosphere heat up in response to the appearance of active regions.

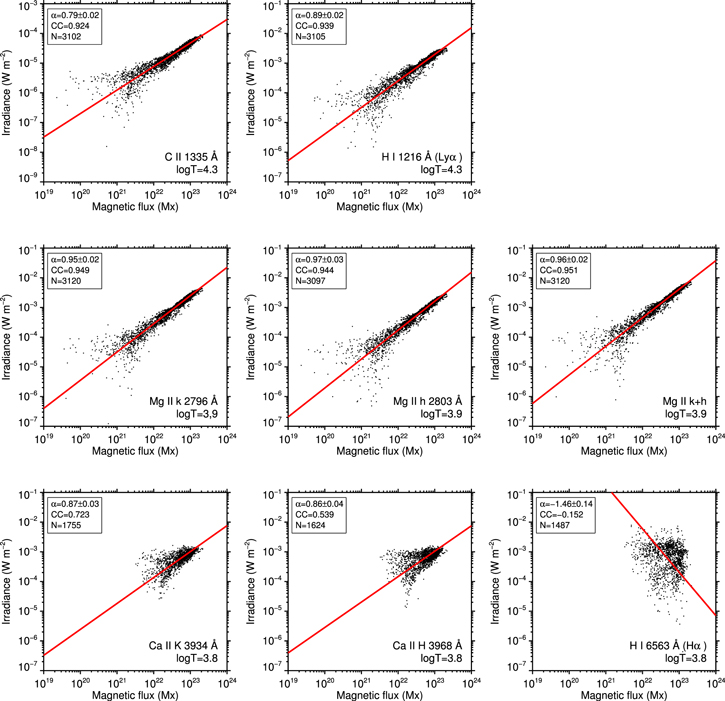
Zoom In Zoom Out Reset image size

Each panel of Figure 2 shows a scatter plot of the variation of a given solar irradiance from its background level (basal flux) versus that of the total unsigned magnetic flux (see Figure 6 in the Appendix for all spectral lines). In each panel, only the data points where both the irradiance F and unsigned flux Φ are positive are plotted, and the number of such data points, N, is shown in the small box in the upper left corner. The power-law index α for the linear fit ($\mathrm{log}F=\alpha \mathrm{log}{\rm{\Phi }}+\beta$) and the correlation coefficient $\mathrm{CC}(\mathrm{log}{\rm{\Phi }},\mathrm{log}F)$ are also provided. The power-law index α, offset β, correlation coefficient CC, and number of data points N for all scatter plots are summarized in Table 2.

Zoom In Zoom Out Reset image size

Table 2. Power-law Indices and Correlations between Irradiance and Total Magnetic Flux

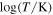
Feature	${\rm{log}}(T/{\rm{K}})$	Power-law Index α	Offset β	Correlation Coefficient CC	Data Points N	LS Deviation
(1)	(2)	(3)	(4)	(5)	(6)	(7)
X-rays 1–8 Å	6–7	1.42 ± 0.04	−38.6 ± 0.8	0.893	3243	0.431
X-rays 5.2–124 Å	6–7	1.16 ± 0.03	−29.9 ± 0.7	0.926	2994	0.247
Fe xv 284 Å	6.4	1.15 ± 0.03	−30.6 ± 0.7	0.919	3009	0.258
Fe xiv 211 Å	6.3	1.15 ± 0.03	−30.9 ± 0.7	0.924	2998	0.248
Fe xii 193+195 Å	6.2	1.14 ± 0.03	−30.5 ± 0.7	0.925	2998	0.246
F10.7 cm radio	∼6	1.24 ± 0.03	−26.8 ± 0.7	0.939	3200	0.225
He ii 256 Å	4.9	1.14 ± 0.03	−30.8 ± 0.7	0.923	3001	0.249
Si iv 1393 Å	4.9	0.90 ± 0.02	−25.3 ± 0.5	0.923	3089	0.215
Si iv 1402 Å	4.9	0.83 ± 0.02	−24.1 ± 0.5	0.914	3096	0.214
C ii 1335 Å	4.3	0.79 ± 0.02	−22.5 ± 0.5	0.924	3102	0.193
H i 1216 Å (Lyα)	4.3	0.89 ± 0.02	−23.3 ± 0.5	0.939	3105	0.193
Mg ii k 2796 Å	(3.9)	0.95 ± 0.02	−24.4 ± 0.5	0.949	3120	0.187
Mg ii h 2803 Å	(3.9)	0.97 ± 0.03	−25.2 ± 0.6	0.944	3097	0.200
Mg ii k+h	(3.9)	0.96 ± 0.02	−24.5 ± 0.6	0.951	3120	0.187
Ca ii K 3934 Å	(3.8)	0.87 ± 0.03	−23.1 ± 0.8	0.723	1755	0.214
Ca ii H 3968 Å	(3.8)	0.86 ± 0.04	−22.7 ± 0.9	0.539	1624	0.273
H i 6563 Å (Hα)	(3.8)	−1.46 ± 0.14	29.9 ± 3.1	−0.152	1487	0.643

Note. The first and second columns show the spectral lines and their formation temperatures, respectively. Columns 3, 4, 5, and 6 provide the power-law index α, offset β, correlation coefficient CC, and the number of data points N of each double logarithmic scatter plot of irradiance versus total magnetic flux. Column 7 presents the least-square deviation of the linear fit to the double logarithmic plot.

Download table as:  ASCIITypeset image

Here, one may find that the data points are often dispersed and sometimes show a two-branched shape at the lower end (the bottom left corner of each panel). Considering the results of, e.g., Pevtsov et al. (2003), in which the data points are located on the power-law line even in the range of Φ = 10¹⁶ Mx, the dispersed or branched tails in this study probably reflect the measurement noise rather than physical origins.

In Figure 2, the total magnetic fluxes and irradiances of the solar-type stars that have been measured in the past are overplotted. The stellar data are located on the extensions of the power-law relations of the solar data, indicating that the atmospheric responses to the magnetic flux are universal for the Sun and Sun-like stars, regardless of age or activity.

Figure 3 shows the power-law indices, α, as a function of formation temperature. The X-ray fluxes (log(T/K) = 6–7) are known to show a power-law relation with an exponent of slightly above unity (α = 1.1–1.8) for the Sun and Sun-like stars (Section 1). We confirmed this trend and also revealed that other coronal XUV lines and radio fluxes show much the same relationship. On the other hand, for the temperatures characteristic of the transition region and chromospheric range (${\rm{log}}(T/{\rm{K}})\lt 6$), the power-law index decreases below unity, indicating that the atmospheric response to the surface magnetic flux falls below linearity.

Zoom In Zoom Out Reset image size

Note here that Hα is omitted from Figure 3 because it has an inverse proportionality with magnetic flux (α < 0). The light curve of Hα enhanced only in the declining phase of the solar cycle (bottom panel of Figure 5), and as a result it showed a negative correlation against magnetic flux with a large scatter (CC = −0.152: Figure 6). A recent Sun-as-a-star observation by Maldonado et al. (2019) indicates a similar anticorrelation between Ca ii K and Hα, and this may be attributed to the difference in the line formation processes: while the Ca ii K flux increases monotonically with increasing chromospheric temperature or mass, Hα can be in absorption or emission depending on the temperature or mass (Cram & Giampapa 1987; Rutten et al. 1989).

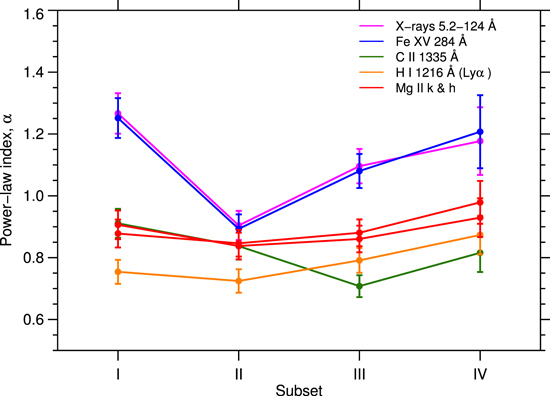
The phase dependence of α is summarized in Figure 4, which shows the α values of representative spectral lines that are measured in four different phases of the solar activity cycle (see Table 4 for all proxies). It is clearly seen that α takes its minimum in Subset II or III, i.e., at the solar maximum or in the declining phase, while it becomes larger in Subset I or IV, i.e., in the rising or minimum phase. In Table 4, the trends are not clear for the chromospheric lines (Ca ii K, Ca ii H, and Hα), possibly because of their narrow dynamic ranges compared to the other proxies.

Zoom In Zoom Out Reset image size

The temperature dependence of power-law scaling relationships between the magnetic flux and radiation fluxes discovered in this study is a powerful tool for understanding the heating mechanism of stellar atmospheres that is common to the Sun and Sun-like stars.

For the coronal regime (${\rm{log}}(T/{\rm{K}})\gt 6$), where the power-law index exceeds unity, theoretical explanations have been provided (Fisher et al. 1998; Takasao et al. 2020; Zhuleku et al. 2020). These include the heating via Alfvén waves (van Ballegooijen et al. 2011) and electric current sheets (Parker 1972, 1988). In the first mechanism, the Alfvén waves excited by shuffling convective motions in the solar/stellar surface propagate upwards along the magnetic field lines and dissipate energy into heat. In the second model, the energy is dissipated in current sheets within braided field-line structures driven by photospheric convection as a nanoscale version of solar flares (nanoflares). Recent numerical modeling of coronal loops considering the effect of turbulent dissipation of Alfvén waves successfully reproduced the power-law index of α = 1.19 for the Sun and Sun-like stars (Shoda & Takasao 2021). Young, fast-rotating stars are known to exhibit high X-ray quiescent luminosity, which is attributed to the enhanced dynamo activity driven by fast stellar rotation (Pizzolato et al. 2003; Wright et al. 2011). Our result of power-law indices being α > 1 for ${\rm{log}}(T/{\rm{K}})\gt 6$ provides the robust view that the same heating mechanism—the energy supply by surface convection, transportation along the magnetic field, and dissipation in the atmosphere—is commonly at work in these stars, regardless of age or activity, to generate the hot coronae.

The Ca ii K emission (${\rm{log}}(T/{\rm{K}})\sim 3.8$) has been found to correlate with surface magnetic flux with power-law indices α = 0.6–1 (e.g., Skumanich et al. 1975; Schrijver et al. 1989), and our study reveals that the tendency of α ≲ 1 is true for the chromospheric lines of Sun-like stars in general. Schrijver et al. (1989) has attributed this tendency to the geometrical effect of magnetic flux tubes, where vertical expansion of the flux tubes is restricted because the tubes are concentrated at the boundaries of convection cells, resulting in a small effective area of the chromosphere. The flux-tube expansion also plays a key role in reflecting the ascending Alfvén waves via drastic density reduction (Cranmer & van Ballegooijen 2005), and this may suppress the efficiency of chromospheric heating by Alfvén waves to a sublinear proportionality with photospheric magnetic flux.

The power-law indices α were also found to depend on the solar cycle. Specifically, they reach minimum values during the maximum phase of the cycle. One possible explanation is that, at maximum, the solar atmosphere is filled with magnetic flux sourced from active regions that cover the sphere, and thus the atmospheric heating becomes saturated. That is, compared to the quiescent phases, the atmosphere is not effectively heated any more even if the new magnetic flux is supplied to the surface. However, the determination of what physical mechanism causes the saturation requires further assessment.

The power-law scaling relationships obtained in this study provide a means to empirically estimate the irradiances over a wide range of wavelengths from Sun-like stars. This allows us to calculate the quiescent radiation fluxes, specifically of XUV emissions, to the (exo)planetary atmospheres and their surfaces derived from the magnetic flux distribution of observed or modeled Sun-like planet-hosting stars. Once the total radial unsigned magnetic flux in the visible hemisphere is obtained from observations or modeling, the irradiance of a given line, F₁, can be estimated using the values in Tables 1 and 2 as ${F}_{1}=\beta {({{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{0})}^{\alpha }+{F}_{0}$, where Φ₁, Φ₀, and F₀ are the observed and basal magnetic fluxes and basal irradiance, respectively.

This stellar output provides observationally constrained input for studying the response of (exo)planetary atmospheres in terms of associated atmospheric escape and impact on atmospheric chemistry, the critical factors of exoplanetary habitability and associated potential biosignatures. On the other hand, because most of the stellar observations are snapshots and usually not synchronized with magnetic field measurements, it is possible that only selected phases of activity variations are reflected in the analysis, causing a scatter in the stellar data of Figure 2. Long-term, multiwavelength monitoring of irradiances and magnetic fields with future solar and space telescopes, probably leveraging numerical modeling, may further reveal the physical mechanisms behind atmospheric responses to surface magnetic field (Toriumi et al. 2017, 2020) and lead to the understanding of stellar flare eruptions (Maehara et al. 2012; Davenport 2016).

The authors thank the anonymous referee for the constructive comments, which improved the quality of the paper. Data are courtesy of the science teams of SDO, GOES, SORCE, SOLIS, and DRAO. HMI is an instrument on board SDO, a mission for NASA's Living With a Star program. ISS data were acquired by SOLIS instruments operated by NISP/NSO/AURA/NSF. This work was supported by JSPS KAKENHI grant Nos. JP20KK0072 (PI: S. Toriumi), JP21H01124 (PI: T. Yokoyama), and JP21H04492 (PI: K. Kusano), and by the NINS program for cross-disciplinary study (grant Nos. 01321802 and 01311904) on Turbulence, Transport, and Heating Dynamics in Laboratory and Astrophysical Plasmas: "SoLaBo-X." V. S. Airapetian was supported by the GSFC Sellers Exoplanet Environments Collaboration (SEEC), which is funded by the NASA Planetary Science Division's Internal Scientist Funding Model (ISFM), NASA's TESS Cycle 1, HST Cycle 27, and NICER Cycle 2 project funds.

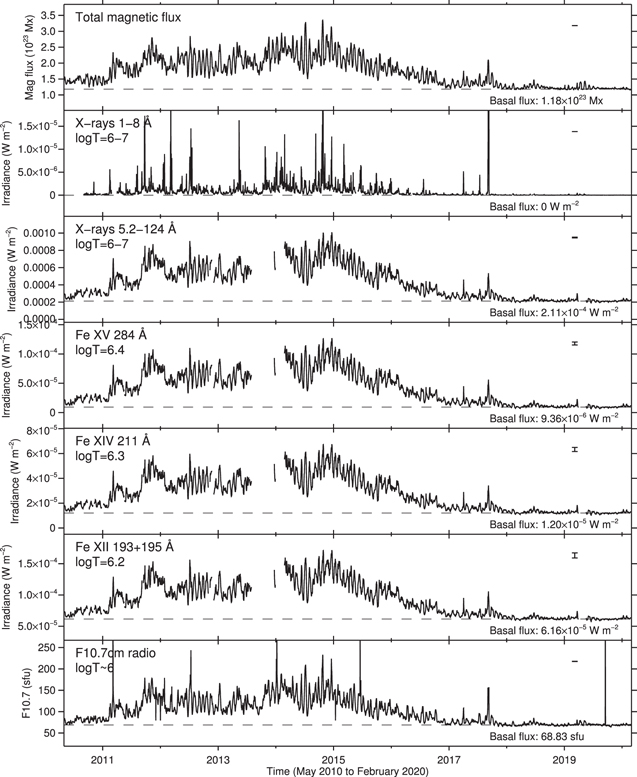
Figure 5 provides the time series of total radial unsigned flux and irradiances of all spectral lines, while Figure 6 shows the scatter plots of total magnetic flux and irradiances of all lines. Table 3 summarizes the characteristics, total hemispheric magnetic fluxes, and irradiances of the stars analyzed with the references. Table 4 presents the power-law indices α of all spectral lines that are measured in four different phases of the solar activity cycle.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Table 3. Characteristics of the Sun-like Stars

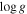
HD	Name	Sp. Type	Teff	$\mathrm{log}g$	Age	Prot	R	Φ	X-rays 5.2–124 Å	Fe xv 284 Å	C ii 1335 Å	Lyα	Mg ii k+h
			(K)		(Myr)	(days)	(R⊙)	(Mx)	(W m−2)	(W m−2)	(W m−2)	(W m−2)	(W m−2)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
1835	BE Cet	G3V	5837	4.47	600	7.78	1.00	4.55 × 1024	4.80 × 10−2, 1.78 × 10−2	⋯	⋯	⋯	6.04 × 10−2
20630	κ1 Cet	G5V	5742	4.49	600	9.3	0.95	2.61 × 1024	2.19 × 10−2, 2.56 × 10−2	2.40 × 10−3	9.50 × 10−4	3.01 × 10−2	7.09 × 10−2
39587	χ1 Ori	G0V	5882	4.34	500	4.83	1.05	2.47 × 1024	3.48 × 10−2, 3.73 × 10−2	5.00 × 10−3	1.52 × 10−3	4.16 × 10−2	1.18 × 10−1
56124		G0V	5848	4.46	4500	18	1.01	4.78 × 1023	9.79 × 10−2	⋯	⋯	⋯	⋯
72905	π1 Uma	G1.5V	5873	4.44	500	4.9	0.95	3.08 × 1024	4.48 × 10−2, 2.96 × 10−2	5.00 × 10−3	1.52 × 10−3	4.22 × 10−2	8.93 × 10−2
73350	V401 Hya	G5V	5802	4.48	510	12.3	0.98	2.43 × 1024	2.05 × 10−2	⋯	⋯	⋯	⋯
76151		G3V	5790	4.55	3600	20.5	1.00	2.62 × 1024	7.78 × 10−3	⋯	⋯	⋯	⋯
82558	LQ Hya	K1V	5000	4.00	50	1.601	0.71	1.39 × 1025	3.24 × 10−1, 2.43 × 10−1	⋯	⋯	5.91 × 10−2	7.27 × 10−2
129333	EK Dra	G1.5V	5845	4.47	120	2.606	0.97	1.52 × 1025	3.03 × 10−1, 2.52 × 10−1	2.20 × 10−2	4.70 × 10−3	⋯	1.26 × 10−1
131156	ξ Boo A	G7V	5570	4.65	200	6.4	0.83	1.13 × 1025	2.58 × 10−2, 2.83 × 10−2	⋯	⋯	3.53 × 10−2	6.19 × 10−2
166435		G1IV	5843	4.44	3800	3.43	0.99	4.94 × 1024	1.12 × 10−1	⋯	⋯	⋯	⋯
175726		G0V	5998	4.41	500	3.92	1.06	1.26 × 1024	4.48 × 10−2	⋯	⋯	⋯	⋯
190771		G2V	5834	4.44	2700	8.8	1.01	3.48 × 1024	4.80 × 10−2	⋯	⋯	⋯	⋯
206860	HN Peg	G0V	5974	4.47	260	4.55	1.04	1.92 × 1024	3.56 × 10−2, 2.52 × 10−2	⋯	⋯	⋯	5.90 × 10−2
Sun	(mean)	G2V	5777	4.44	4600	25.4	1.00	1.73 × 1023	4.24 × 10−4	4.12 × 10−5	1.84 × 10−4	6.77 × 10−3	2.55 × 10−2
	(median)							1.67 × 1023	3.87 × 10−4	3.59 × 10−5	1.82 × 10−4	6.69 × 10−3	2.52 × 10−2
	(max)							3.35 × 1023	1.01 × 10−3	1.27 × 10−4	2.46 × 10−4	8.94 × 10−3	3.06 × 10−2
	(min)							1.16 × 1023	1.85 × 10−4	5.68 × 10−6	1.52 × 10−4	5.60 × 10−3	2.32 × 10−2

Note. The HD number, name, spectral type, effective temperature, surface gravity, age, rotation period, and radius of the stars are shown in Columns 1–8. Column 9 shows the total hemispheric magnetic flux estimated based on the Zeeman broadening of the spectral lines. Columns 10–14 show the irradiances of X-ray 5.2–124 Å, Fe xv 284 Å, C ii 1334.5 + 1335.7 Å, Lyα, and Mg ii k+h (combined) in the literature, all converted to the values at 1 au from the stars. For X-rays, multiple observations are shown (if they exist).

References. Turon et al. (1993), Valenti & Fischer (2005), McDonald et al. (2012), Gonzalez et al. (2010), Cole et al. (2015), Allende Prieto & Lambert (1999), Vidotto et al. (2014), Rosén et al. (2016), Oláh et al. (2016), See et al. (2019), Kochukhov et al. (2020), Telleschi et al. (2005), Ribas et al. (2005), Takeda et al. (2007), Wood & Linsky (2010), Güdel et al. (1997), Wood et al. (2005), Schmitt et al. (1990), Dorren & Guinan (1994).

Download table as:  ASCIITypeset image

Table 4. Power-law Indices for Different Phases of the Solar Activity Cycle

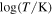
Feature	${\rm{log}}(T/{\rm{K}})$	Power-law Index α	Subset I αI	Subset II αII	Subset III αIII	Subset IV αIV
(1)	(2)	(3)	(4)	(5)	(6)	(7)
X-rays 1–8 Å	6–7	1.42 ± 0.04	1.93 ± 0.12	2.45 ± 0.13	1.78 ± 0.10	1.19 ± 0.09
X-rays 5.2–124 Å	6–7	1.16 ± 0.03	1.27 ± 0.07	0.90 ± 0.05	1.10 ± 0.06	1.18 ± 0.11
Fe xv 284 Å	6.4	1.15 ± 0.03	1.25 ± 0.06	0.89 ± 0.05	1.08 ± 0.06	1.21 ± 0.12
Fe xiv 211 Å	6.3	1.15 ± 0.03	1.25 ± 0.06	0.90 ± 0.05	1.09 ± 0.06	1.16 ± 0.11
Fe xii 193+195 Å	6.2	1.14 ± 0.03	1.25 ± 0.06	0.90 ± 0.05	1.09 ± 0.06	1.14 ± 0.11
F10.7 cm radio	∼6	1.24 ± 0.03	1.40 ± 0.07	1.17 ± 0.05	1.39 ± 0.07	1.21 ± 0.11
He ii 256 Å	4.9	1.14 ± 0.03	1.25 ± 0.06	0.90 ± 0.05	1.08 ± 0.06	1.16 ± 0.11
Si iv 1393 Å	4.9	0.90 ± 0.02	0.85 ± 0.04	0.79 ± 0.04	0.76 ± 0.04	0.94 ± 0.07
Si iv 1402 Å	4.9	0.83 ± 0.02	0.77 ± 0.04	0.76 ± 0.04	0.70 ± 0.04	0.82 ± 0.07
C ii 1335 Å	4.3	0.79 ± 0.02	0.91 ± 0.05	0.84 ± 0.04	0.71 ± 0.04	0.82 ± 0.06
H i 1216 Å (Lyα)	4.3	0.89 ± 0.02	0.75 ± 0.04	0.72 ± 0.04	0.79 ± 0.04	0.87 ± 0.06
Mg ii k 2796 Å	(3.9)	0.95 ± 0.02	0.91 ± 0.05	0.84 ± 0.04	0.86 ± 0.04	0.93 ± 0.06
Mg ii h 2803 Å	(3.9)	0.97 ± 0.03	0.88 ± 0.05	0.85 ± 0.04	0.88 ± 0.04	0.98 ± 0.07
Mg ii k+h	(3.9)	0.96 ± 0.02	0.89 ± 0.05	0.84 ± 0.04	0.87 ± 0.04	0.94 ± 0.06
Ca ii K 3934 Å	(3.8)	0.87 ± 0.03	1.01 ± 0.07	0.90 ± 0.06	0.98 ± 0.07	⋯
Ca ii H 3968 Å	(3.8)	0.86 ± 0.04	1.20 ± 0.08	0.98 ± 0.08	0.69 ± 0.05	⋯
H i 6563 Å (Hα)	(3.8)	−1.46 ± 0.14	1.42 ± 0.17	3.06 ± 1.66	0.87 ± 0.19	⋯

Note. Column 3 shows the power-law index α, taken from Table 2. Columns 4, 5, 6, and 7 are the power-law indices that are measured for the data points in different subsets of the solar activity cycle, which are (I) the rising phase from 2010 May to 2012 August; (II) the solar maximum from 2012 September to 2015 July; (III) the declining phase from 2015 August to 2017 November; and (IV) the solar minimum from 2017 December to 2020 February. There are no α_IV for Ca ii K, Ca ii H, and Hα because the ISS observation terminated in 2017 October.

Download table as:  ASCIITypeset image