Abstract
Asteroseismic large frequency separations possess great diagnostic value. However, their expressions as scaling relations are predicated on homology arguments that may not hold in general, resulting in mass- and temperature-dependent deviations. The first-order asymptotic expressions, which should in principle account for this structural evolution, also deviate more from fitted frequency-separation estimates than the simple scaling relations and exhibit qualitatively different behavior. We present a modified asymptotic estimator and show that these discrepancies can be accounted for by the evolution of the acoustic turning points of the asteroseismic mode cavity, which is typically neglected in first-order asymptotic analysis. This permits us to use a single expression to accurately estimate the large frequency separations of main-sequence, ascending red giant branch, and red clump stellar models, except at transition points between two asymptotic regimes during the subgiant phase of evolution, where the WKB approach fails. The existence of such transition points provides theoretical justification for separately calibrated scaling relations for stars in different evolutionary stages.
Export citation and abstract BibTeX RIS
1. Introduction
Solar-like oscillations—oscillations of the star excited stochastically in convective envelopes—result in photometric and velocity variations that have frequency-domain power spectra that exhibit a comblike structure. Such a comb is composed of peaks at the resonant frequencies of global asteroseismic p-modes, which are (to a good approximation) evenly spaced in the frequency domain with a characteristic spacing Δν, which is called the large frequency separation. Phenomenologically, there exist minor variations in the mode frequency spacing (owing to, e.g., acoustic glitches), and in practice, an average value of Δν is found by least-squares fitting of mode frequencies against their associated radial quantum numbers, with appropriate weights to account for variations of noise and mode amplitudes.
The asymptotic expression for these p-mode frequencies,
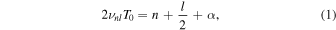
where 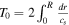 is the sound-travel time, yields an expression for the large frequency separation of radial modes as
is the sound-travel time, yields an expression for the large frequency separation of radial modes as
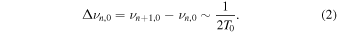
Under the assumption of hydrostatic equilibrium, the sound-travel time and gravitational dynamical time  should be of roughly the same order of magnitude, giving rise to the scaling relation (Ulrich 1986; Christensen-Dalsgaard 1988)
should be of roughly the same order of magnitude, giving rise to the scaling relation (Ulrich 1986; Christensen-Dalsgaard 1988)
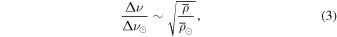
with 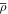 as the mean density of the star, for stars that are essentially homologous to the Sun. This solar-calibrated scaling relation has been historically established to hold relatively well, even for stellar models that exhibit considerable structural differences from the Sun. For this reason, the large separation has proven to be a valuable diagnostic of global properties of stars exhibiting such solar-like oscillations (Chaplin et al. 2014; Pinsonneault et al. 2014; Serenelli et al. 2017).
as the mean density of the star, for stars that are essentially homologous to the Sun. This solar-calibrated scaling relation has been historically established to hold relatively well, even for stellar models that exhibit considerable structural differences from the Sun. For this reason, the large separation has proven to be a valuable diagnostic of global properties of stars exhibiting such solar-like oscillations (Chaplin et al. 2014; Pinsonneault et al. 2014; Serenelli et al. 2017).
Owing to this first-order dependence on the mean density, observational measurements of Δν have been widely applied to determine asteroseismic estimates of stellar masses and radii, either by direct inversion of this scaling relation (e.g., Chaplin et al. 2010) or through a so-called grid-based approach, where an optimal solution is determined from the large separations of a grid of models (e.g., Basu et al. 2011; Chaplin et al. 2014; Pinsonneault et al. 2014). For the latter case, it is generally desirable to be able to accurately estimate Δν from a stellar model without solving for individual mode frequencies, which is quite computationally expensive. The scaling relation is typically used for this purpose.
However, there remain discrepancies (of order a few percent) between the scaling relation predictions compared to fitted values of Δν as computed from detailed frequencies returned from stellar models (i.e., even in the absence of observational errors and unconstrained physics), which prevent its use in such a capacity in the regime of high-precision asteroseismology. White et al. (2011) found that these scaling deviations appear to exhibit some dependence on the effective temperature (and, by proxy, on stellar evolution; see Figure 1), with an apparent second-parameter dependence on stellar metallicity.
Figure 1. Scaling deviations: ratio of fitted Δν vs. scaling relation estimator for solar-metallicity main-sequence/subgiant MESA stellar models with solar-calibrated parameters over a range of stellar masses.
Download figure:
Standard image High-resolution imageExtant approaches to dealing with these deviations vary but are uniformly empirical in nature. For instance, White et al. (2011) fit a parabola to the empirical morphology of the scaling deviation curve, Guggenberger et al. (2016) proposed the use of a damped-sinusoid function (with additional modifications from symbolic regression presented in Guggenberger et al. 2017), and Kallinger et al. (2018) proposed modifying the first-order expression (Equation (1)) to include additional free parameters accounting for acoustic glitches and second-order curvature effects, resulting in additional terms in the scaling relation that have to be calibrated empirically. Sharma et al. (2016) instead sought recourse to explicitly calibrating the scaling deviations against a reference grid of stellar models spanning the desired parameter space. While undoubtedly practical, such approaches lack theoretical insight. Moreover, attempts at empirical fits (without recourse to a model grid) have neglected scaling deviations on the main sequence, despite these stars being, in principle, the most similar to the Sun (and hence ostensibly the easiest to model).
While the sound-travel time may also be used to estimate Δν without requiring individual mode frequencies, there exists some contention as to the correct choice of the upper limit R used to compute it. Strictly speaking, the limit of integration should be the outer boundary of the eigenvalue problem with respect to which the eigenfunctions are computed. However, this boundary is difficult to define. While the photospheric radius is used by default in most evolutionary codes, it returns sound-travel times that are typically lower (and therefore frequency separations higher) than would be consistent with both observational values and values fitted against detailed model frequencies (as in Figure 2). Hekker et al. (2013) noted that this can be remedied by simply extending the domain of integration outward, but the question of ambiguity as to the correct outer boundary remains.
Figure 2. Ratio of fitted Δν vs. the usual asymptotic estimator (i.e., sound-travel time) for the same set of stellar models as in Figure 1.
Download figure:
Standard image High-resolution imageA critical underlying assumption made in all of these analyses is that the phenomenological and asymptotic values of Δν should be similar, which is only true if the phase function α in Equation (1) does not exhibit significant secular variation between modes. This would be the case with, e.g., the contribution to α from an acoustic glitch, where the rapid but oscillatory variations with frequency are canceled out when a global value of Δν is fitted for. However, in this formulation, the value of α as a function of frequency depends on the structure of the entire stellar model, and this assumption may not necessarily hold good. On the other hand, should such secular phase variations exist, their dependence on stellar parameters like the mass and radius is not a priori obvious.
We instead derive an asymptotic estimator for the large frequency separation that captures most of the variation in these phase functions (and so scaling deviations) with a single expression and thereby returns estimates of Δν that are considerably closer to the fitted value than the traditional asymptotic estimator, without any ambiguity as to the outer turning point of the relevant integral. We demonstrate numerically that the validity of this expression is independent of stellar mass, evolutionary stage (with one major exception), and atmospheric model.
2. The WKB Approximation
2.1. Review of Existing Work
In the first-order asymptotic theory of p-modes, the large frequency separation Δν emerges from the phase integral quantization condition
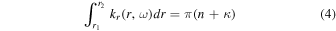
for integer n, where kr is the WKB wave number, r1 and r2 are the turning points of the integral (usually where kr vanishes), and κ is a function of frequency. Here κ depends only on the functional behavior of kr2 at the turning points. In particular, it can be shown that  is constant if
is constant if  at both turning points (Gough 2007; Aerts et al. 2010). To a first approximation, this expression yields the Duvall law,
at both turning points (Gough 2007; Aerts et al. 2010). To a first approximation, this expression yields the Duvall law,
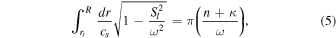
where cs is the sound speed, 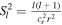 is the Lamb frequency, and
is the Lamb frequency, and 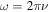 is the angular frequency. Again, the inner turning point of this integral is defined by where the integrand vanishes (or r = 0 for radial modes), and the outer turning point R is the same as that used to evaluate the sound-travel time.
is the angular frequency. Again, the inner turning point of this integral is defined by where the integrand vanishes (or r = 0 for radial modes), and the outer turning point R is the same as that used to evaluate the sound-travel time.
Naturally, higher-order approximations are possible. For instance, Tassoul (1994) derived Equation (1) from a second-order expansion of the asteroseismic equations of motion, using linear combinations of spherical Bessel functions and their derivatives as ansatzen for the eigenfunctions, with a similar phase integral quantization condition emerging for the arguments of these functions. This was in turn taken to fourth order by Roxburgh & Vorontsov (1994) with a similar approach.
On the other hand, the accuracy of the WKB expression can also be improved with more detailed asymptotic analysis (i.e., not setting terms to zero prematurely before performing the WKB analysis). For instance, a more accurate description is afforded by Deubner & Gough (1984),
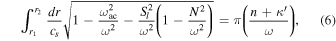
which emerges from just such a more detailed analysis (with still more detail provided in Gough 1993). The integrand in this expression reduces asymptotically to that in Equation (5) far into the interior of the convective envelope of solar-like main-sequence stars, where 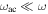 for most p-modes of interest. Here N2 is the Brunt–Väisälä or buoyancy frequency, and κ' is another function of frequency (different, in general, from κ in Equation (5)). However, κ' also only depends on the behavior of the integrand in Equation (6) at the turning points.
for most p-modes of interest. Here N2 is the Brunt–Väisälä or buoyancy frequency, and κ' is another function of frequency (different, in general, from κ in Equation (5)). However, κ' also only depends on the behavior of the integrand in Equation (6) at the turning points.
The formulation of Equation (6) differs from the standard form of the Duvall law in terms of both its explicit dependence on an acoustic cutoff frequency
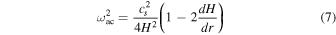
involving 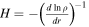 (the density scale height) in the integrand and the locations of the turning points (as the integrands vanish at different places). In particular, the outer turning point is essentially determined by the acoustic cutoff frequency, rather than being defined by the boundary conditions of the eigenvalue problem. The precise form of the acoustic cutoff frequency and other quantities involved in the oscillation equations will depend on the choice of dynamical variable used to perform the WKB analysis. Nonetheless, the resulting eigenvalue equation can typically be put into the form of Equation (6), although different expressions for
(the density scale height) in the integrand and the locations of the turning points (as the integrands vanish at different places). In particular, the outer turning point is essentially determined by the acoustic cutoff frequency, rather than being defined by the boundary conditions of the eigenvalue problem. The precise form of the acoustic cutoff frequency and other quantities involved in the oscillation equations will depend on the choice of dynamical variable used to perform the WKB analysis. Nonetheless, the resulting eigenvalue equation can typically be put into the form of Equation (6), although different expressions for 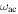 , Sl2, and N2 may have to be used in place of those described here. An illustrative example can be found in Gough (1993).
, Sl2, and N2 may have to be used in place of those described here. An illustrative example can be found in Gough (1993).
With respect to the above formalism, Christensen-Dalsgaard & Perez Hernandez (1992) instead define a phase function α so that
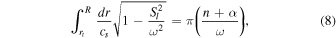
where
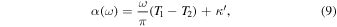
with
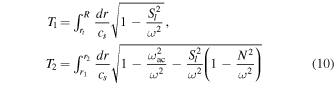
being integrals with dimensions of time appearing on the left-hand side of Equations (5) and (6). This permits the use of Equation (1) with α in place of κ. Whereas the phase functions κ and κ' defined previously depend only locally on the asymptotic properties of the WKB integrands in the neighborhoods of their classical turning points, α as defined in this manner also depends on the global properties of the entire acoustic mode cavity.
2.2. A New Expression
We take the first-order expression (Equation (6)) at face value and assume that the quantities N2 and Sl2 have no parametric dependence on the frequency, and further that all quantities on the right-hand side are continuous functions of the frequency ν. We proceed to expand finite differences as Taylor series. In particular, we consider finite differences of the terms in Equation (6), multiplied throughout by 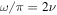 and evaluated at frequencies of adjacent n for the same l,
and evaluated at frequencies of adjacent n for the same l,
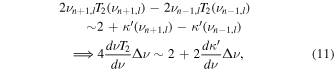
with the quantities on the last line being evaluated at the frequency 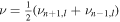 so that the error term is
so that the error term is 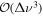 , and where T2 is the left-hand side of Equation (6). This yields the expression
, and where T2 is the left-hand side of Equation (6). This yields the expression
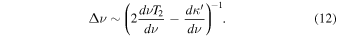
For the first term, we observe that

Since the turning points of the integral are either fixed (for 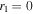 ) or defined to be where the relevant integrand vanishes, the boundary contributions to the above derivative also vanish, leaving us with
) or defined to be where the relevant integrand vanishes, the boundary contributions to the above derivative also vanish, leaving us with
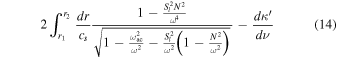
inside the parentheses in Equation (12). For radial modes in particular, we can neglect Sl2, leaving us with
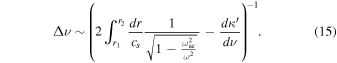
As noted previously, 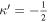 in the ideal WKB scenario of the mode cavity exhibiting asymptotically linear behavior near the classical turning points. On the other hand, if the radicand tends to a constant value near the inner turning point (as would be the case for Sun-like stars, where
in the ideal WKB scenario of the mode cavity exhibiting asymptotically linear behavior near the classical turning points. On the other hand, if the radicand tends to a constant value near the inner turning point (as would be the case for Sun-like stars, where 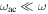 far into the interior), then the behavior of the eigenfunctions near the inner turning point is described by the spherical Bessel function j0 and
far into the interior), then the behavior of the eigenfunctions near the inner turning point is described by the spherical Bessel function j0 and  (Gough 1993). In either case, assuming that it changes very slowly with respect to frequency, its derivative is much smaller than the integral expression. We thus propose the use of a modified integral estimator for the large frequency separation:
(Gough 1993). In either case, assuming that it changes very slowly with respect to frequency, its derivative is much smaller than the integral expression. We thus propose the use of a modified integral estimator for the large frequency separation:
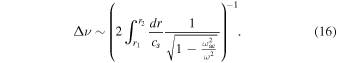
This expression contains an explicit dependence on the frequency. Observationally, however, we are limited to the study of only modes with frequencies near νmax, the frequency of maximum acoustic power. Moving forward, we will evaluate this quantity at νmax.
We note that the denominator of the integrand in Equation (16) vanishes at the outer boundary of the domain of integration, so the integrand becomes singular. Depending on the acoustic cutoff frequency of the stellar model, this may also be the case at the inner boundary. In the ideal WKB regime, this results in the presence of integrable singularities at the end points. We would therefore expect that the evolution of these turning points plays a significant role in how the value of this estimator changes over the course of stellar evolution. Our expression does not contain a prescription for the actual turning points of the asymptotic integral, only that they depend on the formulation of the acoustic cutoff frequency that accompanies the degree of approximation being used.
Moreover, within the domain of integration, we note that the integrand is strictly larger than the 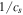 that appears as the integrand of the sound-travel time. Since the integrand is also strictly positive, we conclude that the integral is strictly larger than the sound-travel time. Given that the sound-travel time generally overestimates Δν (i.e., yields too small a value of the integral, as in Figure 2), this is suggestive as at least a zeroth-order mark of improvement.
that appears as the integrand of the sound-travel time. Since the integrand is also strictly positive, we conclude that the integral is strictly larger than the sound-travel time. Given that the sound-travel time generally overestimates Δν (i.e., yields too small a value of the integral, as in Figure 2), this is suggestive as at least a zeroth-order mark of improvement.
3. Benchmarking against Models
Our modified estimator for Δν, Equation (16), was derived under assumptions that may not be strictly valid in all cases. To test how well it actually reproduces the large separation of a model, we compare it against Δν as calculated using the frequencies of a model.
To do this, we compute both Equation (16) and an estimate of Δν from a linear fit to individual mode frequencies for a variety of stellar models constructed with the stellar evolution code MESA, version 10398 (Paxton et al. 2015). We ran evolutionary tracks for stellar masses from 0.8 to 1.6 M⊙ in increments of 0.1 M⊙, using initial helium abundances Y0 and mixing-length parameters αMLT obtained by constructing solar-calibrated models at solar metallicity (using values from Grevesse & Sauval 1998) but with no additional constraints. Frequencies were computed with version 5.1 of the GYRE oscillation code (Townsend & Teitler 2013). The evolution included heavy-element diffusion and gravitational settling, as well as convective overshoot. We compute frequencies for all radial modes up until the maximum acoustic cutoff frequency (i.e., all trapped p-modes).
As noted above, our proposed asymptotic estimator has an explicit frequency dependence, and we evaluate it at the frequency of maximum acoustic power, νmax. While the theoretical underpinnings of νmax are not well understood, it carries diagnostic information on the excitation and damping of stellar modes and hence must depend on the physical conditions in the near-surface layers where the modes are excited. Close to the surface (and outer acoustic turning point), the behavior of the waves is strongly influenced by the acoustic cutoff frequency. Brown et al. (1991) argued that  , since both frequencies are determined by conditions in the near-surface layers; Kjeldsen & Bedding (1995) used this to derive a scaling relation between νmax and near-surface properties. Belkacem et al. (2011) showed that while νmax does indeed depend on
, since both frequencies are determined by conditions in the near-surface layers; Kjeldsen & Bedding (1995) used this to derive a scaling relation between νmax and near-surface properties. Belkacem et al. (2011) showed that while νmax does indeed depend on  , there are also additional dependences on other quantities, such as the turbulent Mach number and the mixing-length parameter. However, to simplify matters, in this work, we evaluate Equation (16) at the value of νmax given by the scaling relation of Kjeldsen & Bedding (1995).
, there are also additional dependences on other quantities, such as the turbulent Mach number and the mixing-length parameter. However, to simplify matters, in this work, we evaluate Equation (16) at the value of νmax given by the scaling relation of Kjeldsen & Bedding (1995).
The expression (Equation (7)) for the acoustic cutoff frequency exhibits rapid variations, owing to both limitations in the MESA models and possibly density discontinuities, which may affect the accuracy of the WKB approximation (in that kr may not vary slowly). In particular, large rapid variations near the turning points will strongly influence the computed value of the integrable singularities there. To avoid this, we use an isothermal homogeneous plane-parallel ideal-gas approximation, as detailed in Aerts et al. (2010). Practically, this means that we use only the leading-order term in Equation (7) when computing the acoustic cutoff frequency. In turn, the value of the integral (Equation (16)) was evaluated using an adaptive Gauss–Kronrod quadrature scheme.
3.1. Results
To compare the results obtained from the integral and frequencies, we compute the logarithms of the ratios between the value of 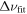 (obtained by a least-squares fit of
(obtained by a least-squares fit of 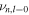 against n) versus the values of our integral estimator in Equation (16), which we plot as circles in subsequent figures. We also do this with the log ratios of
against n) versus the values of our integral estimator in Equation (16), which we plot as circles in subsequent figures. We also do this with the log ratios of 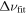 versus the values of the sound-travel time estimator
versus the values of the sound-travel time estimator 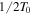 (which we show as triangles), as well as versus the values predicted by the scaling relation (squares). As a more quantitative (but still heuristic) comparison, we compute the root mean square (rms) deviation of these log ratios from zero. An rms deviation of zero means that the estimator exactly coincides with
(which we show as triangles), as well as versus the values predicted by the scaling relation (squares). As a more quantitative (but still heuristic) comparison, we compute the root mean square (rms) deviation of these log ratios from zero. An rms deviation of zero means that the estimator exactly coincides with 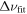 for all models.
for all models.
The top panel of Figure 3 shows the values of the log ratios described above for stellar models along the main sequence and on the subgiant branch. It is visually evident that the agreement between the estimator in Equation (16) and the fitted values of Δν is considerably better than both the scaling relation and the sound-travel time. We find that the scaling relation results in an rms log deviation of about 0.010 dex, compared to 0.025 dex for the sound-travel time and 0.002 dex for our integral estimator.
Figure 3. Log ratio of fitted Δν vs. various estimators for solar-metallicity MESA stellar models with solar-calibrated parameters over a range of stellar masses and ages, with our modified asymptotic estimator in colored points. To guide the eye, we plot with faint markers the quantities in Figures 1 and 2 (with corresponding marker shapes). We break these plots up by evolutionary stage. Top: main-sequence and subgiant stars; middle: ascending RGB; bottom: horizontal branch/red clump models. The agreement is considerably better for our estimator than the usual methods.
Download figure:
Standard image High-resolution imageWhereas the relative deviations from the scaling relation appear to exhibit curlicues for main-sequence stars of different masses (as in Figure 1), we note that the most obvious deviations between our asymptotic estimator and the fitted value of Δν occur as a sharp spike near the main-sequence turnoff during the onset of shell burning (at the core hydrogen exhaustion/subgiant hook for more massive stars). We examine this more closely in Figure 4.
Figure 4. Top: plots of the acoustic cutoff frequency in units of νmax for stellar models at various evolutionary stages along the  track, showing the two extreme asymptotic regimes of the inner turning points for main-sequence and evolved stars and illustrating the failure of the WKB approximation during the transition between them at the main-sequence turnoff. Bottom: log ratio of frequency separations (as in the top panel of Figure 3) for the
track, showing the two extreme asymptotic regimes of the inner turning points for main-sequence and evolved stars and illustrating the failure of the WKB approximation during the transition between them at the main-sequence turnoff. Bottom: log ratio of frequency separations (as in the top panel of Figure 3) for the 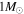 track, with the direction of evolution indicated with arrows. Stellar models corresponding to curves shown in the top panel are marked with points of the same color on lines with corresponding styles in the legend of the bottom panel. An animation showing both panels is available. Its duration is 28 s.
track, with the direction of evolution indicated with arrows. Stellar models corresponding to curves shown in the top panel are marked with points of the same color on lines with corresponding styles in the legend of the bottom panel. An animation showing both panels is available. Its duration is 28 s.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageWe show in the top panel of Figure 4 the acoustic cutoff frequency, in units of νmax, of main-sequence, main-sequence turnoff, and subgiant stellar models with 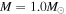 . Following our above discussion of various values of κ in the WKB regime, we see that for the main-sequence star (blue solid curve), the inner turning point is at r = 0, where
. Following our above discussion of various values of κ in the WKB regime, we see that for the main-sequence star (blue solid curve), the inner turning point is at r = 0, where 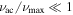 , and the WKB wave function goes as
, and the WKB wave function goes as  , where
, where  , with the same integrand as in Equation (6). On the other hand, for the subgiant star (green dashed curve), the WKB wave function goes as
, with the same integrand as in Equation (6). On the other hand, for the subgiant star (green dashed curve), the WKB wave function goes as 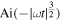 near a first-order classical turning point at
near a first-order classical turning point at 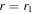 , where
, where 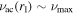 and
and  , and
, and 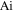 is the Airy function.
is the Airy function.
These represent two distinct asymptotic regimes in which the assumptions underlying the WKB approximation hold well. However, this is not necessarily true during the transition between these two regimes. In particular, for some stellar models near the main-sequence turnoff (orange dotted curve), we have a maximum of the acoustic cutoff frequency with a value very close to νmax. This violates one of the underlying assumptions of the WKB approximation (viz., that kr varies slowly except near classical turning points, which requires in this case that 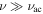 ), and neither of the above asymptotic descriptions is a good approximation for the actual mode eigenfunctions.
), and neither of the above asymptotic descriptions is a good approximation for the actual mode eigenfunctions.
We noted earlier that the radicand in Equation (16) vanishes where 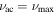 . For first-order turning points, this results in integrable singularities at the end points of integration. However, when there is a maximum point where
. For first-order turning points, this results in integrable singularities at the end points of integration. However, when there is a maximum point where 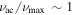 (as would be the case with a second-order turning point), either the integrand changes very rapidly (becoming very large) in a region smaller than the wavelength of the eigenfunction (
(as would be the case with a second-order turning point), either the integrand changes very rapidly (becoming very large) in a region smaller than the wavelength of the eigenfunction ( ), or a nonintegrable singularity is introduced into the domain of integration (
), or a nonintegrable singularity is introduced into the domain of integration ( ), and the convergence of the numerical integration is poor. In these cases, a numerical computation of Equation (16) will be very different from the fitted value of Δν: the orange dotted curve of Figure 4 corresponds to the maximum deviation between Equation (16) and the fitted value of Δν along our
), and the convergence of the numerical integration is poor. In these cases, a numerical computation of Equation (16) will be very different from the fitted value of Δν: the orange dotted curve of Figure 4 corresponds to the maximum deviation between Equation (16) and the fitted value of Δν along our 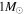 track (as in the orange point in the bottom panel). In principle, the phase function κ, as we have defined it, also becomes discontinuous in the neighborhood of
track (as in the orange point in the bottom panel). In principle, the phase function κ, as we have defined it, also becomes discontinuous in the neighborhood of 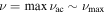 , and its derivative also becomes singular. A proper accounting should permit these two singularities to cancel each other out. However, this is difficult to handle numerically.
, and its derivative also becomes singular. A proper accounting should permit these two singularities to cancel each other out. However, this is difficult to handle numerically.
It is possible that these difficulties can be resolved by a more refined analysis. For instance, strictly speaking, the asymptotic behavior of the WKB wave function near such a second-order stationary point should be given by the parabolic cylinder function (Gough 2007). However, such an analysis is fairly involved and may not as readily yield a simple (and easily computed) expression like Equation (16). Alternatively, one might imagine choosing a set of dynamical variables such that the expression for the cutoff frequency is always singular near the center of the model (Gough 1993), so that this transition point does not emerge. Again, doing so would require a more detailed analysis than we have performed, which we leave beyond the scope of this paper.
3.1.1. RGB and Red Clump Stars
In the lower two panels of Figure 3, we show the log ratios of frequency-separation estimators for ascending red giant branch (RGB; middle panel) and descending RGB and red clump stars (lower panel). Once again, our expression in Equation (16) deviates much less from the fitted Δν than do both the scaling relation prediction and the sound-travel time. However, we note the emergence of terrace-like features in these deviation plots, which ultimately originate from the method by which we compute a fitted value for Δν. In particular, since we have included all modes with frequencies lower than the maximum acoustic cutoff frequency in the least-squares fit, and since the acoustic cutoff frequency changes relative to Δν over the course of stellar evolution, the number of modes used in the fit changes also changes discontinuously over the course of the track, as illustrated in Figure 5. These terraces are therefore a property of our benchmarking methodology, rather than being a feature of our asymptotic estimator.
Figure 5. Frequencies of radial modes (in units of νmax) for stellar models on the ascending RGB from the 1 M⊙ evolutionary track, with modes of the same n at different models being joined with solid lines. The maximum acoustic cutoff frequency in the atmosphere is shown with the red dashed line; only modes below this dashed line have a confined mode cavity, so only these are included in the fit for Δν. As the age of the star increases (with decreasing effective temperature), this cutoff decreases relative to Δν, so the number of modes available to be included in the fit decreases discontinuously.
Download figure:
Standard image High-resolution imageIn addition, we observe that while the scaling relation overpredicts the large frequency separation for ascending RGB stars, it slightly underpredicts it for red clump stars. Since the use of the scaling relation is (implicitly) a homology argument (Belkacem et al. 2013), this indicates that the acoustic structure of red clump stars differs significantly from that of red giant stars. On this basis, Miglio et al. (2012) proposed the use of different correction factors for the scaling relation for first-ascent red giant and red clump stars, precisely to account for these structural differences.
In terms of our formulation, we show in Figure 6 the radial dependence of the acoustic cutoff frequency for two stellar models—one red giant and one red clump—with identical masses and radii. While their acoustic structure is very similar in the outer parts of the star, we see that their modified radial mode cavities have different inner turning points. Accordingly, our integral estimator correctly returns different estimates for Δν for these different types of stars.
Figure 6. Acoustic cutoff frequency (in units of νmax) for two 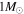 stellar models on the ascending RGB (dotted line) and red clump (solid line) with the same
stellar models on the ascending RGB (dotted line) and red clump (solid line) with the same 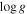 (and therefore the same radii). While their acoustic structure is very similar near the envelope, the inner turning points of the modified radial p-mode cavity are different, as are the estimated values of Δν.
(and therefore the same radii). While their acoustic structure is very similar near the envelope, the inner turning points of the modified radial p-mode cavity are different, as are the estimated values of Δν.
Download figure:
Standard image High-resolution image3.1.2. Dependence on Model Atmospheres
The models previously discussed were constructed with Eddington-gray atmospheres. To examine the dependence of our integral estimator on atmospheric conditions, we also constructed models using Krishna–Swamy model atmospheres, with Y0 and αMLT calibrated separately. Once again, we show the log ratios between our estimator and the fitted Δν in the top panel of Figure 7. Surprisingly, there does not appear to be any significant difference in the structure of the residuals. We interpret this to indicate that the remaining deviations that persist in either case stem from either an insufficiently high order of approximation or issues with our formulation that become significant only in the interior of the star, rather than the atmosphere.
Figure 7. Log ratio of fitted Δν vs. our integral estimator for main-sequence/subgiant models with different physics and/or fundamental parameters. The gray points in the background correspond to the colored points in Figure 3 at solar metallicity and with Eddington-gray atmospheres. Top: models with Krishna–Swamy atmospheres instead of Eddington-gray atmospheres; middle: low-metallicity models (i.e., ![$[\mathrm{Fe}/{\rm{H}}]=-0.5$](https://content.cld.iop.org/journals/0004-637X/870/1/41/revision1/apjaaf1b5ieqn46.gif) ), excluding models with no outer convection zone (where we would not expect global oscillations to be excited at all); bottom: high-metallicity models (i.e.,
), excluding models with no outer convection zone (where we would not expect global oscillations to be excited at all); bottom: high-metallicity models (i.e., ![$[\mathrm{Fe}/{\rm{H}}]=+0.5$](https://content.cld.iop.org/journals/0004-637X/870/1/41/revision1/apjaaf1b5ieqn47.gif) ).
).
Download figure:
Standard image High-resolution imageOne possible such inadequacy in our formulation could be our numerical treatment of the acoustic cutoff frequency. For example, Gough (1993) constructed a different expression for the acoustic cutoff frequency that takes the sphericity of the star into account, which only becomes significant deep in the stellar interior. This is also, therefore, where we expect the expression that we have used to be the most inaccurate. Since a large contribution to the value of our integral expression comes from singularities (integrable or otherwise) at the turning points, it is possible that the remaining error could potentially be considerably reduced or eliminated entirely by using an expression that is more accurate in the interior.
3.1.3. Dependence on Metallicity
To investigate dependences on composition, we also construct stellar models with metallicities ![$[\mathrm{Fe}/{\rm{H}}]=\pm 0.5$](https://content.cld.iop.org/journals/0004-637X/870/1/41/revision1/apjaaf1b5ieqn48.gif) , showing the log ratios between the fitted frequency separation and our estimator in the bottom two panels of Figure 7. We show only models possessing outer convection zones. We note that, aside from some translation along the apparent residual curve, the qualitative features of these residuals are once again essentially unchanged.
, showing the log ratios between the fitted frequency separation and our estimator in the bottom two panels of Figure 7. We show only models possessing outer convection zones. We note that, aside from some translation along the apparent residual curve, the qualitative features of these residuals are once again essentially unchanged.
3.1.4. Δν from Nonradial Modes
Finally, if we relax our previous restriction to radial modes, we arrive at a similar integral expression,
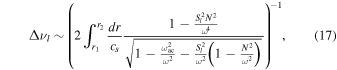
for the large separation of modes with 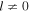 . To test this expression, we evaluate
. To test this expression, we evaluate
by least-squares fitting of 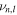 against n for l = 1 and 2 on the same set of stellar models as used in the first panel of Figure 3, again including all modes with frequencies below the maximum acoustic cutoff frequency. Again, we plot the log ratio of these against the corresponding integral estimates (this time from Equation (17)) in Figure 8. We see that for main-sequence stars, our estimator also adequately reproduces the fitted value of Δνl. However, there is a considerable amount of scatter for stars that have evolved off the main sequence, as well as a clear systematic deviation for l = 2.
against n for l = 1 and 2 on the same set of stellar models as used in the first panel of Figure 3, again including all modes with frequencies below the maximum acoustic cutoff frequency. Again, we plot the log ratio of these against the corresponding integral estimates (this time from Equation (17)) in Figure 8. We see that for main-sequence stars, our estimator also adequately reproduces the fitted value of Δνl. However, there is a considerable amount of scatter for stars that have evolved off the main sequence, as well as a clear systematic deviation for l = 2.
Figure 8. Log ratio of fitted Δν vs. various estimators, with the same coloring and markers as in Figure 3. Top: ratios for Δν fitted from and integral expressions with l = 1. Bottom: the same with l = 2.
Download figure:
Standard image High-resolution imageWe attribute the above to difficulties in constructing a well-defined average Δν for nonradial modes with evolved stars. For l = 1, avoided crossings emerge as the star evolves through the subgiant phase, and mixed-mode propagation (i.e., evanescent coupling to a g-mode cavity) becomes possible (Scuflaire 1974; Osaki 1975; Aizenman et al. 1977; Deheuvels & Michel 2011), with further mode splitting emerging when Δν becomes sufficiently small. This g-mode coupling also changes the frequencies of observed l = 2 mixed modes relative to pure p-modes. Mixed modes are described by two quantum numbers, np (the radial quantum number n of the p-mode being coupled) and ng (Unno et al. 1989); in computing Δνl, we have selected for each value of np the frequency of the corresponding mode with the lowest inertia. However, this does not necessarily correspond to the eigenfrequency of a pure p-mode with that value of np.
We illustrate this problem in Figure 9, where we plot the ratio of the least-squares fitted values of 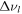 to
to 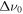 for l = 1, 2. It is clear that this ratio is relatively constant (although not necessarily unity) near the main sequence but shows large variations—both systematic and in terms of scatter between timesteps—for evolved stars. Much of the scatter in Figure 8 is a result of these rapid variations in Δνl, rather than originating from our modified estimator. While our formulation cannot explain the remaining systematic differences for evolved stars (as in the bottom panel of Figure 8, for l = 2), we nonetheless note that these have qualitatively the same morphology as the relative differences between the sound-travel time and the fitted value of Δν. Again, this likely indicates the limitations of our numerical formulation of the acoustic cutoff frequency; a careful accounting (as in Gough 1993) shows that it, too, depends on the degree l (in a somewhat complicated fashion), which is not included in our numerical integration.
for l = 1, 2. It is clear that this ratio is relatively constant (although not necessarily unity) near the main sequence but shows large variations—both systematic and in terms of scatter between timesteps—for evolved stars. Much of the scatter in Figure 8 is a result of these rapid variations in Δνl, rather than originating from our modified estimator. While our formulation cannot explain the remaining systematic differences for evolved stars (as in the bottom panel of Figure 8, for l = 2), we nonetheless note that these have qualitatively the same morphology as the relative differences between the sound-travel time and the fitted value of Δν. Again, this likely indicates the limitations of our numerical formulation of the acoustic cutoff frequency; a careful accounting (as in Gough 1993) shows that it, too, depends on the degree l (in a somewhat complicated fashion), which is not included in our numerical integration.
Figure 9. Ratios of Δνl to 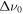 for l = 1 (top) and l = 2 (bottom) for evolutionary tracks of stellar masses 0.8 and
for l = 1 (top) and l = 2 (bottom) for evolutionary tracks of stellar masses 0.8 and 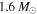 , with colors corresponding to those of Figure 3. Main-sequence models are denoted with circles, while subgiants (with core hydrogen mass fractions
, with colors corresponding to those of Figure 3. Main-sequence models are denoted with circles, while subgiants (with core hydrogen mass fractions 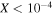 ) are shown with triangles.
) are shown with triangles.
Download figure:
Standard image High-resolution image4. Conclusions
We present a modified asymptotic expression, Equation (16), as an estimator for Δν, the large frequency separation. We find that our estimator, evaluated at νmax, describes the large frequency separation (as obtained by fitting ν against n) more accurately than both the scaling relation and the classical asymptotic estimator, which is the sound-travel time. While the latter can be modified to more closely match the fitted value by adjusting the integration domain somewhat arbitrarily, the turning points of our integral emerge naturally from the theoretical formulation and do not suffer such ambiguity. This result appears to hold good with little variation with respect to the choice of model atmosphere, and modifications to the model metallicity also do not substantially change the qualitative features of the residual deviation. The insensitivity of the residual differences to the choice of model atmosphere indicates that they originate from theoretical issues pertaining to the interior of the stellar models, rather than the surface, as is usually assumed (Hekker et al. 2013).
We also find that our integral expression becomes singular at some point during the main-sequence turnoff; this failure mode is ultimately a consequence of the failure of the WKB regime under these conditions. We show that these singular points occur during a transition between two extreme regimes of asymptotic behavior, owing to structural evolution yielding a qualitative change in the inner turning point of the WKB integral. We argue that this provides theoretical justification for separately calibrated scaling relations for stars at different evolutionary stages.
Moreover, our naive application of the WKB approach appears insufficient to completely describe the behavior of Δν as fitted from nonradial modes, particularly away from the main sequence. However, this may be improved with a more detailed numerical implementation. In any case, such a fit is observationally ill-defined away from the main sequence.
These limitations notwithstanding, we propose the use of this integral expression as an alternative to both the scaling relation and the sound-travel time for estimating Δν, although care should be taken to avoid the singular points where it fails. This expression is particularly well suited to such a use when fitting stellar models to individual mode frequencies, in that the closeness of a model's Δν to observed values can be used as a decision criterion for whether or not said model is sufficiently optimal as to warrant expending additional computational resources to calculate its individual mode frequencies. An accurate asymptotic estimation of Δν will considerably reduce the size of this expensive search space.











