Introduction

A robust observation in the task-switching literature is the interaction between task transition and response transition. When the task repeats, response repetitions lead to performance benefits (e.g., faster response time [RT] and lower error rate [ER]). However, when the task switches, response repetitions typically lead to performance decrements. These performance differences are referred to as response-repetition (RR) effects (for overviews, see Altmann, 2011; Druey, 2014; Gade et al., 2014). Consider the tasks of classifying an object either by its color (blue/red) or its shape (triangle/square). In this case, a left response may represent “blue” in the context of the color task, but “triangle” in the context of the shape task. Interference between these representations would be greatest on a response-repetition task-switch trial, as the response must be recoded with a different representation.

Theoretical accounts for response-repetition costs

Several accounts have been considered to explain RR effects that are not mutually exclusive. Episodic binding accounts (see Altmann, 2011) propose that all task-relevant features—for example, the task context, stimulus, response, and response-related outcomes—are bound within a shared episodic representation (e.g., Frings et al., 2020; Hommel et al., 2001; Prinz, 1990). When a feature of the previous trial repeats, it acts as a retrieval cue for the previous episodic trace. This retrieval results in a cost when at least one feature on the current trial differs from the previous trial, as the episode must be overcome and the response must be selected with a new representation (Schuch & Koch, 2004). Costs are not expected in cases in which either all features of an episode repeat or all features of an episode switch because there is no match between the current event and the retrieved one (see also Benini, et al., 2022; Kandalowski et al., 2020; Meiran, 2000; Rogers & Monsell, 1995; Schmidt et al., 2020; Schneider & Logan, 2005).

Priming and inhibition accounts (Druey, 2014; Hübner & Druey, 2006), on the other hand, assume that responses are automatically inhibited after execution to prevent accidental response re-executions (Smith, 1968). This produces RR costs on task-switch trials when the same response must be produced again. Although this inhibition mechanism is presumably active on task-repetition trials, RR costs are not observed as inhibition is overcompensated by repetition of the stimulus category (i.e., stimulus priming), such that the positive effects of stimulus repetitions outweigh the costs of response repetitions (for a hybrid inhibition-episodic account, see Koch et al., 2018).

Alternatively, reconfiguration accounts assume that task sets are hierarchically organized (Kleinsorge, 1999; Kleinsorge & Heuer, 1999), whereby switches at higher levels (e.g., task) facilitate switches at lower levels (e.g., response) via a general task-set reconfiguration mechanism. Thus, preparing a task switch involves preparing a response switch, but not vice versa. Consequently, response repetitions lead to costs on task-switch trials, as additional reconfiguration is needed to switch back to the recently executed response.

These accounts focus on the relationship between stimulus categorizations and motor responses, with little attention to what happens after the response is produced. However, it has been argued that responses are best construed as outcome-oriented actions—that is, oriented toward the body-related and/or environmental effects resulting from the production of a response (Frings et al., 2020; Hommel et al., 2001). Thus, we propose that changes in the activation of outcome representations are a potential source of RR costs. If so, RR costs should be eliminated, or even reversed, when the same outcome representations are activated across tasks.

The present study

We assume that outcome representations are typically dominated by the body-related sensory effects associated with responses (e.g., tactile feedback and proprioceptive changes resulting from finger movements) and the intended meanings of actions. Given the difficulty in decoupling motor activity from its inherent effects (e.g., removing tactile feedback from manual responses), researchers couple arbitrary environment-related effects, such as changes in sound or visual input, to actions to manipulate the outcome representations (e.g., Kunde, 2001; Schacherer & Hazeltine, 2020). It is proposed that after the co-occurrence of the action and its corresponding outcome, a bidirectional link is established, so that activating the representation of the outcome activates the corresponding motor pattern (e.g., Hommel et al., 2001; for review, see Pfister, 2019). This bidirectional link causes the activation of representations of candidate actions to activate outcome representations and vice versa. Therefore, we designed tasks in which responses were followed by experimentally induced perceptual events (hereafter, manipulated outcomes) to test the role of outcomes in response repetition costs.

Note that manipulated outcomes are presented after RT is measured. Thus, to impact performance, representation of these anticipated outcomes must be activated prior to action execution. Indeed, response selection (and thus, response production) is faster and less error-prone when responses are followed by compatible outcomes, such as when a left keypress is followed by a left-sided light than a right-sided light (Kunde, 2001; see also Koch & Kunde, 2002; Kunde et al., 2004).

In the present study, we explored whether changes in the representation of actions provide a potential source of RR costs. To do this, we instructed participants to produce outcomes that “completed the set.” They were shown either two colors (e.g., red and green) or two shapes (e.g., square and pentagon) and instructed to produce the outcome (e.g., blue, triangle) that completed the color (red–green–blue) or shape (square–pentagon–triangle) set. Across three conditions, we varied the number of manipulated outcomes. In one condition (three manipulated outcomes; 3MO), the outcomes were the same across tasks—that is, a given response, regardless of task, produced a single outcome (e.g., blue–triangle conjunction). In another condition (six manipulated outcomes; 6MO), responses produced task-specific outcomes that did not overlap across tasks (e.g., blue or triangle, depending on the task context). Lastly, we included a condition with no manipulated outcomes (NMO) as in a typical task-switching experiment. In the NMO condition, we assumed that participants conceptualized their responses in terms of the identity of the compound stimulus (e.g., “this is the red–green key” when responding to the red–green stimulus pairing). Thus, like the 6MO condition, there would be six possible “outcomes” as there are six stimulus–response pairings.

When task switches lead to outcome repetitions in the 3MO condition, we predicted minimal RR costs—or even benefits—as responses do not need to be reselected with different outcome representations. We expect that the distinct features of the outcomes (i.e., color and shape) will be integrated because subjects will be rapidly switching between attending to the color and shape of the outcome across trials, making the irrelevant feature difficult to ignore, as in a task-switching procedure with bivalent stimuli (e.g., Rogers & Monsell, 1995). However, when task switches lead to outcome switches in the 6MO condition, or switches in the mental representation of the response in the NMO condition, we predicted RR costs.

Method

Participants

Using an effect size of ƞ2 = .06 (medium effect size) and an alpha of .05, a power analysis for a 2 (response type) × 3 (condition) within-between repeated-measures analysis of variance (ANOVA) using G*Power (Faul et al., 2007) determined that 42 participants (14 for each of our three conditions) would be needed to obtain statistical power of .8 (Cohen, 1988). We tested 32 participants per condition (96 total).

Ninety-six undergraduate students from the University of Iowa participated in partial fulfillment of an introductory psychology course requirement. Seventeen participants whose overall accuracy was less than 80% were discarded and replaced. The final 96 participants were equally divided into three conditions based on the number of experimentally manipulated outcomes: three manipulated outcomes (3MO; Mage = 18.81, SDage = 1.23); six manipulated outcomes (6MO; Mage = 18.75, SDage = 1.16); or no manipulated outcomes (NMO; Mage = 18.56, SDage = 0.80). Vision and hearing were reported as normal or corrected-to-normal. Consent was obtained prior to the experiment. All methods and procedures were approved by the Institutional Review Board at the University of Iowa.

Stimuli and apparatus

The experiment was conducted using PsychoPy (Version 2020.1.1; Peirce et al., 2019), and data were collected using the Pavlovia online server. Participants in all conditions performed the same color task and shape task. Only the outcomes of the responses were manipulated. Color stimuli were three desaturated colors: red (RGB: 209, 133, 151), green (RGB: 143, 185, 162), or blue (RGB: 113, 146, 183). Footnote 1Shape stimuli were three white shapes: triangle, square, or pentagon. Color stimuli were presented 3 cm to left of fixation, while shape stimuli were presented 3 cm to the right of fixation (see Figs. 1 and 2). All stimuli were presented for 2,000 ms and were about 3.3 cm × 3.3 cm on the screen.Footnote 2 Manual responses were the J/K/L keys on a standard QWERTY keyboard. The stimuli used to cue the responses and the responses themselves were identical across all three conditions.

Fig. 1
figure 1

Example stimuli–response–outcome mappings. a In the three manipulated outcomes (3MO) condition, outcomes were shared across tasks (e.g., blue-triangle conjunction). b In the six manipulated outcomes (6MO) condition, outcomes were restricted to one set (e.g., blue or triangle, depending on task context). c In the no manipulated outcomes (NMO) condition, no additional outcomes were presented

Full size image
Fig. 2
figure 2

Response-repetition costs and switch costs for both RT (top) and ER (bottom). White bars represent the 3MO condition; medium-gray bars represent the 6MO condition; and dark-gray bars represent the NMO condition. Error bars represent standard error of the mean. *** represents significance at p < .001; ** represents significance at p < .01; * represents significance at p < .05

Full size image

In the three manipulated outcomes (3MO) condition, outcomes were shared across tasks. For example, the outcomes may have been a blue triangle, red square, or green pentagon (conjunctions counterbalanced across participants). Critically, the outcomes were the same for both the color and shape tasks (Fig. 1a). In the six manipulated outcomes (6MO) condition, outcomes depended on the task set. For the color task, the outcome was a red, green, or blue circle. For the shape task, the outcome was a white square, triangle, or pentagon (Fig. 1b). Finally, participants in the no manipulated outcomes (NMO) condition completed the color and shape tasks with no additional outcomes provided, similar to previous studies assessing RR effects in task-switching (e.g., Druey, 2014; Kleinsorge, 2004; Rogers & Monsell, 1995; Fig. 1c).

Design and procedure

Written instructions were presented on the computer prior to the start of each block. Instructions emphasized both speed and accuracy for all block types. The experiment took approximately 45 minutes to complete.

Stimuli, responses, and the mappings between them were identical across all three conditions. What varied was the number of manipulated outcomes: 3MO, 6MO, or NMO. Instructions for the 3MO and 6MO conditions were identical. Participants were instructed to produce the outcome that “completed the set.” Example instructions were as follows: Color task: “When you see RED and GREEN, make BLUE appear”; Shape task: “When you see the SQUARE and PENTAGON, make the TRIANGLE appear.” Participants were then instructed how to produce the appropriate outcome (e.g., “To make BLUE appear, press the J key”). Note that in the 3MO condition, participants were never instructed to produce the color-shape conjunction (i.e., they were not told “. . . to make the BLUE TRIANGLE appear”). Thus, any differences between the 3MO and 6MO conditions would stem from the participant’s conceptualization of their actions. For the NMO condition, participants were instructed to press the correct key based on the provided instructions (e.g., “When you see RED and GREEN, press the J key”).

For all conditions, each trial began with the onset of a fixation cross for 1,000 ms, followed by presentation of the stimuli for 2,000 ms. On every trial, two stimuli—each belonging to the same set (color, shape)—were presented pseudorandomly either to the left or right of fixation depending on the set (the set–location mapping was counterbalanced across participants). Because the stimuli were univalent, no additional switch cues were used. Tasks were presented in an unpredictable sequence with the constraint that each task was presented an equal number (18) of times per block (e.g., Meiran, 1996). The response interval was 2,000 ms. Outcomes were presented immediately following response production with a duration of 800 ms at the center of the screen. For the 3MO and 6MO conditions, stimuli remained on the screen with the produced outcome, to emphasize the completed set. The next trial began immediately after the conclusion of the outcome. No error feedback was provided when the response was incorrect. If no response was produced, the words “No Key Press” were displayed centrally for 800 ms (same duration as the produced outcome). For the NMO condition, the overall procedure was identical with the exception that no manipulated outcomes were presented following response production; instead, a blank screen was presented for 800 ms. Thus, the trial duration was equivalent across all three conditions.

Participants completed 24 blocks consisting of 36 trials each. The first three blocks were practice blocks, in which participants performed the color task alone, the shape task alone, or the two tasks intermixed (mixed block). In these practice blocks, the response–outcome mappings were presented on the bottom of the screen across trials to remind participants which response produced which outcome. The remaining 21 blocks consisted of six homogenous single-task blocks (three for each task: color or shape) and fifteen mixed blocks. The mixed blocks consisted of 36 single-task trials of either task (18 of each task), intermixed at random. The order of blocks was as follows: two single-task, seven mixed, two single-task, four mixed, two single-task, and four mixed. The order of the single-task blocks (color, shape) was counterbalanced across participants.

Statistical analysis

For all three conditions, the first six blocks (three practice, one color, one shape, one mixed) were excluded from analysis. Thus, we analyzed data from eighteen blocks: four single-task (two color-only, two shape-only)Footnote 3 and 14 mixed blocks. The first two trials in each block were treated as practice and excluded. All responses given within the first 200 ms after stimulus onset or any RTs greater than 2,000 ms were excluded from analysis. Lastly, incorrect trials, trials in which no response was detected, trials following an error, and direct stimulus repetitions were removed from the analysis of RT. For the 18 analyzed blocks, we removed 14.5% of trials from our final RT analysis.

For the analysis of RR costs, we predicted that there would be no RR costs for task-switch trials in the 3MO condition but significant RR costs for task-switch trials in the other conditions. We assume that RR costs reflect the recoding of the meaning of the response and that this recoding is greatly reduced when the manipulated outcomes are identical across task switches. For this analysis, we analyzed data from only task-switch trials in mixed blocks. We conducted a 2 × 3 repeated-measures ANOVA with response type (response-repeat, response-switch) as a within-subjects factor and condition as a between-subjects factor.

Given the nature of our design, we also assessed switch costs—the performance differences between task-repeat and task-switch trials. We predicted that switch costs would be smallest for the 3MO condition because response-outcome representations would require the least updating. Switch costs are thought to reflect either transient trial-to-trial carryover effects (Allport et al., 1994) or the time needed to reconfigure control processes (Rogers & Monsell, 1995; for review, see Kiesel et al., 2010). Because task similarity facilitates task-switching (Arrington et al., 2003), we predicted reduced switch costs in the 3MO condition as the manipulated outcomes made tasks more similar (see also Lukas et al., 2013). For this analysis, we analyzed data from both task-repeat and task-switch trials in mixed blocks and conducted a 2 × 3 repeated-measures ANOVA with task transition (task-repeat, task-switch) as a within-subjects factor and condition as a between-subjects factor.

For all analyses, if there was unequal variance across conditions (Levene’s p < .05), we applied the Brown–Forsythe test statistic for comparisons. Significant main effects and interactions were followed-up with independent-samples t tests to compare across conditions. In addition to null hypothesis significance testing, we report Bayes factors (Lee & Wagenmakers, 2013). We also report the results of a three-way ANOVA with response type and task transition as within-subject factors and condition as a between-subject factor in the Supplementary Materials (Section B). The mean RTs and ERs for all conditions are shown in Table 1.

Table 1 Mean response times (RT) and percentage error rate (ER) for each of the trial types
Full size table

Results and discussion

Response-repetition effects

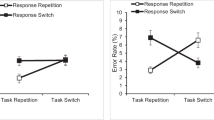
There was a significant main effect of response type (response-repeat: 1,067 ms; response-switch: 1,053 ms), F(1, 93) = 4.98, p = .028, ƞp2 = .051, BF10 = 0.95, The main effect of condition was not significant (3MO: 1,089 ms; 6MO: 1,063 ms; NMO: 1,028 ms), F(2, 93) = 1.42, p = .246, ƞ2 = .028, BF10 = 0.55. Critically, the interaction was significant, F(2, 93) = 9.83, p < .001, ƞp2 = .175, BF10 = 217.14, indicating differences in response-repetition effects across conditions (3MO: −25 ms; 6MO: 33 ms; NMO: 35 ms). Follow-up tests on the interaction revealed a significant difference between the 3MO and 6MO conditions, t(62) = 3.50, p < .001, d = 0.88, BF10 = 34.58; between the 3MO and NMO conditions, t(53.28) = 3.71, p < .001, d = 0.93, BF10 = 60.48; but not between the 6MO and NMO conditions, t(62) = 0.16, p = .877, d = 0.04, BF10 = 0.26. One-sample t tests with 0 ms (i.e., no RR effect) as the reference revealed marginally significant response-repetition RT benefits when response outcomes were shared across tasks (3MO; t(31) = −1.86, p = .072, d = 0.33, BF10 = 0.87), but significant RT costs when response outcomes changed across tasks, 6MO, t(31) = 3.44, p = .002, d = 0.61, BF10 = 20.48; and NMO, t(31) = 3.93, p < .001, d = 0.70, BF10 = 67.48 (Fig. 1d). These results contrast findings of RR costs on task-switch trials and support the proposal that RR costs reflect changes to the representation of an action (Schuch & Koch, 2004).

For ER, both the main effects of response type (response-repeat: 10.1; response-switch: 6.5), F(1, 93) = 71.11, p < .001, ƞp2 = .433, BF10 = 1.21e+9; and condition (3MO: 8.1; 6MO: 10.4; NMO: 6.4), F(2, 93) = 5.65, p = .005, ƞ2 = .082, BF10 = 9.31, were significant. The interaction was also significant, F(2, 93) = 7.72, p < .001, ƞp2 = .142, BF10 = 37.97, revealing differences in response-repetition effects across conditions ((3MO: 2.8; 6MO: 5.9; NMO: 2.0). Follow-up tests on the interaction revealed significant differences between the 3MO and 6MO conditions, t(62) = 2.76, p = .008, d = 0.69, BF10 = 5.80; between the 6MO and NMO conditions, t(62) = 4.07, p < .001, d = 1.02, BF10 = 172.47; but not between the 3MO and NMO conditions, t(62) = 0.79, p = .430, d = 0.20, BF10 = 0.33. The overall pattern of ER suggests that the RT results were not due to a speed–accuracy trade-off.

Switch costs

Both main effects were significant: task transition (repeat: 1,003 ms; switch: 1,058 ms), F(1, 93) = 193.90, p < .001, ƞp2 = .676, BF10 = 5.79e+16; and condition (3MO: 1078 ms; 6MO: 1036 ms; NMO: 978 ms), F(2, 93) = 3.95, p = .022, ƞ2 = .074, BF10 = 1.58. The interaction was also significant, F(2, 93) = 19.86, p < .001, ƞp2 = .299, BF10 = 136276.25, revealing differences in switch costs across conditions (3MO: 33 ms; 6MO: 44 ms; NMO: 91 ms). Follow-up tests on the interaction revealed significant differences between the 3MO and NMO conditions, t(62) = 6.26, p < .001, d = 1.57, BF10 = 259270.87; between the 6MO and NMO conditions, t(62) = 4.49, p < .001, d = 1.12, BF10 = 600.10; but not between the 3MO and 6MO conditions, t(62) = 1.14, p = .260, d = 0.28, BF10 = 0.44 (Fig. 1e).

For ER, neither the main effect of task transition (repeat: 6.9; switch: 7.4), F(1, 93) = 1.40, p = .240, ƞp2 = .015, BF10 = 0.32; nor the interaction, F(2, 93) = 2.82, p = .065, ƞp2 = .057, BF10 = 1.31, were significant. However, the main effect of condition was significant (3MO: 7.5; 6MO: 8.6; NMO: 5.5), F(2, 93) = 18.52, p < .001, ƞ2 = .164, BF10 = 17765.96. Follow-up tests revealed significant differences between all three conditions: 3MO–6MO: t(62) = 2.16, p = .035, d = 0.54, BF10 = 1.77; 3MO–NMO: t(62) = 4.13, p < .001, d = 1.03, BF10 = 202.79; and 6MO–NMO: t(62) = 5.79, p < .001, d = 1.45, BF10 = 47946.57, consistent with a speed–accuracy trade-off.Footnote 4

This pattern of switch costs supports the proposal of hierarchical switching operations within the task space in which the task judgment resides at the top of the hierarchy (e.g., Kleinsorge, 2004; Kleinsorge & Heuer, 1999). If participants conceptualize both tasks as “complete the set”—as instructed in the 3MO and 6MO conditions—then the transition between the judgment on a color trial and the judgment on a shape trial should be facilitated, resulting in smaller switch costs. This may stem from residual activation of the previous trial (Allport et al., 1994) or a decrease in the time needed to reconfigure control processes (Rogers & Monsell, 1995; Rubinstein et al., 2001). These overlapping conceptualizations were presumably not present in the NMO condition, as participants were instructed to respond to either color or shape pairs. Thus, task similarity—defined here in terms of task conceptualization (rather than outcome overlap as predicted)—appears to facilitate task-switching (see Arrington et al., 2003).

General discussion

Consistent with the proposal that response selection operates on representations that include outcomes (Frings et al., 2020; Hommel et al., 2001; Schumacher & Hazeltine, 2016), we observed marginal RR benefits in RT when manipulated outcomes repeated across task-switches (3MO) and significant RR costs in RT when manipulated outcomes (6MO) or mental representations of the response (NMO) switched across task-switches. For ER, in which RR costs were observed across all conditions, costs were of similar size in the 3MO and NMO conditions, but largest in the 6MO condition. The fact that RR costs in RT are nearly identical in the 6MO and NMO condition but significantly less (and negative) in the 3MO condition indicates that it is not simply adding outcomes that reduces the RR costs. Rather, changing the intention associated with the response is critical. Moreover, the SR mappings were identical in all conditions but whether costs or benefits were observed depended on events that occurred immediately following the response. Thus, benefits or costs can be observed regardless of the stimulus sets used to cue responses.

Theoretical implications

According to episodic binding accounts of RR effects (Altmann, 2011), task-relevant features—task context, stimuli, responses, and outcomes—are bound within a unitary episodic trace (Hommel, 2004). The magnitude and direction of the RR effect depends on the numbers of matching and mismatching features on response-repeat and response-switch trials. In the present study, the 3MO condition has one matching pair and four mismatching pairs on response repeat trials, and the 6MO and NMO conditions have no matching feature pairs and three mismatching feature pairs (for details, see Section D of Supplementary Materials). Because there are no repeating features on response-switch trials, the difference score between matching and mismatching feature pairings is identical across conditions. Thus, this framework predicts RR costs across all conditions—which was not observed. However, Altmann (2011) proposed an associative biasing mechanism that may weight the bindings between features differently. In the 3MO condition, the outcome representation may be more strongly weighted than other representations because it is consistent across tasks. In this case, a repeated outcome may lead to the retrieval of the response-outcome mapping from the previous trial, producing RR benefits.

According to the priming and inhibition account (Druey, 2014; Hübner & Druey, 2006), RR costs arise from residual response inhibition from the previous trial. However, this inhibition can be counteracted by positive priming of the stimulus or outcome. In the 3MO condition, RRs exist alongside outcome repetitions. If an outcome representation remains active after responding, then residual outcome activation, paired with outcome anticipation on the next trial, may overcompensate the effects of response inhibition, resulting in RR benefits.

The results are also consistent with the idea of a generalized task-set reconfiguration mechanism (Kleinsorge, 1999; Kleinsorge & Heuer, 1999), if it is assumed that participants structure their task representations primarily in terms of outcomes. Because switches at hierarchically higher levels (e.g., outcomes) facilitate switches at lower levels (e.g., responses), RR costs would be expected in the 6MO and NMO conditions, but not in the 3MO condition—which was observed.

In sum, while the results can be accommodated by a range of existing theories, they impose important constraints on each account, demonstrating that changing the outcome associated with a motor action is a principal source of RR costs.

Switch costs

Although both RR costs and switch costs were affected by the outcome manipulation, the pattern of costs was different: for RT, RR costs were largest when manipulated outcomes did not overlap across tasks (6MO, NMO); whereas switch costs were largest without manipulated outcomes (NMO). For ER, both RR costs and switch costs were largest in the 6MO condition. These increased switch costs in RT are consistent with the proposal of a dimensionally-organized task space (Kleinsorge, 1999), in which task similarity (here, “complete the set”) facilitates switching (Arrington et al., 2003). When tasks share component operations, this reduces the time needed to reconfigure central processes and/or the likelihood of inhibitory carryover effects. Together, the ways outcome representations, and more broadly task conceptualization, can affect task-switching appear complex.Footnote 5

Limitations

In contrast to many RR studies, we used univalent rather than bivalent stimuli. With bivalent stimuli, the risk of response re-executions may be particularly high as stimulus–response bindings may be in a more active state relative to when univalent stimuli are used (Rogers & Monsell, 1995). Moreover, many experiments have used two-choice rather than three-choice tasks, and that may be an important difference. Future work will determine whether these factors play a major role in the pattern of results.

Summary

The present results provide evidence that RR costs and switch costs are affected by changes in response representations that incorporate outcomes. In addition, the different ways in which outcomes affect the two costs highlight how these task-switching measures may stem from different sources. Together, this study illustrates how the selection of actions relies on the retrieval of outcome representations rather than specific stimulus–response mappings.