Introduction

Interest in why performance degrades when people try to perform two activities simultaneously dates back at least to William James (James, 1890). Many theories have been proposed. For example, one class of models assumes that multiple tasks must compete for the same set of limited mental resources (Kahneman, 1973; Navon & Gopher, 1979). Another class assumes that cognitive operations must be performed serially and therefore performance is degraded when two tasks are performed simultaneously because of rapid switching back and forth between the tasks (Pashler, 1994). After these theories were developed, the field of cognitive neuroscience proposed (and largely embraced) the view that humans have multiple memory systems (Eichenbaum & Cohen, 2001; Squire, 2004). Researchers in many other fields are now also debating whether multiple systems might mediate what previously was thought to be a unitary cognitive process. Included in this list are category learning (Ashby & Alfonso-Reese, 1998; Erickson & Kruschke, 1998), recognition memory (Yonelinas, 2002), and logical reasoning (Sloman, 1996). The evidence for multiple systems raises an intriguing question about the origins of dual-task interference: Is dual-task interference mediated within a single system, or by the interaction of multiple systems? More specifically, if a behavior and a dual task are both typically mediated by system A when performed alone, does that same behavior remain under the control of system A under dual-task conditions, or might it instead be transferred to a less-efficient system B? This article tests this hypothesis within the framework of perceptual categorization.

Within the categorization literature, research has focused on two possible learning systems: a declarative system that underlies explicit reasoning and cognitive flexibility, and a procedural system that underlies classic motor skills such as riding a bicycle or tying a tie (Eichenbaum & Cohen, 2001; Squire, 2004). Procedural learning is qualitatively different from declarative learning in a number of important ways. Specifically, procedural learning is slow and incremental, requires immediate and consistent feedback (Willingham, 1998), is strongly tied to motor goals (Willingham et al. 1989), and is not typically available to conscious recollection or awareness.

The evidence for multiple memory systems comes from a wide variety of sources including behavioral, neuroimaging, neuropsychological, and pharmacological studies. To date, the category-learning literature possesses a rich and robust demonstration of behavioral dissociations between tasks thought to recruit procedural versus declarative memory systems (Ashby & Maddox 2005, 2010). This work has been derived almost entirely from investigations of rule-based (RB) versus information-integration (II) category-learning tasks. In their most typical form, participants in each task are shown one stimulus per trial (drawn at random from a large set of category exemplars) and must guess whether it belongs to category ‘A’ or ‘B.’ Category labels are learned slowly through trial and error. The key difference is that the optimal strategy in RB tasks is a verbalizable rule that can be discovered via logical reasoning, whereas in II tasks category assignments are made in a way that defies explicit reasoning. II tasks are thought to recruit procedural learning and require dopamine-dependent reinforcement learning, and RB tasks are thought to rely on declarative mechanisms including working memory and logical reasoning.

Many different empirical dissociations have been reported between RB and II task performance (for reviews, see Ashby and Maddox 2005, 2010). Two of these are especially important to this article. First, switching the response keys of the categories after learning has occurred interferes with II much more than RB categorization (Ashby, Ell, & Waldron, 2003; Maddox, Bohil, & Ing, 2004, 2010; Spiering & Ashby 2008). Sensitivity to this type of response remapping has been used as a signature of procedural learning and control (Crossley & Ashby, in press; Crossley et al. 2012; Willingham et al. 2000). This line of reasoning appeals to the observation that procedural learning should be strongly tied to response-based processes. Second, a dual task thought to recruit working memory and executive function impairs category learning much more in RB than in II tasks (Waldron & Ashby, 2001; Zeithamova & Maddox, 2006).

There is, however, a logical ambiguity in the interpretation of this latter result: Does a concurrent dual-task impair RB performance simply by reducing the learning rate in the declarative system? Or is RB performance impaired because the RB categories are learned procedurally in the presence of the dual task? This latter hypothesis seems plausible because it is thought that the procedural system can learn almost any type of category structureFootnote 1 (given immediate and reliable feedback). This article addresses these questions by first training participants on either II or one of three different RB category structures either with or without a simultaneous dual task known to recruit working memory and executive attention. After the categories are learned, we then switch the response keys to test whether the RB categories were learned using a declarative or procedural strategy. We take large impairments in performance after switching the response keys as indicative of procedural learning and small impairments as indicative of declarative learning. Our results suggest that, with or without the dual task, the declarative memory categorization tasks were learned by declarative systems (regardless of task difficulty).

The nuance in multiple systems

Our experimental question is framed by the hypothesis that humans have multiple category-learning systems. However, some researchers question this assumption (Newell, Dunn, & Kalish, 2011, Newell et al. 2013, Nosofsky, Stanton, & Zaki 2005, Stanton and Nosofsky 2007; for a counter, see Ashby 2014). For example, Nosofsky et al. (2005) proposed that the RB versus II button-switch dissociation was due to cognitive complexity differences between the tasks, Stanton and Nosofsky (2007) proposed that the RB versus II feedback processing dissociation reported by Maddox, Ashby, Ing, and Pickering (2004) was due to perceptual discriminability differences between the tasks, and Newell et al. (2013) argued that the RB versus II dissociation reported by Filoteo, Lauritzen, and Maddox (2010) was because of feedback processing time differences between the tasks. Obviously, no single study can test all of these different hypotheses. The present study, however, focuses on the RB versus II button-switch dissociation, and our design does allow a strong test of the only existing single-system alternative account of this dissociation—namely that it is driven by differences in task complexity.

Thus, even if one is skeptical of the multiple systems claim, the present experiment makes a valuable contribution because it provides a rigorous test of the cognitive complexity hypothesis. In other words, an alternative view of our experiment is that it examines the effects of a button switch under eight different conditions that vary widely on cognitive complexity. The cognitive complexity hypothesis therefore predicts that the magnitude of the button-switch interference should be ordered across our conditions in a very specific way. As we will see, the results strongly disconfirm this prediction. Thus, although this article does not attempt to test between one versus multiple category-learning systems, our results do provide a strong test of one prominent alternative hypothesis that has been used to argue for a single category-learning system.

On the other hand, it seems unlikely that procedural and declarative memory systems—and therefore the associated category-learning mechanisms—are completely independent. In fact, the current multiple-systems view of category learning leaves ample room for rich system interactions. For instance, recent work has shown that the procedural system learns perfectly well even when the declarative system completely controls behavior (Crossley & Ashby, in press). Fleshing out the nuances of these interactions is well beyond the scope of the present article.

Materials and methods

Participants and conditions

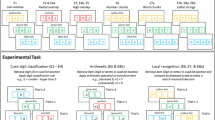
Our experiment included four conditions: The II condition included 30 participants, the RB 4D condition included 16 participants, the RB 6D condition included 36 participants, and the RB Biconditional condition included 32 participants. Every participant served in only one of the four conditions in which they were assigned. Participants in the II, RB 4D, and RB 6D conditions were randomly assigned. Participants in the RB Biconditional condition were run during a separate quarter as a separate study. Sample sizes were determined based on previous research (e.g., Ashby et al. 2003). The RB 6D, RB Biconditional, and II conditions required larger sample sizes than the RB 4D condition because they were more difficult and therefore led to more subjects being excluded from analysis (see the exclusion criteria section of the results section). All participants were undergraduate students from the University of California, Santa Barbara (UCSB) who reported normal or corrected-to-normal vision and received partial course credit in exchange for participation. Each participant completed an approximately 60-min session.

Stimuli and apparatus

The categorization stimuli were colored geometric figures presented on a colored background. The stimuli used in the RB 4D, RB Biconditional, and II conditions varied on four binary-valued dimensions: background color (blue or yellow), embedded symbol color (red or green), number of symbols (1 or 2), and symbol shape (square or circle). This yields a total of 16 possible stimuli in each condition. The stimuli used in the RB 6D condition varied on six binary-valued dimensions. Four of these were the same as in the RB 4D and II conditions. To create six dimensional stimuli, two dimensions were added: (1) rotation—each stimulus was presented as in the RB 4D or II conditions or slightly rotated in a clockwise direction, and (2) background texture (smooth or granular). An example stimulus with each new value (rotated and granular texture) appears in Fig. 1. The addition of two dimensions increased the number of stimuli in the RB 6D condition to 64 and the number of possible one-dimensional rules to 6.

Fig. 1
figure 1

A stimulus from the six-dimensional RB task

Full size image

Each stimulus rectangle was 253x253 pixels in size and was presented on a dark gray background using Matlab and functions from Brainard’s (1997) Psychophysics Toolbox. Responses were made with the ‘D’ and ‘K’ keys on a keyboard; the stimuli were shown on a 19” LCD monitor with a resolution of 1680x1050. In the RB 4D, RB Biconditional, and II conditions, each of the 16 stimuli was repeated 27 times for a total of 432 stimulus presentations. In the RB 6D condition, each stimulus was repeated seven times for a total of 448 stimulus presentations. In all conditions, the presentation order of the stimuli was completely randomized for every participant.

To create the RB 4D and 6D category structures, one dimension was randomly selected to be relevant. The two values on that dimension were then randomly assigned to the two contrasting categories. To create II category structures, one dimension was randomly selected to be irrelevant. Next, one level on each relevant dimension was arbitrarily assigned a numerical value of 1 and the other level was assigned a value of 0. The category assignments were then determined by the following rule: The stimulus belongs to category A if the sum of values on the relevant dimensions is greater than 1.5; otherwise it belongs to category B.

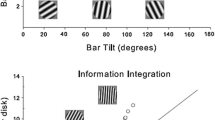
Finally, for the biconditional RB categories, two dimensions were randomly selected as relevant, and the two possible values on each dimension arbitrarily assigned numeric values of 0 and 1. The categories were defined such that if the sum of the values on the two relevant dimensions was either 0 or 2, the stimulus belonged to category A; otherwise, it belonged to category B. This way of defining the categories requires participants to identify both relevant dimensions and to make a conjoint judgment on both dimensions to categorize the stimulus. Examples of possible RB and II category structures using these stimuli are illustrated in Fig. 2.

Fig. 2
figure 2

Top: Example 1 dimensional rule-based categories. The optimal strategy can be verbalized, ‘blue shapes belong to category A, and yellow shapes belong to category B’. Middle: Example Biconditional rule-based categories. The optimal strategy can be verbalized, ‘large blue and small yellow shapes belong to category A, and small blue and large yellow shapes belong to category B.’ Bottom: Example information-integration categories. The optimal classification strategy cannot be simply and concisely verbalized

Full size image

The dual task was the same numerical Stroop task used by (Waldron & Ashby, 2001). In this task, two different digits are randomly chosen on every trial (ranging from 2 to 8), and displayed on each side of the fixation point during the categorization experiment (6.5 cm from the fixation point). One of the digits was displayed in a larger font and occupied 3.3∘ of visual angle. The size of the other digit occupied 1.9∘ of visual angle. On ‘congruent’ trials, the digit with the larger numerical value was displayed in a larger font, whereas on ‘incongruent’ trials the digit with the smaller numerical value was displayed in the larger font. The response keys and feedback for the numerical Stroop task were the same as for the categorization task. The ‘D’ key was used to indicate left, and the ‘K’ key was used to indicate right (matching their locations on a regular keyboard).

Procedure

The experiment was divided into two phases. In the first phase, participants performed the category-learning task only (i.e., no dual task). One possible category structure (there were four possible structures in the RB 4D, RB Biconditional, and II conditions, and six possible structures in the 6D RB condition) was randomly selected without replacement, and participants performed this task until reaching the learning criterion of 12 consecutive correct responses. The category labels ‘A’ and ‘B’ were displayed above the corresponding response keys with every stimulus presentation. After responding to a stimulus, ‘correct’ in green or ‘incorrect’ in red was printed on the screen. The left side of Fig. 3 shows the trial structure and timing for phase 1 of the experiment. Once the learning criterion was met, the participant was informed that the response key locations would switch and that they were required to achieve the learning criterion again on exactly the same category structures. The on-screen category labels shown with each stimulus were reversed to remind participants that the buttons switched.

Fig. 3
figure 3

Sequence of events on a single-task trial (left) and a dual-task trial (right)

Full size image

During phase two, participants performed both the category-learning task as well as the numerical Stroop task. One of the remaining category structures was randomly selected, and participants were required to achieve the learning criterion. The participants were told that the categorization problem would change, and that they would have to perform both the learning and memory (Stroop) tasks simultaneously. Participants were instructed to try their hardest to do well on the memory task, and to do the categorization task with ‘whatever was left’. During this phase, participants were first briefly flashed two numbers, which were then masked with white boxes. Next, the categorization stimulus appeared (again, with labels on-screen). After responding to the stimulus, feedback was given and then a cue indicating either ‘Size’ or ‘Value’ appeared indicating whether to respond to the physically or numerically larger number. Feedback was then given to the Stroop response. The right side of Fig. 3 shows the trial structure and timing for phase 2 of the experiment. Upon achieving criterion, participants were again informed that the response key locations would switch (with reversed on-screen labels) but not the category structures, and they would have to continue performing the same category-learning and memory tasks again until reaching criterion.

Phases 1 and 2 were alternated until all 432 stimuli were seen in the case of the RB 4D, RB Biconditional, and II conditions, and until all 448 stimuli were seen in the case of the RB 6D condition. If a participant exhausted all four category structures, the categories were randomly sampled with replacement at the beginning of each phase thereafter. Prior to performing the experiment, participants watched a brief, self-paced demonstration stepping through a single trial of the experiment with both the Stroop and categorization tasks (e.g., a phase 2 trial) and also performed a ten-trial-long practice session structured like phase 2 of the experiment.

Results

Exclusion criteria

Concurrent performance of a Stroop task and a categorization task is very challenging, and many participants failed to learn one or both components of the task. Moreover, since each participant may complete a different number of problems, the participants that perform the best might contribute more data points than those who perform more poorly. This raises many questions regarding the most appropriate subset of participants to include in our analysis. For example, should we exclude participants that never made it to the button switch phase while under dual-task conditions? Should we consider only one problem of each type per participant, or should we include all problems from each included participant? Should participants be excluded based on their Stroop task performance? Ultimately, there may be no clear right or wrong answer to these questions, and so our approach is to present the results from a wide variety of exclusion criteria in the supplemental material, while focusing on a single set of exclusion criteria in the body of this article. As is demonstrated at length in the supplement, the qualitative pattern of our results is completely independent of exclusion criteria.

For the main article, we employed two exclusion criteria. First, we excluded any participant who failed to solve at least one problem. Since these participants failed to learn a single category problem in more than 400 trials, it seems likely that this exclusion criterion only eliminated participants who were exceptionally unmotivated or confused. Second, we excluded any participant who failed to achieve an average Stroop accuracy of at least 70 %. This exclusion criterion is essential since sound inferences about category-learning performance between conditions cannot be made if Stroop performance between conditions also varies. Altogether, this criterion excluded six participants from the II condition, two from the RB 4D condition, ten from the 6D RB condition, and 15 from the Biconditional RB condition. Figure 4, which shows the number of participants that solved one, two, three, or four problems in each condition, makes it clear that the majority of exclusions in the RB 6D and RB Biconditional conditions were derived from inadequate Stroop performance.

Fig. 4
figure 4

The number of participants in each condition that solved at least one, two, three, or four category problems

Full size image

Figure 4 also makes clear that II and RB tasks are learned in qualitatively different ways. Specifically, every participant in every RB condition that solved at least one problem, also solved the subsequent button switch. Many of these participants (especially in the RB 6D and RB Biconditional conditions) failed to learn the following problem under dual-task conditions. However, of those that did solve the first dual-task problem, all but one in each condition solved the subsequent dual-task button-switch problem. The II condition, on the other hand, was characterized by a much more graded decrement in the number of participants solving one, two, three, or four problems. Indeed, this decrement was not significantly different from problem to problem in the II condition [χ 2(3) = 2.35, p = .50], but was significantly different in all RB conditions [RB 4D: χ 2(3) = 9.44, p < .05; RB 6D: χ 2(3) = 34.16, p < .001; RB Biconditional: χ 2(3) = 45.88, p < .001].

Stroop task performance

Participants performed the concurrent Stroop task with a high degree of accuracy, achieving an overall average of 85.6 % correct. The differences among Stroop task accuracies on RB 4D (84.3 %), RB 6D (86.5 %), RB Biconditional (85.4 %) or II trials (86.6 %) were not significant according to a 4 condition × 2 phase (pre-button switch, post-button switch) repeated measures ANOVA [F(3,114) = 0.41, p = 0.74]. Importantly, the button switch had no detrimental effect on Stroop performance, although there was a significant effect of phase [F(1,93) = 15.76, p < 0.001]. Supplementary Figure s2 shows that this difference was driven by improvements in Stroop performance during the button switch in the RB 4D condition. This suggests that after acquiring the rule, participants were able to perform better on the Stroop task and that the co-mingled interference between tasks was reduced. In summary, participants performed the concurrent Stroop task with high accuracy regardless of category structure and regardless of whether or not the response buttons were switched. These results were expected, given that participants were instructed to perform the Stroop task perfectly and, ‘with what was left over’, to perform the category-learning task.

Category-learning performance

We assessed the statistical significance of all reported effects by performing a two phases (initial learning versus button-switch) ×2 cognitive loads (single-task versus dual-task) ×4 structures (RB 4D, RB 6D, RB Biconditional, II) repeated measures mixed design ANOVA. The ANOVA assumed type 3 sums of squares and used the Satterthwaite approximation for degrees of freedom. The only significant effect in the ANOVA was the phase x structure interaction [F(1,534) = 34.94, p < .001], which was driven by a variety of factors summarized in Table 1 and Fig. 5. The important points are that there were no differences in initial learning between the RB Biconditional and II conditions under either single-task [t(53) = −.26, p = .80, d = .07] or dual-task conditions [t(8) = .38, p = .71, d = .26]. Thus, task difficulty was equated between the II and RB Biconditional conditions.

Fig. 5
figure 5

Top: Trials to criterion during initial learning. Bottom: Button-switch cost. Blue bars are single-task performance, and red bars are dual-task performance. Error bars are 95 % confidence intervals, and horizontal lines indicate significant pairwise comparisons

Full size image
Table 1 Post hoc pairwise comparisons
Full size table

The more critical question is how the button switch affected performance. To address this issue, we computed a button-switch cost, defined as the number of trials to criterion minus 12. Recall that the response keys were switched immediately after the participant reached the learning criterion of 12 correct responses in a row. The participants were informed of this switch and told to continue responding to the same category structures they had just learned until the criterion was reached again. Thus, if the button switch had no effect, then participants would respond correctly on the next 12 trials (i.e., as they had on the previous 12) and the button-switch cost would be 0. The II condition took significantly longer to recover from the button-switch than any RB condition, including the Biconditional condition, under both single-task [t(29) = −5.14, p < .001, d = 1.90] and dual-task conditions [p(18) = −2.59, p < .02, d = 1.22]. Finally, the recovery from the button switch in the Biconditional condition was not significantly different from in the 4D [single-task: t(25) = 1.81, p = .08, d = .71; dual-task: t(10) = −.66, p = .52, d = .40] or in the 6D RB [single-task: t(24) = 1.88, p = .07, d = .76; dual-task: t(5) = .76, p = .48, d = .67] conditions.

In summary, the II and RB Biconditional conditions were matched for difficulty under both single-task and dual-task conditions, yet the button-switch cost was significantly higher than in the other RB conditions only in the II condition. Finally, despite the increased difficulty of the RB Biconditional task relative to the 4D and 6D tasks, the button-switch cost was not significantly different between these RB conditions. These results replicate previous demonstrations that button-switch cost is increased in II relative to RB category structures (Ashby et al. 2003; Maddox et al. 2004, 2010; Spiering & Ashby, 2008). Our novel result is that learning RB categories while performing a concurrent Stroop task, while substantially increasing the difficulty of category learning, does not increase button- switch cost.

Discussion

Many aspects of behavior are widely thought to be governed by learning and memory in qualitatively distinct neurobiological systems. Procedural learning and memory are thought to proceed slowly and incrementally, require immediate and consistent feedback, and be strongly tied to motor resources. Declarative learning is thought to be fast and flexible, and rely on explicit reasoning. Behavior that is thought to be under the domain of the declarative system has long been known to suffer under increased cognitive load, such as occurs in the presence of a concurrent Stroop task (Pashler, 1994). This article asked a novel and fundamental question regarding the nature of this impairment. Does impaired learning under increased cognitive load reflect the diminished resources available to declarative systems, or does it instead reflect a switch of behavioral control to a procedural system? Our results are summarized in the following paragraph and are consistent with the former of these possibilities.

We ran participants in one of four category-learning tasks. One task was most easily solved by recruiting procedural learning, while the other three were conducive to explicit strategies. We examined whether learning in these tasks was impaired when the buttons used to make category judgments were reversed. This was examined under single-task and dual-task conditions. We found that participants struggled to reverse their categorization strategy (i.e., to compensate for a button switch) when their initial learning was hypothesized to require procedural memory, but reversed their strategy with ease when initial learning was hypothesized to be declarative. This was true regardless of whether a dual-task was present, and was independent of task difficulty.

There are several specific findings worth emphasizing here that strongly imply that training under dual-task conditions does not induce a system switch to procedural resources. First, the button switch caused no significant impairment after learning in RB categorization. Impressively, participants largely demonstrated near instant recovery in performance—reacquiring the categories in nearly the minimum possible time (i.e., 12 trials), regardless of the presence of the dual task. Second, performance on the dual task actually improved slightly in the RB 4D condition during the button-switch trials. This implies that the interference caused by the dual task was much higher during initial rule acquisition, but that once the rule was learned (i.e., after reaching criterion), the interference decreased, allowing participants to improve on the dual task.

One confound in our design is that participants always completed single-task problems before they completed dual-task problems. Thus, at the time of the first dual-task button switch, participants had already recovered from at least one prior button switch, and this practice may have reduced the dual-task button-switch cost. While the current data do not allow us to rule this possibility out, note that with the II categories, the button-switch cost was significant under both single- and dual-task conditions, and thus, if there was a practice effect, it did not change the qualitative results in the II condition.

Unfortunately, overall task difficulty when the dual task was presented first was so great that it was impossible to examine initial learning under dual-task conditions. An extensive pilot study showed that when the dual task was introduced from the first trial, most participants failed to learn any II categories or any of the more difficult RB categories. The problem is that any novel category learning is extremely difficult for participants in the presence of a dual task. There are at least two reasons for this difficulty. First, at the beginning of any new task, participants must acquire general knowledge about the task (so-called metalearning). This includes learning what the stimuli look like, learning about the timing and the response keys, and what the feedback means. A simultaneous dual task could interfere with this metalearning, regardless of what memory systems are used to solve the category-learning task.

Second, people often begin with declarative strategies, even in II tasks that require procedural learning for optimal performance. Thus, previous studies have always found some dual-task interference in II tasks. The important point is that this interference is always less than in RB tasks, even when the RB task is considerably easier for participants to learn under single-task conditions.

Another interesting design choice is that we ran this study using a within-subjects design in which each participant always learned category structures of the same type in an attempt to minimize potential interference from one categorization problem to the next. Prior research shows that switching between declarative and procedural category-learning systems is incredibly difficult (Ashby & Crossley, 2010). This prior work suggests that if we had asked participants to switch between RB and II category structures, many would have failed. The most likely outcome is that many participants would have used explicit strategies on all categorization problems, even in the II condition. This is the reason we decided on a within-subjects design. If future research uncovers methods to reliably induce fluid switching between categorization systems, we may return to examine a design in which each participant is exposed to category structures of all types.

Our results are broadly consistent with an ever-growing body of evidence linking RB category learning to declarative systems, and II category learning to procedural systems. Of particular relevance here are prior studies showing that II category learning is impaired after a button switch much more than RB learning (Ashby et al. 2003; Maddox et al. 2004, 2010; Spiering & Ashby, 2008), whereas RB category learning is impaired more under dual-task conditions (Waldron and Ashby, 2001; Zeithamova & Maddox, 2006). On the other hand, the absence of a large button-switch impairment in the Biconditional condition seems a failure to replicate Nosofsky et al. (2005), who showed that RB categorization can incur a substantial button-switch cost if the explicit strategy required in the RB task is made difficult enough (i.e., a conjunction rule). However, one potentially important difference between Nosofsky et al. (2005) and the present work is that we showed the category labels on the screen immediately above the response keys, whereas Nosofsky et al. (2005) did not. Thus, in the Nosofsky et al. experiment, participants had to remember the new locations of the response keys after the button switch and the conjunction rule needed for optimal responding, whereas in our experiment they only needed to remember the biconditional rule. So one possibility is that the button-switch interference observed by Nosofsky et al. with a conjunction rule was actually due to extra working memory demand. Although we know of no direct tests of this hypothesis, there is some supporting evidence (Maddox et al. 2007). Even so, more work is clearly needed on this issue.

Another important caveat is that our results are limited to very early learning, and therefore do not address the question of whether dual-task effects might be quite different following more training. In fact, the evidence for such differences is good. Helie, Waldschmidt, and Ashby (2010) showed that after more than 11,000 trials of training, RB and II tasks both exhibit similar button-switch costs and neither exhibits a significant dual-task cost, presumably reflecting automaticity in task performance.

Another contribution of the present article is that it provides a strong test of the cognitive complexity hypothesis. As mentioned earlier, the only single-system account of the RB versus II button-switch dissociation is that a button-switch interference occurs in the II task because it has greater cognitive complexity than the (rotated) one-dimensional RB task (Nosofsky et al., 2005). The present experiment provides strong tests of this hypothesis because our various conditions differ considerably on cognitive complexity. First, by any definition of complexity, the Biconditional RB task is more complex than the 6D RB task, which is more complex than the 2D RB task. So the cognitive complexity hypothesis predicts that the button-switch costs should be similarly ordered. In contrast to this prediction, no button-switch costs were found in any of these conditions. Second, adding a dual task clearly increases cognitive complexity, so the complexity hypothesis predicts larger button-switch costs in each dual-task condition than in the analogous single-task control. In contrast to this prediction, we found no effect of the dual task on button-switch cost for any of our four category structures—including the II categories. Thus, the complexity hypothesis fails to account for any results described in this article. Instead, the presence or absence of a button-switch cost was perfectly predicted by the multiple systems hypothesis in every condition.

Because so many aspects of behavior are apparently governed by the interaction of multiple learning and memory systems, it is reasonable to think that studying ways to bias which of these systems controls learning might hold promise for enhanced skill acquisition. However, our results reinforce the conclusion of Ashby and Crossley (2010) that switching control from one system to another appears to be more difficult than one might naively expect. In our experiment, it seems that the most efficient strategy for dealing with the dual task might be to divide the workload between declarative and procedural memory systems—declarative systems could perform the numerical Stroop task and procedural systems could perform the category learning. Despite the seeming appeal of this policy, our results suggest that people instead persist in using declarative systems for both tasks. Thus, this study identifies a possible interesting suboptimality in human behavior.