Because of the large amount of information that the visual system is confronted with on one hand, and the limited processing resources that it has available on the other hand, we need a mechanism that allows us to select some information among others: selective attention. How exactly this selection works has been a focus of investigation for decades. Many studies have shown that attentional selection can work on the basis of locations, selecting all the information within a certain area, regardless of the type of information presented at that location (e.g., Downing & Pinker, 1985; Eriksen & Eriksen, 1974; Posner, 1980; Posner, Snyder & Davidson, 1980). For example, Posner and colleagues oriented attention to a location in space using a precue that either appeared directly at that location or pointed toward this location (e.g., Posner & Cohen, 1984). They found that participants were faster and more accurate to react to a target that was presented at the cued location (valid condition) than to a target that was presented at another location (invalid condition). This cueing effect was attributed to the shifting of attention from one location to another.

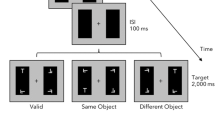
Posner and colleagues’ paradigm (e.g., Posner & Cohen, 1984), however, did not allow distinguishing whether attention was indeed oriented toward locations or rather toward objects at these locations (e.g., Vecera & Farah, 1994). Egly, Driver, and Rafal (1994) developed a paradigm, often referred to as the two-rectangle method, which allowed them to investigate not only space-based but also object-based components of visual attention. Their paradigm was based on Posner and colleagues’ spatial cueing paradigm (e.g., Posner & Cohen, 1984), but it used two elongated rectangles that were presented either to the left and right or above and below a central fixation point (see Fig. 1). A brightening of one of the rectangles’ corners, the cue, oriented attention toward that corner, and participants had to detect a subsequent filling-in of one of the corners, the target. Importantly, this target could either appear directly at the cued location (valid condition) or at one of two uncued locations: either within the same rectangle (invalid-same condition) or at an equidistant location on the corner of the other rectangle (invalid-different condition). Participants were faster to detect the target at the valid condition than any of the two invalid conditions, showing the well-known effect of space-based attention (Posner et al., 1980). In addition, however, participants were faster to detect the target at the invalid-same condition compared to the invalid-different condition. As the target had the same distance to the cue in both types of invalid conditions, Egly et al. (1994) attributed this effect to the object-based component of attention, suggesting that there was an attentional benefit for the entire object (i.e., attention “spreading” along the object’s borders even though only a part of it had been cued; see also Hollingworth, Maxcey-Richard & Vecera, 2012) as well as a cost due to the shifting of attention between objects (see also Lamy & Egeth, 2002). One interpretation of this object-based benefit asserts that an attended object is enhanced at a sensory level and this enhancement includes everything that falls within its borders (Chen & Cave, 2006; Richard, Lee, & Vecera, 2008). Attention seems to be able to even select objects that are solely defined by subjective contours (Moore, Yantis, & Vaughun, 1998) or even hidden portions of occluded objects (Moore & Fulton, 2005).

Fig. 1
figure 1

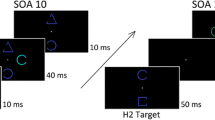
Example of calculation of meridian control scores that look at object-based effects for attentional shifts across the horizontal and vertical meridian separately. Example of a trial with the cue in the upper-left position, dissimilar rectangle color, and L as the target (F are distractors). Please note that the horizontal meridian score (left displays) takes into account only vertical shifts of attention and thus controls for a potential facilitation effect along the horizontal meridian, as suggested by the meridian facilitation theory (e.g., Al-Janabi & Greenberg, 2016; Pilz et al., 2012). The vertical meridian score (right displays), on the other hand, takes into account only horizontal shifts of attention. (Color figure online)

Full size image

In line with these object-based interpretations of the object-based cueing effect, some studies have shown that object appearance can strongly influence object-based attention effects (Avrahami, 1999; Davis & Holmes, 2005; Hecht & Vecera, 2007; Shomstein & Behrmann, 2008; Watson & Kramer, 1999). In particular, Shomstein and Behrmann (2008) have shown that object similarity can influence object-based cueing. They used a variation of the two-rectangle method (Egly et al., 1994), in which the target could appear with different probabilities at the invalid-same or invalid-different location. They manipulated the preview duration of the objects as well as the similarity of the objects by presenting both rectangles filled with the same color (red on a black background) in one experiment, and filled with dissimilar colors (red and blue) in another experiment. The results showed that when the objects were dissimilar from each other, object-based effects were present even at short preview durations. Shomstein and Behrmann (2008) concluded that the dissimilarity of the objects influenced the strength of the object representation as two distinct objects, which in turn increased the object-based effect.

The object-based interpretations of the object-based cueing effect, however, have also been called into question, as the object-based cueing effect seems to be not very robust and is sensitive to a large variety of different factors that seem to be independent of the objects themselves (for a review, see Chen, 2012; Reppa, Schmidt, & Leek, 2012). The object-based cueing effect has been shown, for example, to be dependent on the predictability of the target location (Drummond & Shomstein, 2010; Shomstein & Yantis, 2002, 2004), the attentional distribution or type of orienting (Al-Janabi & Greenberg, 2016; Goldsmith & Yeari, 2003; Macquistan, 1997), recent experience whether the target had appeared on the cued object on the previous trial (Lee, Mozer, Kramer, & Vecera, 2012), task demands (Chen & Huang, 2015; Pilz, Roggeveen, Creighton, Bennet, & Sekuler, 2012), or target-object integration (Al-Janabi & Greenberg, 2016).

Moreover, recent studies have also shown that the object-based cueing effect depends on the orientation of the objects (Al-Janabi & Greenberg, 2016; Pilz et al., 2012). Pilz et al. (2012), for example, investigated object-based cueing effects at the level of the individual participant using nonparametric bootstrapping procedures and showed that, in contrast to space-based effects, object-based effects were very unreliable, being small, absent or even inverted (object-based cueing costs), depending on the orientation of the rectangles. In particular, they found object-based cueing effects for a discrimination task only with horizontally oriented rectangles. Pilz et al. (2012; Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016) concluded that the object-based effects might depend on individual strategies and reflect advantages in directing attention along the horizontal meridian, instead of being caused by object-based attentional effects. Similarly, Harrison and Feldman (2009) also reported effects of rectangle orientation in a different object-based attention paradigm and proposed that so-called object-based effects could be due to a nonobject based horizontal advantage due to a facilitation of symmetry detection across the vertical meridian that might be related to particular attentional scanning strategies (see also Davis & Holmes, 2005).

Together, these studies strongly question whether object-based cueing effects are really object-based (i.e., dependent on the distribution of attention across objects) or merely a by-product of spatial attention, as, for example, a facilitated attentional shift along the horizontal meridian (Harrison & Feldman, 2009; Pilz et al., 2012). Al-Janabi and Greenberg (2016) looked at this question by calculating a meridian control difference score that takes into account only attentional shifts along the vertical meridian and is thus not affected by the horizontal meridian effect. In particular, they compared response latencies at the invalid-same object location for vertically oriented rectangles with latencies at the invalid-different object location for horizontally oriented rectangles (Fig. 1, left displays). They found a significant difference between the two conditions of about 20 ms that suggests the existence of a real object-based contribution to the object-based cueing effects.

The aim of this study was to further test the object-based account of the object-based cueing effect by examining the influence of rectangle similarity and rectangle orientation on it. In particular, we used rare color (Exp. 1), color (Exp. 2A), and shape (Exp. 2B) to make the two rectangles appear more or less similar to each other, as similarity is known to affect how elements are grouped together (Wertheimer, 1923): The more dissimilar the objects are, the more likely it is that different perceptual groups are represented. The idea was that “true” object-based attentional effects should be modulated by this manipulation: The more distinct the objects were perceived from each other, the stronger the object-based cueing effects should be independent of rectangle orientation. A non-object-based explanation purely in terms of horizontal meridian effects (Harrison & Feldman, 2009; Pilz et al., 2012), on the other hand, would not predict any effect of object similarity on rectangle orientation.

Experiment 1 (Rare color dissimilarity)

To investigate whether object similarity can influence rectangle orientation effects, we used color in the first experiment to make the two objects less similar from each other. We used the classic two-rectangle method introduced by Egly et al. (1994), but changed two things. First, instead of using a simple detection paradigm, we used a discrimination task developed by Moore et al. (1998) to maximize potential effects by increasing the difficulty of the task. Participants had to decide as fast as possible which of the two potential target letters (T or L) was presented in one of the rectangle corners. The target letter was always presented together with the distractor letter F at all the other corners. Second, object similarity was manipulated by presenting one of the two objects in 33% of the trials in a dissimilar color (green among blue or blue among green rectangles). If the object-based cueing effects dependent on the object itself, we expected to find larger object-based cueing effects in the dissimilar color condition than in the similar color condition for both rectangle orientations, as the dissimilar color of the rectangles should increase the likelihood that two separate rectangle representations were formed, which should impede attentional shifts between objects. On the other hand, if one assumes that object-based cueing effects were solely due to attentional meridian effects (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012), the similarity of the rectangles should not affect the object-based cueing effects no matter what orientation the rectangles have.

Method

Participants

Twenty-four volunteers (mean age = 24 years; range: 18–43 years) participated in the experiment. All participants had normal or corrected-to-normal vision and were unaware of the purpose of the study. They were mostly students of the University of Tübingen and either received a monetary compensation of €8 or course credit for their participation in the study. One participant had to be replaced because of many key presses of other than the response keys.

Apparatus

Participants were seated in front of the screen with a viewing distance of about 65 cm in a dimly illuminated cabin. The experiment was presented on a 20-in. color CRT monitor (IIyama Vision Master Pro 514 driven by a NVIDIA NVS 300 graphics card, NVIDIA Inc., Santa Clara, CA) with a screen resolution of 1024 × 768 pixels and a refresh rate of 100 Hz. MATLAB software (Version 2012b, MathWorks, Natick, MA) in combination with the Psychtoolbox-3 extensions (Brainard, 1997; Pelli, 1997) was used to present the stimuli and collect responses, which were given via the computer keyboard.

Stimuli

The displays consisted of two rectangles (each subtending 9.15° × 1.32°) that were presented either to the left and right or above and below a central fixation cross (0.62° × 0.62°, gray with a luminance of 35 cd/m2; see Fig. 2a). All stimuli were presented on a white background (0.9 kcd/m2). The distance between the two rectangles corresponded to their height (i.e., rectangles centers were separated by 7.83°), such that the distance between stimuli presented in the corners within the same rectangle or within two different rectangles was the same. Depending on the object similarity condition, both rectangles were either presented in the same color (similar color condition) or in two different colors (dissimilar color condition): green (72 cd/m2) and blue (12 cd/m2 ). We used the letters T and L as target letters and the letter F as distractor letter. Each letter was 0.79° high and 0.62° wide. All letters were black (1.3 cd/m2) and were presented in the corner of the rectangles. They could be oriented in one of four different orientations, tilted by 0°, 90° to the left or the right, and 180°. To cue a location, one corner of the rectangle (1.32° × 1.32°) disappeared and reappeared.

Fig. 2
figure 2

Different displays used in Experiments 1, 2A, and 2B. Depending on the object similarity condition, both rectangles either were similar or dissimilar in color (Exps. 1 and 2A) or shape (Exp. 2B). (Color figure online)

Full size image

Procedure

At the beginning of the experiment, participants were informed about the general purpose and procedure of the experiment and asked to give their informed consent. Next, written instructions about the experiment were given, followed by 20 practice trials, after which questions could be asked. The entire experimental session lasted about 1.5 h.

Figure 3 illustrates the general trial sequence. Each trial started with the presentation of the fixation cross and the two rectangles (fixation display), oriented horizontally or vertically for 1,000 ms. Next, one of the four rectangle corners disappeared for 100 ms in order to cue that location. After that, the fixation display reappeared again for another 200 ms. This was followed by the target display with the target letter and the three distractor letters. The target display was presented until the participant pressed a response key. The task of the participants was to decide as quickly and as correctly as possible whether the target letter was a T or L, independent of the orientation of the letter. Participants used the f and j keys on the computer keyboard for indicating their answer. Which key indicated which target letter was counterbalanced across participants, and a sign was placed below the computer screen to indicate the correct mapping throughout the experiment. If the response was incorrect an error message was presented for 1,500 ms. The next trial started after a blank intertrial interval of a random duration between 500 and 2,000 ms. Participants were asked to maintain fixation throughout the trial. Every 45 trials a break was provided, and participants got a feedback on their performance during that block (mean reaction time and percentage correct). Participants were encouraged to use these breaks between trials to relax.

Fig. 3
figure 3

General trial sequence. Illustrated is an example of vertically presented rectangles with a cue in the upper left corner of the left rectangle and the target L. Not represented is the feedback display at the end of each incorrect trial as well as the intertrial interval (ITI). (Color figure online)

Full size image

Design

The cue appeared equally often in any of the four rectangle corners and was valid in 60% of the trials; each of the two invalid conditions was presented in 20% of the trials. The main color, that is, the color in the similar color condition (blue or green) was counterbalanced across participants. Both rectangles were presented in 67% of the trials in the similar color and in 33% in dissimilar colors, the cued rectangle being in half of these trials the main color (dissimilar main color condition) and in the other half the other (rare) color (dissimilar rare color condition). Depending on the cueing condition, the target letter appeared either in the same location as the cue (valid condition) or at one of two other locations, either within the cued rectangle (invalid-same condition) or in the corner of the other rectangle that was closest to the cue (invalid-different condition). The rectangle orientation was counterbalanced across trials. We combined three cue validity conditions (valid, invalid-same, invalid-different) with three object similarities (similar color, dissimilar main color, dissimilar rare color), two rectangle orientations (horizontal, vertical), four cue locations (upper left, lower left, upper right, lower right corner), and two target letters (T, L). This combination resulted in an overall 1,440 trials (864 valid, 288 invalid-same, 288 invalid-different trials; 960 similar color, 480 dissimilar color trials) per participant, which were presented in 32 experimental blocks of 45 trials each.

Because we were interested in the contribution of object-based and non-object-based attentional effects to the object-based cueing effects, we conducted separate ANOVAs to measure object- and space-based cueing effects. The space-based effect was defined as the difference between the valid and the invalid-same condition, in which no object border has to be crossed.Footnote 1 The object-based effect was defined as the difference between the invalid-same and invalid-different condition, in which a target was presented equidistant to the cued location, but an object border crossing was or was not required.

Results

Responses that did not match one of the two response keys, as well as anticipatory reactions (RT shorter than 150 ms) and misses (RT longer than 2000 ms), were discarded prior to the analyses (0.09% too fast and 0.43% too long). The statistic software R (R Development Core Team, 2008) and in particular the library “ez” (Lawrence, 2011) was used to analyze the data. Whenever necessary, Greenhouse–Geisser corrections were used to account for violations of the sphericity assumption. For all three experiments, mean correct reaction times (RT) and mean percentage correct (PC) were computed separately for each condition.

Space-based effect

We first conducted an ANOVA with the within-factors cue validity (valid, invalid-same), object similarity (similar color, dissimilar main color, dissimilar rare color), and rectangle orientation (horizontal, vertical). The analysis of PC revealed a main effect for cue validity, F(1, 23) = 31.13, p < .001, η2 = .58, as PC were higher in the valid (M = 96%) than in the invalid-same condition (M = 92%), as expected for a space-based cueing effect (e.g., Moore et al., 1998). No other significant main effects or interactions were observed, Fs < 0.71, ps > .45.

Analysis of RT also showed a main effect of cue validity, F(1, 23) = 70.49, p < .001, η2 = .75, RTs being much faster in the valid condition (M = 546 ms) than in the invalid-same condition (M = 651 ms; see Fig. 4), again as expected for a space-based cueing effect. The analysis showed no main effect for object similarity, F(2, 46) = 0.26, p = .68, but a main effect of rectangle orientation, F(1, 23) = 20.87, p < .001, η2 = .48, with RT being faster for horizontal rectangles (M = 593 ms) than for vertical rectangles (M = 606 ms). Interestingly, the space-based cueing effect was modulated by rectangle orientation, F(1, 23) = 19.80, p < .001, η2 = .46, as the cueing effect was larger for vertical than for horizontal rectangles (see Fig. 5a, left graph). The analysis also revealed a significant interaction between rectangle orientation and object similarity, F(2, 46) = 5.14, p = .023, η2 = .18, but no interaction between cue validity and object similarity, F(2, 46) = 1.02, p = .37, and no three-way interaction between cue validity, object similarity and rectangle orientation, F(2, 46) = 3.30, p = .13.

Fig. 4
figure 4

Results of Experiment 1 (rare color). The left graph shows mean reaction time (RT) as a function of cue validity (valid, invalid-same, and invalid-different) and object similarity (similar color, dissimilar main color, and dissimilar rare color) for horizontally oriented rectangles. The right graph shows again RT as a function of cue validity and object similarity, but for vertically oriented rectangles. The error bars correspond to the standard error computed for within-participants designs (Loftus & Masson, 1994). (Color figure online)

Full size image

To estimate the influence of object similarity for the different orientations, horizontal and vertical rectangle orientations were analyzed separately. The space-based cueing effect was reliable for both, for horizontal, F(1, 23) = 60.99, p < .001, η2 = .73, as well as for vertical rectangles, F(1, 23) = 71.38, p < .001, η2 = .76. It was, however, not influenced by object similarity for horizontal or vertical rectangles, as we found no significant interaction between cue validity and object similarity for both, horizontal rectangles, F(2, 46) = 1.97, p = .15, and vertical rectangles, F(2, 46) = 1.52, p = .23. Moreover, we found a significant effect of object similarity for horizontal, F(2, 46) = 4.18, p = .038, η2 = .15, but not for vertical rectangles, F(2, 46) = 1.02, p = .34. Post hoc analyses (Holm-corrected p values) revealed that for horizontal rectangles RT in the similar color condition (M = 593 ms) were significantly slower than in the dissimilar main color condition (M = 584 ms), t(23) = 2.15, p = .010. In addition, responses in the dissimilar main color condition were significantly faster than in the dissimilar rare color condition (M = 601), t(23) = -2.27, p = .010, but there was no significant difference between the same color and the dissimilar rare color condition, t(23) = -1.50, p = .15.

Fig. 5
figure 5

Cueing effects for Experiment 1 (rare color) and 2 (color/shape). Asterisks represent significant effects and asterisks in parentheses represent trends. The interactions between cueing effect and rectangle orientation are not depicted. A The left graph shows the space-based cueing effects (difference between invalid-same and valid condition) as a function of object similarity (similar color, dissimilar main color, dissimilar rare color) and rectangle orientation (horizontal, vertical). The right graph shows the object-based cueing effects (difference between invalid-different and invalid-same condition) as a function of object similarity and rectangle orientation. Error bars represent the standard error computed for within-participants designs (Loftus & Masson, 1994). B Meridian control scores for horizontal attentional shifts across the vertical meridian (vertical meridian score) and for vertical attentional shifts across the horizontal meridian (horizontal meridian score) in Experiment 1. See Fig. 1 and the main text for more explanations. C The left and right graph show the space-based and object-based cueing as a function of object similarity (similar object, dissimilar object) and rectangle orientation (horizontal, vertical) for Experiment 2. Error bars represent the standard error computed for within-participants designs (Loftus & Masson, 1994). D Meridian difference scores in Experiment 2. (Color figure online)

Full size image

Object-based cueing effect

We first conducted an ANOVA with the within factors cue validity (invalid-same, invalid-different), object similarity (similar color, dissimilar main color, dissimilar rare color), and rectangle orientation (horizontal, vertical). Participants were very accurate overall (M > 91%) and no significant effects for PC were found, Fs < 1.68, ps > .21.

RT analysis revealed a main effect for cue validity, F(1, 23) = 24.82, p < .001, η2 = .52. In particular, RTs were significantly faster in the invalid-same (M = 651 ms) than in the invalid-different condition (M = 671 ms), as one would expect for an object-based cueing effect (see Fig. 4). We also observed a main effect of object similarity, F(2, 46) = 3.32, p = .045, η2 = .13, as RT were shorter in the similar color condition (M = 653 ms) than in the two dissimilar color conditions (dissimilar main M = 664 ms, dissimilar rare M = 666 ms), but there was no main effect of rectangle orientation, F(1, 23) = 2.15, p = .16. The object-based cueing effect was, however, strongly modulated by rectangle orientation, F(1, 23) = 15.42, p = .001, η2 = .40, being larger for horizontal than vertical rectangles (see Fig. 5a, right graph) and thus opposite to what we found for the space-based cueing effect. We also found a trend for a three-way interaction between cue validity, object similarity and rectangle orientation, F(2, 46) = 2.89, p = .065, η2 = .11, but no other interactions, Fs < 2.03, ps > .16.

To decompose the interactions, horizontal and vertical rectangle orientations were analyzed separately. The object-based cueing effect was only present for horizontal rectangles, F(1, 23) = 35.54, p < .001, η2 = .61, but not for vertical rectangles, F(1, 23) = 0.14, p = .72. Furthermore, the cueing effect was influenced by object similarity for horizontal, F(2, 46) = 4.55, p = .032, η2 = .17, but not for vertical rectangles, F(2, 46) = 1.32, p = .27. Separate analysis for each object similarity condition for horizontal rectangles revealed that the object-based cueing effect was significant in each of the three object similarity conditions, Fs > 19.59, ps <.001, η2 > .46. In addition, the object-based cueing effect was larger for the dissimilar main color than for the similar color condition, F(1, 23) = 12.67, p = .002, η2 = .36, but none of these two conditions was significantly different from the dissimilar rare color condition, Fs < 2.34, ps > .14. Although there was no significant interaction between cue validity and object similarity for vertical rectangles, by looking at Fig. 5a (right graph) it can be seen that the direction of cueing effects reversed in the similar color condition. An ANOVA for cue validity in the similar color condition suggests the presence of an object-based cueing cost, F(1, 23) = 8.89, p = .007, η2 = .28, which was absent for the two dissimilar color conditions, Fs < 0.88, ps > .36.

Meridian control score

Following Al-Janabi and Greenberg (2016), we also calculated a meridian control score to control for the potential effects of attentional shifts across the horizontal or vertical meridian. In particular, we separated conditions in which a vertical shift of attention was required from those in which a horizontal shift of attention was necessary. To obtain the horizontal meridian control score that only included vertical shifts of attention within and between objects we compared RT in the invalid-same condition for vertical rectangles with RT in the invalid different condition for horizontal rectangles, which directly corresponds to the meridian control difference score calculated by Al-Janabi and Greenberg (2016, see Fig. 1, left displays). Additionally we also calculated the opposite, a vertical meridian score that only included horizontal shits of attention within and between objects, comparing RT in the invalid-same condition for horizontal rectangles with RT in the invalid-different condition for vertical rectangles (see Fig. 1, right displays).

Using t tests, we then tested for the vertical meridian score (i.e., horizontal shifts of attention) as well as the horizontal meridian score (i.e., vertical shifts of attention) and each object similarity condition (similar color, dissimilar main color, dissimilar rare color) whether the score was significantly different from zero. For the vertical meridian control score, the dissimilar main color condition was significantly different from zero, t(23) = 3.28, p = .003, but the other two object similarity conditions were not, similar color, t(23) = 1.24, p = .23, and dissimilar rare color, t(23) = 1.63, p = .12 (see Fig. 5b, left). For the horizontal meridian control score, we found a trend only for the dissimilar rare color condition, t(23) = 2.04, p = .053, and no significant difference for the other two object similarity conditions, similar color, t(23) = -0.52, p = .61, and dissimilar main color, t(23) = 1.43, p = .17 (see Fig. 5b, right).

Discussion

The results of this experiment replicated earlier studies in two ways: First, we found strong space-based cueing effects for both rectangle orientations, reactions in the valid condition being always much faster and more accurate than in the invalid condition within the same object (Al-Janabi & Greenberg, 2016; Pilz et al., 2012). This space-based effect was more pronounced for vertically oriented rectangles than for horizontally oriented ones (Al-Janabi & Greenberg, 2016). Second, for the object-based cueing effects we found a strong effect of rectangle orientation, as this effect was present in its classic form for horizontally oriented rectangles (i.e., longer RT in the invalid-different than in the invalid-same condition), but not for vertically oriented rectangles, for which the effect was even reversed for the same color condition (i.e., an object-based cueing cost). These two observations fit well with the idea of a meridian facilitation effect of attention, which suggests that attention can be more easily oriented along a horizontal axis than along a vertical axis (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012). In particular, according to the meridian theory the space-based cueing effect should be larger for vertical than for horizontal rectangles, as the relevant comparison of conditions for the space-based effect is within rectangles (valid and invalid-same), and thus the necessary attentional shift would be along the horizontal axis for horizontal rectangles and along the vertical axis for vertical rectangles (see Fig., upper displays), leading to more difficult attentional shifts and thus larger cueing effects for vertically oriented rectangles. In contrast, the object-based cueing effect should be larger for horizontal than for vertical rectangles, as the relevant comparison of conditions is between rectangles (invalid-same and invalid-different), and, consequently, a horizontal attentional shift is necessary for vertical rectangles in the invalid-different condition, whereas a vertical attentional shift is required for horizontal rectangles (see Fig. 1, lower displays). This situation should lead to more difficult attentional shifts and thus a larger cueing effect for horizontally oriented rectangles. Moreover, this same mechanism could explain the occurrence of an object-based cost for vertically oriented rectangles if the horizontal shift of attention to the invalid-different condition is faster than the vertical shift of attention to the invalid-same condition due to the facilitation of the attentional shift along the horizontal meridian (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016).

Although the space-based cueing effect was not influenced by object similarity, the object-based cueing effect was larger in the dissimilar main color condition compared to the similar color condition for horizontally oriented rectangles. As can be seen in Fig. 4, this effect can be traced back to shortened invalid-same RT in the dissimilar main color condition and concurrent long invalid-different RT. Moreover, there was an object-based cueing cost for vertically oriented rectangles in the similar color conditions, but not in the dissimilar color conditions. Finally, the meridian differences scores (Al-Janabi & Greenberg, 2016) seemed also to be influenced by object similarity, as the dissimilar color conditions showed object-based effects whereas there were no such effects for the similar color condition, although the interaction between the factors did not reach significance. In particular we found a trend for an object-based attention effect for the dissimilar rare color condition for vertical shifts of attention whereas there was a significant effect for the dissimilar main color condition for horizontal shifts of attention. The observed differences between the two types of dissimilar color conditions suggest that the frequency of the color had an influence on the object-based cueing effects. Furthermore, the object-based effects were strongest for the horizontal rectangle condition and horizontal shifts of attention, and thus might be dependent on the fast shifts of attention along the horizontal meridian.

Taken together, the two effects, space-based and object-based, both seemed to be influenced by the rectangle orientation and the similarity of the objects. The effects are, however, variable and not very strong, and it is unclear whether the frequency of the color change plays an important role for this effect. In Experiments 2A and 2B we aim to exclude effects that could be caused by stimulus probability and thus present the properties of the different objects with comparable frequency.

Experiment 2A and 2B (Color/shape dissimilarity)

Experiments 2A and 2B were designed to see if the previously found influence of object similarity and rectangle orientation on the object-based cueing effects can be replicated for more frequent color changes and extended to another feature, object shape. To see whether the infrequency of the object is a necessary prerequisite to find an effect of object similarity, in Experiment 2A, the dissimilarly colored rectangles appeared in half of the trials; thus, the color change was not rare anymore (see Fig. 2b). In Experiment 2B, we used rectangles with little circular or rectangular parts attached to their sides to make them appear more or less similar (see Fig. 2c). Other than that, the experiment was identical to Experiment 2A.

Method

Except where noted, the method was the same as for Experiment 1.

Participants

For Experiment 2A (color) a new set of 24 participants (mean age = 23 years; range: 19–35 years) took part in the experiment. One of them had already participated in Experiment 1, but all others did not. One participant did not complete the experiment because of technical problems and was replaced. For Experiment 2B (shape), yet another set of 24 volunteers (mean age = 25 years; range: 18–32 years) participated in the experiment. None of the participants had participated in Experiment 1 or 2A. For both experiments, all participants but one were naïve concerning the goal of the study. All had normal or corrected-to-normal vision.

Stimuli

The stimuli for Experiment 2A were exactly the same as in Experiment 1. For Experiment 2B, instead of two dissimilar colors two dissimilar shapes were used. The rectangles had either circular or rectangular appendices that were oriented away from each other, leaving the entire surface of the rectangle intact (see Fig. 2c). This particular shape was used in order to have comparable letter discrimination conditions for the dissimilar shape conditions as for the other two experiments. The rectangles themselves were 9.41° × 1.76°. The extension (rectangular or circular) centered to the height of the rectangles was 1.67° wide (at the widest point) and 4.85° high. The centers of the two rectangles were presented 7.65° apart from each other.

Design

The design of Experiment 2A and 2B was similar to Experiment 1, except that the rectangles were presented in the similar color/shape in half of the trials and in dissimilar colors/shape in the other half of the trials. Thus, each of the four object similarity conditions (both rectangles similar color/shape: both blue/rectangular or both green/circular, both rectangles dissimilar color/shape: one rectangle blue/rectangular and one rectangle green/circular or vice versa) were presented in 25% of the trials. Because of this change, the number of trials per block was now 40, and the overall number of experimental trials for each participant was 1,280.

Results

As in Experiment 1, trials with wrong key presses as well as anticipatory reactions (RT shorter than 150 ms, 0.31%) and misses (RT longer than 2,000 ms) were discarded (0.14%). Mean reaction times (RT) and percentage correct (PC) were computed separately for each condition and participant. As in Experiment 1, separate ANOVAs were conducted for the valid and invalid-same cue validity condition on one hand (space-based effect) and the invalid-same and invalid-different cue validity condition on the other hand (object-based effect). As Experiment 2A and 2B were very similar, we first analyzed whether the pattern of results differed between experiments by producing interactions with the factor experiment (Exp. 2A, Exp. 2B). Because there were no theoretically meaningful interactions, in a second step, we clustered the two experiments together in order to increase the statistical power.

Space-based effect

We conducted an ANOVA with the within-factors cue validity (valid, invalid-same), object similarity (similar object, dissimilar object), and rectangle orientation (horizontal, vertical), and the between-factor experiment (Exp. 2A, Exp. 2B). PCs were as in Experiment 1 overall very high (M > 91.0%). The analysis of PC revealed an interaction between the factors cue validity, orientation, and experiment, F(1, 46) = 4.16, p = .047, η2 = .08, as the space-based cueing effect for Experiment 2A was significantly larger for vertical rectangles (M = 4.3%) than for horizontal rectangles (M = 2.9%), whereas for Experiment 2B the space-based cueing effect for both orientations was very similar (M = 2.3% for horizontal vs. M = 2.0% for vertical rectangles). No main effect for the factor experiment, F(1, 46) = 0.56, p = .46, nor any other significant interactions with the factor experiment were found, Fs < 0.97, ps > .33 for PC. For RT we found a trend for the factor experiment, F(1, 46) = 2.87, p = .097, η2 = .06, as RT were overall faster for Experiment 2A (M = 584 ms) than Experiment 2B (M = 623 ms), but the factor experiment did not interact with any other factor, Fs < 1.22, ps > .274.

We therefore conducted another ANOVA without the between-factor experiment using only the within-factors cue validity (valid, invalid-same), object similarity (similar object, dissimilar object), and rectangle orientation (horizontal, vertical). This ANOVA showed a significant space-based cueing effect for PC, F(1, 47) = 11.16, p = .002, η2 = .19, as participants were more accurate in the valid (M = 95.2%) than in the invalid-same condition (M = 92.3%). No other effects were significant, Fs < 1.64, ps > .21.

For RT the analysis showed again a significant space-based cueing effect, F(1, 47) = 120.28, p < .001, η2 = .72, RT being significantly faster in the valid (M = 561 ms) than in the invalid-same condition (M = 646 ms; see Fig. 6). In addition, we also found a main effect of rectangle orientation, F(1, 47) = 4.96, p = .031, η2 = .10, as RT were slightly faster for horizontal (M = 601 ms) than vertical rectangles (M = 606 ms), but no effect for object similarity, F(1, 47) = 2.62, p = .112. Interestingly, the space-based cueing effect was as in Experiment 1 modulated by rectangle orientation, F(1, 47) = 21.76, p < .001, η2 = .32. As Fig. 5c (left graph) shows, the cueing effect was again larger for vertical than for horizontal rectangles.

Fig. 6
figure 6

Results of Experiment 2 (color/shape). The left and right graph show mean reaction time (RT) as a function of cue validity (valid, invalid-same, and invalid-different) and object similarity (similar object and dissimilar object) for horizontally and vertically oriented rectangles in Experiment 2. The error bars correspond to the standard error computed for within-participants designs (Loftus & Masson, 1994). (Color figure online)

Full size image

Separate analysis for each rectangle orientation confirmed that the space-based cueing effect was significant for both horizontal, F(1, 47) = 101.30, p < .001, η2 = .68, as well as vertical rectangles, F(1, 47) = 120.13, p < .001, η2 = .72. Moreover, there was an interaction between object similarity and rectangle orientation, F(1, 47) = 5.41, p = .024, η2 = .10, suggesting that the two rectangle orientation conditions were only different in the similar object condition (M = 600 ms for horizontal, M = 610 ms for vertical rectangle), but not in the dissimilar object condition (M = 602 ms for both rectangle conditions). No other significant interactions were found, Fs < 0.66, ps > .42.

Object-based effect

As for the space-based effect, we again first conducted an ANOVA with the within factors cue validity (invalid-same, invalid-different), object similarity (similar object, dissimilar object), and rectangle orientation (horizontal, vertical), and the between factor experiment (Exp. 2A, Exp. 2B). The analysis for PC showed a trend only for the interaction between experiment and cue validity, F(1, 46) = 3.63, p = .063, η2 = .07, as the object-based cueing was somewhat larger in experiment 2A (M = 1.4 %) than in experiment 2B (M = 0.2 %). There was no main effect of experiment, F(1, 46) = 1.26, p = .27, and no interactions between the factor experiment and any other factor, Fs < 1.14, ps > .29. For RT there was a trend for the factor experiment, F(1, 46) = 3.83, p = .056, η2 = .08, as RT were again faster for Experiment 2A (M = 628 ms) than Experiment 2B (M = 676 ms), but no interactions between this factor and any other factors, Fs < 1.93, ps > .17.

We therefore eliminated the between-factor experiment and conducted an ANOVA using only the within-factors cue validity (invalid-same, invalid-different), object similarity (similar object, dissimilar object), and rectangle orientation (horizontal, vertical). This analysis revealed a significant object-based cueing effect for PC, F(1, 47) = 5.81, p = .020, η2 = .11, as participants responded more accurately in the invalid-same (M = 92.3 %) than in the invalid-different condition (M = 91.5 %). In addition, there was a trend for an interaction between cue validity and object similarity, F(1, 47) = 3.05, p = .087, η2 = .06, as the object-based cueing effect was a little bit larger for dissimilar (M = 1.4 %) than for similar objects (M = 0.1%). All other factors were not significant, Fs < 1.44, ps > .24.

Analysis of RT also revealed a significant object-based cueing effect, F(1, 47) = 13.58, p = .001, η2 = .22, as RTs were significantly faster in the invalid-same (M = 646 ms) than the invalid-different condition (M = 658 ms; see Fig. 6). In addition, there was a main effect of object similarity, F(1, 47) = 4.25, p = .045, η2 = .08, as RTs were significantly faster in the similar object condition (M = 650 ms) compared to the dissimilar object condition (M = 655 ms). There was no main effect for rectangle orientation, F(1, 47) = 0.49, p = .49, but the object-based cueing effect was again influenced by rectangle orientation, F(1, 47) = 29.49, p < .001, η2 = .39, being as in Experiment 1 larger for horizontal than for vertical rectangles (see Fig. 5c, right graph).

Separate analyses for horizontal and vertical rectangle orientations indicated that the cueing effect was reliable for horizontal, F(1, 47) = 32.51, p < .001, η2 = .41, but not for vertical rectangles, F(1, 47) = 2.58, p = .115; see Fig. 5c (right graph). Most important, the object-based cueing effect was additionally influenced by object similarity, F(1, 47) = 19.97, p < .001, η2 = .30. Separate analyses for the two object similarity conditions indicated that it was present in the dissimilar object condition, F(1, 47) = 22.62, p < .001, η2 = .32, but not in the similar object condition, F(1, 47) = 0.49, p = .49. Even though the absence of the three-way interaction between object-based cueing, object orientation, and object similarity, F(1, 47) = 0.45, p = .51, suggests a similar RT pattern for horizontal-and vertical-oriented rectangles, Fig. 5c (right graph) conveys another impression. To account for the negative object-based cueing effect in the similar object vertical orientation condition, which was not caught by our factorial design, we conducted separate analyses for horizontal and vertical rectangle orientations and investigated how the object-based cueing effect was influenced by similarity. These analyses showed that for horizontal rectangles, the object-based cueing effects were significant for both object conditions, similar object, F(1, 47) = 14.33, p < .001, η2 = .23, as well as dissimilar object, F(1, 47) = 37.75, p < .001, η2 = .45, whereas for vertical rectangles there was a reliable object-based cueing cost for the similar object condition, F(1, 47) = 12.43, p = .001, η2 = .21, but not for the dissimilar object condition, F(1, 23) = 0.78, p = .38. Finally, the object-based cueing effects were modulated by similarity for both rectangle orientations, horizontal, F(1, 47) = 7.73, p = .008, η2 = .14, as well as for vertical, F(1, 47) = 9.22, p = .004, η2 = .16. No other significant interactions were found, Fs < 1.77, ps > .19.

Meridian control score

As in Experiment 1, we calculated a meridian control score (Al-Janabi & Greenberg, 2016) to control for the potential effects of attentional shifts across the horizontal or vertical meridian. Again, separate t tests were conducted for the vertical meridian score (i.e., horizontal shifts of attention) as well as the horizontal meridian score (i.e., vertical shifts of attention) and each object similarity condition (similar color, dissimilar color). For the vertical meridian control score the dissimilar object condition was significantly different from zero, t(47) = 3.40, p = .001, but not the similar object condition, t(47) = 0.70, p = .49 (see Fig. 5d, left). For the horizontal meridian score, we found the same pattern of results, a significant difference from zero for the dissimilar object condition, t(47) = 4.17, p < .001, but not the similar object condition, t(47) = 0.21, p = .84 (see Fig. 5d, right).

Discussion

In line with Experiment 1, we found strong space-based cueing effects for both rectangle orientations. Again, the space-based effect was larger for vertical than for horizontal rectangles. We also found an effect of rectangle orientation for the object-based effect, as there was an object-based cueing effect for horizontal rectangles, but no overall effect for vertical rectangles. As explained before, these results support the attentional meridian theory (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012).

As in Experiment 1, the space-based cueing effect was not influenced by object similarity. Theoretically most important, the object-based effect still depended on object similarity in Experiment 2, and the way in which object similarity was manipulated seems not to influence the general pattern of results. In particular, we found object-based cueing effects for both object similarity conditions with horizontal rectangles, the effect being larger for rectangles presented in dissimilar colors/shapes than in the similar color/shape. For vertically oriented rectangles, however, we found an object-based cueing cost for the similar color/shape condition and no object-based effect for the dissimilar color/shape condition. As explained previously, these object-based cueing effects and costs can be explained by the attentional meridian theory (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012). The meridian differences scores (Al-Janabi & Greenberg, 2016) that allowed us to look at vertical and horizontal shifts of attention separately showed object-based effects for both vertical and horizontal shifts of attention, but only when the two objects were dissimilar in color/shape.

In summary, our results suggest that the rectangle-orientation effect can be influenced by the similarity of the objects using dissimilar colors or shapes, even if the dissimilarity of objects is not a rare event, as in Experiment 1. Moreover, the similarity of the objects strongly affects the meridian controlled object-based effect for both types of attentional shifts. These results are in line with the attentional meridian theory (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012), but also suggest the existence of a “true” object-based attentional component (Chen & Cave, 2006; Egly et al., 1994, Hollingworth et al., 2012; Richard et al., 2008), as will be discussed in more detail in the General Discussion.

General Discussion

This study investigated whether the object-based cueing effect (Egly et al., 1994) is caused by object-based attention or - in contrast to the original interpretation - rather by non-object-based attentional effects. In particular, as recent studies found that the object-based cueing effect is influenced by the particular way the object are oriented, it has been suggested that object-based cueing effects are not really due to attention selecting the objects, but rather due to attention being more easily shifted along the horizontal meridian (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz, et al., 2012). We manipulated the similarity of the two objects used in the standard two-rectangle paradigm (Egly et al., 1994), comparing conditions, in which both objects were presented either in similar or in dissimilar colors (Exps. 1 and 2A) or shapes (Exp. 2B). We expected object similarity to have an impact on the object-based cueing effect regardless of rectangle orientation if these effects were due to object-based attention, but not if they were due to attentional facilitation along the horizontal meridian. The idea behind this was that as the meridian effect does not rely on the object itself, it should be independent of factors manipulating the strength of the object representation. In contrast, real object-based effects should depend on the strength of the object representation: The more dissimilar the objects were from each other, the more likely it should have been that separate object representations of each object were created and thus that attention would be limited to one object instead of including both objects.

Our results were mixed: On one hand, we found that object-based cueing depended on the orientation of the rectangles, finding a classic object-based cueing effect for horizontally presented rectangles, and no effect or even an object-based cueing cost for vertically presented rectangles. Showing that the pattern of results varies substantially with the orientation of the rectangles is in line with the interpretation of a facilitation of attentional allocation along the horizontal meridian, which would increase RT in the invalid-different condition compared to the valid/invalid-same condition for horizontally oriented rectangles, but show just the opposite pattern for vertically oriented rectangles (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012). On the other hand, we found that the object-based effect cueing was modulated by object similarity: The cueing effect was larger and the object-based cost less strong when the two objects differed in their color or shape compared to when they were similar. It also didn’t matter how exactly we manipulated object similarity, as the effect was very similar in all three experiments, whether the manipulation was a rare or a frequent color change or even a shape change.

Interestingly, controlling for the potential effects of facilitated horizontal shifts of attention by calculating a meridian control score (Al-Janabi & Greenberg, 2016), we found object-based effects only in conditions in which the two objects were dissimilar and not when they were similar. Moreover, we found object-based effects for both, the vertical meridian score (i.e., horizontal shifts of attention) and the horizontal meridian score (i.e., vertical shifts of attention). These results suggest that the traditional object-based cueing effect might be to a large part due to the facilitation of attentional shifts along the horizontal meridian, while at the same time we could show that an object-based component exists, as long as the objects are clearly represented as different. The lack of any object-based effect in the similar object condition is in contrast to the findings of Al-Janabi and Greenberg (2016), who found evidence for object-based selection, even with similar objects (Exp. 2). It is possible that our dissimilarity manipulation caused not only the different objects to be represented more as separate entities but also that, at the same time, the similarity might have led to a more combined representation of the two entities as being two parts of one single object. Such a perceived contrast of the representations for similar and dissimilar entities might have eliminated potential object-based effects in the similar object condition.

To account for the overall pattern of results of this study, we suggest that despite a strong non-object-based component of the object-based cueing effect, there is an object-based component that usually is concealed by the meridian effect, but starts to get visible if the object representation is strong enough, as, for example, when the objects are dissimilar, as in our study. In particular, the meridian effect and the object effect work in the same direction for horizontally oriented rectangles, and thus we can see an increase in the size of the cueing effect when the two rectangles are dissimilar in color or shape than when they are similar. For vertically oriented rectangles, on the other hand, the meridian effect and the object effect go in opposite directions. Thus, evidence for the object-based component can only be seen when the size of the object effect is large enough to override the meridian effect. Indeed, when both rectangles differed in their color/shape, the object-based cueing cost found for conditions when both rectangles were similar was eliminated (and numerically even positive). Thus, when the rectangles are perceived as dissimilar from each other, the object-based effect starts to get strong enough to overcome the meridian effect that goes in the opposite direction. This interpretation is supported by the meridian control scores that show object-based effects for horizontal as well as vertical shifts of attention, but only in the dissimilar object conditions.

Recently, Roque and Boot (2015) suggested that the concreteness or realism of the object might play a role in the object-based cueing effect and might be responsible for the different sizes of object-based effects reported in different studies. To investigate this proposition, they manipulated the concreteness of the object by comparing object-based cueing effects for black and white photorealistic pictures of a spoon, vectorized pictures of the same images that conserved the shape and shading of the original image, and a rectangle that only conserved the shading of the vector image. They could not find any effect of the realism of the objects on the object-based cueing effect. In a second experiment, they made the objects dissimilar from each other, using photorealistic images of a spoon and a fork together. Again they did not find any object-based cueing effects. These findings suggested that object similarity does not play a role for object-based cueing effects and is thus in contrast with our findings. The authors, however, did not compare their spoon–fork condition directly with a spoon–spoon or fork–fork condition. It is possible that the dissimilarity of the objects needs to be apparent by comparing it to a similar object condition to show an effect of object similarity.

As mentioned in the introduction, Shomstein and Behrmann (2008, Exp. 4) also used dissimilarly colored rectangles to strengthen the object representation of the rectangles in a way similar to how we did in this study. They found strong object-based cueing effects for dissimilarly colored rectangles compared to no object-based cueing effects with rectangle outlines or with rectangles filled with the similar color. Based on these results, Shomstein and Behrmann (2008) suggested that if the object representation is sufficiently robust (e.g., using dissimilar colors), evidence for object-based attention can be found. In particular, the cue might not only cue a location but also a color, and shifting attention from one color to another could be more difficult than shifting attention within the similar color. Their study, however, differed from our study in several ways: In Shomstein and Behrmann’s study (2008), rectangle orientation was blocked across participants, which means that they were not able to directly investigate the influence of object similarity on rectangle orientation. Furthermore, Shomstein and Behrmann (2008) used a particular modification of the Egly et al. (1994) two-rectangle method, in which the probability that a target would appear in one of the two invalid conditions (invalid-same and invalid-different) was manipulated, being either 41.7% or 8.3% (with probability condition counterbalanced across participants). It is possible that this probability manipulation might have engaged different, more endogenous attentional mechanisms than in the usual two-rectangle paradigm, which might in turn differentially affect object-based cueing effects. Thus, our study allows a number of new insights: For one, we can show that dissimilarly colored objects strengthen object-based cueing effects, even when the invalid conditions have the same probability as in the classic two-rectangle paradigm. We also show that the outline difference of objects can be enough to strengthen the object representation, when similar colored and dissimilarly colored objects are presented within the same experiment. In addition, our results suggest that shape can have a similar effect as color. Finally, they show that the effect of the strength of the object representation can influence the rectangle orientation effect.

In summary, our study supports the notion that attention can be oriented toward entire objects and that the object-based cueing effects found with the Egly et al.’s (Egly et al. 1994) two-rectangle method can reflect this object-based attention mechanism, as we could find object-based effects with dissimilar objects for both rectangle orientations. Our results also show, however, that object-based attentional selection strongly depends on how much the objects presented on the screen are represented as separate or not. The existence of an object-based attention component would be consistent with recent studies showing lexical-based object effects using Chinese characters (Li & Logan, 2008; Liu, Wang, & Zhou, 2011) or with studies showing object-based attention effects in other paradigms than cueing paradigms (e.g., Duncan, 1984; Kramer & Jacobson, 1991) that are difficult to explain with non-object-based attentional effects alone as the attentional meridian effect (Al-Janabi & Greenberg, 2016; Barnas & Greenberg, 2016; Harrison & Feldman, 2009; Pilz et al., 2012). It is, however, also obvious from our study that the object-based cueing effect can be contaminated in large part by effects that are not object related, supporting studies that show how much the object-based cueing effect is dependent on many different factors, including the orientation of the rectangles (Al-Janabi & Greenberg, 2016; Pilz et al., 2012). Thus, it might be more reasonable to employ other paradigms when investigating object-based attention, as, for example, paradigms that rely on the flanker compatibility effect developed by Eriksen and Eriksen (1974, e.g., Driver & Baylis, 1989; Kramer & Jacobson, 1991) and that are not dependent on the shifting of attention to locations with a cue, or with paradigms, in which the configuration of elements itself attracts attention as demonstrated in the studies by Kimchi and colleagues (e.g., Kimchi, Yeshurun, & Cohen-Savransky, 2007; Kimchi, Yeshurun, Spehar, & Pirkner, in press). At the very least, future studies need to control for the orientation of the objects to ensure that it is not the spatial layout of cue and target instead of the object structure that drive the observed effects.