2D Phase-Based RFID Localization for On-Site Landslide Monitoring
Abstract
:1. Introduction
2. Instrumentation and Methods
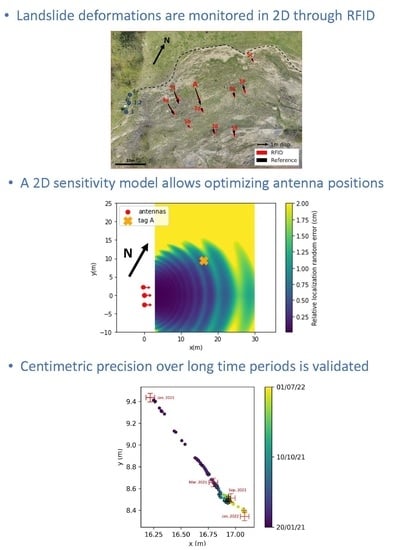
2.1. Experimental Site: Harmalière Landslide
2.2. RFID Instrumentation and Localization
2.2.1. RFID Instrumentation
2.2.2. RFID Localization Scheme
3. Theoretical Model
3.1. Localization Model
3.1.1. One Dimensional TD-PD
3.1.2. 2D Relative Displacement Approach
3.2. Geometrical Localization Sensitivity
3.3. Phase Error Model: Multipath, Phase Standard Deviation and Radiation Pattern
3.3.1. Multipath Propagation Model
3.3.2. Two Types of Phase Error
4. Harmalière Landslide Monitoring
4.1. Real Phase Data
4.2. Application of the Model to a Real Geometry
4.2.1. Random Localization Error of the Experimental Field
4.2.2. Systematic Localization Bias of the Experimental Field
- The direction that produces the least bias variation is a displacement, which corresponds to the quasi rotational symmetry of the system.
- A horizontal displacement along yields a small localization error. This confirms previous studies and demonstrates a centimeter precision for the RFID technique in the horizontal plane [18].
- A vertical displacement along undergoes several strong bias oscillations (Figure 5c). The subsequent localization error is a cumulative effect of both the strong multipath interference and the small vertical aperture of the measurement system.
| Dir. | ||||
|---|---|---|---|---|
| Bias | ||||
| max. bias | <1 cm | <1 cm | 10 cm | |
| (1 cm ) | (20 cm) | |||
| max. bias | 1 cm | 1 cm | 2 cm | |
| (1 cm) | (15 cm) | |||
| max. bias | 1 cm | <1 cm | 70 cm | |
| (5 cm) | (110 cm) | |||
4.3. Surface Displacement Monitoring Results
4.3.1. 2D Relative Displacement for One Tag
4.3.2. 2D Localization for All Tags
4.4. Discussion
4.5. Localization Error and Reference Measurements
4.5.1. Discussion on Antenna Position
4.5.2. Perspective for Improving Data Availability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote sensing for landslide investigations: An overview of recent achievements and perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Lu, Z. Remote sensing of landslides—A review. Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef] [Green Version]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Strozzi, T.; Farina, P.; Corsini, A.; Ambrosi, C.; Thüring, M.; Zilger, J.; Wiesmann, A.; Wegmüller, U.; Werner, C. Survey and monitoring of landslide displacements by means of L-band satellite SAR interferometry. Landslides 2005, 2, 193–201. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-based differential interferometry SAR: A review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 43–70. [Google Scholar] [CrossRef]
- Tarchi, D.; Casagli, N.; Fanti, R.; Leva, D.D.; Luzi, G.; Pasuto, A.; Pieraccini, M.; Silvano, S. Landslide monitoring by using ground-based SAR interferometry: An example of application to the Tessina landslide in Italy. Eng. Geol. 2003, 68, 15–30. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef] [Green Version]
- Helmstetter, A.; Garambois, S. Seismic monitoring of Séchilienne rockslide (French Alps): Analysis of seismic signals and their correlation with rainfalls. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Aryal, A.; Brooks, B.A.; Reid, M.E.; Bawden, G.W.; Pawlak, G.R. Displacement fields from point cloud data: Application of particle imaging velocimetry to landslide geodesy. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Benoit, L.; Briole, P.; Martin, O.; Thom, C.; Malet, J.P.; Ulrich, P. Monitoring landslide displacements with the Geocube wireless network of low-cost GPS. Eng. Geol. 2015, 195, 111–121. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.; Jiang, S.H.; Huang, F.; Chang, Z. A web-based GPS system for displacement monitoring and failure mechanism analysis of reservoir landslide. Sci. Rep. 2017, 7, 17171. [Google Scholar] [CrossRef] [Green Version]
- Šegina, E.; Peternel, T.; Urbančič, T.; Realini, E.; Zupan, M.; Jež, J.; Caldera, S.; Gatti, A.; Tagliaferro, G.; Consoli, A.; et al. Monitoring Surface Displacement of a Deep-Seated Landslide by a Low-Cost and near Real-Time GNSS System. Remote Sens. 2020, 12, 3375. [Google Scholar] [CrossRef]
- Dong, M.; Wu, H.; Hu, H.; Azzam, R.; Zhang, L.; Zheng, Z.; Gong, X. Deformation prediction of unstable slopes based on real-time monitoring and deepar model. Sensors 2020, 21, 14. [Google Scholar] [CrossRef]
- Intrieri, E.; Gigli, G.; Gracchi, T.; Nocentini, M.; Lombardi, L.; Mugnai, F.; Frodella, W.; Bertolini, G.; Carnevale, E.; Favalli, M.; et al. Application of an ultra-wide band sensor-free wireless network for ground monitoring. Eng. Geol. 2018, 238, 1–14. [Google Scholar] [CrossRef]
- Mucchi, L.; Jayousi, S.; Martinelli, A.; Caputo, S.; Intrieri, E.; Gigli, G.; Gracchi, T.; Mugnai, F.; Favalli, M.; Fornaciai, A.; et al. A flexible wireless sensor network based on ultra-wide band technology for ground instability monitoring. Sensors 2018, 18, 2948. [Google Scholar] [CrossRef]
- Schneider, J.M.; Turowski, J.M.; Rickenmann, D.; Hegglin, R.; Arrigo, S.; Mao, L.; Kirchner, J.W. Scaling relationships between bed load volumes, transport distances, and stream power in steep mountain channels. J. Geophys. Res. Earth Surf. 2014, 119, 533–549. [Google Scholar] [CrossRef]
- Breton, M.L.; Liébault, F.; Baillet, L.; Charléty, A.; Larose, E.; Tedjini, S. Dense and longdterm monitoring of Earth surface processes with passive RFID—A review. arXiv 2021, arXiv:2112.11965. [Google Scholar]
- Le Breton, M.; Baillet, L.; Larose, E.; Rey, E.; Benech, P.; Jongmans, D.; Guyoton, F.; Jaboyedoff, M. Passive radio-frequency identification ranging, a dense and weather-robust technique for landslide displacement monitoring. Eng. Geol. 2019, 250, 1–10. [Google Scholar] [CrossRef]
- Le Breton, M.; Baillet, L.; Larose, E.; Rey, E.; Benech, P.; Jongmans, D.; Guyoton, F. Outdoor uhf rfid: Phase stabilization for real-world applications. IEEE J. Radio Freq. Identif. 2017, 1, 279–290. [Google Scholar] [CrossRef]
- Le Breton, M. Suivi Temporel d’un Glissement de Terrain à l’Aide d’Étiquettes RFID Passives, Couplé à l’Observation de Pluviométrie et de Bruit Sismique Ambiant. Ph.D. Thesis, Université Grenoble Alpes (ComUE), Grenoble, France, 2019. [Google Scholar]
- Intrieri, E.; Gigli, G.; Mugnai, F.; Fanti, R.; Casagli, N. Design and implementation of a landslide early warning system. Eng. Geol. 2012, 147, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth-Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Balaji, R.; Malathi, R.; Priya, M.; Kannammal, K. A Comprehensive Nomenclature Of RFID Localization. In Proceedings of the 2020 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 22–24 January 2020; pp. 1–9. [Google Scholar]
- Miesen, R.; Ebelt, R.; Kirsch, F.; Schäfer, T.; Li, G.; Wang, H.; Vossiek, M. Where is the tag? IEEE Microw. Mag. 2011, 12, S49–S63. [Google Scholar] [CrossRef]
- Ni, L.M.; Liu, Y.; Lau, Y.C.; Patil, A.P. LANDMARC: Indoor location sensing using active RFID. In Proceedings of the 1st IEEE International Conference on Pervasive Computing and Communications, 2003.(PerCom 2003), Fort Worth, TX, USA, 23–26 March 2003; pp. 407–415. [Google Scholar]
- Subedi, S.; Pauls, E.; Zhang, Y.D. Accurate localization and tracking of a passive RFID reader based on RSSI measurements. IEEE J. Radio Freq. Identif. 2017, 1, 144–154. [Google Scholar] [CrossRef]
- Rohmat Rose, N.D.; Low, T.J.; Ahmad, M. 3D trilateration localization using RSSI in indoor environment. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 385–391. [Google Scholar]
- Martinelli, F. A robot localization system combining RSSI and phase shift in UHF-RFID signals. IEEE Trans. Control. Syst. Technol. 2015, 23, 1782–1796. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, Q.; Pang, J.; Xu, H.; Li, P. PRDL: Relative localization method of RFID tags via phase and RSSI based on deep learning. IEEE Access 2019, 7, 20249–20261. [Google Scholar] [CrossRef]
- Scherhäufl, M.; Pichler, M.; Stelzer, A. UHF RFID localization based on evaluation of backscattered tag signals. IEEE Trans. Instrum. Meas. 2015, 64, 2889–2899. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, N.; Malekian, R.; Xiao, F.; Wang, R. TrackT: Accurate tracking of RFID tags with mm-level accuracy using first-order taylor series approximation. Ad Hoc Netw. 2016, 53, 132–144. [Google Scholar] [CrossRef]
- Zhou, C.; Griffin, J.D. Accurate phase-based ranging measurements for backscatter RFID tags. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 152–155. [Google Scholar] [CrossRef]
- Li, C.; Mo, L.; Zhang, D. Review on UHF RFID localization methods. IEEE J. Radio Freq. Identif. 2019, 3, 205–215. [Google Scholar] [CrossRef]
- Huiting, J.; Flisijn, H.; Kokkeler, A.B.; Smit, G.J. Exploiting phase measurements of EPC Gen2 RFID tags. In Proceedings of the 2013 IEEE International Conference on RFID-Technologies and Applications (RFID-TA), Johor Bahru, Malaysia, 4–5 September 2013; pp. 1–6. [Google Scholar]
- Pelka, M.; Bollmeyer, C.; Hellbrück, H. Accurate radio distance estimation by phase measurements with multiple frequencies. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 142–151. [Google Scholar]
- Nikitin, P.V.; Martinez, R.; Ramamurthy, S.; Leland, H.; Spiess, G.; Rao, K. Phase based spatial identification of UHF RFID tags. In Proceedings of the 2010 IEEE International Conference on RFID (IEEE RFID 2010), Orlando, FL, USA, 14–16 April 2010; pp. 102–109. [Google Scholar]
- Povalac, A.; Sebesta, J. Phase difference of arrival distance estimation for RFID tags in frequency domain. In Proceedings of the 2011 IEEE International Conference on RFID-Technologies and Applications, Sitges, Spain, 15–16 September 2011; pp. 188–193. [Google Scholar]
- Scherhäufl, M.; Pichler, M.; Stelzer, A. UHF RFID localization based on phase evaluation of passive tag arrays. IEEE Trans. Instrum. Meas. 2014, 64, 913–922. [Google Scholar] [CrossRef]
- Buffi, A.; Nepa, P.; Cioni, R. SARFID on drone: Drone-based UHF-RFID tag localization. In Proceedings of the 2017 IEEE International Conference on RFID Technology & Application (RFID-TA), Warsaw, Poland, 20–22 September 2017; pp. 40–44. [Google Scholar]
- Buffi, A.; Motroni, A.; Nepa, P.; Tellini, B.; Cioni, R. A SAR-based measurement method for passive-tag positioning with a flying UHF-RFID reader. IEEE Trans. Instrum. Meas. 2018, 68, 845–853. [Google Scholar] [CrossRef]
- Motroni, A.; Nepa, P.; Magnago, V.; Buffi, A.; Tellini, B.; Fontanelli, D.; Macii, D. SAR-based indoor localization of UHF-RFID tags via mobile robot. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–8. [Google Scholar]
- Bernardini, F.; Buffi, A.; Motroni, A.; Nepa, P.; Tellini, B.; Tripicchio, P.; Unetti, M. Particle swarm optimization in SAR-based method enabling real-time 3D positioning of UHF-RFID tags. IEEE J. Radio Freq. Identif. 2020, 4, 300–313. [Google Scholar] [CrossRef]
- Gareis, M.; Fenske, P.; Carlowitz, C.; Vossiek, M. Particle filter-based SAR approach and trajectory optimization for real-time 3D UHF-RFID tag localization. In Proceedings of the 2020 IEEE International Conference on RFID (RFID), Orlando, FL, USA, 28 September–16 October 2020; pp. 1–8. [Google Scholar]
- Monjuvent, G. La transfluence Durance-Isère Essai de synthèse du Quaternaire du bassin du Drac’(Alpes françaises). Géol. Alp. 1973, 49, 57–118. [Google Scholar]
- Jongmans, D.; Bièvre, G.; Renalier, F.; Schwartz, S.; Beaurez, N.; Orengo, Y. Geophysical investigation of a large landslide in glaciolacustrine clays in the Trièves area (French Alps). Eng. Geol. 2009, 109, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Fiolleau, S.; Borgniet, L.; Jongmans, D.; Bièvre, G.; Chambon, G. Using UAV’s imagery and LiDAR to accurately monitor Harmalière (France) landslide evolution. In Geophysical Research Abstracts; European Geosciences Union: Munchen, Germany, 2019; Volume 21. [Google Scholar]
- Fiolleau, S.; Jongmans, D.; Bièvre, G.; Chambon, G.; Lacroix, P.; Helmstetter, A.; Wathelet, M.; Demierre, M. Multi-method investigation of mass transfer mechanisms in a retrogressive clayey landslide (Harmalière, French Alps). Landslides 2021, 18, 1981–2000. [Google Scholar] [CrossRef]
- Norrdine, A. An algebraic solution to the multilateration problem. In Proceedings of the 15th International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; Volume 1315. [Google Scholar]
- Conn, A.R.; Gould, N.I.; Toint, P.L. Trust Region Methods; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Van Loan, C.F. Generalizing the singular value decomposition. SIAM J. Numer. Anal. 1976, 13, 76–83. [Google Scholar] [CrossRef]
- Anton, H.; Rorres, C. Elementary Linear Algebra: Applications Version; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Golub, G.; Kahan, W. Calculating the singular values and pseudo-inverse of a matrix. J. Soc. Ind. Appl. Math. Ser. Numer. Anal. 1965, 2, 205–224. [Google Scholar] [CrossRef]
- Wang, G.; Qian, C.; Cui, K.; Shi, X.; Ding, H.; Xi, W.; Zhao, J.; Han, J. A Universal Method to Combat Multipaths for RFID Sensing. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 277–286. [Google Scholar]
- Faseth, T.; Winkler, M.; Arthaber, H.; Magerl, G. The influence of multipath propagation on phase-based narrowband positioning principles in UHF RFID. In Proceedings of the 2011 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications, Torino, Italy, 12–16 September 2011; pp. 1144–1147. [Google Scholar]
- Rembold, B. Optimum modulation efficiency and sideband backscatter power response of RFID-tags. Frequenz 2009, 63, 9–13. [Google Scholar] [CrossRef]
- ITU-R P. 523-7; Electrical Characteristics of the Surface of the Earth. ITU-R: Geneva, Switzerland, 1992.
- Lytle, R.J. Measurement of earth medium electrical characteristics: Techniques, results, and applications. IEEE Trans. Geosci. Electron. 1974, 12, 81–101. [Google Scholar] [CrossRef] [Green Version]
- Azzouzi, S.; Cremer, M.; Dettmar, U.; Kronberger, R.; Knie, T. New measurement results for the localization of uhf rfid transponders using an angle of arrival (aoa) approach. In Proceedings of the 2011 IEEE International Conference on RFID, Sitges, Spain, 15–16 September 2011; pp. 91–97. [Google Scholar]
- Sun, S.L.; Deng, Z.L. Multi-sensor optimal information fusion Kalman filter. Automatica 2004, 40, 1017–1023. [Google Scholar] [CrossRef]
- Sarkka, S.; Viikari, V.V.; Huusko, M.; Jaakkola, K. Phase-based UHF RFID tracking with nonlinear Kalman filtering and smoothing. IEEE Sens. J. 2011, 12, 904–910. [Google Scholar] [CrossRef]










| Antenna No. | x (m) | y (m) | z (m) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0.018 | −0.034 | 1.55 |
| 3 | 0.013 | −2.608 | 0.256 |
| 4 | −0.338 | 2.148 | 0.287 |
| (m) | 3 | ||
| (m) | 1 | ||
| Ground relative permittivity | 2.4 | ||
| Tag | 51 | A | 4e | 26 | 55 | 5f | 2d | 5c | 59 | 5b |
|---|---|---|---|---|---|---|---|---|---|---|
| Total disp (m) | 1.54 | 1.37 | 1.20 | 0.81 | 0.75 | 0.85 | 0.69 | 0.67 | 0.74 | 0.56 |
| Reference (m) | 1.57 | 1.45 | 1.28 | 0.81 | 0.79 | 0.74 | 0.77 | 0.74 | 0.72 | 0.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charléty, A.; Le Breton, M.; Larose, E.; Baillet, L. 2D Phase-Based RFID Localization for On-Site Landslide Monitoring. Remote Sens. 2022, 14, 3577. https://doi.org/10.3390/rs14153577
Charléty A, Le Breton M, Larose E, Baillet L. 2D Phase-Based RFID Localization for On-Site Landslide Monitoring. Remote Sensing. 2022; 14(15):3577. https://doi.org/10.3390/rs14153577
Chicago/Turabian StyleCharléty, Arthur, Mathieu Le Breton, Eric Larose, and Laurent Baillet. 2022. "2D Phase-Based RFID Localization for On-Site Landslide Monitoring" Remote Sensing 14, no. 15: 3577. https://doi.org/10.3390/rs14153577