Field Line Resonances and Cavity Modes at Earth and Jupiter

Introduction

Ultra-low-frequency (ULF) waves are ubiquitous in the magnetospheres of Earth and Jupiter, and their presence in other magnetized planets is very likely. These waves, defined at Earth as having periods from 0.2 to 600 s (e.g., Kivelson, 1995), play a major role in transporting energy and momentum throughout the magnetosphere, as well as mediating changes in the field-aligned currents. ULF waves are generally described using the theory of magnetohydrodynamics (MHD), which allows for three distinct wave modes, labelled the slow (or ion acoustic) mode, the intermediate (or shear Alfvén) mode, and the fast (or magnetosonic) mode. On a global scale, the slow mode does not play a major role, and so the rest of this review will concentrate on the Alfven and fast mode.

In MHD theory, the shear Alfvén mode is guided along the magnetic field, and carries a field-aligned current. This mode propagates along the field line at the Alfvén speed, defined as

where ω is the wave frequency, k_|| is the wave number along the magnetic field, B is the magnetic field strength and ρ is the mass density. On closed magnetic field lines, this wave can propagate from one ionosphere to the conjugate ionosphere forming a standing wave between the two ionospheres. When such a structure is excited by mode coupling from a fast mode wave, it is called a field line resonance (Chen and Hasegawa, 1974; Southwood, 1974). Since the magnetic field strength, the mass density, and the length of the field line vary from one field line to the next, this mode creates a range of frequencies that can be used as a proxy for the mass density along the field line. The study of these frequencies to determine the mass density has been termed “magnetoseismology” (e.g., Menk and Waters, 2013).

On the other hand, the fast mode propagates more isotropically, so that it is not guided along a field line, with a dispersion relation in a low-β plasma (with β = 2μ₀p/B² being the ratio of plasma pressure to magnetic field pressure) given by

Here k is the total wave number, k_⊥ is the perpendicular wave number and c_s is the sound speed. Since this mode can propagate in all directions, it will tend to fill up any regions of space. Due to the inhomogeneity of magnetospheric plasmas, this mode can form resonant cavities in regions where the plasma density is significantly different from the surrounding regions.

Since ULF waves have wavelengths that can be comparable to the size of the whole magnetosphere, the standard Wentzel-Kramers-Broulliin (WKB) theory (e.g., Stix, 1992), which implies that the wave propagates without reflection when the gradient scale length of the wave speed is much longer than the wavelength, is violated. In the limit of a discontinuous change in the Alfvén speed (for the shear mode) or the magnetosonic speed (for the fast mode), the reflection coefficient can be written as

Here V₁ is the wave speed in the incident region and V₂ is the wave speed in the outer region. In a similar manner, for reflections of shear Alfvén waves from the ionosphere, the reflection coefficient can be written as

where Σ_P is the Pedersen conductance and ${\Sigma }_A=1/{\mathrm{\mu }}_0{V}_A$ is sometimes called the “Alfvén conductance.” It should be noted that in the presence of a finite Hall conductance in the ionosphere, the Pedersen conductance in Equation 4 can be modified by a term describing the coupling of the shear Alfvén wave to the fast mode (e.g., Lysak and Yoshikawa, 2006).

Equations 3 and 4 indicate that the strongest reflections occur when the discontinuity in the wave speed is very large, or in the case of the ionosphere, if the Alfvén conductance is very different than to the Pedersen conductance. As a reference point, it can be noted that an Alfvén speed of 1,000 km/s corresponds to 0.796 mho, or a conductance of 1 mho corresponds to 796 km/s. Therefore, cavity modes and field line resonances can be excited with only weak damping when the contrast between the parameters of the two regions is strong.

Since the magnetic fields of Earth and Jupiter are relatively smooth in most regions, the strong gradients needed to provide a strong reflection of these modes mostly occur due to the change in density. The differences between the density structure of the two magnetospheres leads to differences in the types of modes they can support. In the next section of this review, we will discuss the density profiles for the two magnetospheres. Then in subsequent sections, we will discuss field line resonances and cavity mode structures in both magnetospheres. Finally we will introduce a new type of resonant mode that is unique to Jupiter, a shear Alfvén mode resonance in the low density region between the ionosphere and plasma sheet.

Density Structure of the Magnetospheres of Earth and Jupiter

Next, we discuss the density profiles at the two planets, working our way outward from the planet’s surface starting with the ionosphere. The ionosphere at Earth is very well studied through measurements from sounding rockets, radar measurements from the ground and low-Earth orbiting satellites (e.g., Kelley, 1989). The density in the ionosphere generally peaks at densities of 10⁵–10⁶ cm⁻³ at the peak of the F-layer, at about 200 km. There are large variations in these parameters due to sunlit vs dark conditions as well as effects due to magnetic storm activity in the magnetosphere. An empirical model including these variations is the International Reference Ionosphere (IRI; Bilitza et al., 2017; Alken et al., 2021). The ionosphere is largely populated by heavy ions such as O⁺ and NO⁺, with protons becoming the dominant ion at higher altitudes, above about 1,000 km.

The Jovian ionosphere is much less understood, since the measurement techniques listed in the previous paragraph are not possible. Radio occultation techniques have been used from both Voyager and Galileo, leading to similar densities of 10⁵–10⁶ cm⁻³ (e.g, McConnell et al., 1982; Hinson et al., 1997, 1998), while a more recent study by Mendillo et al. (2022) has indicated that peak densities are at 10⁵ cm⁻³. Measurements from the Microwave Radiometer instrument on Juno have suggested that even higher densities, up to 10⁹ cm⁻³ might be present (Hodges et al., 2020). Modeling results (e.g., Millward et al., 2002) are consistent with the lower densities. These results also indicate that at Jupiter, the dominant ion at altitudes below about 1,000 km is H₃⁺, which is an ion that can only exist under dense, cold conditions (e.g., Yelle and Miller, 2004). At higher altitudes, this ion dissociates and protons are the dominant ion.

Recent Juno measurements have provided measurements of the electron density in the topside ionosphere by using electromagnetic wave resonances (e.g., Elliott et al., 2021; Sulaiman et al., 2022). These measurements show that the plasma density is frequently below 100 cm⁻³ at radial distances below 2 R_J, and can reach values as low as 10^–2 cm⁻³. These measurements are supported by direct observations of the low energy plasma by the Juno Auroral Distributions Experiment (JADE) on Juno (Allegrini et al., 2021). Because of the strong Jovian magnetic field, which is the order of 1 G (or 100 μT) at 2 R_J, the Alfvén speed is essentially equal to the speed of light at this and higher altitudes. In the Earth’s auroral zone, the plasma density is also low, with densities less than 1 cm⁻³ at 2 R_E where the magnetic field is about 5 μT, which gives an Alfvén speed of about 100,000 km/s or one-third of the speed of light.

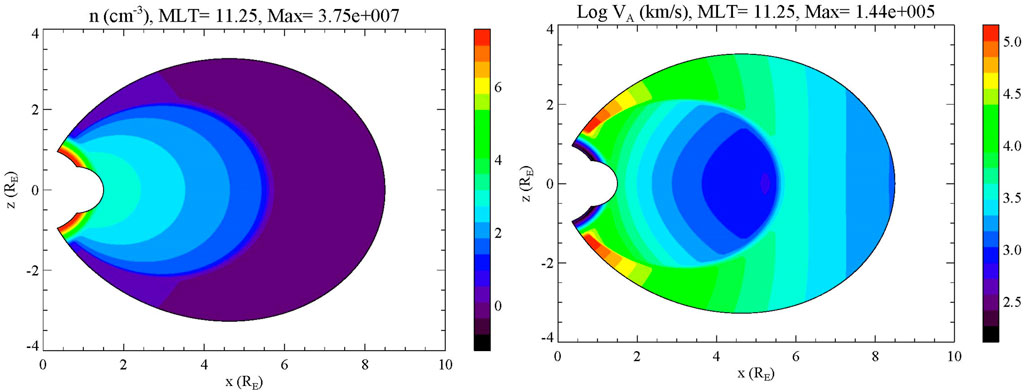
Another contrast is that Earth possesses a rather dense plasmasphere, which extends to about 4–6 R_E and has densities up to about 1,000 cm⁻³ (e.g., Gallagher et al., 2000, 2021). The plasmaspheric mass density can also be determined by considering the frequency of field line resonances, a research area known as magnetoseismology (e.g,. Takahashi and Anderson, 1992; Denton, 2006; Waters et al., 2006), which confirms these densities. The plasmasphere often has a rather sharp edge, the plasmapause, that can act to reflect fast mode waves (as described above), forming cavity mode resonances in the plasmasphere (Waters et al., 2002; Takahashi et al., 2018), sometimes called virtual resonances since the plasmapause is not a perfect reflector (Lee, 1998). A density model for the dipole regions of Earth’s magnetosphere is given in Figure 1. In contrast, a similar plasmasphere is not present at Jupiter, likely due to the rapid rotation of the planet and the inner magnetosphere. The centrifugal acceleration overcomes the gravitational acceleration at Jupiter at radial distances greater than 2.24 R_J (e.g., Ray et al., 2009), and so a stable, corotating plasmasphere such as is found at Earth does not seem to form at Jupiter.

FIGURE 1. Density (left) and Alfvén speed (right) for a dipole model of Earth’s magnetosphere.

Moving farther out in the magnetospheres, at Earth the geomagnetic tail contains a plasma sheet that is largely composed of solar wind ions, with a minor fraction consisting of ions accelerated up from the ionosphere. Typical parameters of the central plasma sheet (e.g., Hughes, 1995) are a density of 0.3 cm⁻³ and a magnetic field strength of 10 nT, which gives an Alfvén speed of 400 km/s, assuming a hydrogen plasma. This plasma sheet is surrounded by a low-density lobe, with typical parameters of a magnetic field of 20 nT and a density of 0.01 cm⁻³, giving an Alfvén speed of about 4,400 km/s. In contrast, Jupiter contains a plasma disk that is largely composed of plasma originating at the moon Io, whose volcanoes emit sulfur and oxygen which is then ionized and transported outward by centrifugal forces (Bagenal and Delamere, 2011). At a radial distance of 20 R_J, this plasma has a density of about 1 cm⁻³ and a magnetic field strength of 20 nT, according to the model of Connerney et al. (1981) (The updated model of Connerney et al., 2020, has a slightly lower field.). This gives an Alfvén speed of 100 km/s, assuming an average mass of 16 amu. However, in the case of Jupiter, the lobe regions appear to be very empty, with Alfvén speeds approaching the speed of light. Figure 2 (updated from Lysak and Song, 2020) gives the magnetic field, density and Alfvén speed for a model based on Bagenal and Delamere (2011) and Connerney et al. (2020).

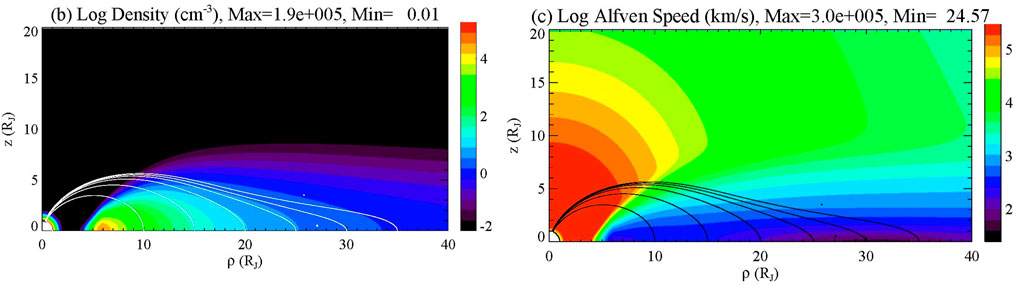
FIGURE 2. A meridional cut of the density (left) and Alfvén speed (right) for a model of Jupiter’s magnetosphere (adapted from Lysak and Song (2020), updated with the Connerney et al. (2020) magnetic field model) with ρ being the cylindrical distance from Jupiter’s magnetic axis and z is the distance above the equatorial plane. Representative model field lines are indicated by the white lines in the left figure and black lines in the right.

A final distinction between the two magnetospheres is that the solar wind impacts the Earth’s plasma sheet much more than at Jupiter. Changing solar wind conditions can lead to reconnection occurring at distances of 20 R_E during magnetospheric substorms, while reconnection at Jupiter is thought to occur much farther out. Woch et al. (2002) note that the transition between inward (toward Jupiter) and outward flows occurs at distances greater than 70 R_J. Thus, the Jovian tail is more likely to be able to support field line resonances at larger radial distances from the planet than at Earth.

Field Line Resonances and Cavity Modes at Earth

The study of field line resonances has a long history, starting from the seminal reports of Dungey (1954) and Tamao (1964). This was put on a firm footing by the work of Cummings et al. (1969), who used a dipolar coordinate system to compute the resonant frequencies of both toroidal modes (with a magnetic perturbation in the azimuthal direction) and poloidal modes (with the magnetic field in the radial direction at the equator). This work was extended by Singer et al. (1981), who included non-dipolar fields with an azimuthal dependence to determine the resonant frequencies as a function of local time.

A major observational advance was made by Samson (1972), who concluded from the polarization of the field-line resonances that they were excited as a result of Kelvin-Helmholtz instability at the magnetopause. This instability leads to the formation of compressional (fast mode) waves that propagate across field lines until they hit a field line whose resonant frequency matches the frequency of the fast mode waves. This resonant point is generally at smaller radial distances than the classical turning point of the fast mode waves, indicating that tunneling from the turning point to the resonant point should occur. The theory of this process was discussed by Zhu and Kivelson (1988) by using a box model in which the field lines are straightened out. Numerical studies of this process in a dipole model were carried out by Lee and Lysak (1989, 1990), who noted that tunneling was not necessary in the dipole model due to the curvature of the field lines.

At lower L-shells, field line resonances have often been used to determine the plasma mass density, an area called magnetoseismology. For example, Takahashi and Anderson (1992) used measurements from the magnetometer aboard the AMPTE CCE satellite to determine the inferred density and Alfvén speed within the L = 7 L shell. These observations clearly show FLRs with frequencies of a few tens of milliHertz, with a jump in the frequencies at L = 4 to 5, indicating the presence of the plasmapause. Denton et al. (2006) generalized the plasma density model used in previous studies, which assumed a power law distribution of density, by using observations of multiple FLR harmonics to fit to a polynomial distribution of the density. They found that at L shells of 6–8, while the electron density was well fit by a single power law, the mass density distribution had a peak near the equator, which suggested that heavy ions were concentrated near the equator.

Fewer studies have reported on field line resonances at higher L shells. This may be because the tail is frequently disrupted by storm and substorm processes during which the tail is dramatically reconfigured, making a standing resonance more difficult to sustain. Another point is that the FLR frequencies can become very low. There have been a few indications of such low frequency FLRs. Samson et al. (1996) reported FLRs in the 1–3 mHz range at L = 7 near midnight local times from ground based observations. Rankin et al. (2000) noted that resonances in this frequency range could be explained by considering the stretched magnetic topology in the midnight region. The most extreme examples of low frequency FLRs in the tail were presented by Zheng et al. (2006), who showed coordinated observations of FLRs from Cluster at 19 R_E at about 1.1 mHz, or a period of 15 min together with ground observations on conjugate field lines at the same frequency. These authors also reported FLRs at 2.5 mHz from GOES-12 and Geotail at 9 R_E, and Polar at 2 mHz at 10.5 R_E as well as at 1.5 mHz at 14 R_E. Therefore when conditions permit, field line resonances can be seen throughout the magnetosphere and into the near-Earth magnetotail.

In contrast with the relatively common observations of FLRs in the magnetosphere, cavity mode oscillations have been more difficult to observe. One early example was provided by Kivelson et al. (1984) and Kivelson and Southwood (1986) of global pulsations in the 5–8 min range (2–3 mHz) in the dayside magnetosphere. On the dayside, the plasmapause and the magnetopause provide strong gradients that can act to confine these cavity modes on the dayside. On the other hand, on the nightside, there is no comparable boundary to the magnetopause to confine these modes. In contrast, Samson et al. (1992) have suggested that field line resonances at discrete frequencies of 1.3, 1.9, 2.6 and 3.3 mHz were associated modes propagating in a waveguide formed in the magnetotail. Modeling efforts (Wright, 1994; Keller and Lysak, 2001) have shown the possibility of supporting such modes, but direct observation of the fields in this waveguide have proven elusive. As with the FLRs, this may be because the dynamics of the magnetotail may disrupt for formation of these very long period waves.

On the other hand, the plasmasphere is also capable of supporting cavity modes. Lee (1996) studied the possibility of plasmaspheric cavity modes. He noted that the imperfect reflection of waves at the plasmaspheric boundary suggested that these modes should be called virtual resonances rather than pure cavity modes. Whatever such modes are called, a recent study by Takahashi et al. (2018) has provided some of the best evidence for the excitation of these oscillations in the dayside magnetosphere in response to the impact of an interplanetary shock using data from the Van Allen Probes mission.

We have examined this event using a ULF wave code set in a dipolar geometry that has been used in a number of previous papers (e.g., Lysak et al., 2013; Lysak et al., 2015; Lysak et al., 2020). This code uses non-orthogonal coordinates to address the differences between a dipolar geometry appropriate to the magnetosphere and the spherical geometry of the ionosphere. The model equations are Maxwell’s equations, coupled with ionospheric currents given by Ohm’s Law. Thus the equations modeled are

Here σ_P and σ_H are the Pedersen and Hall conductivities, respectively, and $\widehat{\mathbf{b}}$ is the direction of the magnetic field. The permittivity ${\epsilon }_{\perp }={\epsilon }_0\left(1+c^2/V_A^2\right)$ includes the effects of the displacement and polarization currents.

This code was run with a density profile modeled after wave observations by the Van Allen Probes mission. Cavity modes with frequencies of 13 mHz, 30 and 43 mHz were found in the simulation, very close to observed values of 13 mHz, 26 and 40 mHz. Figure 3 (from Takahashi et al., 2018) shows the density profile used in the model (panel a), the spectrum of both the cavity modes (panel b, indicated by the azimuthal, or E_φ component of the electric field) and the field line resonances (the E_ν component, panel c). It can be seen that the cavity modes are not strictly confined within the plasmasphere. Note that Figure 3A givesthe electron density, not the mass density. In the simulations, we assume that the plasmasphere is mainly hydrogen, although it is likely that there is some population of heavy ions. In addition, the simulations have assumed a slightly lower density than the observations to account for the fact that the magnetic field is compressed on the dayside, leading to larger Alfvén speeds.

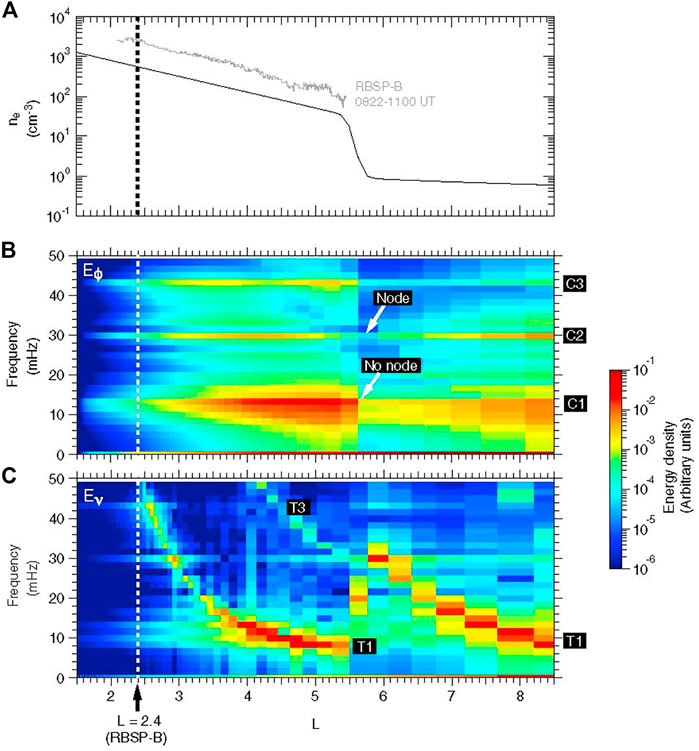
FIGURE 3. (A) Density assumed in a model of cavity mode oscillations. Solid line gives the model profile, and lighter line gives density determined from Van Allen Probes wave data; (B) Spectral energy density for the azimuthal component of the electric field (Eφ). Three harmonics of the cavity mode are indicated by C1, C2 and C3; (C) Spectral energy density for the radial component of the electric field (Eν) showing field line resonances. The fundamental mode is indicated by T1 and the third harmonic by T3 (Takahashi et al., 2018).

A final type of resonant cavity is the topside ionosphere, which supports modes in what has been called the Ionospheric Alfvén Resonator (IAR, Polyakov and Rapaport, 1981; Lysak, 1991; Lysak and Yoshikawa, 2006). This resonator is formed by the rapid decrease in the plasma density above the ionosphere, which leads to a rapidly increasing Alfvén speed. As opposed to the time scales of minutes for the field line resonances, the IAR has resonant periods of seconds, roughly the time that it takes an Alfvén wave from the ionosphere to reflect from the peak in the Alfvén speed that usually occurs at 3,000–6,000 km altitude. The wave frequency in this resonator scales with the Alfvén speed at the ionosphere divided by the ionospheric scale height, V_AI/2h, times a factor that depends on the ionospheric conductance. These rapid reflections can accelerate the effect of phase mixing, which can produce narrow scales due to the perpendicular gradients of the Alfvén speed. Such scales can also be produced by ionospheric feedback interactions due to fluctuations in the ionospheric conductance (Lysak, 1991; Lysak and Song, 2002). At these narrow scales, the Alfvén wave can develop a parallel electric field that can accelerate auroral particles. These parallel electric fields fluctuate on a time scale of a few seconds, comparable to the electron transit time through the region (as a reference point, a 100 eV electron travels at about 1 R_E/s). Thus, electrons passing through this region will all feel a different degree of acceleration, producing the broadband electron distribution often called the Alfvénic aurora (e.g., Chaston et al., 2002; Chaston et al., 2003).

Field Line Resonances and Cavity Modes at Jupiter

Given the larger size of Jupiter’s magnetosphere, one might expect that field line resonances at Jupiter would occur at lower frequencies than at Earth. This remains true despite the fact that the magnetic field is stronger at Jupiter while densities are not that much different than on Earth, leading to larger Alfvén speeds. The best evidence for field line resonances at Jupiter are the so-called Quasi-Periodic Oscillations with periods of 10–60 min that have been observed in the aurora by the Hubble Space Telescope (Nichols et al., 2017) and by the Japanese Subaru satellite (Watanabe et al., 2018) in the infrared. Observations from Voyager 2 have also shown magnetic fluctuations in this period range (Khurana and Kivelson, 1989). Similar observations from Galileo have been reported by Wilson and Dougherty (2000). A detailed study of these oscillations was done by Manners et al. (2018), Manners and Masters (2019), and Manners and Masters (2020). Manners and Masters (2019) used a box model to analyze these observations, and showed that there are maxima in the power in the transverse magnetic fields at periods of about 22, 14, 7 and 4 min at a radial distance of 23 R_J. In the box model used in this work, these oscillations corresponded to the first, third, seventh and 11th harmonics of the field line resonance. In particular, all of these modes have antinodes in the magnetic field at the equator, indicative of the driving source.

These observations were tested in a more realistic magnetosphere by Lysak and Song (2020). As shown above in Figure 2, we used the magnetic field model of Connerney et al. (1981) and the plasma model of Bagenal and Delamere (2011). We then performed an eigenvalue analysis to determine the resonant frequencies and a time-domain simulation for the M = 23 field line (where M refers to the distance of the equatorial crossing, in Jovian radii) to confirm the mode structure of these waves. These frequencies and the corresponding period (in minutes) are shown in Figure 4 (Lysak and Song, 2020). We found a rich set of frequencies in the 10–40 min range could be supported by the model. The modes observed by Manners and Masters (2019) here corresponded to modes 6, 10, 18, and 32, with periods of 22.4, 13.0, 7.1 and 3.9 min, respectively (here we are counting the fundamental as mode 1, with the first harmonic being mode 2, and so on). The time domain simulations supported the idea that these harmonics could be excited by a bipolar pulse in the electric field, corresponding to a shear flow in the magnetotail. Such sheared flows might be expected in this region of the Jovian magnetosphere where the co-rotation of the plasma with the planet is breaking down. As this break down is associated with the generation of auroral field-aligned currents, these waves could potentially produced the observed oscillations in the aurora.

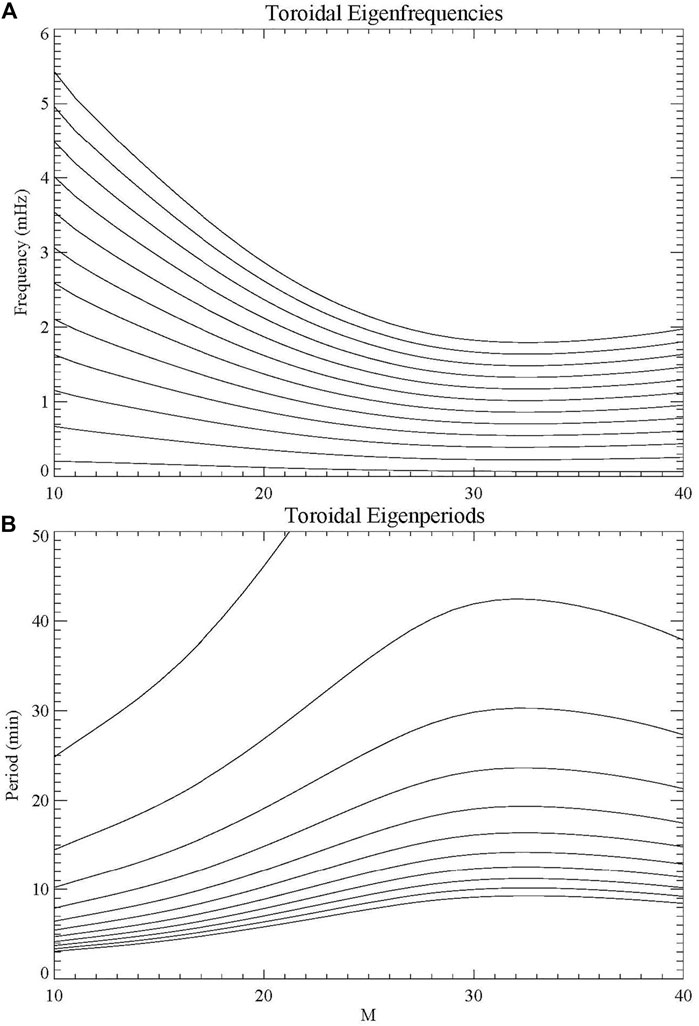
FIGURE 4. Eigenfrequencies as a function of M-shell for first 12 eigenmodes for the density and Alfvén speed given in Figure 3. (A) Frequencies in mHz; (B) Periods in minutes. Note that the fundamental mode, which has periods greater than 80 min for all values of M, is not shown in panel b (Lysak and Song, 2020).

Manners and Masters (2020) investigated the local time dependence of ULF waves in the Jovian magnetosphere, including compressional waves (fast mode) as well as transverse waves (Alfvén mode). The two modes were observed in the range of periods from 10 to 60 min, with periods of 15, 30 and 40 min being dominant. The distribution of the waves were similar in the noon and midnight sectors, suggesting that the compressional waves were ducted through the plasma disk from a dayside source to the nightside. However, they observed greater wave power within 10 R_J than at radial distances of greater than 40 R_J, suggesting that the source of these waves was internal rather than imposed from the magnetopause by, for example, dynamic pressure pulses in the solar wind or by Kelvin-Helmholtz instabilities.

One obvious possibility for an internal source is the motion of the moon Io (and to a lesser extent, Ganymede and Europa) through the magnetosphere (or more precisely, by the motion of the co-rotating plasma past the moon). It has long been known that this interaction gives rise to “Alfvén wings” that couple Io with the ionosphere of Jupiter (e.g., Goertz, 1980; Neubauer, 1980; Acuña et al., 1981; Belcher et al., 1981; Gurnett and Goertz, 1981; Bagenal, 1983; Crary, 1997; Chust et al., 2005; Hinton et al., 2019). While much of this work has focused on transverse Alfvén waves, Glassmeier et al. (1989) observed both transverse and compressional waves in the plasma torus. It seems reasonable that as the co-rotating plasma impacts and is diverted around Io, compressions in the magnetic field would be excited. These waves could be trapped in the Io plasma torus itself (denoted as a “torus resonance” by Manners and Masters (2020)), or could leak out to fill the plasma sheet that forms tailward of the Io plasma torus. As noted above, the dense plasma of heavy ions produced by the Io interaction would lead to strong cavity oscillations. In addition, the Iogenic plasma moves outward under the influence of the centrifugal force. However, this motion is not smooth but rather is in the form of irregular interchange motions that would seem like a natural source of ULF waves. Further study is clearly needed to investigate these types of cavity modes at Jupiter.

As noted above, there is also a sharp decrease in the plasma density in the topside ionosphere of Jupiter (e.g., Allegrini et al., 2021; Elliott et al., 2021), which should lead to an ionospheric Alfvén resonator at Jupiter. As at Earth, this can produce a broadband acceleration of electrons, which are often the dominant form of electron distribution in the Jovian auroral zone. It is worth noting that the magnetic field strength at Jupiter is an order of magnitude bigger than at Earth while the plasma densities are comparable, so that the Alfvén speed is roughly an order of magnitude larger at Jupiter. However, the scale heights of the ionosphere, which scale with the planetary radius, is also an order of magnitude larger than at Earth, so that the IAR frequencies are comparable. However, at Jupiter, it is a 30 keV electron that travels at about 1 R_J/s. Thus, the Alfvénic acceleration process should produce broadband electrons in this energy range.

However, recent observations from Juno indicate that while broadband electrons are frequently seen on field lines connecting to the main auroral emissions, the corresponding Alfvén waves are often not observed on the same field lines (Mauk et al., 2020). This could be because the acceleration is taking place at altitudes above the spacecraft, or that the broadband acceleration in this case is due to some other mechanism, such as acceleration by whistler mode waves (Elliott et al., 2018). Another possibility is that the magnetic field may be below the observational threshold, since the density in this region is very low, the Alfvén speed is high, and so the magnetic field perturbation would be very small. Juno does not carry a low-frequency electric field measurement, so this hypothesis is difficult to put to the test. Alfvén waves are observed in the regions equatorward of the main auroral emissions (Sulaiman et al., 2022) where the density is higher, which may give some support to this suggestion.

There is a clearer signature of Alfvénic acceleration in the flux tube connected to Io (and probably Ganymede and Europa as well). As noted above, Io provides a strong source for Alfvén wave emissions. Szalay et al. (2018), using Juno observations, have observed both broadband acceleration and Alfvén wave turbulence in this region, suggesting that the IAR may be active on these field lines. Moreover, Szalay et al. (2020) have also observed broadband proton acceleration, consistent with an Alfvénic acceleration process. Thus, while more observations will help to clarify these issues, it appears likely that Alfvénic acceleration is dominant on the Io flux tube.

A new resonant cavity that appears to be unique in the Jovian magnetosphere is what could be called a lobe resonator in the very low density region between the ionosphere and the heavy ion plasma disk. This region has an Alfvén speed that is nearly the speed of light, while the ionosphere and the plasma disk have Alfvén speeds below 1,000 km/s. This makes a strong contrast in Alfvén speeds that leads to strong reflection according to Equation 3. This resonator has a period of a few minutes, intermediate between the seconds of the IAR and the tens of minutes for field line resonances. Evidence for this cavity was presented by Lysak et al. (2021a), who were modeling field lines in the main aurora. However, reflections at the boundary of the plasma disk are particularly important in the Io interaction since these reflections return to the ionosphere, producing the elongated tail observed in the aurora. This tail consists of multiple spots when observed with high resolution (e.g., Mura et al., 2018; Moirano et al., 2021). Figure 5 shows a snapshot of a simulation we did (Lysak et al., 2021b) of the Io plasma interaction. This plot shows E_ν, the component of the perpendicular electric field that points radially outward near the equator and poleward near the poles, with green and yellow colors indicating radially outward fields and blue and violet being inward. In this run, the source due to Io has been moving across the system, generating Alfvén waves. At this longitude, Io is at its maximum magnetic latitude of about 10°. The contrast in the angle of the field patterns between the low Alfvén speed disk, which covers roughly from −10° to 20° latitude in the figure, and the lobe region of high Alfvén speed can be observed. It can also be seen that the electric fields reverse on each bounce from the disk, consistent with Equation 3 since in this case, V₂ < V₁. Understanding this resonant cavity will be key to determining the structure of the Io auroral tail as well as the interaction of other moons with the Jovian magnetosphere.

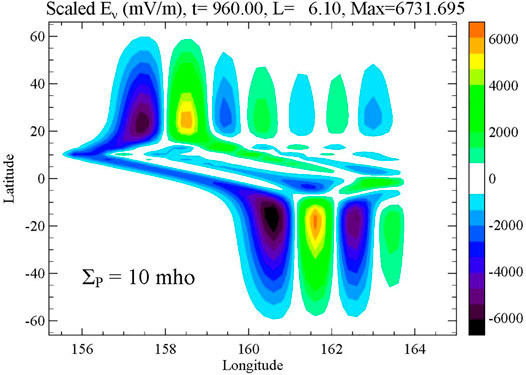
FIGURE 5. Snapshot of the radial electric field in a simulation of Io’s interaction with the Jovian magnetosphere (Lysak et al., 2021b). The location of Io is at the leading spot on the left side of the figure. The Alfvén waves generated by the Io interaction are shown. Note that the waves in the dense plasma disk near the equator are propagating more slowly than in the low density lobe region at higher latitudes. The reflections at the boundary of the plasma disk can be seen.

Summary and Conclusion

The theories and observations presented here show that resonant Alfvén wave structures, whether field line resonances for the shear Alfvén mode or cavity resonances for the fast mode, are ubiquitous in the magnetospheres of Earth and Jupiter, and no doubt in other planetary magnetospheres as well. To summarize the results of the papers covered in this review:

1. The magnetospheres of both Earth and Jupiter can support field line resonances consisting of shear Alfvén waves propagating from one ionosphere to the conjugate ionosphere. At Earth, these resonances have periods of minutes, while at Jupiter the periods are tens of minutes.

2. At Earth, the plasmasphere can support cavity modes, also with periods of a few minutes. Coupling between these cavity modes and the field line resonances are important in the dynamics of the magnetosphere. In contrast, at Jupiter, there is not a well defined plasmasphere, so this type of mode cannot exist.

3. On the other hand, Jupiter has a plasma disk consisting of heavy ions due to plasma originating at the moon Io. This disk can support cavity modes with periods of tens of minutes and could couple to the field line resonances at similar frequencies as well. At Earth, there do not seem to be many observations of such resonances in the tail plasma sheet. This is perhaps due to the fact that the geomagnetic tail is often disrupted by substorm dynamics.

4. The magnetospheres of both planets can support an ionospheric Alfvén resonator due to the rapid decrease of density above the ionosphere. These resonances have periods of seconds in both cases, and can contribute to the broadband acceleration of electrons and ions associated with the Alfvénic aurora. In the case of Jupiter, this acceleration is particularly important in the interaction of Io with the co-rotating plasma.

5. At Jupiter, there is also a lobe resonator in the high Alfvén speed region between the ionosphere and the plasma disk, with periods of minutes. This resonator affects the Alfvénic interaction between Io and Jupiter, and leads to the extended auroral tail that is initiated on the Io flux tube. This type of resonator does not appear to be active at Earth.

In conclusion, these various interactions due to the inhomogeneous Alfvén speed play an important role in the short time dynamics of the magnetospheres of Earth and Jupiter. Understanding these interactions will lead to greater understanding of the formation of aurora and the acceleration of particles at these magnetospheres as well as those of other planets, both within our Solar System and in other systems.

Author Contributions

RL is the sole author of this paper and is solely responsible for its content.

Funding

The research behind this research has been supported by a National Science Foundation grant AGS-1840891 and a National Aeronautical and Space Administration grant 80NSSC20K1269. Computing support has been provided by the Minnesota Supercomputer Institute.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor KT declared a shared group NSF with the author at the time of review.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work has benefited from numerous conversations with colleagues both with regard to the Earth-based and Jupiter-based aspects of the work. In particular, I acknowledge contributions from Yan Song and Sadie Elliott (University of Minnesota), Colin Waters and Murray Sciffer (Newcastle University, Australia), Kazue Takahashi and Barry Mauk (Johns Hopkins University Applied Physics Lab), Ali Sulaiman and Bill Kurth (University of Iowa), Fran Bagenal (University of Colorado), and H. Arthur Manners and Adam Masters (Imperial College London).

References