On-Chip Broadband Mid-Infrared Supercontinuum Generation Based on Highly Nonlinear Chalcogenide Glass Waveguides

Introduction

Capturing the distinctive spectral fingerprints of molecules in the infrared (IR) region is of vital importance in molecular spectroscopy applications for environmental and health monitoring [1–3]. IR spectroscopy is considered the gold standard for molecular structures identification by detecting the distinctive spectral fingerprints of molecules in IR region covering 3–12 μm [4]. As laser-based light sources directly accessing the IR region, supercontinuum generations (SCGs) have attracted great attention due to their broad bandwidth, spatial coherence, and high brightness compared with the current mid-infrared sources [5]. Especially, when the SCG can be achieved in photonic integrated waveguides, the SCG platforms benefit from high lithography accuracy, dramatic compactness, high yield, and low power consumption [6, 7]. Typically, a femtosecond pulse laser is used to pump the nonlinear waveguide which has a wide transmission range and high nonlinear refractive index (n₂) with dispersion engineered for broadband SCG. However, up to now, very few demonstrations successfully extended the reach into the mid-IR [7].

Recently, SCG based on chalcogenide glasses (ChGs) has shown particular potential, which are well known for their wide transparency window, high Kerr nonlinearity, and low two-photon absorption and are promising material platforms for photonic integrated nonlinear devices [8]. More importantly, as amorphous materials, the optical and mechanical properties of ChGs can be optimized by adjusting the composition. To date, a few of ChG-based fibers and waveguides have been fabricated and used for their practical applications. For example, a robust SCG with a high average power of 550 mW can be used as IR source to detect CS₂ gas [5]. A stable and repeatable SCG with a power of around 20 mW was experimentally demonstrated using the Ge-As-Se/Ge-As-S rib waveguide, and an absorption spectrum of the polystyrene film has been obtained [9]. Very recently, our work on improved 2-micron optical interconnection using on-chip chalcogenide glass photonic integration has shown the promising prospect for photonic integration at the MIR waveband [10].

Yet, achieving MIR SCG with long wavelength of more than 10 μm in chip-scale waveguides remains a challenge. For SCG based on on-chip photonic waveguides, dispersion engineering is an efficient way to extend the SC to longer wavelengths. Multilayer waveguide structures have been proposed to flatten waveguide dispersion with multiple zero dispersion wavelengths (ZDWs), which can be used to generate broadband SC [11, 12]. Moreover, soliton-induced dispersive wave (DW) generation is an ideal mechanism that can coherently and efficiently broaden SC over a large frequency span [13] and enable ultrabroadband SCG without complex waveguide structures [7, 14, 15]. In addition, the mode at longer wavelengths expands significantly outside of the waveguide and does not overlap well with that at shorter wavelengths. The high NA would ensure a high light confinement at all wavelengths, which provides a substantial increase in the effective nonlinearity, and modes overlap over a broad wavelength span. Therefore, for broadband SCG, proper waveguide structure design is of vital importance to achieve a balance between MIR wave confinement and dispersion engineering in such waveguide.

In this work, a highly nonlinear chalcogenide waveguide with a Ge-As-Se-Te glass core and Ge-Se glass upper and lower cladding with NA of 2.07 is proposed and designed. A broadband SC from 2 to 13 μm assisted by dispersive wave generation is numerically demonstrated by launching a 120 fs, 800 W peak power pulse in such a waveguide. In addition, we propose a fabrication scheme to realize the precise manipulation of dispersion design. The proposed SCG holds great potential for the compact trace gas sensing and biomedical diagnostics.

Concept and Waveguide Structure

Among the ChG family, the ChGs based on sulfur and selenium show the transparency cutoff between 10 and 15 μm due to their higher phonon energies. The telluride (Te) glasses have lower phonon energies, resulting in broader transmission windows extending to more than 20 μm [16] and higher third-order nonlinearity [17]. However, the Te ChG has a poor transmittance in the short wavelength below 3 μm and is easy to crystallize. Here, we prepare and purify a Te-Se hybrid glass Ge₂₀As₂₀Te₄₅Se₁₅ (Ge-As-Te-Se) with a wide transmission window covering 2–16 μm region and superior thermal stability against crystallization during the film deposition process, which is chosen as the core material. The nontoxic Ge_21.5Se_78.5 chalcogenide glass is chosen as the upper and lower cladding, as shown in Figure 1A.

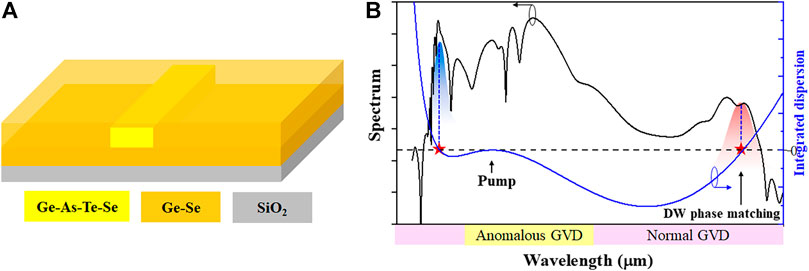
FIGURE 1. (A) The structure of the proposed all-chalcogenide waveguide. (B) Schematic presentation of soliton-induced dispersive wave (DW) generation: a DW related to soliton can be stimulated when the spectral regions satisfy zero-phase mismatching (where ${\beta }_{int}$ = 0). By this time, the pump laser is located at the anomalous GVD region to support soliton, while DWs are in the normal GVD region.

The transmission spectrum of the core and cladding glasses is shown in Figure 2A. Moreover, an IR ellipsometer (IR-VASE MARK II, J. A. Woollam Co.) has been used to characterize the refractive indices of the core and cladding glasses, as shown in Figure 2B. Using our measured refractive index, the nonlinear refractive index (n₂) can be determined by the following equation [18]:

where n₀ is the linear refractive index and the calculated $n_2 = 2.85\times {10}^{-17}$ m²/W at 5.8 μm.

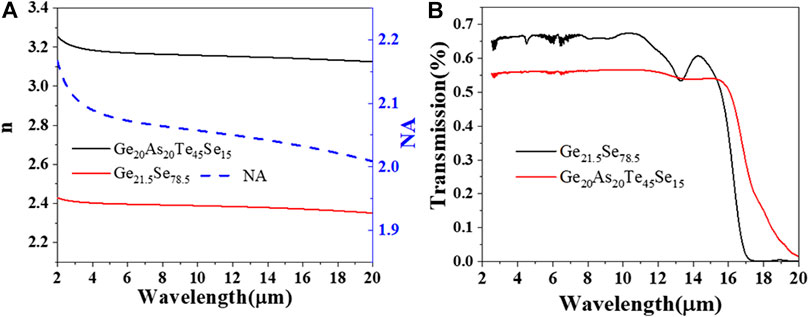
FIGURE 2. (A) Optical transmission spectra of the Ge-As-Te-Se and Ge-Se bulk glasses. (B) Measured linear refractive index of the Ge-As-Te-Se and Ge-Se ChG film and correspondingly calculated NA.

SCG occurs when a sufficiently powerful femtosecond pulse propagates through nonlinear nanophotonic waveguides and generally experiences a temporal compression and spectral broadening. Especially, the high-order soliton dynamics will be induced when the pulse laser propagates in a flat and low anomalous group velocity dispersion (GVD) region [19], facilitating a self-phase modulation (SPM) enabling spectral broadening and temporal compression, and the degree is proportional to the soliton number [20]. The soliton number (N) determines the relative interaction intensity between nonlinearity and dispersion, and the soliton number is often designed to be $1\le N\le 10$, leading to effective self-compression. The generalized nonlinear Schrodinger equation (GNLSE) is used for investigating the evolution of the envelope $A(z,t)$ based on such waveguides [21]:

where $\alpha$ and ${\beta }_m$ are the loss and dispersion, representing the linear optical effects, while $\gamma$ and $R\left(t^{\text{'}}\right)$ in the right side represent various nonlinear effects. The approximation ${\gamma }_1=\gamma /{\omega }_0$ has been employed [22]. $\gamma$ denotes the Kerr coefficient of the waveguide and can be calculated using the following equation [21]:

where $F\left(x,y\right)$ is the vector electric field, n₂ is the nonlinear refractive index of materials, $\lambda$ is the wavelength, and β denotes the propagation constant. The Taylor series expansion of the propagation constant relative to pump pulse (${\omega }_0$) can be expressed as follows [19].

where ${\beta }_n\left({\omega }_0\right)=d^n\beta /d{\omega }^n$. The group velocity dispersion (GVD) profile can be calculated through the equation $D =-\left(2\pi c/{\lambda }^2\right)\cdot {\beta }_2= -\left(\lambda /c\right)\cdot \left(d^2{n}_{eff}/d{\lambda }^2\right)$, where $n_{eff}$ is the effective refractive index. Taking into account material dispersions of Ge₂₀As₂₀Te₄₅Se₁₅ and Ge_21.5Se_78.5 (Figure 2B), the effective refractive index value as a function of wavelength is obtained using finite element method. $R\left(t\right)$ is the Raman response function:

where τ₁ and τ₂ are the Raman period and lifetime. There is no publication for Raman response function for Ge₂₀As₂₀Te₄₅Se₁₅. Here, the coefficients of As₂Se₃ chalcogenide glass have been used for the simulation [22].

At the compression point, the effects of high-order dispersion (HOD) on the propagating solitons will cause the energy conversion from the soliton to a spectral region in the normal GVD regime, causing the emission of dispersive waves (DWs) [19]. The phase-matching condition of DW generation can be given with the same phase constant of the soliton pulse and the linear waves [13]:

where β, ${\omega }_s,$$v_g=1/{\beta }_1\left({\omega }_s\right)\text{, and P }$ are the mode propagation vector, soliton central angular frequency, soliton group velocity, and pulse peak power, respectively. In Eq. 6, the nonlinear phase shift is always small and can be neglected; thus, the left side is the integrated dispersion ${\beta }_{int}$. Therefore, the phase-matching condition can be simplified to the following form with a Taylor expansion:

The phase-matching condition of the zero-integrated dispersion determines the location of DWs [23, 24]. Figure 1B shows the principle of soliton-induced DW generation [19]. When the spectral regions satisfy zero-phase mismatching (where ${\beta }_{int}$ = 0), a DW related to soliton can be stimulated. By this time, the pump laser is located at anomalous GVD region to support soliton, while DWs are in the normal GVD region.

As for ChG-based SCG, the laser-induced damage threshold (LDT) is important when dumping femtosecond pulse with high peak power into the waveguides. The intensity threshold Ith can be calculated by the following equation [25]:

where P_cr is the critical average powers when the observable modification on the surface is induced, P_peak, D, R, and τ are the corresponding peak power, diameter of the beam spot, repetition rate, and pulse duration, respectively.

Results and Discussion

Dispersion Engineering for DWs Phase Matching

Firstly, the effects of structural parameters on dispersion and integrated dispersion are systematically investigated. Figures 3A,C show the calculated GVD with different widths and heights for both fundamental TM and TE modes. Two zero dispersion wavelengths (ZDWs) can be obtained with engineered dispersion in the MIR region for these two modes. At short wavelengths, the material dispersion dominated a ZWD, leading to first DW generation. And at longer wavelengths, the waveguide dispersion can compensate a large anomalous material GVD in the MIR, reaching a second ZDW. Thus, the second ZWD is moved as waveguide structure changes. When increasing the width (W, the waveguide height remains the same, H = 2.7 μm) and height (H, the waveguide width remains the same, W = 3.75 μm), the second ZWD is moved from short to long wavelengths gradually, which are shown in Figures 3A,C.

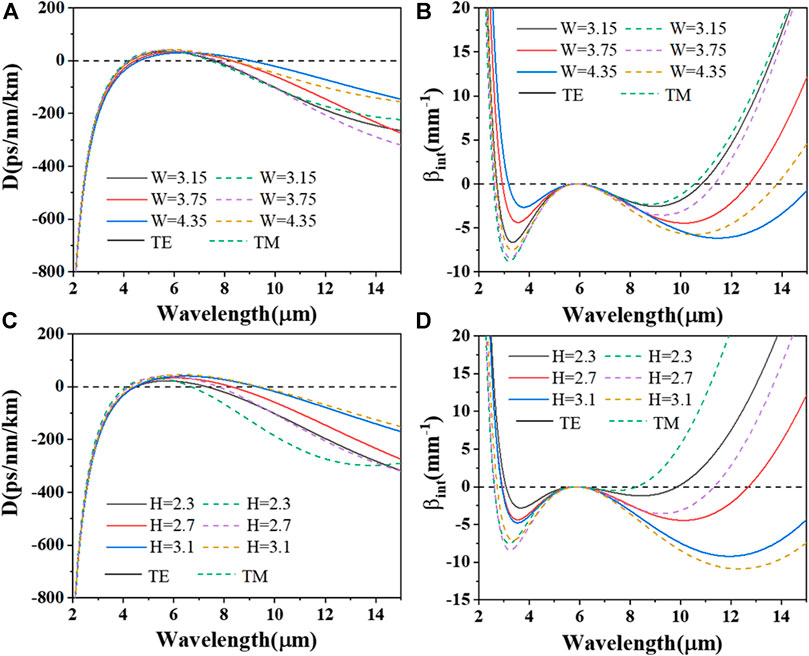
FIGURE 3. (A,C) GVD profiles and (B,D) integrated dispersion profiles with different structural parameters changed. (A,B) The waveguide width W (H = 2.7 μm). (C,D) The waveguide height H (W = 3.75 μm).

Then, the integrated dispersion β_int (Figures 3B,D) can be calculated as increasing the waveguide widths W and heights H (which have the same trends as Figures 3A,C) when pumped at 5.8 μm, where two DW phase-matching points can be found in MIR range. The first phase-matching point shifts toward shorter wavelength and the second one shifts toward longer wavelength by increasing W and H of the waveguide. It is noteworthy that although the phase-matching point can shift toward much longer wavelength, the dispersion barrier between pump and DW phase-matching point will also significantly increase, greatly limiting spectral conversion efficiency from soliton to dispersive waves [7]. Therefore, a good balance between bandwidth and efficiency of SCG can be achieved by careful dispersion engineering and choosing appropriate pump wavelength.

Broadband MIR Supercontinuum Generation

Based on the above, in order to obtain broadband SC with relatively high conversion efficiency from soliton to dispersive waves, a GVD profile with two ZWDs located at 4.47 and 8.10 μm for the fundamental TE mode is achieved by setting the structural parameters as W = 3.75 μm and H = 2.7 μm, as shown in Figure 4A. When pumped at 5.8 μm, Figure 4A shows the calculated integrated dispersion of the waveguide when pumped at 5.8 μm, in which two dispersive wave phase-matching points at 2.94 and 12.7 μm can be found, and the dispersion barrier between pump and DW phase-matching point is less than 5 mm⁻¹, leading to efficient broadband SCG.

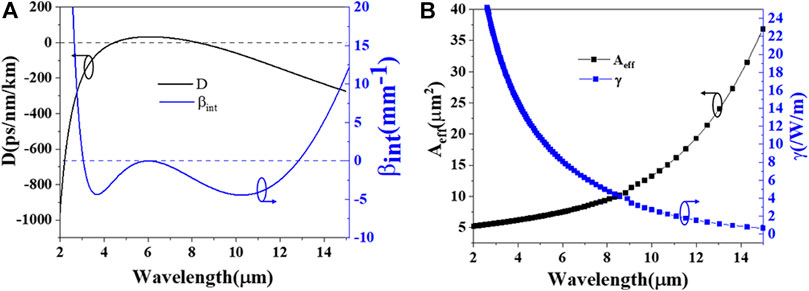
FIGURE 4. (A) Calculated GVD profile and corresponding integrated dispersion. (B) The effective mode area A_eff and nonlinear coefficient γ of the fundamental TE mode in the optimized waveguide (W = 3.75 μm; H = 2.7 μm).

Figure 4B shows the effective mode area and corresponding nonlinear coefficient of the TE mode in the optimized waveguide. The effective mode area increases from 5.2 to 31.5 μm² with the wavelength from 2 to 14 μm, and γ decreases due to the increased mode area and relatively low confinement. At 5.8 μm, the effective mode area is 7.42 μm², with a corresponding nonlinear coefficient of 8.32/W/m. A chirp-free hyperbolic secant pulse at 5.8 μm with a peak power of 800 W and FWHM 120 fs is launched into the above-optimized waveguide. At such a pump scheme, the calculated power intensity is 10.78 GW/cm². Zhao, Z. et al. [26] experimentally demonstrated MIR SCG pumped by an fs pulse at 4.5 μm with ∼150 fs, 1 KHz, average power of 9 mW in a Ge₂₀As₂₀Te₄₅Se₁₅-based step fiber, and corresponding power intensity of ∼15.6 GW/cm². Although the LDT of Ge₂₀As₂₀Te₄₅Se₁₅ glasses was not measured, the launched power intensity is higher than ours. Besides, Hongya Ou et al. [27] measured the LDT of Ge₁₅Sb₂₅Se₆₀ glasses, and the results indicated that laser-induced damage occurs at a beam intensity of 3674 GW∕cm² for the Ge₁₅Sb₂₅Se₆₀ bulk glass. Therefore, we are convinced that our proposed waveguide will not be damaged at such peak power intensity.

Figure 5 shows the spectral evolution along the waveguide, and the SCG can be achieved over 11 μm spectral range with power fluctuation of −40 dB when the waveguide with the length of 5 mm is pumped by an fs pulse with peak power P = 800 W, pump wavelength λ₀ = 5.8 μm, and t_FWHM = 120 fs. The effects of peak power P and center wavelength λ₀ of the pump pulse are also investigated with the 120 fs input pulses. As shown in Figure 6, the bandwidth of SC gets larger, and the two-DW generation can be observed gradually as the peak power P increases. Figure 7A shows the calculated integrated dispersion profile for different pump central wavelengths, which indicates the DW phase-matching wavelength can be tuned, as shown in Figure 7B. When pumped at 5.2 μm, the phase-matching wavelength of the DW can even be extended to 13 μm, while the flatness will be limited due to relatively larger dispersion barrier, compared with that pumped at 6.4 μm. According to this result, we can adjust the pump wavelength to generate broader and flatter spectrum.

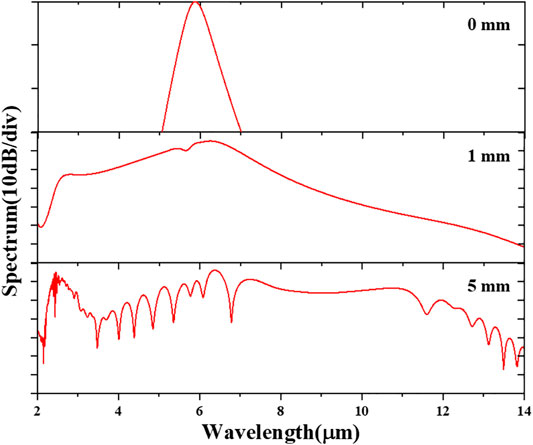
FIGURE 5. Simulated SC results of different waveguide lengths L with peak power P = 800 W, pump wavelength λ₀ = 5.8 μm, and t_FWHM = 120 fs.

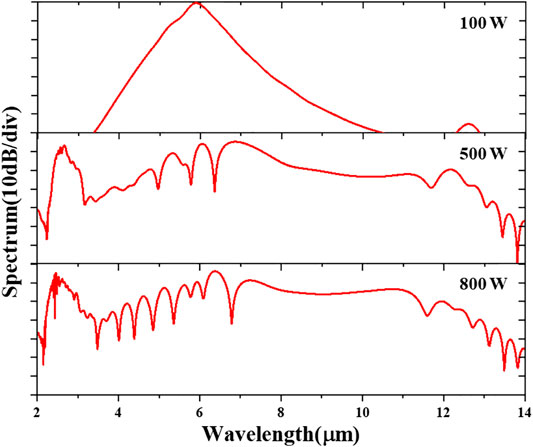
FIGURE 6. Simulated SC results of different peak powers P with waveguide length L = 5 mm, pump wavelength λ₀ = 5.8 μm, and t_FWHM = 120 fs.

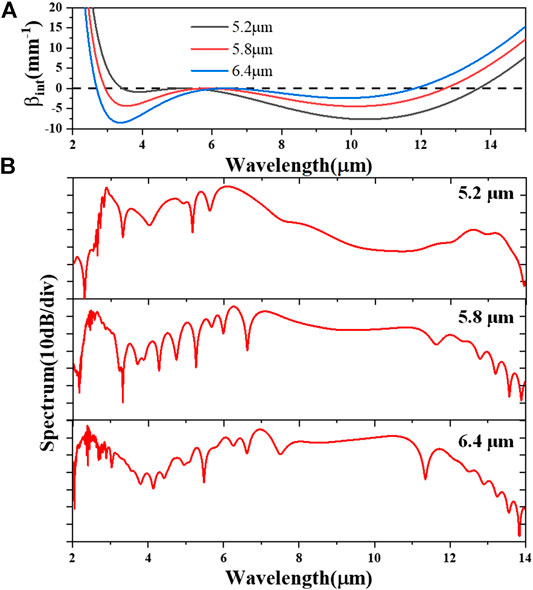
FIGURE 7. Simulated (A) integrated dispersion profiles and (B) SC results of different pump wavelength λ₀ with waveguide length L = 5 mm, peak power P = 800 W, and t_FWHM = 120 fs.

Table 1 summarizes the SC bandwidth with different peak powers P and center wavelength λ₀. When such waveguide with 5 mm length is pumped by a 120 fs pulse with a central wavelength of 6.4 μm and peak power of 800 W, the spectrum expands from 2.05 to 13.18 μm at −40 dB, covering three octaves. To the best of our knowledge, the long-wavelength edge of SC spectrum to ∼13 μm in photonic integrated waveguides is firstly demonstrated. Furthermore, a comparison of our result with other proposed designs by employing various materials is shown in Table 2. These waveguides in Table 2 have various nonlinear coefficients ranging from the lowest being 0.1/W/m to the highest being 630/W/m due to different material platforms, waveguide structures, and central pump wavelength. Among them, although AlGaAs-OI platform offers almost two-order larger nonlinear coefficient than Ge-As-Te-Se in this work, the absorption loss of silica substrate and ultra-small size of the waveguide would limit the practical spectral application in the MIR region. It is noteworthy that nonlinear coefficient gets lower as the pump wavelength increases, while launching the pump pulse at longer wavelength will extend the long-wavelength edge of SC (Table 1). It benefits from higher nonlinear coefficient of our waveguide keeping 8.32/W/m even pumped at wavelength of 5.8 μm, which contributes to the broadband SCG.

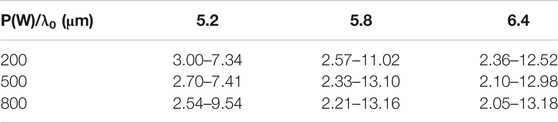
TABLE 1. SCG (−40 dB) with different pump powers P and central wavelength λ₀ (the unit of the spectrum is μm).

TABLE 2. Comparison of MIR SCG reported in chip-scale waveguides.

Figures 8A,B show the evolution of the SC generation process during pump pulses propagates along the waveguide, providing us with a description of the soliton dynamics during the propagation. For the SCG, the stronger nonlinear effects compared with dispersion effects of pump pulse are designed to enable a soliton number ($N^2=L_D/L_N, L_D>L_N$, $L_D=T^2/\left|{\beta }_2\right|\text{, }{L}_N={\left(\gamma P\right)}^{-1}$, where $T$ is the pump pulse duration) greater than one, so that self-phase modulation (SPM) determining spectrum broadening and soliton self-compression occur [21]. In this work, the duration $T$ and peak power P of pump pulse were set to 120 fs and 800 W, and the soliton number is correspondingly 3.4. Theoretically, SCG usually occurs initially at the first compression point L_c, which is inversely proportional to soliton number ($L_c\propto L_D/N$ ). As shown in Figure 8B, the spectrum is firstly broadened due to SPM before the first compression point which is at around 1.5 mm. After the first compression point, the propagating pulse separates at a much shorter distance due to the soliton splitting effect [21], and dips in the SC spectra can be observed due to a spectral interference of the split solitons, as shown in the temporal evolution in Figure 8B. Moreover, the temporal evolution indicates the output temporal pulse envelope of SC, the soliton fission effect (soliton splits into two components) and temporal compression effect can be observed, and the output pulse duration of the main pulse is accordingly around 20 fs.

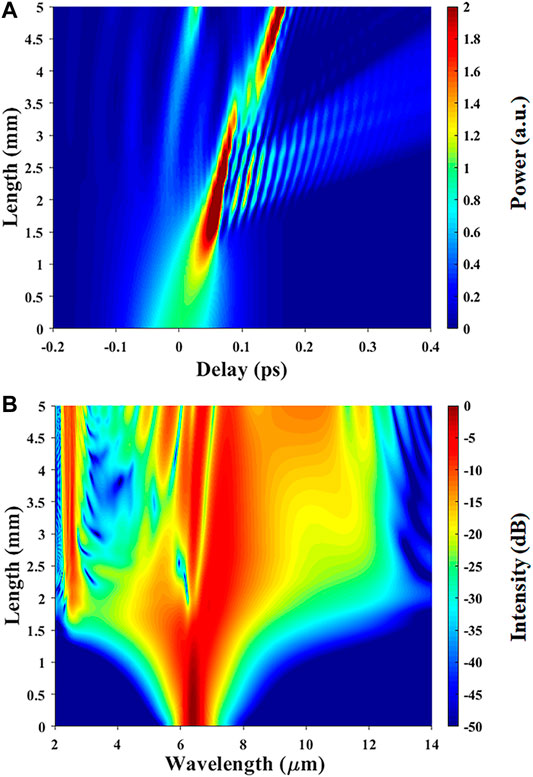
FIGURE 8. (A) Temporal and (B) spectral evolutions (dB scale) of the pump pulse along 5 mm waveguide.

Owing to high-order dispersion and high-order nonlinear effects, if the pump pulse maintains enough energy for broadening the spectrum, the DW can continuously obtain energy from the soliton self-compression process enabling sufficient spectral broadening. This mechanism allows robust generation of DWs, and such DWs emission can efficiently enable broadband SCG in photonic chip-scale waveguides.

Analysis of Fabrication Procedures

Figure 9 explores our ChG waveguide nanofabrication procedure. Firstly, a 6 μm thick Ge-Se lower cladding layer and a 3.75 μm thick Ge-As-Te-Se core layer are deposited by a way of thermal evaporation on a silicon substrate with 3 μm thick thermal oxidation layer. Then, the wafer is purged with nitrogen to form a dry and clean surface on a hot plate at 130°C for 5 min. After that, a 2 nm thick Al₂O₃ protective layer is applied to prevent the ChG from being oxidized during removing residues resist by inductive coupled plasma etching (ICP-RIE). Afterward, e-beam lithography (EBL) and inductive coupled plasma etching (ICP-RIE) are used to fabricate waveguide, then the residual photoresist of the chip is removed. Finally, the upper cladding was thermally deposited onto the patterned wafer. The all-ChG strip waveguides are fabricated. To reduce the insertion loss, inverse tapers will be designed and fabricated at both ends of the waveguide.

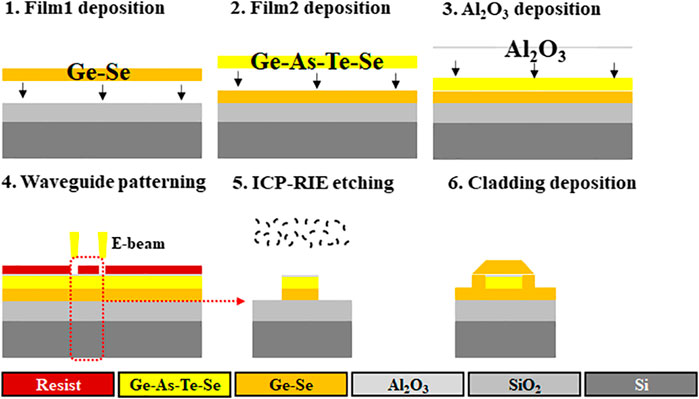
FIGURE 9. A fabrication scheme for the chalcogenide waveguide with a Ge-As-Se-Te core and Ge-Se upper and lower cladding.

Conclusion

A broadband SCG covering the 2–13 μm wavelength has been numerically demonstrated in a compact and high NA Ge-As-Te-Se/Ge-Se chalcogenide waveguide. The influences of geometrical parameters and laser operating conditions are systematically investigated. The DW generation can be observed gradually when increasing the peak power of pump laser, which is conducive to broadening and flattening SCG. This work reveals the potential application for compact, chip-based broadband laser source in detecting fingerprints of the molecules.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

DX, BZ, and YH designed the structure of the waveguide and simulated and analyzed the supercontinuum spectra; ZY, PZ, HC, and LL prepared the glasses; HS, MZ, YZ, and ZL participated in the discussion of the mechanism of the broadband SC generation.

Funding

The work was supported by the Key Project in Broadband Communication and New Network of the Ministry of Science and Technology (MOST) (2018YFB1801003), National Key R&D Program of China under Grant 2019YFA0706303; National Science Foundation of China (NSFC) (61975242, 62035018, U1701661, U2001601), Key Project for Science and Technology of Guangzhou City (201904020048), The Science and Technology Planning Project of Guangdong Province (2019A1515010774), Science Foundation of Guangzhou City (202002030103).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References