1. Introduction
Snow-sampling methods have a multitude of applications and challenges. As snow properties change over days, or even hours, and as sampling can be destructive to the snow properties being measured, sampling methods must be as efficient as possible. Time spent laying out a sampling grid or moving from point to point can affect the number of observations that can be made, and can affect the snow properties if not done properly.
Here we compare point-sampling methods for surveys such as depth, penetration resistance and surface conditions. These can be thought of as minimal-support observations (Reference Blöschl and SivapalanBlöschl and Sivapalan, 1995), and they commonly enable the observer to make many more observations in a day than large-support tests such as the rutschblock.
Such point-observation surveys are usually performed to spatially describe snow qualities of an area or spatial processes affecting the area (Reference Schweizer, Kronholm, Jamieson and BirkelandSchweizer and others, 2008). Examples include finding the spatial extent of snow layers (Reference KronholmKronholm, 2004) for use in avalanche forecasting or obtaining good spatial visualizations of water storage in the snowpack (D. Cline and others, http://www.nohrsc.nws.gov/cline/clpx.html).
2. Related Work
A few previous sampling-method evaluations and comparisons exist. Currently, the most common way to compare and defend methods is lag-bin distributions, as used by Reference KronholmKronholm (2004) and Reference Bellaire, Schweizer and CampbellBellaire and Schweizer (2008). These distributions can be thought of as histograms showing how many point pairs in a sample exist in a given lag bin for possible variogram-type analysis.
Variograms measure the spatial correlation at different distances, or lag bins, within a field, and therefore they measure the continuity of similar measurements well. This can be useful for tracing the two-dimensional extent of traits such as snow layers (Reference KronholmKronholm, 2004) or wind and terrain affectation (Reference Deems, Fassnacht and ElderDeems and others, 2006). The lag-bin type of evaluation, then, comes from the understanding that the more points in a lag bin, the better that sampling method will capture spatial correlation at that lag.
An in-depth analysis performed by Reference Kronholm and BirkelandKronholm and Birkeland (2007) analyzed different sampling methods and how they reproduced a known range, sill and nugget for a spherical variogram model generated from a small subset of generated random fields. This type of analysis directly analyzed histograms of error, which addressed the accuracy question much more thoroughly than lag-bin analysis.
Development of new sampling methods seems limited. Most current methods derive from grid-type structures, with their grid spacing varying to capture information on different spatial scales. These include the LH grids (Reference Birkeland, Kronholm, Logan and GanjuBirkeland and others, 2004), the MT grids (Reference Birkeland, Kronholm, Logan and GanjuBirkeland and others, 2004) and the Swiss grid (Reference KronholmKronholm, 2004; Reference Kronholm, Schneebeli and SchweizerKronholm and others, 2004). Some studies (D. Cline and others, http://www.nohrsc.nws.gov/cline/clpx.html; Reference Bellaire, Schweizer and CampbellBellaire and Schweizer, 2008) utilize a sampling method with random locations placed within and organized by an overall grid, but provide minimal analysis of the method.
Gridded methods can be easier to divide into an orderly day of work, but they often require extensive laying out. Pure uniform random distributions are near impossible to divide up and sample logically without destroying the area in the process. However, they continue to be highly desirable due to their accuracy (Reference Kronholm and BirkelandKronholm and Birkeland, 2007). We feel this leaves a gap, which defined our objectives – to design a sampling method with:
Efficient and minimally destructive layout and sampling.
Similar spatial modelling accuracy to other current methods.
Such a method would have an orderly implementation of random points, without needing to lay out a grid; thereby obtaining its accuracy via randomness and its efficiency via some imposed order.
3. Methods and Data
Using the gstat package (Reference Pebesma and WesselingPebesma and Wesseling, 1998) in the R Project for Statistical Computing (R Development Core Team, 2006), we performed a Monte Carlo simulation to compare the fitted variogram models for 1024 real datasets to fitted variogram models of samples of that data. We give details of the datasets, sampling methods, inclusion of randomness and the variograms in the following subsections.
3.1. Dataset
We use naturally occurring datasets. Digital elevation model (DEM) data, having both spatial correlation and occasional fractal dimension, show the same general qualities of snow cover (Reference Deems, Fassnacht and ElderDeems and others, 2006).
We used four 1:50 000 parcels of DEM data from Geobase.ca (Geobase Orthoimage 2005–10, http://www.geobase.ca): 93b, 93e, 93f and 93h. Each parcel contains 16 grids with 1201 × 1201 elevation points. We trimmed each 1201 × 1201 grid down to 1000 × 1000 and then, due to the O(n2) computational demands of the variogram, we additionally split that into sixteen 250 × 250 point grids.
This gave 1024 grids of data, each with 62 500 points. Each can be thought to model a 25 × 25 m grid with possible samples every 10cm. When sampling a point between two known values, we used the closest known value. As discussed below (section 3.4), we operated on the residuals of the elevation values left after removing linear trends from each grid.
This dataset enables us to examine enough data points to assess each sampling method over a variety of spatially correlated data, including a wide variance of ranges and many fractal and linear variograms (e.g. Reference Deems, Fassnacht and ElderDeems and others, 2006).
Generally, normal distributions do not model snow data well, and log-normal distributions perform only slightly better (Reference KronholmKronholm, 2004). However, while investigating a subset of the data for log-normal trends, we compared the trends in the real data with the Swiss grid samples (described below) of those data.
We found that, although 8–18% of the Swiss grid samples showed a significance at ρ < 0.05 fit for a log-normal distribution, (dependent on fit method, KS/Lillefors, Anderson-Darling and Cramer-von Mises tests were used through the Nortest R package; Reference GrossGross, 2006), none of the corresponding real datasets showed ρ < 0.05 fit to a log-normal model. Thus, we did not include normal or log-normal fit as a basis for choosing the dataset.
3.2. Sampling
We compare gridded, gridded-random, linear-random and pure-random sampling methods. Figure 1 shows visual layouts of the four sample methods used.
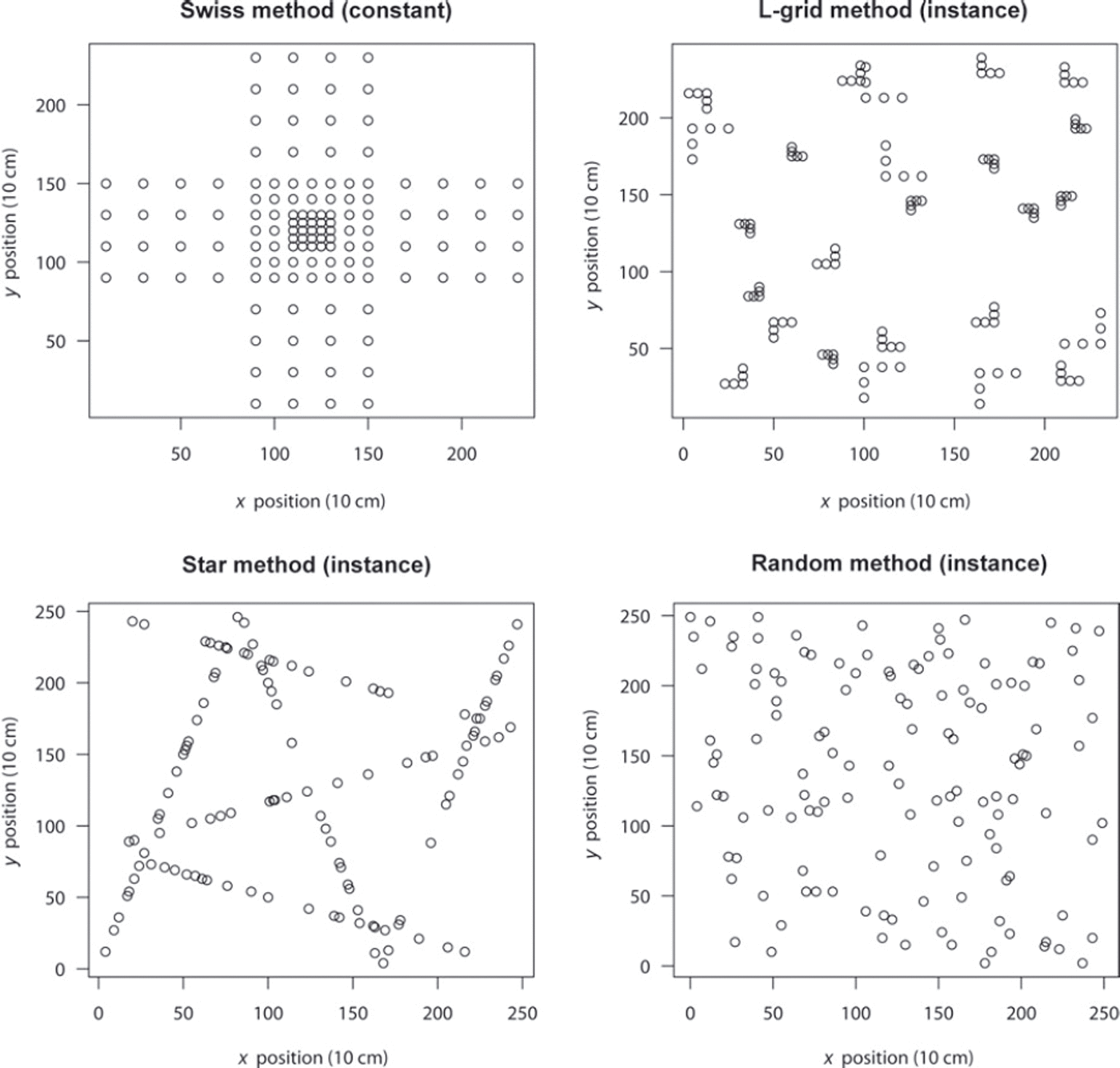
Fig. 1. The four sampling methods used. Note that the three methods that contain randomness (Random, Star and L-grid) varied with every instance. Each grid consists of 250 × 250 points, which we show here as 10 cm spacing.
Due to the extensive analysis provided by Reference KronholmKronholm (2004), we use the Swiss grid as the representative grid method. For the gridded-random method we choose the L-grid (D. Cline and others, http://www.nohrsc.nws.gov/cline/clpx.html; Reference Bellaire, Schweizer and CampbellBellaire and Schweizer, 2008), which enjoys relatively wide use. A simple uniform random-sample distribution served as the pure-random sample.
To approximately equalize its number of points and maintain its original spacing, we add an additional outer layer (16 points) to the Swiss grid. The 16 additional points give it the most sample points (129) of the methods. Random sampling consisted of 125 points, Star consisted of 126 points (21 points per line over 6 transects) and L-grid consisted of 125 points (5 points per grid over 25 equal grids).
Our method, Star, fills the linear-random niche, as we could find no others. It consists of six transects which always divide up the area the same way, as shown in Figure 1. Each transect has the same number of sample locations. Only the spacing between points varies randomly from sample to sample and transect to transect.
After one winter of use, we found the effective minimum spacing varies by the type of sampling being performed (Reference Shea, Jamieson, Schweitzer and van HerwijnenShea and Jamieson, 2009). For point crystal size measurements, our smallest usable spacing was 10 cm. For measurements that require larger support or equipment, the smallest spacing may be larger to prevent overlap of measurement effects.
To use Star, one begins at the top of observer’s left and traverses across the area to one-third of the way down the opposite (right) side, sampling at uniform random intervals along the way. This forms transect one. From there, the user repeats the random sampling process, turning and traversing again to a point two-thirds down the left side, and turns again – still sampling – to traverse to the lower right corner. This forms transects two and three, respectively. The same ’by thirds’ spacing structures transects four, five and six, which are essentially a 90• counterclockwise rotation of the first three transects over the same area.
Star’s efficiency comes from a number of qualities. Most notably, the user always travels a known and reasonable distance, including a small number of turns, to sample an area. Here, on the 25 m squares, the user would traverse 184 m total with only six turns, including the traverse on the bottom from the end of transect three to the start of transect four. To sample the Swiss grid in the most efficient way would take 191 m of travel with 18 turns.
The L-grid does not have a constant travel distance, since the positions of the Ls in the method vary. As a lower bound (when all of the Ls are as small as possible and ideally stacked linearly with respect to one another) the user would travel just under 160 m. However, the user would make 75 turns: one for each L, one to head toward the next L and one to align themselves along the new L. At the upper distance bound (using the largest L size and with Ls placed in opposite corners of their grids) the user would travel >240 m, again with 75 turns.
Finding the shortest distance to travel and minimal required turning for the random-sampling method is a very difficult problem, and we do not present its efficiency here. However, the high number of turns required to perform L-grid sampling should give the reader an intuitive sense of why pure-random sampling methods remain essentially unusable in the field.
Thus, we feel the structure of Star adequately fulfils our objective of efficiency and minimal destructiveness as the user can stay on one line at a time on skis or on foot; the remainder of this paper focuses on the comparative accuracy of the method.
3.3. Randomness
For the three methods containing randomness – Random, L-grid and Star – the simulation varied that randomness for every sample layout. For Star, the spacing along each sampling transect varied. For Random, the x and y coordinates for each point varied. For L-grid, the axis point of each L within each grid, the spacing between points and the orientation of the L varied. So, the layouts in Figure 1 are only one instance of many random variations used.
When the formative process varies, so should the measurement spacing (Reference Blöschl and SivapalanBlöschl and Sivapalan, 1995). This variation in spacing ‘catches’ and identifies correlation by being itself an independent function of what it measures. Thus the attractiveness of random methods comes from process-independent variance in the sample method. In other words, randomness does not oscillate in step with any measured data (other than random data), and it may help discover the operation of unknown formative process scales.
However, this means that methods which use randomness must maintain it. Even if the locations of a sample are decided randomly once, one cannot easily know whether that single instance lies at the extreme end of a random distribution, or the more desirable median of a random distribution. Thus, if we selected a single instance of Star, L-grid or (pure) Random methods, it could introduce bias or skew, and our results would be very different.
3.4. Variogram
For each real data grid and its four samples, we produced omnidirectional variograms using Reference CressieCressie’s (1993) robust method. Each semivariance, calculated over 15 bins with respect to residuals left after linear trend removal, then provided a basis for fitting a variogram model. We removed all linear trends, regardless of significance, because we prioritized removing all linear anisotropy over retaining the original data values.
The general variogram, shown in Equation (1) (Reference O’Sullivan and UnwinO’Sullivan and Unwin, 2003), simply finds the squared difference between all n residual value pairs (zi , zj ) within a lag bin of width 2Δ and given lag distance, d ± Δ wide, from each other:

Cressie found that, although this general form has no bias, it can have skew because the squared factor amplifies large outliers. His robust model calculates the variogram ![]() based on transformed differences of (Reference CressieCressie, 1993) with a numerical denominator to account for the bias this introduces:
based on transformed differences of (Reference CressieCressie, 1993) with a numerical denominator to account for the bias this introduces:
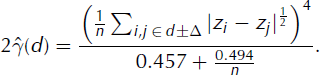
After calculating the variogram, we fit a standard spherical model γ (Equation (3)). The model has range, a, sill, c, and nugget, c 0, and is defined up to the range d = a. After that, we use the linear function γ(d) = c, where c = c 1 + c 0. This means c 1 represents the y-axis distance over which the semivariance rises from nugget c 0 to sill c (Reference O’Sullivan and UnwinO’Sullivan and Unwin, 2003):
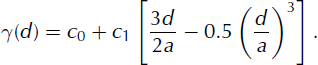
We present the model and its use on a single real data variogram in Figure 2. It can be seen that the variogram can serve as a tool for relating to physical-process scales, as the range demonstrates the physical extent at which measurements cease being similar to one another.
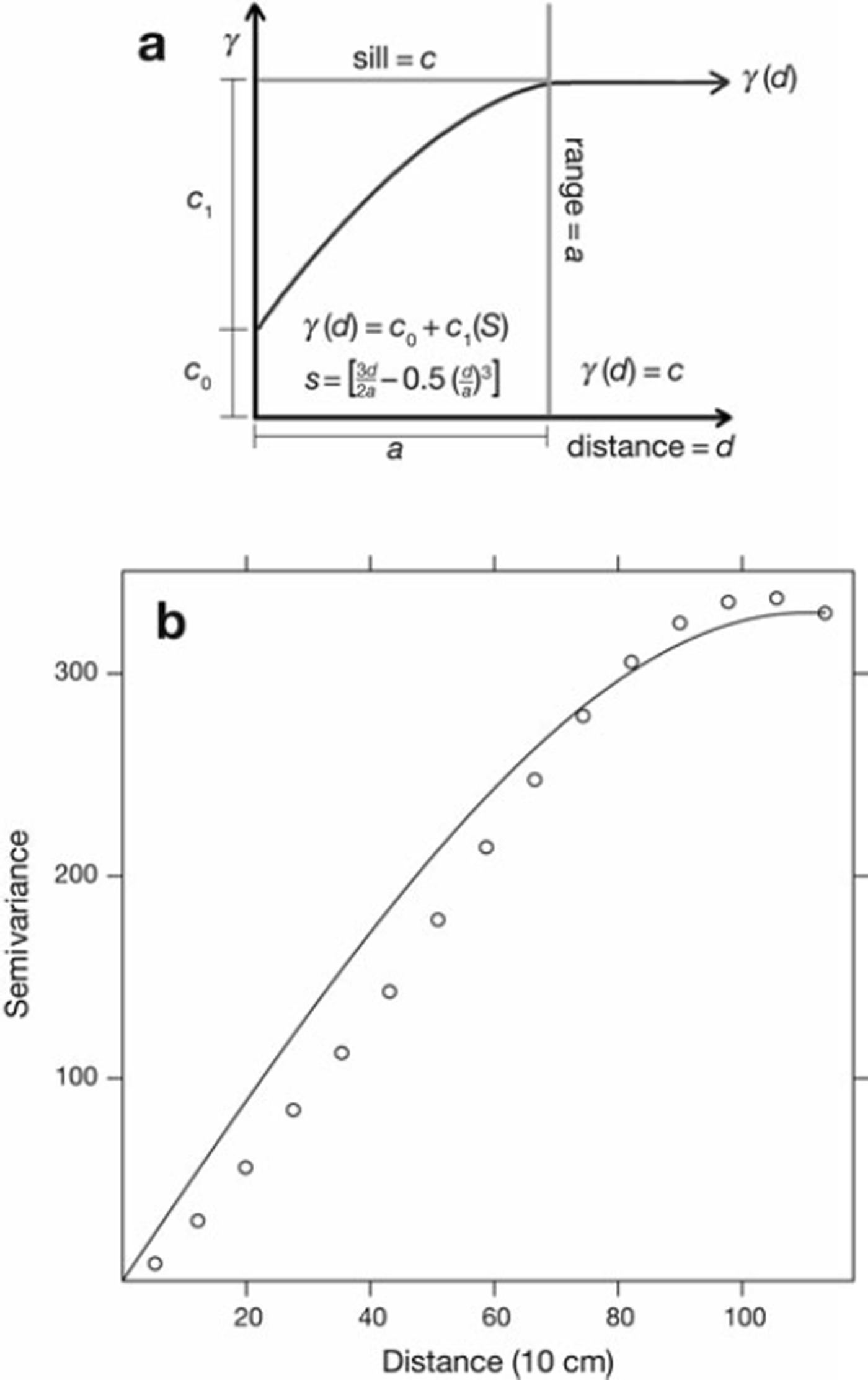
Fig. 2. (a) A diagram showing how the equations of the spherical variogram model determine range. (b) An example variogram and fit spherical model. The spherical model shows a reasonable, but not perfect, fit to the variogram.
Due to its current prevalence in snow literature as a measure for evaluating data, as well as sampling methods (Reference KronholmKronholm, 2004; Reference Bellaire, Schweizer and CampbellBellaire and Schweizer, 2008), we select the omnidirectional variogram and a spherical model. We utilize least squares to fit the spherical model form to each variogram.
Use of these methods allows us to compare Star to the Swiss and random models, which have been previously compared (Reference Kronholm and BirkelandKronholm and Birkeland, 2007). However, such a set-up - and the variogram in particular - has many limitations. In section 4.4 we briefly discuss the limitations of the spherical model and omnidirectional variogram.
As previous work has already reported the variances of all spherical semivariogram model attributes (range, a, sill, c, and nugget, c 0) across different sampling methods excepting Star (Reference Kronholm and BirkelandKronholm and Birkeland, 2007), we choose to simply present the error in range, a, to comparatively demonstrate Star’s fitness as a sampling method.
Reference Kronholm and BirkelandKronholm and Birkeland (2007) showed that those sampling methods which performed well in range comparisons also performed well in sill comparisons. Here, after removing linear trends individually for each dataset, the remaining sill values complicate comparison across datasets, and thus we refer to the relation present in that work. Then, the nugget can be thought of as a measure of how much small-scale process detail a method can capture. It may also be interesting for additional comparison in the future, but here we focus on the larger perspective of spatial correlation detection.
4. Results
On completion of the Monte Carlo simulation, there were four possible cases of how each sample’s variogram model could compare with that of the original real data model. With a least-squares-fit method for the spherical model in Equation (3), the real data model could converge on a spatial correlation range, the sample data could converge on an spatial correlation range, and the two did not necessarily happen together.
Non-convergences imply that the variogram would be better served by a linear model, a fractal model or any number of other possibilities. Fractal variograms rise up to a levelling-off point (pseudo-sill) before rising again to another levelling-off point. We show an example from our dataset in Figure 3.
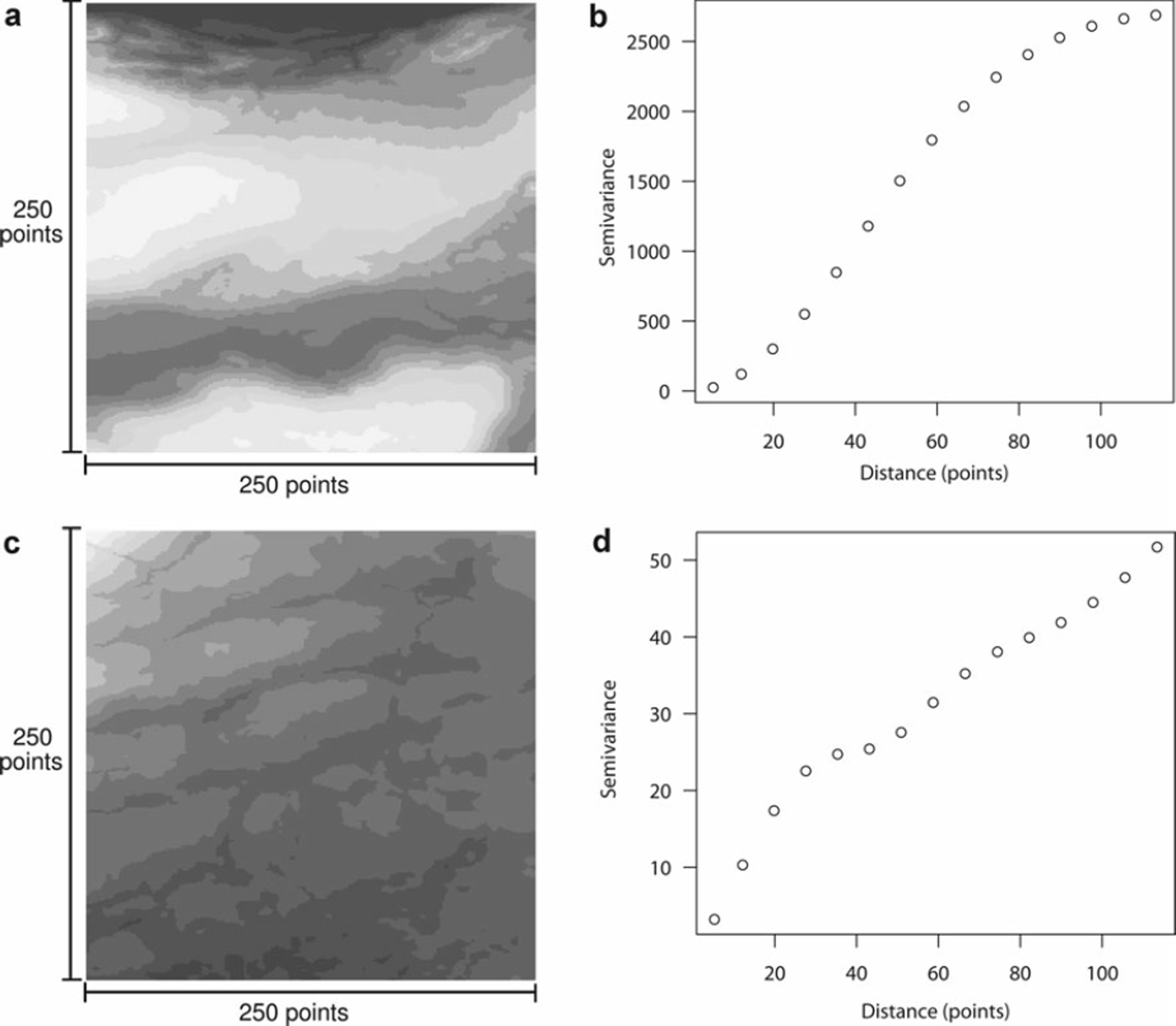
Fig. 3. (a, c) Two example datasets, both from Geobase grid 093b04, presented in greyscale varying with the point values. Each has the semi-variance rise of its corresponding variogram shown on the right. The variogram in (b) should be more properly fit with a Gaussian model than a spherical one. Compare to the variogram plot in (d), which presents a complex fractal character of multiple ranges, or ‘spatial correlation within spatial correlation’.
These fractal variograms imply spatial correlation within spatial correlation and, although they can be interesting and useful (Reference Deems, Fassnacht and ElderDeems and others, 2006), they often reduce to a non-converged model when spherical models attempt to fit to them. This comes from the spherical model’s inability to fit multiple ranges and sills and thus reducing, by least squares, to fitting none of them.
Even more visually near-spherical variograms, such as the semivariance rise of the Gaussian-type variogram shown in Figure 3c, can reduce to a linear, non-converged fit. The fitting mechanism (in this case least squares) must attempt to fit the lesser rising slope at the low distances and thus may undershoot and miss the sill when it does occur at higher distances.
As the spherical model must curve eventually, these non-convergences present with very large ranges, often several orders of magnitude larger than the data extent. Thus, unless otherwise noted, we define a converged spherical model as one having a range of 500 points or fewer. This definition includes spatial correlation within the 25 m area and twice that width in a hypothetical prediction beyond it.
This hypothetical extension, though not statistically significant, is used in other sources in practice (Reference KronholmKronholm, 2004), and thus for comparison consistency we include those extents in our analysis here. Also, where possible, we present results for different definitions of convergence at less than 500 points.
This gives us four possible categories, each with some unique subset of the 1024 tests, as not all the real data converged on a good fit to the spherical model:
Common non-convergence (CNC): Where neither real data nor sample data variograms converged on a spherical model.
False convergence (FC): Where the sample data variogram converged on a spherical model but no spherical model fit the real data variogram.
False non-convergence (FNC): Where the real data variogram fit a spherical model, but the sample data variogram did not converge on a spherical model.
Common convergence (CC): Where both the real data and sample data variograms converged on a spherical model, though not necessarily the same one.
The main validation of accuracy lies in the common convergences and common non-convergences, but we examine the particulars of each category in turn. How often a sampling method ends up in the right category can be at least as important as how well it performs in any one category.
Without knowing how often a sampling method correctly or incorrectly detects the existence of spatial structure in the underlying data, one cannot put faith in the structures that the sample does detect. For, as this paper shows, some instances of ‘detected’ structure may not have been present at all; and conversely, some structures that should have been found went unnoticed. We consider spatial correlation to be a measure of spatial structure, and we consider spherical model fit to be a measure of detection, but false spatial structure detection, whether by false presence or false absence, should be of concern by any measure.
4.1. Common convergence
Finding the total number of correct convergences involves a simple intersection. If C(real) represents the set of real datasets which converge on a spherical model fit, and C(sample) represents the set of sample datasets which converge on a spherical model fit, then the intersection of the two gives the common convergence (CC):
Though only part of the picture, the number of times a sampling method shows spatial correlation correctly can be a measure of its performance. The correct convergence of a sample measures how often it detects spatial correlation when it exists in the real data.
Consider, for example, an ideal sampling method which has a common convergence of 100%, and a common non-convergence of 100%. Then, every time our sample converged, we could know the real data actually demonstrated some kind of spatial structure - here, variance - such that it fits a spherical model with a reasonable range. In reality, when samples have common convergence only 75% of the time or less on these elevation data, we know that at least 2 5% of our linear variograms should have been reasonably spherical, but which data compose that 25% is unknown.
When both real data and sample data fit a spherical model well, the next question becomes: how well? To answer this, we find the residuals in ranges for the common convergences. For example, if the real data present with a range a r = 200, and the sample with a range a s = 400, although they both converge, the sample data range is not very accurate with an error of —200 points (—20 m).
Figure 4 shows histograms for the range differences for all common convergences with ranges less than 500 points (50 m). If the ranges of the sample set model variograms are denoted as a(sample) and the ranges of the real dataset model variograms as a(real), then the histograms display a(reali) — a(samplei),V(reali, sample i) ∈ CC for each sampling method. Note that for range errors, medians represent bias; in Figure 4 all medians are positive and thus imply that these four sampling methods generally underestimate the range.
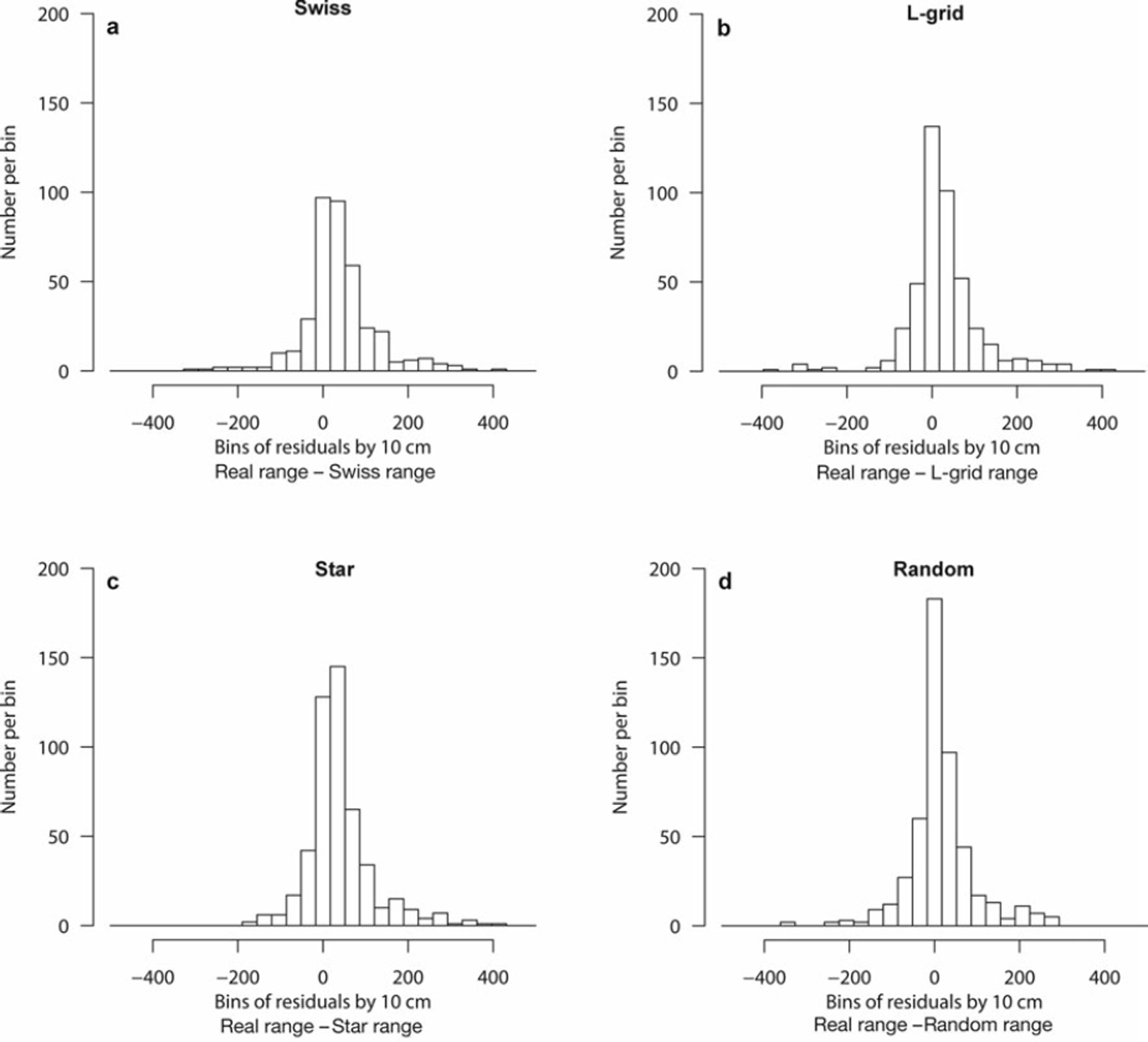
Fig. 4. Histogram distributions of range errors for n correct common convergences. (a) Swiss: n = 384, median = 31.6 points (3.1 m), standard deviation = 86.5 points (8.7 m). (b) L-grid: n = 447, median = 16.3 points (1.6 m), standard deviation = 85.8 points (8.6 m). (c) Star: n = 496, median = 25.2 points (2.5 m), standard deviation = 77.3 points (7.7 m). (d) Random: n = 498, median = 8.2 points (0.8 m), standard deviation 77.9 points (7.8 m).
One can see that both more accurate convergence and higher incidence of common convergence are highly desirable, as is higher incidence of common non-convergence (see section 4.4). The common convergence numbers are shown over different definitions of convergence range in Figure 5a.
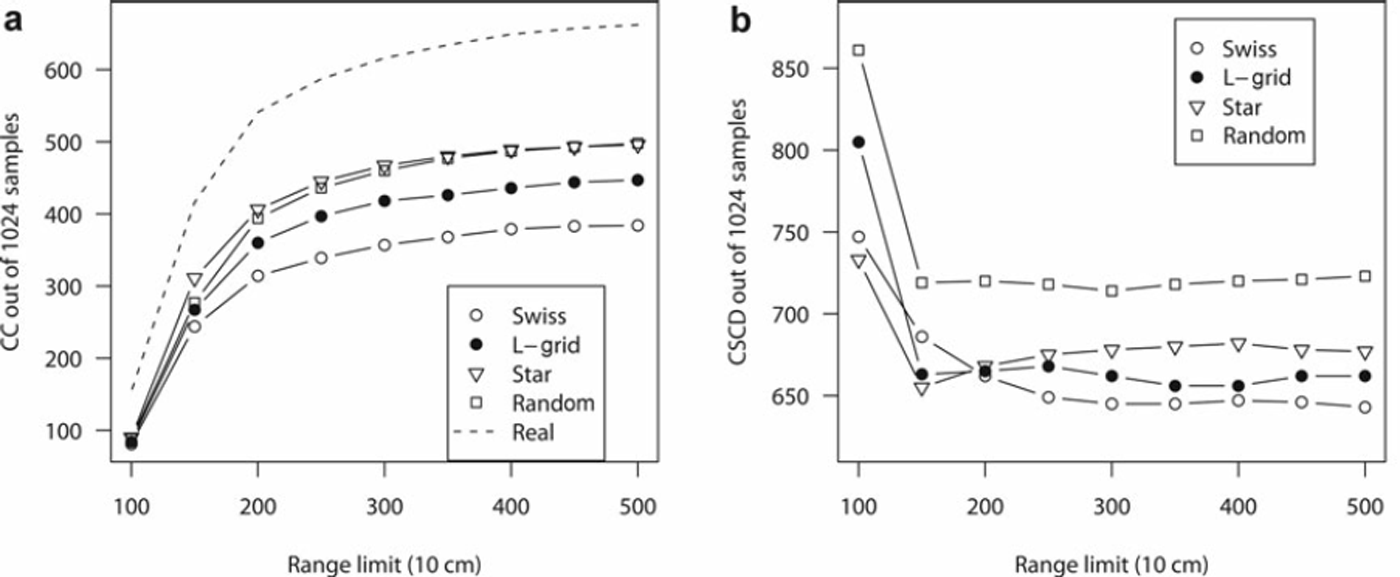
Fig. 5. (a) Common convergence (CC) and (b) correct spatial correlation detection (CSCD) graphs. Definitions vary by what range limit we choose to define as a good spherical model fit, and we show the results over various definitions of convergence, 10–50 m. Note the instability at 150 points (15 m) and less for CSCD; the corresponding ranges in the CC graph show that relatively few data points exist at this definition and thus we do not obtain a good model.
4.2. False convergence
We derive a sample’s false convergence, FC, by the set difference of converged samples, C(sample), with the set of common convergences, CC, from Equation (4):
Of all the methods, Star has the most false convergence: the error of finding, via a spherical model, spatial trends where none exist in the real data. The Swiss method errs on the side of more false non-convergences, whereas both L-grid and Random more evenly distribute their false convergence and false non-convergence. Table 1 shows the FC values for ranges less than 500 points.
Table 1. Chi-squared analysis for categorical FC and FNC tendencies. O(FC) and O(FNC) represent observed false convergence and false non-convergence rates out of 1024 samples for each sample method, with convergence being a model fit at range a < 500 points. E(FC) and E(FNC) represent the weighted expected FC and FNC rates out of the n = 1391 total false results represented by the four samples. Finally, (O – E)2/E represents the standardized squared difference between observed and expected values, which when summed yield the χ2 statistic of 52.05. With degrees of freedom, f = 3, this implies categorical distinctness at ρ < 0.001 across incorrect spatial correlation detection results per method

The reason for Star’s false convergences comes from its pockets of concentrated points near the outer areas of the sample. In Figure 1, areas of greater and lesser concentration of points can be seen. In the few instances where small spatial correlation happens to exist in those areas in the real data, Star emphasizes it enough to cause the spherical model to converge falsely.
To examine these tendencies between samples, we performed a simple type of cluster analysis through quadrat counts (e.g. Reference O’Sullivan and UnwinO’Sullivan and Unwin, 2003) every 50 points square (5 × 5 m). This means, by definition, the L-grid contained five points per quadrat. The Swiss grid showed quadrat count ranges between 0 (the outer corners) and 41 (centre quadrat). The random grid ranged from 4.88 to 5.09 samples per quadrat, with no readily apparent pattern. The Star method ranged from 0 to 12.68 per quadrat, with all four quadrats with more than 12 samples on the outermost rim. One can see these clusters near the edges in Figure 1.
Examination of the categorical chi-squared analysis of the FC and FNC categories in Table 1 indicates that a main distinction between the samples can be quantified by the most populated quadrat on the outer rim. In the case of random and L-grid, the most populated quadrat in the outer rim is approximately 5, for Star it is more than 12 and for Swiss it is only 4.
For the low bias in distribution (an unbiased distribution would have every quadrat count equal to 5), we see low contributions to the χ2 total. For the two methods with bias, Star and Swiss, we see high contributions to the χ2 total, with the Swiss method demonstrating the most categorical bias. Note that here bias does not mean error; rather, it demonstrates a method’s tendency to have more FNC or FC within its total false results (FNC U FC) relative to the other samples.
Also of interest is that although four quadrats of the Star method along the outer edges averaged more than 12 samples over the 1024 runs, all of the outer edge quadrats together averaged to 5.22 samples per quadrat, explaining the success of Star in finding spatial correlation over the dataset.
4.3. False non-convergence
We can derive a sample method’s false non-convergence (FNC) by the set difference between the set of converged real data C(real) versus the set of common convergences, CC from Equation (4):
The numbers for false non-convergence appear in Table 1. Overall, the Swiss grid shows the greatest tendency to not converge on a good spherical model fit when the real data do. This means it is more likely to present a linear semivariogram (or a very large, poorly fitting spherical model) when the real data present stronger spatial correlation. We feel that this occurs due to the points being concentrated in the centre with very few near the edges, as discussed above. Such a method may only detect spatial correlation in that area well. Indeed, other sampling methods (such as the MT2004 grid described by Reference Kronholm and BirkelandKronholm and Birkeland, 2007) have been developed to try to spread the points over a larger area while retaining the field advantages of gridded construction.
4.4. Common non-convergence
To be a correct model of the real data, a sampling method should not only converge upon a range with a given model (here, the spherical one in Equation (3)), but also not converge when the model does not fit the real data well. We can find the common non-convergence (CNC) via the set difference of all real data models, {real}, with the union of both convergence sets, C(sample) and C(real), given by:
Though all real data show visual spatial correlation, some real data instances do not fit a spherical semivariogram model well. Two examples are shown in Figure 3, where we can see obvious spatial patches which we would like to discover using our sampling method, but the corresponding variograms next to the images are obviously non-spherical.
In fact, from the low numbers of real data instances which did not converge, we observe that (although common in snow data analysis) spherical variograms, and even variograms in general, are not necessarily good solve-all tools for detecting patterns and process effects.
Nevertheless, CNC, along with CC, completes the set of correct spatial correlation answers a sampling method can produce via the variogram and a model. Though technically uninteresting, as CNC does not discover any spatial correlation, it assists in calculating the correct spatial correlation detection total for a sampling method, as discussed in the next subsection.
4.5. Correct spatial correlation detection
When we know the common convergences from Equation (4) and the number of common non-convergences from Equation (7), we know the total number of correct spatial correlation answers a given sampling method finds. This total gives the measure of correct spatial correlation detection (CSCD) for a sample:
Figure 5b shows the numbers of correct spatial correlation detections for each sample over various ranges. In this case, rather than simply using 500 points (50 m) as a general convergence measure, we find how many correct answers each sample detected for ranges of 500–100 points, at intervals of 50 points (5 m). Since linear and other non-spherical variograms forced to fit spherical models can be identified by extremely large range values, this initially assists in finding which should be converging on a good model fit, and for lower ranges simply reduces the window of good fits we need to analyze.
As the number of converged simulation data points becomes fewer and fewer, it becomes easier and easier to use a so-called ‘ignorant’ sampling algorithm. For example, being picky enough to only consider ranges of <100 points (10 m) leaves us with so few real data convergences (154 of 1024 samples) that we could theoretically not sample anything at all, and thus never converge, and still achieve the ’correct’ answer (non-convergence) over 80% of the time. This should give some intuitive sense of the instability demonstrated at the left edge of Figure 5b at ranges of 150 points and fewer.
Finally, we note from Figure 5b that, even in a best case, no sampling method detects spatial correlation correctly better than three out of four times. Considering various definitions of range, the three non-random sampling methods perform comparatively.
5. Discussion
Above all, this paper demonstrates that different sampling methods have different strengths and weaknesses. Of course, all statistical strengths and weaknesses presented here depend greatly on the spherical model fit.
But given that, for the smallest range error bias per known converging variogram model, the L-grid seems the obvious choice. For focus at the centre of an area, the Swiss grid may assist in revealing details there with its point concentration. For detection of unknown ranges of a process, the Star properly matches or rejects a spherical fit when the data do more often than the other methods, implying better correlation across varied datasets. In addition, Star has efficient design and a small standard deviation of range error in its common convergences. Of course, the pure-random model presents the best correlation and smallest error of all but remains very inefficient to properly implement in the field.
6. Conclusions
Given the strengths and weaknesses of each sampling method and the range of applications for each method, we cannot simply say one method presents the best mix. Ease of use allows one to obtain the most points in a given time. Mathematical robustness allows one to feel more confident in the results.
As an initial design of a sampling method intended to make randomness usable and efficient in the field, the Star method shows promise for linear-random sampling methods in general, due to its ease of layout plus comparably accurate spatial correlation detection. One could spend some time minimizing the clustering effects in the corners to improve Star and better approach a purely random distribution.
However, when measuring spatial variability on snow, we cannot really know what the variability range is without measuring every single point. Thus, when using the variogram, we only know the spatial correlation range of our measurements, and a little about how good our measurement methods probably are. Furthermore, when we find spatial correlation in our sample data without knowing every measurable point, false convergence and false non-convergence will occur with any sampling method, and Figure 5b shows that, even in the best case, FC or FNC will occur at least one out of four times for these sampling methods using this dataset.
The greatest question posed by this paper centres around how to model spatial correlation in snow. The real data we use had visual spatial correlation in every sample; however, the spherical model converged on a reasonable fit to the semivariograms of those data fewer than two out of three times. It may be possible to scale a sampling method to extend well beyond the expected range, which would then obtain more robust measurements of spatial correlation. However, the destructiveness of snow sampling often presents a barrier to adaptive sample method scaling.
Furthermore, when manually treated to detect anisotropy, to discover better fits with different models or to use techniques other than the variogram, the sample data will probably be much less limited than presented here. Thus, investigating how variograms, or other process detection and correlation tools, can be best used with the particulars of snow-science sampling may prove useful.
7. Acknowledgements
We thank L. Bentley and G. Margrave for their thoughtful comments on a draft of this paper. In addition, the paper greatly benefited from careful review by K. Kronholm and another reviewer. For financial support, we gratefully thank the Natural Sciences and Engineering Research Council of Canada, HeliCat Canada, the Canadian Avalanche Association, Mike Wiegele Helicopter Skiing, Teck Mining Company, Canada West Ski Areas Association, the Association of Canadian Mountain Guides, Backcountry Lodges of British Columbia and the Canadian Ski Guides Association.










