Skip to main content
SpringerLink
Log in

A Strain Energy Density Potential for Non-Crystalline Solids Using Molecular Interactions

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

Abstract

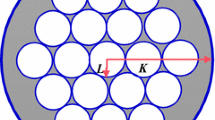
Non-crystalline solids have important applications in engineering and science. To predict the stress-strain behaviour of these materials, this work constructs an efficient strain energy density function using the concepts of molecular interactions. Considering hard contact between molecules, strain energy density of materials is defined in terms of packing fraction (volume occupied by the molecules per unit volume of the material) in deformed configurations. The packing fraction is represented in terms of strain invariants of right Cauchy-Green deformation tensor. Constitutive model obtained from the present strain energy density function is applied for predicting finite deformations of the materials like uniaxial extension, equibiaxial extension, and pure dilation. We observe that increasing reference packing fraction increases the Cauchy stress components. Results obtained from the present theoretical model is compared with experimental results of flexible polyurethane foam materials. We obtain good agreement with the experimental results. The present strain energy density function can be applied for predicting deformation as well as stress-strain behaviour of any other micro/nano components used in engineering systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.

Similar content being viewed by others

REFERENCES

  1. M. L. Falk and C. E. Maloney, “Simulating the mechanical response of amorphous solids using atomistic methods,” Eur. Phys. J. B. 75 (4), 405–413 (2010). https://doi.org/10.1140/epjb/e2010-00157-7

    Article  ADS  CAS  Google Scholar 

  2. R. Xu and Y. Xu, Modern Inorganic Synthetic Chemistry, 2nd ed. (Elsevier, 2017).

    Google Scholar 

  3. Zb. H. Stachurski, “On structure and properties of amorphous materials,” Mater. 4 (9), 1564–1598 (2011). https://doi.org/10.3390/ma4091564

  4. J. Mort, “Applications of amorphous materials,” Phys. Technol. 11 (4), 134–141 (1980). https://doi.org/10.1088/0305-4624/11/4/I02

    Article  ADS  Google Scholar 

  5. A. J. M. Spencer, Continuum Mechanics (Dover Publ., 2004).

    Google Scholar 

  6. R. W. Ogden, “Large deformation isotropic elasticity - on the correlation of theory and experiment for incompressible rubberlike solids,” Proc. Math. Phys. 326 (1567), 565–584 (1972). https://doi.org/10.1098/rspa.1972.0026

    Article  CAS  Google Scholar 

  7. M. Mooney, “A theory of large elastic deformation,” J. Appl. Phys. 11 (9), 582–592 (1940). https://doi.org/10.1063/1.1712836

    Article  ADS  Google Scholar 

  8. R. S. Rivlin and E. K. Rideal, “Large elastic deformations of isotropic materials IV. further developments of the general theory,” Philos. Trans. Roy. Soc. A 241 (835), 379–397 (1948). https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.1948.0024

    ADS  MathSciNet  Google Scholar 

  9. A. N. Gent, Engineering with Rubber (Carl Hanser Verlag, Munich, 2001).

    Google Scholar 

  10. W. K. Liu, E G. Karpov, S. Zhang, and H. S. Park, “An introduction to computational nanomechanics and materials,” Comput. Meth. Appl. Mech. Eng. 193, 1529–1578 (2004). https://doi.org/10.1016/j.cma.2003.12.008

    Article  MathSciNet  Google Scholar 

  11. D. Garcia-Gonzalez, A. Jrusalem, S. Garzon-Hernandez, et al. “A continuum mechanics constitutive framework for transverse isotropic soft tissues,” J. Mech. Phys. Solids. 112, 209–224 (2018). https://doi.org/10.1016/j.jmps.2017.12.001

    Article  ADS  MathSciNet  Google Scholar 

  12. D. A. McQuarrie, Statistical Mechanics (Viva Books Private Limited, New Delhi, 2008).

    Google Scholar 

  13. V. K. Devendiran, R. K. Sandeep, K. Kannan, and K. R. Rajagopal, “A thermodynamically consistent constitutive equation for describing the response exhibited by several alloys and the study of a meaningful physical problem,” Int. J. Solids Struct. 108, 1–10 (2017). https://doi.org/10.1016/j.ijsolstr.2016.07.036

    Article  CAS  Google Scholar 

  14. N. Sakaguch, M. Niinomi, and T. Akahori, “Tensile deformation behavior of ti-nb-ta-zr biomedical alloys,” Mater. Trans. 45, 1113–1119 (2004). https://doi.org/10.2320/matertrans.45.1113

    Article  CAS  Google Scholar 

  15. Y. L. Hao, S. J. Li, S. Y. Sun et al., “Super-elastic titanium alloy with unstable plastic deformation,” Appl. Phys. Lett. 87 (9), 091906 (2005). https://doi.org/10.1063/1.2037192

  16. F.Q. Hou, S.J. Li, Y.L. Hao, and R. Yang, “Nonlinear elastic deformation behaviour of ti-30nb12zr alloys,” Scr. Mater. 63 (1), 54–57 (2010). https://doi.org/10.1016/j.scriptamat.2010.03.011

    Article  CAS  Google Scholar 

  17. X. Zhang, Z. Chen, and Y. Liu, The Material Point Method (Academic Press, Oxford, 2017).

    Book  Google Scholar 

  18. D. F. Jones and L. R. G. Treloar, “The properties of rubber in pure homogeneous strain,” J. Phys. D: Appl. Phys. 8 (11), 1285–1304 (1975). https://doi.org/10.1088/0022-3727/8/11/007

    Article  ADS  Google Scholar 

  19. P. Steinmann, M. Hossain, and G. Possart, “Hyperelastic models for rubber-like materials: consistent tangent operators and suitability for treloars data,” Arch. Appl. Mech. 82, 1183–1217 (2012). https://doi.org/10.1007/s00419-012-0610-z

    Article  ADS  Google Scholar 

  20. B. R. Seth, Generalized Strain Measure with Applications to Physical Problems, MRC Technical Report No. 248 (Math. Res. Center, Medison, 1964).

  21. K. Hashiguchi, Elatoplasticity Theory (Springer-Verlag, Berlin Heidelberg, 2013).

    Google Scholar 

  22. M. Hossain and P. Steinmann, “More hyperelastic models for rubber-like materials: consistent tangent operators and comparative study,” J. Mech. Behav. Mater. 22 (1–2), 27–50 (2013). https://doi.org/10.1515/jmbm-2012-0007

    Article  CAS  Google Scholar 

  23. E. M. Arruda and M. C. Boyce, “Evolution of plastic anisotropy in amorphous polymers during finite straining,” Int. J. Plast. 9 (6), 697–720 (1993). https://doi.org/10.1016/0749-6419(93)90034-N

    Article  CAS  Google Scholar 

  24. O. Yeoh, “Hyperelastic material models for finite element analysis of rubber,” J. Nat. Rubber Res. 12, 142–153 (1997).

    CAS  Google Scholar 

  25. J. Lambert-Diani and C. Rey, “New phenomenological behavior laws for rubbers and thermoplastic elastomers,” Eur. J. Mech. A/Solids 18 (6), 1027–1043 (1999). https://doi.org/10.1016/S0997-7538(99)00147-3

    Article  ADS  Google Scholar 

  26. O. Lopez-Pamies, “A new I1-based hyperelastic model for rubber elastic materials,” C. R. - Mec. 338 (1), 3–11 (2010). https://doi.org/10.1016/j.crme.2009.12.007

    Article  ADS  CAS  Google Scholar 

  27. L. C. S. Nunes, “Mechanical characterization of hyperelastic polydimethylsiloxane by simple shear test,” Mater. Sci. Eng. A. 528 (3), 1799–1804 (2011). https://doi.org/10.1016/j.msea.2010.11.025

    Article  CAS  Google Scholar 

  28. P. M. Gullett, M. F. Horstemeyer, M. I. Baskes, and H. Fang, “A deformation gradient tensor and strain tensors for atomistic simulations,” Model. Simul. Mater. Sci. Eng. 16 (1), 015001 (2007). https://doi.org/10.1088/0965-0393/16/1/015001

  29. J. Ghanbari and R. Naghdabadi, “Multiscale nonlinear constitutive modeling of carbon nanostructures based on interatomic potentials,” Comput. Mater. Contin. 10 (1), 41–64 (2009). https://doi.org/10.3970/cmc.2009.010.041

    Article  Google Scholar 

  30. P. M. Morse, “Diatomic molecules according to the wave mechanics. II. Vibrational levels.” Phys. Rev. 34 (1), 57–64 (1929). https://doi.org/10.1103/PhysRev.34.57

    Article  ADS  CAS  Google Scholar 

  31. J. Li and A. K. Soh, “Modeling of the plastic deformation of nanostructured materials with grain size gradient,” Int. J. Plast. 39, 88–102 (2012). https://doi.org/10.1016/j.ijplas.2012.06.004

    Article  CAS  Google Scholar 

  32. B. Vorselaars, A. V. Lyulin, and M. A. J. Michels, “Deforming glassy polystyrene: Influence of pressure, thermal history, and deformation mode on yielding and hardening.” J. Chem. Phys. 130 (7), 074905 (2009). https://doi.org/10.1063/1.3077859

  33. F. Yang, S. Ghosh, and L. J. Lee. “Molecular dynamics simulation based size and rate dependent constitutive model of polystyrene thin films,” Comput. Mech. 50, 169–184 (2012). https://doi.org/10.1007/s00466-012-0714-x

    Article  MathSciNet  Google Scholar 

  34. M. Jafari, S. Ziaei-Rad, and N. Nouri, “Modeling of the plastic deformation of polycrystalline materials in micro and nano level using finite element method,” J. Nano Res. 22, 41–60 (2013). https://doi.org/10.4028/www.scientific.net/JNanoR.22.41

    Article  CAS  Google Scholar 

  35. A. V. Konovalov, “Constitutive relations for metals under high-temperature plastic strains,” Mech. Solids 44 (1), 98–104 (2009). https://doi.org/10.3103/S0025654409010105

    Article  ADS  Google Scholar 

  36. D. L. Bykov, D. N. Konovalov, and V. A. Peleshko, “Constitutive relations for calculating the processes of quasistatic deformation, damage, and fracture of bodies (Including those with concentrators) made of filled polymer materials,” Mech. Solids 46 (6), 839–855 (2011). https://doi.org/10.3103/S0025654411060045

    Article  ADS  Google Scholar 

  37. S. Mukherjee and A.K. Mandal, “A generalized strain energy function using fractional powers: Application to isotropy, transverse isotropy, orthotropy, and residual stress symmetry,” Int. J. Non-Lin. Mech. 128, 103617 (2021). https://doi.org/10.1016/j.ijnonlinmec.2020.103617

  38. S. Mukherjee and A. K. Mandal, “Static and dynamic characteristics of a compound sphere using initial stress reference independence,” Int. J. Non-Lin. Mech. 136, 103787 (2021). https://doi.org/10.1016/j.ijnonlinmec.2021.103787

  39. S. Mukherjee and A. K. Mandal, “Extended gent models for residually stressed thick spheres and cylinders,” Int. J. Non-Lin. Mech. 137, 103804 (2021). https://doi.org/10.1016/j.ijnonlinmec.2021.103804

  40. L. Rao V and S. Das, “Drag force on a liquid domain moving inside a membrane sheet surrounded by aqueous medium,” J. Fluid Mech. 779, 468–482 (2015). https://doi.org/10.1017/jfm.2015.434

    Article  ADS  MathSciNet  Google Scholar 

  41. P. Mahata, A. Shrivastava, C. K. Sahu, et al., “Electrostatic interaction with a rigid curved domain causes nonlinear deformation of a thin elastic sheet: Implications for biosystems,” Phys. B: Condens. Matter. 646, 414274 (2022). https://doi.org/10.1016/j.physb.2022.414274

  42. P. Mahata and L. Vennamneni, “Deformation of an elastic membrane interacting electrostatically with a rigid curved domain: implications to biosystems,” Arch. Appl. Mech. 91, 1–17 (2021). https://doi.org/10.1007/s00419-020-01785-1

    Article  Google Scholar 

  43. P. Mahata and S. Das, “Generation of wavy structure on lipid membrane by peripheral proteins: A linear elastic analysis,” FEBS Lett. 591, 1333–1348 (2017). https://doi.org/10.1002/1873-3468.12661

    Article  CAS  PubMed  Google Scholar 

  44. P. Mahata, L. Singhal, R. Prasad et al., “Computational investigation for deformation of lipid membrane by BAR proteins due to electrostatic interaction,” Mater. Today: Proc. 61, 1–9 (2022).

    CAS  Google Scholar 

  45. S. Mukherjee and P. Mahata, “Computational investigation for endocytosis of CoVID-19 virus SARS-CoV-2 in cell membrane,” Proc. Inst. Mech. Eng., Part C 235 (24), 7331–7342 (2021). https://doi.org/10.1177/09544062211029984

    Article  CAS  Google Scholar 

  46. F. Lin, J. S. Peng, S. F. Xue, and J. Yang, “An indirect method to determine nonlinear elastic shear stress-strain constitutive relationships for nonlinear torsional deformation of Al-1%Si shaft,” Mech. Solids 57 (5), 1173–1193 (2022). https://doi.org/10.3103/S0025654422050090

    Article  ADS  Google Scholar 

  47. N. F. Carnahan and K. E. Starling, “Equation of state for nonattracting rigid spheres,” J. Chem. Phys. 5 1(2), 635–636 (1969). https://doi.org/10.1063/1.1672048

  48. F. Lado, “Equation of state of the hard disk fluid from approximate integral equations,” J. Chem. Phys. 49 (7), 3092–3096 (1968). https://doi.org/10.1063/1.1670553

    Article  ADS  CAS  Google Scholar 

  49. E. Leutheusser, “Exact solution of the Percus-Yevick equation for a hard-core fluid in odd dimensions,” Phys. A: Stat. Mech. 127 (3), 667–676 (1984). https://doi.org/10.1016/0378-4371(84)90050-5

    Article  MathSciNet  Google Scholar 

  50. Y. Song, E. A. Mason, and R. M. Stratt, “Why does the carnahan-starling equation work so well?” J. Phys. Chem. 93, 6916–6919 (1989).

    Article  CAS  Google Scholar 

  51. F. H. Ree and W. G. Hoover, “Fifth and sixth virial coefficients for hard spheres and hard disks,” J. Chem. Phys. 40, 939–950 (1964). https://doi.org/10.1063/1.1725286

    Article  ADS  MathSciNet  Google Scholar 

  52. Y. Song and E. A. Mason, “Statistical-mechanical theory of a new analytical equation of state,” J. Chem. Phys. 91 (12), 7840–7853 (1989). https://doi.org/10.1063/1.457252

  53. P. Mahata and S. L. Das, “Two-dimensional convex-molecule fluid model for surface adsorption of proteins: Effect of soft interaction on adsorption equilibria,” Phys. Rev. E 90 (6), 062713 (2014). https://doi.org/10.1103/PhysRevE.90.062713

  54. J. H. Weiner, Statistical Mechanics of Elasticity, 2nd ed. (Dover Publications, New York, 2017).

    Google Scholar 

  55. W. H. El-Ratal and P. K. Mallick, “Elastic response of flexible polyurethane foams in uniaxial tension,” J. Eng. Mater. Technol.-T. ASME, 118, 157–161 (1996). https://doi.org/10.1115/1.2804881

    Article  Google Scholar 

Download references

ACKNOWLEDGMENTS

The authors would like to thank the anonymous referees for their valuable suggestions to enhance the quality of the paper.

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Birla Institute of Technology, 835215, Mesra, Ranchi, India

    Raj Kumar & Paritosh Mahata

Authors
  1. Raj Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Paritosh Mahata
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Raj Kumar or Paritosh Mahata.

Ethics declarations

The authors of this work declare that they have no conflicts of interest.

Additional information

Publisher’s Note.

Allerton Press remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, R., Mahata, P. A Strain Energy Density Potential for Non-Crystalline Solids Using Molecular Interactions. Mech. Solids 58, 2097–2114 (2023). https://doi.org/10.3103/S0025654423601052

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0025654423601052

Keywords:

Search

Navigation