Abstract
It is shown that the isovector np-pair number operator can be realized in the O(5) quasi-spin  basis. The computation of the isovector np-pair number is demonstrated for even-even and odd-odd ds-shell nuclei described by the charge-independent mean field plus isovector pairing model restricted within the O(5) seniority-zero subspace, thereby binding energies and low-lying
basis. The computation of the isovector np-pair number is demonstrated for even-even and odd-odd ds-shell nuclei described by the charge-independent mean field plus isovector pairing model restricted within the O(5) seniority-zero subspace, thereby binding energies and low-lying  excited states of these ds-shell nuclei are fit, along with estimates for the isovector neutron-proton pairing contributions. For reasonable neutron-proton pairing strengths the isovector np-pairing energy contribution to the total binding energy in odd-odd N = Z nuclei is systematically larger than that in the even-even nuclei. In sum, the results suggest that the isovector np-pairing mode is favored in odd-odd N = Z nuclei; and additionally, a decrease in the double binding-energy difference for odd-odd nuclei is primarily due to the symmetry and Wigner energy contributions to the binding energy.
excited states of these ds-shell nuclei are fit, along with estimates for the isovector neutron-proton pairing contributions. For reasonable neutron-proton pairing strengths the isovector np-pairing energy contribution to the total binding energy in odd-odd N = Z nuclei is systematically larger than that in the even-even nuclei. In sum, the results suggest that the isovector np-pairing mode is favored in odd-odd N = Z nuclei; and additionally, a decrease in the double binding-energy difference for odd-odd nuclei is primarily due to the symmetry and Wigner energy contributions to the binding energy.
Export citation and abstract BibTeX RIS
In atomic nuclei it is evident from both theoretical and experimental studies that in addition to neutron-neutron (nn) and proton-proton (pp) pairing, neutron-proton (np) pairing is also very important, especially in 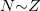 nuclei [1–8]. Though isoscalar
nuclei [1–8]. Though isoscalar 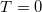 np-pairing in nuclei becomes important in the high-energy regime [9,10], isovector
np-pairing in nuclei becomes important in the high-energy regime [9,10], isovector 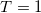 np-pairing often dominates in the low-energy regime [8,11], where the shell model mean field plus isovector pairing seems to provide a simple and clear picture of the np-pairing correlations [7,12–14]. Exact solution of the charge-independent mean field plus isovector pairing has been reported in [15,16]. However, since the basis used in [15,16] is equivalent to the tensor product of relevant O(5) irreducible representations (irreps) adapted to the
np-pairing often dominates in the low-energy regime [8,11], where the shell model mean field plus isovector pairing seems to provide a simple and clear picture of the np-pairing correlations [7,12–14]. Exact solution of the charge-independent mean field plus isovector pairing has been reported in [15,16]. However, since the basis used in [15,16] is equivalent to the tensor product of relevant O(5) irreducible representations (irreps) adapted to the 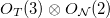 subgroup which is related to the isospin and the number of valence nucleons, it is not possible to define a simple operator that counts the number of isovector np-pairs, so the corresponding two-body np-pairing interaction related to the isovector np-pairing energy contribution is often used to account for the number of isovector np-pairs instead [17].
subgroup which is related to the isospin and the number of valence nucleons, it is not possible to define a simple operator that counts the number of isovector np-pairs, so the corresponding two-body np-pairing interaction related to the isovector np-pairing energy contribution is often used to account for the number of isovector np-pairs instead [17].
Besides shell model calculations based on various algorithms with effective interactions [18], which have been proven to be very successful in describing ds-shell nuclei, model calculations based on group theoretic or algebraic labelling scheme within a multi-particle subspace of the same shell model configuration is equally feasible [12,13,19], which is equivalent to choosing a complete set of orthonormal eigenstates of a set of commuting operators, or the subgroup invariants [20] constructed from the single-particle creation and annihilation operators of the shell model mean field. Moreover, though the agreement of the standard shell model results [18] with experiment suggests that the isovector and isoscalar pairing interactions are realistic, the actual interaction strengths are subject to considerable uncertainty due to the fact that the competition of the isovector and isoscalar pairing, deformation, and other correlations leads to a very complex picture [8]. Therefore, in order to address the aforementioned issue more directly, in this work, we only consider isovector pairing corresponding to the J = 0 and T = 1 two-body interactions adopted in the standard shell model calculations [18] within a spherical mean field in the charge-independent form with a Hamiltonian that can be written as [7,12–16]

where p is the number of j-orbits of the mean field considered, 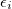 is the single-particle energy in the i-th orbit,
is the single-particle energy in the i-th orbit, 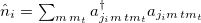 is the valence nucleon number operator in the i-th j-orbit,
is the valence nucleon number operator in the i-th j-orbit, 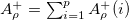 and
and 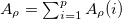 [
[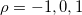 ] are collective J = 0 and T = 1 nn-, np-, and pp-pairing operators with
] are collective J = 0 and T = 1 nn-, np-, and pp-pairing operators with 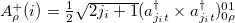 ,
, 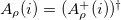 , in which
, in which  stands for the angular momentum and isospin coupling with
stands for the angular momentum and isospin coupling with  and
and 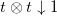 , and G > 0 is the overall isovector pairing strength. Here
, and G > 0 is the overall isovector pairing strength. Here 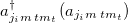 is the creation (annihilation) operator for a valence nucleon in the i-th j-orbit with isospin
is the creation (annihilation) operator for a valence nucleon in the i-th j-orbit with isospin 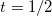 and angular momentum projection m and isospin projection mt
. In order to demonstrate the evaluation of the number of isovector np-pairs, some low-lying
and angular momentum projection m and isospin projection mt
. In order to demonstrate the evaluation of the number of isovector np-pairs, some low-lying 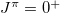 level energies of even-even and odd-odd
level energies of even-even and odd-odd  nuclei up to the middle of the ds-shell outside the
nuclei up to the middle of the ds-shell outside the 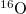 core are fit by the charge-independent mean field plus isovector pairing. To fit binding energies and some low-lying
core are fit by the charge-independent mean field plus isovector pairing. To fit binding energies and some low-lying 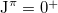 level energies of these nuclei, in addition to
level energies of these nuclei, in addition to 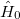 shown in (1), the Coulomb energy and the symmetry energy (with the isospin-dependent part of the Wigner energy contribution) are considered with the same model Hamiltonian as that used in [21]:
shown in (1), the Coulomb energy and the symmetry energy (with the isospin-dependent part of the Wigner energy contribution) are considered with the same model Hamiltonian as that used in [21]:

where 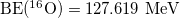 is the binding energy of the
is the binding energy of the  core taken as the experimental value,
core taken as the experimental value, 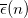 is the average binding energy per valence nucleon in the ds-shell with
is the average binding energy per valence nucleon in the ds-shell with  ,
, 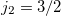 , and
, and 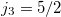 orbits, of which the function of
orbits, of which the function of  is determined from a best fit to binding energies of all ds-shell nuclei considered,
is determined from a best fit to binding energies of all ds-shell nuclei considered,

is the Coulomb energy [22], and

is the parameter of the symmetry energy, of which the first term is taken to be the empirical global symmetry energy parameter provided in [22], while 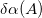 is adjusted according to the experimental binding energy of the nucleus with a given mass number A needed to account for the local deviation from the first term when the Hamiltonian (2) is used. The experimentally deduced single-particle energies above the
is adjusted according to the experimental binding energy of the nucleus with a given mass number A needed to account for the local deviation from the first term when the Hamiltonian (2) is used. The experimentally deduced single-particle energies above the 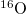 core with
core with 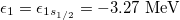 ,
, 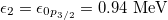 ,
, 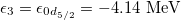 [21] are taken. In order to get a better fitting quality for the low-lying
[21] are taken. In order to get a better fitting quality for the low-lying 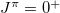 level energies, the overall isovector pairing strength is taken as
level energies, the overall isovector pairing strength is taken as 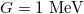 for all the nuclei fitted, which is very close to the value used in [23] with
for all the nuclei fitted, which is very close to the value used in [23] with 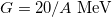 . Comparing to the standard shell model calculations in the ds-shell [18], the empirical Coulomb energy, the symmetry energy, and the average binding energy terms are introduced to replace the other two-body interaction terms of the standard shell model calculations [18], except for J = 1 and T = 0 isoscalar pairing related to the J = 1 and T = 0 matrix elements of the two-body interaction in the standard shell model calculation [18], which is not included in (2). Therefore, (2) can be considered as an approximation to the standard shell model Hamiltonian focusing on the isovector pairing only, from which the number of the isovector np-pairs in low-lying
. Comparing to the standard shell model calculations in the ds-shell [18], the empirical Coulomb energy, the symmetry energy, and the average binding energy terms are introduced to replace the other two-body interaction terms of the standard shell model calculations [18], except for J = 1 and T = 0 isoscalar pairing related to the J = 1 and T = 0 matrix elements of the two-body interaction in the standard shell model calculation [18], which is not included in (2). Therefore, (2) can be considered as an approximation to the standard shell model Hamiltonian focusing on the isovector pairing only, from which the number of the isovector np-pairs in low-lying 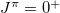 states can be estimated reasonably under the condition that the J = 1 and T = 0 isoscalar pairing can be neglected.
states can be estimated reasonably under the condition that the J = 1 and T = 0 isoscalar pairing can be neglected.
For convenience, we choose the proton and neutron quasi-spin 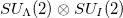 group as the subgroup of O(5) with generators of the proton quasi-spin group
group as the subgroup of O(5) with generators of the proton quasi-spin group 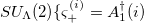 ,
, 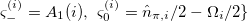 and those of the neutron quasi-spin group
and those of the neutron quasi-spin group 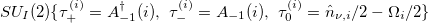 . Details of the relation between the group chain
. Details of the relation between the group chain 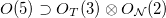 and
and 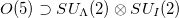 are provided in [24] and shown in the Supplementary Material Supplementarymaterial.pdf (SM), which provides details of the O(5) basis and the reduced matrix elements needed in the calculation. For any orbit, the irreducible representation (irrep) of O(5) is denoted by
are provided in [24] and shown in the Supplementary Material Supplementarymaterial.pdf (SM), which provides details of the O(5) basis and the reduced matrix elements needed in the calculation. For any orbit, the irreducible representation (irrep) of O(5) is denoted by 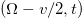 , where the O(5) seniority number of valence nucleons v and the reduced isospin t indicate that there are v nucleons coupled to the isospin t, which are free from the angular momentum
, where the O(5) seniority number of valence nucleons v and the reduced isospin t indicate that there are v nucleons coupled to the isospin t, which are free from the angular momentum 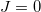 and
and 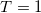 pairs. The orthonormal basis vectors of
pairs. The orthonormal basis vectors of 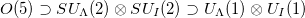 are labeled as [12,13,24]
are labeled as [12,13,24]
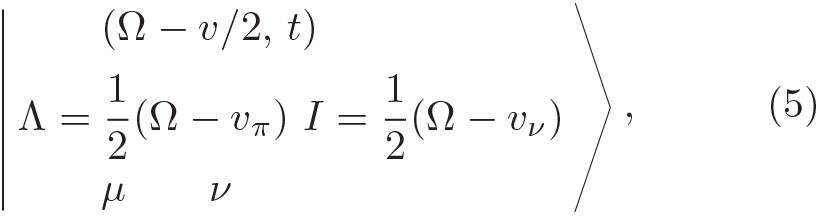
where μ and ν are eigenvalues of  and
and 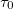 , respectively, Λ and I are the proton and neutron quasi-spin quantum numbers, in which
, respectively, Λ and I are the proton and neutron quasi-spin quantum numbers, in which 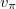 and
and 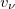 are the proton and neutron seniority numbers, respectively, with [24]
are the proton and neutron seniority numbers, respectively, with [24]

where  and
and  , indicating that there are
, indicating that there are 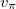 and
and 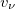 valence protons and neutrons not coupled to J = 0 pp- and nn-pairs, respectively. However, there may be a portion of the valence protons and neutrons that are coupled into J = 0 np-pairs, which is indicated by the number q. As is clearly indicated in (6), besides the number of valence protons or neutrons in the np-pairs q, there are
valence protons and neutrons not coupled to J = 0 pp- and nn-pairs, respectively. However, there may be a portion of the valence protons and neutrons that are coupled into J = 0 np-pairs, which is indicated by the number q. As is clearly indicated in (6), besides the number of valence protons or neutrons in the np-pairs q, there are 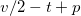 valence protons and
valence protons and 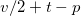 valence neutrons with total v valence nucleons that are coupled to the reduced isospin t with
valence neutrons with total v valence nucleons that are coupled to the reduced isospin t with 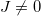 . Thus, q is the number of isovector np-pairs in a given orbit, which shows that the isovector np-pair number operator is well defined in the
. Thus, q is the number of isovector np-pairs in a given orbit, which shows that the isovector np-pair number operator is well defined in the 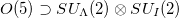 labelling scheme.
labelling scheme.
The Hamiltonian (2) is diagonalized within the O(5) seniority-zero subspace spanned by the tensor product basis 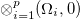 in the
in the 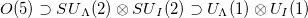 labelling scheme with p = 3. Eigenstates of (2) within the O(5) seniority-zero
labelling scheme with p = 3. Eigenstates of (2) within the O(5) seniority-zero  subspace are denoted as
subspace are denoted as
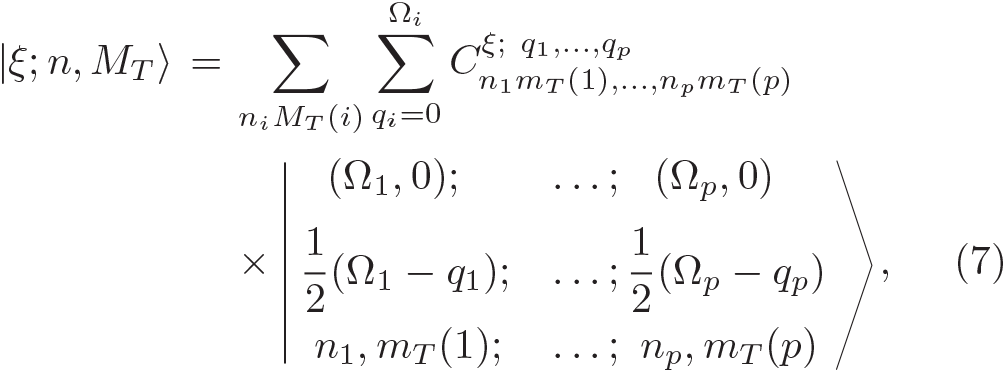
where the eigenstate  with total number of valence nucleons
with total number of valence nucleons 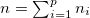 and total isospin projection
and total isospin projection  is expended in terms of the p copies of the O(5) tensor product basis
is expended in terms of the p copies of the O(5) tensor product basis 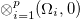 in the
in the 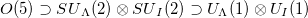 labelling scheme with
labelling scheme with

for 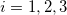 ,
, 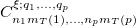 is the corresponding expansion coefficient, and ξ labels the ξ-th eigenstate with the same n and MT
. Since
is the corresponding expansion coefficient, and ξ labels the ξ-th eigenstate with the same n and MT
. Since 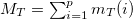 is a good quantum number, this diagonalization scheme is similar to the MT
-scheme realized in the
is a good quantum number, this diagonalization scheme is similar to the MT
-scheme realized in the 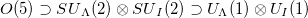 basis, which is equivalent to the MT
-scheme with
basis, which is equivalent to the MT
-scheme with 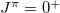 states adopted in the standard shell model calculation [18]. The details of the O(5) basis and the reduced matrix elements needed in the calculation are shown in the SM. Moreover, it is clearly shown that the eigenstate (7) is a linear combination of the O(5) tensor product states with different proton and neutron seniority numbers
states adopted in the standard shell model calculation [18]. The details of the O(5) basis and the reduced matrix elements needed in the calculation are shown in the SM. Moreover, it is clearly shown that the eigenstate (7) is a linear combination of the O(5) tensor product states with different proton and neutron seniority numbers 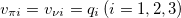 for
for 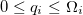 , where qi
is exactly the number of T = 1 np-pairs in the i-th orbit. The main difference from the standard shell model basis is that only J = 0 and T = 1 pairing operators are used in the construction of (7). Other O(5) seniority-nonzero states constructed by (
, where qi
is exactly the number of T = 1 np-pairs in the i-th orbit. The main difference from the standard shell model basis is that only J = 0 and T = 1 pairing operators are used in the construction of (7). Other O(5) seniority-nonzero states constructed by (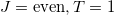 ) and (
) and (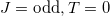 ) pair operators coupled to J = 0 and at least with the total O(5) seniority number v = 4 are not considered as an approximation, of which
) pair operators coupled to J = 0 and at least with the total O(5) seniority number v = 4 are not considered as an approximation, of which 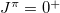 isovector pairing matrix elements are comparatively small, so that these seniority-nonzero states have less contribution to the low-lying
isovector pairing matrix elements are comparatively small, so that these seniority-nonzero states have less contribution to the low-lying 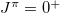 states as long as the isoscalar pairing interaction is negligible. As shown in our previous works [21,25–27], such an approximation seems adequate as far as binding energies and a few low-lying
states as long as the isoscalar pairing interaction is negligible. As shown in our previous works [21,25–27], such an approximation seems adequate as far as binding energies and a few low-lying 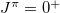 level energies are concerned.
level energies are concerned.
The best fit to the binding energies and a few lowest 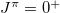 level energies of these nuclei yields
level energies of these nuclei yields

of which the first constant is very close to the value of the average binding energy per valence nucleon with 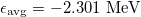 used in [21], and the contribution from the second term to the binding, which is related to the other two-body interactions in the standard shell model calculation [18] becomes smaller because a relatively larger pairing strength is used in the present calculation, while the third term is related to the three-body interaction as an additional correction. The parameter
used in [21], and the contribution from the second term to the binding, which is related to the other two-body interactions in the standard shell model calculation [18] becomes smaller because a relatively larger pairing strength is used in the present calculation, while the third term is related to the three-body interaction as an additional correction. The parameter 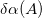 (in MeV), which is obtained from the fitting, is given by
(in MeV), which is obtained from the fitting, is given by 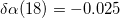 ,
, 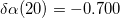 ,
, 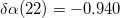 ,
, 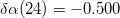 ,
, 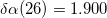 , and
, and  . Since the binding energies and a few low-lying
. Since the binding energies and a few low-lying  level energies of even-even and odd-odd
level energies of even-even and odd-odd 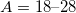 nuclei were fit together, there remain deviations between the fitted and experimental binding energies, with a root mean square deviation
nuclei were fit together, there remain deviations between the fitted and experimental binding energies, with a root mean square deviation 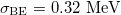 , except
, except  and
and 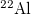 for which
for which 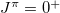 level energies are not available experimentally. Table 1 shows the lowest experimentally known
level energies are not available experimentally. Table 1 shows the lowest experimentally known 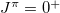 level energies (in MeV) of these even-even and odd-odd ds-shell nuclei. The corresponding shell model results obtained by using the KSHELL code [28] with the USD (W) interaction [29] are also provided for comparison. Though direct computation of the overlaps of the
level energies (in MeV) of these even-even and odd-odd ds-shell nuclei. The corresponding shell model results obtained by using the KSHELL code [28] with the USD (W) interaction [29] are also provided for comparison. Though direct computation of the overlaps of the 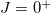 states of this model with those of the shell model is not an easy task, the results provided in table 1 show that the low-lying
states of this model with those of the shell model is not an easy task, the results provided in table 1 show that the low-lying 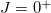 level energies fitted by the O(5) model restricted within the O(5) seniority-zero subspace are comparable with those of the standard shell model calculation. The root mean square deviation for these excited
level energies fitted by the O(5) model restricted within the O(5) seniority-zero subspace are comparable with those of the standard shell model calculation. The root mean square deviation for these excited 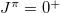 level energies is
level energies is  in this O(5) model and 0.36 MeV in the standard shell model, while the average deviation of the excited levels,
in this O(5) model and 0.36 MeV in the standard shell model, while the average deviation of the excited levels,  , where the sum is over all the excited level energies of these nuclei fitted, is
, where the sum is over all the excited level energies of these nuclei fitted, is 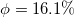 in the O(5) model and
in the O(5) model and 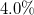 in the standard shell model calculation, respectively.
in the standard shell model calculation, respectively.
Table 1:. Binding energy (BE) (in MeV) and a few lowest  level energies (in MeV) of the 22 even-even and odd-odd ds-shell nuclei fit by (2) (Th), where
level energies (in MeV) of the 22 even-even and odd-odd ds-shell nuclei fit by (2) (Th), where 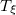 denotes the ξ-th excited state with the same T, the experimental data (Exp) are taken from [30] and [31] for the evaluated isobaric analogue states, "–" indicates the corresponding energy level was not observed in experiments, and the standard shell model results (SM) are obtained by using the KSHELL code [28] with the USD (W) interaction [29], and the parameters of (2) are the same as those used in fitting the binding energies.
denotes the ξ-th excited state with the same T, the experimental data (Exp) are taken from [30] and [31] for the evaluated isobaric analogue states, "–" indicates the corresponding energy level was not observed in experiments, and the standard shell model results (SM) are obtained by using the KSHELL code [28] with the USD (W) interaction [29], and the parameters of (2) are the same as those used in fitting the binding energies.

| Exp | Th | SM |
| Exp | Th | SM |
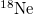
| Exp | Th | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 139.81 | 140.00 | 137.37 | 137.31 | 132.14 | 132.04 | |||||

| 0 | 0 | 0 |
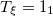
| 1.04 | 1.04 | 1.19 |
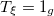
| 0 | 0 | 0 |
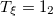
| 3.63 | 5.71 | 4.32 |

| 4.75 | 6.75 | 5.51 |
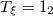
| 3.58 | 5.71 | 4.32 |
| Exp | Th | SM |
| Exp | Th | SM |
| Exp | Th | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 151.37 | 151.20 | 154.40 | 154.40 | 160.65 | 160.41 | |||||
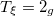
| 0 | 0 | 0 |
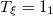
| 3.53 | 1.23 | 3.49 |

| 0 | 0 | 0 |
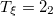
| 4.46 | 5.07 | 5.04 |
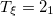
| 6.52 | 6.80 | 6.52 |
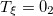
| 6.73 | 5.90 | 6.76 |
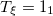
| 13.64 | 11.33 | 13.64 | ||||||||

| 16.73 | 16.90 | 16.66 |
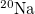
| Exp | Th | SM |
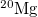
| Exp | Th | SM |
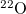
| Exp | Th | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 145.97 | 145.97 | 134.56 | 133.84 | 162.04 | 161.45 | |||||
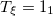
| 3.09 | 1.48 | 3.49 |
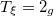
| 0 | 0 | 0 |
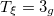
| 0 | 0 | 0 |
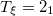
| 6.53 | 7.05 | 6.52 |
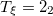
| – | 5.07 | 5.04 |
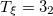
| 4.91 | 4.35 | 4.62 |
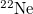
| Exp | Th | SM |
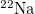
| Exp | Th | SM |
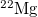
| Exp | Th | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 177.77 | 178.23 | 174.15 | 174.14 | 168.58 | 168.86 | |||||
| 0 | 0 | 0 |
| 0.66 | 0.36 | 0.66 |
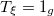
| 0 | 0 | 0 |
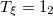
| 6.24 | 5.03 | 6.34 |
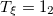
| – | 5.39 | 7.01 |
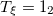
| 5.95 | 5.03 | 6.34 |

| Exp | Th | SM |
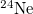
| Exp | Th | SM |
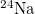
| Exp | Th | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 133.28 | 133.33 | 191.84 | 191.60 | 193.52 | 193.52 | |||||
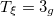
| 0 | 0 | 0 |
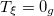
| 0 | 0 | 0 |

| 3.68 | 0.37 | 3.33 |

| 4.77 | 4.30 | 4.66 |
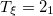
| 5.97 | 6.24 | 5.88 |
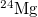
| Exp | Th | SM |
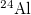
| Exp | Th | SM |
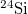
| Exp. | Th. | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 198.26 | 198.85 | 183.59 | 183.59 | 172.01 | 171.52 | |||||
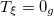
| 0 | 0 | 0 |
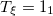
| – | 0.48 | 3.33 |
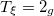
| 0 | 0 | 0 |

| 6.43 | 5.16 | 7.56 |

| 5.96 | 6.35 | 5.88 | ||||
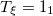
| 13.04 | 10.49 | 12.87 | ||||||||
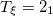
| 15.44 | 16.35 | 15.43 |
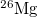
| Exp | Th | SM |
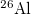
| Exp | Th | SM |
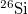
| Exp | Th | SM |

| Exp | Th | SM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BE | 216.68 | 216.78 | 211.89 | 211.89 | 206.04 | 206.09 | 247.74 | 247.67 | |||||||
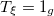
| 0 | 0 | 0 |
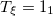
| 0.23 | 0.23 | 0.08 |
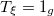
| 0 | 0 | 0 |
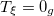
| 0 | 0 | 0 |
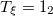
| 3.59 | 4.24 | 3.68 |
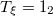
| 3.75 | 4.47 | 3.76 |
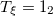
| 3.36 | 4.24 | 3.68 |
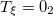
| 4.98 | 4.25 | 5.01 |
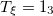
| 4.97 | 5.13 | 5.20 |

| 5.20 | 5.36 | 5.29 |
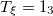
| 4.83 | 5.13 | 5.20 |
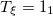
| 10.27 | 10.27 | 10.29 |
In addition, when the ground state of the nucleus is not a 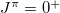 state, which cannot be determined from present calculation for
state, which cannot be determined from present calculation for  states only, the eigenenergy of (2) is given by
states only, the eigenenergy of (2) is given by

where  is the excitation energy of the ξ-th excited state with isospin T and J = 0. The theoretical value of
is the excitation energy of the ξ-th excited state with isospin T and J = 0. The theoretical value of 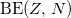 is adjusted to reproduce a reasonable value of the excitation energy
is adjusted to reproduce a reasonable value of the excitation energy 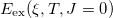 . Due to the Coulomb energy contribution and the freedom in adjusting the binding energy with a reasonable value of the excitation energy in this case, there is about a few hundreds of keV energy difference in these excitation energies of mirror nuclei with
. Due to the Coulomb energy contribution and the freedom in adjusting the binding energy with a reasonable value of the excitation energy in this case, there is about a few hundreds of keV energy difference in these excitation energies of mirror nuclei with 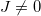 ground state as shown in table 1.
ground state as shown in table 1.
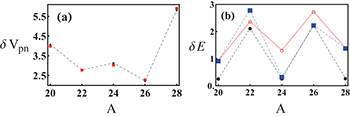
Panel (a) of fig. 1 shows the double binding-energy difference defined as [32]

These results show that the 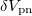 are comparatively smaller for odd-odd N = Z nuclei with A = 22 and 26. Since the one- and two-body interaction dominating average binding energy term (9) and the Coulomb energy term of (2) only contribute an overall Z- and N-independent constant to
are comparatively smaller for odd-odd N = Z nuclei with A = 22 and 26. Since the one- and two-body interaction dominating average binding energy term (9) and the Coulomb energy term of (2) only contribute an overall Z- and N-independent constant to 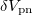 , the symmetry energy seems to be the main source that alters the pairing gap staggering pattern. This is consistent with the claim made in [5] that the double binding-energy difference (11) actually provides evidence for the importance of the Wigner energy contribution to the binding energy, and additionaly demonstrates that the isovector np-pairing energy contribution is relatively large in the even-even N = Z nuclei [21]. Alternatively, instead of
, the symmetry energy seems to be the main source that alters the pairing gap staggering pattern. This is consistent with the claim made in [5] that the double binding-energy difference (11) actually provides evidence for the importance of the Wigner energy contribution to the binding energy, and additionaly demonstrates that the isovector np-pairing energy contribution is relatively large in the even-even N = Z nuclei [21]. Alternatively, instead of 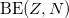 , we also calculated the double pairing energy difference defined as
, we also calculated the double pairing energy difference defined as

where

is the lowest  state expectation value of either
state expectation value of either 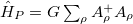 or
or 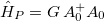 , of which the former is the total pairing energy contribution, while the latter is the isovector np-pairing energy contribution to the binding energy. By substituting
, of which the former is the total pairing energy contribution, while the latter is the isovector np-pairing energy contribution to the binding energy. By substituting 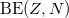 used in (11) with
used in (11) with

which removes the symmetry energy contribution to the binding energy, the resultant  obtained from (11) should be close to the double pairing energy difference (12). And indeed, as shown in panel (b) of fig. 1, the value of
obtained from (11) should be close to the double pairing energy difference (12). And indeed, as shown in panel (b) of fig. 1, the value of 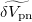 is very close to the
is very close to the 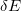 values calculated with the total pairing energy and the np-pairing energy contribution to the binding energy. Most noticeably, in comparison to
values calculated with the total pairing energy and the np-pairing energy contribution to the binding energy. Most noticeably, in comparison to 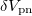 , the staggering pattern is clearly evident, and, to the contrary, the actual np-pairing energy in the odd-odd N = Z nuclei turns out to be comparatively strong, which shows that the Wigner energy contribution plays the important role in the lowest
, the staggering pattern is clearly evident, and, to the contrary, the actual np-pairing energy in the odd-odd N = Z nuclei turns out to be comparatively strong, which shows that the Wigner energy contribution plays the important role in the lowest  states of odd-odd N = Z nuclei. Table 2 shows the actual nn-, pp-, and np-pairing energy at the ground state or the lowest
states of odd-odd N = Z nuclei. Table 2 shows the actual nn-, pp-, and np-pairing energy at the ground state or the lowest 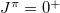 excited state of (2) for these nuclei defined by
excited state of (2) for these nuclei defined by

and the percentage of the isovector np-pairing energy with respect to the total pairing energy

It can be seen from the results that  in the
in the 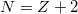 nuclei is the same as
nuclei is the same as  in the
in the 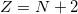 mirror nuclei, while
mirror nuclei, while 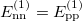 in the N = Z nuclei due to the charge-independent approximation adopted. However,
in the N = Z nuclei due to the charge-independent approximation adopted. However, 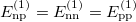 in even-even N = Z nuclei, while
in even-even N = Z nuclei, while 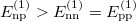 in odd-odd N = Z nuclei, shows that the isovector np-pairing energy contribution to the binding energy is the largest in odd-odd N = Z nuclei in comparison to that in the adjacent
in odd-odd N = Z nuclei, shows that the isovector np-pairing energy contribution to the binding energy is the largest in odd-odd N = Z nuclei in comparison to that in the adjacent  and even-even N = Z nuclei.
and even-even N = Z nuclei.
Fig. 1: (a) The double binding-energy difference 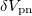 (in MeV) defined in (11) for even-even and odd-odd
(in MeV) defined in (11) for even-even and odd-odd  -shell nuclei, where the (red) solid squares are the experimental data, and the (black) dots connected with the dashed lines are the results of the present model. (b) The double pairing energy difference (in MeV) defined in (12), where the (red) open circles connected with the solid lines are calculated from (12) with the isovector np-pairing energy, the (black) solid dots connected with the dashed lines are calculated from (12) with the total pairing energy, and the (blue) solid squares connected with the dashed lines are
-shell nuclei, where the (red) solid squares are the experimental data, and the (black) dots connected with the dashed lines are the results of the present model. (b) The double pairing energy difference (in MeV) defined in (12), where the (red) open circles connected with the solid lines are calculated from (12) with the isovector np-pairing energy, the (black) solid dots connected with the dashed lines are calculated from (12) with the total pairing energy, and the (blue) solid squares connected with the dashed lines are  values calculated from (11) with
values calculated from (11) with 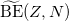 .
.
Download figure:
Standard imageTable 2:. The isovector np-, nn-, and pp-pairing energy contribution (in MeV) to the binding energy and the percentage of the isovector np-pairing energy with respect to the total pairing energy  in the 22 even-even and odd-odd ds-shell nuclei described within the seniority-zero subspace of the model, where the average number of the isovector np-pairs
in the 22 even-even and odd-odd ds-shell nuclei described within the seniority-zero subspace of the model, where the average number of the isovector np-pairs 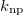 and its fluctuation
and its fluctuation 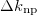 , and the isovector np-pair occupation number
, and the isovector np-pair occupation number 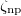 in the
in the 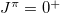 ground state or the lowest
ground state or the lowest 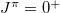 state of these nuclei are also shown.
state of these nuclei are also shown.
| Nucleus | n | Isospin |

|
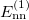
|
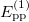
|
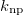
|
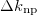
|

|
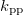
|
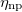
|
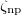
|
|---|---|---|---|---|---|---|---|---|---|---|---|
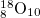
| 2 |
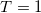
| 0 | 5.036 | 0 | 0 | 0 | 1 | 0 | 0% | 0% |
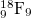
| 2 |
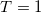
| 5.036 | 0 | 0 | 1 | 0 | 0 | 0 | 100% | 100% |
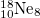
| 2 |
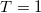
| 0 | 0 | 5.036 | 0 | 0 | 0 | 1 | 0% | 0% |
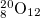
| 4 |
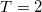
| 0 | 7.945 | 0 | 0 | 0 | 2 | 0 | 0% | 0% |

| 4 |
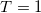
| 2.568 | 2.568 | 0 | 1 | 0 | 1 | 0 | 50% | 50% |
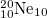
| 4 |
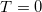
| 3.707 | 3.707 | 3.707 | 0.497 | 0.865 | 0.7515 | 0.7515 | 33.33% | 24.85% |
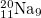
| 4 |
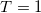
| 2.568 | 0 | 2.568 | 1 | 0 | 0 | 1 | 50% | 50% |

| 4 |
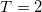
| 0 | 0 | 7.945 | 0 | 0 | 0 | 2 | 0% | 0% |

| 6 |
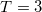
| 0 | 8.666 | 0 | 0 | 0 | 3 | 0 | 0% | 0% |
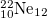
| 6 |
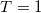
| 2.226 | 7.356 | 4.444 | 0.205 | 0.606 | 1.8975 | 0.8975 | 15.87% | 6.83% |
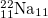
| 6 |

| 9.573 | 2.226 | 2.226 | 1.756 | 0.940 | 0.622 | 0.622 | 68.25% | 58.53% |
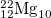
| 6 |

| 2.226 | 4.444 | 7.356 | 0.205 | 0.606 | 0.8975 | 1.8975 | 15.87% | 6.83% |
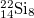
| 6 |
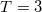
| 0 | 0 | 8.666 | 0 | 0 | 0 | 3 | 0% | 0% |

| 8 |
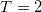
| 1.600 | 8.393 | 4.756 | 0.083 | 0.159 | 2.9585 | 0.9585 | 10.85% | 2.08% |
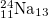
| 8 |

| 5.061 | 4.167 | 2.681 | 1.404 | 0.645 | 1.798 | 0.798 | 42.49% | 35.10% |
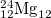
| 8 |
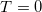
| 6.000 | 6.000 | 6.000 | 0.711 | 1.342 | 1.6445 | 1.6445 | 33.33% | 17.78% |
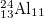
| 8 |
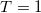
| 5.061 | 2.681 | 4.167 | 1.404 | 0.645 | 0.798 | 1.798 | 42.49% | 35.10% |
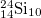
| 8 |
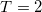
| 1.600 | 4.756 | 8.393 | 0.083 | 0.159 | 0.9585 | 2.9585 | 10.85% | 2.08% |
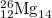
| 10 |
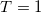
| 3.615 | 7.917 | 7.186 | 0.234 | 0.449 | 2.883 | 1.883 | 19.31% | 4.68% |

| 10 |

| 11.489 | 3.615 | 3.615 | 1.792 | 1.179 | 1.604 | 1.604 | 61.38% | 35.84% |
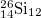
| 10 |

| 3.615 | 7.186 | 7.917 | 0.234 | 0.449 | 1.883 | 2.883 | 19.31% | 4.68% |
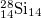
| 12 |
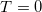
| 6.847 | 6.847 | 6.847 | 0.585 | 1.066 | 2.7075 | 2.7075 | 33.33% | 9.75% |
Finally, the average number of the isovector np-pairs in the lowest 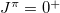 state can be defined as
state can be defined as

with 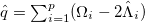 . Hence, the average number of nn-pairs and that of pp-pairs are given by
. Hence, the average number of nn-pairs and that of pp-pairs are given by

These values for the each nucleus at the lowest 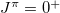 state are shown in table 2. Since the number of isovector np-pairs is not a conserved quantity in general, its fluctuation in the lowest
state are shown in table 2. Since the number of isovector np-pairs is not a conserved quantity in general, its fluctuation in the lowest 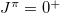 state of these nuclei defined as
state of these nuclei defined as

is also provided. It can be observed from table 2 that the 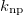 value is a definite integer for nuclei with less than or equal to one valence neutron or proton, for which the
value is a definite integer for nuclei with less than or equal to one valence neutron or proton, for which the 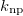 value is also easily countable, while (17) must be used for evaluating
value is also easily countable, while (17) must be used for evaluating 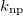 for nuclei with more valence neutrons and protons. It is obvious that the
for nuclei with more valence neutrons and protons. It is obvious that the  value is indeed relatively large in the odd-odd N = Z nuclei, which is consistent to the larger isovector np-pairing energy contribution to the binding energy shown in table 2, while the average number of the isovector np-pairs
value is indeed relatively large in the odd-odd N = Z nuclei, which is consistent to the larger isovector np-pairing energy contribution to the binding energy shown in table 2, while the average number of the isovector np-pairs 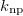 in the even-even nuclei is considerably small with very large fluctuation. The
in the even-even nuclei is considerably small with very large fluctuation. The 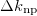 value in these even-even N = Z nuclei is almost two times of the corresponding average value. Though the isovector np-pair occupation number defined as
value in these even-even N = Z nuclei is almost two times of the corresponding average value. Though the isovector np-pair occupation number defined as

where 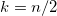 , in the even-even N = Z nuclei is small, the isovector np-pairing energy is still comparable to the nn- or pp-pairing energy. Table 2 shows that the isovector np-pairing energy per pair
, in the even-even N = Z nuclei is small, the isovector np-pairing energy is still comparable to the nn- or pp-pairing energy. Table 2 shows that the isovector np-pairing energy per pair 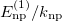 is 2.31 and 4.63 times of
is 2.31 and 4.63 times of  in
in 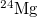 and
and 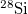 , respectively. In short, the number of isovector np-pairs is larger in odd-odd N = Z nuclei as described by the charge-independent mean field plus isovector pairing model.
, respectively. In short, the number of isovector np-pairs is larger in odd-odd N = Z nuclei as described by the charge-independent mean field plus isovector pairing model.
In summary, it is shown that the isvector np-pair number operator can be realized in the neutron and proton quasi-spin 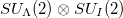 chain, in which the average number of the isovector np-pairs and its fluctuation can be evaluated. The evaluation is demonstrated in the charge-independent mean field plus isovector pairing model, thereby binding energies and low-lying
chain, in which the average number of the isovector np-pairs and its fluctuation can be evaluated. The evaluation is demonstrated in the charge-independent mean field plus isovector pairing model, thereby binding energies and low-lying 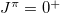 excited states of even-even and odd-odd
excited states of even-even and odd-odd 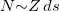 -shell nuclei are fit, and in turn, the isovector np-, nn-, and pp-pairing energy contributions to the binding energy in the even-even and odd-odd ds-shell nuclei are estimated. The results corroborate earlier findings [25,26] that the isovector np-pairing energy contribution to the lowest
-shell nuclei are fit, and in turn, the isovector np-, nn-, and pp-pairing energy contributions to the binding energy in the even-even and odd-odd ds-shell nuclei are estimated. The results corroborate earlier findings [25,26] that the isovector np-pairing energy contribution to the lowest 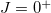 level energy in the odd-odd N = Z nuclei is systematically larger than that in the even-even nuclei. It is also observed that the decrease in the double binding-energy difference for the odd-odd nuclei is mainly due to the symmetry energy, which includes the Wigner energy contribution, that alters the pairing staggering patten. Particularly, the average number of the isovector np-pairs in the
level energy in the odd-odd N = Z nuclei is systematically larger than that in the even-even nuclei. It is also observed that the decrease in the double binding-energy difference for the odd-odd nuclei is mainly due to the symmetry energy, which includes the Wigner energy contribution, that alters the pairing staggering patten. Particularly, the average number of the isovector np-pairs in the 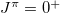 ground state or the lowest
ground state or the lowest 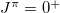 excited state of the even-even and odd-odd ds-shell nuclei are evaluated, which shows that the average number of the isovector np-pairs
excited state of the even-even and odd-odd ds-shell nuclei are evaluated, which shows that the average number of the isovector np-pairs  in the even-even N = Z nuclei is considerably small with very large fluctuation in comparison to that in the odd-odd N = Z nuclei, and leads to the conclusion that the isovector np-pairs increase in number in odd-odd N = Z nuclei. On the other hand, although the isovector np-pair occupation number in the even-even N = Z nuclei is rather small, the isovector np-pairing energy per pair is systematically larger than the nn- or pp-pairing energy per pair. It should be stated that the purpose of this work is mainly to provide the precise definition of the isovector np-pair number operator. The computation of the isovector np-pair number, however, is demonstrated for the even-even and odd-odd
in the even-even N = Z nuclei is considerably small with very large fluctuation in comparison to that in the odd-odd N = Z nuclei, and leads to the conclusion that the isovector np-pairs increase in number in odd-odd N = Z nuclei. On the other hand, although the isovector np-pair occupation number in the even-even N = Z nuclei is rather small, the isovector np-pairing energy per pair is systematically larger than the nn- or pp-pairing energy per pair. It should be stated that the purpose of this work is mainly to provide the precise definition of the isovector np-pair number operator. The computation of the isovector np-pair number, however, is demonstrated for the even-even and odd-odd 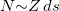 -shell nuclei described by the isovector pairing model restricted within the O(5) seniority-zero subspace only, where the isoscalar np-pairs are not involved. In order to reveal the actual np-pair contents in these
-shell nuclei described by the isovector pairing model restricted within the O(5) seniority-zero subspace only, where the isoscalar np-pairs are not involved. In order to reveal the actual np-pair contents in these 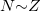 nuclei, other O(5) seniority-nonzero configurations must be considered, for which an alternative O(8) model [33–35] should be more convenient. Nevertheless, as has been shown in our recent work on the O(8) model [36], not only the binding energies and the low-lying
nuclei, other O(5) seniority-nonzero configurations must be considered, for which an alternative O(8) model [33–35] should be more convenient. Nevertheless, as has been shown in our recent work on the O(8) model [36], not only the binding energies and the low-lying 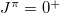 level energies shown in table 1, but also the isovector pairing energy contributions to the binding energies provided in table 2 are the same as those calculated from the O(8) model, where the isoscalar np-pairs are also involved. Therefore, the conclusion of the present work on the isovector pairing energy contribution to the binding energies of these ds-shell nuclei is still valid even in the presence of isoscalar np-pairs.
level energies shown in table 1, but also the isovector pairing energy contributions to the binding energies provided in table 2 are the same as those calculated from the O(8) model, where the isoscalar np-pairs are also involved. Therefore, the conclusion of the present work on the isovector pairing energy contribution to the binding energies of these ds-shell nuclei is still valid even in the presence of isoscalar np-pairs.
Acknowledgments
Support from the National Natural Science Foundation of China (11675071, 11975009), the Liaoning Provincial Universities Overseas Training Program (2019GJWYB024), the U. S. National Science Foundation (OIA-1738287 and PHY-1913728), U. S. Department of Energy (DE-SC0005248), the Southeastern Universities Research Association, and the LSU-LNNU joint research program (9961) is acknowledged.