Abstract
Quantum entanglement is the most famous type of quantum correlation between elements of a quantum system that has a basic role in quantum communication protocols like quantum cryptography, teleportation and Bell inequality detection. However, it has already been shown that various applications in quantum information theory do not require entanglement. Quantum discord as a new kind of quantum correlations beyond entanglement, is the most popular candidate for general quantum correlations. In this paper, first we find the entanglement witness in a particular multipartite quantum system which consists of a N-partite system in 2n-dimensional space. Then we give an exact analytical formula for the quantum discord of this system. At the end of the paper, we investigate the additivity relation of the quantum correlation and show that this relation is satisfied for a N-partite system with 2n-dimensional space.
Export citation and abstract BibTeX RIS
Introduction
Quantum entanglement is one of the most important features of quantum mechanics [1,2]. Many quantum information applications require the sharing of entangled particles. The answer to the question as to whether particles are entangled or not, is an important subject for the researchers. The Peres-Horodecki criterion is a necessary and sufficient condition, for the joint density matrix ρ of two quantum mechanical systems A and B, to be separable [3,4]. It is also called the PPT criterion, for positive partial transpose, whereas for higher dimensions there exist in general only necessary conditions for separability. The PPT condition is also a necessary and sufficient condition for Hilbert spaces 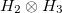 .
.
For characterizing entanglement, entanglement witness (EW) [4,5] is important for detecting the presence of entanglement. The EWs are nonpositive Hermitian operators which allow us to distinguish a specific entangled state from the separable ones. In other words, for a given entangled state ρ, the entanglement witness is an observable W whose expectation value is non-negative on any separable state and strictly negative on the quantum state ρ. Convex optimization is a useful tool for quantum optimization problems such as a test for distinguishing an entangled from a separable quantum state [6–11]. In addition to distinguishing the entangled states from the separable ones, another matter is to determine the amount of the correlation between the components of the quantum system. To this end, entanglement is the key resource of quantum information processing. It plays an important role in many quantum processing such as quantum teleportation, quantum key distribution, and quantum algorithm [12]. One can define several types of entanglement measures, for instance, entanglement of formation [13] and the concurrence [14,15]. However, it is shown that quantum entanglement is not the only kind of quantum correlations. Quantum systems without any entanglement can still have another kind of quantum correlation called quantum discord. Quantum discord was first introduced in [16,17]. Zhang and Chen in [18] briefly reviewed the concepts and properties of quantum discord. In general, there are several measures of discord including the original measure of discord, Gaussian discord, relative entropy-based discord, geometric discord, global discord. In [19] the dynamics of quantum discord under noisy channels, namely, the Pauli channels  ,
, 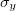 ,
,  and the depolarizing channel is studied. In this paper, we choose the quantum discord based on relative entropy as the quantum correlation measure that is distance-based discord and defined as the minimal distance of a quantum state and all states with zero discord [20,21].
and the depolarizing channel is studied. In this paper, we choose the quantum discord based on relative entropy as the quantum correlation measure that is distance-based discord and defined as the minimal distance of a quantum state and all states with zero discord [20,21].
In [22] the entanglement witness and quantum discord based on relative entropy are obtained for three-qubit and tripartite systems in the four-dimensional space. In this paper, inspired by the work [22] we find the entanglement witness of a N-partite system with 2n dimension space. Then using the concept of relative entropy as a distance measure of correlations we give an exact explicit formula for quantum discord of these states. Finally, we investigate the additivity relation of the quantum correlation for the N-partite system with 2n-dimensional space. The organization of this paper is as follows:
In the next section we review the definition of quantum discord based on relative entropy. In the following two section we obtain the entanglement witness and quantum discord based on relative entropy for a N-partite system in 2n-dimension space. Then we investigate the additivity relation of quantum correlations in this system. We conclude in the last section.
Distance measure of correlations
Briefly, the nonclassical correlations based on relative entropy are defined as [20]




where 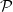 is the set of all product states that have the form
is the set of all product states that have the form 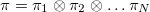 and
and 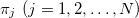 is the reduced state of the j-th subsystem. The set of classical states,
is the reduced state of the j-th subsystem. The set of classical states,  , contains mixtures of locally distinguishable states
, contains mixtures of locally distinguishable states 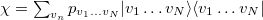 , where
, where 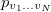 is a joint probability distribution and local states
is a joint probability distribution and local states 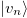 are an orthonormal basis. The correlations of these states are identified as classical correlations [20,23,24].
are an orthonormal basis. The correlations of these states are identified as classical correlations [20,23,24]. 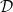 is the set of all separable states of the form
is the set of all separable states of the form 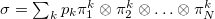 . The relative entropy between two quantum states ρ and χ is given by
. The relative entropy between two quantum states ρ and χ is given by

where 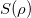 is the von Neumann entropy of ρ and
is the von Neumann entropy of ρ and 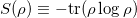 .
.
EW of N-partite systems in 2n-dimensional space
If a pure state 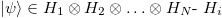 is the Hilbert space of the i-th subsystem which can be written in the form
is the Hilbert space of the i-th subsystem which can be written in the form 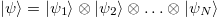 , where
, where 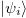 is a pure state of the i-th subsystem, it is said to be separable, otherwise it is called entangled. When a system is in an entangled pure state, it is not possible to assign states to its subsystems. This will be true, in the appropriate sense, for the mixed state case as well. A mixed state of the composite system is described by a density matrix ρ acting on
is a pure state of the i-th subsystem, it is said to be separable, otherwise it is called entangled. When a system is in an entangled pure state, it is not possible to assign states to its subsystems. This will be true, in the appropriate sense, for the mixed state case as well. A mixed state of the composite system is described by a density matrix ρ acting on 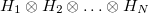 . ρ is separable if there exist
. ρ is separable if there exist 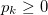 ,
, 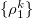 ,
, 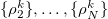 which are mixed states of the respective subsystems such that
which are mixed states of the respective subsystems such that 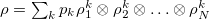 , where
, where 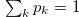 . Any violation of the condition of separation of the state makes it entangled. The most general approach to study the entanglement of quantum states in higher-dimensional physical systems is based on the notion of entanglement witnesses. In general, a Hermitian operator (or an observable) is called EW if it has a positive expectation value with all separable states while it possesses at least one negative eigenvalue. Mathematically, this means that for the Hermitian operator W, we must check the two properties: firstly,
. Any violation of the condition of separation of the state makes it entangled. The most general approach to study the entanglement of quantum states in higher-dimensional physical systems is based on the notion of entanglement witnesses. In general, a Hermitian operator (or an observable) is called EW if it has a positive expectation value with all separable states while it possesses at least one negative eigenvalue. Mathematically, this means that for the Hermitian operator W, we must check the two properties: firstly, 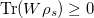 for all separable states
for all separable states 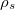 , secondly Tr
, secondly Tr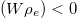 for some entangled state
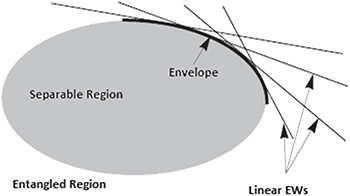
for some entangled state 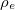 . In fact in quantum information theory, an entanglement witness is a functional which distinguishes a specific entangled state from the separable ones [25]. Each linear EW separates the separable region from the entanglement one. The set of such linear EWs is a family of curves whose envelope can be considered as a nonlinear entanglement witness. Figure 1 shows this nonlinear witness.
. In fact in quantum information theory, an entanglement witness is a functional which distinguishes a specific entangled state from the separable ones [25]. Each linear EW separates the separable region from the entanglement one. The set of such linear EWs is a family of curves whose envelope can be considered as a nonlinear entanglement witness. Figure 1 shows this nonlinear witness.
Fig. 1: Nonlinear EW is the envelope of a family of linear EWs.
Download figure:
Standard imageIn this section, we consider the N-partite systems where each of the local dimensions is 2n and find the separability condition for these states.
To this end, suppose that the entanglement witness W is in the following form [26]:
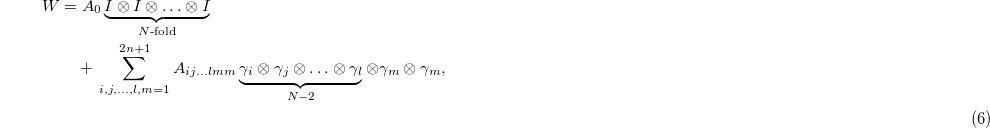
where 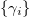 are Dirac matrices (see appendix) [27] and I denotes the identity matrix of dimension 2n. Note that here we choose maximally anticommuting sets of
are Dirac matrices (see appendix) [27] and I denotes the identity matrix of dimension 2n. Note that here we choose maximally anticommuting sets of 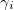 . Throughout the paper, we remove the tensor products. For example, instead of
. Throughout the paper, we remove the tensor products. For example, instead of 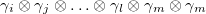 , we use the notation
, we use the notation 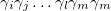 . Note that A0 is a nonzero positive real parameter,
. Note that A0 is a nonzero positive real parameter,  are operators with
are operators with 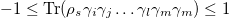 for every separable
for every separable 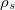 , and
, and 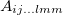 are real parameters whose ranges must be determined such that W becomes an EW. We define the arbitrary N-partite product state as
are real parameters whose ranges must be determined such that W becomes an EW. We define the arbitrary N-partite product state as 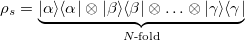 . For the Hermitian operators
. For the Hermitian operators  , we consider the maps
, we consider the maps 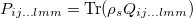 for any product state such that these maps map the convex set of product states into a bounded convex region which will be named feasible region. In other words, in order for W to be an entanglement witness, it must satisfy the condition
for any product state such that these maps map the convex set of product states into a bounded convex region which will be named feasible region. In other words, in order for W to be an entanglement witness, it must satisfy the condition  . This condition takes the following form:
. This condition takes the following form:

where

Note that in the above equation, the number of 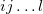 is N – 2. To proof of the inequality eq. (7) assume
is N – 2. To proof of the inequality eq. (7) assume
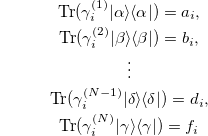
(where the superscripts  in
in 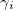 , denote the first, second, ..., N-th party, respectively) and
, denote the first, second, ..., N-th party, respectively) and
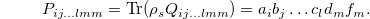
Hence we get

where
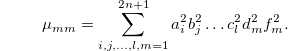
Since 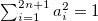 and also the similar relations hold for bi,..., ci, di and fi, then we have
and also the similar relations hold for bi,..., ci, di and fi, then we have

Hence, the convex optimization problem is in the following form:
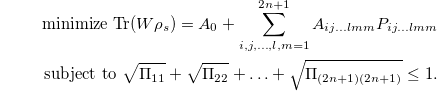
By solving this problem, we arrive at the following condition:

So, with the following condition:

W is an entanglement witness.
In the rest of this section, we are going to obtain the detection condition for generic density matrix. To do this, consider the following density matrix:

then we have
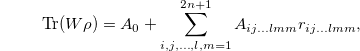
and by using eq. (11) and eq. (12), the convex optimization problem takes the form
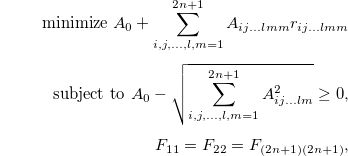
where
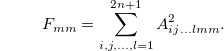
Using the convex optimization method, one can show that

where
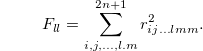
In order to find the PPT conditions of the density matrix, eq. (13), we consider the following assumptions: In the general form of a N-particles density matrix, the coefficients of  are
are 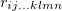 , but we choose these coefficients such that if
, but we choose these coefficients such that if 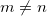 , then
, then 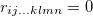 and also for any
and also for any 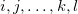 , we consider
, we consider  . So the subscript m appears twice in
. So the subscript m appears twice in 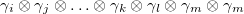 . The reason for this choice is that we are able to obtain the eigenvalues of the density matrix, otherwise, it is very difficult to gain the eigenvalues of it. So, by these conditions, the density matrix, eq. (13), has the following form:
. The reason for this choice is that we are able to obtain the eigenvalues of the density matrix, otherwise, it is very difficult to gain the eigenvalues of it. So, by these conditions, the density matrix, eq. (13), has the following form:

Now we are going to find the PPT condition of the density matrix, eq. (15). To this end, we rewrite it as the following form:

where
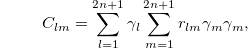
and
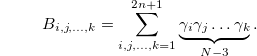
The eigenvalues of  are
are  , where
, where 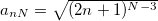 ., and the eigenvalues of Clm are
., and the eigenvalues of Clm are

where  . Finally, the PPT condition of the density matrix is as follows:
. Finally, the PPT condition of the density matrix is as follows:

Furthermore, for the density matrix of the form of eq. (15), the detection condition, eq. (14), is as the following form:
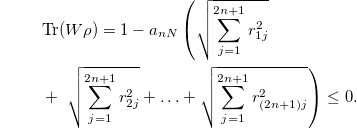
If Tr(Wρ) = 0, i.e.,
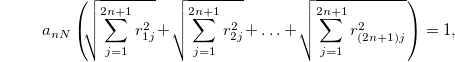
then ρ is separable, because we can write it as
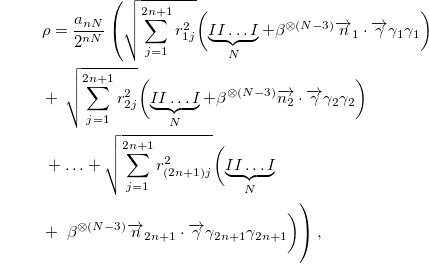
with
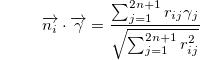
and
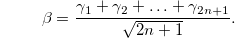
The terms in parentheses are projection operators and ρ is a convex combination of separable terms, hence ρ is separable.
Quantum discord of a N-partite system
We first recall a result regarding the closest classical states (CCS) and the closest separable states (CSS) of a generic state ρ in [28].
Theorem: Given a generic state 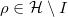 and
and 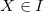 ,
, 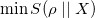 is achieved when ρ and X have common eigenbasis. Here, I is a special subset of the Hilbert space
is achieved when ρ and X have common eigenbasis. Here, I is a special subset of the Hilbert space 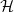 .
.
We should mention that obtaining the CCS and CSS of a generic state is still a very difficult problem. In fact, using the above result one can obtain the CCS and CSS of a generic state ρ when the eigenvectors of ρ and X are parallel.
Now, we focus on the density matrix in the form of eq. (15) and find an exact analytical formula for the quantum discord of this density matrix using the concept of relative entropy as a distance measure of correlations (eq. (2)). Now from eq. (2), to determine D, we have

The classical states contain mixtures of locally distinguishable states, hence we take the CCS of ρ as

Let us choose χ as 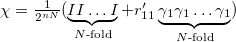 , then we obtain
, then we obtain

To maximize the above equation, by calculating the gradient of the above equation with respect to 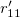 and make it zero, one can show that
and make it zero, one can show that 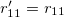 .
.
Hence quantum discord of N-partite systems in 2n dimensions is given by

Subadditivity relation
One of the basic question related to the measure of correlations is the additivity of the proposed measures. In this section, we discuss the subadditivity relation for the states given by eq. (15) and show that the subadditivity relation is satisfied for this density matrix. To this end, we use the relative entropy-based definitions of quantum correlations, which is completely applicable for multipartite systems of arbitrary dimensions. Defining the total mutual information as 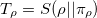 and classical correlation as
and classical correlation as 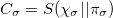 , the subadditivity relation that is
, the subadditivity relation that is 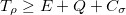 , can be checked. To simplify the investigation of the subadditivity relation between quantum correlations, we consider the special case that is
, can be checked. To simplify the investigation of the subadditivity relation between quantum correlations, we consider the special case that is
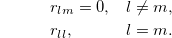
So we arrive at the following density matrix:

The PPT condition for this density matrix is as follows:

and then the detection condition of entanglement is 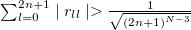 . In [28], the analytical technique for finding the closest separable states (CSS) of 2n-dimensional Bell diagonal states is provided. Following the calculations of it, we can write the closest separable states (CSS) of the density matrix, eq. (22), as
. In [28], the analytical technique for finding the closest separable states (CSS) of 2n-dimensional Bell diagonal states is provided. Following the calculations of it, we can write the closest separable states (CSS) of the density matrix, eq. (22), as

The eigenvectors of ρ and σ are parallel [28] and so  ; on the other hand, since σ is a separable state, then
; on the other hand, since σ is a separable state, then 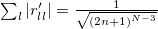 . Using these two facts, we get
. Using these two facts, we get

For simplicity, we assume that all of  is positive. Then by some calculations, we obtain the additivity relation between quantum correlations as the following form:
is positive. Then by some calculations, we obtain the additivity relation between quantum correlations as the following form:

then using eq. (23) we have 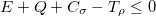 , that is the correlations of the state in eq. (15) are subadditive.
, that is the correlations of the state in eq. (15) are subadditive.
Conclusion
In this paper we have studied the system which consists of a N-partite system with 2n-dimensional Hilbert space in each subsystem. In the first step, we have found the entanglement witness for this system, then we have computed the quantum discord based on relative entropy. At the end of the paper, we have found the closest separable state (CSS) for a N-partite system of 2n-dimensional space and have analyzed the subadditivity relation between the quantum correlations of this system.
Acknowledgments
This research has been supported by Farhangian University of Tehran, Tabriz University and Shabestar Branch Islamic Azad University.
Appendix: gamma matrices
The gamma matrices,  ,
, 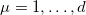 , are the set of d matrices that satisfy the following anticommutation relations:
, are the set of d matrices that satisfy the following anticommutation relations:

where 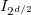 is the identity matrix with dimension
is the identity matrix with dimension  . These matrices are also called Dirac matrices and generate a matrix representation of the Clifford algebra with 2d dimension. One element of this algebra can be obtained by product all of the γ matrices:
. These matrices are also called Dirac matrices and generate a matrix representation of the Clifford algebra with 2d dimension. One element of this algebra can be obtained by product all of the γ matrices:
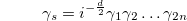
that commute with all gamma matrices and 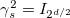 . By adding this matrix with other gamma matrices, anticommutation relations have the following form:
. By adding this matrix with other gamma matrices, anticommutation relations have the following form:

In the case of d = 2, the Dirac matrices are the Pauli matrices all of which are Hermitian:

It is also possible to construct higher-dimensional gamma matrices that generalize to even dimensions as follows:
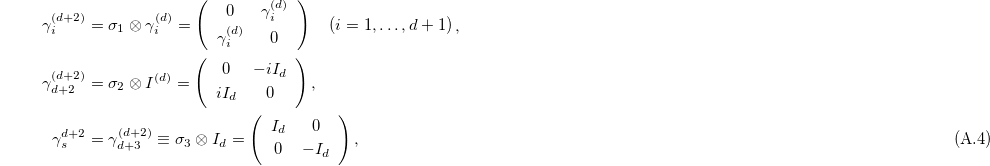
where Id is the unitary matrix in 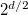 dimensions. It can be shown that if
dimensions. It can be shown that if 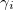 satisfy eq. (A.2) in d-dimension, then the same relation exists for
satisfy eq. (A.2) in d-dimension, then the same relation exists for 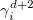 .
.
As eq. (A.2) shows, we can indicate the γ matrices in odd dimensions through obtaining the γ matrices of dimension d – 1 where 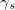 was added to them. In this case the γ matrices are not all algebraically independent, in contrast to the even case.
was added to them. In this case the γ matrices are not all algebraically independent, in contrast to the even case.