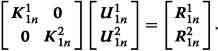Domain decomposition involving subdomain separable space representations for solving parametric problems in complex geometries

Abstract

A domain decomposition technique combined with an enhanced geometry mapping based on the use of NURBS is considered for solving parametrized models in complex geometries (non simply connected) within the so-called proper generalized decomposition (PGD) framework, enabling the expression of the solution in each subdomain in a fully separated form, involving both the space and the model parameters. NURBS allow a compact and powerful domain mapping into a fully separated reference geometry, while the PGD allows recovering an affine structure of the problem in the reference domain, facilitating the use of the standard PGD solver for computing the parametric solution in each subdomain first, and then by enforcing the interface transmission conditions, in the whole domain.

Introduction

Proper generalized decomposition (PGD) is based on the use of separated representations, fact that alleviates the computational complexity when solving multidimensional problems by reducing them to a sequence of lower dimensional problems. PGD was successfully applied for addressing four problem typologies:

• Transient models can be decomposed into a series of space and time problems, leading to a non-incremental integrator where the solution history is computed simultaneously instead of incrementally as most of time integrators perform. The interested reader can refer to [7] and the numerous references therein;

• Parametric models can be decomposed into a series of space, time and parameter problems, enabling the calculation of the whole solution history for any value of the parameters involved in the model and here assumed as model extra-coordinates, as described in [8, 10] and the numerous references therein;

• The solution of models defined in a degenerated domain (like plate, shells, beam, ... geometries) where at least one of its characteristic dimensions is much smaller than the others, can be successfully accomplished within the separated representation framework, where each dimension is treated sequentially, weakly coupled with the others, reducing the 3D problem to a sequence of one-dimensional ones (or a series of two and one dimensional problems) which alleviates the meshing issues usually encountered when performing 3D analyses in this kind of domains [7].

• Problems defined in non-degenerated but non-separable domains that could become separable in a domain decomposition framework.

This work concerns the fourth problem typology, that is, the one related to space-separation with domain decomposition.

In the past it was claimed that this kind of decomposition works well when the domain can be expressed from the cartesian product of one-dimensional domains, or a two-dimensional and a one-dimensional ones as it is the case when addressing plates and shell geometries, laminates or extruded profiles. More complex geometries, non-separable in a direct way, can be separated by using appropriate mappings [2, 13, 14] or penalty techniques [13], and thus, fully space-separated representation can be applied to reduce the computational cost of solving 3D problems to the one characteristic of the solution of 2D or 1D problems.

However, the proposed mappings generality remains quite limited when the domain shape complexity increases. In [1] we proposed a two levels discretization, the coarser to parametrize the shape and the finest for approximating the problem solution, being the main remaining challenges: (i) the accurate geometry parametrization, looking for its most compact representation when that geometry is being considered as a model parameter (a very valuable route in shape optimization); and (ii) the affine expression of the problem defined in the reference (fully separable) domain to ensure the efficiency of the separated representation constructor (PGD solver).

For alleviating the just referred issues domain decomposition techniques could be envisaged. Domain decomposition techniques have been widely employed in a diversity of applications. Some techniques are based on the subdomains overlapping, other consider non-overlaping coupling strategies. Among the overlapping-based strategies we can mention the classical Schwartz [27] or the more recent and versatile Arlequin technique and its variants [3,4,5]. Among the non-overlapping ones we can mention the mortar-based techniques [6, 23], the FETI strategy and its variants [11, 12] and the LATIN-multiscale and LATIN-multidomain approaches widely developed by Ladeveze and coauthors [18,19,20,21] [22]. These works considered multi-domain coupled with space-time separated representations, however in our knowledge, never separated representations involving either space coordinates or parametric extra-coordinates were considered within the framework of domain decomposition. Authors proposed different techniques based on domain decomposition, within the Arlequin coupling paradigm [25] and within a more standard decomposition (without overlapping) technique, assembling parametric patches [15].

Recently, in [16] we proposed a powerful mapping able to represent complex CAD geometries (employing NURBS) and able to efficiently parametrize complex mappings while recover efficiently an affine decomposition of the differential operators involved in the model. However, the presented technology only applied in simply connected domains, that is, for example in 2D domains without holes.

In the present work the technique proposed in [16] is extended for addressing non simply connected domains. For that purpose, we consider the mapping proposed in [16] in tandem with a domain decomposition technique, where the required continuity is ensured at the patches interface level. The proposed technique will be applied in some numerical experiments to prove its potential.

Geometrical mapping and domain decomposition

To use the full potential of the PGD technique for solving parametric and high dimensional problems defined in non-regular geometries (non rectangular or hexahedral) it is necessary to map the problem from the non-regular physical domain, $\Omega _{\varvec{x}}$, into a regular (in the sense of separable) computational domain, $\Omega _{\varvec{\xi }}$. A schematic geometric mapping is shown in Fig. 1. It can be noticed that the geometric mapping should ensure a separable nature of the problem. Recently, the authors have proposed a general and easily separable mapping in conjunction with the NURBS basis functions [16] for the geometry description. This technique makes possible using the PGD for solving parametric problems in 2D and 3D non-separable domains.

Fig. 1

A schematic representation of the geometrical mapping: a Physical domain; b Computational domain

Fig. 2

Schematic representation of the conversion of a domain with an internal hole into a simply connected computational domain (the two sided arrow shows the continuity constraint): a Physical domain; b computational domain

This technique can be generalized for solving problems in non simply connected domains as the one illustrated in Fig. 2 containing a hole, by transforming it into a simply-connected domain. For that purpose, one could cut the domain creating a new boundary connecting the inner and outer boundaries and then applying in it the continuity constraints when solving the problem, for guaranteeing the solution periodicity across this artificial boundary. More details regarding the enforcement of the continuity constraints will be presented later in subsequent sections.

Although the above mentioned procedure could be used to convert any domain with one internal hole into a simply connected domain, the mapping could become very complex in some cases affecting the solution efficiency. It also must be noted that in the case of domains with many holes this technique needs more than a simple single cut, making difficult the proposed procedure.

To overcome this difficulty, it is proposed in the current work to use more than one computational domain while applying the PGD in each computational domain (subdomain). In this approach, the physical domain would be decomposed into some relatively simple subdomains or patches and then each patch mapped into a separable computational domain.

To preserve the continuity of the solution on the subdomain interfaces, appropriate continuity constraints must be applied between adjacent patches expressed in their computational domains.

A schematic representation of this multi-patch technique is shown in Figs. 3 and 4 for domains containing one and two internal holes, respectively. Such domain decomposition is possible for other topologies addressed later. Details concerning the continuity enforcement between adjacent patches will be presented in the following sections.

Fig. 3

Schematic representation of the multi-patch approach for a domain containing one internal hole: a Patches in the physical domain; b Continuity constraints between adjacent patches; c Patches in the computational domain

Fig. 4

A schematic representation of multi-patch approach for a domain containing two internal holes: a Patches in the physical domain; b Continuity constraints between adjacent patches; c Patches in the computational domain

Problem formulation

For the sake of simplicity and without loss of generality in the present work we evaluate the proposed multi-domain technique by considering the nonlinear heat equation with a temperature dependent thermal conductivity, expressed from:

$$\begin{aligned} \frac{\partial }{\partial x} \left( k(u)\frac{\partial u}{\partial x}\right) + \frac{\partial }{\partial y} \left( k(u)\frac{\partial u}{\partial y}\right) + f = 0, \end{aligned}$$

(1)

where u is the unknown temperature field defined in physical domain $\Omega _{\varvec{x}}$, k(u) is the temperature dependent thermal conductivity and f is the distributed heat source. The nonlinear models will be addressed by using an adequate linearization. In the context of the PGD addressed later, the simplest route consists in evaluating the nonlinear terms, the conductivity in the present case, from the temperature field computed at the previous iteration.

The physical domain, $\Omega _{\varvec{x}}$, results from the union of non-overlapping subdomains or patches $\Omega _{\varvec{x}}^s$.

$$\begin{aligned} \Omega _{\varvec{x}}=\bigcup _{s=1}^{N_p} \Omega _{\varvec{x}}^s, \end{aligned}$$

(2)

where $N_p$ is the total number of patches.

The weighted residual form of Eq. (1) reads

$$\begin{aligned} B(w,u)=L(w) \end{aligned}$$

(3)

where w and u are the test and trial functions respectively, and B and L the associated bi-linear and linear forms.

The problem can be expressed in the variational form

$$\begin{aligned} I=\frac{1}{2} B(u,u) - L(u). \end{aligned}$$

(4)

The unknown field $u(\varvec{x})$ must be obtained in such a way that minimize the functional I in Eq. (4). In the proposed multi-patch technique, a penalty method is used to enforce the Dirichlet boundary conditions, by considering the extended variational form

$$\begin{aligned} I^{\alpha }=\frac{1}{2} B(u,u) - L(u)+\frac{1}{2}\int _{\Gamma _D} \alpha (u-{{\bar{u}}})^2 d\Gamma , \end{aligned}$$

(5)

where ${{\bar{u}}}$ is the prescribed value of the field on the Dirichlet boundary $\Gamma _D$ and $\alpha$ is the associated penalty parameter. By minimizing the functional it results

$$\begin{aligned}&\int _{\Omega _{\varvec{x}}} {\tilde{k}} \left( \frac{\partial u^*}{\partial x} \frac{\partial u}{\partial x} + \frac{\partial u^*}{\partial y} \frac{\partial u}{\partial y} \right) d \Omega + \int _{\Gamma _D} \alpha u^* u d \Gamma = \nonumber \\&\ \int _{\Omega _{\varvec{x}}} u^* f d \Omega + \int _{\Gamma _N} u^* {{\bar{q}}} d \Gamma + \int _{\Gamma _D} \alpha u^* {{\bar{u}}} d \Gamma , \end{aligned}$$

(6)

where ${\tilde{k}}$ represents the conductivity linearization and ${{\bar{q}}}$ is the prescribed heat flux on the Neumann boundary $\Gamma _N$. In Eq. (6), $u^*$ is the first variation of the field variable u.

Solution procedure

The use of NURBS enables the efficient description of general curves, surfaces and volumes. According to the notation introduced in Appendix A, the mapping from the physical to the computational domain in the 2D case reads

$$\begin{aligned} \varvec{x}=\sum ^n_{i=1} \sum ^m_{j=1} R^{pq}_{ij} (\varvec{\xi }) \varvec{P}_{ij}^s\ ,\ \ \ \ \ \ \ \varvec{x} \in \Omega _{\varvec{x}}^s\ ,\ \ \varvec{\xi }\in \Omega _{\varvec{\xi }}^s \end{aligned}$$

(7)

where are $R^{pq}_{ij} (\varvec{\xi })$ are the NURBS-based shape functions, $\varvec{P}^s_{ij}$ refers to the control points (the vertices of the so-called control net) related to the s-th patch in the physical domain. Eq. (7) expresses the geometrical mapping, with $\varvec{\xi }$ in the computational domain $\Omega _{\varvec{\xi }}^s$ to a point $\varvec{x}$ in physical domain $\Omega _{\varvec{x}}^s$.

The previous equation allows not only transforming the domain, but also transforming the differential operators and computing the transformation Jacobian (see Appendix A).

Even if the computational domain in which the physical one is mapped, is fully separable by construction, the differential operators are not, because of the fact that the just referred shape functions involved in the geometry mapping are not separated. Thus, to obtain a separated representation of a generic function $g(\varvec{x})$ into the computational domain, it suffices looking for the separated form

$$\begin{aligned} g(\varvec{\xi }) \approx \sum ^{N_G}_{i=1} \prod ^{N_D}_{j=1} {\varvec{M}}^T_j(\xi _j) \varvec{G}_{ji}, \end{aligned}$$

(8)

with $\varvec{M}_j(\xi _j)$ the vector of approximation functions involving the j-th coordinate and $\varvec{G}_{ji}$ is the vector of coefficients of the i-th mode in the j-th coordinate direction. $N_D$ is the total number of problem dimensions (in the present case $N_D=2$ if the problem is 2D or $N_D>2$ when some problem parameters are considered as model extra-coordinates) and $N_G$ is the number of modes needed for reaching the desired accuracy (as described in Appendix B).

Thus, the so-called Separated Approximate Representation –SAR– proceeds by enforcing in a weak form the equality $g(\varvec{\xi }) = g(\varvec{x}(\varvec{\xi }))$ in $\Omega _{\varvec{\xi }}^s$, with $g(\varvec{\xi })$ expressed in the separated form (8), following the procedure deeply addressed in our former works [9, 16], to finally obtain the coefficients $\varvec{G}_{ji}$.

This procedure, the just described SAR, is then applied for expressing both the Jacobian and the differential operator transformation (see Appendix C), in an affine form, making possible the application of the standard PGD procedure.

Thus, the separated representation of the temperature field $u(\varvec{\xi })$ in the computational subdomain $\Omega _{\varvec{\xi }}^s$ reads at the n-enrichment (the dependence on the subdomain considered, referred by the upper-script $\bullet ^s$, is omitted for the sake of notational simplicity)

$$\begin{aligned} u^n(\varvec{\xi }) \approx \sum ^{n-1}_{i=1} \prod ^{N_D}_{j=1} \varvec{M}^T_j \varvec{U}_{ji} + \prod ^{N_D}_{j=1} \varvec{M}^T_j \varvec{U}_{jn}, \end{aligned}$$

(9)

where $\varvec{U}_{jn}$, $j=1,2,\dots ,N_D$ must be calculated from the problem weak form by using the standard fixed-point alternated directions fixed point algorithm [9].

When updating the function concerned by the d-coordinate (in the present case $d=1$ or $d=2$), the test function reads:

$$\begin{aligned} u^{*d}(\varvec{\xi }) = {\varvec{M}_d^T \varvec{U}_{dn}^{*d} \prod ^{N_D}_{ \begin{array}{c} j=1 \\ j\ne d \end{array}} \varvec{M}^T_j \varvec{U}_{jn}}, \end{aligned}$$

(10)

that allows updating coefficients $\varvec{U}_{dn}$.

Nonlinear models can be addressed by computing nonlinear terms at the current solution (for instance $u^{n-1}(\varvec{\xi })$) whose affine description can be recovered by applying again the SAR. For additional details the interested reader can refer to [16].

Enforcing continuity constraints

As stated before, continuity constraints must be enforced between adjacent patches to enforce the continuity of the field. The continuity constraints may be defined between opposite sides of a single patch or between sides of adjacent patches. In the former case, the standard fixed point iterative method involved in the PGD constructor, can be applied for solving the resulting system of nonlinear algebraic equations.

Application of the continuity constraints between the adjacent edges of a multi-patch topology is more complex and the standard fixed point iterative approach is not longer applicable. In this case, a multi-action fixed point iterative approach is proposed in the present work to solve the system of nonlinear algebraic equations. These techniques are discussed in the following subsections.

Single patch PGD with continuity constraints

As previously discussed a valuable approach to solve the problem in a domain containing an internal hole consists of applying a cut line and transform the non simply connected region into a simply connected one as shown schematically in Fig. 2.

A continuity constraint then should be enforce to ensure the continuity of the field along that cut-line. In this approach, the problem can be solved using a single patch (one computational domain). Consider, for instance, that the continuity constraint is defined between the edges parallel to $\xi$ axis, that according to Eq. (9) implies some constraints to be applied in the modes concerning the direction $\eta$.

In other words, when operating with $\varvec{M} _2^T \varvec{U} _{2n}$, the constraint reads:

$$\begin{aligned} \left( \varvec{M} _2^T \varvec{U} _{2n} \right) \bigg |_{\eta =0} = \left( \varvec{M} _2^T \varvec{U} _{2n} \right) \bigg |_{\eta =1}. \end{aligned}$$

(11)

When using standard piecewise linear functions for expressing $\varvec{M}_2$, verifying the Kroenecker delta property, the previous constraint implies that the first and last degree of freedom coincides. That is, in ${\mathcal {N}}_2$ nodes are used for approximating the modes involving the $\eta$ coordinate, the previous continuity constraint simply reads

$$\begin{aligned} \varvec{U}_{2n}\bigg |_1=\varvec{U}_{2n}\bigg |_{{\mathcal {N}}_2}, \end{aligned}$$

(12)

that can be directly enforced when looking for the coefficients $\varvec{U} _{2n}$.

Multi-patch PGD with continuity constraints

When more than one computational domain is considered, the continuity constraint and fixed point iteration schema becomes more complex. To explain the basic idea and the procedure, three sample topologies for computational domains are considered. More complex cases are considered in subsequent sections.

Fig. 5

First topology: multi-patch computational domains and a single continuity constraint

First topology

For the first sample topology, consider the two patches shown in Fig. 5. There is a single continuity constraint and is shown in that figure. Consider in the n-th enrichment step, we would like to find $\varvec{U}_{dn}^s$, where s is the patch number, and d is the space direction ($d=1$ for $\xi$ and $d=2$ for $\eta$).

The continuity constraint (see Fig. 5) indicates that the unknown field at the edge BC of patch 1 must be equal to the field at the edge BC of patch 2. Therefore, the modes involving the $\eta$ direction in patch 1 must be the same as the modes in this same direction in patch 2. In addition, the value of the modes involving the $\xi$ direction at the common boundary must match. To make it more clear, refer to Fig. 6. This figure shows schematic representation of modes in $\xi$ and $\eta$ directions for two patches 1 and 2. To satisfy the continuity between two patches, Fig. 6a, b show that the modes of $\xi$ should have same value at the patches interface. On the other hand, Fig. 6c, d show that the modes of $\eta$ should be same function for both patches. Mathematically, the continuity constraint for this sample topology is defined as:

(13)

Fig. 6

Schematic representation of modes and continuity constraint for two patches of the first topology: (a, b) modes in $\xi$ direction; (c, d) modes in $\eta$ direction

The PGD system of algebraic equations regarding direction d of patch s at the n-th enrichment step reads (see [16]):

$$\begin{aligned} \varvec{K}_{dn}^s \varvec{U}_{dn}^s = \varvec{R}_{dn}^s. \end{aligned}$$

(14)

To solve the equations and obtain the n-th enrichment modes, a modified fixed point iteration approach is used here considering the continuity constraint given in Eq. (13). This modified fixed point schema consists of the three steps:

• 1. Regarding the continuity constraint given in the first row of Eq. (13), the system to be solved reads

  

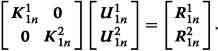  (15)

• 2. Regarding the continuity constraint given in the second row of Eq. (13), the system to be solved reads

  $$\begin{aligned} \left[ \begin{array}{c} \varvec{K}_{2n}^1 \end{array} \right] \left[ \begin{array}{c} \varvec{U}_{2n}^1 \end{array}\right] = \left[ \begin{array}{c} \varvec{R}_{2n}^1 \end{array}\right] . \end{aligned}$$

  (16)

• 3. If other parameters are involved as extra-coordinates, that can be represented by a generic d, $d>2$, the associated degrees of freedom results from

  $$\begin{aligned} \left[ \varvec{K}_{dn}^1 + \varvec{K}_{dn}^2 \right] \left[ \varvec{U}_{dn}^1 \right] = \left[ \varvec{R}_{dn}^1 + \varvec{R}_{dn}^2 \right] . \end{aligned}$$

  (17)

The Eqs. (15)–(17) are located in the inner loop of fixed point algorithm. It is clear that the first row of Eq. (13) must be considered when solving Eq. (15) and it consists of simple matrix operations. Each system of Eqs. in (15)–(17) is solved by a direct system solver.

Second topology

The second sample topology consists of three patches shown in Fig. 7. The continuity constraints are also shown in that figure. Consider in the n-th enrichment step, we would like to find $\varvec{U}_{dn}^s$, where s is the patch number, and d is the space direction ($d=1$ for $\xi$ and $d=2$ for $\eta$).

The continuity constraint 1 (in reference to Fig. 7) indicates that the unknown field at the edge BC of patch 1 must be equal to the field at the edge BC of patch 2. Therefore, the modes involving the $\eta$ direction in patch 1 must be the same as the ones in this same direction in patch 2. In addition, the value of the modes involving the $\xi$ direction at the common boundary must match, i.e.:

(18)

Fig. 7

Second topology: multi-patch computational domains and continuity constraints

The same rationale applies for enforcing the continuity constraint 2 (see Fig. 7). To make it more clear, the modes involving $\xi$ direction in patch 2 must be the same as the modes in $\xi$ direction in patch 3. And, the modes involving $\eta$ direction must match at the common interface of patches 2 and 3. That reads:

(19)

The PGD system of algebraic equations regarding direction d of patch s at the n-th enrichment step reads

$$\begin{aligned} \varvec{K}_{dn}^s \varvec{U}_{dn}^s = \varvec{R}_{dn}^s. \end{aligned}$$

(20)

The modified fixed point schema consists of the three steps:

• 1. Regarding the continuity constraint 1 given in Eq. (18), the system to be solved reads

  

  (21)

• 2. Regarding the continuity constraint 2 given in Eq. (19), the system to be solved reads

  $$\begin{aligned} \left[ \begin{array}{cc} \varvec{K}_{2n}^1+\varvec{K}_{2n}^2 &{} \varvec{0} \\ \varvec{0} &{} \varvec{K}_{2n}^3 \end{array} \right] \left[ \begin{array}{c} \varvec{U}_{2n}^1 \\ \varvec{U}_{2n}^3 \end{array}\right] = \left[ \begin{array}{c} \varvec{R}_{2n}^1 + \varvec{R}_{2n}^2\\ \varvec{R}_{2n}^3 \end{array}\right] . \end{aligned}$$

  (22)

• 3. If other parameters are involved as extra-coordinates, that can be represented by a generic d, $d>2$, the associated degrees of freedom results from

  $$\begin{aligned} \left[ \varvec{K}_{dn}^1 + \varvec{K}_{dn}^2 + \varvec{K}_{dn}^3 \right] \left[ \varvec{U}_{dn}^1 \right] = \left[ \varvec{R}_{dn}^1 + \varvec{R}_{dn}^2 + \varvec{R}_{dn}^3 \right] . \end{aligned}$$

  (23)

Fig. 8

Second topology: multi-patch computational domains and continuity constraints

The systems of Eqs. (21)–(23) constitute the solution procedure. In other words, the Eqs. (21)–(23) are placed in the inner loop of fixed point algorithm. Each system of Eqs. in (21)–(23) is solved by a direct system solver but the whole process is iterative.

Third topology

For the third sample topology, we consider a computational domain composed of the four patches shown in Fig. 8 that shows the four continuity constraints.

By using the notation that was used previously, the continuity of the filed along all adjacent edges, the continuity constraints 1 to 4 are given in Table 1. Note that the operator $\mathrm {Flip}(\cdot )$ that appears in some terms of Table 1 acts on a vector, by reversing the elements of the vector. It also acts in a similar way on the associated matrices. For example concerning the second constraint, $\eta$ increases in patch 2 while the associated coordinate, $\xi$ in patch 3 decreases.

Table 1 Continuity constraints in the second analyzed topology, where ${\mathcal {N}}_1$ and ${\mathcal {N}}_2$ are the same in all the subdomains

Taking into account the usual PGD update given by Eq. (20) and the continuity constraints given in Table 1, the procedure reads:

• 1. Compute the less-constrained modes where only the constraints in the last column of Table 1 are enforce in a direct manner,

  $$\begin{aligned} \left[ \begin{array}{cccc} \varvec{K}_{1n}^2 &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{K}_{2n}^3 &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{K}_{1n}^4 &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{K}_{2n}^1 \\ \end{array} \right] \left[ \begin{array}{c} \varvec{U}_{1n}^2 \\ \varvec{U}_{2n}^3 \\ \varvec{U}_{1n}^4 \\ \varvec{U}_{2n}^1 \\ \end{array}\right] = \left[ \begin{array}{c} \varvec{R}_{1n}^2 \\ \varvec{R}_{2n}^3 \\ \varvec{R}_{1n}^4 \\ \varvec{R}_{2n}^1 \\ \end{array}\right] . \end{aligned}$$

  (24)

• 2. The most constrained modes are then calculated, in fact only one because the first column in Table 1 implies that it propagates along all the connected patches. This mode reads

  $$\begin{aligned}&\left[ \varvec{K}_{2n}^2 + \mathrm {Flip} (\varvec{K}_{1n}^3) + \mathrm {Flip} (\varvec{K}_{2n}^4) + \varvec{K}_{1n}^1 \right] \left[ \varvec{U}_{2n}^2 \right] = \nonumber \\&\left[ \varvec{R}_{2n}^2 + \mathrm {Flip} (\varvec{R}_{1n}^3) + \mathrm {Flip} (\varvec{R}_{2n}^4) + \varvec{R}_{1n}^1 \right] . \end{aligned}$$

  (25)

• 3. If other parameters are involved as extra-coordinates, that can be represented by a generic d, $d>2$, the associated degrees of freedom results from

  $$\begin{aligned} \left[ \varvec{K}_{dn}^1 + \varvec{K}_{dn}^2 + \varvec{K}_{dn}^3 + \varvec{K}_{dn}^4 \right] \left[ \varvec{U}_{dn}^1 \right] = \left[ \varvec{R}_{dn}^1 + \varvec{R}_{dn}^2 + \varvec{R}_{dn}^3 + \varvec{R}_{dn}^4 \right] . \end{aligned}$$

  (26)

Similar to the previous topology, the systems of Eqs. (24)–(26) are placed in the inner loop of fixed point algorithm. In each iteration of the fixed point procedure, the system of Eqs. in (24)–(26) should be solved by a direct system solver.

Numerical examples

In this section some numerical examples are presented to evaluate the applicability and potential of the proposed multi-patch separable PGD technique.

First case study

The first numerical example concerns the Poisson problem in a circular domain containing an internal hole. The problem domain, its dimensions and the control net that is used for representing the physical domain from NURBS are shown in Fig. 9. The domain is transformed into a simply-connected domain by using a cut-line, the segment AC, shown in Fig. 10(left).

The computational domain and the continuity constraint are shown in Fig. 10(right). To construct the NURBS basis, the order of the B-Spline basis functions is of two concerning the dimension $\xi$ and one concerning $\eta$. The knot vectors $\varvec{\kappa }_\xi$ and $\varvec{\kappa }_\eta$ (introduced in Appendix A) are given by

$$\begin{aligned} \varvec{\kappa }_\xi =[0,0,0,0.25,0.25,0.5,0.5,0.75,0.75,1,1,1]^T, \end{aligned}$$

(27)

and

$$\begin{aligned} \varvec{\kappa }_\eta =[0,0,1,1]^T, \end{aligned}$$

(28)

respectively.

Homogeneous Dirichlet boundary conditions are enforced on both boundaries, the inner and outer, that is, on the boundaries ABA and CDC of the computational domain depicted in Fig. 10.

The heat source f(x, y) in Eq. (1) reads:

$$\begin{aligned} f(x,y) = \frac{4}{5} \left( 4x^2 + 4y^2 -4y + 1 \right) -8. \end{aligned}$$

(29)

This particular choice leads to the exact solution

$$\begin{aligned} u(x,y)=-\frac{1}{5}(x^2+y^2-1)\left( x^2+(y-1)^2-9\right) . \end{aligned}$$

(30)

Fig. 9

Physical domain related to the Poisson problem, with the dimensions and the control net related to the NURBS-based geometry description

Fig. 10

Geometry mapping and the continuity constraint: a Physical domain; b Computational domain

The separated representation of the physical coordinates $x(\xi ,\eta )$ and $y(\xi ,\eta )$ (according to Appendix C) involve a single mode for the former and two modes for the last, represented in Figs. 11 and 12, for x and y, respectively.

Fig. 11

Separated representation of $x(\xi ,\eta )$ involving a single mode

Fig. 12

Separated representation of $y(\xi ,\eta )$ involving two modes

The modes involved in the separated representation of the solution involved 41 nodes for the modes affecting the $\xi$ coordinate and 21 the ones concerning $\eta$.

The first five modes involved in the separated representation of $u(\xi ,\eta )$ are shown in Fig. 13. The contours of the reconstructed field in the physical and computational domains are shown in Fig. 14. The computed PGD solution is compared with exact one in Fig. 15 along the line $x=0$ for $1<y<4$, proving the excellent accuracy of the computed solution.

Fig. 13

First five modes involved in the separated representation of $u(\xi ,\eta )$ related to the first case study

Fig. 14

Contours of the reconstructed solution: a Physical domain; b Computational domain

Fig. 15

Comparison of the PGD results with exact one on $x=0$ for $1<y<4$

Second case study

The second case study concerns a domaine containing two holes. The problem domain is divided into 8 subdomains or patches. The dimensions of the physical domain and the control nets related to the NURB representation of the geometry are shown in Fig. 16.

The patches in the physical and computational domains and the continuity constraints are shown in Figs. 17 and 18, respectively. In the present numerical study all the patches have the same structure, therefore, the same knot vectors are used for all patches, in particular

$$ \begin{aligned} \varvec{\kappa }_\xi =[0,0,0,1,1,1]^T \ \& \ \varvec{\kappa }_\eta =[0,0,1,1]^T. \end{aligned}$$

(31)

Fig. 16

Geometry and control net concerned by the second case study

A nonzero Dirichlet boundary condition is enforced on the boundary of both internal holes, with ${\overline{u}}=100$ and ${\overline{u}}=10$ on the left and right holes respectively, that will be enforced by using the penalty technique discussed before. In the present case, a temperature dependent thermal conductivity is considered, according to $k(u)=1+0.04u$. No thermal source is considered, i.e., $f(x,y)=0$.

The 9 continuity constraints which are shown in Fig. 18 are expressed in detail in Table 2. These continuity constraints will be considered as previously discussed.

Fig. 17

Patches in the physical domain and continuity constraints associated to the second case study

Fig. 18

Patches in the computational domain and continuity constraints associated to the second case study

The three steps procedure previously described is here applied again, where the third step does not apply because there are not extra-coordinates to be addressed:

• 1. The modes that concerns each subdomain, with as only constraints the ones reported in the last column of Table 2, leads to the system

  $$\begin{aligned}&\left[ \begin{array}{ccccccc} \varvec{K}_{1n}^1 &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{K}_{1n}^2 + \mathrm {Flip} (\varvec{K}_{1n}^8) &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{K}_{1n}^3 &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{K}_{1n}^4 &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{K}_{1n}^5 &{} \varvec{0} &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{K}_{1n}^6 &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{K}_{1n}^7 \\ \end{array} \right] \left[ \begin{array}{c} \varvec{U}_{1n}^1 \\ \varvec{U}_{1n}^2 \\ \varvec{U}_{1n}^3 \\ \varvec{U}_{1n}^4 \\ \varvec{U}_{1n}^5 \\ \varvec{U}_{1n}^6 \\ \varvec{U}_{1n}^7 \\ \end{array} \right] = \nonumber \\&\left[ \begin{array}{c} \varvec{R}_{1n}^1 \\ \varvec{R}_{1n}^2 + \mathrm {Flip} (\varvec{R}_{1n}^8) \\ \varvec{R}_{1n}^3 \\ \varvec{R}_{1n}^4 \\ \varvec{R}_{1n}^5 \\ \varvec{R}_{1n}^6 \\ \varvec{R}_{1n}^7 \\ \end{array} \right] . \end{aligned}$$

  (32)

• 2. The second step concerns the calculation of the modes that propagate throughout different patches for ensuring the continuity (first column in Table 2). It is easy to see that in the present case these modes verify the system

  $$\begin{aligned}&\left[ \begin{array}{cc} \varvec{K}_{2n}^1 + \varvec{K}_{2n}^2 + \varvec{K}_{2n}^3 + \varvec{K}_{2n}^4 &{} \varvec{0} \\ \varvec{0} &{} \varvec{K}_{2n}^5 +\varvec{K}_{2n}^6 + \varvec{K}_{2n}^7 + \varvec{K}_{2n}^8 \\ \end{array} \right] \left[ \begin{array}{c} \varvec{U}_{2n}^1 \\ \varvec{U}_{2n}^8 \\ \end{array} \right] = \nonumber \\&\left[ \begin{array}{c} \varvec{R}_{2n}^1 + \varvec{R}_{2n}^2 + \varvec{R}_{2n}^3 + \varvec{R}_{2n}^4 \\ \varvec{R}_{2n}^5 + \varvec{R}_{2n}^6 + \varvec{R}_{2n}^7 + \varvec{R}_{2n}^8 \\ \end{array} \right] . \end{aligned}$$

  (33)

Table 2 Continuity constraints to be enforced in the second use case, with ${\mathcal {N}}_1 = {\mathcal {N}}_2 \equiv {\mathcal {N}}$ for all the subdomains

In the present case study the 1D discretizations of modes involving the $\xi$ and $\eta$ coordinates is done by using 21 nodes in each direction. The contours of the reconstructed solution, in the physical u(x, y) and computational $u(\xi ,\eta )$ domains, are shown in Figs. 19 and 20, respectively.

The first six modes involved in the solution $u(\xi ,\eta )$, are shown for the eight patches in Fig. 21. To evaluate the PGD results, the problem is also solved by using the finite element method with linear quadrilateral elements. The solution on the upper edge of the domain, $y=3$, is plotted in Fig. 22 for both PGD and finite element solutions, proving the excellent accuracy of the PGD-based solution.

Fig. 19

Reconstructed solution in the physical domain in the second case study

Fig. 20

Reconstructed solution in the computational domain in the second case study

Fig. 21

First six modes in the eight patches

Fig. 22

Comparison of the PGD and the finite element solutions on the upper edge of the domain, $y=3$

Third case study

In the last case study we are including parameters as model extra-coordinates. In particular the domain geometry is parameterized here and the field variable is not only a function of coordinates $\xi$ and $\eta$ but also it is a function of few extra-parameters describing the domain shape.

We solve the Laplace equation, in the domain shown in Fig. 23, where the internal hole has a shape represented by the four digits NACA profile that involves three parameters M, P and T [24]. Thus, the problem involves 5 coordinates, the space ones, $\xi$ and $\eta$, and the three extra-coordinates M, P and T, that within the PGD rationale, its solution will reduce to a sequence of five one-dimensional problems.

The physical domain consists of the internal boundary (where a null normal gradient is enforced) and an outer boundary (ellipse) on which the solution in enforced (Dirichlet boundary condition), $u(x,y)=x$. A single computational domain (single patch) is used here to map the physical domain. The geometry mapping and continuity constraint are shown in Fig. 23. Both internal and external boundaries are described by using NURBS, each involving 31 control points.

The continuity constraint is very simple as previously discussed, it reduces to

(34)

Fig. 23

Physical and computational domain related to the third case study

The ranges of the parameters describing the shape are: $M\in [0,5]\%$, $P\in [35,50]\%$ and $T\in [15,30]\%$. The 1D discretization is done by using 11 nodes in each directions $\xi$, M, P and T and 31 nodes in the $\eta$ direction. The contours of the reconstructed solution, $u(\xi ,\eta ,M,P,T)$, in the physical domain are shown in Fig. 24 for four different choices of the parameters defining the internal shape. The first six modes involved in the solution separated representation are shown in Fig. 25.

Fig. 24

Reconstructed solution for four choices of the internal shape

Fig. 25

Six first modes involved in the parametric separated representation of $u(\xi ,\eta ,M,P,T)$

Conclusions

The present paper proposed a valuable methodology for addressing complex geometries non simply connected, while enabling a fully separated representation with respect to the space coordinates as well as on some problem parameters, considered as model extra-coordinates within the PGD rationale.

The proposed technique combines domain decomposition, a geometrical description based on the use of NURBS and the use of the PGD for recovering an affine representation after the mapping that transforms complex geometries into fully separated ones.

Model extra-coordinates can be easily included in the formalism, that only needs make special care on the continuity enforcement across the subdomains interfaces.

Appendix A: NURBS-based geometry description

NURBS enables accurately representing the geometry of curves, surfaces and volumes, being nowadays a usual technology employed in CAD. For the sake of completeness this appendix revisits the main concepts involved in the NURBS construction. For additional details refer to [26].

NURBS result from weighted combinations of B-spline functions. To define a set of n B-spline functions of order p in a univariate parametric space $\xi \in [0,1]$, the knot vector $\varvec{\kappa }_\xi$ is defined as follows.

$$\begin{aligned} \varvec{\kappa }_\xi =[\xi _1, \xi _2, \dots ,\xi _{n+p+1}]^T. \end{aligned}$$

(35)

Denote $N_{ap}(\xi )$ as the B-spline basis function of order p in the a-th knot span $\xi \in [\xi _a, \xi _{a+1}]$. The following recursive equations can be used to compute the univariate B-spline basis function $N_{ap}(\xi )$ [26]

$$\begin{aligned} N_{a0}(\xi )= & {} \left\{ \begin{array}{ll} 1 &{} \xi _a \le \xi < \xi _{a+1} \\ 0 &{} \mathrm {otherwise} \end{array} \right. \ , \ \ \ \ \ \mathrm {for} \ \ \ p=0 \end{aligned}$$

(36)

$$\begin{aligned} N_{ap} (\xi )= & {} \frac{\xi - \xi _a}{\xi _{a+p} - \xi _a} N_{a(p-1)} + \frac{\xi _{a+p+1} - \xi }{\xi _{a+p+1} - \xi _{a+1}} N_{(a+1)(p-1)} \ , \ \ \ \ \mathrm {for} \ \ \ \ p>0 \end{aligned}$$

(37)

A proper choice of the knot vector allows obtaining rich behavior of the basis functions and enough flexibility to describe complex geometries. The NURBS basis functions can be obtained using a rational weighted sum of the B-splines basis functions. With $w_i$ the weight, the univariate NURBS basis function, $R^p_i (\xi )$ reads [26]

$$\begin{aligned} R^p_i (\xi )=\frac{N_{ip}(\xi )w_i}{\sum ^n_{\alpha =1} N_{\alpha p}(\xi ) w_\alpha }. \end{aligned}$$

(38)

The bivariate NURBS basis functions $R^{pq}_{ij} (\xi ,\eta )$ in 2D domains can be obtained using tensor product of univariate basis functions.

$$\begin{aligned} R^{pq}_{ij}(\varvec{\xi }) = \frac{N_{ip}(\xi ) N_{jq}(\eta ) w_{ij}}{\sum ^n_{\alpha =1} \sum ^m_{\beta =1} N_{\alpha p}(\xi ) N_{\beta q}(\eta ) w_{\alpha \beta }}. \end{aligned}$$

(39)

In the above equation p and q are the order of B-splines in directions $\xi$ and $\eta$, respectively and $\varvec{\xi }= (\xi ,\eta )$ is the coordinates vector in the computational domain. In this equation, $w_{ij}$ denotes the geometry related weight parameter. The knot vector $\varvec{\kappa }_\eta$ applying in the coordinates $\eta$ read

$$\begin{aligned} \varvec{\kappa }_\eta =[\eta _1,\eta _2, \dots , \eta _{m+q+1}]^T,\ \ \ \ \ \ \ \ \ \eta \in [0,1], \end{aligned}$$

(40)

being n and m the number of basis functions in directions $\xi$ and $\eta$ respectively. Using the NURBS basis functions just described, the bivariate physical domain $\Omega _{\varvec{x}}$ can be described from

$$\begin{aligned} \varvec{x}=\sum ^n_{i=1} \sum ^m_{j=1} R^{pq}_{ij} (\varvec{\xi }) \varvec{P}_{ij}\ ,\ \ \ \ \ \ \ \varvec{x} \in \Omega _{\varvec{x}}\ ,\ \ \varvec{\xi }\in \Omega _{\varvec{\xi }}, \end{aligned}$$

(41)

where, $\varvec{P}$ refers to the control points (the vertices of the so-called control net) in the physical domain.

Equation (41) represent a one to one relation that maps any point $\varvec{\xi }$ in the computational domain $\Omega _{\varvec{\xi }}$ to a point $\varvec{x}$ in physical domain $\Omega _{\varvec{x}}$.

Now, using the notation $(x,y) \equiv (x_1,x_2)$ and $(\xi ,\eta ) \equiv (\xi _1,\xi _2)$, for facilitating the mapping description compactness, the terms involved in the transformation of the differential operator from $\Omega _{\varvec{x}}$ to $\Omega _{\varvec{\xi }}$ read

$$\begin{aligned} \frac{\partial {\varvec{x}}}{\partial \xi _a}=\sum ^n_{i=1} \sum ^m_{j=1} \frac{\partial R^{pq}_{ij}(\varvec{\xi })}{\partial \xi _a} \varvec{P}_{ij}\ ,\ \ \ \ \ \ \ a,b=1,2. \end{aligned}$$

(42)

More details and derivations regarding basic concepts and computations of NURBS basis functions and their derivatives could be found in [26]. Note that the geometric mapping given in Eq. (41) and its derivatives in Eq. (42) leads to a non-separable mapping in the sense of the PGD technique, compromising the effectiveness of the PGD solver. To overcome this difficulty, we apply a Separated Approximate Representation (SAR) of the Jacobian of the transformation [16], revisited in Appendix B.

Appendix B: Separated approximate representation (SAR)

Consider the generic function $g(\varvec{x})$ defined in the physical domain $\Omega _{\varvec{x}}$ and its counterpart, $g(\varvec{\xi })$, in the computational domain $\Omega _{\varvec{\xi }}$. A separated approximate representation of $g(\varvec{\xi })$ in the computational domain $\Omega _{\varvec{\xi }}$ reads

$$\begin{aligned} g(\varvec{\xi }) \approx \sum ^{N_G}_{i=1} \prod ^{N_D}_{j=1} {\varvec{M}}^T_j(\xi _j) \varvec{G}_{ji}, \end{aligned}$$

(43)

where, $\varvec{M}_j(\xi _j)$ is the vector of approximation functions in term of j-th coordinate direction and $\varvec{G}_{ji}$ is the vector of coefficients of the i-th mode in the j-th coordinate direction. $N_D$ is the total number of problem dimensions (considering both geometric space and parametric solution space) and $N_G$ is the number of modes which are used to represent the separated representation of function $g(\varvec{\xi })$. Generally, any type of approximation functions $\varvec{M}_j(\xi _j)$ could be used to approximate the modes in each direction but the piecewise linear Lagrange interpolation functions (which are common in the FEM) are used here for simplicity. More details and procedure for calculating the unknown coefficients vector $\varvec{G}_{ji}$ was addressed in [9, 16, 17].

Appendix C: Separable geometry mapping (SGM)

The most appealing features of the PGD is reducing of a high dimensional problem to a series of problems defined in lower dimensional spaces. As stated before, to apply this method in non-regular geometries, one needs first to map the problem from the physical domain, $\Omega _{\varvec{x}}$, into is counterpart, the so-called computational domain, $\Omega _{\varvec{\xi }}$. The main issue, as previously discussed, is the non-separable expression of the terms related to the Jacobian of the coordinate transformation. The derivatives transform according to

$$\begin{aligned} \left[ \begin{array}{c} \partial (\cdot ) / \partial x \\ \partial (\cdot ) / \partial y \end{array} \right] = \varvec{h} \left[ \begin{array}{c} \partial (\cdot ) / \partial \xi \\ \partial (\cdot ) / \partial \eta \end{array} \right] , \end{aligned}$$

(44)

where $\varvec{h}$ is the inverse of the Jacobian tensor, $\varvec{J}$.

The coordinate transformation (41) leads to non separable expressions in Eq. (44) that compromise the PGD effectiveness. An alternative procedure consists in constructing a separated representation of the coordinates mapping, $\varvec{x}(\varvec{\xi })$, as follows:

$$\begin{aligned} x(\varvec{\xi })=\sum ^{N_X}_{i=1} \prod ^{N_D}_{j=1} \varvec{M}^T_j \varvec{X}_{ji}, \end{aligned}$$

(45)

and

$$\begin{aligned} y(\varvec{\xi })=\sum ^{N_Y}_{i=1} \prod ^{N_D}_{j=1} \varvec{M}^T_j \varvec{Y}_{ji}, \end{aligned}$$

(46)

where, $N_X$ and $N_Y$ are the number of modes required to reach the desired level of accuracy in the SAR of $x(\varvec{\xi })$ and $y(\varvec{\xi })$, respectively. Using the same rationale, we can derive the SAR of Jacobian determinant, $|\varvec{J}(\varvec{\xi })|$, and the all 4 elements of the transformation derivatives tensor, $\varvec{h}(\varvec{\xi })$, as follows:

$$\begin{aligned} | \varvec{J} |=\sum ^{N_J}_{i=1} \prod ^{N_D}_{j=1} \varvec{M}^T_j \varvec{J}_{ji}, \end{aligned}$$

(47)

and

$$\begin{aligned} h_{ab} (\varvec{\xi })=\sum ^{N_{H^{ab}}}_{i=1} \prod ^{N_D}_{j=1} \varvec{M}^T_j \varvec{H}^{ab}_{ji},\ \ \ \ a,b=1,2. \end{aligned}$$

(48)

More details regarding separated geometry mapping and its performance in parametric solution of field problems are given in [16].