On the stability of Rayleigh–Taylor problem for stratified rotating viscoelastic fluids

Abstract

We investigate the stability of Rayleigh–Taylor (RT) problem of the stratified incompressible viscoelastic fluids under the rotation and the gravity in a horizontal periodic domain, in which the rotation axis is parallel to the direction of gravity, the two fluids are immiscible, and the heavier fluid lies on the lighter one. We establish a stability condition for the RT problem. Moreover, we prove that, under the stability condition, the RT problem enjoys a unique strong solution, which exponentially decays with respect to time. In addition, we note that the stability condition is independent of rotation angular velocity, and the rotation has no destabilizing effect.

1 Introduction

Considering two completely plane-parallel layers of immiscible fluids, the heavier on top of the lighter one and both subject to the earth’s gravity, it is well-known that such equilibrium state is unstable to sustain small disturbances, and this unstable disturbance will grow and lead to a release of potential energy as the heavier fluid moves down under the gravitational force and the lighter one is displaced upwards. This phenomenon was first studied by Rayleigh [33] and then Taylor [34], and therefore is called the Rayleigh–Taylor (RT) instability. In the last decades, this phenomenon has been extensively investigated from both physical and numerical aspects, see [3, 8, 17, 19, 23, 36] for examples. It has been also widely investigated how the RT instability evolves under the effects of other physical factors, internal surface tension [9, 38], magnetic fields [3, 4, 18, 21, 22, 24, 25], and so on.

Recently, Jiang et al. [16, 27] have found that the elasticity can inhibit the RT instability based on the following idea, i.e., Oldroyd–B model of an incompressible viscoelastic fluid in the presence of a uniform gravitational field in a three-dimensional domain Ω:

$$ \left \{ \textstyle\begin{array}{l} \rho\partial_{t} \mathbf {v}+\rho\mathbf {v}\cdot\nabla\mathbf {v}+\nabla p=\mu\Delta\mathbf {v}+\kappa\operatorname{div}(\rho U U^{T})-g\rho e_{3},\\ \partial_{t}U+\mathbf {v}\cdot\nabla U-\nabla\mathbf {v} U=0,\\ \operatorname{div}\mathbf {v}=0. \end{array}\displaystyle \right . $$

(1.1)

Here $\mathbf {v}:=\mathbf{v}(t,{x})$, $p:=p(t,{x})$, and ${U}:={U}(t,{x})$ represent velocity, pressure, and deformation tensor (a $3\times3$ matrix-valued function), respectively. $\rho, \mu >0$, $\kappa>0$, $g>0$ stand for the density, viscosity coefficient, elasticity coefficient, and gravitational constant, respectively. ${e}_{3}:=(0,0,1)^{\mathrm{T}}$ is the vertical unit vector, and $-g{e}_{3}$ denotes the gravitational force. We mention that the well-posedness problem of (1.1) without gravity $-\rho ge_{3}$ has been widely studied, see [28–31] for examples, the corresponding compressible case has also been investigated in [11–15].

Recently, Baldwin et al. investigated the effect of rotation on the RT instability by an experiment. Motivated by the experiment of Baldwin et al. and the mathematical result of Jiang et al. [16, 27], we further mathematically investigate the effect of rotation on the RT instability in the stratified viscoelastic fluids in this article. Before stating our result, we shall introduce the mathematical model.

1.1 Stratified rotating VRT problem in Eulerian coordinates

We consider the stratified incompressible viscoelastic fluids under the rotation and the gravity in a layer domain, in which the rotation axis is parallel to the direction of gravity. Moreover, the two fluids are immiscible, and the heavier fluid lies on the lighter one. Referring to the motion equations (1.1) and the motion equations of stratified viscous fluids (see [20]), we can easily write out the mathematical model of stratified viscoelastic fluids without internal surface tension:

$$\{\begin{array}{ll}{\rho }_{\pm }{\partial }_t{\mathbf{v}}_{\pm }+{\rho }_{\pm }{\mathbf{v}}_{\pm }\cdot \mathrm{\nabla }{\mathbf{v}}_{\pm }+div\mathbb{S}(p_{\pm }^g,{\mathbf{v}}_{\pm },U_{\pm })+2{\rho }_{\pm }(\mathbf{a}\times {\mathbf{v}}_{\pm })=0& \text{in }{\mathrm{\Omega }}_{\pm }(t),\\ {\partial }_t{U}_{\pm }+{\mathbf{v}}_{\pm }\cdot \mathrm{\nabla }{U}_{\pm }=\mathrm{\nabla }{\mathbf{v}}_{\pm }{U}_{\pm }& \text{in }{\mathrm{\Omega }}_{\pm }(t),\\ div{\mathbf{v}}_{\pm }=0& \text{in }{\mathrm{\Omega }}_{\pm }(t),\\ d_t+v_1{\partial }_{1}d+v_2{\partial }_{2}d=v_3& \text{on }\mathbb{T},\\ 〚{\mathbf{v}}_{\pm }〛=0,〚\mathbb{S}(p_{\pm }^g,{\mathbf{v}}_{\pm },U_{\pm })〛\nu =gd〚\rho 〛\nu & \text{on }\mathrm{\Sigma }(t),\\ {\mathbf{v}}_{\pm }=0& \text{on }{\mathrm{\Sigma }}_{\pm },\\ {\mathbf{v}}_{\pm }{|}_{t=0}={\mathbf{v}}_{\pm }^0,U_{\pm }{|}_{t=0}=U_{\pm }^0& \text{in }{\mathrm{\Omega }}_{\pm }(0),\\ d{|}_{t=0}=d_0& \text{on }\mathrm{\Sigma }(0),\end{array}$$

(1.2)

where $\mathbb {S}(p_{\pm}^{g},\mathbf {v}_{\pm}, U_{\pm}):=p_{\pm}^{g} I-\mu_{\pm}\mathbb {D}(\mathbf {v}_{\pm})-\kappa_{\pm}\rho_{\pm}(U_{\pm}U_{\pm}^{T}-I)$ and $p_{\pm}^{g}:=p_{\pm}+g\rho_{\pm}x_{3}$. Next we shall introduce the notations appearing in the above mathematical model.

Equations (1.2)₁–(1.2)₂ describe the motion of the lower lighter and upper heavier viscoelastic fluids driven by the gravitational field along the negative $x_{3}$-direction, which occupy the two time-dependent disjoint open subsets $\Omega_{+}(t)$ and $\Omega_{-}(t)$ at time t, respectively. The fluids are incompressible by (1.2)₃. The two fluids interact with each other by the interfacial jump conditions (1.2)₅ and the motion of a free interface (1.2)₄, in which $d:=d(x_{1},x_{2},t)$ represents the displacement function of the point at the interface. (1.2)₆ describes the non-slip boundary condition of the velocities on both upper and lower fixed flat boundaries, and the initial statuses of the two fluids are described by (1.2)₇–(1.2)₈.

The notations $f_{-}$ and $f_{+}$ in (1.2) denote the values of the quantity f in the lower and upper fluids, respectively. The term $2\rho_{\pm}(\mathbf {a}\times\mathbf {v}_{\pm})$ represents the Coriolis force with constant rotation angular velocity $\mathbf{a}=(0,0,a)$ about the vertical direction [5]. $\mathbb {D}(\mathbf {v}_{\pm}):=\nabla\mathbf {v}_{\pm}+(\nabla\mathbf {v}_{\pm})^{\mathrm{T}}$ denotes viscous stress tension. The superscript T and the capital letter I stand for the transposition and the $3\times3$ identity matrix, respectively. The notations $f^{0}$ or $f_{0}$ represent the initial data of f.

In this article, we consider that the domain Ω occupied by the two fluids is horizontal periodic, thus we denote

(1.3)

where we have defined that $\mathbb{T}_{i}=2\pi L_{i}(\mathbb{R}/\mathbb {Z})$ and $\mathbb{T}=\mathbb{T}_{1}\times\mathbb{T}_{2}$. Moreover, we have the following expressions:

$$ \begin{gathered} \Omega_{+}(t)=\bigl\{ (x_{h},x_{3}) \mid x_{h}\in\mathbb{T}, d(x_{h},t)< x_{3}< m\bigr\} , \\ \Omega_{-}(t)=\bigl\{ (x_{h},x_{3}) \mid x_{h}\in\mathbb{T}, -l< x_{3}< d(x_{h},t)\bigr\} ,\qquad\Omega(t)=\Omega_{+}(t)\cup\Omega _{-}(t), \\ \Sigma(t):=\bigl\{ \bigl(x_{h},d(x_{h},t)\bigr)\mid x_{h}\in\mathbb{T}\bigr\} , \\ \Sigma_{-}:=\mathbb{T}\times\{x_{3}=-l\}\quad\mbox{and}\quad \Sigma _{+}:=\mathbb{T}\times\{x_{3}=m\}. \end{gathered} $$

Finally, we explain the interfacial jump conditions (1.2)₅. The mathematical notation $〚\cdot 〛$ represents

$$〚f_{\pm }〛:=f_{+}{|}_{\mathrm{\Sigma }(t)}-f_{-}{|}_{\mathrm{\Sigma }(t)},$$

where $f_{\pm}|_{\Sigma(t)}$ denote the traces of the quantities $f_{\pm}$ on $\Sigma(t)$. From the physical point of view, the velocity of two viscous fluids meeting at a free boundary is continuous across the interface and the jump in the normal stress is proportional to the mean curvature of the surface multiplied by the normal to the surface (see [38]). Thus, we have the jump conditions $〚v〛=0$ on $\Sigma(t)$ and

$$〚\mathbb{S}(p_{\pm },v_{\pm },U_{\pm })〛\nu =\vartheta \mathcal{C}\nu \text{on }\mathrm{\Sigma }(t),$$

where we have defined that

$$ \begin{aligned} \mathbb{S}(p_{\pm},v_{\pm},U_{\pm}):=p_{\pm}I- \mu_{\pm}\mathbb{D}(v_{\pm})-\kappa_{\pm} \rho_{\pm}\bigl(U_{\pm}U^{\mathrm{T}}_{\pm}-I \bigr), \end{aligned} $$

(1.4)

and ν represents the unit normal vector on $\Sigma(t)$, ϑ the surface tension coefficient, and $\mathcal{C}$ twice the mean curvature of the internal surface $\Sigma(t)$. Here we only focus on the elasticity effect upon the RT instability, then the surface tension is omitted. Thus we obtain the second jump condition in (1.2)₅. In addition, since the density of the lower fluid is lighter than the upper one, we have

$$〚{\rho }_{\pm }〛>0.$$

Problem (1.2) enjoys the following stratified equilibrium state solution:

$$ \bigl(\mathbf {v},U,d,p^{g}\bigr)=\bigl(0,I,\bar{d} , \bar{p}^{g}\bigr), $$

where $\bar{d}\in(-l,m)$. We should point out that $\bar{p}^{g}$ can be uniquely computed out by hydrostatics, which depends on the variable $x_{3}$ and $\rho_{\pm}$ and is continuous with respect to $x_{3}\in (-l,m)$. Without loss of generality, we assume that $\bar{d}=0$ in this article. If d̄ is not zero, we can adjust the $x_{3}$ coordinate to make $\bar{d}=0$. Thus d can be regarded as a displacement function away from the plane

$$ \Sigma:=\mathbb {T}\times\{0\}. $$

To simplify problem (1.2), we introduce the indicator function χ:

$$ \chi_{\Omega_{+}(t)}=\left \{ \textstyle\begin{array}{l@{\quad}l} 1,& x\in\Omega_{+}(t);\\ 0,& x\in\Omega_{+}^{c}(t), \end{array}\displaystyle \right . \qquad \chi_{\Omega_{-}(t)}=\left \{ \textstyle\begin{array}{l@{\quad}l} 1,& x\in\Omega_{-}(t);\\ 0,& x\in\Omega_{-}^{c}(t). \end{array}\displaystyle \right . $$

Then we define that

$$ \begin{gathered} \rho=\rho_{+} \chi_{\Omega_{+}(t)}+\rho_{-} \chi_{\Omega_{-}(t)},\qquad\mu =\mu_{+}\chi_{\Omega_{+}(t)}+\mu_{-}\chi_{\Omega_{-}(t)},\\ \kappa=\kappa_{+}\chi_{\Omega_{+}(t)}+\kappa_{-}\chi_{\Omega_{-}(t)}, \qquad\mathbf {v}=\mathbf {v}_{+}\chi_{\Omega_{+}(t)}+\mathbf {v}_{-}\chi_{\Omega _{-}(t)},\\ U=U_{+}\chi_{\Omega_{+}(t)}+U_{-}\chi_{\Omega_{-}(t)}, \qquad p=p_{+}\chi_{\Omega _{+}(t)}+p_{-}\chi_{\Omega_{-}(t)},\\ v_{0}=v_{+}^{0}\chi_{\Omega_{+}(t)}+v_{-}^{0}\chi_{\Omega_{-}(t)},\qquad U_{0}=U_{+}^{0}(t)\chi_{\Omega_{+}(t)}+U_{-}^{0}(t)\chi_{\Omega_{-}(t)}, \end{gathered} $$

and denote the perturbation quantity around the equilibrium state $(0,I,0,\bar{p}^{g})$ by

$$ \mathbf{v}=\mathbf{v}-0,\qquad \sigma=p^{g}-\bar{p}^{g}, \qquad V=U-I,\qquad d=d-0. $$

Thus we have the following perturbation form for problem (1.2):

(1.5)

where $\Sigma_{-}^{+}:=\Sigma_{+}\cup\Sigma_{-}$, and $\mathbb {S}(\sigma, \mathbf {v},V+I)$ is defined by (1.4) with $(\sigma, \mathbf {v},V+I)$ in place of $(p_{\pm}, \mathbf {v}_{\pm},U_{\pm})$. Here and in what follows, the subscript ± has been omitted in the jump notation $〚\cdot 〛$ for simplicity. Thus the equilibrium-state solution of (1.5) is $(\mathbf {v} ,V,d,\sigma)=(0,0,0,0)$. In this article, we call the initial-boundary value problem (1.5) the stratified rotation viscoelastic Rayleigh–Taylor (SRVRT) problem.

1.2 Reformulation in Lagrangian coordinates

It is difficult to investigate the well-posedness of the SRVRT problem due to the movement of the free interface $\Sigma(t)$ and the changes of the domain $\Omega_{\pm}(t)$ in Eulerian coordinates. Therefore we switch the problem to Lagrangian coordinates, so that the interface and the domains stay fixed in time. To this purpose, we define the fixed Lagrangian domains $\Omega_{+}:=\mathbb {T}\times(0,m)$, $\Omega_{-}=\mathbb {T}\times(-l,0)$, and $\Omega:=\Omega_{+}\cup\Omega_{-}$, and assume that there exist invertible mappings

$$ \xi_{\pm}^{0}:\Omega_{\pm}\rightarrow \Omega_{\pm}(0) $$

such that

$$ \Sigma(0)=\xi_{\pm}^{0}(\Sigma),\qquad \Sigma_{+}= \xi_{+}^{0}(\Sigma_{+}),\qquad \Sigma _{-}=\xi_{-}^{0}(\Sigma_{-}), $$

(1.6)

and

$$ \operatorname{det}(\nabla\xi_{0})=1. $$

(1.7)

The first condition in (1.6) means that the initial interface $\Sigma(0)$ is parameterized by the mapping $\xi_{\pm}^{0}$ defined on Σ, while the latter two conditions in (1.6) mean that $\xi_{\pm}^{0}$ map the fixed upper and lower boundaries into themselves. Let $\xi_{\pm}$ be the flow maps, which are solutions to

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \partial_{t}\xi_{\pm}(y,t)=\mathbf {v}_{\pm}(\xi_{\pm}(y,t),t)&\text{in } \Omega_{\pm},\\ \xi_{\pm}(y,0)=\xi_{\pm}^{0}(y) &\text{in } \Omega_{\pm}. \end{array}\displaystyle \right . $$

We call $(x,t)$ with $x=\xi(y,t)$ and $(y,t)\in\Omega\times \mathbb {R}^{+}$ the Eulerian coordinates and Lagrangian coordinates, respectively.

We further assume that $\xi_{\pm}(\cdot,t)$ are invertible and

$$ \Omega_{\pm}(t)=\xi_{\pm}(\Omega_{\pm},t) $$

in order to switch back from Lagrangian to Eulerian coordinates. Since $\mathbf {v}_{\pm}$ and $\xi_{\pm}^{0}$ are all continuous across the surface Σ, we have

$$ \Sigma(t)=\xi_{\pm}(\Sigma,t). $$

In other words, the Eulerian domains of upper and lower fluids are the image of $\Omega_{\pm}$ under the mapping $\xi_{\pm}$, and the free interface is the image of Σ under the mappings $\xi_{\pm}(t,\cdot)$. Recalling the non-slip boundary condition $\mathbf {v}_{\pm}|_{\Sigma_{\pm}}=0$, we have

$$ y=\xi_{\pm}(y,t)\quad\text{on } \Sigma_{\pm}. $$

Using the incompressible condition, we can derive that

$$ \operatorname{det}(\nabla\xi_{\pm})=1\quad\text{in } \Omega_{\pm}$$

(1.8)

as well as the initial condition (1.7), please refer to [32, Proposition 1.4] for the derivation.

In Lagrangian coordinates, we can use the Jacobi matrix of $\xi_{\pm}(y,t)$ to define the deformation tensor $\tilde{U}_{\pm}(y,t)$:

$$ \tilde{U}_{\pm}(y,t):=\nabla\xi_{\pm}(y,t),\quad \text{i.e.}, \tilde {U}_{ij}=\partial\bigl(\xi_{\pm}(y,t) \bigr)_{i}, $$

where $\partial_{j}$ stands for the partial derivative with respect to the jth component of the spatial variables. In Eulerian coordinates, the deformation tensor can be rewritten as follows:

$$ U_{\pm}(x,t):=\tilde{U}_{\pm}\bigl(\xi_{\pm}^{-1}(x,t),t \bigr). $$

Using the chain rule, it is easy to verify that $U_{\pm}(x,t)$ enjoys the transport equation

$$ \partial_{t} U_{\pm}+\mathbf {v}_{\pm}\cdot\nabla U_{\pm}=\nabla\mathbf {v}_{\pm}U_{\pm}\quad\mbox{in } \Omega_{\pm}(t). $$

Now, we define $\xi=\chi_{+}\xi_{+}+\chi_{-}\xi_{-}$, $\eta=\xi-y$, and the Lagrangian unknowns

$$ (u,q) (y,t)=(\mathbf {v},\sigma) \bigl(\xi(y,t),t\bigr)\quad\mbox{for } (y,t)\in \Omega\times \mathbb {R}^{+}, $$

then the motion equations of u and q in Lagrangian coordinates the evolution equations read as follows:

$$\{\begin{array}{ll}{\eta }_t=u& \text{in}\mathrm{\Omega },\\ \rho u_t+{div}_{\mathcal{A}}{\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)+2\rho a(u_1{e}_2-u_2{e}_1)=0& \text{in }\mathrm{\Omega },\\ {div}_{\mathcal{A}}u=0& \text{in }\mathrm{\Omega },\\ 〚u〛=〚\eta 〛=0,〚{\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)-g\rho {\eta }_{3}I〛\mathbf{n}=0& \text{on }\mathrm{\Sigma },\\ u=0,\eta =0& \text{on }{\mathrm{\Sigma }}_{-}^{+},\\ u{|}_{t=0}=u_0,\eta {|}_{t=0}={\eta }_0& \text{in }\mathrm{\Omega },\end{array}$$

(1.9)

where we have defined that

$$\begin{aligned}& \mathbb {S}_{\mathcal {A}}(q,u,\nabla\eta+I):=qI-\mu \mathbb {D}_{\mathcal {A}}(u)-\kappa\rho \bigl(\mathbb {D}(\eta)+\nabla\eta\nabla \eta^{T}\bigr), \end{aligned}$$

(1.10)

$$\begin{aligned}& \mathbb {D}_{\mathcal {A}}(u):=\nabla_{\mathcal {A}}u+( \nabla_{\mathcal {A}}u)^{\mathrm{T}}, \end{aligned}$$

(1.11)

$$\begin{aligned}& \mathbf {n}:=\frac{\partial_{1}(\eta+y)\times\partial_{2}(\eta +y)}{ \vert \partial_{1}(\eta+y)\times\partial_{2}(\eta+y) \vert }\bigg|_{\Sigma}=\frac{\mathcal {A} e_{3}}{ \vert \mathcal {A} e_{3} \vert }\bigg|_{\Sigma} \end{aligned}$$

(1.12)

for the unit normal to $\Sigma(t)=\xi(\Sigma,t)$. Since $〚\eta 〛=0$ on Σ, then

$$〚{\partial }_1\eta 〛=〚{\partial }_2\eta 〛=0\text{on }\mathrm{\Sigma }.$$

Thus the definition of n in (1.12) makes sense. We call problem (1.9) the transformed SRVRT problem. In this article, we prove that the transformed SRVRT problem is stable under proper conditions, see Theorem 2.1.

Next, we further introduce the notations involving $\mathcal {A}$. The matrix $\mathcal {A}$ is defined by the relation

$$ \mathcal {A}^{\mathrm{T}}=(\nabla\xi)^{-1}:=( \partial_{j}\xi_{i})_{3\times3}^{-1}. $$

(1.13)

We define the differential operator $\nabla_{\mathcal {A}}$ by

$$ \begin{aligned} &\nabla_{\mathcal{A}}w:=( \nabla_{\mathcal{A}} w_{1},\nabla_{\mathcal{A}}w_{2}, \nabla_{\mathcal{A}}w_{3})^{\mathrm {T}}, \\ &\nabla_{\mathcal{A}}w_{i}:=(\mathcal{A}_{1k} \partial_{k}w_{i}, \mathcal{A}_{2k} \partial_{k}w_{i},\mathcal{A}_{3k}\partial _{k}w_{i})^{\mathrm{T}}, \end{aligned} $$

(1.14)

where $\mathcal {A}_{ij}$ is the $(i,j)$th entry of $\mathcal{A}$, $w:=(w_{1},w_{2},w_{3})^{\mathrm{T}}$, and we have used the Einstein convention of summation over repeated indices. The differential operator $\operatorname {div}_{\mathcal {A}}$ is defined by

$$ \operatorname{div}_{\mathcal{A}}(f_{1},f_{2},f_{3})= (\operatorname{div}_{\mathcal{A}}f_{1},\operatorname{div} _{\mathcal{A}}f_{2},\operatorname{div}_{\mathcal{A}}f_{3})^{\mathrm{T}}\quad \mbox{and} \quad\operatorname{div}_{\mathcal{A}}f_{i}:= \mathcal{A}_{lk}\partial_{k}f_{il} $$

(1.15)

for the vector function $f_{i}:=(f_{i1},f_{i2},f_{i3})^{T}$. In addition,

$$ \Delta_{\mathcal {A}} X:=\operatorname {div}_{\mathcal {A}} \nabla_{\mathcal {A}} X. $$

(1.16)

Finally, we introduce some properties of $\mathcal {A}$. Recalling the definition of $\mathcal {A}$ and (1.8), we have

$$ \mathcal {A}=\bigl(\mathcal {A}^{*}_{ij}\bigr)_{3\times3}, $$

(1.17)

where $\mathcal {A}^{*}_{ij}$ represents the algebraic complement minor of the $(i,j)$th entry of the matrix $(\partial_{j}\xi_{i})_{3\times3}$. In addition, we have

$$ \mathcal{A}_{ji}\partial_{l} \xi_{j}=\mathcal{A}_{ij}\partial_{j}\xi _{l}=\delta_{il} $$

(1.18)

and

$$ \begin{aligned} \partial_{k} \mathcal{A}^{\ast}_{ik}=0 \quad\mbox{or} \quad\partial _{k} \mathcal{A}_{ik}=0, \end{aligned} $$

(1.19)

where we have defined that $\delta_{il}=1$ for $i=l$ and $\delta _{il}=0$ for $i\neq l$. Thus

$$ \operatorname {div}_{\mathcal {A}_{t}} u=\partial_{l}( \partial_{t}\mathcal {A}_{kl}u_{k}). $$

(1.20)

The rest of this paper is organized as follows. In Sect. 2, we present the stability result of the transformed SRVRT problem. Then, in Sect. 3, we deduce some preliminary estimates, while in Sect. 4 we derive a priori estimates of η and u. Finally, in Sect. 5, we derive an exponential decay estimate which, together with the local well-posedness result of the transformed SRVRT problem, yields the desired stability result of the transformed SRVRT problem.

2 Main results

Before stating our main result, we shall derive the stability condition for the transformed SRVRT problem. To begin with, we introduce some notations, which are used throughout this article.

• (1) Simplified function spaces:

  

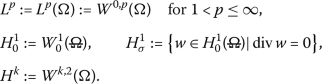
• (2) Simplified norms:

  $$\begin{array}{c}{\parallel \cdot \parallel }_k:={\parallel \cdot \parallel }_{H^k}={\parallel \cdot \parallel }_{W^{k,2}}\text{for }k\ge 0,\\ |〚w〛{|}_s:={\parallel w_{+}{|}_{\mathrm{\Sigma }}-w_{-}{|}_{\mathrm{\Sigma }}\parallel }_{H^s(\mathbb{T})}\text{for }s\in R,\\ |w{|}_s:=\{\begin{array}{ll}{\parallel w_{+}{|}_{\mathrm{\Sigma }}-w_{-}{|}_{\mathrm{\Sigma }}\parallel }_{H^s(\mathbb{T})}& \text{for }{w}_{+}{|}_{\mathrm{\Sigma }}\ne w_{-}{|}_{\mathrm{\Sigma }},\\ {\parallel w_{+}{|}_{\mathrm{\Sigma }}\parallel }_{H^s(\mathbb{T})}& \text{for }{w}_{+}{|}_{\mathrm{\Sigma }}=w_{-}{|}_{\mathrm{\Sigma }},\end{array}\\ {\parallel \cdot \parallel }_{i,k}^2:={\sum }_{{\alpha }_1+{\alpha }_2=i}{\parallel {\partial }_1^{{\alpha }_1}{\partial }_2^{{\alpha }_2}\cdot \parallel }_k^2\text{for non-negative integer }k.\end{array}$$

• (3) Energy and functionals:

  $$\begin{array}{c}\mathcal{E}(t):={\parallel u(t)\parallel }_2^2+{\parallel u_t\parallel }_0^2+{\parallel \eta (t)\parallel }_3^2+{\parallel \mathrm{\nabla }q(t)\parallel }_0^2+|〚q(t)〛{|}_{1/2}^2,\\ \mathcal{D}(t):={\parallel (u,\eta )(t)\parallel }_3^2+{\parallel u_t\parallel }_1^2+{\parallel \mathrm{\nabla }q(t)\parallel }_1^2+|〚q(t)〛{|}_{3/2}^2.\end{array}$$

• (4) Other notations:

  $$ \begin{gathered} f\in H^{k+\frac{1}{2}} \text{ denotes } f(y_{h},0)\in H^{k+\frac {1}{2}}(\mathbb {T})\quad \text{for } f=(y_{h},y_{3}), y_{h}=(y_{1},y_{2}), \\ \partial_{h}^{i} \text{ denotes } \partial_{1}^{\alpha_{1}} \partial_{2}^{\alpha _{2}} \quad\text{for any } \alpha_{1}+ \alpha_{2}=i, \\ a\lesssim b\hbox{ means that }a\leq cb,\qquad a\gtrsim b\hbox{ means that }a\geq cb, \end{gathered} $$

  where the letter c denotes a positive constant depending on the domain and the known physical parameters in the transformed SRVRT problem.

Now we start to derive the stability condition. We assume that $(u,\eta )$ is very small, thus we can neglect the small terms of the second order (i.e., the nonlinear terms) in (1.9) and obtain the following linearized transformed SRVRT problem:

$$\{\begin{array}{ll}{\eta }_t=u& \text{in }\mathrm{\Omega },\\ \rho u_t+\mathrm{\nabla }q+2\rho a(u_1{e}_2-u_2{e}_1)=\mu \mathrm{\Delta }u+\kappa \rho div\mathbb{D}(\eta )& \text{in }\mathrm{\Omega },\\ divu=0& \text{in }\mathrm{\Omega },\\ 〚u〛=〚\eta 〛=0,〚(q-g\rho {\eta }_3)I-\mathbb{D}(\mu u+\kappa \rho \eta )〛e_3=0& \text{on }\mathrm{\Sigma },\\ u=0,\eta =0& \text{on }{\mathrm{\Sigma }}_{-}^{+},\\ u{|}_{t=0}=u_0,\eta {|}_{t=0}={\eta }_0& \text{in }\mathrm{\Omega }.\end{array}$$

(2.1)

It is convenient to analyze the physical and mathematical mechanisms in the transformed SRVRT problem based on the linearized problem.

Exploiting the standard method, we shall look for the normal mode solutions of (2.1) in the following form:

$$ u(y,t)=\tilde{u}(y)e^{\lambda t},\qquad q(y,t)=\tilde{q}(y)e^{\lambda t},\qquad \eta(y,t)=\tilde{\eta}(y)e^{\lambda t} \quad\text{for some constant } \lambda>0. $$

Inserting these ansatz into (2.1) yields the following eigenvalue problem:

$$\{\begin{array}{ll}\lambda \tilde{\eta }=\tilde{u}& \text{in }\mathrm{\Omega },\\ \lambda \rho \tilde{u}+\mathrm{\nabla }\tilde{q}+2\rho a({\tilde{u}}_1{e}_2-{\tilde{u}}_2{e}_1)=\mu \mathrm{\Delta }\tilde{u}+\kappa \rho div\mathbb{D}(\tilde{\eta })& \text{in }\mathrm{\Omega },\\ div\tilde{u}=0& \text{in }\mathrm{\Omega },\\ 〚\tilde{u}〛=0,〚(\tilde{q}-g\rho {\eta }_3)I-\mathbb{D}(\mu \tilde{u}+\kappa \rho \tilde{\eta })〛e_3=0& \text{on }\mathrm{\Sigma },\\ \tilde{u}=0,\tilde{\eta }=0& \text{on }{\mathrm{\Sigma }}_{-}^{+}.\end{array}$$

(2.2)

Replacing η̃ by (2.2)₁, we arrive at the boundary value problem:

$$\{\begin{array}{ll}{\lambda }^2\rho \tilde{u}+\lambda \mathrm{\nabla }\tilde{q}-div\mathbb{D}((\lambda \mu +\kappa \rho )\tilde{u})+2\rho a({\tilde{u}}_1{e}_2-{\tilde{u}}_2{e}_1)=0& \text{in }\mathrm{\Omega },\\ div\tilde{u}=0& \text{in }\mathrm{\Omega },\\ 〚\tilde{u}〛=0,〚(\tilde{q}-g\rho {\eta }_3)I-\mathbb{D}(\mu \tilde{u}+\kappa \rho \tilde{\eta })〛e_3=0& \text{on }\mathrm{\Sigma },\\ \tilde{u}=0,\tilde{\eta }=0& \text{on }{\mathrm{\Sigma }}_{-}^{+}.\end{array}$$

(2.3)

Multiplying (2.3)₁ by ũ in $L^{2}$ and exploiting the formula of integration by parts and conditions (2.3)₂–(2.3)₄, one has

$${\lambda }^2{\parallel \sqrt{\rho }\tilde{u}\parallel }_0^2=g〚\rho 〛|{\tilde{u}}_3{|}_0^2-\frac{1}{2}{\parallel \sqrt{\kappa \rho }\mathbb{D}(\tilde{u})\parallel }_0^2-\frac{1}{2}{\parallel \sqrt{\lambda \mu }\mathbb{D}(\tilde{u})\parallel }_0^2+2\rho a{\int }_{\mathrm{\Omega }}({\tilde{u}}_2{e}_1-{\tilde{u}}_1{e}_2)\cdot \tilde{u}\mathrm{d}y.$$

Noting that

$$ 2\rho a \int_{\Omega}(\tilde{u}_{2}e_{1}-\tilde{u}_{1}e_{2})\cdot\tilde{u}\,\mathrm {d}y=0, $$

thus we derive that

$$ \lambda^{2} \Vert \sqrt{\rho}\tilde{u} \Vert _{0}^{2}= \tilde{E}(\tilde{u}) -\frac{1}{2} \bigl\Vert \sqrt{\lambda\mu} \mathbb {D}(\tilde{u}) \bigr\Vert _{0}^{2}, $$

(2.4)

where we have defined that

$$\tilde{E}(\tilde{u}):=g〚\rho 〛|{\tilde{u}}_3{|}_0^2-\frac{1}{2}{\parallel \sqrt{\kappa \rho }\mathbb{D}(\tilde{u})\parallel }_0^2.$$

(2.5)

Using the point of view of energy, if $\tilde{E}(\tilde{u})<0$ for some ũ, then the linearized SRVRT problem may be stable. Hence, we have the stability criterion: if $\mathrm{C}_{\mathrm{r}} <1$ (i.e., the elasticity coefficient κ is appropriately large), any solution to the linearized stratified VRT problem enjoys some stability estimate, where we have defined that

$${\mathrm{C}}_{\mathrm{r}}:=\underset{u\in H_{\sigma }^1}{sup}\frac{2g〚\rho 〛|u_3{|}_0^2}{{\parallel \sqrt{\kappa \rho }\mathbb{D}(u)\parallel }_0^2}.$$

(2.6)

In this article, we will rigorously prove that the transformed SRVRT problem (1.9) is stable. More precisely, we have the following mathematical result.

Theorem 2.1

Let $a\geq0$. Under the stability condition $\mathrm{C}_{\mathrm{r}}<1$, there is a sufficiently small constant $\delta>0$ such that for any $(u_{0},\eta _{0})\in H^{2}\times H^{3}$ enjoying the following conditions:

• (1) $u_{0}=0$ on $\Sigma_{-}^{+}$ and $\operatorname {div}_{\mathcal {A}_{0}} u_{0}=0$;

• (2) $\operatorname{det}(\nabla\eta_{0}+I)=1$, $\eta_{0}=0$ on $\Sigma_{-}^{+}$ and $〚{\eta }_0〛=0$ on Σ;

• (3) $\|u_{0}\|_{2}+\|\eta_{0}\|_{3}\leq\delta$;

• (4) the initial value $(u_{0},\eta_{0})$ satisfies the compatibility condition

  $$〚{\mathbb{S}}_{{\mathcal{A}}_0}(0,u_0,\mathrm{\nabla }{\eta }_0+I){\mathbf{n}}_0-{\mathbf{n}}_0\cdot ({\mathbb{S}}_{{\mathcal{A}}_0}(0,u_0,\mathrm{\nabla }{\eta }_0+I){\mathbf{n}}_0){\mathbf{n}}_0〛=0,$$

  then the transformed SRVRT problem (1.9) possesses a unique global solution $(u,\eta)\in C^{0}([0,\infty), H^{2}\times H^{3})$ with an associated perturbation pressure q. Furthermore, $(\eta,u,q)$ has the following exponential stability estimate:

  $$ \mathcal {E}(t)\leq c e^{-ct}\bigl( \Vert u_{0} \Vert _{2}^{2}+ \Vert \eta_{0} \Vert _{3}^{2}\bigr), $$

  (2.7)

  where $\mathcal {A}_{0}$ and $\mathbf {n}_{0}$ denote the initial data of $\mathcal {A}$ and n, respectively, and are defined by $\eta_{0}$, and the positive constants δ and c depend on the domain and the physical parameters in the transformed SRVRT problem.

Remark 2.1

In view of the proof of Theorem 2.1, we can easily observe that Theorem 2.1 still holds if $\Omega=\{x\in \mathbb {R}^{3}|{-}l< x_{3}< m\}$ or one of $\kappa_{+}$ and $\kappa _{-}$ is non-zero and sufficiently large. Moreover, if $\kappa_{+}=\kappa _{-}$, then the stability condition is equivalent to $\kappa>\kappa_{c}$, where we have defined that

$${\kappa }_c:=\underset{w\in H_{\sigma }^1}{sup}\frac{2g〚\rho 〛|w_3{|}_0^2}{{\parallel \sqrt{\rho }\mathbb{D}(w)\parallel }_0^2}.$$

It should be noted that the stability condition is independent of a. Thus Theorem 2.1 presents that the rotation has no destabilizing effect. Next we briefly introduce the proof of Theorem 2.1. The key step of the proof is to deduce an a priori exponential decay estimate (2.7). To this purpose, we naturally construct an energy inequality of differential form

$$ \frac{\mathrm{d}}{\mathrm{d}t}\tilde {\mathcal {E}}(t)+\tilde {\mathcal {D}}(t)\lesssim \sqrt {\mathcal {E}}\mathcal {D}$$

(2.8)

for some energy functional $\tilde {\mathcal {E}}(t)$ (see (5.7) for the definition) and dissipative functional $\tilde {\mathcal {D}}(t)$ (see (5.8) for the definition). Moreover, $\tilde {\mathcal {E}}(t)$ and $\tilde {\mathcal {D}}(t)$ are equivalent to $\mathcal{E}(t)$ and $\mathcal{D}(t)$, respectively, and $\tilde {\mathcal {E}}(t)$ can be controlled by $\mathcal{D}(t)$. In particular, if $\mathcal{E}$ is sufficiently small, we further have

$$ \frac{\mathrm{d}}{\mathrm{d}t}\tilde {\mathcal {E}}(t)+\mathcal{D}(t)\lesssim 0, $$

which implies the desired exponential decay estimate by Gronwall’s inequality. Thus, by a local well-posedness result of the transformed SRVRT problem, we immediately get Theorem 2.1.

Here we mention the derivation of (2.8). Recently, Jiang et al. [27] have proved that the elasticity can inhibit the RT instability based on the energy method. To obtain (2.8), we naturally use the energy method in [27] to prove Theorem 2.1. However, we need some more complicated mathematical techniques for the estimate of $\|\eta\|_{3}$. Thus our derivation of the estimate of $\|\eta\|_{3}$ is very different with the one in [27]. In fact, since $w:=u+(\kappa\rho/\mu)\eta$ may not be continuous on Σ, we shall apply the regularity theory of one-phase steady Stokes problem to the momentum equations of upper and lower viscoelastic fluids. Thus we derive an energy inequality of $\| \eta\|_{3}$, which has some norms of $y_{h}$-derivative (i.e., horizontal derivative) of $(u,\eta)$, see Lemma 4.2 for details. Moreover, we also derive a series of energy inequalities of $y_{h}$-derivative in the energy inequalities of $y_{h}$-derivative of $(u,\eta)$, see Lemmas 4.1 and 4.4 for details, which can close the norms involving $y_{h}$-derivative in the energy inequality of $\|\eta\|_{3}$. Thus, we can still exploit a standard energy method to establish the energy inequality (2.8). It should be noted that $\tilde {\mathcal {E}}(t)$ contains some negative terms involving gravity. To control the non-positive terms, we shall use the stability condition based on the physical idea that the stabilizing terms of elasticity can control the non-positive term, see Lemma 4.3 for details. Thus we derive the equivalence of $\tilde {\mathcal {E}}$ and $\mathcal {E}$. Of course, we will also use the stability condition in the derivation of the dissipative functional $\mathcal {D}$.

3 Preliminary estimates

The key step in the proof of Theorem 2.1 is to derive a priori exponential stability estimate for the transformed SRVRT problem (1.9). To this purpose, let $(u,\eta)$ be a solution of the transformed SRVRT problem and satisfy

$$ \sup_{0\leq t\leq T}\sqrt{ \bigl\Vert \eta(t) \bigr\Vert _{3}+ \bigl\Vert u(t) \bigr\Vert _{2}}\leq\delta \in(0,1)\quad\text{for some } T>0, $$

(3.1)

where the initial data of $(u,\eta)$ enjoys assumptions (1)–(4) in Theorem 2.1, and δ is sufficiently small. We mention that the smallness condition (3.1) depends on Ω and other physical parameters in the transformed SRVRT problem, and will be repeatedly used throughout the rest of the article. Moreover, we assume that the solution $(u,\eta)$ possesses proper regularity, so that the procedure of formal derivation makes sense.

In order to exploit the regularity theory of the (steady) Stokes problem in the derivation of a priori estimates, we shall write (1.9)₂–(1.9)₅ as the following nonhomogeneous form, in which the terms on the left-hand side of the equations are linear:

$$\{\begin{array}{ll}\rho u_t+\mathrm{\nabla }q-div\mathbb{D}(\mu u+\kappa \rho \eta )+2\rho a(u_1{e}_2-u_2{e}_1)=\mathcal{N}& \text{in }\mathrm{\Omega },\\ divu=-{div}_{\tilde{\mathcal{A}}}u& \text{in }\mathrm{\Omega },\\ 〚u〛=0,〚(qI-\mathbb{D}(\mu u+\kappa \rho \eta )-g\rho {\eta }_3)e_3〛=\mathcal{M}& \text{on }\mathrm{\Sigma },\\ u=0,\eta =0& \text{on }{\mathrm{\Sigma }}_{-}^{+},\end{array}$$

(3.2)

where we have defined that

$$\begin{aligned}& \tilde {\mathcal {A}}:=\mathcal {A}-I, \end{aligned}$$

(3.3)

$$\begin{aligned}& \mathcal {N}:=\operatorname {div}\bigl(\mu \mathbb {D}_{\tilde{\mathcal {A}}}(u)+\kappa \rho\nabla \eta\nabla\eta^{T}\bigr) -\operatorname {div}_{\tilde{\mathcal {A}}}\mathbb {S}_{\mathcal {A}}(q,u, \nabla\eta+I), \end{aligned}$$

(3.4)

$$\mathcal{M}:=〚\mu {\mathbb{D}}_{\tilde{\mathcal{A}}}(u)+\kappa \rho \mathrm{\nabla }\eta \mathrm{\nabla }{\eta }^T〛e_3+〚({\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)-g\rho {\eta }_{3}I)〛(e_3-\mathbf{n}),$$

(3.5)

and $\mathbb {D}_{\tilde {\mathcal {A}}}(u)$ and $\operatorname {div}_{\tilde {\mathcal {A}}}$ are defined by (1.11) and (1.15) with $\tilde {\mathcal {A}}$ in place of $\mathcal {A}$, respectively. Since $\det(\nabla\xi_{0})=1$, we have $\det(\nabla\xi)=1$, i.e., $\det(\nabla\eta+I)=1$.

This section is devoted to the derivation of preliminary estimates for $(\eta,u)$. To begin with, we shall recall some important inequalities, these inequalities will be frequently used in the rest of the article.

• (1) Sobolev’s embedding inequalities [1, Theorem 4.12]:

  $$\begin{aligned}& \Vert f \Vert _{L^{p}}\lesssim \Vert f \Vert _{1}\quad\text{for } 2\leq p\leq6, \end{aligned}$$

  (3.6)
  $$\begin{aligned}& \Vert f \Vert _{C^{0}(\bar{\Omega})}\lesssim \Vert f \Vert _{2}. \end{aligned}$$

  (3.7)

• (2) Korn’s inequality [10, Lemma 10.7]:

  $$ \Vert w \Vert _{1}\lesssim \bigl\Vert \mathbb {D}(w) \bigr\Vert _{0}\quad\text{for any } w\in H_{0}^{1}. $$

  (3.8)

• (3) Interpolation inequality $H^{j}$ ([1, Theorem 5.2]):

  $$ \Vert f \Vert _{j} \leq \Vert f \Vert _{0}^{1-\frac{j}{i}} \Vert f \Vert _{i}^{\frac{j}{i}} \leq C_{\varepsilon} \Vert f \Vert _{0}+\varepsilon \Vert f \Vert _{i} \quad\text{for any }0\leq j< i, \varepsilon>0, $$

  (3.9)

  where the constant $C_{\varepsilon}$ depends on the domain and ε.

• (4) Estimates of the product of functions in Sobolev spaces [26]:

  $$\begin{aligned}& \Vert f\psi \Vert _{j}\lesssim \left \{ \textstyle\begin{array}{l@{\quad}l} \Vert f \Vert _{1} \Vert \psi \Vert _{1}&\text{for }j=0,\\ \Vert f \Vert _{j} \Vert \psi \Vert _{2}&\text{for }0\leq j\leq2,\\ \Vert f \Vert _{2} \Vert \psi \Vert _{3}+ \Vert f \Vert _{3} \Vert \psi \Vert _{2} &\text{for }j=3, \end{array}\displaystyle \right . \end{aligned}$$

  (3.10)
  $$\begin{aligned}& \Vert \phi\varphi \Vert _{H^{\frac{3}{2}}(\mathbb {T})} \lesssim \Vert \phi \Vert _{H^{\frac{3}{2}}(\mathbb {T})} \Vert \varphi \Vert _{H^{\frac{3}{2}}(\mathbb {T})}, \end{aligned}$$

  (3.11)
  $$\begin{aligned}& \Vert \phi\varphi \Vert _{H^{-\frac{1}{2}}(\mathbb {T})} \lesssim \Vert \phi \Vert _{L^{4}(\mathbb {T})} \Vert \varphi \Vert _{L^{4}(\mathbb {T})}, \end{aligned}$$

  (3.12)
  $$\begin{aligned}& \Vert \phi\varphi \Vert _{H^{\frac{1}{2}}(\mathbb {T})} \lesssim \Vert \phi \Vert _{W^{1,\gamma}(\mathbb {T})} \Vert \varphi \Vert _{H^{\frac{1}{2}}(\mathbb {T})} \quad \text{for any }\gamma>2. \end{aligned}$$

  (3.13)

• (5) Trace theorems [1, Theorem 7.58]:

  $$\begin{aligned}& \bigl\Vert f(x_{h},0) \bigr\Vert _{W^{k,4}(\mathbb {T})} \lesssim \Vert f \Vert _{k+1}\quad\mbox{for any integer } k\geq0, \end{aligned}$$

  (3.14)
  $$\begin{aligned}& \bigl\Vert f(x_{h},0) \bigr\Vert _{H^{k+\frac{1}{2}}(\mathbb {T})} \lesssim \Vert f \Vert _{k+1}\quad\mbox{for any } k\geq0, \end{aligned}$$

  (3.15)
  $$\begin{aligned}& \vert u_{3} \vert _{-\frac{1}{2}}\lesssim \Vert u \Vert _{0}+ \Vert \operatorname {div}u \Vert _{0}\quad\mbox{for any } u:=(u_{1},u_{2},u_{3})\in H_{0}^{1}, \end{aligned}$$

  (3.16)

  where (3.16) can be derived by integration by parts and the inverse trace theorem. We mention that (3.6)–(3.10) also hold for the bounded domain.

Now, we start the derivation of some preliminary estimates. First, we derive bounds for divη. Since

$$ \det(\nabla\xi_{0})=\det\bigl(\nabla(\eta_{0}+y)\bigr)=\det( \nabla\eta _{0}+I)=1, $$

one can derive from (1.9)₁ that

$$ \det(\nabla\eta+I)=1. $$

Then, using the determinant expansion theorem, we have

$$ \begin{aligned}\det(\nabla\eta+I)= {}& \begin{vmatrix} \partial_{1}\eta_{1}+1 & \partial_{2} \eta_{1} & \partial_{3}\eta_{1} \\ \partial_{1}\eta_{2} & \partial_{2} \eta_{2}+1 & \partial_{3}\eta_{2} \\ \partial_{1}\eta_{3} & \partial_{2} \eta_{3} & \partial_{3}\eta_{3}+1 \end{vmatrix} \\ ={}&\det\nabla\eta+\frac{1}{2}\bigl((\operatorname {div}\eta)^{2}- \operatorname{tr}(\nabla\eta )^{2}\bigr)+\operatorname {div}\eta+1=1. \end{aligned} $$

Consequently,

$$ \operatorname {div}\eta=\frac{1}{2}\bigl(\operatorname{tr}(\nabla \eta)^{2}-(\operatorname {div}\eta )^{2}\bigr)-\det\nabla\eta. $$

(3.17)

Making use of (3.17), (3.10), and (3.1), we have

$$\begin{aligned}[b] \Vert \operatorname {div}\eta \Vert _{2} \lesssim{}& \bigl\Vert (\operatorname {div}\eta)^{2} \bigr\Vert _{2}+ \bigl\Vert \operatorname{tr}( \nabla \eta)^{2} \bigr\Vert _{2}+ \Vert \det\nabla\eta \Vert _{2} \\ \lesssim{}& \Vert \operatorname {div}\eta \Vert _{2} \Vert \eta \Vert _{3}+ \Vert \nabla\eta \Vert _{2} \Vert \nabla\eta \Vert _{2}+ \Vert \nabla \eta \Vert _{2}^{3} \\ \lesssim{}& \Vert \nabla\eta \Vert _{2}^{2}\bigl(1+ \Vert \nabla\eta \Vert _{2}\bigr) \lesssim \Vert \eta \Vert _{3}^{2}.\end{aligned} $$

(3.18)

Second, we estimate for $\mathcal {A}$ and $\tilde {\mathcal {A}}$. Using (3.10) and (1.17), we have

$$ \begin{aligned} \Vert \mathcal {A} \Vert _{2} \lesssim& 1+ \Vert \eta \Vert _{3}\bigl(1+ \Vert \eta \Vert _{3}\bigr)\lesssim1. \end{aligned} $$

(3.19)

Similarly, we can deduce from (1.9)₁ that

$$\begin{aligned}& \Vert \mathcal {A}_{t} \Vert _{j}\lesssim \Vert u \Vert _{j+1}\quad\text{for }0\leq j\leq2, \end{aligned}$$

(3.20)

$$\begin{aligned}& \Vert \mathcal {A}_{tt} \Vert _{0}\lesssim \Vert u_{t} \Vert _{1}+ \Vert u \Vert _{2}. \end{aligned}$$

(3.21)

Since δ is sufficiently small, we have the following relation:

$$ \mathcal {A} ^{T}=I-\nabla\eta+(\nabla\eta)^{2}\sum _{i=0}^{\infty}(-\nabla \eta)^{i} =I-\nabla \eta+(\nabla\eta)^{2}\mathcal {A}^{T}, $$

which yields that

$$ \tilde {\mathcal {A}}^{T}=(\nabla\eta)^{2}\mathcal {A}^{T}- \nabla\eta. $$

(3.22)

Using (3.22), (3.19), and (3.10), we can estimate that

$$ \Vert \tilde {\mathcal {A}}\Vert _{j}\lesssim \Vert \nabla\eta \Vert _{2}^{2} \Vert \mathcal {A} \Vert _{j}+ \Vert \eta \Vert _{j}\lesssim \Vert \eta \Vert _{j+1} \quad\text{for }0\leq j\leq2. $$

(3.23)

In addition, exploiting (3.23), (3.19), and (3.8), we can easily deduce that, for any $w\in H_{0}^{1}$,

$$\begin{aligned}& \bigl\Vert \mathbb {D}_{\mathcal {A}}(w) \bigr\Vert \lesssim \Vert w \Vert _{1}, \end{aligned}$$

(3.24)

$$\begin{aligned}& \Vert w \Vert _{1}\lesssim \bigl\Vert \mathbb {D}(w) \bigr\Vert _{0}\lesssim \bigl\Vert \mathbb {D}_{\tilde {\mathcal {A}}}(w) \bigr\Vert _{0}+ \bigl\Vert \mathbb {D}_{\mathcal {A}}(w) \bigr\Vert _{0} \lesssim \Vert \eta \Vert _{3} \Vert w \Vert _{1}+ \bigl\Vert \mathbb {D}_{\mathcal {A}}(w) \bigr\Vert _{0}, \end{aligned}$$

(3.25)

which yield that, for sufficiently small δ,

$$ \Vert w \Vert _{1}\lesssim \bigl\Vert \mathbb {D}_{\mathcal {A}}(w) \bigr\Vert _{0}\lesssim \Vert w \Vert _{1}\quad\text{for any } w\in H_{0}^{1}. $$

(3.26)

Finally, we estimate the nonlinear terms $\mathcal {N}$ and $\mathcal {M}$. Recalling the definition of $\mathcal {N}$, we use (3.23), (3.19), and (3.10) to infer that

$$ \begin{aligned}[b] \Vert \mathcal {N} \Vert _{1} ={}& \bigl\Vert \kappa\rho \operatorname {div}\bigl(\nabla\eta\nabla\eta^{T}\bigr)+\mu \operatorname {div}\mathbb {D}_{\tilde {\mathcal {A}}}(u)+\mu \operatorname {div}_{\tilde {\mathcal {A}}} \mathbb {D}_{\mathcal {A}}(u) \\ &+\kappa\rho \operatorname {div}_{\tilde {\mathcal {A}}} \mathbb {D}(\eta)-\operatorname {div}_{\tilde {\mathcal {A}}}(qI)+\kappa \rho \operatorname {div}_{\tilde {\mathcal {A}}}\bigl(\nabla\eta\nabla\eta^{T}\bigr) \bigr\Vert _{1} \\ \lesssim{}& \bigl\Vert \nabla\eta\nabla\eta^{T} \bigr\Vert _{2}+ \bigl\Vert \mathbb {D}_{\tilde {\mathcal {A}}}(u) \bigr\Vert _{2}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \bigl\Vert \mathbb {D}_{\mathcal {A}}(u) \bigr\Vert _{2} \\ &+ \Vert \tilde {\mathcal {A}}\Vert _{2} \bigl\Vert \mathbb {D}(\eta) \bigr\Vert _{2}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert \nabla q \Vert _{1}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \bigl\Vert \nabla\eta\nabla \eta^{T} \bigr\Vert _{2} \\ \lesssim{}& \Vert \eta \Vert _{3}^{2}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert u \Vert _{3}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert \mathcal {A} \Vert _{2} \Vert u \Vert _{3}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert \eta \Vert _{3} \\ &+ \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert \nabla q \Vert _{1}+ \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert \eta \Vert _{3}^{2} \\ \lesssim{}& \Vert \eta \Vert _{3}\bigl( \bigl\Vert (u,\eta) \bigr\Vert _{3}+ \Vert \nabla q \Vert _{1}\bigr). \end{aligned} $$

(3.27)

Following the argument of (3.27), one has

$$ \begin{aligned}[b] \Vert \mathcal {N} \Vert _{0} \lesssim{}& \Vert \eta \Vert _{2} \Vert \eta \Vert _{3}+ \Vert \tilde {\mathcal {A}}\Vert _{2}\bigl( \Vert u \Vert _{2}+ \Vert \mathcal {A} \Vert _{2} \Vert u \Vert _{2}+ \Vert \eta \Vert _{2}+ \Vert \nabla q \Vert _{0}+ \Vert \eta \Vert _{2} \Vert \eta \Vert _{3}\bigr) \\ \lesssim{}& \Vert \eta \Vert _{3}\bigl( \bigl\Vert (u,\eta) \bigr\Vert _{2}+ \Vert \nabla q \Vert _{0}\bigr). \end{aligned} $$

(3.28)

Since we have the following relation

$$ \mathcal {A} e_{3}=\partial_{1}(\eta+y)\times \partial_{2}(\eta+y) =e_{3}+e_{1}\times \partial_{2}\eta+\partial_{1}\eta\times e_{2}+ \partial _{1}\eta\times\partial_{2}\eta, $$

(3.29)

making use of (3.29), (3.10), and (3.7), we find that, for sufficiently small δ,

$$ \bigl\Vert |\mathcal {A} e_{3} \vert ^{-1} \bigr\Vert _{2}\lesssim1 \quad\text{and}\quad \big\Vert 1-|\mathcal {A} e_{3}| \big\Vert _{2}\lesssim \Vert \eta \Vert _{3}. $$

(3.30)

Exploiting (3.30), (3.23), (3.19), and (3.10), one estimates that

$$ \biggl\Vert \frac{\mathcal {A} e_{3}}{ \vert \mathcal {A} e_{3} \vert } \biggr\Vert _{2} \lesssim 1\quad\text{and} \quad \biggl\Vert \frac{\mathcal {A} e_{3}}{ \vert \mathcal {A} e_{3} \vert }-e_{3} \biggr\Vert _{2}\lesssim \Vert \eta \Vert _{3}. $$

(3.31)

Consequently, exploiting the estimates (3.31), (3.23), (3.19), (3.15), (3.11), and (3.10), one has

$$\begin{array}{rl}|\mathcal{M}{|}_{\frac{3}{2}}\le & |〚\mu {\mathbb{D}}_{\tilde{\mathcal{A}}}(u)+\kappa \rho \mathrm{\nabla }\eta \mathrm{\nabla }{\eta }^T〛e_3{|}_{\frac{3}{2}}\\ & +|〚{\mathbb{S}}_{\mathcal{A}}(0,u,\mathrm{\nabla }\eta +I)-g\rho {\eta }_{3}I〛(e_3-\mathbf{n}){|}_{\frac{3}{2}}+|〚qI〛(e_3-\mathbf{n}){|}_{\frac{3}{2}}\\ \lesssim & {\parallel \mu {\mathbb{D}}_{\tilde{\mathcal{A}}}(u)+\kappa \rho \mathrm{\nabla }\eta \mathrm{\nabla }{\eta }^T\parallel }_2\\ & +{\parallel ({\mathbb{S}}_{\mathcal{A}}(0,u,\mathrm{\nabla }\eta +I)-g\rho {\eta }_{3}I)(e_3-\frac{\mathcal{A}{e}_3}{|\mathcal{A}{e}_3|})\parallel }_2+|〚qI〛(e_3-\mathbf{n}){|}_{\frac{3}{2}}\\ \lesssim & {\parallel \eta \parallel }_3({\parallel (u,\eta )\parallel }_3+|〚q〛{|}_{\frac{3}{2}}).\end{array}$$

(3.32)

Similarly, we can derive from (3.14) and (3.13) that

$$|\mathcal{M}{|}_{\frac{1}{2}}\lesssim {\parallel \eta \parallel }_3({\parallel (u,\eta )\parallel }_2+|〚q〛{|}_{\frac{1}{2}}).$$

(3.33)

4 Estimates of η and u

In this section, we aim to deduce some estimates of η and u.

4.1 Estimates of η

This subsection is devoted to the derivation of the $y_{h}$-derivative estimates of η, the $H^{3}$-norm estimate of η, and some positive definiteness estimate under the stability condition.

Lemma 4.1

We have, for $0\leq i\leq2$,

$$ \begin{aligned}[b] &\frac{\mathrm {d}}{\mathrm {d}t} \biggl( \int_{\Omega}\rho\partial_{h}^{i}\eta \cdot \partial_{h}^{i} u \,\mathrm {d}y+\frac{1}{4} \bigl\Vert \sqrt{\mu} \mathbb {D}\bigl(\partial_{h}^{i} \eta\bigr) \bigr\Vert _{0}^{2} \biggr)-\tilde{E}\bigl(\partial_{h}^{i} \eta \bigr) \\ &\quad\lesssim \Vert u \Vert _{i,0}^{2}+ \Vert \eta \Vert _{i,0} \Vert u \Vert _{i,0}+\sqrt{\mathcal {E}}\mathcal {D}. \end{aligned} $$

(4.1)

Proof

Applying $\partial_{h}^{i}$ to (3.2), we have

$$\{\begin{array}{ll}\rho {\partial }_h^i{u}_t+\mathrm{\nabla }{\partial }_h^{i}q-div{\partial }_h^i\mathbb{D}(\mu u+\kappa \rho \eta )+2\rho a{\partial }_h^i(u_1{e}_2-u_2{e}_1)={\partial }_h^i\mathcal{N}& \text{in }\mathrm{\Omega },\\ div{\partial }_h^{i}u=-{\partial }_h^i{div}_{\tilde{\mathcal{A}}}u& \text{in }\mathrm{\Omega },\\ 〚{\partial }_h^{i}u〛=〚{\partial }_h^i\eta 〛=0,〚{\partial }_h^i(qI-\mathbb{D}(\mu u+\kappa \rho \eta )-g\rho {\eta }_3)e_3〛={\partial }_h^i\mathcal{M}& \text{on }\mathrm{\Sigma },\\ {\partial }_h^{i}u=0,{\partial }_h^i\eta =0& \text{on }{\mathrm{\Sigma }}_{-}^{+}.\end{array}$$

(4.2)

Multiplying (4.2)₁ by $\partial_{h}^{i}\eta$ in $L^{2}$, one obtains

$$\begin{aligned}[b] \frac{\mathrm {d}}{\mathrm {d}t} \int_{\Omega}\rho\partial_{h}^{i}\eta\cdot \partial _{h}^{i}u\,\mathrm {d}y={}& \int_{\Omega}\partial_{h}^{i}\bigl(\operatorname {div}\mathbb {D}(\mu u+\kappa\rho\eta )-\nabla q\bigr)\cdot\partial_{h}^{i} \eta \,\mathrm {d}y+ \int_{\Omega}\rho \bigl\vert \partial_{h}^{i}u \bigr\vert ^{2}\,\mathrm {d}y\\ &+ \int_{\Omega}\partial_{h}^{i}\mathcal {N}\cdot \partial_{h}^{i}\eta \,\mathrm {d}y+2 \int _{\Omega}\rho a\partial_{h}^{i}(u_{2}e_{1}-u_{1}e_{2}) \cdot\partial_{h}^{i}\eta \,\mathrm {d}y\\:= {}&\sum _{k=1}^{4} I_{k}.\end{aligned} $$

(4.3)

Next, we estimate for $I_{1}$–$I_{4}$.

Using the integration by parts, the boundary conditions in (4.2)₄, and the second jump condition in (4.2)₃, we have

$$\begin{array}{rl}{I}_1=& {\int }_{\mathrm{\Omega }}div{\partial }_h^i(\mathbb{D}(\mu u+\kappa \rho \eta )-qI)\cdot {\partial }_h^i\eta \mathrm{d}y\\ =& {\int }_{\mathrm{\Sigma }}〚{\partial }_h^i(qI-\mathbb{D}(\mu u+\kappa \rho \eta )-g\rho {\eta }_3)e_3〛\cdot {\partial }_h^i\eta \mathrm{d}{y}_h+{\int }_{\mathrm{\Sigma }}〚{\partial }_h^i(g\rho {\eta }_3)〛e_3\cdot {\partial }_h^i\eta \mathrm{d}{y}_h\\ & +{\int }_{\mathrm{\Omega }}{\partial }_h^i(qI):\mathrm{\nabla }\left({\partial }_h^i\eta \right)\mathrm{d}y-{\int }_{\mathrm{\Omega }}\mu {\partial }_h^i\mathbb{D}(u):\mathrm{\nabla }\left({\partial }_h^i\eta \right)\mathrm{d}y\\ & -{\int }_{\mathrm{\Omega }}\kappa \rho {\partial }_h^i\mathbb{D}(\eta ):\mathrm{\nabla }\left({\partial }_h^i\eta \right)\mathrm{d}y\\ =& \tilde{E}\left({\partial }_h^i\eta \right)-\frac{1}{4}\frac{\mathrm{d}}{\mathrm{d}t}{\parallel \sqrt{\mu }\mathbb{D}\left({\partial }_h^i\eta \right)\parallel }_0^2+I_5+I_6,\end{array}$$

(4.4)

where

$$\begin{aligned}& I_{5}= \int_{\Sigma}\partial_{h}^{i}\mathcal {M}\cdot \partial _{h}^{i}\eta \,\mathrm {d}y_{h}, \end{aligned}$$

(4.5)

$$\begin{aligned}& I_{6}= \int_{\Omega}\partial_{h}^{i}q\operatorname {div}\partial _{h}^{i}\eta \,\mathrm {d}y. \end{aligned}$$

(4.6)

Therefore, putting (4.4) into (4.3) and using Hölder’s inequality, we have

$$ \begin{aligned} [b]&\frac{\mathrm {d}}{\mathrm {d}t} \biggl( \int_{\Omega}\rho\partial_{h}^{i}\eta \cdot \partial_{h}^{i} u \,\mathrm {d}y+\frac{1}{4} \bigl\Vert \sqrt{\mu} \mathbb {D}\bigl(\partial_{h}^{i} \eta\bigr) \bigr\Vert _{0}^{2} \biggr)-\tilde{E}\bigl(\partial_{h}^{i} \eta \bigr) \\ &\quad\lesssim \Vert u \Vert _{i,0}^{2}+ \Vert \eta \Vert _{i,0} \Vert u \Vert _{i,0}+I_{3}+I_{5}+I_{6}. \end{aligned} $$

(4.7)

Exploiting the formula of integration by parts, (3.32), and (3.27), one obtains

$$ \begin{aligned} [b]I_{3}={}&\left \{ \textstyle\begin{array}{l@{\quad}l} -\int_{\Omega}\partial_{h}\mathcal {N}\cdot\partial_{h}^{3}\eta \,\mathrm {d}y\lesssim \Vert \mathcal {N} \Vert _{1} \Vert \eta \Vert _{3}&\mbox{for }i=2,\\ \int_{\Omega}\partial_{h}^{i}\mathcal {N}\cdot\partial_{h}^{i}\eta \,\mathrm {d}y\lesssim \Vert \mathcal {N} \Vert _{i} \Vert \eta \Vert _{i}&\mbox{for }i=0,1, \end{array}\displaystyle \right . \\ \lesssim{}& \Vert \mathcal {N} \Vert _{1} \Vert \eta \Vert _{3} \lesssim\sqrt{\mathcal {E}}\mathcal {D}, \end{aligned} $$

(4.8)

and

$$ \begin{aligned}[b] I_{5}={}&\left \{ \textstyle\begin{array}{l@{\quad}l} -\int_{\Sigma}\partial_{h}\mathcal {M}\cdot\partial_{h}^{3}\eta \,\mathrm {d}y_{h}\lesssim \vert \partial_{h}\mathcal {M} \vert _{\frac{1}{2}} \vert \partial _{h}^{3}\eta \vert _{-\frac{1}{2}}&\mbox{for }i=2,\\ \int_{\Sigma}\partial_{h}^{i}\mathcal {M}\cdot\partial_{h}^{i}\eta \,\mathrm {d}y_{h}\lesssim \vert \mathcal {M} \vert _{i} \vert \eta \vert _{i}&\mbox{for }i=0,1, \end{array}\displaystyle \right . \\ \lesssim{}& \vert \mathcal {M} \vert _{\frac{3}{2}} \vert \eta \vert _{\frac{5}{2}} \lesssim\sqrt{\mathcal {E}}\mathcal {D}. \end{aligned} $$

(4.9)

Using Hölder’s inequality and (3.18), we can get that

$$ I_{6}\lesssim \bigl\Vert \partial_{h}^{i}q \bigr\Vert _{0} \bigl\Vert \operatorname {div}\partial _{h}^{i} \eta \bigr\Vert _{0}\lesssim \sqrt {\mathcal {E}}\mathcal {D}\quad\text{for }i=1,2. $$

(4.10)

Next we turn to estimate for $I_{6}$ with $i=0$. We can deduce from (3.17) that

$$ \begin{aligned} [b]\operatorname {div}\eta ={}&\frac{1}{2}\bigl( \operatorname{tr}(\nabla\eta)^{2}-(\operatorname {div}\eta)^{2}\bigr)-\det \nabla \eta \\ ={}&\partial_{1}\eta_{2}\partial_{2} \eta_{1}+\partial_{2}\eta_{3}\partial _{3}\eta_{2}+\partial_{3}\eta_{1} \partial_{1}\eta_{3} -\partial_{1} \eta_{1}\partial_{2}\eta_{2}-\partial_{1} \eta_{1}\partial_{3}\eta _{3}- \partial_{2}\eta_{2}\partial_{3}\eta_{3} \\ &+\partial_{1}\eta_{1}(\partial_{2} \eta_{3}\partial_{3}\eta_{2}-\partial _{2}\eta_{2}\partial_{3}\eta_{3}) + \partial_{2}\eta_{1}(\partial_{1}\eta_{2} \partial_{3}\eta_{3}-\partial _{1} \eta_{3}\partial_{3}\eta_{2}) \\ &+\partial_{3}\eta_{1}(\partial_{1} \eta_{3}\partial_{2}\eta_{2}-\partial _{1}\eta_{2}\partial_{2}\eta_{3}), \end{aligned} $$

(4.11)

which yields that

$$ \operatorname {div}\eta=\operatorname {div}\psi, $$

(4.12)

where we have defined that

$$ \psi:= \begin{pmatrix} -\eta_{1}(\partial_{2}\eta_{2}+\partial_{3}\eta_{3})+\eta_{1}(\partial_{2}\eta _{3}\partial_{3}\eta_{2}-\partial_{2}\eta_{2}\partial_{3}\eta_{3})\\ \eta_{1}\partial_{1}\eta_{2}-\eta_{2}\partial_{3}\eta_{3}+\eta_{1}(\partial _{1}\eta_{2}\partial_{3}\eta_{3}-\partial_{1}\eta_{3}\partial_{3}\eta_{2})\\ \eta_{1}\partial_{1}\eta_{3}+\eta_{2}\partial_{2}\eta_{2}+\eta_{1}(\partial _{1}\eta_{3}\partial_{2}\eta_{2}-\partial_{1}\eta_{2}\partial_{2}\eta_{3}) \end{pmatrix} . $$

Using the integration by parts, (3.15), and (3.10), we obtain that

$$\begin{array}{rl}{I}_6=& -{\int }_{\mathrm{\Sigma }}〚q〛e_3\cdot \psi \mathrm{d}{y}_h-{\int }_{\mathrm{\Omega }}\psi \cdot \mathrm{\nabla }q\mathrm{d}y\\ \lesssim & {\parallel \psi \parallel }_1({\parallel \mathrm{\nabla }q\parallel }_0+|〚q〛{|}_{\frac{1}{2}})\lesssim {\parallel \eta \parallel }_3^2({\parallel \mathrm{\nabla }q\parallel }_0+|〚q〛{|}_{\frac{1}{2}})\lesssim \sqrt{\mathcal{E}}\mathcal{D}.\end{array}$$

(4.13)

Finally, inserting (4.8)–(4.10) and (4.13) into (4.7), we immediately deduce (4.1). □

In order to estimate η in $H^{3}$-norm, problem (3.2) shall be rewritten as the following two one-phase steady Stokes problems:

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} -\mu_{\pm}\Delta w_{\pm}+\nabla q_{\pm}=\mathcal {G}_{\pm}&\text{in } {\Omega },\\ \operatorname {div}w_{\pm}=\mathcal {H}_{\pm}&\text{in } {\Omega},\\ w_{\pm}=w_{\pm}|_{\Sigma}&\text{on } \Sigma,\\ w_{\pm}=0 &\text{on } \Sigma_{-}^{+}, \end{array}\displaystyle \right . $$

(4.14)

where

$$\begin{aligned}& \mathcal {H}_{\pm}:= \biggl(\frac{\kappa\rho}{\mu} \operatorname {div}\eta- \operatorname {div}_{\tilde {\mathcal {A}}} u \biggr)\chi_{\Omega_{\pm}}, \end{aligned}$$

(4.15)

$$\begin{aligned}& \mathcal {G}_{\pm}:=\bigl(\mu\nabla \mathcal {H}_{\pm}+\mathcal {N}-\rho u_{t} +2\rho a(u_{2}e_{1}-u_{1}e_{2}) \bigr)\chi_{\Omega_{\pm}}, \end{aligned}$$

(4.16)

$$\begin{aligned}& w_{\pm}:= \biggl(u+\frac{\kappa\rho}{\mu}\eta \biggr) \chi_{\Omega_{\pm}}, \end{aligned}$$

(4.17)

and $(w_{\pm},w_{\pm}|_{\Sigma})$ enjoys the following relation:

$$ \int_{\Omega_{\pm}} \mathcal {H}_{\pm} \,\mathrm {d}y= \int_{\Sigma}w_{\pm}|_{\Sigma}\cdot(\mp e_{3})\,\mathrm {d}y_{h}. $$

(4.18)

Lemma 4.2

We have

$$ \frac{\mathrm {d}}{\mathrm {d}t} \biggl\Vert \sqrt{\frac{\kappa\rho}{\mu}}\eta \biggr\Vert _{3}^{2}+ \bigl\Vert (\eta,u) \bigr\Vert _{3}^{2}+ \Vert \nabla q \Vert _{1}^{2} \lesssim\sum_{i=0}^{2} \bigl\Vert ( \eta,u) \bigr\Vert _{i,1}^{2}+ \Vert u_{t} \Vert _{1}^{2}+\mathcal {ED}. $$

(4.19)

Proof

Applying the classical regularity of one-phase Stokes problem in [35] to (4.14), one has

$$ \Vert w_{\pm} \Vert _{3}^{2}+ \Vert \nabla q_{\pm} \Vert _{1}^{2}\lesssim \Vert \mathcal {G}_{\pm} \Vert _{1}^{2}+ \Vert \mathcal {H}_{\pm} \Vert _{2}^{2}+ \vert w_{\pm} \vert _{\Sigma}|_{\frac{5}{2}}^{2}, $$

(4.20)

which yields that

$$ \Vert w \Vert _{3}^{2}+ \Vert \nabla q \Vert _{1}^{2}\lesssim \Vert \mathcal {G} \Vert _{1}^{2}+ \Vert \mathcal {H} \Vert _{2}^{2}+ \vert w \vert _{\frac{5}{2}}^{2}, $$

(4.21)

where we have defined that $w=w_{+}\chi_{\Omega_{+}}+w_{-}\chi_{\Omega _{-}}$, $\mathcal {G}=\mathcal {G}_{+}\chi_{\Omega_{+}}+\mathcal {G}_{-}\chi_{\Omega_{-}}$, and $\mathcal {H}=\mathcal {H}_{+}\chi_{\Omega_{+}}+\mathcal {H}_{-}\chi_{\Omega_{-}}$.

Since

$$ \Vert w \Vert _{3}^{2}=\frac{\mathrm {d}}{\mathrm {d}t} \biggl\Vert \sqrt{\frac{\kappa \rho}{\mu}}\eta \biggr\Vert _{3}^{2} + \Vert u \Vert _{3}^{2}+ \biggl\Vert \frac{\kappa\rho}{\mu}\eta \biggr\Vert _{3}^{2}, $$

(4.22)

inserting the above equation into (4.20) yields

$$ \frac{\mathrm {d}}{\mathrm {d}t} \biggl\Vert \sqrt{\frac{\kappa\rho}{\mu}}\eta \biggr\Vert _{3}^{2} + \Vert u \Vert _{3}^{2}+ \biggl\Vert \frac{\kappa\rho}{\mu}\eta \biggr\Vert _{3}^{2}+ \Vert \nabla q \Vert _{1}^{2} \lesssim \Vert \mathcal {G} \Vert _{1}^{2}+ \Vert \mathcal {H} \Vert _{2}^{2}+ \vert w \vert _{\frac{5}{2}}^{2}. $$

(4.23)

Making use of (3.27), (3.23), (3.18), (3.15), and (3.7), we have

$$\begin{aligned}& \begin{aligned}[b] \Vert \mathcal {G} \Vert _{1}\lesssim{}& \Vert u \Vert _{1}+ \Vert u_{t} \Vert _{1}+ \Vert \mathcal {H} \Vert _{2}+ \Vert \mathcal {N} \Vert _{1} \\ \lesssim{}& \Vert u \Vert _{1}+ \Vert u_{t} \Vert _{1}+ \Vert \operatorname {div}\eta \Vert _{2}+ \Vert \operatorname {div}_{\tilde {\mathcal {A}}}u \Vert _{2}+ \Vert \mathcal {N} \Vert _{1} \\ \lesssim{}& \Vert u \Vert _{1}+ \Vert u_{t} \Vert _{1}+ \Vert \eta \Vert _{3}\bigl( \bigl\Vert (u,\eta) \bigr\Vert _{3}+ \Vert \nabla q \Vert _{1}\bigr) \\ \lesssim{}& \Vert u \Vert _{1}+ \Vert u_{t} \Vert _{1}+\sqrt{ \mathcal {ED}},\end{aligned} \end{aligned}$$

(4.24)

$$\begin{aligned}& \Vert \mathcal {H} \Vert _{2}^{2} = \biggl\Vert \frac{\kappa \rho}{\mu} \operatorname {div}\eta-\operatorname {div}_{\tilde {\mathcal {A}}}u \biggr\Vert _{2}^{2} \lesssim\bigl( \Vert \eta \Vert _{3}^{2}+ \Vert \eta \Vert _{3} \Vert u \Vert _{3}\bigr)^{2}\lesssim \mathcal {ED} \end{aligned}$$

(4.25)

and

$$ \vert w \vert _{\frac{5}{2}}^{2}= \vert w \vert _{2+\frac{1}{2}}^{2} \lesssim\sum_{i=0}^{2} \Vert w \Vert _{i,1}^{2} \lesssim\sum _{i=0}^{2} \bigl\Vert (\eta,u) \bigr\Vert _{i,1}^{2}. $$

(4.26)

Putting (4.24)–(4.26) into (4.23) yields (4.19). □

In order to control the negative terms containing g and η, we will establish the following positive definiteness estimate.

Lemma 4.3

We have

$$ \bigl\Vert \partial_{h}^{i}\eta \bigr\Vert _{1}^{2}\lesssim-\tilde{E}\bigl(\partial _{h}^{i}\eta\bigr)+ \Vert \eta \Vert _{3}^{3}\quad\textit{for }0\leq i\leq2. $$

(4.27)

Proof

It is obvious that (4.27) holds with any $\varphi\in H_{\sigma}^{1}$ in place of $\partial_{h}^{i}\eta$. In fact, recalling the definition of $\mathrm{C}_{\mathrm{r}}$ in (2.6), we have

$$-g〚\rho 〛|{\phi }_3{|}_0^2\ge -\frac{{\mathrm{C}}_{\mathrm{r}}}{2}{\parallel \sqrt{\kappa \rho }\mathbb{D}(u)\parallel }_0^2,$$

(4.28)

which implies that

$$ -\tilde{E}(\varphi)\geq\frac{1}{2} \bigl\Vert \sqrt{\kappa\rho} \mathbb {D}( \varphi) \bigr\Vert _{0}^{2}-\frac{\mathrm{C}_{\mathrm{r}}}{2} \bigl\Vert \sqrt{\kappa\rho} \mathbb {D}(\varphi) \bigr\Vert _{0}^{2} \gtrsim \bigl\Vert \mathbb {D}(\varphi) \bigr\Vert _{0}^{2}. $$

Therefore, together with $\mathrm{C}_{\mathrm{r}}<1$ and Korn’s inequality (3.8), it implies that

$$ \Vert \varphi \Vert _{1}^{2}\lesssim \bigl\Vert \mathbb {D}(\varphi) \bigr\Vert _{0}^{2}\lesssim- \tilde{E}(\varphi)\quad\text{for any }\varphi\in H_{\sigma}^{1}. $$

(4.29)

To further deduce (4.27) from (4.29), we shall introduce Bogovskii’s function with the standing-wave form. We have the following conclusion:

Let $\Omega'$ be a bounded Lipschitz domain. For any given $f\in L^{2}(\Omega')$ satisfying $\int_{\Omega'}f\,\mathrm {d}y=0$, there exists a Bogovskii’s function $\tilde{\mathcal {B}}\in H_{0}^{1}(\Omega')$ such that $\operatorname {div}\tilde{\mathcal {B}}[f]=f$ and

$$ \bigl\Vert \tilde{B}[f] \bigr\Vert _{H^{1}(\Omega')}\leq c \Vert f \Vert _{L^{2}(\Omega')}, $$

(4.30)

where the constant c only depends on the domain $\Omega'$ (see [6], Theorem 10.11 or [7], Lemma III.3.1).

The above Bogovskii’s function defined on a bounded domain can be extended to the horizontal periodic domain Ω. In fact, we define that

$$ \mathbb {C}:=\bigl\{ (y_{1},y_{2},y_{3}) \in \mathbb {R}^{3}|0< y_{1}< 2\pi L_{1}, 0< y_{2}< 2\pi L_{2}, -l< y_{3}< \tau\bigr\} . $$

(4.31)

Then $\mathbb{C}$ is a bounded Lipschitz domain. We can use Bogovskii’s function defined on $\mathbb {C}$ and an approach of horizontally translational extension to infer that, for any given $g\in L^{2}$ satisfying $\int_{\mathbb {C}} g \,\mathrm {d}y=0$, there exists a horizontally periodic Bogovskii’s function $\mathcal {B}[g]\in H_{0}^{1}$ such that

$$\begin{aligned}& \operatorname {div}\mathcal {B}[g]=g, \end{aligned}$$

(4.32)

$$\begin{aligned}& \bigl\Vert \mathcal {B}[g] \bigr\Vert _{1}\leq c \Vert g \Vert _{0}, \end{aligned}$$

(4.33)

$$\begin{aligned}& \bigl(\mathcal {B}[g]\bigr) (2\pi k_{1} L_{1},2\pi k_{2} L_{2}, y_{3})=0 \end{aligned}$$

(4.34)

for any integers $k_{1}$ and $k_{2}$. We call $\mathcal {B}[g]$ Bogovskii’s function in a standing-wave form due to property (4.34).

Since $\operatorname {div}\partial_{h}^{i}\eta\in L^{2}$ and $\int_{\Omega} \operatorname {div}\partial_{h}^{i}\eta \,\mathrm {d}y=0$, then we can apply Bogovskii’s function to divη. Thus, using (4.30) and (3.18), we can infer that

$$ \bigl\Vert \mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i} \eta\bigr] \bigr\Vert _{1}\lesssim \bigl\Vert \operatorname {div}\partial_{h}^{i}\eta \bigr\Vert _{0}\lesssim \Vert \eta \Vert _{3}^{2}. $$

(4.35)

Obviously, $-\tilde{E}(\partial_{h}^{i}\eta)$ can be rewritten as follows:

$$\begin{array}{rl}-\tilde{E}\left({\partial }_h^i\eta \right)=& -\tilde{E}({\partial }_h^i\eta -\mathcal{B}[div{\partial }_h^i\eta ]+\mathcal{B}[div{\partial }_h^i\eta ])\\ =& -\tilde{E}({\partial }_h^i\eta -\mathcal{B}[div{\partial }_h^i\eta ])\\ & +\frac{1}{2}(2{\int }_{\mathrm{\Omega }}\kappa \rho \mathbb{D}\left({\partial }_h^i\eta \right):\mathbb{D}\left(\mathcal{B}[div{\partial }_h^i\eta ]\right)\mathrm{d}y-{\parallel \sqrt{\kappa \rho }\mathbb{D}\left(\mathcal{B}[div{\partial }_h^i\eta ]\right)\parallel }_0^2)\\ & -g〚\rho 〛(2{\int }_{\mathrm{\Sigma }}{\partial }_h^i{\eta }_3{\mathcal{B}}_3[div{\partial }_h^i\eta ]\mathrm{d}{y}_h-|{\mathcal{B}}_3[div{\partial }_h^i\eta ]{|}_0^2)\\ =:& I_7+I_8+I_9.\end{array}$$

(4.36)

Since $\partial_{h}^{i}\eta-\mathcal {B}[\operatorname {div}\partial_{h}^{i}\eta]\in H_{\sigma}^{1}$, thus, using (4.29) and the Cauchy–Schwarz inequality, we obtain

$$ \begin{aligned}[b] &\frac{1}{2} \bigl\Vert \mathbb {D} \bigl(\partial_{h}^{i}\eta\bigr) \bigr\Vert _{0}^{2}- \bigl\Vert \mathbb {D}\bigl(\mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i}\eta\bigr]\bigr) \bigr\Vert _{0}^{2} \\ &\quad\leq \bigl\Vert \mathbb {D}\bigl(\partial_{h}^{i}\eta\bigr) \bigr\Vert _{0}^{2}+ \bigl\Vert \mathbb {D}\bigl(\mathcal {B}\bigl[ \operatorname {div}\partial_{h}^{i}\eta\bigr]\bigr) \bigr\Vert _{0}^{2} -2 \int_{\Omega} \mathbb {D}\bigl(\partial_{h}^{i}\eta \bigr):\mathbb {D}\bigl(\mathcal {B}\bigl[\operatorname {div}\partial _{h}^{i}\eta \bigr]\bigr)\,\mathrm {d}y\\ &\quad= \bigl\Vert \mathbb {D}\bigl(\partial_{h}^{i}\eta-\mathcal {B} \bigl[\operatorname {div}\partial_{h}^{i}\eta \bigr]\bigr) \bigr\Vert _{0}^{2}\lesssim I_{7}. \end{aligned} $$

(4.37)

In addition, we use (4.35), (3.15), and (3.1) to estimate that

$$ \begin{aligned}[b] & \vert I_{8}+I_{9} \vert + \bigl\Vert \mathbb {D}\bigl(\mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i} \eta \bigr]\bigr) \bigr\Vert _{0}^{2} \\ &\quad\lesssim \bigl\vert \mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i} \eta\bigr] \bigr\vert _{0}\bigl( \bigl\vert \partial_{h}^{i} \eta_{3} \bigr\vert _{0}+ \bigl\vert \mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i}\eta \bigr] \bigr\vert _{0} \bigr) \\ &\qquad{}+ \bigl\Vert \mathbb {D}\bigl(\mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i} \eta\bigr]\bigr) \bigr\Vert _{0}\bigl( \bigl\Vert \mathbb {D}\bigl( \partial_{h}^{i}\eta\bigr) \bigr\Vert _{0}+ \bigl\Vert \mathbb {D}\bigl(\mathcal {B}\bigl[\operatorname {div}\partial _{h}^{i} \eta\bigr]\bigr) \bigr\Vert _{0}\bigr) \\ &\quad\lesssim \bigl\Vert \mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i} \eta\bigr] \bigr\Vert _{1}\bigl( \bigl\Vert \partial_{h}^{i} \eta \bigr\Vert _{1}+ \bigl\Vert \mathcal {B}\bigl[\operatorname {div}\partial_{h}^{i}\eta \bigr] \bigr\Vert _{1} \bigr) \\ &\quad\lesssim \Vert \eta \Vert _{3}^{3}. \end{aligned} $$

(4.38)

Thanks to (4.37) and (4.38), we deduce from (4.36) that

$$ \frac{1}{2} \bigl\Vert \mathbb {D}\bigl(\partial_{h}^{i} \eta\bigr) \bigr\Vert _{0}^{2}\lesssim -\tilde{E}\bigl( \partial_{h}^{i}\bigr)+ \Vert \eta \Vert _{3}^{3}, $$

which, together with Korn’s inequality (3.8), yields (4.27). □

4.2 Estimates of u

In this subsection, we deduce the $y_{h}$-derivative estimate of u, the temporal derivative estimates, and the elliptic estimates for $(u,q)$ in sequence.

Lemma 4.4

We have

$$ \frac{\mathrm {d}}{\mathrm {d}t} \biggl( \int_{\Omega}\rho \bigl\vert \partial_{h}^{i}u \bigr\vert ^{2}\,\mathrm {d}y-\tilde{E}\bigl(\partial_{h}^{i} \eta\bigr) \biggr)+c \bigl\Vert \sqrt{\mu }\mathbb{D}\bigl(\partial_{h}^{i}u \bigr) \bigr\Vert _{0}^{2}\lesssim \sqrt {\mathcal {E}}\mathcal {D}\quad\textit{for }i=1,2. $$

(4.39)

Proof

The derivation of Lemma 4.4 is very similar to the one of Lemma 4.1. Multiplying (4.2) by $\partial_{h}^{i}u$, and integrating the resulting identity over Ω, we have

$$ \begin{aligned}[b] \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d}t} \int_{\Omega}\rho \bigl\vert \partial _{h}^{i}u \bigr\vert ^{2}\,\mathrm {d}y={}&{-} \int_{\Omega}\partial_{h}^{i}\bigl(\nabla q- \operatorname {div}\mathbb {D}(\mu u+\kappa\rho \eta)\bigr)\cdot\partial_{h}^{i}u \,\mathrm {d}y+ \int_{\Omega}\partial_{h}^{i}\mathcal {N}\cdot \partial_{h}^{i}u \,\mathrm {d}y\\ &+2 \int_{\Omega}\rho a \partial_{h}^{i}(u_{2}e_{1}-u_{1}e_{2}) \cdot\partial _{h}^{i}u\,\mathrm {d}y. \end{aligned} $$

(4.40)

Noting that

$$ 2 \int_{\Omega}\rho a \partial_{h}^{i}(u_{2}e_{1}-u_{1}e_{2}) \cdot\partial _{h}^{i}u\,\mathrm {d}y=0, $$

following the argument of (4.7), we have

$$ \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d}t} \biggl( \int_{\Omega}\rho \bigl\vert \partial _{h}^{i}u \bigr\vert ^{2}\,\mathrm {d}y-\tilde{E}\bigl(\partial_{h}^{i} \eta\bigr) \biggr) +\frac{1}{2} \bigl\Vert \sqrt{\mu}\mathbb{D}\bigl( \partial_{h}^{i}u\bigr) \bigr\Vert _{0}^{2} :=I_{10}+I_{11}, $$

(4.41)

where we have defined that

$$\begin{aligned}& I_{10}:= \int_{\Omega} \mathcal {N}\cdot\partial_{h}^{i}u\,\mathrm {d}y+ \int_{\Sigma}\partial_{h}^{i}\mathcal {M} \cdot \partial_{h}^{i}u\,\mathrm {d}y_{h}, \end{aligned}$$

(4.42)

$$\begin{aligned}& I_{11}:= \int_{\Omega}\partial_{h}^{i}q\operatorname {div}\partial _{h}^{i}u\,\mathrm {d}y. \end{aligned}$$

(4.43)

Following the argument of (4.8) and (4.9), we have

$$ I_{10}\lesssim \sqrt {\mathcal {E}}\mathcal {D}. $$

(4.44)

By (3.2)₂, one further gets

$$ I_{11}=- \int_{\Omega}\partial_{h}^{i}q \partial_{h}^{i}\operatorname {div}_{\tilde {\mathcal {A}}}u\,\mathrm {d}y\lesssim \Vert \nabla q \Vert _{1} \Vert \operatorname {div}_{\tilde {\mathcal {A}}} u \Vert _{2}\lesssim \sqrt {\mathcal {E}}\mathcal {D}. $$

(4.45)

Finally, we put the result (4.44) and (4.45) into (4.41), and get (4.39). This completes the proof of Lemma 4.4. □

Lemma 4.5

We have

$$\begin{array}{rl}& \frac{\mathrm{d}}{\mathrm{d}t}({\parallel \sqrt{\rho }(u(t),u_t)\parallel }_0^2-\tilde{E}(u)-\tilde{E}(\eta )-{\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y-{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h)\\ & +c{\parallel (u,u_t)\parallel }_1^2\lesssim \sqrt{\mathcal{E}}\mathcal{D}.\end{array}$$

(4.46)

Proof

Since $〚\eta 〛=0$, one has

$$〚\mathcal{A}{e}_3〛=0.$$

(4.47)

Recalling the definition of n in (1.11) and the second jump condition in (1.9)₄, we get

$$〚{\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)\mathcal{A}{e}_3〛=〚{\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)〛\mathcal{A}{e}_3=g〚\rho 〛{\eta }_3\mathcal{A}{e}_3\text{on }\mathrm{\Sigma }.$$

(4.48)

Hence, multiplying (1.9)₂ by u in $L^{2}$ and using (1.19), the jump condition (4.48), and the relation

$$ 2 \int_{\Omega}\rho a(u_{1}e_{2}-u_{2}e_{1}) \cdot u\,\mathrm {d}y=0, $$

we have

$$\begin{array}{rl}& \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}({\parallel \sqrt{\rho }u\parallel }_0^2-\tilde{E}(\eta ))+\frac{1}{2}{\parallel \sqrt{\mu }{\mathbb{D}}_{\mathcal{A}}(u)\parallel }_0^2\\ & =-{\int }_{\mathrm{\Omega }}\kappa \rho (\mathrm{\nabla }\eta \mathrm{\nabla }{\eta }^T:{\mathrm{\nabla }}_{\mathcal{A}}{u}^T+\mathbb{D}(\eta ):{\mathrm{\nabla }}_{\tilde{\mathcal{A}}}{u}^T)\mathrm{d}y+g〚\rho 〛{\int }_{\mathrm{\Sigma }}{\eta }_3\tilde{\mathcal{A}}{e}_3\cdot u\mathrm{d}{y}_h=:K_1.\end{array}$$

(4.49)

It is easy to estimate that

$$ K_{1}\lesssim \Vert \eta \Vert _{3}^{2} \Vert \mathcal {A} \Vert _{2} \Vert u \Vert _{1}+ \Vert \eta \Vert _{3} \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert u \Vert _{1} + \Vert \eta \Vert _{2} \Vert \tilde {\mathcal {A}}\Vert _{1} \Vert u \Vert _{1} \lesssim \sqrt {\mathcal {E}}\mathcal {D}. $$

(4.50)

Inserting the above estimate into (4.49) yields that

$$ \begin{gathered} \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d}t} \bigl( \Vert \sqrt{\rho}u \Vert _{0}^{2}-\tilde{E}(\eta) \bigr) +\frac{1}{2} \bigl\Vert \sqrt{\mu} \mathbb {D}_{\mathcal {A}}(u) \bigr\Vert _{0}^{2} \lesssim \sqrt {\mathcal {E}}\mathcal {D}. \end{gathered} $$

(4.51)

Next we turn to estimate $u_{t}$. Differentiating (1.9)₂–(1.9)₄ and the jump condition (4.48), we use (1.20) to deduce that

$$\{\begin{array}{ll}\rho u_{tt}+{div}_{\mathcal{A}}\mathcal{V}+2{\partial }_t(\rho a(u_1{e}_2-u_2{e}_1))& \\ =-{div}_{{\mathcal{A}}_t}{\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)-\mu {div}_{\mathcal{A}}{\mathbb{D}}_{{\mathcal{A}}_t}(u)& \text{in }\mathrm{\Omega },\\ {div}_{\mathcal{A}}{u}_t=-{\partial }_l({\partial }_t{\mathcal{A}}_{kl}{u}_k)& \text{in }\mathrm{\Omega },\\ 〚\mathcal{V}-g\rho u_{3}I〛\mathcal{A}{e}_3=〚g\rho {\eta }_{3}I-{\mathbb{S}}_A(q,u,\mathrm{\nabla }\eta +I)〛{\mathcal{A}}_t{e}_3+〚\mu {\mathbb{D}}_{{\mathcal{A}}_t}(u)〛\mathcal{A}{e}_3& \text{on }\mathrm{\Sigma },\\ u_t=0,{\eta }_t=0& \text{on }{\mathrm{\Sigma }}_{-}^{+},\end{array}$$

(4.52)

where we have defined that

$$ \mathcal {V}:=\mathbb {S}_{\mathcal {A}}(q_{t}, u_{t},0)-\kappa\rho\bigl(\mathbb {D}(u)+\nabla u\nabla \eta^{T}+ \nabla\eta\nabla u^{T}\bigr). $$

(4.53)

Multiplying (4.52)₁ by $u_{t}$ in $L^{2}$ and exploiting (4.52)₂–(4.52)₄, we have

$$\begin{array}{rl}& \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}({\parallel \sqrt{\rho }{u}_t\parallel }_0^2-\tilde{E}(u))+\frac{1}{2}{\parallel \sqrt{\mu }{\mathbb{D}}_{\mathcal{A}}(u_t)\parallel }_0^2\\ & =-{\int }_{\mathrm{\Omega }}{q}_t{\partial }_l({\partial }_t{\mathcal{A}}_{kl}{u}_k)\mathrm{d}y-{\int }_{\mathrm{\Omega }}(\kappa \rho (\mathrm{\nabla }u\mathrm{\nabla }{\eta }^T+\mathrm{\nabla }\eta \mathrm{\nabla }{u}^T):{\mathrm{\nabla }}_{\mathcal{A}}{u}_t^T+\kappa \rho \mathbb{D}(u):{\mathrm{\nabla }}_{\tilde{\mathcal{A}}}{u}_t^T)\mathrm{d}y\\ & -{\int }_{\mathrm{\Omega }}({div}_{{\mathcal{A}}_t}{\mathbb{S}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)+\mu {div}_{\mathcal{A}}{\mathbb{D}}_{{\mathcal{A}}_t}(u))\cdot u_t\mathrm{d}y\\ & +{\int }_{\mathrm{\Sigma }}(〚g\rho {\eta }_{3}I-{\mathbb{D}}_{\mathcal{A}}(q,u,\mathrm{\nabla }\eta +I)〛{\mathcal{A}}_t{e}_3+〚\mu {\mathbb{D}}_{{\mathcal{A}}_t}(u)〛\mathcal{A}{e}_3+g\rho u_3\tilde{\mathcal{A}}{e}_3)\cdot u_t\mathrm{d}{y}_h\\ & +2{\int }_{\mathrm{\Omega }}\rho a{\partial }_t(u_2{e}_1-u_1{e}_2)\cdot u_t\mathrm{d}y\\ & =:\sum _{i=2}^6{K}_i.\end{array}$$

(4.54)

We can estimate the integrals $K_{3}$–$K_{6}$ as follows:

$$\begin{aligned}& K_{3}\lesssim \bigl\Vert \nabla u\nabla \eta^{T}+\nabla \eta\nabla u^{T} \bigr\Vert _{0} \bigl\Vert \nabla_{\mathcal {A}} u_{t}^{T} \bigr\Vert _{0} + \bigl\Vert \mathbb {D}(u) \bigr\Vert _{0} \bigl\Vert \nabla_{\tilde {\mathcal {A}}}u_{t}^{T} \bigr\Vert _{0} \lesssim \sqrt {\mathcal {E}}\mathcal {D}, \end{aligned}$$

(4.55)

$$\begin{aligned}& \begin{aligned}[b]K_{4}\lesssim{}& \Vert u_{t} \Vert _{0} \bigl\Vert \operatorname {div}_{\mathcal {A}_{t}}\mathbb {S}_{\mathcal {A}}(q,u,\nabla\eta+I) \bigr\Vert _{0} + \Vert u_{t} \Vert _{0} \bigl\Vert \operatorname {div}_{\mathcal {A}}\mathbb {D}_{\mathcal {A}_{t}}(u) \bigr\Vert _{0} \\ \lesssim{}& \Vert u_{t} \Vert _{0} \Vert \mathcal {A}_{t} \Vert _{2}\bigl( \Vert \nabla q \Vert _{0}+ \bigl\Vert \mathbb {D}_{\mathcal {A}}(u) \bigr\Vert _{1}+ \bigl\Vert \mathbb {D}(\eta) \bigr\Vert _{1} + \bigl\Vert \nabla\eta \nabla\eta^{T} \bigr\Vert _{1}\bigr) \\ &+ \Vert u_{t} \Vert _{0} \Vert \mathcal {A} \Vert _{2} \Vert \mathcal {A}_{t} \Vert _{2} \Vert u \Vert _{2} \lesssim \sqrt {\mathcal {E}}\mathcal {D}, \end{aligned} \end{aligned}$$

(4.56)

$$\begin{array}{rl}{K}_5\lesssim & |u_t{|}_0(|〚g\rho {\eta }_{3}I-{\mathbb{S}}_{\mathcal{A}}(0,u,\mathrm{\nabla }\eta +I)〛{\mathcal{A}}_t{e}_3\\ & +〚\mu {\mathbb{D}}_{{\mathcal{A}}_t}(u)〛\mathcal{A}{e}_3+g〚\rho 〛u_3\tilde{\mathcal{A}}{e}_3{|}_0+|〚q〛{\mathcal{A}}_t{|}_0)\\ \lesssim & {\parallel u_t\parallel }_1({\parallel {\eta }_3{\mathcal{A}}_t\parallel }_1+{\parallel {\mathbb{S}}_{\mathcal{A}}(0,u,\mathrm{\nabla }\eta +I){\mathcal{A}}_t\parallel }_1\\ & +{\parallel {\mathbb{D}}_{{\mathcal{A}}_t}(u)\mathcal{A}\parallel }_1+{\parallel u_3\tilde{\mathcal{A}}\parallel }_1+|〚q〛{|}_{\frac{1}{2}}{\parallel {\mathcal{A}}_t\parallel }_{W^{1,4}(\mathbb{T})})\\ \lesssim & {\parallel u_t\parallel }_1({\parallel {\mathcal{A}}_t\parallel }_1({\parallel {\eta }_3\parallel }_2+{\parallel \mathcal{A}\parallel }_2{\parallel u\parallel }_3+{\parallel \eta \parallel }_3+{\parallel \eta \parallel }_3^2)\\ & +{\parallel \tilde{\mathcal{A}}\parallel }_2{\parallel u\parallel }_1+|〚q〛{|}_{\frac{1}{2}}{\parallel {\mathcal{A}}_t\parallel }_2)\\ \lesssim & \sqrt{\mathcal{E}}\mathcal{D},\end{array}$$

(4.57)

$$\begin{aligned}& K_{6}= 2 \int_{\Omega}\rho a \partial_{t}(u_{2}e_{1}-u_{1}e_{2}) \cdot u_{t}\,\mathrm {d}y=0. \end{aligned}$$

(4.58)

By (4.47), one has

$$〚{\mathcal{A}}_t{e}_3〛=0.$$

In order to estimate $K_{2}$, we use partial integrations and get

$$\begin{array}{rl}{K}_2=& {\int }_{\mathrm{\Omega }}{\partial }_l{q}_t{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y+{\int }_{\mathrm{\Sigma }}〚q_t〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h\\ =& \frac{\mathrm{d}}{\mathrm{d}t}({\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y+{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h)+K_7,\end{array}$$

(4.59)

where we have defined that

$$\begin{array}{rl}{K}_7& :=-({\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t({\partial }_t{\mathcal{A}}_{kl}{u}_k)\mathrm{d}y+{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u_t\mathrm{d}{y}_h)-{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_{tt}\cdot u\mathrm{d}{y}_h\\ & =:K_8+K_9.\end{array}$$

(4.60)

Exploiting (3.21) for $\mathcal {A}_{tt}$, we have

$$K_8\lesssim {\parallel \mathrm{\nabla }q\parallel }_0({\parallel u_t\parallel }_1{\parallel {\mathcal{A}}_t\parallel }_1+{\parallel {\mathcal{A}}_{tt}\parallel }_0{\parallel u\parallel }_2)+{\parallel {\mathcal{A}}_t\parallel }_2{\parallel u_t\parallel }_1|〚q〛{|}_0\lesssim \sqrt{\mathcal{E}}\mathcal{D}.$$

(4.61)

Since

$$ \mathcal {A}_{tt} e_{3}=e_{1}\times \partial_{2} u_{t}+\partial_{1}u_{t} \times e_{2}+\partial_{1} u_{t}\times \partial_{2}\eta+ 2\partial_{1} u\times\partial_{2} u+\partial_{1}\eta\times\partial _{2}u_{t}, $$

one can exploit (3.14) and (3.12) to derive that

$$\begin{array}{rl}{K}_9\lesssim & |u_t{|}_0({\parallel u\parallel }_2\left(\right|〚{\partial }_{1}q〛{|}_0+|〚{\partial }_{2}q〛{|}_0)+{\parallel u\parallel }_3|〚q〛{|}_0)(1+{\parallel \eta \parallel }_3)\\ & +{\parallel u\parallel }_2{\parallel u_t(y_h,0)\parallel }_{L^4(\mathbb{T})}{\parallel {\partial }_1{\partial }_2\eta (y_h,0)\parallel }_{L^4(\mathbb{T})}|〚q〛{|}_0\\ & +{\parallel u\parallel }_2{\parallel u\parallel }_3|{\partial }_{2}u{|}_0|〚q〛{|}_0\\ \lesssim & \sqrt{\mathcal{E}}\mathcal{D}.\end{array}$$

(4.62)

Exploiting (4.55)–(4.62), we can derive from (4.54) that

$$\begin{array}{rl}& \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}({\parallel \sqrt{\rho }{u}_t\parallel }_0^2-\tilde{E}(u)-{\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y-{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h)\\ & +\frac{1}{2}{\parallel \sqrt{\mu }{\mathbb{D}}_{\mathcal{A}}(u_t)\parallel }_0^2\lesssim \sqrt{\mathcal{E}}\mathcal{D}.\end{array}$$

(4.63)

Finally, adding (4.63) to (4.51) and exploiting (3.26), we get (4.46). □

Next, we use the stratified steady Stokes regularity theory to estimate $(u,q)$. Problem (3.2) can be rewritten as the following standard form of the stratified steady Stokes problem:

$$\{\begin{array}{ll}-\mu \mathrm{\Delta }u-\kappa \rho \mathrm{\Delta }\eta +\mathrm{\nabla }q=\mathcal{G}& \text{in }\mathrm{\Omega },\\ divu=-{div}_{\tilde{\mathcal{A}}}u& \text{in }\mathrm{\Omega },\\ 〚u〛=0,〚(qI-\mu \mathbb{D}(u))e_3〛=\mathcal{K}& \text{on }\mathrm{\Sigma },\\ u=0& \text{on }{\mathrm{\Sigma }}_{-}^{+},\end{array}$$

(4.64)

where

$$\mathcal{K}:=g〚\rho 〛{\eta }_3{e}_3+〚\kappa \rho \mathbb{D}(\eta )e_3〛+\mathcal{M}.$$

Next, we obtain the following regularity result for problem (4.64).

Lemma 4.6

Let δ be sufficiently small, we have

$${\parallel u\parallel }_2^2+{\parallel \mathrm{\nabla }q\parallel }_0^2+|〚q〛{|}_{\frac{1}{2}}^2\lesssim {\parallel \eta \parallel }_3^2+{\parallel (u,u_t)\parallel }_0^2,$$

(4.65)

$${\parallel u\parallel }_3^2+{\parallel \mathrm{\nabla }q\parallel }_1^2+|〚q〛{|}_{\frac{3}{2}}^2\lesssim {\parallel \eta \parallel }_3^2+{\parallel (u,u_t)\parallel }_1^2.$$

(4.66)

Proof

Applying the classical regularity of stratified Stokes problem in [37, Theorem 3.1] to (4.64), we obtain that, for $k=2$ and $k=3$,

$$\begin{array}{rl}& {\parallel u\parallel }_k+{\parallel \mathrm{\nabla }q\parallel }_{k-2}+|〚q〛{|}_{k-\frac{3}{2}}\\ & \lesssim {\parallel \mathcal{G}\parallel }_{k-2}+{\parallel {div}_{\tilde{\mathcal{A}}}u\parallel }_{k-1}+|\mathcal{K}{|}_{k-\frac{3}{2}}\\ & \lesssim {\parallel \eta \parallel }_k+{\parallel (u,u_t)\parallel }_{k-2}+{\parallel \mathcal{N}\parallel }_{k-2}+{\parallel \mathcal{H}\parallel }_{k-1}+|\mathcal{M}{|}_{k-\frac{3}{2}}+{\parallel \eta \parallel }_3{\parallel u\parallel }_k,\end{array}$$

(4.67)

where we have exploited (3.23), (3.10), and (3.15) to estimate the second inequality in (4.67).

Since

$$ \Vert \mathcal {H} \Vert _{1}\lesssim \Vert \operatorname {div}\eta \Vert _{1}+ \Vert \operatorname {div}_{\tilde {\mathcal {A}}} \Vert _{1} \lesssim \Vert \eta \Vert _{3}^{2}+ \Vert \eta \Vert _{3} \Vert u \Vert _{2}, $$

(4.68)

then, making use of (4.68), (3.33), and (3.28), for sufficiently small δ, we derive from (4.67) with $k=2$ that

$${\parallel u\parallel }_2+{\parallel \mathrm{\nabla }q\parallel }_0+|〚q〛{|}_{\frac{1}{2}}\lesssim {\parallel (u,u_t)\parallel }_0+{\parallel \eta \parallel }_3(1+|〚q〛{|}_{\frac{1}{2}}+{\parallel \mathrm{\nabla }q\parallel }_0),$$

(4.69)

which immediately implies (4.65).

Similarly, exploiting the estimates (3.32) and (3.27), for sufficiently small δ, we also get from (4.67) with $k=3$ that

$${\parallel u\parallel }_3+{\parallel \mathrm{\nabla }q\parallel }_1+|〚q〛{|}_{\frac{3}{2}}\lesssim {\parallel (u,u_t)\parallel }_1+{\parallel \eta \parallel }_3(1+{\parallel u\parallel }_3+|〚q〛{|}_{\frac{3}{2}}+{\parallel \mathrm{\nabla }q\parallel }_1),$$

(4.70)

which implies (4.66). □

Next we establish an estimate for $u_{t}(0)$.

Lemma 4.7

Let δ be sufficiently small, we have

$$ \bigl\Vert u_{t}(0) \bigr\Vert \lesssim \Vert \eta_{0} \Vert _{3}+ \Vert u_{0} \Vert _{2}. $$

(4.71)

Proof

We denote $w:=\mathcal {A}^{T} u$ as in [2], then

$$divw=0,w{|}_{{\mathrm{\Sigma }}_{-}^{+}}=0,〚{\partial }_t{w}_3〛=0,$$

(4.72)

$$\begin{aligned}& \Vert w_{t} \Vert _{0}\lesssim \Vert u_{t} \Vert _{0}+ \Vert u \Vert _{2}^{2}. \end{aligned}$$

(4.73)

Now, multiplying (3.2)₁ by $w_{t}$ in $L^{2}$ and exploiting condition (4.72), we get

$$\begin{array}{rl}{\int }_{\mathrm{\Omega }}\rho |u_t{|}^2\mathrm{d}y=& {\int }_{\mathrm{\Sigma }}〚q〛{\partial }_t{w}_3\mathrm{d}{y}_h\\ & +{\int }_{\mathrm{\Omega }}(div\mathbb{D}(\mu u+\kappa \rho \eta )+2\rho a(u_1{e}_2-u_2{e}_1)+\mathcal{N})\cdot w_t\mathrm{d}y\\ & -{\int }_{\mathrm{\Omega }}\rho u_t\cdot (\left({\tilde{\mathcal{A}}}^T{u}_t\right)+{\mathcal{A}}_t^{T}u)\mathrm{d}y\\ =:& K_{10}+K_{11}+K_{12}.\end{array}$$

(4.74)

Exploiting (4.73), (3.33), (3.28), and (3.16), we have

$$\begin{array}{rl}{K}_{10}& \lesssim |〚q〛{|}_{\frac{1}{2}}|{\partial }_t{w}_3{|}_{-\frac{1}{2}}\lesssim |〚q〛{|}_{\frac{1}{2}}{\parallel w_t\parallel }_0\lesssim |〚q〛{|}_{\frac{1}{2}}({\parallel u_t\parallel }_0+{\parallel u\parallel }_2)\\ & \lesssim |(〚(\mathbb{D}(\mu u+\kappa \rho \eta )+g\rho {\eta }_3)e_3〛+\mathcal{M}){|}_{\frac{1}{2}}({\parallel u_t\parallel }_0+{\parallel u\parallel }_2)\\ & \lesssim ({\parallel (u,\eta )\parallel }_2+{\parallel \eta \parallel }_3({\parallel (u,\eta )\parallel }_2+|〚q〛{|}_{\frac{1}{2}}))({\parallel u_t\parallel }_0+{\parallel u\parallel }_2),\end{array}$$

(4.75)

$$\begin{aligned}& \begin{aligned}[b] K_{11}\lesssim{}&\bigl( \bigl\Vert (u,\eta) \bigr\Vert _{2}+ \Vert \mathcal {N} \Vert _{0}\bigr) \Vert w_{t} \Vert _{0} \lesssim \bigl( \bigl\Vert (u,\eta) \bigr\Vert _{2}+ \Vert \eta \Vert _{3} \Vert \nabla q \Vert _{0}\bigr) \Vert w_{t} \Vert _{0} \\ \lesssim{}&\bigl( \bigl\Vert (u,\eta) \bigr\Vert _{2}+ \Vert \eta \Vert _{3} \Vert \nabla q \Vert _{0}\bigr) \bigl( \Vert u_{t} \Vert _{0}+ \Vert u \Vert _{2}^{2}\bigr), \end{aligned} \end{aligned}$$

(4.76)

$$\begin{aligned}& K_{12}\lesssim \Vert \tilde {\mathcal {A}}\Vert _{2} \Vert u_{t} \Vert _{0}^{2}+ \Vert u \Vert _{2} \Vert \mathcal {A}_{t} \Vert _{0} \Vert u_{t} \Vert _{0} \lesssim \Vert \eta \Vert _{3} \Vert u_{t} \Vert _{0}^{2}+ \Vert u \Vert _{2}^{2} \Vert u_{t} \Vert _{0}. \end{aligned}$$

(4.77)

Therefore, making use of (4.75), (4.77), (4.65), the smallness condition (3.1), and Young’s inequality, we deduce that

$$ \Vert u_{t} \Vert _{0}^{2} \lesssim \Vert u \Vert _{2}^{2}+ \Vert \eta \Vert _{3}^{2}, $$

(4.78)

which yields (4.71). Furthermore, by (4.65) and (3.1), we deduce that

$$ \mathcal {E}\leq c_{e}^{2}\bigl( \Vert u \Vert _{2}^{2}+ \Vert \eta \Vert _{3}^{2} \bigr)\leq c_{e}^{2}\delta^{2}, $$

(4.79)

where $c_{e}$ depends on the domain and other known physical parameters. □

5 Exponential stability

We are in the position to deduce (2.7). By Lemmas 4.1–4.5, (3.26), (4.27), and Young’s inequality, there exist positive constants $c_{1}$–$c_{4}$ such that

$$\begin{aligned}& c_{1} \bigl\Vert \partial_{h}^{i} \eta \bigr\Vert _{1}^{2}\leq-\tilde{E}\bigl(\partial _{h}^{i}\eta\bigr)+ \Vert \eta \Vert _{3}^{3}, \end{aligned}$$

(5.1)

$$\begin{aligned}& \frac{\mathrm {d}}{\mathrm {d}t} \biggl( \int_{\Omega}\rho\partial_{h}^{i}\eta\cdot \partial_{h}^{i} u \,\mathrm {d}y+\frac{1}{4} \bigl\Vert \sqrt{\mu} \mathbb {D}\bigl(\partial _{h}^{i} \eta\bigr) \bigr\Vert _{0}^{2} \biggr)-\frac{1}{2}\tilde{E}\bigl( \partial_{h}^{i}\eta\bigr) \leq c_{2}\bigl( \bigl\Vert \partial_{h}^{i}u \bigr\Vert _{1}^{2} +\sqrt{\mathcal {E}}\mathcal {D}\bigr), \end{aligned}$$

(5.2)

$$\begin{aligned}& \frac{\mathrm {d}}{\mathrm {d}t} \biggl\Vert \sqrt{\frac{\kappa\rho}{\mu}}\eta \biggr\Vert _{3}^{2} + \bigl\Vert (\eta,u) \bigr\Vert _{3}^{2}+ \Vert \nabla q \Vert _{1}^{2} \leq c_{2} \Biggl(\sum_{i=0}^{2} \bigl\Vert \bigl(\partial_{h}^{i}\eta,\partial _{h}^{i}u\bigr) \bigr\Vert _{1}^{2}+ \Vert u_{t} \Vert _{1}^{2}+\sqrt {\mathcal {E}}\mathcal {D}\Biggr), \end{aligned}$$

(5.3)

$$\begin{aligned}& \frac{\mathrm {d}}{\mathrm {d}t} \biggl( \int_{\Omega}\rho \bigl\vert \partial_{h}^{i}u \bigr\vert ^{2}\,\mathrm {d}y-\tilde{E}\bigl(\partial_{h}^{i} \eta\bigr) \biggr) +c_{3} \bigl\Vert \partial_{h}^{i}u \bigr\Vert _{1}^{2}\leq c_{2}\sqrt {\mathcal {E}}\mathcal {D}, \end{aligned}$$

(5.4)

$$\begin{array}{rl}& \frac{\mathrm{d}}{\mathrm{d}t}({\parallel \sqrt{\rho }(u(t),u_t)\parallel }_0^2-\tilde{E}(u)-\tilde{E}(\eta )-{\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y-{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h)\\ & +c_4{\parallel (u,u_t)\parallel }_1^2\le c_2\sqrt{\mathcal{E}}\mathcal{D}.\end{array}$$

(5.5)

Thus, we can derive from the above four inequalities (5.2)–(5.5) that

$$ \frac{\mathrm{d}}{\mathrm{d}t}\tilde{\mathcal {E}}(t)+\tilde{\mathcal {D}}(t)\leq c_{2}(1+c_{5}+c_{6}+c_{7})\sqrt {\mathcal {E}}\mathcal {D}, $$

(5.6)

where we have defined that

$$\begin{array}{rl}\tilde{\mathcal{E}}(t):=& c_5\sum _{i=0}^2({\int }_{\mathrm{\Omega }}\rho {\partial }_h^i\eta \cdot {\partial }_h^{i}u\mathrm{d}y+\frac{1}{4}{\parallel \sqrt{\mu }\mathbb{D}\left({\partial }_h^i\eta \right)\parallel }_0^2)\\ & +{\parallel \sqrt{\frac{\kappa \rho }{\mu }}\eta \parallel }_3^2+c_6\sum _{i=1}^2\left({\int }_{\mathrm{\Omega }}\rho \right|{\partial }_h^{i}u{|}^2\mathrm{d}y-\tilde{E}\left({\partial }_h^i\eta \right))\\ & +c_7({\parallel \sqrt{\rho }(u(t),u_t)\parallel }_0^2-\tilde{E}(u)-\tilde{E}(\eta )\\ & -{\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y-{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h)\end{array}$$

(5.7)

and

$$ \begin{aligned} [b]\tilde{\mathcal {D}}(t):={}&{-}\frac{c_{5}}{2} \tilde{E}\bigl(\partial_{h}^{i}\eta\bigr)-c_{2}\sum _{i=1}^{2} \bigl\Vert \partial_{h}^{i} \eta \bigr\Vert _{1}^{2} + (c_{6}c_{3}-c_{2}-c_{5}c_{2} )\sum_{i=0}^{2} \bigl\Vert \partial _{h}^{i}u \bigr\Vert _{1}^{2} \\ &+ \bigl\Vert (\eta,u) \bigr\Vert _{3}^{2}+ \Vert \nabla q \Vert _{1}^{2}+(c_{4}c_{7}-c_{2}) \bigl\Vert (u,u_{t}) \bigr\Vert _{1}^{2}. \end{aligned} $$

(5.8)

By (4.66) and (4.27), there exist constants $\tilde{c}_{5}$–$\tilde{c}_{7}$ and $c_{8}$ such that

$$ c_{8}\mathcal{D}(t)\leq\tilde{\mathcal{D}}(t) $$

for any $c_{5}>\tilde{c}_{5}$, $c_{6}>\tilde{c}_{6}$, and $c_{7}>\tilde{c}_{7}$. Thus, by (4.79), for any $\delta\leq c_{8}/2c_{e}c_{2}(1+c_{5}+c_{6}+c_{7})$, we have

$$ \frac{\mathrm{d}}{\mathrm{d}t}\tilde{\mathcal {E}}(t)+\frac{c_{8}}{2}\mathcal {D}(t) \leq0. $$

(5.9)

Noting that

$$|{\int }_{\mathrm{\Omega }}{\partial }_{l}q{\partial }_t{\mathcal{A}}_{kl}{u}_k\mathrm{d}y+{\int }_{\mathrm{\Sigma }}〚q〛{\mathcal{A}}_t{e}_3\cdot u\mathrm{d}{y}_h|\lesssim {\parallel u\parallel }_2^2({\parallel \mathrm{\nabla }q\parallel }_0+|〚q〛{|}_0),$$

we utilize (4.65), (4.29), (4.27), (3.8), and the Cauchy–Schwarz inequality to see that there exist sufficiently large $c_{6}$ and sufficiently small $c_{7}$ such that

$$ \mathcal {E}(t)\lesssim\tilde{\mathcal {E}}(t) $$

(5.10)

for any sufficiently small δ. Obviously, $\tilde{\mathcal {E}}\lesssim \mathcal {D}$. Thus, by (5.9), we can deduce that

$$ \frac{\mathrm{d}}{\mathrm{d}t}\tilde {\mathcal {E}}+c\tilde {\mathcal {E}}(t)\leq0, $$

from which, together with (5.10), we have

$$ \mathcal {E}(t)\lesssim \tilde {\mathcal {E}}(0)e^{-ct}, $$

(5.11)

where we have defined that

$$ \tilde{\mathcal{E}}(0):= \Vert \eta_{0} \Vert _{3}^{2}+ \Vert u_{0} \Vert _{2}^{2}+ \bigl\Vert u_{t}(0) \bigr\Vert _{0}^{2}. $$

On the other hand, by (4.71) we obtain

$$ \tilde {\mathcal {E}}(0)\lesssim \Vert u_{0} \Vert _{2}^{2}+ \Vert \eta_{0} \Vert _{3}^{2}, $$

which, together with (5.11), yields

$$ \mathcal {E}(t)\lesssim\bigl( \Vert u_{0} \Vert _{2}^{2}+ \Vert \eta_{0} \Vert _{3}^{2}\bigr)e^{-ct}. $$

(5.12)

Consequently, we get Theorem 2.1 from the above a priori stability estimate (5.12) and the following local well-posedness of the transformed SRVRT problem.

Proposition 5.1

Let $(u_{0},\eta_{0})$ satisfy assumptions (1)–(4) in Theorem 2.1 and δ be sufficiently small, then the transformed SRVRT problem (1.9) possesses a unique global strong solution $(u,\eta)\in C^{0}([0,T),H^{2}\times H^{3})$ with an associated perturbation pressure q for some $T>0$. Moreover, $(u,\eta,q)$ enjoys the following estimate:

$$ \sup_{0\leq t\leq T} \mathcal{E}(t)+ \int_{0}^{T}\mathcal{D}(\tau )\,\mathrm{d}\tau< \infty. $$

(5.13)

Proof

Xu et al. [39] have established the local and global well-posedness results of the one-layer viscoelastic fluid model with upper free boundary. Exploiting the regularity theory for the stratified viscous flows in [38], we can easily extend the well-posedness results in [39] to the transformed SRVRT problem by a standard iteration method, and thus obtain Proposition 5.1. □

6 Conclusion

We investigate the stability of RT problem of the stratified incompressible viscoelastic fluids under the rotation and the gravity in a horizontal periodic domain, in which the rotation axis is parallel to the direction of gravity, the two fluids are immiscible, and the heavier fluid lies on the lighter one. We establish a stability condition for the RT problem. Moreover, we prove that, under the stability condition, the RT problem enjoys a unique solution which exponentially decays with respect to time. In addition, we note that the stability condition is independent of rotation angular velocity and the rotation has no destabilizing effect. However, we can observe that the rotation has no stabilizing effect from the experiment of Baldwin et al. Hence we will try to prove mathematically the stabilizing effect of the rotation in the future.