Evaluation of Egyptian code provisions for seismic design of moment-resisting-frame multi-story buildings

Abstract

Since the occurrence of the Cairo earthquake on October 1992, the design of structures for earthquakes became a major demand enforced in the Egyptian design codes. The seismic response of building structures can be estimated through utilization of a variety of analysis methods that range from simple equivalent static analysis to complex nonlinear dynamic analysis. The traditional approach is to employ equivalent static analysis methods, while current design practice is moving toward an increased emphasis on the nonlinear analysis method. The Egyptian code provisions for building seismic design adopt the traditional approach of equivalent static load method as the main method for evaluating seismic actions and recommend the response spectrum method for nonsymmetrical buildings. This study aims to evaluate the Egyptian code provisions for the seismic design of moment-resistant frame multi-story building through using nonlinear time history analysis. The analysis procedures are evaluated for their ability to predict deformation demands in terms of inter-story drifts, potential failure mechanisms and story shear force demands. The results of the analysis of the different approaches are used to evaluate the advantages, limitations, and ease of application of each approach for seismic analysis.

Introduction

Occurrences of recent earthquakes in different parts of the world and the resulting losses, especially human lives, have highlighted the structural inadequacy of buildings to carry seismic loads. The great losses due to the Cairo earthquake on October 1992 (Ms 5.4) were mainly related to the fact that at the time of construction, the buildings were designed to resist only vertical loads and had insufficient lateral resistance. Thus, the columns and beam column connections were found to have inadequate shear capacity, ductility, and confinement in plastic hinges. This earthquake illustrated the vulnerability of the building stock, especially older structures, due to design, detailing, construction, and maintenance issues (Khater 1992; Badawi and Mourad 1994; Mourad et al. 2000). So there is an urgent need for assessment of existing buildings in terms of seismic performance and to continuously upgrade the seismic codes for the design of new buildings. The design of structures for earthquakes became a major demand enforced in the Egyptian design codes that motivated the Ministry of Housing and Buildings to update the Egyptian codes regularly, taking into account the seismic loads. Since October 1992, a set of Egyptian codes have been released to prevent building collapse and/or control major damages of structural elements. Many advances in earthquake engineering have been made from the observation of the performance of real structures that have been subject to a severe earthquake. Analytical modeling, including finite element analysis, has an important role, but its limitations must be recognized. For many engineered structures, satisfactory seismic performance requires careful attention to analysis, design, and detailing and good construction practice. Safety is thus achieved by the successful integration of analysis, design, and construction.

Building code restrictive seismic design provisions and building system type and configuration have remarkable implications on the seismic performance of reinforced concrete moment-framed structures. The specifications permit the designer to utilize a variety of methods for seismic analysis that range from simple equivalent static analysis to complex nonlinear dynamic analysis (UBC 1997; AIJ 1999; SEAOC 1999; ICC 2003; ECS 2004; ASCE 2005; ECP 2007, 2008). For building structures, it is common practice to utilize a simplified approach, such as equivalent static load. This approach has several shortcomings, which have been accepted due to its simplicity and a lack of alternative practical approaches. Such approach may be regarded as force based since the method’s primary emphasis is on the forces within the structure. In recent years, there has been a shift of attention away from linear methods of seismic analyses to nonlinear methods which put emphasis on the displacements within the structure. Thus, nonlinear analysis methods that are capable of realistically predicting the deformations imposed by earthquakes on structures are needed. In response to this need, nonlinear static analysis procedures have appeared in national resource documents such as the ATC-40 report on seismic evaluation and retrofit of concrete buildings (ATC 1996) and the FEMA-356 pre-standard on seismic rehabilitation of buildings (FEMA 2000). Such analysis methods are useful for predicting inelastic displacement capacities while simultaneously offering a compromise between the oversimplification of linear static analysis and the inherent complexity of nonlinear dynamic analysis. The latest Egyptian code for load and forces (ECP 2008) and most of the international participating building codes depend on the traditional approach of equivalent static load method as the main method for evaluating seismic actions on symmetrical buildings (UBC 1997; AIJ 1999; ECS 2004; ECP 2008). For nonsymmetrical buildings, ECP (2008) recommended the response spectrum method to be used for building seismic analysis and design, which was considered to be a more accurate method of analysis than the equivalent static load method (Chopra 1995; Paz and Leigh 2003).

The structural response is a function of building mass, stiffness, and material damping (Ghosh and Fanella 2003; Abdel Raheem et al. 2010); however, ECP(2008) gives an empirical expression to calculate the equivalent static load of seismic action depending on the total building weight only, neglecting the effect of building stiffness and material damping on the structural response. This study aims to evaluate the way Egyptian code seismic provisions treat the consideration of seismic loads and analysis methods during the seismic design of buildings, to discuss the alternative solutions for cases wherein existing provisions do not lead to satisfactory results, and to quantify the effect of building lateral stiffness and diaphragm flexibility on the structural response so that designers can be aware of the likely impact of their decisions. The evaluation of Egyptian code seismic provisions and simplified methods is performed through comparison with a more refined approach whereas an effort is made to quantitatively assess the relative importance of various design and analysis assumptions. Nonlinear time history (TH) analysis has been performed to evaluate equivalent static load (ESL) and response spectrum (RS) analysis methods; a set of time history records have been used. A parametric study is carried out to evaluate the design parameter effects on the building seismic demands in different approaches of analysis and to assess the fundamental period, total base shear, displacements, and story drifts for the three methods of analysis; the design parameters include the building lateral stiffness and floor diaphragm in-plane stiffness. The results show that the building lateral stiffness and floor diaphragm in-plane stiffness have a significant influence on the shear and displacement demands calculated from response spectrum and nonlinear time history methods. The ESL method is overestimated and not accurate for calculating seismic action.

Methods

Egyptian code seismic provisions

Until the beginning of the last decade, consideration of seismic loading was absent from national codes in Egypt. Buildings were typically designed to resist gravity loads, and the only means of lateral load resistance was provided through the consideration of wind loads in some cases. The first official code of practice to consider seismic loading was published by the Ministry of Housing, Utilities and New Communities in 1989-the Reinforced Concrete Code (ECP 1989). However, the code overlooked a number of basic seismic considerations, including the influence of soil conditions and the dynamic characteristics of buildings. More importantly, for the Greater Cairo area, a crude approach was adopted whereby an arbitrary percentage of building weight was proposed as lateral seismic loading. The loading code issued on December 1993 (ECP 1993), following the 1992 earthquake, provided an approach for determining seismic loads for different types of structures. Although this code represented an improvement in comparison with previous regulations (ECP 1989), it still adopted significantly simplified assumptions in terms of loading considerations and design procedures. More recently, in 2004 a new loading code (ECP 2004a) was issued and dealt with most of the shortcomings present in preceding standards, particularly on the loading side. The new code largely follows the same framework adopted in EC8 (ECS 2004; UBC 1997). It introduces the concept of response spectra and codified force reduction factors for the design of structures and includes safety verifications relevant to ultimate and serviceability limit states. The Egyptian code gradually introduced ductility concepts and detailing procedures through its versions (ECP 2001, 2004b, 2007), although these aspects of the code still need considerable improvement and development.

Table 1 illustrates the base shear formulas with the related parameters to present the major changes to the seismic provisions in different Egyptian code of practice (ECP) editions released from 1993 to 2008 and the Regulations for Earthquake Resistant Design of Buildings in Egypt issued by the Egyptian Society for Earthquake Engineering (ESEE) (Sobaih et al. 1988). It has been found that there is high variation between the base shear and base moment obtained using the ECP versions specified in the different analysis methods and in comparison with the ESEE. The major difference between ECP (1993) and ECS (2004) was remarked by the new adoption of the response spectrum method that presented pseudo-acceleration anchored to peak ground acceleration (PGA). Also, the soil parameter has a big effect on the response spectrum curve. On the other hand, the two newest provisions ECP (2004a,b) and ECP (2008) have a similar base shear formulation except for the existence of the importance factor γ_I either in the response spectrum or in the base shear equation which yields final identical base shear. It is clear from the initial comparison how the base shear value obtained from ECP (2004a, 2008) is greater than the value obtained from ECP(1993).

Table 1 Egyptian code provisions for seismic design development from 1992 up to 2008 (El-Arab 2011 )

The ESEE presented the response spectrum method in addition to the equivalent static load with many factors not taken into consideration in ECP (2004a, 2008) like M(material), R(risk), and Q(construction quality factors). All of these factors are still neglected in all ECP editions till 2008. Most recent seismic codes, including the 2008 draft of the Egyptian code for design loads on structures (ECP 2008), are developed with two performance levels: one with the intent of limiting damage during frequent moderate earthquakes, namely the serviceability limit state, and the other ensuring collapse prevention during a major earthquake, namely the ultimate limit state. Earthquake engineering research has proven that deformability is a governing factor in satisfying seismic codes’ life safety requirement as well as damage limitation (FEMA 2007).

The period of vibration is a fundamental parameter in the force-based design of structures as this parameter defines the spectral acceleration and thus the base shear force to which the building should be designed. This paper takes a critical look at the way in which seismic design codes around the world have allowed the designer to estimate the period of vibration for use in both linear static and dynamic analysis (Crowley and Pinho 2010). The fundamental period of a building is a key parameter for the seismic design of a building structure using the equivalent lateral force procedure. As the building period cannot be analytically calculated before the building is designed, periods from the empirical period formulas recommended in seismic design codes or from finite element analysis with assumed mass and stiffness are used during the preliminary design stage. The form of the formulas for the RC and steel MRFs in ATC3-06 (ATC 1978; Goel and Chopra 1997) [6] was developed based on the assumption that lateral forces are distributed linearly over the height of a building and that the deflections of the building are controlled by drift limitation.

Seismic analysis procedures

In the preliminary design process, equivalent static seismic forces are used to determine the design internal forces of structural members using linear elastic analyses of structure and, in turn, determine the design member strength demands. Such static seismic forces are simply determined corresponding to the elastic design acceleration spectrum divided by a structural strength reduction factor particularly called the response modification factor R (UBC 1997), the structural behavior factor q (ECS 2004), or the structural factor D_s (AIJ 1999). Usually, the elastic design spectrum, which is often related to 5% or 10% probability of exceedance in 50 years, is defined smoothly as a reasonable representation of the seismic action demand on the structure at the site of interest. The adopted strength reduction factor is thus intended to represent an expected inelastic response demand or expected damage level demand of the whole structure, which may be induced during earthquake excitation (Thuat 2012).

ESL method

According to ECP (2008), the seismic base shear force, F_b, for each horizontal direction in which the building is analyzed, shall be determined using the following expression:

$$F_{\mathrm{b}}=\gamma \times S_{\mathrm{d}}\left(T_1\right)\times \lambda \times W/g,$$

(1)

where S_d (T₁) is the ordinate of the design spectrum at period T₁; T₁ is the fundamental period of vibration of the building for lateral motion in the direction considered; W is the total weight of the building, above the foundation level; g is the gravity acceleration; γ is the importance factor of the building; and λ is the effective modal mass correction factor, the value of which is equal to λ = 0.85 for T ≤ 2 T_c and n> 2 stories, where T_c is the upper limit of the period of the constant spectral acceleration branch as shown in Figure 1 and n is the number of stories.

Figure 1

ECP ( 2008 ) design response spectrum for different subsoil classes.

The value of the fundamental period of vibration, T, is determined using the following expression:

$$T=C_{\mathrm{t}}\times H^{3/4},$$

(2)

where C_t is a factor determined according to the structural system and building material and is equal to 0.075 in the case of a moment-resistant space concrete frame, and H is the height of the building (m), from the foundation or from the top of a rigid basement. The ordinate of the design spectrum, S_d (T₁), can be determined from

$$S_{\mathrm{d}}\left(T\right)=\frac{2.5}{R}\times a_{\mathrm{g}}\times \gamma \times S\times \eta \left[\frac{T_{\mathrm{c}}}{T}\right]\ge \left[0.2\right]\times a_{\mathrm{g}}\times \gamma ,$$

(3)

where a _g is the design ground acceleration for the reference return period, T_c is the upper limit of the period of the constant spectral acceleration branch as shown in Figure 1,η is the design damping correction factor for the horizontal elastic response spectrum where a reference value of η= 1 corresponds to a normal 5% viscous damping ratio (in the case of RC buildings),S is the soil factor, γ is the importance factor and R is the reduction factor according the statical system of the structure. The total base shear, F_b, shall be determined by applying horizontal forces F _i to each story mass m _i and shall be distributed as follows:

$$F_i=\left[\frac{z_i\times W_i}{{\displaystyle {\sum }_{j=1}^n{z}_j\times W_j}}\right]\times F_{\mathrm{b}},$$

(4)

where F _i is the horizontal force acting on story i; F_b is the seismic base shear force (Equation 1); z _i and z _j are the heights of masses m _i and m _j above the foundation level, respectively; W _i and W _j are the weights of masses m _i and m _j , respectively; and n is the number of stories above the foundation level. Equation 4 gives a linear shear distribution depending only on the height of the story.

Modal RS method

The modal response spectrum analysis is applicable for all types of buildings, while the lateral force method of analysis has many restrictions on its use due to the ‘fear’ that it would provide un-conservative results in certain conditions; however, in spite of this disadvantage, the method is still widely used due to its ease of application (Crowley and Pinho 2010). Response spectrum analysis includes sufficient modes of vibration to capture participation of at least 90% of the structure’s mass in each of two orthogonal directions (Kunnath and Kalkan 2004). Figure 1 shows the design response spectrum curve for the current case of study; it shall be noted that ECP(2008) includes a damping coefficient in the elastic response spectra equations. Hence, no damping ratio has been used in the analysis of this method. As specified in most design codes, the shape of the target elastic acceleration spectrum is characterized by the seismic intensity expressed in terms of the expected design PGA, a_g, and the effect of soil ground types expressed in terms of the response spectral periods T_b and T_c. Various values of T_b and T_c were considered corresponding to different soil ground types (from A-type of hard rock to D-type of soft soil).

Many codes recognize that the period of vibration from the simplified period-height equation is more realistic, having been directly obtained from the measured periods of vibration of buildings subject to earthquake ground motions, but that when higher modes are important (in tall and/or irregular structures), the modal response spectrum method gives a more realistic profile of the lateral forces. Hence, these codes (NBCC 2005;ASCE 2005) require the designer to check whether the modal base shear force is less than 85% of the base shear force from the equivalent lateral force method. If this is the case, then the modal forces, but not the drifts, should be multiplied by 0.85 V/V_t, where V is the base shear from the lateral force method and V_t is the base shear from the required modal combination. Even when higher modes are not important and the designers are allowed to use the linear static method, but they decide to calculate the period of vibration from the Rayleigh method, many codes apply an upper bound to the period of vibration from the Rayleigh method. This is another procedure which is used to safeguard against unrealistically high periods of vibration used in the design to lower the base shear forces (Crowley and Pinho 2010).

Nonlinear TH method

Nonlinear time history analysis is by far the most comprehensive method for seismic analysis. The earthquake record in the form of acceleration time history is input at the base of the structure. The response of the structure is computed at each second for the entire duration of an earthquake. This method differs from response spectrum analysis because the effect of ‘time’ is considered. That is, stresses and deformations in the structure at an instant are considered as an initial boundary condition for computation of stresses in the next step. Furthermore, nonlinearities that commonly occur during an earthquake can be included in the time history analysis. Such nonlinearities cannot be easily incorporated in response spectrum analysis. Unlike the response spectrum method, nonlinear time history analysis does not assume a specific method for mode combination. Hence, results are realistic and not conservative. Furthermore, this method is equivalent to getting 100% mass participation using response spectrum analysis. Full mass participation is necessary to generate correct earthquake forces. Usually, only 90% to 95% participation is obtained in response spectrum analysis. All types of nonlinearities can be accounted for in this analysis. This could be very important when seismic retrofit involves energy dissipation by yielding of members or plastic hinge rotation. However, this method is very expensive and time-consuming to perform. Large amounts of information are generated. Furthermore, input earthquake is never known with certainty. Hence, three to five different histories should be used, further increasing the cost.

Since the results of the time history depend mainly on the characteristic of the used acceleration time history records and the shapes of their corresponding elastic response spectra (Kunnath and Kalkan 2004), the reason of using the inelastic TH method is to verify the results obtained by other code-specific analysis procedures (ESL and RS methods) against a time history record. Nonlinear time history analysis was performed taking into consideration the P-Δ and large displacements effect. A constant damping ratio of 0.05 has been taken for RC buildings. The inelastic time history analysis is performed using the direct integration technique considering a time step of 0.005 s. Nonlinear analysis could be used to justify a design that would not satisfy the prescriptive building code requirements. Story drifts and floor accelerations are important indicators of damage to nonstructural components and overall building performance. For nonlinear seismic analyses, a total seismic mass including self-weight and floor cover ‘dead load’ (DL) plus 50% of ‘live load’ (LL) (1.0DL + 0.5LL) is considered (ASCE 2005).

Description of building structure

During the past two decades, the building environment in Egypt had extensively utilized medium-rise RC buildings having 12 stories, which is the maximum height allowed by the local authorities in most districts. These buildings are built with different configurations and structural systems having varying stiffness parameters that may have great influence on their seismic behavior. Two samples of typical buildings with 6 and 12 stories are chosen for this study as shown in Figure 2; the building’s layout is essentially bisymmetric in plan, has regular plans of four equal bays with a typical bay width of 5 m in both directions, and is representative of benchmark typical buildings in current practice in Egypt. The height of every story (column height) is taken equal to 3 m, as a normal height for residential buildings. Beams are assumed on all grid lines, and the base columns are assumed to be fixed to the foundation.

Figure 2

Configuration of a sample building model. (a) Plan configuration. (b) Elevation configuration for 6-story and 12-story buildings.

The building structural elements have been first designed according to the Egyptian code of practice (ECP 2007,2008) under static loads assuming un-cracked sections for beam and slabs in the analysis. Square columns were used with different cross sections to represent the change in lateral stiffness. Also, different slab thicknesses were used to represent the change of diaphragm flexibility. These sections have been checked under seismic actions using the Egyptian code for load and forces (ECP 2008) to satisfy the Egyptian code requirements taking into consideration the effect of earthquake loads. The minimum safe column cross section under static and dynamic loads, to satisfy the Egyptian code requirements (ECP 2007, 2008), is 0.4 × 0.4 m for the 6-story building and 0.6 × 0.6 m for the 12-story building.

The materials used in the design are C300 for concrete and St52 for steel, and the material for the building structure is taken as a reinforced concrete with the following constant properties: modulus of elasticity E = 25 GPa, Poisson ratio μ = 0.2, density of 24 kN/m³, f_c = 28 MPa, f_y = 355 MPa, and minimum steel reinforcement ratio ρ = 0.0035.

For gravity load design, dead loads include the self-weight of the structure, a typical floor cover of 1.5 kN/m², and partition (wall) load intensity of 1.5 kN/m³ including plastering and assuming typical wall thickness of 0.25 m. A live load of 2.5kN/m² is considered. On the other hand, for seismic design purposes, a total seismic mass including self-weight and floor cover plus 50% of live load is considered. The seismic design has been carried out assuming a soil type ‘C’ as per referring to dense/stiff soil, an importance factor of 1.0, and a seismic zone 5B, and the shape of the spectrum is type 1 as per Egyptian zoning system with a design ground acceleration, a_g, of 0.30 g associated with the code reference probability of exceedance of 10% in 50 years.

Finite element model

A three-dimensional mathematical model of the physical structure will be used that represents the spatial distribution of the mass and stiffness of the structure to an extent that is adequate for the calculation of the significant features of the building’s dynamic response. All structures are modeled and analyzed in this paper using ETABS and Sap2000 (Computers and Structures, Inc 2003, 2007, 2011[a, b]). The building is modeled as a three-dimensional (3D) frame structure using frame elements for columns, longitudinal beams, and transverse beams and shell element for slabs. The structures are assumed to have a rigid foundation; therefore, the soil foundation interaction and foundation flexibility effects are ignored.

The seismic zone considered in this study is zone 5B, and the shape of the spectrum is type 1, as shown in Figure 2. The two models are considered as residential buildings with an importance factor γ = 1. The soil is considered to be stiff soil, which presents soil class C and a soil factor S = 1.5. The reduction factor, R, is taken considering that the vertical loads and the total base shear are totally resisted by the frame structure without using shear walls or bracings (R = 6). It should be noted that ECP(2008) recommends that in the application of the ESL method, the building should meet the criteria for regularity in both plan and elevation, and with calculated structural period T not greater than 2 s or 4T_c (1 s for the selected soil class C). In the ESL method, according to ECP (2008), the base shear is determined as a percentage of the total building weight that gives a value of 7.2% of the total weight of the building in the 6-story building and 4.3% in the 12-story building.

Input seismic excitation

It is impossible to predict ground motion characteristics that may occur in the future at a construction site because the property of the ground motion is interrelated with many factors such as fault mechanism, seismic wave propagation from source to site, and the amplification characteristics of the ground. The important factors of ground motions affecting the structure’s response results are peak ground acceleration, frequency contents, duration of ground motion, and shapes of the waveform. Egypt is a region of moderate seismicity, where infrequent moderate to large earthquakes have occurred in the past. However, there is a serious lack of strong motion records of engineering interest in the region. Therefore, the use of a large number of artificial or natural earthquake records from the literature is indispensible for the nonlinear time history analysis. The seismic design guidelines provide an acceleration response spectrum for estimating the design seismic force of a structure. Accordingly, the input ground motion applied to the dynamic response analysis of structures would be appropriate for the ground motion history which is highly related with design seismic force. A suite of nine ground motion records from seven different earthquakes (PEER 2012) are selected for the purpose of understanding the input ground motion effect, as listed in Table 2.

Table 2 Characteristics of earthquake ground motion records used in the analysis

A suite of nine ground motion acceleration time history records, representing a wide range of intensity and frequency contents, are selected and used in the study. Those records are downloaded from the website of the Pacific Earthquake Engineering Research Center (PEER 2012). The earthquake records are listed in Table 2 by their magnitude, PGA, peak ground velocity (PGV), and peak ground displacement (PGD). Figure 3 shows the elastic pseudo-acceleration response spectra of the earthquake motions for 5% damping; the figure shows significant variation in the frequency contents and the response characteristics. The ground motion records are grouped into three levels depending on the peak ground acceleration as low (0.1 up to 0.3 g), moderate (0.4 up to 0.6 g), and high (0.7 up to 0.9 g). The records are chosen such that the period ratio (T₁/T_g and T₂/T_g; adjacent building period over the ground motion characteristic period) has a wide range.

Figure 3

Associated 5%damped response spectrum for the nine records.

Results and discussion

This study aims to evaluate the way Egyptian code seismic provisions treat the consideration of seismic loads and analysis methods during the seismic design of buildings, to discuss the alternative solutions for cases wherein existing provisions do not lead to satisfactory results, and to quantify the effect of building lateral stiffness and diaphragm flexibility on the structural response so that designers can be aware of the likely impact of their decisions. The evaluation of Egyptian code seismic provisions and simplified methods is performed through comparison with a more refined approach whereas an effort is made to quantitatively assess the relative importance of various design and analysis assumptions. TH analysis has been performed to evaluate ESL and RS analysis methods; a set of time history records have been used. A parametric study is carried out to evaluate the design parameter effects on the building seismic demands in different approaches of analysis and to assess the fundamental period, total base shear, displacements, and story drifts for the three methods of analysis; the design parameters include the building lateral stiffness and floor diaphragm in-plane stiffness. This paper compares seismic provisions in the Egyptian code for loads (ECP 2008) to highlight the differences in dealing with the seismic design of moment-resisting-frame buildings.

Effect of building model lateral stiffness

The 6-story and 12-story building models have been studied to evaluate the effect of the lateral stiffness on determination and evaluation of fundamental period, base shear, displacement, and story drift. A constant beam and slab sections with rigid diaphragm assumption are considered in the analysis with different column cross sections to present the change in lateral stiffness as shown in Table 3.

Table 3 Building structural element dimensions for different lateral stiffness models

Natural vibration analysis

The period of vibration is a fundamental parameter in the force-based design of structures as this parameter defines the spectral acceleration and thus the base shear force to which the building should be designed. This study takes a critical look at the way in which seismic design codes around the world have allowed the designer to estimate the period of vibration for use in both linear static and dynamic analyses. In most building design projects, empirical building period formulas are used to initiate the design process (Kwon and Kim 2010).

The fundamental period of vibration, T, is a function of the stiffness of the lateral load-resisting system and the building mass. The fundamental period in ECP (2008), T, is not influenced by the change of the column cross section but depends only on the building height. Table 4 presents different fundamental periods for the buildings studied, as obtained from structural analysis using finite element models and empirical expression in ECP (2008) and other international building codes. In both 6-story and 12-story buildings, the periods computed from empirical expressions are significantly shorter than those computed from structural models especially for flexible building structures. As the building’s lateral stiffness increases, the fundamental period decreases. Table 4 shows the disparity between the fundamental period of vibration from the empirical period-height equation from different codes and the period of vibration from the eigenvalue or Rayleigh analysis of a bare frame model. The fundamental period estimated by the ECP-201 empirical equation is underestimated especially for flexible models; the fundamental period reaches 179% and 159% in models LS1 and LS5, respectively. Many codes recognize that the period of vibration from the simplified period-height equation is more realistic, having been directly obtained from the measured periods of vibration of buildings subject to earthquake ground motions, but that when higher modes are important (in tall and/or irregular structures), the modal response spectrum method gives a more realistic profile of the lateral forces. However, the empirical equation should be calibrated to obtain a conservative estimate for the base shear.

Table 4 Fundamental period of the RC moment-resisting-frame building

Base shear demands for different lateral stiffness models

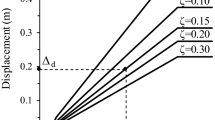
The ESL, dynamic modal RS, and TH analyses are employed, and a comparison of base shear and maximum displacement at the building top is provided as shown in Figures 4 and 5. The response is quantified by the formulation of maximum displacements and shear forces for which each response quantity result is calculated by ETABS to represent a measure of the probable maximum magnitude for that quantity. The resulting maximum and minimum responses provide a range for which the actual structural response of the building is expected to fall within. The results of the analyses show that the time history analysis (Av, average; MinEnv, minimum envelope; MaxEnv, maximum envelope of response demands) is the most appropriate method in capturing the behavior of this particular building under dynamic loading. The ESL method depends on the building weight and the fundamental period calculated from the empirical equation, and the ESL overestimates the base shear and displacement response demands. The seismic demands using ESL has more reliability for the 6-story building than that for the 12-story building (fundamental mode with longer period). The RS underestimates the seismic response demands and should be calibrated for the bare frame eigenvalue to calculate the fundamental vibration period.

Figure 4

Story base shear calculated for different lateral stiffness models. (a) 6-story building. (b) 12-story building.

Figure 5

Displacement calculated for different lateral stiffness models. (a) 6-story building. (b) 12-story building.

Story shear and lateral drift demands

To show the effect of the column rigidity on the shear distribution, the displacements and the story drifts in the case of 6-story and 12-story buildings have been calculated using the three different methods of analysis (ESL, RS, and time history for the nine records ‘Av, MinEnv, and MaxEnv’) and shown in Figures 6 and 7. As the lateral stiffness increases, the story shear demands increase while the story displacement and inter-story drift decrease, with the assumption that the diaphragm is rigid enough to distribute uniformly the lateral loads on the vertical elements. Therefore, the displacements and the story drifts for the external and the internal columns are the same.

Figure 6

Effect of lateral stiffness on seismic responses for 6-story models. (a) LS1. (b) LS4.

Figure 7

Effect of lateral stiffness on seismic responses for 12-story models. (a) LS5. (b) LS9.

In the 6-story building model LS4 with stiff lateral stiffness, the story shear, displacement, and inter-story drift calculated from the ESL method closely match the average response calculated from the time history method. The story shear, displacement, and inter-story drift are significantly overestimated using the ESL method and underestimated using the RS method for flexible lateral stiffness design of buildings (LS1).

In the 12-story building, the story shear, displacement, and inter-story drift are significantly overestimated using the ESL method and underestimated using the RS method for flexible lateral stiffness design of buildings (LS5 to LS9). The tangent inclination angle of RS and Av inter-story drift show a slight change over the building height. The shear distribution along the stories displays a nonlinear pattern and depends on the column cross section.

Effect of floor diaphragm in-plane stiffness on seismic demands

The vertical distribution of forces from the simple equivalent lateral force method, which is commonly used for designing the lateral force-resisting system, is based on assumptions for elastic mode shapes of structures with rigid diaphragms (Fleischman and Farrow 2001; SEAOC 1999). Therefore, for structures with flexible diaphragms, the diaphragm design forces calculated according to the code methods may not be appropriate. When a structure with a flexible diaphragm is considered to have a rigid diaphragm, the period will be underestimated. For structures with periods on the descending branch of the spectral acceleration period plot, this may result in some structural base shears being slightly overestimated. However, the actual displacement will be greater than predicted. That is, the structure with a flexible diaphragm will have larger displacements along the diaphragm length compared with the displacements because of a rigid diaphragm assumption. This unaccounted increased displacement, because of a rigid diaphragm assumption, may increase the possibility of damage because of structural pounding with neighboring structures. It will also affect the distribution of forces between vertical lateral force-resisting ‘VLFR’ elements, which may be critical if they, or the elements they are connected to, do not possess sufficient strength or ductility (Sadashiva et al. 2012).

The code empirical methods under-predict the fundamental natural period of structures with flexible diaphragms. This effect on period calculation means that the design forces are likely to be overestimated, which is conservative. Fundamental natural period increased with increasing diaphragm flexibility. A critical level of diaphragm flexibility exists when the mass tributary to the lateral system and the remainder of the diaphragm mass act independently. Diaphragm flexibility effects on seismic demands are higher for short-period structures than for medium- or long-period structures For the diaphragm flexibility effect study, simple models of 6-story and 12-story building structures are developed with different floor in-plane stiffness ‘diaphragm flexibility’ using slab thicknesses that range from 0.15 to 0.30 along with a grid beam of 0.25× 0.60 cross section as shown in Table 5. Flexible diaphragm effects were evaluated by conducting time history analyses and comparing the responses of structures with rigid and flexible diaphragms.

Table 5 Building structural element dimensions for different floor diaphragm in-plane stiffness models

Table 6a,b presents different fundamental periods, for 6-story and 12-story buildings, as obtained from structural analysis using finite element models and empirical expression in ECP (2008) and other international building codes. In both 6-story and 12-story buildings, the periods computed from empirical expressions are significantly shorter than those computed from structural models especially for flexible diaphragm. As the floor in-plan stiffness increases, the fundamental period decreases. The fundamental period estimated by the ECP-201 empirical equation is underestimated especially for flexible diaphragm models; the fundamental period reaches 179% and 159% in models DS1 and DS5, respectively. The 6-story building models DS1-1 to DS4-1 are laterally flexible; as the diaphragm stiffness increases, the fundamental period slightly decreases in contact to behavior trend with models DS1-2 to DS4-2 that are relatively laterally rigid(the fundamental period decreases as the diaphragm stiffness increases), while for the 12-story models, the fundamental period decreases as the diaphragm stiffness increases.

Table 6 Estimation of the fundamental period for different building models

The base shear for the eight different models calculated from the three methods of analysis for both 6-story and 12-story buildings, is shown in Figure 8. As the floor diaphragm in-plane stiffness increases, the base shear increases, while story displacement response displays almost no change in the case of 6-story and 12-story models except for the ESL that displays a significant decrease of story displacement demand. The base shear and story displacement responses calculated from the ESL method are significantly larger than those calculated from RS and TH methods. The base shear and story displacement calculated from RS for the different models are slightly smaller than the average response ‘Av’ calculated from TH methods, which means that the actual base shear on the buildings is smaller than the base shear calculated from ECP (2008).

Figure 8

Floor diaphragm in-plane stiffness effect on seismic response demands. (a) 6-story building. (b) 12-story building.

Effect of floor diaphragm in-plane stiffness on story shear and drift demands

To show the effect of the floor diaphragm in-plane stiffness on the shear distribution, the displacements and the story drifts in the case of 6-story and 12-story buildings have been calculated using the three different methods of analysis as shown in Figures 9 and 10. In all models of 6-story and 12-story buildings, the displacement calculated from the ESL method is significantly larger than the displacement calculated from the RS and nonlinear TH methods. In the case of the RS and TH methods, the tangent inclination of the displacement curve and the curvature of the story drift in the case of the relatively flexible diaphragm, model DS1-1 in the 6-story building and model DS5-1 in the 12-story building, are significantly larger than those of the relatively rigid diaphragm, model DS4-1 in the 6-story building and model DS5-1 in the 12-story building. This means that the change in the floor diaphragm in-plane stiffness has a significant effect on the shear distribution and the floor displacement.

Figure 9

Effect of floor diaphragm in-plane stiffness on seismic response demands for 6-story building. (a) DS1-1. (b) DS4-1.

Figure 10

Effect of floor diaphragm in-plane stiffness on seismic response demands for 12-story building. (a) DS5-1. (b) DS8-1.

Conclusions

In this study, nonlinear TH analysis, for nine different time history records, has been used to evaluate the ESL and RS methods, adopted in the Egyptian code for load and forces (ECP 2008). These expressions depend on building weight only and do not take into consideration the effect of the building dynamic characteristics. The evaluation of Egyptian code seismic provisions and simplified methods is performed through comparison with a more refined approach whereas an effort is made to quantitatively assess the relative importance of various design and analysis assumptions that have to be made when building seismic design is taken into consideration, based on the study of the dynamic response of different buildings. The main findings of the study are summarized as follows:

The empirical expression for calculating the fundamental period of vibration by ECP (2008) underestimates the fundamental period compared to the structural model. As the lateral stiffness increases, the fundamental period for the structural model decreases; this means that the fundamental period is not only a function of building height but also a function of lateral stiffness.

For flexible diaphragm, the fundamental period calculated from the structural model is larger than the fundamental period calculated from the ECP (2008) empirical expression, which means that the change in the floor diaphragm in-plane stiffness has a significant effect on the fundamental period of vibration. It can be seen from the study that the main important role of the slab is actually to act as a deep beam in transferring the horizontal loads from the slabs to the vertical lateral force-resisting system. Increased diaphragm flexibility changes the demands on the whole structure. That is, it increases the structural period, and this affects the forces entering the structures thereby changing the force demands and displacements of the elements. It changes the distribution of forces between the vertical lateral force-resisting elements. Diaphragm flexibility resulted in the interior fames to resist a larger proportion of the lateral load than the exterior frames. Floor deflections increased because of diaphragm flexibility, with higher increases obtained at the first floor than at other floors.

The fundamental natural period of structures increased because of diaphragm flexibility. The flexible diaphragms result in greater floor displacements compared with rigid diaphragms of equivalent buildings. Also, the shears on the interior frames with larger tributary areas increased because of diaphragm flexibility. The above diaphragm flexibility effects amplified when the number of spans was increased or when the number of stories was decreased.

The code empirical methods under-predict the fundamental natural period of structures with flexible diaphragms. This effect on period calculation means that the design forces are likely to be overestimated, which is conservative. Fundamental natural period increased with increasing diaphragm flexibility. A critical level of diaphragm flexibility exists when the mass tributary to the lateral system and the remainder of the diaphragm mass act independently. Diaphragm flexibility effects on seismic demands are higher for short-period structures than for medium- or long-period structures.

The increase of the lateral stiffness and/or floor diaphragm in-plane stiffness increases the total building base shear. However, the increase of RS and/or nonlinear TH base shear is different from the increase of ESL base shear, which depends only on the building weight. This means that the base shear is not only a function of the building weight but also a function of the building rigidity.

The nonlinear TH base shear, in all studied models, is smaller than the ESL base shear. This means the ECP-201 empirical expressions for calculating the base shear are overestimated. The results show that the ESL method is overestimated and not accurate for calculating seismic action.

The displacements and story drifts calculated from the ESL method don’t significantly change with the change of the column and/or floor diaphragm in-plane stiffness. On the contrary, the displacements and story drifts calculated from RS and TH methods change more significantly with the change of the lateral and floor diaphragm in-plane stiffness. This means that the linear shear distribution assumed in ECP-201 is not adequately accurate and depends on the building rigidity and the linear shear distribution is inconvenient.

The building lateral stiffness and floor diaphragm in-plane stiffness have a significant effect on the story shear, overturning moment, story displacement, and inter-story drift demands calculated from the response spectrum and nonlinear time history methods.

It should also be highlighted that the lessons learnt from the catastrophic consequences of recent earthquakes, revisions in the seismic design code, and the developments in the material and workmanship characteristics are mandatory for significant improved quality of newer constructions in Egypt.

A future investigation as an extension of this research based on the present study is recommended for the evaluation of the Egyptian code under the effect of low, medium, and high ductility demands; the pushover analysis for calculating the seismic demands and its compatibility with the Egyptian code methods; and the effect of masonry infill on the seismic behavior of buildings designed according to the Egyptian code.

Author’s information

Shehata E. ABDEL RAHEEM, Assoc. Prof. of Earthquake, Bridge, Structural and Geotechnical Engineering; 2009, Civil Engineering Department, Faculty of Engineering, Assiut University, Egypt. Doctor of Engineering; 2003 and Japan Society for the Promotion of Science fellow; 2006, Hokkaido University, Japan. Alexander von Humboldt fellow; 2005, Kassel University, Germany. He has published more than 60 papers in the field of structural engineering, structural analysis, earthquake engineering, soil structure interaction, seismic pounding, structural control, and nonlinear dynamic of offshore structures. He is a previous member of the Japan Society of Civil Engineers. He reviewed many papers for international journals. He is currently working as an engineering counselor at the general project management of Taibah University. He is Assoc. Prof. of Earthquake, Structural and Geotechnical Engineering, Faculty of Engineering, Taibah University, Madinah Munawarh, Kingdom of Saudi Arabia.