Abstract
Here we discuss the thermodynamics of the hydrolysis of four fluorinated lithium salts widely used in aprotic electrolytes for lithium-ion batteries: lithium hexafluorophosphate (LiPF6), lithium bis(trifluoromethylsulfoyl)imide (LiTFSI), lithium bis(fluorosulfonyl)imide (LiFSI) and the hybrid salt lithium fluorosulfonyl-trifluorofulfonyl imide (LiFTFSI). We performed density functional theory calculations at the B3LYP/6–31++G** level of theory using an implicit solvation model, to derive the electronic structures, vibrational properties and the thermodynamic stability of reagents, reaction intermediates and hydrolysis products. We combined ab initio thermodynamic evaluations in solution with thermochemical cycles to derive the variation of the Gibbs energy of heterogeneous reactions, where the precipitation of solid products is considered. Our analysis has been performed at three different temperatures to investigate the possible influence of the temperature on the formation of the reaction products. Overall, the use of imide-based anions limits the spontaneous hydrolysis, by hindering the formation of POF3 differently from LiPF6. All FSI- TFSI- and FTFSI-hydrolyses lead to the precipitation of solid LiOH and, to a lesser extent, of solid LiF. In comparison with other salts, LiTFSI apparently holds down more efficiently the precipitation of solid LiF and limits the onset of the self-feeding salt degradation mechanisms.
Export citation and abstract BibTeX RIS

This is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial No Derivatives 4.0 License (CC BY-NC-ND, http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial reuse, distribution, and reproduction in any medium, provided the original work is not changed in any way and is properly cited. For permission for commercial reuse, please email: permissions@ioppublishing.org.
The hydrolysis of lithium salts in aprotic electrolytes plays a key role in the degradation chemistry in Li-ion batteries (LIBs). 1–6 Thus, in order, to enhance the battery life, mitigation strategies have been developed mainly by minimizing the amount of free water in the electrolytes through sequestration by electrode fillers 6,7 or functional separators. 8,9
Among all lithium salts used in LIBs, 10–15 lithium hexafluorophosphate (LiPF6) is by large the most common thanks to its optimal balancing between chemical, thermal and electrochemical stability, toxicity and safety, compared to LiClO4, LiAsF6, LiBF4 and LiSO3CF3. 16,17 Other lithium salts like lithium bis(oxalate)borate (LiBOB), 18 lithium bis(trifluoromethylsulfoyl)imide (LiTFSI) 19 and lithium bis(fluorosulfonyl)imide (LiFSI) 20 have also been proposed and studied in the research literature to improve sustainability and hazard mitigation. Hydrolysis in all cases is an issue 20 as the presence of the inevitable water traces opens the door to parasitic chemical recations 1,17,21–26 and alters the composition and stability of the solid electrolyte interphases (SEI) spontaneously grown over the electrode surfaces. 2,5,11 In fact, like all the other electrolyte components (i.e. solvent blend, soluble additives), lithium salts participate to the sequence of irreversible reactions occurring spontaneously between electrolyte and electrodes, both in open circuit conditions (chemical reactivity) and upon polarization (electrochemical reactivity). 5,27,28 The most detrimental parasitic process involving the highly-fluorinated lithium salts is the release of HF, that is highly reactive and aggressive towards the positive electrodes and the counter collectors. 29–34
Experimental and computational studies about the spontaneous reactivity of lithium salts in LIBs with water have been reported by many authors, focusing mainly on the kinetics of HF release and the reactivity with the solvent molecules (i.e. organic carbonates or ethers). 1,21–25,29,31 Reaction mechanisms have been proposed based on experimental or computational evidences 29,31 but the thermodynamics of these processes remains unclear. The methodological aspect that mainly limits the comprehension of the thermodynamics of these chemical reactions deals with the complexity of these multiphase and multicomponent systems: both experimentally and computationally it is not easy to identify and decouple the impact of the major specific homogeneous or heterogeneous reactions and quantify the underlying thermodynamic quantities (i.e. Gibbs energies of reaction and equilibrium constants).
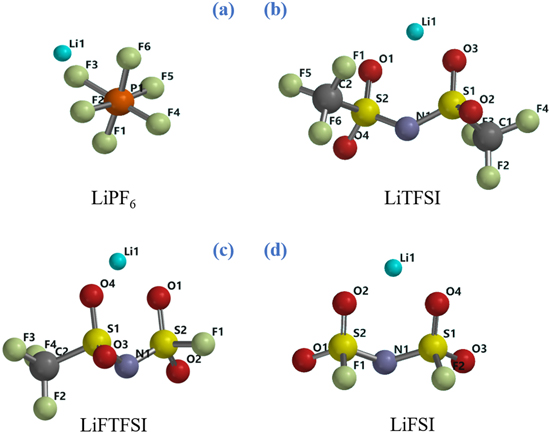
In this study we tackle the thermodynamic description at various temperatures of the hydrolysis of LiPF6, LiFSI, LiTFSI and the hybrid salt lithium fluorosulfonyl-trifluorofulfonyl imide (LiFTFSI) by electronic structure calculations by density functional theory (DFT) performed in a simulated solvent: the chemical structure of these salts is presented in Fig. 1. Here we also apply thermodynamic cycles to combine the ab initio thermodynamic descriptions of reactions in the solvent media with the precipitation of insoluble LiF(s) and LiOH(s). Our aim is to describe how the hydrolysis of these lithium salts onsets the nucleation of SEI components on electrodes through spontaneous chemical paths driven by the favourable reaction thermodynamics.
Figure 1. Chemical structures of the four lithium salts: (a) lithium hexafluorophosphate; (b) lithium bis(trifluoromethylsulfonyl)imide; (c) lithium fluorosulfonlyl-trifluoromethylsulfonyl imide; (d) bis(fluorosulfonyl) imide.
Download figure:
Standard image High-resolution imageOur study starts from the state-of-the-art salts widely adopted in commercial Li-ion battery formulations, i.e. LiPF6: its hydrolysis has been studied before and here we compare our prediction with previous reports. Starting from the consensus concerning the hydrolysis of lithium hexafluorophosphate, we propose hydrolysis mechanisms for LFSI, LiTFSI and LiFTFSI in analogy to LiPF6, considering the inevitable changes and adaptations. As far as we know, this is the first study to report a comparative analysis of the hydrolysis of imide-based lithium salts using LiPF6 as benchmark.
Methods
Electronic structure calculations by DFT have been performed by using the Spartan18 software
35
: the hybrid functional B3LYP
36
has been adopted with the 6–31++G** basis set.
37
The choice of the B3LYP/6–31++G** method has been made to balance between computational costs and the accuracy. Stereo-conformers have been identified by exploiting molecular mechanics routines embedded in the Spartan18 software. Equilibrium geometries for all molecules and conformers have been obtained by full structural relaxations of the atomic positions. Solvation has been simulated by adopting an implicit solvation model (Polarizable Continuum Model, PCM
38
) mimicking a polar environment (ε = 37.22). Vibrational frequencies and zero-point energies have been computed for all chemical species. The total Gibbs energies of a generic molecular species i (either neutral or charged) have been calculated at various temperatures, i.e.  by evaluating the corresponding partition functions and considering zero-point energies. Isolated atoms and monatomic ions thermodynamics have been computed using Gaussian09 package
39
adopting the same level of theory. Free Gibbs Energy of reactions have been calculated as stoichiometrically-weighed differences between Gibbs Free Energy products or intermediates and reactants.
by evaluating the corresponding partition functions and considering zero-point energies. Isolated atoms and monatomic ions thermodynamics have been computed using Gaussian09 package
39
adopting the same level of theory. Free Gibbs Energy of reactions have been calculated as stoichiometrically-weighed differences between Gibbs Free Energy products or intermediates and reactants.
The computational accuracy of the adopted B3LYP/6–31++G** method has been evaluated by comparing the thermodynamics of selected reactions with similar calculations performed by more advanced functionals (M06–2X/6–31++G**; ωB97X-D/6–31++G**) 40,41 or methods at higher level of theory (MP2/6–31++G**), assuming in all cases the same basis set. 42 Two reactions have been considered in vacuum, namely (a) LiPF6 → LiF + PF5 and (b) LiPF6 + H2O → HF + LiOH + PF5. The corresponding Gibbs energy of reaction at 298 K in vacuum are:
- Reaction (a): 130, 147, 172, 147 kJ mol−1 for B3LYP, ωB97X-D, M06–2X and MP2, respectively.
- Reaction (b): 210, 228, 237, 229 kJ mol−1 for B3LYP, ωB97X-D, M06–2X and MP2, respectively.
The relative accuracy of the three functionals in respect to the benchmark MP2 method have been calculated as average between the two relative calculated errors; the final estimated relative errors are: 9.9, 0.1 and 10.3% for B3LYP, ωB97X-D andM06–2X, respectively. Apart from the outperforming and computationally expensive ωB97X-D functional, B3LYP and M06–2X show a similar computational accuracy. In the view of a balanced compromise between computational costs and accuracy we adopted B3LYP.
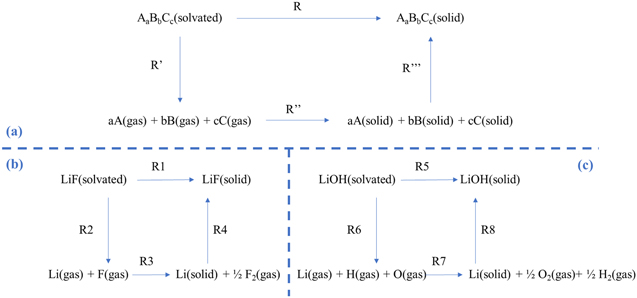
To evaluate the thermodynamic of heterogeneous reactions leading to the precipitation of LiF(s) and LiOH(s), we considered the thermodynamic cycles shown in Fig. 2. Cycles have been drawn by modifying an approach already used by us for oxides, peroxides and superoxides for aprotic lithium oxygen batteries 43
Figure 2. (a) General reactions cycle suitable to evaluate any thermodynamic quantity related to the precipitation reaction (R) of a general substance AaBbCc. (b) Reaction cycle for the evaluation of the precipitation thermodynamics of LiF(s); (c) Reaction cycle for the evaluation of the precipitation thermodynamics of LiOH(s).
Download figure:
Standard image High-resolution imageThe precipitation thermodynamics of a generic substance AaBbCc can be derived by combining computational data on molecules, either solvated or in the gas phase, obtained by electronic structure calculations or similar methods, with assessed literature thermodynamic quantities.
44
By assuming the generic thermodynamic cycle shown in Fig. 2a, one may calculate the Gibbs energy of reaction R,  by the equations summarized in Table I.
by the equations summarized in Table I.
Table I. Thermodynamic equations necessary to derive the Gibbs energies of the precipitation reaction of the generic substance AaBbCc from computational and literature data.  is the computational DFT total Gibbs energy of the generic specie i in the state jat a given temperature T,
is the computational DFT total Gibbs energy of the generic specie i in the state jat a given temperature T,  is the formation Gibbs energy at the same temperature T of the monatomic gas i retrieved from the literature databases as well as the
is the formation Gibbs energy at the same temperature T of the monatomic gas i retrieved from the literature databases as well as the  that is the Gibbs energy of formation of the solid specie AaBbCc.
that is the Gibbs energy of formation of the solid specie AaBbCc.
| Reactions | |
|---|---|
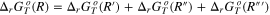
| (R) |
| Atomization reaction of AaBbCc(solvated) | |
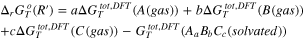
| (R') |
| Formation reaction of the monatomic gas | |

| (R') |
| Formation reaction of the AaBbCc(solid) | |
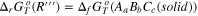
| (R'') |
Turning to the precipitation of LiOH(s) and LiF(s), we can derive the corresponding Gibbs energy of precipitation (reactions R1 and R5) by the following equations:
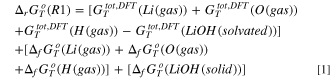
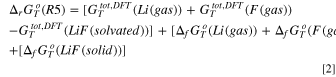
being all symbols defined in line to the caption of Table I. By using this approach, it is possible to evaluate the thermodynamics of the same reaction paths at different temperatures by retrieving the correct literature data from the database 44 and computing DFT Gibbs total energies at the same temperature. All supporting thermodynamic data collected from the literature are reported in the supplementary information (SI) Table SI.
Results
LiPF6 hydrolysis in simulated aprotic media
Li+ is strongly coordinated by the PF6‾ anion in the simulated solvent through electrostatic interactions with the partial negative charges of three fluorine atoms. Following the atomic labels shown in Fig. 1, the interatomic distances are Li1---F3 = 2.007 Å, Li1---F2 = 2.028 Å, Li1---F6 = 2.015 Å being the Li1---P1 distance 2.575 Å.
It is widely known that LiPF6 undergoes in aprotic solvents two competitive dissociation reactions: 45–48
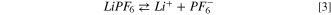
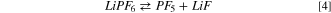
being the first the usual ionic dissociation and the second a Lewis acid/base equilibrium. The calculated Gibbs energy of both reactions at 298 K are positive, i.e.64 kJ mol−1 and 92 kJ mol−1, respectively. The ionic dissociation of reaction 3 is driven by the solvation of Li+ ions in dielectric media 48 whereas reaction 4 is negligible below 60 °C in consideration to the large values of free reaction energy. This last equilibrium is commonly considered as the onset reaction of the thermal aging of LiPF6-based electrolytes in presence of traces of water. In fact, above 60 °C the PF5 molecule easily react with water giving:
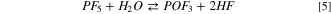
Our calculations suggest for 5 a Gibbs energy of reaction at 298 K of −51 kJ mol−1. In the literature many authors reported that at room temperature 5 is slow, and the consensus suggests a LiPF6 limited degradation through the formation of LiF: 45,46
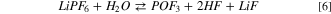
being our computational prediction for the corresponding Gibbs energy of reactionat 298 K  = 41 kJ mol−1.
= 41 kJ mol−1.
Besides these known mechanisms, one can also speculate that LiPF6 can react with water and irreversibly break in fragments leading to the release of LiOH through an Arrhenius acid/base equilibrium in solution:
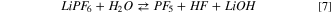
The formation of HPF6 is excluded since it is vibrationally unstable and spontaneously evolves in a coordinated adduct PF5···HF, constituted by two weakly interacting fragments. Overall, the computed thermodynamics of this process is very endergonic ( = 186 kJ mol−1 at 298 K) and it is unlikely to occur. Generally speaking, the thermodynamic landscape of the hydrolysis of LiPF6 in solution outlined from our calculation does not clarify the strong tendency of this solvated salt to easily degrade in presence of traces of water.
= 186 kJ mol−1 at 298 K) and it is unlikely to occur. Generally speaking, the thermodynamic landscape of the hydrolysis of LiPF6 in solution outlined from our calculation does not clarify the strong tendency of this solvated salt to easily degrade in presence of traces of water.
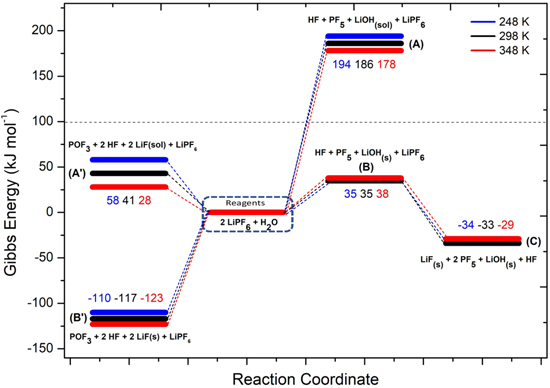
A different picture can be drawn by considering the precipitation of solid LiOH(s) and LiF(s). In Fig. 3 the potential energy surface (PES) of the hydrolysis mechanism of lithium hexafluorophosphate considering the precipitation of solids is shown at three different temperatures. These heterogeneous reaction channels show smaller or even negative energy barriers and therefore are thermodynamically feasible in the 248–348 K temperature range:
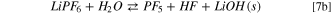
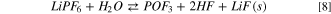
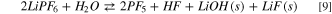
being the corresponding Gibbs energies of reaction at 298 K 35, –117 and −68 kJ mol−1, respectively. On passing, one can note that the precipitation of LiOH(s) as a first hydrolysis products decrease the Gibbs energy of reaction from 186 (7) to 35 kJ mol−1 (7b) at 298 K: this energy barrier is therefore small enough to start the LiPF6 hydrolysis at room temperature observed experimentally. 45,46 Overall, this thermodynamic path nicely matches with the experimental evidence in model studies 45,46 as well as the reported presence of oxofluorides, LiOH(s) and LiF(s) in the composition of passivation films grown over negative electrodes in aprotic LIBs. 27
Figure 3. Potential Energy Surface for LiPF6 hydrolysis reaction (numerical values are the energy differences in respect to the reagents at the various temperatures).
Download figure:
Standard image High-resolution imageThe summary of the  values for reactions involved in the hydrolysis of LiPF6 are reported in the SI, Table SII.
values for reactions involved in the hydrolysis of LiPF6 are reported in the SI, Table SII.
LiFSI hydrolysis in simulated aprotic media
Li+ cation is coordinated by FSI− anion in simulated aprotic solvent via electrostatic interactions with partial negative charges of O2 and O4 atoms (see Fig. 1). Following the atomic labels depicted in Fig. 1, the interatomic distances Li1---O2 and Li1---O4 are identical (1.88 Å) and the value of angle S2-N1-S1 is 122°. The two fluorine atoms and computed structure of LiFSI are in syn configuration.
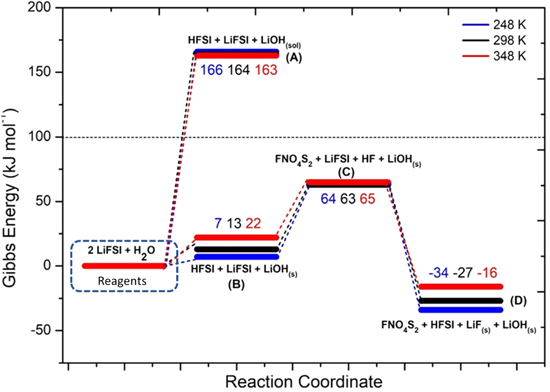
In Fig. 4 the potential energy surface (PES) of the hydrolysis mechanism of LiFSI is shown.
Figure 4. Potential Energy Surface for LiFSI hydrolysis reaction (numerical values are the energy differences in respect to the initial state: i.e. 2LiFSI + H2O at the various temperatures).
Download figure:
Standard image High-resolution imageThis reaction pathway starts with the acid/base equilibrium between LiFSI and water (10–11):
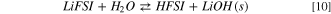
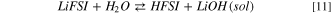
The precipitation of LiOH drives the thermodynamics, being the computed Gibbs reaction energy to give solid lithium hydroxide (10) 13 kJ mol−1 at 298 K, whereas the reaction to the solvated LiOH(sol) (11) has a  = 164 kJ mol−1 at 298 K.This different thermodynamic landscape suggests that LiFSI can react with water leading to the precipitation of lithium hydroxide and forming HFSI, especially for temperatures below 298 K.
= 164 kJ mol−1 at 298 K.This different thermodynamic landscape suggests that LiFSI can react with water leading to the precipitation of lithium hydroxide and forming HFSI, especially for temperatures below 298 K.
The structure of HFSI is shown in the SI, Fig. S1 (available online at stacks.iop.org/JES/168/100514/mmedia); it can react again through reaction (12):
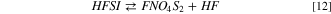
This reaction is endergonic and consists in the neutral loss of hydrofluoric acid from HFSI. The main product of the 12 reaction is the molecular fragment FNO4S2 (see SI, Fig. S1). The minimal energy barrier to climb to activate this process is as high as 43–57 kJ mol−1, in respect to the reagent molecule (HFSI). This value is high enough to expect a limited reactivity through this channel, even smaller if large activation barriers occur. Therefore, in comparison to LiPF6 hydrolysis, LiFSI is less prone to release HF. On the other hand, the equilibrium of the overall hydrolysis shifts to the products side including in the reactive pathway also reaction (13):

This reaction is strongly exergonic with a computed  = −90 kJ mol−1 at 298 K and likely drives a shift of the overall equilibrium in favour of the hydrolysis products. It is to be noted that the precipitation of LiF(s) results in the release of another HFSI molecule that can react again, through reaction (12), thus opening the door to a self-feeding process.
= −90 kJ mol−1 at 298 K and likely drives a shift of the overall equilibrium in favour of the hydrolysis products. It is to be noted that the precipitation of LiF(s) results in the release of another HFSI molecule that can react again, through reaction (12), thus opening the door to a self-feeding process.
Turning to the effect of temperature, the hydrolysis of LiFSI is enhanced at low temperature being favoured the precipitation of solid products.
The summary of the  values for reactions involved in the hydrolysis of LiFSI are reported in the SI, Table SIII.
values for reactions involved in the hydrolysis of LiFSI are reported in the SI, Table SIII.
LiTFSI hydrolysis in simulated aprotic media
Li+ cation is coordinated by the TFSI− anion by coulombic interactions between the positively charged metal ion and the negatively charged sulphonyl groups: the distances between Li1-O1 and L1-O2 are both 1.60 Å (see Fig. 1). Both trifluoromethyl groups are in the anti configuration. In Fig. 5 the potential energy surface (PES) of the LiTFSI hydrolysis process is displayed.
Figure 5. Potential Energy Surface (PES) for the LiTFSI hydrolysis reaction at three temperatures (numerical values are the energy differences in respect to the initial state: i.e. 2LiTFSI + H2O at the various temperatures).
Download figure:
Standard image High-resolution imageAlso in this case, the hydrolysis begins with the acid/base equilibrium between LiTFSI and water:
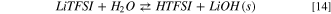
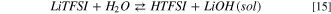
Like LiPF6 and LiFSI, the precipitation of solid lithium hydroxide leads to a Gibbs energy of reaction 14 of 13 kJ mol−1 at 298 K, approximately 150 kJ mol−1 smaller compared to the formation of solvated LiOH(sol).
The precipitation of lithium hydroxide occurs in parallel to the formation of the solvated acid HTFSI, being its structure shown in the SI, Fig. S2. The proton is coordinated by the electron pair on the nitrogen atom.
The release of hydrofluoric acid starting from HTFSI through reaction 16 is an endergonic reaction:

The abstraction of a fluorine atom from −CF3 is thermodynamically expensive due to the strength of the covalent C–F bond. The structure of the fragment molecule C2F5NO4S2 released in reaction 16 is shown in the SI, Fig. S2. Being the energy barrier to release HF as high as 63 kJ mol−1 at room temperature in respect to HTFSI, this path is unlikely to occur also in consideration of the additional energy costs due to the possible kinetic activation energies and reaction 15 (i.e. 13 kJ mol−1 at 298 K). Overall HF release by hydrolysis is likely strongly limited in the case of LiTFSI, in comparison to LiFSI and LiPF6.
Again, the thermodynamics of the overall hydrolysis is shifted towards the products by the strongly exergonic character of reaction 17:

The computed Gibbs energy of reaction 17 is −91kJ mol−1, leading to a final product blend constituted by LiF(s)+LiOH(s)+HTFSI(sol)+C2F5NO4S2(sol). Also in this case, the final HTFSI molecule can react again through reactions 16–17 opening also in this case a self-feeding reaction channel.
The summary of the  values for reactions involved in the hydrolysis of LiTFSI are reported in the SI, Table SIV.
values for reactions involved in the hydrolysis of LiTFSI are reported in the SI, Table SIV.
LiFTFSI hydrolysis in simulated aprotic media
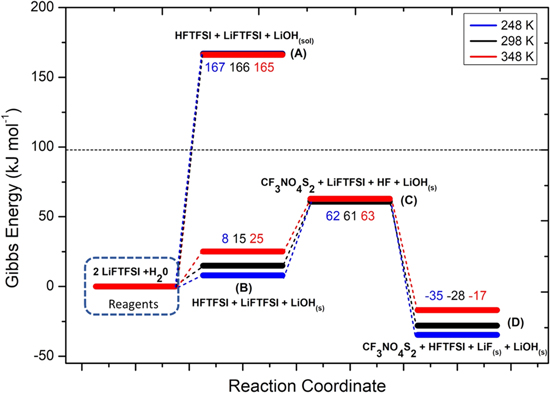
Li+ is coordinated to FTFSI− anion trough electrostatic interaction between Li cation and partial negative charges on oxygen atoms (see Fig. 1). The distance between Li1 and O4 is 1.86 Å and the distances between Li1 and O2 is 1.88 Å.This ionic couple is asymmetric due to the different substitution of sulphur atoms: S2 atom is linked to two oxygens and one fluorine atom (F1) while S1 is connected totwo oxygens and one CF3 group. In Fig. 6 the potential energy surface (PES) for the LiFTFSI hydrolysis mechanism is shown.
Figure 6. Potential Energy Surface (PES) of the LiFTFSI hydrolysis reaction, calculated at three temperatures (numerical values are the energy differences in respect to the initial state: i.e. 2LiFTFSI + H2O at the various temperatures).
Download figure:
Standard image High-resolution imageThe hydrolysis of LiFTFSI starts from the acid/base equilibrium between LiFTFSI and water, as described in reactions 18 and 19:
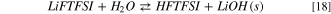
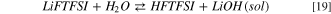
As expected, the precipitation of lithium hydroxide drives the thermodynamics with a Gibbs reaction energy for 18 of 15 kJ mol−1 at 298 K; on the contrary  where LiOH is solvated, is 166 kJ mol−1.
where LiOH is solvated, is 166 kJ mol−1.
The structure of the acid HFTFSI is shown in the SI, Fig. S3. Following the general scheme already outlined for the FSI and the TFSI anions, HFTFSI can break in fragments to release hydrofluoric acid following the reaction 20:
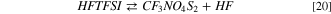
The Gibbs reaction energy of 20 is 46 kJ mol−1 at 298 K, a value very close to reaction 12. This value is expected since the HF release originates from the cleavage of the S–F bond, like in reaction 12, differently from the more expensive break of the C–F bond in reaction 16 (see above). The other reaction product of 20 is the fragment molecule CF3NO4S2: its molecular structure is shown in the SI, Fig. S3.
Overall, the combination of reaction 18 and 20 leads to an energy barrier of 61 kJ mol−1 (thermodynamic limit), without considering the kinetic activation energies. This threshold matches the similar path of the FSI-hydrolysis (i.e. reactions 10–12), whereas it is 15 kJ mol−1 smaller compared to the combined path of the HF release (14–16) from LiTFSI. Once formed, the HF molecule can easily react with LiFTFSI to give solid LiF(s) following reaction 21:
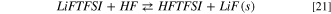
This reaction is exergonic and  = −89 kJ mol−1 at 298 K and leads to the release of HFTFSI, that can feed back reaction 20 and thus possibly opens the door to a chain reactivity.
= −89 kJ mol−1 at 298 K and leads to the release of HFTFSI, that can feed back reaction 20 and thus possibly opens the door to a chain reactivity.
The summary of the  values for reactions involved in the hydrolysis of LiFTFSI are reported in the SI, Table SV.
values for reactions involved in the hydrolysis of LiFTFSI are reported in the SI, Table SV.
Imide based salts vs lithium hexafluorophosphate
The comparison among the various hydrolysis mechanisms here proposed allow to identify three main common reaction steps:
- 1.The LiOH(s) precipitation;
- 2.The HF release;
- 3.The LiF(s) precipitation.
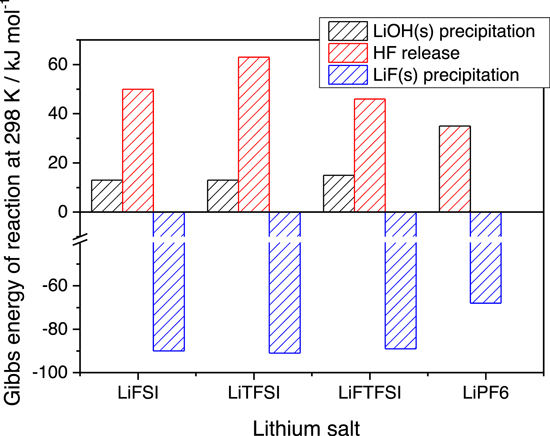
The comparison of the Gibbs reaction energies at 298 K is shown in the Fig. 7 for these three main reaction steps.
Figure 7. Comparison of the Gibbs energy of reactions of the three key-determining reactions in the lithium salt hydrolysis (note that the LiOH(s) precipitation and HF release steps occurs simultaneously in reaction 7b for LiPF6).
Download figure:
Standard image High-resolution imageAll imide-based salts show an energy barrier below 15 kJ mol−1 at room temperature for the formation of LiOH(s). On the other hand, the HF release is strongly endergonic for all lithium imides being the corresponding  50 kJ mol−1. The final hydrolysis step, that also feedback the process (see above) is the LiF(s) precipitation that is in all cases strongly exergonic, therefore driving the overall hydrolysis. In this respected LiPF6 is a compromise, as in reaction 7b the precipitation of LiOH(s) and the HF release are simultaneous: the corresponding Gibbs energy of reaction is larger compared to all the LiOH(s) from imides, whereas it is smaller compared to HF release from imides.
50 kJ mol−1. The final hydrolysis step, that also feedback the process (see above) is the LiF(s) precipitation that is in all cases strongly exergonic, therefore driving the overall hydrolysis. In this respected LiPF6 is a compromise, as in reaction 7b the precipitation of LiOH(s) and the HF release are simultaneous: the corresponding Gibbs energy of reaction is larger compared to all the LiOH(s) from imides, whereas it is smaller compared to HF release from imides.
The different thermodynamic landscape of the hydrolysis of imides compared to LiPF6 necessarily impact the chemical nature of the native passivation layer over electrodes grown in aprotic lithium batteries. In fact, the inorganic phases formed during the hydrolysis can accumulate over the electrodes starting the accumulation of the SEI even in open circuit conditions. Overall, the use of imide-based lithium salts likely leads to LiOH(s)-richer SEI layer over electrodes but likely hinders a massive accumulation of LiF(s) due to the strongly endergonic HF release steps, especially in the case of LiTFSI. A SEI richer in LiOH(s) and poorer in LiF(s) is expected to facilitate the lithium ionic mobility from and into the electrode active material thank to the larger ionic conductivities. 27 On passing it is important to underline that SEI grown on negative electrodes or passivation films deposited on positive electrodes are the results of the complex interplay between the chemically driven salt hydrolysis (that is the goal of this study), the electrochemical degradation of the electrolyte constituents (solvents, additives, salts), and the spontaneous reactivity of soluble and insoluble chemical species (electrolyte components as well as byproducts originating from degradations) with the reduced/oxidized active material in the electrodes. Thus, salt hydrolysis plays a role that must be taken into account in the view of the larger complexity of the entire battery chemistry.
Conclusions
In this manuscript we tackled the analysis of the thermodynamics of hydrolysis in solvent media of four lithium salts used in lithium-ion batteries: LiPF6, LiTFSI, LiFSI and LIFTFSI. We performed density functional theory calculations at the B3LYP/6–31++G** level of theory using an implicit solvation model, to derive the electronic structures, vibrational properties and the thermodynamic stability of reagents, reaction intermediates and hydrolysis products. Using these thermodynamic quantities, also combined with literature assessed values for solid phases like LiOH(s) and LiF(s), we outlined a realistic thermodynamic description of the tendency of these four salts to decompose by direct reaction with water following specific degradation paths. Our analysis has been performed at three different temperatures to account for the possible role played by the thermal effects. Overall, the use of imide-based anions limits the spontaneous hydrolysis, by hindering the formation of POF3 that on the contrary largely occurs for LiPF6. The hydrolyses of the (perfluroalkylsulfonyl)imide anions are driven by the precipitation of solid LiOH(s) and, to a lesser extent, of LiF(s). In particular, LiTFSI apparently holds down more efficiently the precipitation of LiF(s) than the other anions and limits the onset of self-feeding salt degradation mechanisms.
Acknowledgments
The authors would like to acknowledge the financial support from the European UnionHorizon 2020 research and innovation programme within the Si-DRIVE project; grant agreement No. 814464.