Abstract
In this study, the authors focused on the preparation and characterization of Lead-free ferroelectric ceramics known as Sr1−XBi2+2X/3Nb2O9: SBBNX, where 0.0≤ × ≤0.4. The ceramics were synthesized using a conventional solid-state reaction route. The researchers performed X-ray diffraction (XRD) analysis to confirm the phase formation and employed the Rietveld refinement technique. The results indicated that the prepared SBBNX ceramics exhibited a single phase with an orthorhombic structure, specifically belonging to the A21am space group. All samples were subjected to analysis using field emission scanning electron microscopy (FESEM) to investigate their surface morphology. The micrographs revealed a uniform distribution of grains (of size 2–4 μm ) on the surface, with distinct grain boundaries. An increasing trend in both the dielectric constant (from 99 to 220 at room temperature) and transition temperature (from 396 °C to 490 °C) was noted with an increase of Bi content in SBN. The researchers estimated the activation energies by analyzing the Arrhenius plots of the ac conductivity. The obtained values ranged from 0.62 to 1.25 eV, indicating the presence of motion of oxygen vacancies in the SBBNX ceramics. The primary objective of this study was to optimize the Sr/Bi ratio in SBBNX ceramics to enhance their potential use in non-volatile random access memory (NVRAM) applications and high-temperature piezoelectric devices.

Highlights
This study focuses on the impact of substituting smaller Bi3+ for larger Sr2+ in SrBi2Nb2O9 ceramic.
X-ray diffraction (XRD) analysis indicates the successful diffusion of Bi3+ ions at the A-site (Sr2+, ionic radius = 1.44 Å) within the SBN lattice, instead of the B-site (Nb5+, ionic radius = 0.64 Å), resulting in the formation of solid solutions.
Field emission scanning electron microscopy (FESEM) images reveal well-defined grains with distinct boundaries. With an increase in Bi substitution, the shape of the grains transforms into elongated plate structures.
Notably, the maximum room temperature dielectric constant and piezoelectric constant are observed in Sr1-XBi2+2X/3Nb2O9 ceramics, specifically at x = 0.3.
Export citation and abstract BibTeX RIS
The multifunctional Aurivillius family of ferroelectric ceramics has garnered significant attention due to their wide range of applications in various devices, including nonvolatile random access memory (NVRAM), optical memory, electro-optic devices, and high-temperature piezoelectric devices. These ceramics possess favourable characteristics such as lead-free composition, high Curie temperatures, and exceptional fatigue resistance. 1–4 The high fatigue resistance exhibited by Aurivillius ceramics is particularly crucial for devices that undergo repetitive electrical cycles, such as NVRAM, electro-optic devices, and high-temperature piezoelectric devices. Moreover, the ferroelectric properties inherent in Aurivillius ceramics are exploited in optical memory applications. The remarkable multifunctionality of Aurivillius ceramics positions them as potential candidates for numerous electronic devices and emerging technologies. 5
Over the past three decades, researchers and scientists have shown great interest in bismuth-layered ferroelectric materials (BLSFs) and their solid solutions among various Aurivillius ceramics. 6–8 These materials have been extensively investigated due to their diverse applications in the aforementioned devices. The presence of a bismuth layer in these compounds enables the manipulation of their structural, electrical, and ferroelectric properties. Among the different BLSF materials, SrBi2Nb2O9 (SBN) has been extensively studied because its structure and electrical properties are similar to other fatigue-free layered oxides, such as SrBi2Ta2O9 (SBT), SrBi2NbTaO9 (SBNT), SrBi4Ta4O15, and SrBi2Nb2O9 (SBN). Consequently, SBN can serve as a base material for these oxides. SBN is considered superior to SBT due to its larger remnant polarization, high fatigue resistance, high mechanical quality factor, and transition temperature. 9,10 However, during the sintering process, the volatile nature of Bi2O3 leads to the creation of oxygen vacancies in SBN, posing a challenge. To overcome this issue, SBN ceramics are doped with different elements to reduce vacancy concentration and enhance their electrical properties. It has also been observed that strontium deficiency or an excess of bismuth in SBN ceramics can significantly improve their dielectric and ferroelectric properties. 11–13 Researchers have invested considerable effort in enhancing the dielectric and ferroelectric properties of SBN ceramics through various synthesis mechanisms or element substitutions. Dopants can be substituted in the Bi2O3 layer and/or at the A or B-site of the perovskite-like unit. Millan et al. 14,15 substituted Bi3+ in the [Bi2O2]2+ layers with lower or higher valency cations, such as Pb2+, Sb3+, Bi3+ Sn2+ or Te4+. Their study reported an improvement in the dielectric properties of BLSF ceramics with increasing Bi concentration in the [Bi2O2]2+ layers. 14,15 Yun Wu et al. 16 and Subbarao et al. 17–19 demonstrated that the transition temperature (Tc) decreased with the substitution of Sr2+ by Ba2+ and Pb2+, while it increased with Ca2+. Furthermore, the substitution of Bi3+ and La3+ for Sr2+ led to an increase in Tc with increasing Bi3+ concentration and a decrease with La3+ concentration. 16 These studies suggest that substituting cations of smaller size at the Sr-site in SBN, enhances both the transition temperature and dielectric constant of these ceramics, while larger cations result in a decrease in these properties. Therefore, optimizing Sr substitution appears to be crucial for ceramics for electronic devices. The current study focuses on the development of lead-free Bi-excess SBN ceramics, specifically Sr1−XBi2+2X/3Nb2O9: SBBNX (X = 0.0–0.4), using the conventional solid-state reaction method. We examine the effects of Bi3+ substitution on the structural, dielectric, electrical, ferroelectric, and piezoelectric properties of SBN ceramics. These findings provide valuable insights for designing and optimizing multifunctional SBN ferroelectric ceramics for various electronic applications, including nonvolatile random-access memory, optical memory, and high-temperature piezoelectric devices.
Experimental Process
The lead-free ceramic powders Sr1−XBi2+2X/3Nb2O9 (abbreviated as SBBNX) with varying compositions (X = 0.0, 0.1, 0.2, 0.3, and 0.4) were successfully synthesized through the conventional solid-state reaction route. Raw materials including Strontium carbonate (SrCO3, 99.99%, Sigma-Aldrich), Bismuth oxide (Bi2O3, 99.9%, CDH), and Niobium oxide (Nb2O5, 99.99%, Alfa Aesar) were used for the synthesis. The raw powders were weighed by the stoichiometric ratio and subjected to ball milling for 24 h in an acetone medium with Zirconia balls. Subsequently, the resulting powders were dried at a temperature of 100 °C for a duration of 4 h. Subsequently, the dried powders were calcined at an optimized temperature of 800 °C for 4 h, with a heating rate of 3 °C m−1, followed by 2 h of hand grinding. To form pellets, the calcined powders were mixed with 5 wt. % polyvinyl alcohol (PVA) as a binder and pressed into circular disks with a diameter of approximately 10 mm and thickness of about 1.5 mm using a uniaxial Hydraulic press. Finally, the pellets for each composition were sintered at an optimized temperature of 1100 °C for 3 h in a closed alumina crucible with a heating rate of approximately 3 °C min−1. For structural analysis, X-ray diffraction (XRD) patterns of the prepared Sr1−XBi2+2X/3Nb2O9: SBBNX (X = 0.0, 0.1, 0.2, 0.3, and 0.4) were recorded at room temperature using a BRUKER D8 X-ray diffractometer. The measurement was conducted at 40 kV and 40 mA in the range of 10° ≤ 2θ ≤ 70° with Cu-Kα radiation (λ = 1.5406 Å). The density of the specimens was determined using Archimedes' principle. RAMAN spectroscopy was performed using a Renishaw In-Via Reflex Micro-Raman spectrometer to examine the lattice vibrations. Microstructure investigation was conducted using field emission scanning electron microscopy (FESEM) (Model no. TESCAN MIRA 3). For electrical measurements, the pellets of each composition were polished with silicon carbide to obtain flat and parallel surfaces with a thickness of approximately 1 mm. The pellets were coated with silver on both sides and fired at 500 °C for 30 min. Dielectric measurements were recorded as a function of temperature from 30 °C to 500 °C in the frequency range of 20 Hz to 1 MHz using an Impedance analyzer (Wayne Kerr 6500B) with an oscillation amplitude of 1 volt. P-E hysteresis measurements were conducted at room temperature using an automatic P-E hysteresis loop tracer based on the standard Sawyer-Tower Circuit. The piezoelectric coefficients (d33 (pC/N)) were measured using a Piezo test PM 300 piezometer.
Results and Discussion
The X-ray diffraction (XRD) patterns of Sr1−XBi2+2X/3Nb2O9 (0≤ × ≤0.4) ceramics are depicted in Fig. 1. The successful indexing of the diffraction peaks using standard powder diffraction data for SBN (JCPDS card no. 86–1190) confirms the absence of any secondary phases. This confirms the high purity of the prepared SBBNX (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics. Notably, the peak corresponding to the (115) plane exhibits the highest intensity, consistent with the highest diffraction (112 m + 1) peak of BLSFs ceramics. 20 The inset in Fig. 1 provides an enlarged view of the diffraction peaks (115) for all SBBN ceramics. Figure 1b inset shows that the most intense peak (115) at 2θ ≈ 29° undergoes a slight shift towards higher angles with an increasing doping concentration of Bi. This shift in the XRD peak can be attributed to lattice shrinkage resulting from the substitution of the smaller ionic radius of Bi3+ ions (ionic radius = 0.96 Å) for the larger ionic radius of Sr2+, ionic radius = 1.44 Å) at the A-site of the pseudo-perovskite structure. 21 Similar behaviour was observed in the case of (Na0.5Bi0.5) substitution at the Sr-site of SBN. 22 These XRD findings indicate that Bi3+ ions (ionic radius = 0.96 Å) on substitution could have successfully diffused at the A-site (Sr2+, ionic radius = 1.44 Å) instead of the B-site (Nb5+, ionic radius = 0.64 Å) within the SBN lattice, resulting in the formation of solid solutions for these compositions. To verify the structures of Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics and determine the extent of substitution, XRD Rietveld refinements were conducted with an A21am space group at room temperature using the Full Prof software (Version 3.00 June 2015-JGP-JRC), a standard computer program. The least-square refinement method was employed with a Pseudo-Voigt function to obtain the lattice parameters and unit cell volume and their obtained values along with refinements parameters are summarized in Table I.
Figure 1. (a) Room temperature XRD patterns of Sr1−xBi2+2x/3Nb2O9 sintered pellets for X = 0.0–0.04; (b) along with shifting peak (115) with increasing of bismuth content.
Download figure:
Standard image High-resolution imageTable I. The crystal data (Lattice constants (a, b and c), Unit cell volume (V), Average Crystallite size (D) and refinement factors of Sr1−xBi2+2x/3Nb2O9 obtained from X-ray powder diffraction data.
| Lattice parameters | R-Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | a[Å] | b[Å] | c[Å] | V[Å]3 | D (nm) | Rp | Rwp | Rexp | χ2 | S |
| 0.0 | 5.5064 | 5.5053 | 25.0724 | 760.0541 | 33.08 | 29.9 | 30.2 | 23.99 | 1.58 | 1.26 |
| 0.1 | 5.5047 | 5.5078 | 25.3511 | 759.0405 | 24.44 | 36.4 | 33.6 | 27.02 | 1.55 | 1.24 |
| 0.2 | 5.5045 | 5.5027 | 25.0355 | 759.3201 | 27.69 | 30.7 | 29.6 | 25.45 | 1.36 | 1.16 |
| 0.3 | 5.5031 | 5.4990 | 25.0261 | 757.3301 | 29.43 | 29.0 | 29.0 | 24.36 | 1.42 | 1.19 |
| 0.4 | 5.5101 | 5.5122 | 25.0751 | 761.5129 | 28.79 | 36.2 | 32.2 | 26.93 | 1.43 | 1.20 |
Figures 2a–2e showcase the Rietveld refinement results of the XRD patterns for Sr1−xBi2+2X/3Nb2O9 with X = 0.0 − 0.4. Atomic positions for SrBi2Nb2O9 were used as the starting model in refinements reported by Ismunandar et al. 23 During the refinement process, the occupancies of Nb5+ and Oxygen atoms (O(1), O(2), O(3), O(4) and O(5)) were kept constant at 1, while the occupancies of Sr2+ and Bi3+ were varied. Notably, the obtained occupancy values (not shown here) for Sr2+ and Bi3+ at various sites (Sr-site and Bismuth-site) were found to be lower than the reported values for SBN. 24 This disordering phenomenon between A-sites and bismuth sites has been investigated by 24 in bilayer systems with A = Sr2+, Ca2+, and Ba2+ where they suggest that the disordering becomes more pronounced with the increasing ionic radii of the doping element. 25 In our case the ionic radius of Bi3+ is lower than Sr2+, hence this disordering is not less pronounced.
Figure 2. Rietveld refinement of Sr1−XBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageThe R-factors are defined as: 26
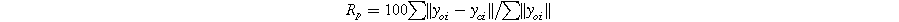
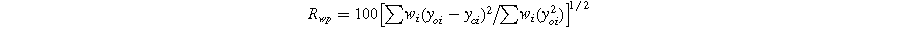
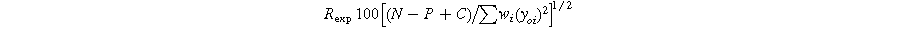
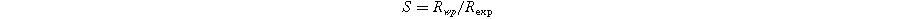
The refinement parameters for all compositions are summarized in Table I. The χ2 values, ranging from 1.57 to 1.33, indicate a strong agreement between the experimental data (solid dashed red line) and the theoretical data (solid black line) shown in Fig. 2.
Figures 3a–3d illustrate the changes in lattice parameters, unit cell volume, orthorhombicity, and orthorhombic distortion as a function of Bi content (X). It is evident that the substitution of larger Sr2+ ions with smaller Bi3+ ions results in a decrease in the values of b and c parameters. This trend in the reduction of unit cell volume has been also reported by other researchers, 11,12,27–29 potentially attributed to the structural constraint caused by the [Bi2O2]2+ layers positioned between the perovskite-like units. 27 The decrease in lattice constant induces lattice strain and distortion, which subsequently impacts the electrical properties of SBBNX ceramics. In the inset of Fig. 3d, it is observed that the value of (b/a = 0.9985) for X = 0.0 is close to 1, indicating a close-to-tetragonal structure. However, as the Bi content increases, the (b/a) value decreases, signifying a more pronounced orthorhombic structure. On the right axis of Fig. 3d, the orthorhombicity is shown to increase with X, which is highly significant and contributes to enhanced dielectric properties. 30
Figure 3. Variation of (a) Lattice constants (a), (b); (b) Lattice constant (c); (c) Unit cell volume (V); and (d) Orthorhombic distortion and Orthorhomicity with Bi Composition (X).
Download figure:
Standard image High-resolution imageThe average crystallite size of the samples was calculated from the XRD patterns using the Debye-Scherer formula: 31
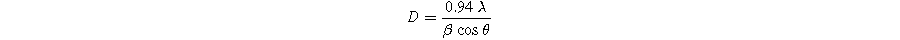
In the formula, D represents the crystallite size, λ denotes the wavelength of the X-ray beam (λ = 1.5406 Å), β indicates the full width at half maximum (FWHM), and θ represents the diffraction angle. The obtained values for the average crystallite size are listed in Table I. In comparison to the undoped SBN sample (D = 33.08 nm), the Bi-substituted SBN samples exhibited a lower value of D, ranging from 24.44 nm to 28.79 nm. An increasing trend in the crystallite size was observed with an increase in Bi concentration for X ≤ 0.3, after which it started to decrease.
The density was determined using the Archimedes principle. To calculate the X-ray density ( ), the following relationship
32
was utilized.
), the following relationship
32
was utilized.
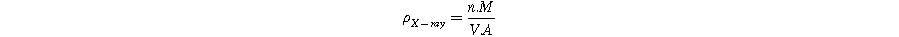
Here, n represents the number of molecules per unit volume, M denotes the molecular weight of the material, V represents the volume of the unit cell, and A signifies Avogadro's number. The porosity (P) of all samples was computed by employing the experimental density ( ) measured through the Archimedes principle and the X-ray density (
) measured through the Archimedes principle and the X-ray density ( ). The formula used for this calculation
32
is as follows :
). The formula used for this calculation
32
is as follows :
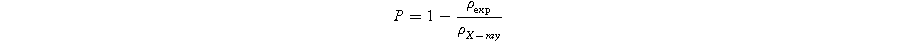
The relative density (%) along with the porosity values are presented in Fig. 4. The data in the figure demonstrate that all the Bi-substituted SBN samples exhibit a relative density greater than 95%. Among the compositions of Sr1−xBi2+2X/3Nb2O9 ceramics, the sample with X = 0.3 showed the highest relative density as compared to the other compositions. This observation is also evident in the SEM micrographs.
Figure 4. Variation of (a) Relative density %; and (b) Porosity as a function of Bi concentration in Sr1−XBi2+2X/3Nb2O9 ceramics.
Download figure:
Standard image High-resolution imageFigures 5a–5e display the field emission scanning electron microscopy (FESEM) micrographs of Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics. In all ceramic compositions, the presence of randomly oriented plate-like grains of different sizes is observed, which is a distinctive characteristic of the BLSFs family. This phenomenon arises due to the anisotropic nature of the crystal structure. 33,34 The micrographs also reveal well-defined grains and grain boundaries with strong packing, confirming the highly dense structure of the prepared SBBNX ceramics. The average grain size, estimated using Image J software, is shown in Fig. 5f, ranging from 2–4 μm. Initially, the average grain size increases with an increase in bismuth concentration up to X = 0.3. However, beyond X = 0.3, the grain size starts to decrease, as indicated in the inset of Fig. 5. The variation in grain sizes could be attributed to the partial substitution of bismuth ions for strontium ions and the sintering temperature. In this study, the sintering temperature was maintained at 1100 °C for all compositions, and thus the substitution of smaller Bi3+ ions for larger Sr2+ ions could be the main reason for the observed variations in grain sizes. Additionally, the incorporation of bismuth into the system might have promoted the formation of low melting point mixtures at grain boundaries during sintering, increasing the diffusion distance between the grains and resulting in smaller grain sizes in the sintered samples. 35 Furthermore, it can be observed from the SEM images that for X ≤ 0.3 in SBBNX ceramics, the shape of the grains is relatively similar. However, with a further increase in Bi concentration in Sr1−XBi2+2X/3Nb2O9 ceramics, the shape of the grains transitions from a plate-like structure to elongated round shapes along the c direction.
Figure 5. Field emission scanning electron microscope (FESEM) micrographs of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageFigures 6a–6e present the room temperature Raman spectra of Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics within the frequency range of 50 to 1000 cm−1. The spectra exhibit sharp phonon modes characteristic of SBBNX ceramics, observed at approximately 175, 207, 271, 576, and 838 cm−1 for X = 0.0. These modes correspond to the orthorhombic phase with space group A21am, consistent with previous reports on SBN. 31,36–40 The high-frequency Raman modes (<200 cm−1) are associated with the vibrations of NbO6 octahedra and lattice translations involving cation motion, while the low-frequency modes (<200 cm−1) are attributed to the motion of the heavier Bi3+ ions. 36 The lowest Raman mode observed at 175 cm−1, originating from the A-site vibration, undergoes a shift towards higher frequencies. The mode at 576 cm−1 (Eg mode) corresponds to a rigid sublattice mode. 41 The highest frequency mode detected at 837 cm−1 arises from the vibration of oxygen ions (O4, O5) in the Nb-O plane (Eg mode). Additionally, the mode at approximately 207 cm−1 (F2μ mode), which represents a torsional bending mode, emerges due to the distortion of NbO6 octahedra. 42 As the Bi concentration increases in Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics, the Raman modes at 175 cm−1 and 207 cm−1 shift towards higher wavenumbers, indicating an augmentation in the distortion of NbO6 octahedra.
Figure 6. Raman spectra of ceramics of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageThe phase composition of SBBNX ceramics was determined by deconvoluting the experimental Raman spectra into individual Gaussian and Lorentzian components, as depicted in Fig. 7. The convoluted spectra in Fig. 7 reveal that the intensity ratio (i.e. I207/I175) of the 207 cm−1 mode to the 175 cm−1 mode decreases with increasing X in Sr1−XBi2+2X/3Nb2O9 and becomes equal at X = 0.3. Moreover, the 207 cm−1 mode broadens, and the 175 cm−1 mode disappears for higher bismuth substitution, indicating a significant bending of NbO6 octahedra. 37 The mode at 576 cm−1 shifts to 579 cm−1 as the Bi concentration increases from X = 0.0 to 0.3 and then decreases back to 576 cm−1. This shift suggests slight changes in the displacements of positive and negative ions. The peak position of the 837 cm−1 mode slightly shifts towards higher frequency with increasing bismuth content, indicating the stretching of the octahedral NbO6 in the a-b plane 39 as a result of a higher concentration of bismuth in SBN. These results align with the theoretical findings for SBN. 36,38 Furthermore, with a further increase in Bi concentration at X = 0.4, the peak intensity decreases even more, suggesting structural distortion caused by an inhomogeneous distribution. This finding confirms that the optimal concentration for Bi substitution in SBBNX ceramics is X = 0.3.
Figure 7. The convoluted Raman spectra of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageFigures 8 and 9 depict the frequency dependence of  and
and  respectively, on a log-log scale for Sr1−XBi2+2X/3Nb2O9 (X = 0.0 − 0.4) ceramics at selected temperatures. Here,
respectively, on a log-log scale for Sr1−XBi2+2X/3Nb2O9 (X = 0.0 − 0.4) ceramics at selected temperatures. Here,  and
and  are the real and imaginary parts of dielectric constant respectively. Both
are the real and imaginary parts of dielectric constant respectively. Both  and
and  plots exhibit strong dispersion in the low-frequency region for all compositions (X = 0.0–0.4). Additionally, two distinct regions of dispersion can be observed: a plateau region in the high-frequency range and a pronounced frequency dispersion in the low-frequency region. The observed dispersion at low frequency can be attributed to the accumulation of space charge in Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics.
43
This type of behaviour in the real and imaginary parts of the dielectric constant is commonly observed in conductive materials with non-negligible ionic conductivity. It is known as low-frequency dielectric dispersion (LFDD) and is a characteristic feature of ferroelectrics.
44,45
Comparing
plots exhibit strong dispersion in the low-frequency region for all compositions (X = 0.0–0.4). Additionally, two distinct regions of dispersion can be observed: a plateau region in the high-frequency range and a pronounced frequency dispersion in the low-frequency region. The observed dispersion at low frequency can be attributed to the accumulation of space charge in Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics.
43
This type of behaviour in the real and imaginary parts of the dielectric constant is commonly observed in conductive materials with non-negligible ionic conductivity. It is known as low-frequency dielectric dispersion (LFDD) and is a characteristic feature of ferroelectrics.
44,45
Comparing  and
and  plots it can be observed that the dispersion in
plots it can be observed that the dispersion in  is stronger than in
is stronger than in  suggesting that
suggesting that  is influenced by direct current (dc) conductivity in Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics. The absence of dielectric dispersion at higher frequencies in both
is influenced by direct current (dc) conductivity in Sr1−XBi2+2X/3Nb2O9 (X = 0.0, 0.1, 0.2, 0.3, and 0.4) ceramics. The absence of dielectric dispersion at higher frequencies in both  and
and  in SBBNX ceramics indicates that the dispersion is associated with space charge effects.
46
in SBBNX ceramics indicates that the dispersion is associated with space charge effects.
46
Figure 8. Frequency dependence of dielectric constant ( ) on the log-log scale at different temperatures of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
) on the log-log scale at different temperatures of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageFigure 9. Frequency dependence of dielectric constant ( ) on the log-log scale at different temperatures of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
) on the log-log scale at different temperatures of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageFigures 10a–10e illustrate the temperature dependence of the dielectric constant ( ) for Sr1−XBi2+2X/3Nb2O9, (0.0≤ × ≤0.4) ceramics at different frequencies. The dielectric parameters measured at 1 kHz for Sr1−XBi2+2X/3Nb2O9 ceramics are summarized in Table II. The value of the dielectric constant (
) for Sr1−XBi2+2X/3Nb2O9, (0.0≤ × ≤0.4) ceramics at different frequencies. The dielectric parameters measured at 1 kHz for Sr1−XBi2+2X/3Nb2O9 ceramics are summarized in Table II. The value of the dielectric constant ( ) at room temperature increases with an increase in bismuth concentration. This rise in
) at room temperature increases with an increase in bismuth concentration. This rise in  indicates an increase in polarizability, which is attributed to the expansion of rattling space.
45
The transition temperature (Tc) for pure SBN has been reported by various researchers in the range of 400 °C–435 °C, with a peak value of the dielectric constant ranging from 700 to 1000.
5,47–49
The study demonstrated that the Tc value, representing the peak of the ferroelectric transition, exhibited an increase as the Bi3+ content increased in the SBN composition. In the case of pure SBBNX with X = 0.0, it is evident from the curves that the transition temperature (Tc) occurs at 396 °C, with a peak value of the dielectric constant (
indicates an increase in polarizability, which is attributed to the expansion of rattling space.
45
The transition temperature (Tc) for pure SBN has been reported by various researchers in the range of 400 °C–435 °C, with a peak value of the dielectric constant ranging from 700 to 1000.
5,47–49
The study demonstrated that the Tc value, representing the peak of the ferroelectric transition, exhibited an increase as the Bi3+ content increased in the SBN composition. In the case of pure SBBNX with X = 0.0, it is evident from the curves that the transition temperature (Tc) occurs at 396 °C, with a peak value of the dielectric constant ( = 634) measured at 1 kHz as shown in the inset of Fig. 10f and presented in Table II. This rise in Tc can be attributed to larger structural distortion in the NbO6 octahedra, which is confirmed by the XRD study shown in Fig. 3d. When a significant amount of smaller Bi3+ ions substitute for larger Sr2+ ions in Sr1−XBi2+2X/3Nb2O9 ceramics, it creates large cation vacancies.
50
These vacancies generate stresses in the perovskite unit cell, resulting in an increased mismatch between the perovskite unit cell and a Bi2O2 layer, leading to structural distortion in the NbO6 octahedra.
= 634) measured at 1 kHz as shown in the inset of Fig. 10f and presented in Table II. This rise in Tc can be attributed to larger structural distortion in the NbO6 octahedra, which is confirmed by the XRD study shown in Fig. 3d. When a significant amount of smaller Bi3+ ions substitute for larger Sr2+ ions in Sr1−XBi2+2X/3Nb2O9 ceramics, it creates large cation vacancies.
50
These vacancies generate stresses in the perovskite unit cell, resulting in an increased mismatch between the perovskite unit cell and a Bi2O2 layer, leading to structural distortion in the NbO6 octahedra.
Figure 10. Temperature dependence of Dielectric constant ( ) at various frequencies of Sr1−xBi2+2X/3Nb2O9 ceramics (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4; and (f) Variation of Transition temperature and dielectric constant with Bi composition (X).
) at various frequencies of Sr1−xBi2+2X/3Nb2O9 ceramics (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4; and (f) Variation of Transition temperature and dielectric constant with Bi composition (X).
Download figure:
Standard image High-resolution imageTable II. Dielectric properties of Sr1−xBi2+2X/3Nb2O9 ceramics measured at 1 KHz.
| X |

|

|

| Tolerance factor | Tc °C |
|---|---|---|---|---|---|
| at Tc | at RT |

| (t) | ||
| 0.0 | 772 | 99 | 3.58 | 0.9846 | 396 |
| 0.1 | 1436 | 133 | 1.27 | 0.9568 | 416 |
| 0.2 | 1661 | 140 | 1.03 | 0.9291 | 446 |
| 0.3 | 1177 | 153 | 1.91 | 0.9014 | 460 |
| 0.4 | 810 | 220 | 1.93 | 0.8736 | 490 |
Consequently, the mismatch between the perovskite-like unit and the Bi2O2 layer is expected to intensify, leading to more significant distortion in the [NbO6] octahedra compared to the stoichiometric composition of SBN. These structural distortions have been found to contribute to a larger ferroelectric spontaneous polarization and higher Curie temperatures. 51
As a result, the transition temperature increases with an increase in Bi concentration in Sr1−XBi2+2X/3Nb2O9 ceramics. Previous studies have reported that thin films synthesized with Sr-deficient and Bi-excess compositions (Sr0.8Bi2.2M2O9) (M = Nb, Ta) exhibit a transition temperature of 400 °C with an 8 times higher dielectric constant at Tc compared to the room temperature value. 11 Moreover, the literature contains numerous reports indicating that ceramics/thin films synthesized with Sr-deficient and Bi-excess SBN/SBT compositions exhibit enhanced dielectric properties compared to stoichiometric compositions. In our study, Sr1−XBi2+2X/3Nb2O9 ceramics with X = 0.3 were observed to exhibit improved dielectric properties. Additionally, frequency dispersion in Tc has been observed in X ≥0.3 SBBNX ceramics, suggesting a non-Debye nature in these materials.
The transition temperature exhibits a direct correlation with the tolerance factor, as defined by Goldschmidt's equation:
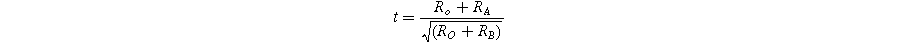
In this context, RA , RB, and Ro denote the effective ionic radii of the A-site (Sr2+, Bi3+), B-site (Nb5+), and oxygen ions, respectively. 46 For Sr1−XBi2+2X/3Nb2O9, the modified tolerance factor (t) can be expressed as follows: 47
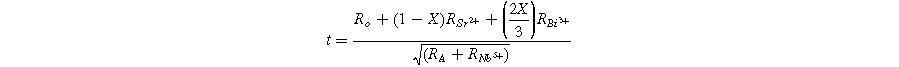
In the above relation, RSr 2+, RBi 3+ and RNb 5+ denote the ionic radii of Sr2+, Bi3+ and Nb5+, respectively. The ionic radii used for Sr2+, Bi3+, and Nb5+ are 1.44 Å, 0.96 Å, and 0.64 Å, respectively. 48 Previous studies have indicated that as the tolerance factor decreases, the structural distortion and transition temperature (Tc) increase. 49 The calculated tolerance factor (t) values are listed in Table II. Considering the same coordination number, the ionic radius of Bi3+ (r = 0.96 Å) is smaller than that of Sr2+ (r = 1.44 Å). This larger ionic radius of Sr2+ reduces the tolerance factor as Bi doping increases at the Sr-site, consequently raising the transition temperature in SBBNX ceramics. The perovskite unit's tolerance factor (t) is typically 0.86 for SBN. 50 In our study, the calculated values of t ranged from 0.9844 to 0.8735. These findings align with previously reported results for SBN. 51
Figures 11a–11e illustrate the temperature dependence of the dielectric tangent loss (tanδ) for Sr1−XBi2+2X/3Nb2O9 ceramics at different frequencies. Initially, tanδ remains almost constant up to a certain temperature, but beyond that temperature (particularly at 400 °C), its value increases. This increase can be attributed to a higher concentration of charge carriers at elevated temperatures and a larger distortion in NbO6 octahedra. 27 Furthermore, tanδ is observed to be higher at low frequencies, indicating that the dipoles are unable to respond to the applied AC field, resulting in a decrease in tanδ with increasing frequency, as explained by Koop's theory. 20,52 The room temperature tanδ values for different X are summarized in Table II, revealing an increase in tanδ with higher Bi concentration.
Figure 11. Temperature dependence of dielectric loss (tanδ) at various frequencies of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageThe relaxor behaviour of ferroelectric ceramics is typically characterized by frequency dispersion (ΔT) and diffusivity parameters (γ). These two parameters were employed to describe the relaxor behaviour of Sr1−XBi2+2X/3Nb2O9 ceramics, as listed in Table III. The frequency dispersion in transition temperature (ΔT) increases from 0 °C to 6 °C with increasing Bi concentration, with the onset of frequency dispersion occurring at X = 0.2. This enhanced value of ΔT suggests that the substitution of smaller Bi3+ for larger Sr2+ ions leads to relaxor behaviour in Sr1−XBi2+2X/3Nb2O9 ferroelectric ceramics, similar to observations in Nd3+ doped SBN. 17,38 The diffuse nature of relaxor behaviour near the transition temperature can be described by the Curie-Weiss law for T > Tm, as proposed by Uchino and Nomura: 53
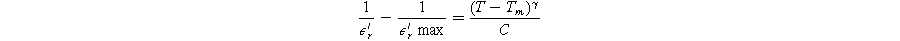
Here, γ and C represent the diffusivity and Curie-Weiss constant, respectively. The value of γ falls within the range of 1 to 2, where γ = 1 corresponds to normal ferroelectrics and γ = 2 represents ideal relaxor ferroelectrics.
33
Figures 12a–12e depicts the plots of  vs
vs  at 10 kHz for Sr1−XBi2+2X/3Nb2O9 ceramics. By performing linear fitting of the experimental data using the above equation, the values of γ were calculated and are listed in Table III. An enhancement in the value of γ is observed, ranging from 1.12 (X = 0.0) to 1.89 (X = 0.4). In general, relaxor behaviour occurs when at least two cations occupy the same crystallographic site (either A or B) and exhibit local ordering.
38,53
With the introduction of Bi3+ at the Sr-site, there is a possibility of disorder in the arrangement of cations at both the Sr-site (in the perovskite-like unit) and bismuth sites (in the (Bi2O2)2+ layers). It becomes evident that the distribution of cations at the Sr-site and bismuth site is not homogeneous at the microscopic scale.
54,55
Such compositional disorder leads to microscopic heterogeneity in the structure, consisting of microdomains with slightly different chemical compositions.
56
at 10 kHz for Sr1−XBi2+2X/3Nb2O9 ceramics. By performing linear fitting of the experimental data using the above equation, the values of γ were calculated and are listed in Table III. An enhancement in the value of γ is observed, ranging from 1.12 (X = 0.0) to 1.89 (X = 0.4). In general, relaxor behaviour occurs when at least two cations occupy the same crystallographic site (either A or B) and exhibit local ordering.
38,53
With the introduction of Bi3+ at the Sr-site, there is a possibility of disorder in the arrangement of cations at both the Sr-site (in the perovskite-like unit) and bismuth sites (in the (Bi2O2)2+ layers). It becomes evident that the distribution of cations at the Sr-site and bismuth site is not homogeneous at the microscopic scale.
54,55
Such compositional disorder leads to microscopic heterogeneity in the structure, consisting of microdomains with slightly different chemical compositions.
56
Table III. The Relaxor behaviour of Sr1−XBi2+2X/3Nb2O9 ceramics measured at 10 kHz.
| X | Frequency |

|

| To (K) | Curie constant C (K) | Diffusivity ( ) ) |
|---|---|---|---|---|---|---|
| 0.0 | 1 KHz | 396 | 0 | 638 | 2.27E+04 | 1.12 |
| 1 MHz | 396 | |||||
| 0.1 | 1 KHz | 416 | 0 | 668 | 2.76E+04 | 1.16 |
| 1 MHz | 416 | |||||
| 0.2 | 1 KHz | 446 | 2 | 682 | 3.81E+04 | 0.97 |
| 1 MHz | 444 | |||||
| 0.3 | 1 KHz | 460 | 2 | 712 | 6.31E+04 | 1.20 |
| 1 MHz | 458 | |||||
| 0.4 | 1 KHz | 490 | 6 | 722 | 1.05E+05 | 1.89 |
| 1 MHz | 484 |
Figure 12. Modified Curie-Weiss law fitted curves of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X= 0.0; (b) X= 0.1; (c) X= 0.2; (d) X= 0.3; and (e) X= 0.4.
Download figure:
Standard image High-resolution imageFigures 13a–13e illustrate the frequency dependence of total AC conductivity (σac ) as a function of temperature for all compositions (0.0 ≤ × ≤0.4). The AC conductivity was determined using the following relation:
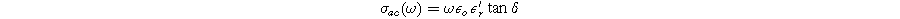
Here, ω = 2πf (f being the frequency used), εo
represents the permittivity of vacuum (8.854 × 10−12 F m−1),  is the dielectric constant, and tanδ is the dielectric loss tangent. The AC conductivity is directly linked to the dielectric properties of any material. The curves exhibit a linear response at higher temperatures and low frequencies, independent of frequency. However, at higher frequencies, the AC conductivity increases according to the power law
is the dielectric constant, and tanδ is the dielectric loss tangent. The AC conductivity is directly linked to the dielectric properties of any material. The curves exhibit a linear response at higher temperatures and low frequencies, independent of frequency. However, at higher frequencies, the AC conductivity increases according to the power law  (0≤ s ≤1) for all compositions (0.0≤ × ≤0.4).
(0≤ s ≤1) for all compositions (0.0≤ × ≤0.4).
Figure 13. Frequency dependence of ac conductivity at various temperatures of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageThis dispersive behaviour of total conductivity in ionic conducting materials is explained by A. K. Jonscher's power law, known as the universal Power Law (UPL): 44
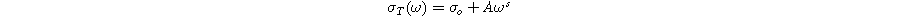
The first term,  is frequency independent and represents the DC conductivity, while the second term is a purely dispersive component of AC conductivity that depends on the measured frequency and parameters A and s. The parameter "s" indicates the extent of interaction between charge carriers and the lattice, while "A" remains frequency-independent but may vary with temperature.
46
An increasing trend in
is frequency independent and represents the DC conductivity, while the second term is a purely dispersive component of AC conductivity that depends on the measured frequency and parameters A and s. The parameter "s" indicates the extent of interaction between charge carriers and the lattice, while "A" remains frequency-independent but may vary with temperature.
46
An increasing trend in  values was observed with increasing frequency and temperature, following Jonscher's power law. At room temperature, the AC conductivity values were found to be on the order of 10−10 S cm−1 for all samples. The increase in
values was observed with increasing frequency and temperature, following Jonscher's power law. At room temperature, the AC conductivity values were found to be on the order of 10−10 S cm−1 for all samples. The increase in  values with temperature can be attributed to the generation of more mobile charge carriers at higher temperatures. It can be observed from Figs. 13a–13e that
values with temperature can be attributed to the generation of more mobile charge carriers at higher temperatures. It can be observed from Figs. 13a–13e that  values decrease with increasing Bi concentration at all temperatures studied. This decrease may be attributed to a reduction in the concentration of mobile charge carriers with increasing Bi concentration. Hence, we can conclude that electrical conduction is dependent on the dopant (Bi) and the concentration of mobile charge carriers (oxygen vacancies). The decrease in conductivity could be linked to a reduction in the conduction path and the emergence of defects due to the substitution of smaller Bi3+ for larger radii Sr2 ions in SBBNX ceramics.
values decrease with increasing Bi concentration at all temperatures studied. This decrease may be attributed to a reduction in the concentration of mobile charge carriers with increasing Bi concentration. Hence, we can conclude that electrical conduction is dependent on the dopant (Bi) and the concentration of mobile charge carriers (oxygen vacancies). The decrease in conductivity could be linked to a reduction in the conduction path and the emergence of defects due to the substitution of smaller Bi3+ for larger radii Sr2 ions in SBBNX ceramics.
Figures 14a–14e display the Arrhenius plot of AC conductivity at different frequencies used in the measurement for various compositions. Based on the different slopes in the plot of  vs (
vs ( ), the plot can be divided into three regions: region 1 (200 °C–280 °C), region 2 (280 °C–350 °C), and Region 3 (350 °C–500 °C). In Region 1, the AC conductivity was found to be independent of temperature and increased with increasing frequency, indicating frequency dispersion at low temperatures, which is an ideal characteristic of ceramics with a plate-like structure.
56
In Region 2,
), the plot can be divided into three regions: region 1 (200 °C–280 °C), region 2 (280 °C–350 °C), and Region 3 (350 °C–500 °C). In Region 1, the AC conductivity was found to be independent of temperature and increased with increasing frequency, indicating frequency dispersion at low temperatures, which is an ideal characteristic of ceramics with a plate-like structure.
56
In Region 2,  increases sharply and exhibits an anomaly near the transition temperature for all samples. This increase in
increases sharply and exhibits an anomaly near the transition temperature for all samples. This increase in  values with temperature can be explained by the formation of oxygen vacancies during the sintering process, which increases with temperature. As the temperature rises, the number of mobile charge carriers increases, leading to an increase in AC conductivity. In region 3 (at high temperatures), the curves converge and become independent of frequency, indicating the onset of intrinsic conductivity that occurs at higher temperatures in these types of ceramics.
57
In the high-temperature region, the conductivity demonstrates frequency-independent behaviour due to thermal activation in SBBNX ceramics.
58
values with temperature can be explained by the formation of oxygen vacancies during the sintering process, which increases with temperature. As the temperature rises, the number of mobile charge carriers increases, leading to an increase in AC conductivity. In region 3 (at high temperatures), the curves converge and become independent of frequency, indicating the onset of intrinsic conductivity that occurs at higher temperatures in these types of ceramics.
57
In the high-temperature region, the conductivity demonstrates frequency-independent behaviour due to thermal activation in SBBNX ceramics.
58
Figure 14. Arrhenius plots for AC conductivity of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageThe activation energy for AC conduction was determined from the slope of the curves for all samples at 10 kHz in different temperature regions using the Arrhenius relation:
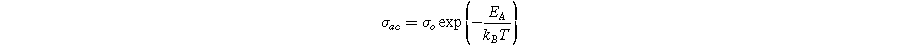
Here,  is a pre-exponential factor,
is a pre-exponential factor,  is the activation energy, and kB
(
is the activation energy, and kB
( J s−1) is the Boltzmann constant. The values of EA in different regions (regions 1 and 2) are listed in Table IV. It can be observed that EA values are lower in Region 2 compared to Region 1, possibly due to the ferroelectric-to-paraelectric phase transition at 396 °C–490 °C for X = 0.0 − 0.4 in SBBNX ceramics. The different EA values in each region suggest the presence of multiple conduction mechanisms. The EA values increase from 0.97 eV (X = 0.0) to 1.33 eV (X = 0.4) by substituting smaller Bi3+ for larger Sr2+ ions in Sr1−xBi2+2X/3Nb2O9. These values are close to the activation energy (1 eV) and confirm the influence of ionized oxygen in the thermal activation process. These values are consistent with the reported values for SBN.
46,59–61
The DC conductivity was estimated by extrapolating the AC conductivity curves. The variation of
J s−1) is the Boltzmann constant. The values of EA in different regions (regions 1 and 2) are listed in Table IV. It can be observed that EA values are lower in Region 2 compared to Region 1, possibly due to the ferroelectric-to-paraelectric phase transition at 396 °C–490 °C for X = 0.0 − 0.4 in SBBNX ceramics. The different EA values in each region suggest the presence of multiple conduction mechanisms. The EA values increase from 0.97 eV (X = 0.0) to 1.33 eV (X = 0.4) by substituting smaller Bi3+ for larger Sr2+ ions in Sr1−xBi2+2X/3Nb2O9. These values are close to the activation energy (1 eV) and confirm the influence of ionized oxygen in the thermal activation process. These values are consistent with the reported values for SBN.
46,59–61
The DC conductivity was estimated by extrapolating the AC conductivity curves. The variation of  as a function of the inverse of temperature for all samples is shown in Fig. 15. An increase in
as a function of the inverse of temperature for all samples is shown in Fig. 15. An increase in  values for all compositions was observed with an increase in temperature, supporting the sample's negative temperature coefficient of resistance (NTCR) behaviour.
62
values for all compositions was observed with an increase in temperature, supporting the sample's negative temperature coefficient of resistance (NTCR) behaviour.
62
Table IV. Electrical properties of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
| Composition | σac (S/cm) 10 kHz | σdc (S/cm) | AC activation energy | DC activation energy | |||
|---|---|---|---|---|---|---|---|
| X | at RT (30 °C) 
|

| EA (eV) | EA (eV) | |||
| Region 1 | Region 2 | Region 1 | Region 2 | Region 3 | |||
| 0.0 | 2.07 | 31.0 | 0.62 | 1.55 | 0.78 | 1.35 | 0.24 |
| 0.1 | 7.50 | 2.36 | 1.18 | 0.36 | 1.58 | 1.00 | 0.08 |
| 0.2 | 1.59 | 3.17 | 1.06 | 0.30 | 1.36 | 0.88 | 0.08 |
| 0.3 | 1.97 | 7.65 | 1.25 | 0.15 | 1.54 | 0.87 | 0.13 |
| 0.4 | 0.66 | 9.45 | 1.08 | 0.15 | 1.53 | 0.81 | 0.003 |
Figure 15. Arrhenius plots for DC conductivity of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageTwo predominant conduction mechanisms were observed in different temperature ranges. At temperatures below the transition temperature, it is expected that the electrical conduction is primarily influenced by extrinsic defects, such as unintentionally introduced impurities. Conversely, at higher temperatures surpassing the transition temperature, conduction is presumed to be primarily governed by intrinsic defects. The variation in the presence of oxygen vacancies determines the charge carriers responsible for both intrinsic and extrinsic conduction in these two temperature regions. Consequently, the charge carriers play a crucial role in the conduction and relaxation processes observed in the SBBNX ceramics. It was also observed that  decreases from 7.89 × 10−7 S cm−1 for X = 0.0 to 6.74 × 10−10 S cm−1 for X = 0.4 with increasing Bi concentration in SBN and the values were found in the range of 10−7 − 10−10 S cm−1 which are approximately 2 orders of magnitude lower than that reported in the literature.
46,61
The activation energy EA for dc conduction in SBBNX ceramics was estimated using the Arrhenius relation and the resulting EA values obtained from the slope of the curves at higher temperatures are listed in Table III, which are consistent with literature findings.
10,37,60,61
Oxygen vacancies, which are defects formed due to the volatilization of Bismuth during the sintering process, play a crucial role in conduction at high temperatures and contribute to a peak in the dielectric loss at the transition temperature.
63
decreases from 7.89 × 10−7 S cm−1 for X = 0.0 to 6.74 × 10−10 S cm−1 for X = 0.4 with increasing Bi concentration in SBN and the values were found in the range of 10−7 − 10−10 S cm−1 which are approximately 2 orders of magnitude lower than that reported in the literature.
46,61
The activation energy EA for dc conduction in SBBNX ceramics was estimated using the Arrhenius relation and the resulting EA values obtained from the slope of the curves at higher temperatures are listed in Table III, which are consistent with literature findings.
10,37,60,61
Oxygen vacancies, which are defects formed due to the volatilization of Bismuth during the sintering process, play a crucial role in conduction at high temperatures and contribute to a peak in the dielectric loss at the transition temperature.
63
Figure 16 displays the polarization-electric field (P-E) hysteresis loop of bismuth-substituted SBN ceramic specimens measured at room temperature. The remnant polarization (Pr) and coercive field (Ec ) values calculated from the loops are summarized in Table V. The addition of Bi in SBBNX ceramics leads to narrower loops. Specifically, for pure SBN (X = 0.0), the remnant polarization (2Pr) is 0.262 μC cm−2 with a coercive field (Ec) of 19.926 kV cm−1. As the value of X increases in Sr1−xBi2+2X/3Nb2O9, 2Pr increases to 0.396 μC cm−2 for X = 0.3 and then decreases to 0.314 μC cm−2 for X = 0.4. The coercive field initially increases up to X = 0.2 and then decreases. The sample with X = 0.3 exhibited to have the highest value of 2Pr with the minimum coercive field as shown in Table V. The P-E loops were also used to estimate the energy storage density (W) and discharge efficiency (η) of SBBNX ceramics using an expression reported elsewhere. 64 The obtained values of W and η are also presented in Table V, with the highest energy storage density of 21.6 mJ cm−3 and efficiency of 64.3% achieved for X = 0.3 in Sr1−xBi2+2X/3Nb2O9.
Figure 16. PE Hysteresis loops of Sr1−xBi2+2X/3Nb2O9 ceramics for (a) X = 0.0; (b) X = 0.1; (c) X = 0.2; (d) X = 0.3; and (e) X = 0.4.
Download figure:
Standard image High-resolution imageTable V. The Ferroelectric and piezoelectric properties of Sr. 1−xBi2+2X/3Nb2O9.
| Composition | 2Pr | 2Ec | d33 | Storage density | Efficiency |
|---|---|---|---|---|---|
| (X) | (μC/cm2) | (KV/cm) | (pC/N) | ( ) ) |

|
| 0.0 | 0.26 | 19.93 | 14 | 12.7 | 51.8 |
| 0.1 | 0.23 | 20.83 | 12 | 14.9 | 53.5 |
| 0.2 | 0.20 | 21.22 | 17 | 17.2 | 55.4 |
| 0.3 | 0.39 | 14.67 | 21 | 21.6 | 64.3 |
| 0.4 | 0.32 | 15.59 | 13 | 19.8 | 58.7 |
The 2Pr value obtained in our study is notably lower than the previously reported value for SBN. 63 This reduction in 2Pr can be attributed to several factors. First, it is connected to the challenge of domain switching, which arises due to a decrease in crystal grain size and a reduction in the unit cell volume. 65,66 Additionally, the decrease in 2Pr can be attributed to the heightened presence of oxygen vacancies in Aurivillius-type ceramics, induced by the volatilization of Bi3+ ions at high temperatures. In the presence of an external electric field, these oxygen vacancies tend to migrate towards domain walls with lower energy, effectively anchoring the domain walls and impeding their switching. This, in turn, leads to a reduction in 2Pr. 67 Furthermore, a noticeable decrease in structural distortion and an increase in oxygen vacancies near domain boundaries occur due to the accumulation of (Bi2O2)2+ layers. These changes in the material's structure also contribute to the overall decrease in 2Pr. 68
For piezoelectric measurements, all the samples were subjected to a DC electric field of 3 kV mm−1 for 1 h in a silicone oil bath. The observed values of the piezoelectric coefficient (d33 in pC/N) are provided in Table V. It was observed that the value of d33 initially increases and then decreases with an increase in Bi content at the Sr-site in SBN. The sample with a composition of X = 0.3 exhibited a higher d33 value compared to the other samples. For X ≤ 0.3, lower drive energy is required for domain wall movement, leading to higher piezoelectricity due to reduced domain activity. However, for X > 0.3, an increase in Bi content increases oxygen vacancies, hindering domain movement and resulting in higher ageing in ceramics and lower piezoelectricity. 60
Conclusions
We investigated the impact of Bi3+ on the crystal structure, microstructure, dielectric, ferroelectric, and piezoelectric properties of Sr1−XBi2+2X/3Nb2O9 (SBBNx) ceramics with X ranging from 0.0 to 0.4. All compounds crystallized into an orthorhombic structure with a slight decrease in cell volume when X varies from 0.0 to 0.4. The X-ray diffraction (XRD) data of SBBNx were well supported by Rietveld refinement analysis. Scanning electron microscopy (SEM) images revealed a plate-like structure characterized by well-defined grains and grain boundaries, which is typical of bismuth-layered structure ferroelectric (BLSF) ceramics. The dielectric constant exhibited an initial increase for X ≤ 0.3 and then decreased. Additionally, there was a systematic enhancement in the transition temperature from 396 °C (for X = 0.0) to 490 °C (for X = 0.4) with an increase in Bi3+ concentration at the Sr2+ site in SBN. The values of γ were found to be 0.97 and 1.89 for X = 0.2 and X = 0.4, respectively, indicating normal ferroelectric and relaxor behaviour. The electrical conductivity study revealed that the conductivity behaviour is governed by oxygen vacancies, and the AC conductivity values for Bi-substituted SBN were lower than those of undoped SBN. The ferroelectric and piezoelectric properties showed enhancement, with high remnant polarization Pr = 0.39 μC cm−2 and low coercive field (Ec =14.67 KV cm−1). A high piezoelectric coefficient (d33 = 22 pC/N) was observed for X = 0.3. Such compositions could be excellent materials both for highly stable ferroelectric memory devices and for high-temperature piezoelectric applications.
Acknowledgments
The author, R. Singh, expresses gratitude to the Research Laboratory, Department of Physics, Gargi College, University of Delhi, New Delhi, for their invaluable research support. Additionally, the authors extend their appreciation to the USIC, Department of Physics and Astrophysics, University of Delhi, India for conducting the XRD and Raman spectroscopy measurements. Special thanks are also extended to Prof. Binay Kumar for providing the piezoelectric measurement facility. R. Singh acknowledges the continuous support from Prof. Gyantosh Kumar Jha, Principal of ARSD College, University of Delhi.

















