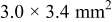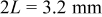Abstract
Electrical conductivity relaxations were measured at a fixed temperature  on proton-conducting
on proton-conducting  upon sudden changes of oxygen activity in fixed water-vapor activity atmospheres and vice versa, in the ranges of
upon sudden changes of oxygen activity in fixed water-vapor activity atmospheres and vice versa, in the ranges of  and
and  , respectively. It has been confirmed that the conductivity relaxes generally with two different relaxation times or twofold, but always nonmonotonically upon hydration/dehydration and monotonically upon oxidation/reduction. This twofold relaxation is attributed to the superposition of the two chemical diffusion processes of component H and O, driven by either the water or oxygen chemical potential gradient. The analytic solution to the conductivity relaxation, be it monotonic or nonmonotonic, is presented in closed form and thereby evaluated the two chemical diffusivities governing the hydration and oxidation kinetics, respectively.
, respectively. It has been confirmed that the conductivity relaxes generally with two different relaxation times or twofold, but always nonmonotonically upon hydration/dehydration and monotonically upon oxidation/reduction. This twofold relaxation is attributed to the superposition of the two chemical diffusion processes of component H and O, driven by either the water or oxygen chemical potential gradient. The analytic solution to the conductivity relaxation, be it monotonic or nonmonotonic, is presented in closed form and thereby evaluated the two chemical diffusivities governing the hydration and oxidation kinetics, respectively.
Export citation and abstract BibTeX RIS
In the process of measurement of the equilibrium (total) electrical conductivity on a proton-conducting oxide  against oxygen activity
against oxygen activity  and water-vapor activity
and water-vapor activity  , it was observed (henceforth referred to as Ref. 1) that upon hydration or dehydration in fixed
, it was observed (henceforth referred to as Ref. 1) that upon hydration or dehydration in fixed  atmospheres, the conductivity relaxes always nonmonotonically to a new equilibrium value, leaving an extremum (minimum for hydration and maximum for dehydration) in between, while the relaxation during oxidation or reduction is always monotonic, irrespective of
atmospheres, the conductivity relaxes always nonmonotonically to a new equilibrium value, leaving an extremum (minimum for hydration and maximum for dehydration) in between, while the relaxation during oxidation or reduction is always monotonic, irrespective of  in fixed
in fixed  atmospheres. The hydration kinetics of a proton conductor oxide used to be understood as being due to the chemical diffusion of
atmospheres. The hydration kinetics of a proton conductor oxide used to be understood as being due to the chemical diffusion of  or ambipolar diffusion of oxide ions (or vacancies) and protons.2, 3 One thus expected a usual monotonic relaxation of conductivity as in chemical diffusion of oxygen in acceptor-doped
or ambipolar diffusion of oxide ions (or vacancies) and protons.2, 3 One thus expected a usual monotonic relaxation of conductivity as in chemical diffusion of oxygen in acceptor-doped  under an oxygen potential gradient.4 In this light, this nonmonotonic relaxation behavior was quite unusual.
under an oxygen potential gradient.4 In this light, this nonmonotonic relaxation behavior was quite unusual.
In Ref. 1, Yoo et al. interpreted the nonmonotonic relaxation upon hydration or dehydration as being due to the superposition of two chemical diffusion processes of chemical components H and O, or the ambipolar diffusion of protons ( or equivalently
or equivalently  ) and holes
) and holes  and of oxygen vacancies
and of oxygen vacancies  and holes, both down the water chemical potential gradient imposed. Upon hydration, for instance, in-diffusion of H reduces the concentration of holes via the reaction
and holes, both down the water chemical potential gradient imposed. Upon hydration, for instance, in-diffusion of H reduces the concentration of holes via the reaction  , but in-diffusion of O increases the hole concentration via
, but in-diffusion of O increases the hole concentration via  , thus leading to a twofold nonmonotonic variation of the conductivity with time. On the basis of this picture, Yoo et al. presented a closed-form solution for conductivity relaxation upon hydration/dehydration, and thereby evaluated with sufficient accuracy the two chemical diffusivities,
, thus leading to a twofold nonmonotonic variation of the conductivity with time. On the basis of this picture, Yoo et al. presented a closed-form solution for conductivity relaxation upon hydration/dehydration, and thereby evaluated with sufficient accuracy the two chemical diffusivities,  and
and  , for H and O, respectively. Almost at the same time, Yu et al.5 also confirmed experimentally by optical spectroscopic means these decoupled chemical diffusion processes upon hydration of Fe-doped
, for H and O, respectively. Almost at the same time, Yu et al.5 also confirmed experimentally by optical spectroscopic means these decoupled chemical diffusion processes upon hydration of Fe-doped  .
.
The redox relaxation in the presence of protons was also interpreted in the same line as twofold but in counter directions, that is, chemical diffusion of O down the oxygen potential gradient and unmixing of H up the gradient. This counter diffusion of O and H should lead to a monotonic conductivity relaxation in appearance but still involves two chemical diffusivities,  and
and  , in principle. For the system of
, in principle. For the system of  , however, its relaxation kinetics was found to be essentially determined by oxygen chemical diffusivity
, however, its relaxation kinetics was found to be essentially determined by oxygen chemical diffusivity  only.
only.
The picture of twofold relaxation and the analytic solution developed in Ref. 1 appear very convincing but have so far been tried on a single specific system,  only. It is necessary to reconfirm the picture and solution by trying on another system of proton conductor oxide, at which the present work is thus aimed. To this end, the conductivity relaxation was measured at
only. It is necessary to reconfirm the picture and solution by trying on another system of proton conductor oxide, at which the present work is thus aimed. To this end, the conductivity relaxation was measured at  on another proton conductor
on another proton conductor  upon hydration and dehydration back in fixed
upon hydration and dehydration back in fixed  atmospheres and upon oxidation and reduction back in fixed
atmospheres and upon oxidation and reduction back in fixed  atmospheres, both in the same ranges as in Ref. 1. We hereby report the results in comparison with those reported earlier on
atmospheres, both in the same ranges as in Ref. 1. We hereby report the results in comparison with those reported earlier on  in Ref. 1.
in Ref. 1.
Experimental
The experimental procedures have been detailed in Ref. 1. Briefly, the specimen with the nominal composition  was prepared via a solid-state reaction route. The sintered sample was of single phase by X-ray diffractometry and ca. 99% or higher density, with a mean grain size of
was prepared via a solid-state reaction route. The sintered sample was of single phase by X-ray diffractometry and ca. 99% or higher density, with a mean grain size of  . The sample was cut into parallelepipeds measuring
. The sample was cut into parallelepipeds measuring  , and Pt electrodes were appropriately attached in a four-probe arrangement for conductivity relaxation measurement.
, and Pt electrodes were appropriately attached in a four-probe arrangement for conductivity relaxation measurement.
DC four-probe conductivity of the specimen was monitored with time at a fixed temperature of  , upon abruptly changing the water-vapor activity
, upon abruptly changing the water-vapor activity  , while keeping the oxygen activity
, while keeping the oxygen activity  fixed and vice versa, in a reaction chamber as detailed elsewhere.6 Oxygen activity was controlled by
fixed and vice versa, in a reaction chamber as detailed elsewhere.6 Oxygen activity was controlled by  gas mixtures in the range of
gas mixtures in the range of  and monitored by zirconia-based oxygen sensors. Water vapor pressure was controlled in the range of
and monitored by zirconia-based oxygen sensors. Water vapor pressure was controlled in the range of  by passing the atmosphere gas through liquid water at controlled temperatures and measured by a hygrometer (Hygro-M4, General Eastern Instruments, U.S.A.). Oxygen activity windows were each kept no greater than an order of magnitude
by passing the atmosphere gas through liquid water at controlled temperatures and measured by a hygrometer (Hygro-M4, General Eastern Instruments, U.S.A.). Oxygen activity windows were each kept no greater than an order of magnitude  and water-vapor activity windows no greater than a half order of magnitude
and water-vapor activity windows no greater than a half order of magnitude  so that the relevant chemical diffusivities could be regarded as constant across each window.
so that the relevant chemical diffusivities could be regarded as constant across each window.
Results and Discussion
Equilibrium conductivity
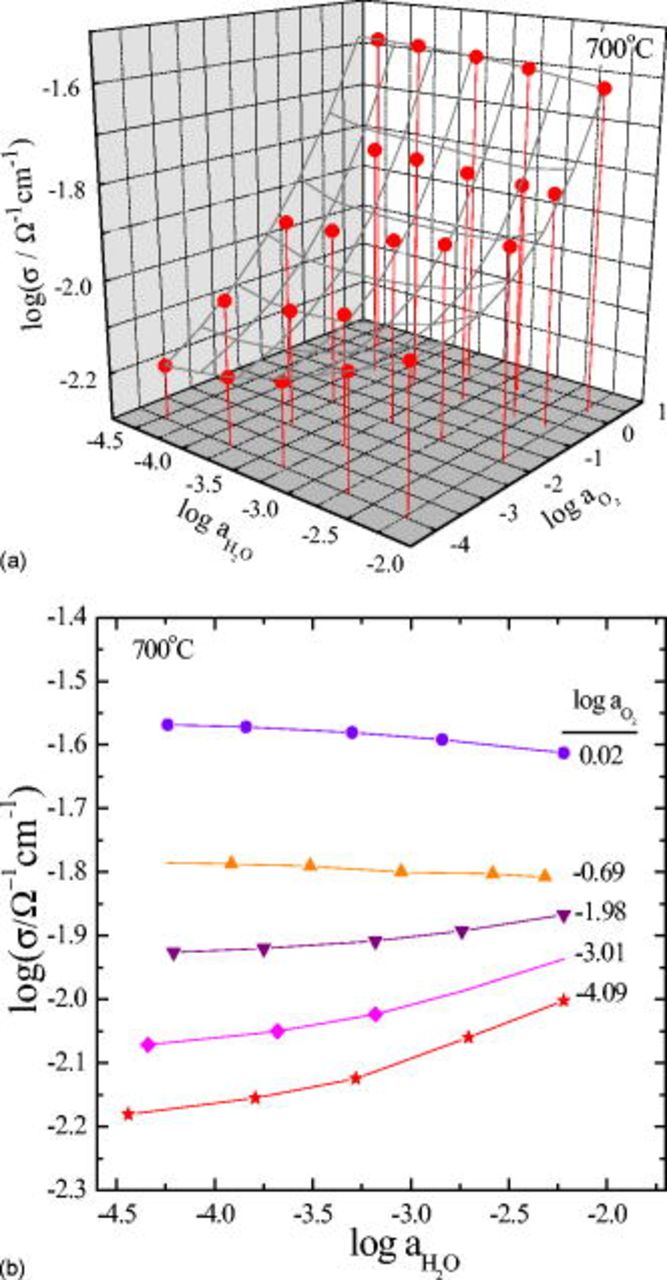
The values for equilibrium conductivity were collected after the conductivity relaxed from an initial equilibrium value to a new equilibrium value after abruptly changing either oxygen partial pressure or water vapor pressure while the other was kept constant. They are represented over a plane of  vs
vs  in Fig. 1a to show a general landscape of the
in Fig. 1a to show a general landscape of the  isotherm in the thermodynamic configuration space. As is seen, the conductivity monotonically increases with
isotherm in the thermodynamic configuration space. As is seen, the conductivity monotonically increases with  at a fixed
at a fixed  . With increasing
. With increasing  , however, the conductivity somewhat increases in reducing atmospheres but tends to decrease as the atmo- sphere gets more and more oxidizing (see Fig. 1b). Remembering that the charge carriers of the present system are oxygen vacancies
, however, the conductivity somewhat increases in reducing atmospheres but tends to decrease as the atmo- sphere gets more and more oxidizing (see Fig. 1b). Remembering that the charge carriers of the present system are oxygen vacancies  , protons
, protons  , and holes
, and holes  in the thermodynamic conditions examined,1, 7 it is suggested that the increasing proton conductivity overrides the decreasing hole conductivity with increasing
in the thermodynamic conditions examined,1, 7 it is suggested that the increasing proton conductivity overrides the decreasing hole conductivity with increasing  in the reducing atmospheres, but as the atmosphere goes more and more oxidizing, the situation is gradually reversed.
in the reducing atmospheres, but as the atmosphere goes more and more oxidizing, the situation is gradually reversed.
Figure 1. Equilibrium conductivity isotherm of  at
at  in three-dimensional representation over a plane
in three-dimensional representation over a plane  vs
vs  (a), and in two-dimensional representation at different
(a), and in two-dimensional representation at different  (b). Solid lines for visual guidance.
(b). Solid lines for visual guidance.
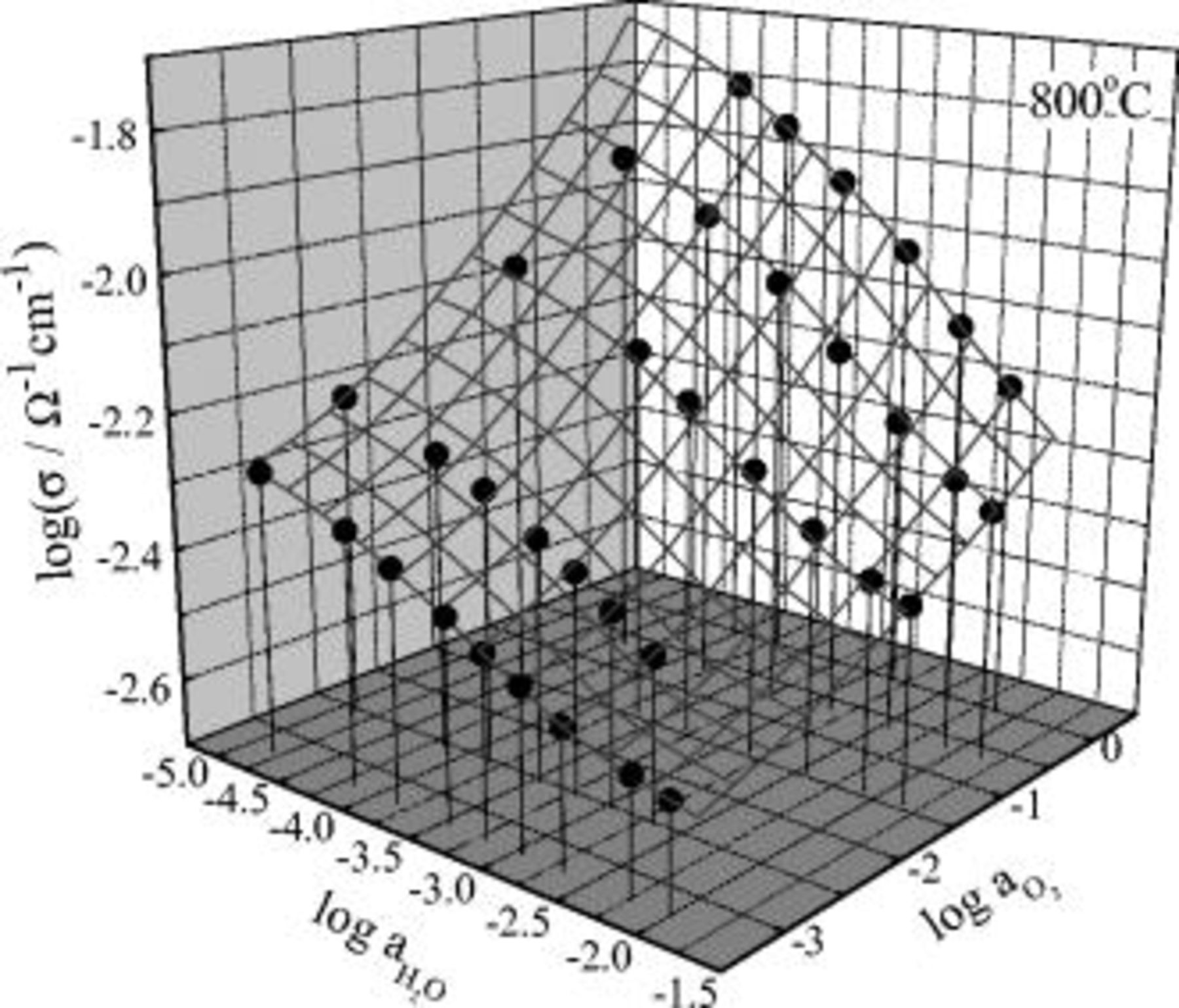
The conductivity variation against  of the present system is contrasted with that of the earlier system
of the present system is contrasted with that of the earlier system  ,1 in that for the latter the total conductivity always decreases with increasing
,1 in that for the latter the total conductivity always decreases with increasing  irrespective of
irrespective of  in the atmosphere, as shown in Fig. 2. This contrast is obviously attributed to a difference in defect formation reaction equilibrium constants involved, but detailed treatment is out of the scope of the present work.
in the atmosphere, as shown in Fig. 2. This contrast is obviously attributed to a difference in defect formation reaction equilibrium constants involved, but detailed treatment is out of the scope of the present work.
Figure 2. The conductivity isotherm of  at
at  in three-dimensional representation. Note that the conductivity always decreases with increasing
in three-dimensional representation. Note that the conductivity always decreases with increasing  in any fixed oxygen activity atmosphere. (From Ref. 1.)
in any fixed oxygen activity atmosphere. (From Ref. 1.)
Conductivity relaxations
Upon hydration/dehydration
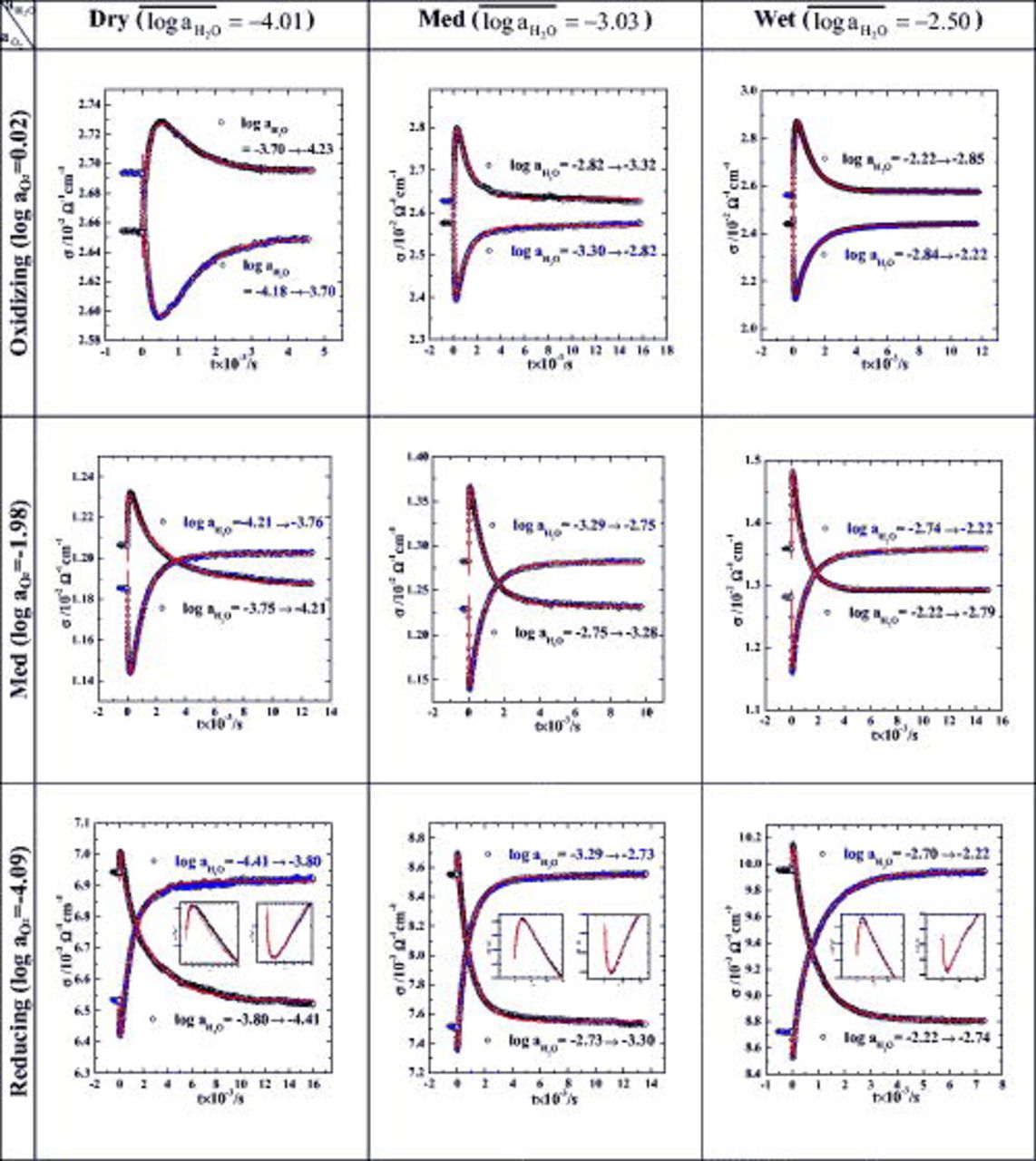
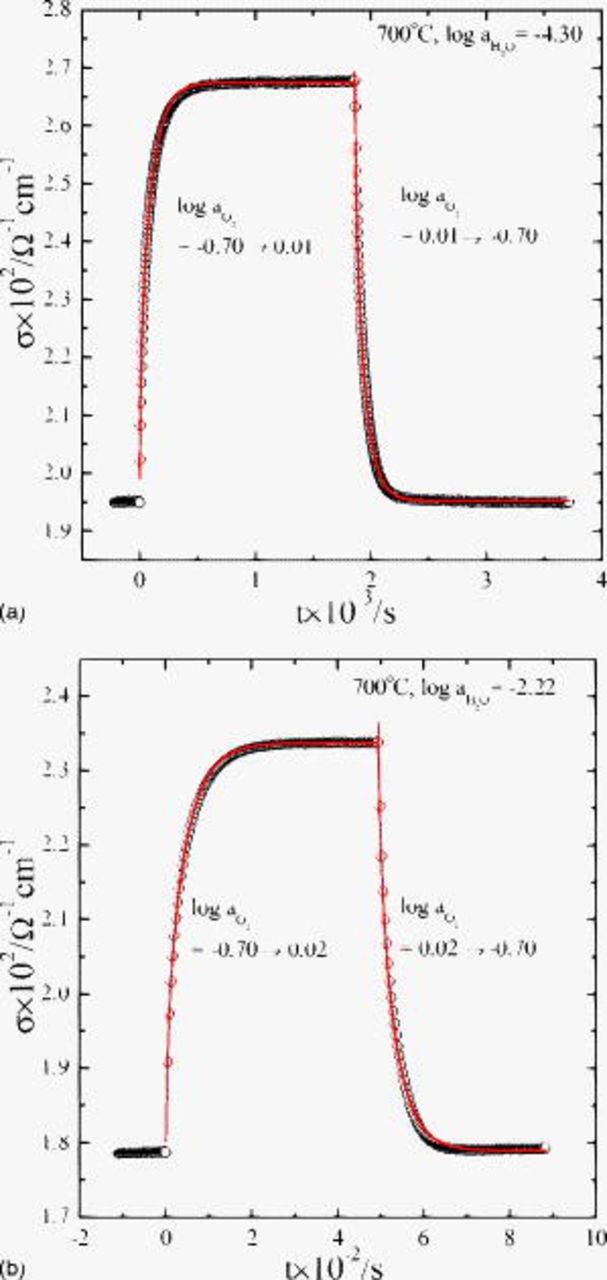
Fig- ure 3 shows the typical behavior of conductivity relaxation upon hydration and subsequent dehydration back across the same  window in a fixed
window in a fixed  atmosphere
atmosphere  . Whenthe water vapor suddenly steps up
. Whenthe water vapor suddenly steps up  , the conductivity first decreases rather sharply and then relatively slowly increases, leaving a minimum in between, toward a new equilibrium value. When
, the conductivity first decreases rather sharply and then relatively slowly increases, leaving a minimum in between, toward a new equilibrium value. When  subsequently steps back down to the original value
subsequently steps back down to the original value  , the conductivity relaxes in exactly the opposite sense: first sharply increases and then slowly decreases, leaving a maximum in between, to the original conductivity value. While its nonmonotonic feature remains the same as in Fig. 3, the kinetics of conductivity relaxation appears dependent on
, the conductivity relaxes in exactly the opposite sense: first sharply increases and then slowly decreases, leaving a maximum in between, to the original conductivity value. While its nonmonotonic feature remains the same as in Fig. 3, the kinetics of conductivity relaxation appears dependent on  as well as
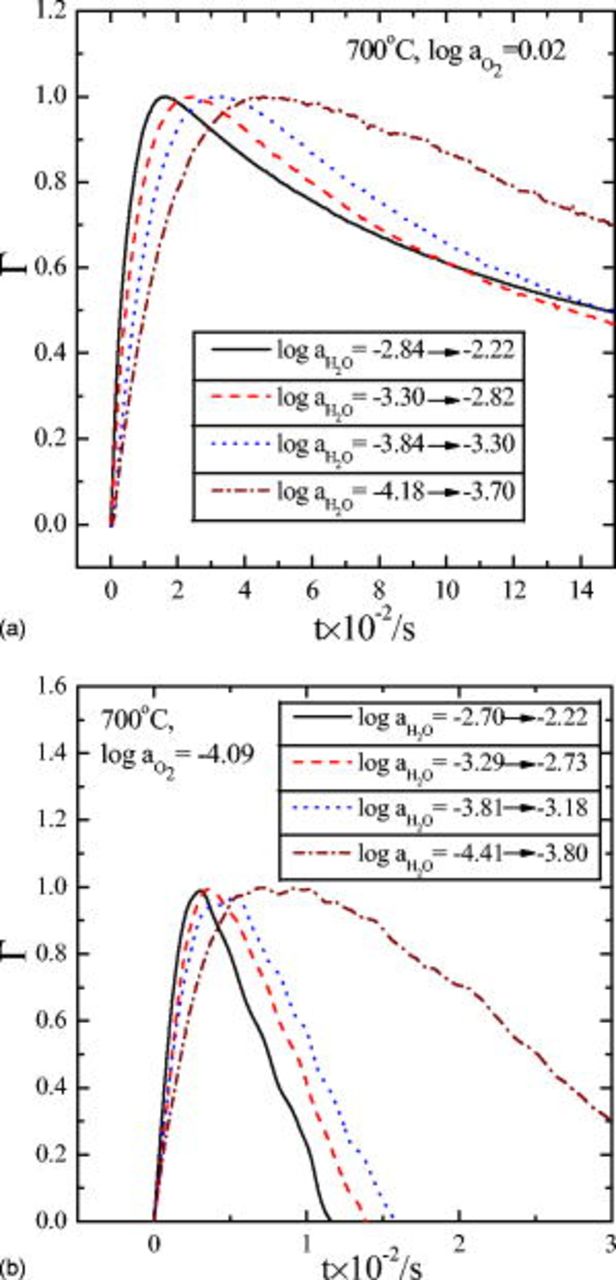
as well as  in their ranges examined, as shown in Fig. 4. It is seen that the initial relaxation gets faster, thus exhibiting the extremum (the minimum or maximum) earlier as the atmosphere gets wetter and more reducing. This kinetic characteristic is more clearly summarized in Fig. 5, where the relative conductivity change with respect to the maximum span of the change, Γ, at different humidity is plotted against time in the most oxidizing atmosphere (a) and in the most reducing atmosphere (b).
in their ranges examined, as shown in Fig. 4. It is seen that the initial relaxation gets faster, thus exhibiting the extremum (the minimum or maximum) earlier as the atmosphere gets wetter and more reducing. This kinetic characteristic is more clearly summarized in Fig. 5, where the relative conductivity change with respect to the maximum span of the change, Γ, at different humidity is plotted against time in the most oxidizing atmosphere (a) and in the most reducing atmosphere (b).
Figure 3. Typical conductivity relaxation of  upon hydration and then dehydration back at
upon hydration and then dehydration back at  . Note the conductivity varies in a nonmonotonic mode to exhibit a minimum (hydration) and a maximum (dehydration). Solid line, the best fitted to Eq. 6a, 6b in the text.
. Note the conductivity varies in a nonmonotonic mode to exhibit a minimum (hydration) and a maximum (dehydration). Solid line, the best fitted to Eq. 6a, 6b in the text.
Figure 4. Conductivity relaxations upon hydration and reverse of  at
at  vs
vs  and
and  . Insets in the bottom row are the exploded views of the initial fast relaxations. Note that as the atmosphere gets wetter and more reducing, the initial relaxation gets faster, thus exhibiting the extremum earlier. Solid lines are all the best-fitted to Eq. 6a, 6b in text.
. Insets in the bottom row are the exploded views of the initial fast relaxations. Note that as the atmosphere gets wetter and more reducing, the initial relaxation gets faster, thus exhibiting the extremum earlier. Solid lines are all the best-fitted to Eq. 6a, 6b in text.
Figure 5. Relative conductivity change Γ vs time upon hydration in oxidizing atmosphere (a) and reducing atmosphere (b). Note the time for  or the extremum depends on the atmosphere.
or the extremum depends on the atmosphere.
It is interesting to compare the characteristic nonmonotonic behavior of the present system (Fig. 3 or Fig. 4) with that of its cousin  (see Fig. 6). One can see that the present oxide
(see Fig. 6). One can see that the present oxide  always displays the sharper, and thus much more conspicuous, extrema against time. This difference points to the fact that the twofold kinetics, rendering the conductivity to change in the opposite sense, should be faster for the present system than the earlier.
always displays the sharper, and thus much more conspicuous, extrema against time. This difference points to the fact that the twofold kinetics, rendering the conductivity to change in the opposite sense, should be faster for the present system than the earlier.
Figure 6. Comparison of the relative conductivity variation vs time for  (solid line) and
(solid line) and  (dashed line) upon hydration at
(dashed line) upon hydration at  in the similar atmospheres.
in the similar atmospheres.
Upon oxidation/reduction
Figures 7a and 7b show, respectively, the typical conductivity relaxation behaviors upon oxidation and reduction back in dry atmosphere (a) and wet atmosphere (b). There is nothing peculiar: in any case, the conductivity relaxes always monotonically and apparently singlefold, as usually observed in oxygen potential gradients,4 in agreement with the earlier  in Ref. 1.
in Ref. 1.
Figure 7. Conductivity relaxation of  at
at  in dry atmosphere (a) and wet atmosphere (b). Note that the relaxation is singlefold monotonic irrespective of humidity. The solid lines are the best-fitted to Eq. 6a, 6b in text.
in dry atmosphere (a) and wet atmosphere (b). Note that the relaxation is singlefold monotonic irrespective of humidity. The solid lines are the best-fitted to Eq. 6a, 6b in text.
Quantitative analyses
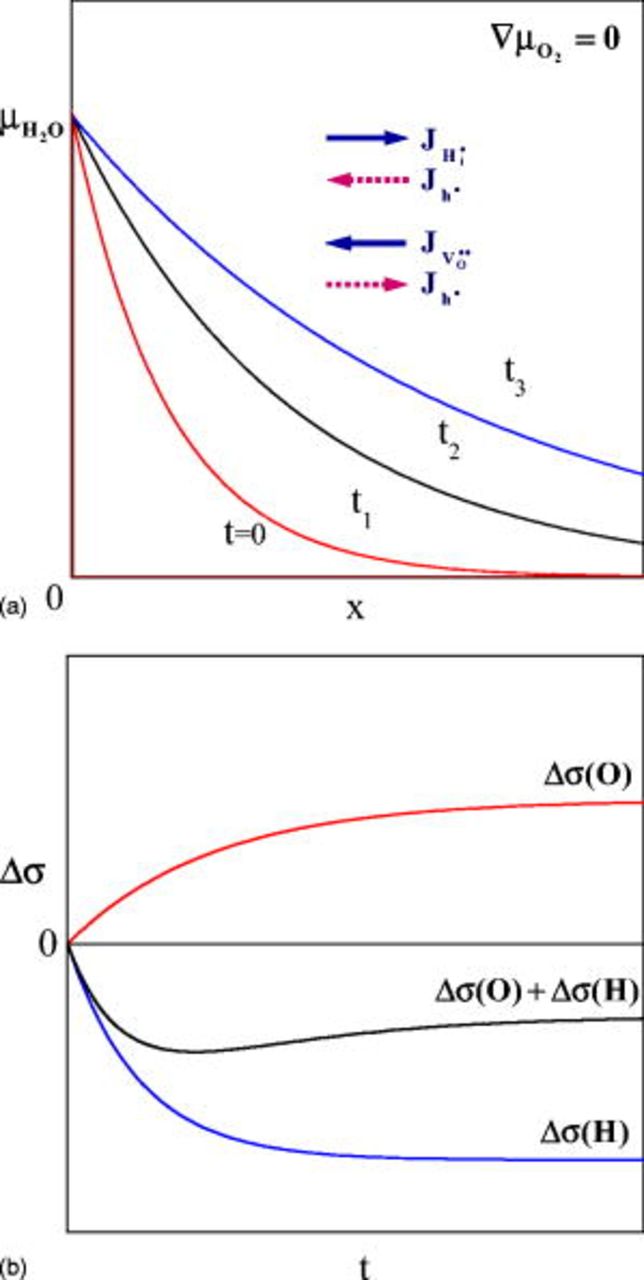
Things happening upon hydration/dehydration or upon oxidation/reduction have already been detailed in Ref. 1. They are briefly as illustrated in Fig. 8 and 9: Upon hydration and dehydration, water does not diffuse via an ambipolar diffusion of  and
and  (or
(or  and
and  in terms of defects) as had been envisaged.2, 3 They first decompose into H and O, probably on the surface of the oxide, and each diffuse independently with the mediation of holes (Fig. 8a). The in-diffusion of O (or equivalently, out-diffusion of
in terms of defects) as had been envisaged.2, 3 They first decompose into H and O, probably on the surface of the oxide, and each diffuse independently with the mediation of holes (Fig. 8a). The in-diffusion of O (or equivalently, out-diffusion of  ) tends to enhance the conductivity
) tends to enhance the conductivity  by increasing the hole concentration, and the in-diffusion of H (or equivalently,
by increasing the hole concentration, and the in-diffusion of H (or equivalently,  ) tends to reduce it
) tends to reduce it  by reducing the hole concentration. Thus, the overall conductivity variation
by reducing the hole concentration. Thus, the overall conductivity variation  during hydration (or dehydration) is always nonmono-tonic, because the effects of the two chemical diffusion processes are opposite (see Fig. 8b).
during hydration (or dehydration) is always nonmono-tonic, because the effects of the two chemical diffusion processes are opposite (see Fig. 8b).
Figure 8. (a) Decoupled diffusion fluxes of components H and O and temporal variation of water vapor chemical potential during hydration  . (b) Expected conductivity variation Δσ as the superposition of the effect by H-diffusion
. (b) Expected conductivity variation Δσ as the superposition of the effect by H-diffusion  and O-diffusion
and O-diffusion  with time. (From Ref. 1.)
with time. (From Ref. 1.)
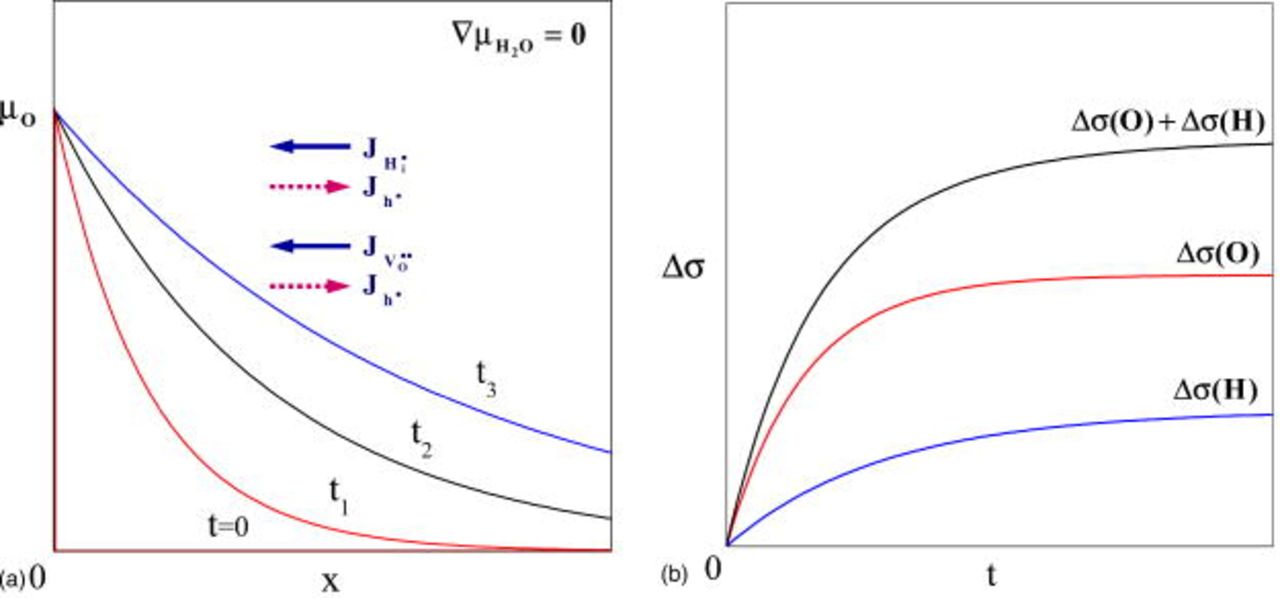
During oxidation or reduction, the two fluxes of O and H (the latter due to unmixing in an oxygen potential gradient) will always be antiparallel (Fig. 9a), while their effects on conductivity change  should always be in the same direction, leading to a monotonic relaxation (Fig. 8b). This monotonic but, in principle, twofold behavior is analogous to the conductivity relaxation of single-crystal
should always be in the same direction, leading to a monotonic relaxation (Fig. 8b). This monotonic but, in principle, twofold behavior is analogous to the conductivity relaxation of single-crystal  under oxygen potential gradient.8 In this system, the conductivity relaxation during oxidation or reduction has been found to be due to the decoupled chemical diffusion of oxygen vacancies and Ti interstitials with the help of electrons, with local defect equilibrium broken down. Quantitatively, the fluxes of component H (denoted by the subscript i) and O (by the subscript v), that are due to the ambipolar diffusion of charged components
under oxygen potential gradient.8 In this system, the conductivity relaxation during oxidation or reduction has been found to be due to the decoupled chemical diffusion of oxygen vacancies and Ti interstitials with the help of electrons, with local defect equilibrium broken down. Quantitatively, the fluxes of component H (denoted by the subscript i) and O (by the subscript v), that are due to the ambipolar diffusion of charged components  and
and  +(or in terms of defects,
+(or in terms of defects,  ) and
) and  and
and  (or
(or  ), respectively may each be represented during hydration or dehydration in a homogeneous
), respectively may each be represented during hydration or dehydration in a homogeneous  atmosphere as
atmosphere as
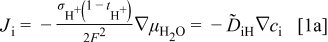
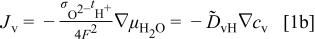
and during oxidation or reduction in a homogeneous water-vapor activity atmosphere as
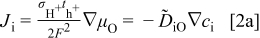
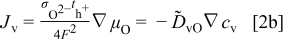
considering the charge neutrality among the charged components  and the local ionization and chemical equilibria among the charged and chemical components
and the local ionization and chemical equilibria among the charged and chemical components  . For more detailed derivation, the reader is referred to Ref. 1. The four chemical diffusivities are defined, respectively, as
. For more detailed derivation, the reader is referred to Ref. 1. The four chemical diffusivities are defined, respectively, as
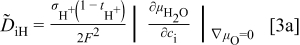
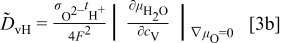
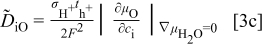

where  denotes the Faraday constant, and
denotes the Faraday constant, and  and
and  the partial electrical conductivity and transference number of the
the partial electrical conductivity and transference number of the  -type carriers (
-type carriers ( ,
,  ,
,  , in terms of charged components), respectively. The quantities within the absolute-value signs (∣ ∣) are corresponding thermodynamic factors or more appropriately, the conversion factors converting a chemical potential gradient to the relevant gradients of defect concentrations
, in terms of charged components), respectively. The quantities within the absolute-value signs (∣ ∣) are corresponding thermodynamic factors or more appropriately, the conversion factors converting a chemical potential gradient to the relevant gradients of defect concentrations  or
or  . It is emphasized that
. It is emphasized that  is the chemical diffusivity of component O in the conventional Wagner sense.9
is the chemical diffusivity of component O in the conventional Wagner sense.9
Figure 9. (a) Decoupled diffusion fluxes of components H and O and temporal variation of oxygen chemical potential during oxidation  . (b) Expected conductivity variation Δσ as the superposition of the effect by H-diffusion
. (b) Expected conductivity variation Δσ as the superposition of the effect by H-diffusion  and O-diffusion
and O-diffusion  with time. (From Ref. 1.)
with time. (From Ref. 1.)
The overall conductivity relaxation is the manifestation of the two decoupled chemical diffusion processes, where the spatial average of conductivity of a specimen  may be given in terms of the temporal variation of the mean concentration of H and O (or equivalently
may be given in terms of the temporal variation of the mean concentration of H and O (or equivalently  and
and  in terms of defects) in the oxide as1, 10
in terms of defects) in the oxide as1, 10
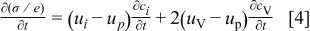
where  represents the electrochemical mobility of the
represents the electrochemical mobility of the  -type carrier (
-type carrier ( ,
,  ,
,  in terms of defects). Assuming no internal reaction among the carriers, one has
in terms of defects). Assuming no internal reaction among the carriers, one has
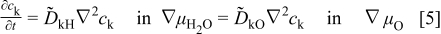
for each of the ionic carriers  . By substituting the trigonometric series solutions for a two-dimensional geometry of the specimen
. By substituting the trigonometric series solutions for a two-dimensional geometry of the specimen  to Eq. 5 into Eq. 4, one finally obtains1
to Eq. 5 into Eq. 4, one finally obtains1

with
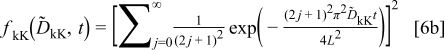
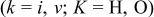
where  are the constants each involving the initial and final concentration of the relevant carriers (defects) and their electrochemical mobilities.10 It is noted that
are the constants each involving the initial and final concentration of the relevant carriers (defects) and their electrochemical mobilities.10 It is noted that  corresponds to the final equilibrium state conductivity because
corresponds to the final equilibrium state conductivity because  as
as  .
.
The conductivity relaxations during hydration/dehydration and oxidation/reduction are each fittedto Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a, yielding the best fitted values for the relevant chemical diffusivities in Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d. As delineated by the solid lines in Fig. 3, 4 and 7, the present analytic solution, Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a, is sufficiently precise to describe all the conductivity relaxations, whether upon hydration/dehydration or oxidation/reduction. This sufficiently high precision of the closed-form solution, Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a, indicates that the overall relaxation kinetics are essentially governed exclusively by the superposed chemical diffusion processes.6 Otherwise, or if the surface reaction kinetics were not negligible compared to the diffusion processes, such highly precise fitting would be unlikely.6 The two chemical diffusivities  and
and  are consequently evaluated as the fitting parameters from the hydration/dehydration relaxations and another two
are consequently evaluated as the fitting parameters from the hydration/dehydration relaxations and another two  and
and  from the oxidation/reduction relaxations. The oxidation/reduction relaxations are all described by a single diffusivity
from the oxidation/reduction relaxations. The oxidation/reduction relaxations are all described by a single diffusivity  , that is, singlefold relaxation in any case, in agreement with the earlier study in Ref. 1.
, that is, singlefold relaxation in any case, in agreement with the earlier study in Ref. 1.
At this point, one may suspect which of the two numerical values, as evaluated by fitting, is for which diffusivity of H and O in each case. In hydration/dehydration relaxations, it is straightforward because the fluxes of H and O are in parallel in any case and hence, their contributions to the conductivity change are opposite (see Fig. 8b). In the case of oxidation or reduction relaxations, one may suspect that it would be not so straightforward if the relaxation were twofold because the relaxation is monotonic. There will be, however, a sound logical criterion to discern the two diffusivities  and
and  . The relaxations in dry atmosphere, which are always singlefold monotonic, are obviously due to the chemical diffusion of oxygen
. The relaxations in dry atmosphere, which are always singlefold monotonic, are obviously due to the chemical diffusion of oxygen  , because there is little concentration of protons and oxygen vacancies are in the majority due to the doped acceptors
, because there is little concentration of protons and oxygen vacancies are in the majority due to the doped acceptors  . This chemical diffusivity of oxygen may not differ significantly, even in the wet atmosphere. Thus, the diffusivity of similar size, which would be evaluated in wet atmosphere, must then be due to the component oxygen.
. This chemical diffusivity of oxygen may not differ significantly, even in the wet atmosphere. Thus, the diffusivity of similar size, which would be evaluated in wet atmosphere, must then be due to the component oxygen.
One may now ask why, unlike the hydration/dehydration relaxations, the redox relaxations are always singlefold, no matter whether dry or wet, where only one chemical diffusivity  , that is the chemical diffusivity of oxygen per se, is evaluated. This is mathematically because the contribution of protons
, that is the chemical diffusivity of oxygen per se, is evaluated. This is mathematically because the contribution of protons  to the conductivity change in an oxygen potential gradient is negligible compared to the contribution by oxygen vacancies
to the conductivity change in an oxygen potential gradient is negligible compared to the contribution by oxygen vacancies  (see Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a). Thus, there may be two possibilities:10 either the chemical diffusion of H
(see Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a). Thus, there may be two possibilities:10 either the chemical diffusion of H  is so sluggish in the oxygen potential gradient imposed so that one can hardly see its effect on the conductivity change in an experimentally viable time range, or the amplification factor
is so sluggish in the oxygen potential gradient imposed so that one can hardly see its effect on the conductivity change in an experimentally viable time range, or the amplification factor  in Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a itself is negligible in any case. For a detailed discus-sion of the manifestation of the twofold kinetics, the reader is referred to Ref. 10. Both possibilities indicate
in Eq. 1a, 1b, 2a, 2b, 3a, 3b, 3c, 3d, 6a itself is negligible in any case. For a detailed discus-sion of the manifestation of the twofold kinetics, the reader is referred to Ref. 10. Both possibilities indicate
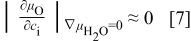
that is, the oxygen chemical potential has little to do with the proton concentration, as guessed intuitively.
The numerical values for the four diffusivities, in which  in any case, are all tabulated in Table I. One can see that the two numerical values for a diffusivity, as obtained from a process of either oxidation or hydration and its reverse process, are in satisfactory agreement (within a factor of 1.5 on average and a factor of 2.6 in the worst) with each other, which again strongly supports the fact that the surface reaction step was indeed fast enough compared to the solid-state diffusion processes.
in any case, are all tabulated in Table I. One can see that the two numerical values for a diffusivity, as obtained from a process of either oxidation or hydration and its reverse process, are in satisfactory agreement (within a factor of 1.5 on average and a factor of 2.6 in the worst) with each other, which again strongly supports the fact that the surface reaction step was indeed fast enough compared to the solid-state diffusion processes.
Table I. The four chemical diffusivities evaluated from oxidation/reduction relaxations ( ,
,  ) and from hydration/dehydration ones (
) and from hydration/dehydration ones ( ,
,  ).
).
|
|
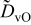 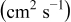
|
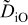 
|
|---|---|---|---|
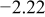
|

|
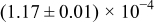
|
|
|
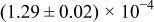
|
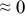
| |
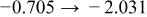
|
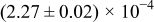
|
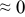
| |
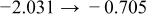
|
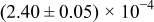
|
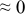
| |
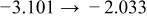
|
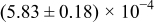
|
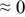
| |

|
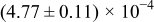
|
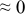
| |
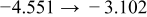
|
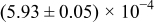
|
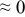
| |
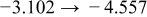
|
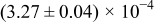
|
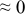
| |
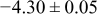
|
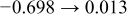
|

|
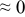
|
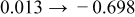
|
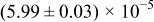
|
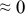
| |
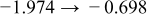
|

|
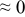
| |

|
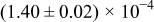
|
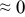
| |
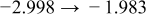
|

|
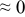
| |
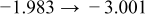
|
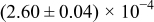
|
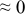
| |
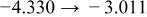
|
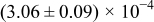
|
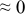
| |
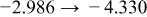
|
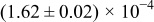
|
| |
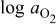
|
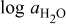
|
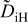 
|
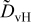 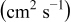
|
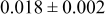
|
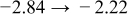
|
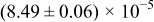
|
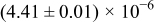
|
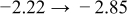
|
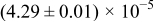
|
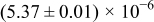
| |
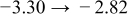
|
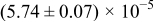
|
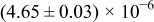
| |
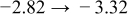
|
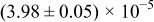
|
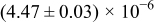
| |
|
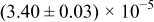
|
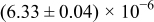
| |
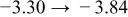
|
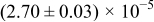
|

| |
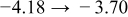
|
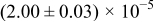
|

| |
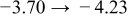
|
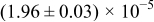
|
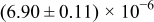
| |
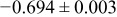
|
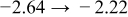
|
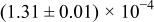
|
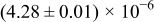
|
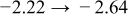
|
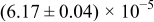
|
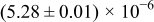
| |
|
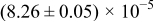
|
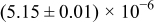
| |
|

|

| |

|
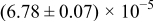
|
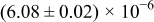
| |
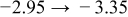
|
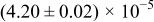
|
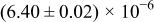
| |

|
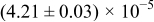
|
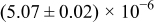
| |

|
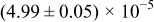
|

| |
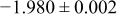
|
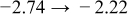
|
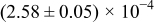
|
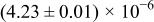
|
|

|
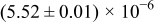
| |
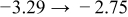
|
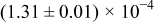
|
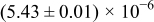
| |
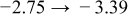
|
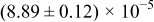
|
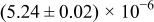
| |
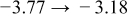
|
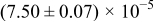
|
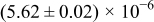
| |
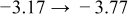
|

|
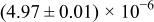
| |
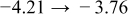
|
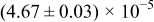
|
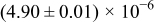
| |
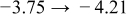
|
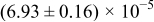
|
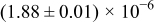
| |
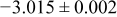
|
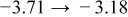
|
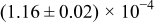
|
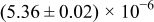
|
|
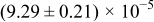
|
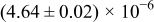
| |
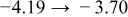
|
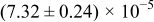
|
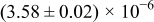
| |
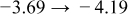
|
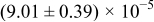
|
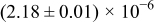
| |
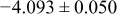
|

|
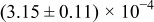
|
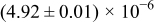
|
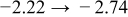
|
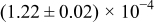
|
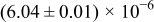
| |
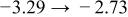
|

|

| |
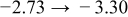
|
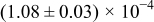
|
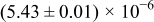
| |

|
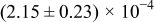
|
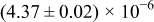
| |
|
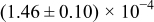
|
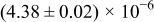
| |
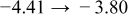
|
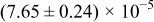
|
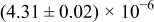
| |
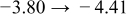
|
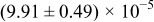
|
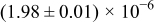
|
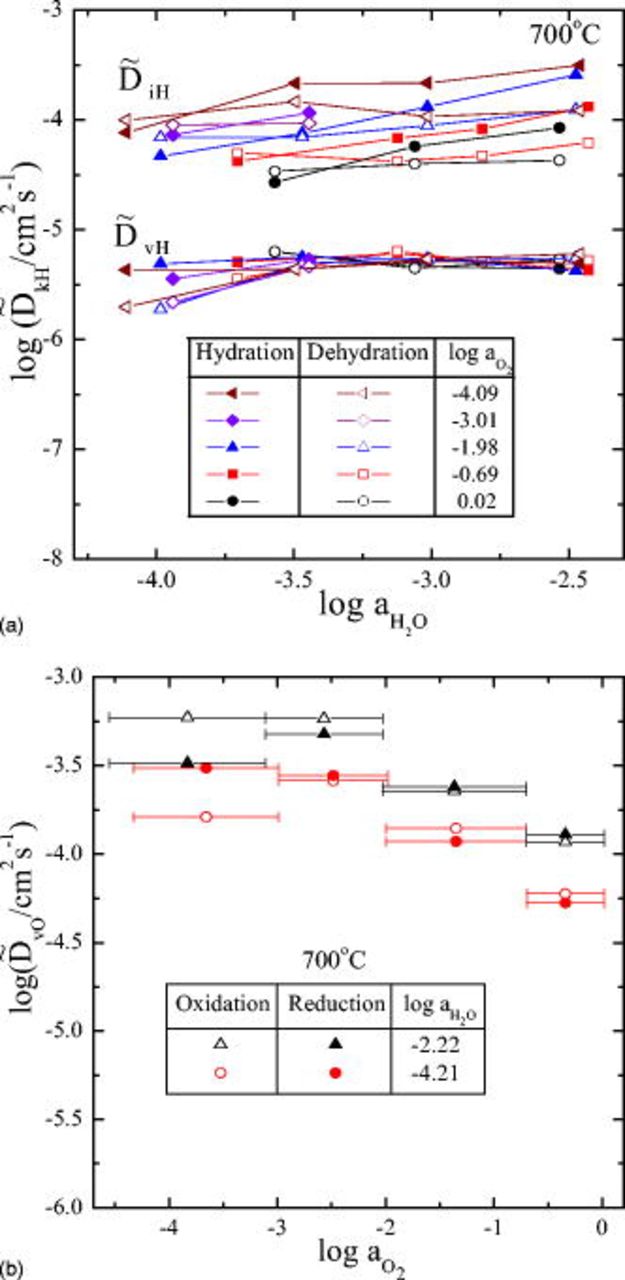
The diffusivities in Table I are plotted against water-vapor activity and oxygen activity in Fig. 10a and 10b, respectively. It is seen that  tends to increase in the range of
tends to increase in the range of  with increasing
with increasing  in a fixed
in a fixed  atmosphere at a fixed temperature of
atmosphere at a fixed temperature of  , while
, while  appears rather insensitive to
appears rather insensitive to  in its range examined.
in its range examined.  appears to decrease in the range of
appears to decrease in the range of  with increasing
with increasing  in the range of
in the range of  , while
, while  whether wet or dry.
whether wet or dry.
Figure 10. (a)The chemical diffusivities vs water vapor activity governing the hydration/dehydration kinetics in different oxygen activity atmospheres, and (b) the oxygen diffusivity vs oxygen activity governing the oxidation/reduction kinetics in dry  and wet atmosphere
and wet atmosphere  for
for  at
at  . Note that the oxidation/reduction kinetics is governed by oxygen chemical diffusion no matter whether wet or dry.
. Note that the oxidation/reduction kinetics is governed by oxygen chemical diffusion no matter whether wet or dry.
Finally, we compare the diffusivities of the present system with those of the earlier system, though the measurement temperatures differ by  (in Fig. 11), where the mean value of
(in Fig. 11), where the mean value of  (of a process and its reverse) is plotted against the mean value of
(of a process and its reverse) is plotted against the mean value of  and
and  . One can see in Fig. 11a that in general, the present system
. One can see in Fig. 11a that in general, the present system  has smaller
has smaller  but larger
but larger  than those of
than those of  , as expected from Fig. 6. However,
, as expected from Fig. 6. However,  values are about the same in magnitude as well as variation trend for both systems (see Fig. 11b).
values are about the same in magnitude as well as variation trend for both systems (see Fig. 11b).
Figure 11. Comparison of the chemical diffusivities for hydration/dehydration kinetics 
 (a), and for oxidation/reduction
(a), and for oxidation/reduction  (b). Closed symbols for
(b). Closed symbols for  at
at  ; open symbols for
; open symbols for  at
at  .
.
Conclusions
It has been reconfirmed that hydration or dehydration proceeds twofold nonmonotonically and oxidation/reduction singlefold monotonically, that is due to decoupled chemical diffusion of H and O with the mediation of holes under either water or oxygen chemical potential gradient. It is also confirmed that the analytic solution for the twofold relaxation proposed in Ref. 1 has general validity and that has yielded the numerical values for the two chemical diffusivities of H and O, respectively, under either oxygen or water chemical potential gradient. In water chemical potential gradients, H chemical diffusion is always faster than O upon hydration/dehydration, but hydrogen diffusion is negligible under oxygen potential gradient no matter whether wet or dry.
Acknowledgments
This work was financially supported through the 21C Frontier Program by the Center for Advanced Materials Processing, Ministry of Knowledge and Economy, Korea.
Seoul National University assisted in meeting the publication costs of this article.
Footnotes
- a
The actual cross section of the present specimen is
 (see Experimental section), but only for the sake of mathematical simplicity, the cross section has been assumed to be a square to take
(see Experimental section), but only for the sake of mathematical simplicity, the cross section has been assumed to be a square to take  , which causes no significant error in the present context.
, which causes no significant error in the present context.