1 Introduction

Infectious diseases have always been major concerns from the ancient times from the first pandemic that started in 165 A.D. called as the Plague of Galen. Since that time many epidemics are mentioned in the literature. The current pandemic has come from coronavirus infection. The first human corona virus, B814, was found in 1965 from an adult who had been reported for having common cold [1]. At the beginning of this century, Severe Acute Respiratory Syndrome (SARS), from the family of human corona virus, was first recognized in Hanoi, Vietnam from a middle-aged businessman who travelled extensively in South-East Asia. He was admitted to a hospital in Hanoi on 26 February 2003 with high fever, dry cough, muscle pain and mild sore throat [2]. The incubation period for SARS is normally 2–7 days and symptoms are likely to be produced during this period. The common symptoms include mild respiratory symptoms, and fever. Sometimes it is associated with chills, rigors, and other symptoms like headache, malaise, and muscle pain. During these days, the outbreak of SARS-CoV had affected people in a large scale with 8000 cases and approximately 800 deaths as reported in [1, 3, 4]. Similarly, Middle East Respiratory Syndrome coronavirus or MERS-CoV (MERS) is a viral respiratory disease caused by a human corona virus. It was first reported in Saudi Arabia in the year 2012. The virus was found to be capable of transmitting from some animals to human beings through a carrier or fluid medium. During that time, people were infected through direct contact or indirect contact with infected people/animals. The source of the virus is still not fully known but it is expected to originate from bats and transmitted to camels [4]. The clinical symptoms were mild respiratory symptoms, severe acute respiratory disease and death. There was also a portion of asymptomatic individuals. Some common symptoms included fever, cough and shortness of breath, sometimes pneumonia and gastrointestinal problems like diarrhea. Approximately 2500 cases were reported and 35.7% of the patients with MERS-COV had died.

Recently, the COVID-19 outbreak was declared an epidemic disease by the World Health Organization on March 11, 2020. In a very short period of time, almost every person is directly or indirectly affected by it because of the virus’ potential of rapid transmission. The virus was first reported in Wuhan City of China on November 17, 2019 [5,6,7]. In the beginning, it was suspected as severe pneumonia but later it was identified as the human corona virus. On February 11, 2020, the Director-General of WHO announced that the disease caused by this new coronavirus, SARS-CoV-2, was to be officially named COVID-19 [5].

In the absence of proper treatment and vaccination for a year, it has affected more than 215 millions of people around the world and has caused 4.48 million deaths world-wide. People of older age and certain underlying medical problems like cardiovascular diseases, diabetes, chronic respiratory disease and cancer are more vulnerable to this disease [8,9,10,11]. It spreads from the infected people through direct contacts such as spitting, sneezing and coughing. The virus causes both upper and lower respiratory tract infection in human body. So, symptoms vary from one person to another. The life span of COVID-19 infection is considered in five stages: incubation period, time of testing, detection of symptoms, quarantine and recovery. The transmission of the COVID-19 infections is normally increased by the high infection rate, recombination rate and mutation rate. According to various studies, mutation of the virus is also happening which a cause of alarm [12, 13]. Due to the onset of various strains/waves of the virus, such as Alpha, beta, Gamma, Delta, and the most alarming, Omicron [14], affect on human lives in terms of employment, economic stability, loss of lives has been dire. There are good initiatives being taken by most nations to curb the rate of infection. Country-wise vaccination drives were started and are still going on; however complete vaccination will require an ample amount of time due to many reasons. To name a few, lack of awareness in rural region and slow formulation and manufacturing speed of vaccines due to the huge amount population of the world. It is also observed that the vaccinated people still remain susceptible to re-infection when contacted with infected people after a certain amount of time. It has been demonstrated that India has comparatively less mortality rate but the rate of infection is a concern [15]. Even after continuous lockdowns, it is still recommended that we continue the precautionary measures like wearing a face mask, sanitizing of hands, and maintaining social distance to be safe. Till date, most countries are facing a chaotic and disastrous situation which is predicted to continue in subsequent waves [16,17,18].

The disease is still the deadliest in the absence of proper treatment and less vaccinated people. Many researchers and scientists are giving efforts to provide solutions, approaches and preventive measures to control the pandemic [19,20,21]. It is still an ongoing process to find appropriate solutions for the health sector workers. However, the mathematical model presented in this paper can provide the predictions on various stages of COVID-19. In this regards, various dynamical models [22,23,24,25,26,27,28,29,30,31] have been presented and various recommendations on how the spread rate of infection could be less if the infected persons are completely in isolation, reducing contact and increasing trace of infected persons may reduce the transmission rate and how social distancing between potentially infected individuals and healthy individuals can reduce the spread have been proposed. Sufficient vitamins, tonics, supplements and medication to stop spread in non-infected people and vaccine-effort and social distancing parameters may control the transmission of COVID. In many articles, the findings of the dynamical models are validated with the clinical data collected from various countries like China, Italy, India, Saudi Arabia, Brazil, etc. The effects of antiviral [32] in COVID-19 infection have also been presented and its dynamical characterization has been done. Another dynamical approach [33] for prioritization of vaccination has been investigated. The effects of BCG vaccine [34] on the COVID-19 have also been reported and the effects of anti-SARS-CoV-2 antibodies in infections and recovery have been investigated by Ref. [35]. It was also found by Ref. [36] that in case roll out of vaccines are not upto speed, then permanent drug treatment should be focused on. Some other interesting models ([37,38,39,40]) on vaccination and prioritization have been reported in literature and it is concluded that vaccination is an efficient tool to stop the spread of infections.

In literature, a mathematical model is a strong tool which plays a major role in predicting the behaviour of any infectious disease and its control [19, 41, 42]. Improvements and generalization of the models existing in literature are always required to give better solutions and predictions. Considering this fact, an improved dynamical model to study the impacts of vaccinations in the spread of COVID-19 is developed. The equilibrium points (both disease-free and endemic) is found and non-negativity and invariant region of the solutions is presented (Table 1). The reproduction number and local stability analysis at equilibrium points for the COVID-19 model are also studied. Numerical approach with NDSolver in Mathematica is employed to compute the simulations. Furthermore, the simulated results are compared with an existing model for validation. It is recommended that the speed of vaccination drive and efficacy of vaccine should be increased to control the pandemic situation and make the normal life.

Table 1 Parameters definition
Full size table

2 Dynamical model for community transmission

When a resident/citizen with no national/international travel history spreads the virus in the community and partial lockdown has been enforced by the government. It becomes a situation when it is very difficult to control the infection and giving full freedom to force of the security personals. If situation is not controlled at this phase then it would become endemic stage where there will be many deaths due to infection with this virus. To develop the dynamical model, the following hypotheses during community transmission of coronavirus are considered [6, 8, 10, 11, 42]:

Fig. 1
figure 1

Flow diagram for the proposed model

Full size image
H1: :

The natural birth and death rate of susceptible population is positive i.e., \(B_1>0\) and \(\mu >0\).

H2: :

The immunization rate is positive viz. rate at which the number of susceptible population is transferred to vaccination population i.e., \(a>0\).

H3: :

Uninfected home quarantine population rate is positive viz. rate at which the number of people from home quarantine is transferred to susceptible population i.e., \(\epsilon _1>0\).

H4: :

Infected home quarantine population rate is positive viz. rate at which the number of people from home quarantine is transferred to infected population i.e., \(\delta _1>0\).

H5: :

Contact rate of infection between susceptible and infected people is positive i.e., \(\beta _1>0\).

H6: :

Quarantine rate is positive viz. rate at which the number of people from susceptible populations are transferred to home quarantine population compartment i.e., \(\lambda _1>0\).

H7: :

Hospitalized rate is positive viz. rate at which the number of infected people has shifted to hospital i.e., \(\eta _1>0\).

H8: :

Recovered rate is positive viz. rate at which the number of people recovered from infection i.e., \(\gamma _1>0\).

H9: :

COVID-19 death rate is positive viz. rate of death induced by the disease i.e., \(\mu _1>0\).

H10: :

The rate at which a vaccinated population is transferred to susceptible population again due to non-availability of antibodies in the vaccinated population i.e., \(b>0\), because, no vaccine is provides \(100\%\) protection from COVID-19 infection.

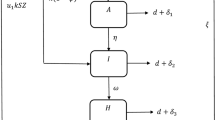
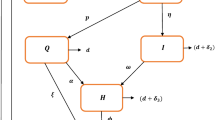
A flow diagram for the spread of COVID-19 within the human population is illustrated in Fig. 1. To express this situation, a dynamical model based on the above hypotheses is developed and expressed mathematically as:

$$\begin{aligned} \begin{aligned} \frac{dS_1}{dt}&= B_1 - \mu S_1 - \lambda _1 S_1 - \beta _1 S_1 I_1 - a S_1 + b V_1 - \epsilon _1 Q_1\\ \frac{dI_1}{dt}&= \beta _1 S_1 I_1 - (\mu + \mu _1 + \eta _1)I_1 + \delta _1 Q_1\\ \frac{dV_1}{dt}&= a S_1 -b V_1 - \mu V_1\\ \frac{dQ_1}{dt}&= -(\mu + \delta _1)Q_1 + \lambda _1 S_1 - \epsilon _1 Q_1\\ \frac{dQ_2}{dt}&= -(\mu + \mu _1 + \gamma _1)Q_2 + \eta _1 I_1\\ \frac{dR_1}{dt}&= - \mu R_1 + \gamma _1 Q_2 \end{aligned} \end{aligned}$$
(1)

subject to following the initial conditions,

$$\begin{aligned} \begin{aligned} S_1(0)&=S_{10}, I_1(0)=I_{10}, V_1(0)=V_{10}, \\ Q_1(0)&=Q_{10}, Q_2(0)=Q_{20}, R_1(0)=R_{10}. \end{aligned} \end{aligned}$$
(2)

The parametric values during the non-infected and infected equilibrium points are listed in Table 2. The non-negativity and invariant region for the proposed model are discussed in the successive subsections where the solutions will persist. For this model, the equilibrium points have been obtained by considering the rate of change of the population to be zero.

Table 2 Parameter values
Full size table

2.1 Non-negativity of the solutions

Lemma 1

The analytical solution of model (1) i.e., \(S_1(t),I_1(t),V_1(t)\), \(Q_1(t),Q_2(t),R_1(t)\) with initial values \(S_1(0)>0\), \(I_1(0) \ge 0\), \(V_1(0) \ge 0\), \(Q_1(0) \ge 0\), \(Q_2(0) \ge 0\), \(R_1(0) \ge 0\) are non-negative for all \(t>0\).

Proof

The first equation of the model (1), i.e., equation (1a) can be written as,

$$\begin{aligned}&\frac{d}{dt} \Big [ S_1(t) exp \left\{ \int ^{t}_{0} \beta _1 I_1(x) dx + (\mu + \lambda _1 +a)t\right\} \Big ]\\&= \big [ B_1 + bV_1(t) - \epsilon _1 Q_1(t) \big ] \ exp \\&\quad \left\{ \int ^{t}_{0}\beta _1 I_1(x) dx + (\mu + \lambda _1 +a)t\right\} \end{aligned}$$

After simplifying the equation, we get

$$\begin{aligned} &S_1(t) = exp \left\{ -\int ^{t}_{0} \beta _1 I_1(x) dx - (\mu + \lambda _1 +a)t\right\} \\ &\quad \times \Bigg [ \int ^{t}_{0}(B_1 + bV_1(y) - \epsilon _1 Q_1(y)) \\&\quad \times exp \left\{ \int ^{y}_{0}\beta _1 I_1(x) dx + (\mu _1 + \lambda _1 +a)y\right\} dy \Bigg ] \\&\quad + S_1(0) \ exp \left\{ -\int ^{y}_{0} \beta _1 I_1(x) dx \!-\! (\mu + \lambda _1 +a)y\right\} \!>\! 0. \end{aligned}$$
(3)

Subsequently, we can also prove that \(I_1(0) \ge 0\), \(V_1(0) \ge 0\), \(Q_1(0) \ge 0\), \(Q_2(0) \ge 0\), \(R_1(0) \ge 0\) (see [43, 44]). Thus, the solutions \(S_1(t), I_1(t), V_1(t)\), \(Q_1(t), Q_2(t), R_1(t)\) stay positive for all \(t>0\). \(\qquad\qquad\qquad\qquad\qquad\square \)

2.2 Invariant region

Let us assume, \(N_1(t)\) is the total sum of all compartment populations, i.e.,

$$\begin{aligned} N_1(t) = S_1(t)+ I_1(t)+ V_1(t)+ Q_1(t)+ Q_2(t)+ R_1(t). \end{aligned}$$

Then,

$$\begin{aligned} \frac{dN_1}{dt}= B_1 - \mu N_1 - \mu _1 (I_1 + Q_2). \end{aligned}$$

In the absence of COVID-19 infection,

$$\begin{aligned} \frac{dN_1}{dt}= B_1 - \mu N_1. \end{aligned}$$

Hence, the total population will bound to \(\frac{B_1}{\mu }\) at \(t\rightarrow \infty \). Therefore, all solutions of this model will be finite and exist in the following region [45]:

$$\begin{aligned}&\Lambda = \left\{ \left( S_1,I_1,V_1,Q_1,Q_2,R_1\right) \in R_6^+: S_1,I_1,V_1,Q_1,Q_2,R_1\nonumber \right. \\&\quad \left. \le \frac{B_1}{\mu } \right\} \end{aligned}$$
(4)

2.3 Equilibrium points

It is well known that if the system is stable, it will be at the equilibrium points. After doing the rigorous calculation for this model, we get the following equilibrium points:

  • Non-infected equilibrium point

    $$\begin{aligned} E_1^*=\left( S_1^*,I_1^*,V_1^*,Q_1^*,Q_2^*,R_1^*\right) =\left( 1,0,0,0,0,0\right) \end{aligned}$$
    (5)

  • Infected equilibrium point

    $$\begin{aligned} \bar{E_1}=\left( \bar{S_1},\bar{I_1},\bar{V_1},\bar{Q_1},\bar{Q_2},\bar{R_1}\right) \end{aligned}$$
    (6)

where, \(\bar{S_1} = \frac{B_1 (-b-\mu )(-\delta _1 - \epsilon _1 - \mu )}{\epsilon _1 \lambda _1 (-b-\mu )+ (-\delta _1 - \epsilon _1 - \mu )(ab-(-b-\mu )(-a-\lambda _1 - \mu - \beta _1 \bar{I_1}))}\),

      \(\bar{V_1}=\frac{a \bar{S_1}}{b+\mu }\), \(\bar{Q_1}=\frac{\lambda _1 \bar{S_1}}{\delta _1 + \epsilon _1 + \mu }\), \(\bar{Q_2}= \frac{\eta _1 \bar{I_1}}{\gamma _1 + \mu + \mu _1}\), \(\bar{R_1}= \frac{\gamma _1 \eta _1 \bar{I_1}}{\mu (\gamma _1 + \mu + \mu _1)}\).

3 Analysis of the COVID-19 model

For an epidemiological model, the basic reproduction number denotes the number of secondary infections caused by one infectious individual, it is calculated in the next subsection. Then, we discuss whether the equilibrium points for the proposed model are stable or unstable.

3.1 Reproduction number

The system of Eq. (1) can be written in another form,

$$\begin{aligned} \frac{dX}{dt}=P(X)-Q(X) \end{aligned}$$
(7)

where,

$$\begin{aligned} X= \begin{pmatrix} I_1\\ V_1\\ Q_1\\ Q_2\\ R_1\\ S_1 \end{pmatrix}, \quad P(X)= \begin{pmatrix} \beta _1 I_1 S_1\\ 0\\ 0\\ 0\\ 0\\ 0 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} Q(X)= \begin{pmatrix} -\delta _1 Q_1 + (\eta _1 + \mu + \mu _1)I_1\\ -a S_1 + b V_1 + \mu V_1\\ -\lambda _1 S_1 + (\eta _1 + \mu + \epsilon _1)Q_1\\ -\eta _1 I_1 + (\gamma _1 + \mu + \mu _1)Q_2\\ -\gamma _1 Q_2 + \mu R_1\\ -B_1 + a S_1 -b V_1 + \beta _1 S_1 I_1 - \epsilon _1 Q_1 + \lambda _1 S_1 + \mu S_1 \end{pmatrix} \end{aligned}$$

Then, we calculate the Jacobian matrix for P(X) and Q(X) at \(E_1^*\),

$$\begin{aligned}&m = J[P(X)]\vert _{E^*_1} \\&=\begin{pmatrix} \eta _1 + \mu + \mu _1 &{} 0 &{} -\delta _1 &{} 0 &{} 0 &{} 0\\ 0 &{} b+\mu &{} 0 &{} 0 &{} 0 &{} -a\\ 0 &{} 0 &{} \eta _1 + \mu + \epsilon _1 &{} 0 &{} 0 &{} -\lambda _1\\ -\eta _1 &{} 0 &{} 0 &{} \gamma _1 + \mu + \mu _1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \gamma _1 &{} \mu \\ \beta _1 &{} -b &{} -\epsilon _1 &{} 0 &{} 0 &{} a + \lambda _1 + \mu \end{pmatrix} \end{aligned}$$

Similarly, we can calculate, \(n=J\left[ Q(X)\right] \vert _{E^*_1}\).

Finally, we deduce the basic reproduction number after calculating the spectral radius, i.e., of \(\mathbb {R}_0=\rho (m n^{-1})\), we get

$$\begin{aligned} \mathbb {R}_0 = \frac{\beta _1 Nr}{b D_1+ \mu D_2}, \end{aligned}$$
(8)

where, \(Nr=(b(\delta _1(\lambda _1 + \mu ) + \mu (\epsilon _1 + \lambda _1 + \mu )) + \mu (a(\delta _1 + \epsilon _1 + \mu ) + \delta _1(\lambda _1 + \mu ) + \mu (\epsilon _1 + \lambda _1 + \mu )))\),

\(D_1=(\delta _1 \beta _1 \lambda _1 + (\delta _1(\lambda _1 + \mu ) + \mu (\epsilon _1 + \lambda _1 + \mu ))(\eta _1 + \mu + \mu _1))\),

\(D_2=(\delta _1 \beta _1 \lambda _1 + a(\delta _1 + \epsilon _1 + \mu )(\eta _1 + \mu + \mu _1) + (\delta _1(\lambda _1 + \mu ) +\mu (\delta _1 + \epsilon _1 + \mu ))(\eta _1 + \mu + \mu _1))\).

3.2 Local stability at non-infected equilibrium point

Theorem 1

The non-infected equilibrium point of model (1) is asymptotically stable if the reproduction number is less than 1, i.e., \(\mathbb {R}_0 < 1\), otherwise it is unstable.

Proof

The Jacobian matrix for the present model at non-infected equilibrium point (see [41, 43]) is

$$\begin{aligned}&J\vert _{E^*_1} = \begin{pmatrix} {-a -\lambda _1 - \mu } &{} -\beta _1 &{} b &{} \epsilon _1 &{} 0 &{} 0\\ 0 &{} {\beta _1 - \eta _1 - \mu - \mu _1} &{} 0 &{} \delta _1 &{} 0 &{} 0\\ a &{} 0 &{} -b - \mu &{} 0 &{} 0 &{} 0\\ \lambda _1 &{} 0 &{} 0 &{} {-\delta _1 - \epsilon _1 - \mu } &{} 0 &{} 0\\ 0 &{} \eta _1 &{} 0 &{} 0 &{} {-\gamma _1 - \mu - \mu _1} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \gamma _1 &{} -\mu \end{pmatrix} \end{aligned}$$

\(\hfill\square \)

After solving characteristic equation for the above matrix, we directly get the following characteristic roots:

$$\begin{aligned} p_1= & {} -\mu ,\\ p_2= & {} -\gamma - \mu - \mu _1,\\ p_3= & {} -\delta _1 - \epsilon _1 - \mu \end{aligned}$$

The other three characteristic roots can be derived from the following equation

$$\begin{aligned} p^3 + A_1 \ p^2 + A_2 \ p + A_3 = 0, \end{aligned}$$
(9)

where, \(A_1 = b + \eta _1 = \lambda _1 + 3\mu + \mu _1 - \epsilon _1 \lambda _1 -\beta _1 +a\),

$$\begin{aligned}A_2 &= a + b \beta _1 + b\eta _1 + b\lambda _1 - \beta _1\lambda _1 + \eta _1 \lambda _1 + 2b\mu \\&\quad + 2 \eta _1 \mu + 2 \lambda _1 \mu + 3 \mu ^2 + b \mu _1^2 + \lambda _1\mu _1 \\&\quad + 2 \mu \mu _1 - \beta _1 \lambda _1\delta _1 - b \epsilon _1 \lambda _1 + \beta _1 \epsilon _1 \lambda _1 - \eta _1 \epsilon _1 \lambda _1 \\&\quad - 2\epsilon _1 \lambda _1 \mu - \epsilon _1 \lambda _1 \mu _1 \\A_3 &= a \mu - b\beta _1 \lambda _1 + b \eta _1 \lambda _1 - b \beta _1 \mu + b \eta _1 \mu + b \lambda _1 \mu \\&\quad - \beta _1 \lambda _1 \mu + \eta _1 \lambda _1 \mu + b \mu ^2 + \eta _1 \mu ^2 + \lambda _1 \mu ^2 + \mu ^3 + b \lambda _1 \mu _1 \\&\quad + b \mu \mu _1 + \lambda _1 \mu \mu _1 + \mu ^2 \mu _1 + \beta _1 b \lambda _1 \delta _1 + b \beta _1 \epsilon _1 \lambda _1 \\&\quad - b \epsilon _1 \eta _1 \lambda _1 + \beta _1 \delta _1 \lambda _1 \mu - b \epsilon _1 \delta _1 \mu + \beta _1 \epsilon _1 \lambda _1 \mu - \epsilon _1 \lambda _1 \eta _1 \mu \\&\quad - \epsilon _1 \lambda _1 \mu ^2 - b \epsilon _1 \lambda _1 \mu _1 - \epsilon _1 \lambda _1 \mu _1 \mu \end{aligned}$$

Using Routh-Hurwitz Criterion [43], it is easy to examine that the real part of the characteristic roots are negative, if \(\mathbb {R}_0 < 1\). Hence, this equilibrium point is local stable for this condition otherwise; it is unstable, for the model (1).

3.3 Local stability at infected equilibrium point

Theorem 2

The infected equilibrium point, \(\bar{E_1}=\left( \bar{S_1},\bar{I_1},\bar{V_1},\bar{Q_1},\bar{Q_2},\bar{R_1}\right) \) is locally asymptotically stable if the reproduction number is greater than 1, i.e., \(\mathbb {R}_0 > 1\).

Proof

The Jacobian matrix at the infected equilibrium point is formed as (see [44]):

$$\begin{aligned}&J\vert _{\bar{E_1}}= \begin{pmatrix} -a - \bar{I_1} \beta _1 - \lambda _1 - \mu &{} -\bar{S_1} \beta _1 &{} b &{} \epsilon _1 &{} 0 &{} 0\\ \bar{I_1} \beta _1 &{} \bar{S_1} \beta _1 - \eta _1 - \mu - \mu _1 &{} 0 &{} \delta _1 &{} 0 &{} 0\\ a &{} 0 &{} -b - \mu &{} 0 &{} 0 &{} 0\\ \lambda _1 &{} 0 &{} 0 &{} -\delta _1 - \epsilon _1 - \mu &{} 0 &{} 0\\ 0 &{} \eta _1 &{} 0 &{} 0 &{} -\gamma _1 - \mu - \mu _1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu \end{pmatrix} \end{aligned}$$

\(\hfill\square \)

After solving the characteristics equation of above matrix, we get two characteristic roots,

$$\begin{aligned} p_1= & {} -\mu \\ p_2= & {} -\gamma _1 - \mu - \mu _1. \end{aligned}$$

And the other four eigenvalues can be derived from the following equation,

$$\begin{aligned}&\lambda _1 \times (b+p+\mu ) \times (-\bar{S_1} \beta _1 (\delta _1 + \epsilon _1) \\&\quad + \epsilon _1(p + \eta _1 + \mu + \mu _1)) + \\&(-p - \delta _1 - \epsilon _1 - \mu ) \times (ab(p - \bar{S_1} \beta _1 + \eta _1 + \mu + \mu _1)\\&\quad \times (-b-p-\mu )\\&(\bar{I_1} \bar{S_1} \beta _1^2 + (a+p+\bar{I_1} \beta _1 + \lambda _1 + \mu ) \times (p- \bar{S_1} \beta _1 + \eta _1\\&\quad + \mu + \mu _1))) = 0 \end{aligned}$$

Similarly, we can report the local stability for the current model at the infected or epidemic equilibrium point using the Routh-Hurwitz criterion. It is derived that real parts of all the eigenvalues are negative and real when the reproduction number is greater than 1, so, it is asymptotically stable.

4 Sensitivity analysis

This model is constructed with consideration of some key parameters which possess close similarity to the actual disease. In this section, we analyze the variation in the basic reproduction number (\(\mathbb {R}_0\)) due to changes in the inputs (different parameters) with the help of sensitivity analysis [46]. This study is important because it provides insight into which parameters require a great deal of attention and has the most effect in the basic reproduction number. Therefore, highly sensitive parameter values must be collected with caution as a slight change in that parameter can cause a huge quantitative change in the amount of concern and may also produce qualitatively different outcomes. To control the rapid spread of a disease, we need to be informed about the factors that can potentially cause the spread of a disease so that effective measures against them can be taken well in advance for lessen the transmission. On the other side, the insensitive parameters don’t require much attention.

The sensitivity index of a parameter [46], say x, is given by

$$\begin{aligned} E_x = \frac{x}{\mathbb {R}_0} \frac{\partial \mathbb {R}_0}{\partial x}. \end{aligned}$$

Table 3 shows the different parameters taken along with their values calculated from a data set and their sensitivity indices. From this table, it is noted that the values of \(E_{\beta _1}\), \(E_a\), \(E_{\mu }\) and \(E_{\epsilon _1}\) are positive and the increase of these parameters will tend to increase the value of \(\mathbb {R}_0\). Further noticed that the values of \(E_b\), \(E_{\delta _1}\), \(E_{\lambda _1}\), \(E_{\eta _1}\) and \(E_{\mu _1}\) are negative and the increase of these parameters will tend to decrease the value of \(\mathbb {R}_0\). Moreover, it is reveal that an increase of a positive parameter, sensitivity index will amount to more spread of the virus, whereas increase of a negative sensitivity index will result in the curb in spreading the epidemic. Furthermore, the following observations are recorded based on sensitivity analysis:

  • \(\beta _1\) is the most sensitive parameter. The value of \(E_{\beta _1}\) is positive, it indicates that if contact rate of infection between susceptible and infected people increases, the value of \(\mathbb {R}_0\) will increase, which will make it difficult to stop the spread of COVID-19.

  • \(\delta _1\) is a very sensitive parameter and it increases its sensitivity as it is increased from 0.01 to 0.4. Since the value of \(E_{\delta _1}\) is negative, it indicates that as infected home quarantine population rate is increased, \(\mathbb {R}_0\) will decrease, which is effective in the containment of COVID-19.

  • \(E_{\eta _1}\) decreases as \(\eta _1\) is increases from 0.02 to 0.2. Since \(E_{\eta _1}\) is negative, i.e., if the rate at which the number of infected people are shifted to hospital is increased with better healthcare and facilities, then the pandemic can be controlled. It is one of the most sensitive parameters.

  • \(\lambda _1\) increases in sensitivity from 0.01 to 0.5 but initially decreases for some values near 0.01. Other than that, it indicates that if the rate at which the number of people from susceptible population are transferred to home quarantine population compartment increases, it will be effective in controlling the community spread of COVID-19.

  • a, b, \(\mu \) and \(\epsilon _1\) are comparatively less sensitive than the other parameters, as discussed above.

Table 3 Sensitivity Index Table
Full size table

5 Numerical results and discussion

In this section, numerical results to examine the dynamical behavior of various types of population like Population of susceptible persons (\(S_1\)), Population of infected persons (\(I_1\)), Population of home isolation persons (\(Q_1\)), Population of quarantine persons in hospital (\(Q_2\)), Population of recovery persons (\(R_1\)), Population of vaccinated persons (\(V_1\)) are computed by NDSolver in Mathematica and illustrated through Figs. 2, 3, 4, 5, 6, 7, 8 and 9. In this study, two sets of data are considered: one set of data (\(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.001\), \(b=0.1\)), when the reproduction number is less than 1 (\(\mathbb {R}_0<1\)) which means “each existing infection causes less than one new infection, i.e., the disease will decline and eventually die out”, used to plot the Figs. 2,  4, 5 and 6. And the second set of data (\(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.1\), \(b=0.01\)), where the reproduction number is greater than 1 (\(\mathbb {R}_0>1\)) which means “each existing infection causes more than one new infection, i.e., the disease will be transmitted between people, and there may be an outbreak or epidemic” used to plot the Figs. 3, 7, 8 and 9. The dynamical behaviour of all the population for non-infected equilibrium point and infected equilibrium points are listed in Tables 4 and 5, respectively. Tables show that initially each population is changing rapidly with time however the variations in population are not much after some time (\(t=40\)).

Fig. 2
figure 2

Dynamical behaviour of population at non-infected equilibrium point during community transmission, when \(\mathbb {R}_0=0.87607\)

Full size image
Fig. 3
figure 3

Dynamical behaviour of population at non-infected equilibrium point during community transmission, when \(\mathbb {R}_0=1.12424\)

Full size image
Fig. 4
figure 4

Dynamical behaviour of population with respect to time at non-infected equilibrium state when initial values (\(S_{10}=0.88\), \(I_{10}=0.04\), \(Q_{10}=0.08\), \(Q_{20}=0\), \(R_{10}=0\), \(V_{10}=0\)) and parameter values \(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(b=0.1\) for various values of a

Full size image
Fig. 5
figure 5

Dynamical behaviour of population with respect to time at non-infected equilibrium state when initial values (\(S_{10}=0.88\), \(I_{10}=0.04\), \(Q_{10}=0.08\), \(Q_{20}=0\), \(R_{10}=0\), \(V_{10}=0\)) and parameter values \(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.001\) for various values of b

Full size image
Fig. 6
figure 6

Dynamical behaviour of population with respect to time at non-infected equilibrium state when initial values (\(S_{10}=0.88\), \(I_{10}=0.04\), \(Q_{10}=0.08\), \(Q_{20}=0\), \(R_{10}=0\), \(V_{10}=0\)) and parameter values \(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(a=0.001\), \(b=0.1\) for various values of \(\epsilon _1\)

Full size image
Fig. 7
figure 7

Dynamical behaviour of population with respect to time at infected equilibrium state when initial values (\(S_{10}=0.88\), \(I_{10}=0.04\), \(Q_{10}=0.08\), \(Q_{20}=0\), \(R_{10}=0\), \(V_{10}=0\)) and parameter values \(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(b=0.01\) for various values of a

Full size image
Fig. 8
figure 8

Dynamical behaviour of population with respect to time at infected equilibrium state when initial values (\(S_{10}=0.88\), \(I_{10}=0.04\), \(Q_{10}=0.08\), \(Q_{20}=0\), \(R_{10}=0\), \(V_{10}=0\)) and parameter values \(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.1\) for various values of b

Full size image
Fig. 9
figure 9

Dynamical behaviour of population with respect to time at infected equilibrium state when initial values (\(S_{10}=0.88\), \(I_{10}=0.04\), \(Q_{10}=0.08\), \(Q_{20}=0\), \(R_{10}=0\), \(V_{10}=0\)) and parameter values \(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(a=0.1\), \(b=0.01\) for various values of \(\epsilon _1\)

Full size image
Table 4 Time series at non-infected equilibrium point (Fig. 2)
Full size table
Table 5 Time series at infected equilibrium point (Fig. 3)
Full size table

5.1 Validation of the model

To validate the proposed model for Response of Vaccination on Community Transmission of COVID-19, a comparative analysis between the behaviour of all the populations (except vaccination) of existing model [6] and behaviour of all the populations of proposed model has been predicated through Fig. 2a and b for \(\mathbb {R}_0=0.87607\). It is reported that behaviour of five populations (susceptible persons, infected persons, home isolation persons, quarantine persons in hospital, and recovery persons) are very similar for both existing and proposed model. Same comparative analysis between existing model [6] and proposed model for \(\mathbb {R}_0=1.12424\) has been computed through Fig. 3a and b and noted that the nature of different populations is same. It is further noted from Figs. 2 and 3 that there is quantitative difference in populations between existing model [6] and proposed model due to one extra population (vaccination) is incorporated. Furthermore, it is concluded that the proposed model is more generalized form and able to recommend the response of vaccination during the community transmission.

5.2 Dynamical behavior of population for \(\mathbb {R}_0<1\)

In this subsection, first set of data (\(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.001\), \(b=0.1\)) which is for reproduction number less than one, is considered. The responses in dynamical behaviour of population under the effects of the vaccination rates, efficacy rate of vaccines and transferring rate of home isolation to susceptible are computed through Figs. 4, 5 and 6, respectively.

The effects of vaccination rates (\(a=0, 0.001, 0.01, 0.02, 0.03, 0.04, 0.05\)) on dynamical behaviour of all populations for fixed values of pertinent parameters \(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(b=0.1\) are shown in Fig. 4a–f. From Fig. 4a, it is depicted that the susceptible populations decrease with the increase in time and vaccination rate which is positive indication of vaccination drive. Figure 4b illustrated that the infected populations are decreasing with the increase in time and vaccination rate. This indicates that we are able to control the peak infection value which is more important if we can’t control the disease at early stage. Figure 4c reveals that the vaccinated populations are increasing with the increase in time and vaccination rate which is obvious and validate our model. Since, vaccinated populations definitely increase when vaccination drive will be more. Figure 4d reported that the home-isolation populations are decreasing with the increase in time and vaccination rate which is directly related to the vaccination drive and its responses. If the number of infected person will reduce with increasing the vaccination drive then the number of home-isolation populations will also reduce. Figure 4e shows that the hospitalization populations are declining more rapidly than the home-isolation population with the increase in time and vaccination rates. Figure 4f discloses that the recovered populations are also decreasing because of less infected and susceptible populations with increasing the time and vaccination rate. From Fig. 4a–f, it is clearly depicted that populations are approaching to some finite value, which is non-infected equilibrium point (\(E_1^*\)) after some time.

Figure 5a–f illustrate the effects of efficacy rate of vaccines, i.e., \(b=0.05, 0.10, 0.15, 0.20, 0.25, 0.30\) on the dynamical behaviour of all populations (susceptible persons, infected persons, home isolation persons, quarantine persons in hospital, recovered persons and vaccinated persons) at fixed values of other parameters \(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.001\). It is reported that populations follow the exponential growth/decay rule. Figure 5a inferred that with the increase in time and efficacy rate of vaccines, the susceptible populations are varying slowly and not much variation is recorded. However, there is significant difference in the susceptible persons between vaccinated and non-vaccinated. Figure 5b shows that the infected populations are rapidly decreasing with the increase in time and efficacy rate of vaccines which is positive indication of the responses of efficacy rate. Figure 5c examines that the vaccinated populations are increasing with the increase in time and efficacy rate of vaccines, which clearly indicate that if more efficient vaccine is being used to the susceptible populations then the persons will be safer as compared to less efficacy vaccinated persons. Figure 5d noticed that the home-isolation populations are not changing significantly with the increase in time and efficacy rate of vaccines because it is more related to the infected persons. If the infected persons are more than home-isolation populations will be more. From Fig. 5e, it is reported that the hospitalization populations are declining more rapidly as compared to home-isolation with the increase in time and efficiency rate of vaccines. It is further concluded that more efficient vaccine will protect the infections and provide the provide the protection in fighting with virus. Due to that the hospitalization populations will be less with highly efficient vaccination. Figure 5f reveals that the recovered populations are also decreasing significantly with the increase in time and efficacy rate of vaccines because of less infected and susceptible populations. From Fig. 5a–f, it is finally concluded that all populations are approaching at equilibrium point \(E_1^*\) after some time which shows the stability of the analysis.

The variations in dynamical behaviour of populations (susceptible persons, infected persons, home isolation persons, quarantine persons in hospital, recovered persons and vaccinated persons) under the effects of different values of transferring rate of home isolation to susceptible, i.e., \(\epsilon _1=0, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30\) at fixed values of other parameters \(B_1=0.04\), \(\beta _1=0.2\), \(\lambda _1=0.1\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.03\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(a=0.001\), \(b=0.1\) are depicted through the Fig. 6a–f. It is noted that populations are varying exponentially with the time. Figure 6a illustrates that with the increase in time and rate of transferring of home isolation to susceptible population in the presence of vaccination, the susceptible populations are quite decreasing. In the Fig. 6b, the infected populations are rapidly decreasing with the increase in time and the rate of transferring of home isolation to susceptible populations in the presence of vaccination. Figure 6c reveals that the vaccinated populations are increasing with the increase in time and \(\epsilon _1\). Figure 6d shows that the home-isolation populations are decreasing significantly with the increase in time and \(\epsilon _1\). From Fig. 6e, it is recorded that the hospitalization populations are diminishing slightly with the increase in time and \(\epsilon _1\). Figure 6f depicts that the recovered population are also reducing with the increase in time and \(\epsilon _1\) because of less infected and susceptible populations and less hospital quarantine populations. From Fig. 6a–f, it is good to mention that all populations are approaching at equilibrium point (\(E_1^*\)) after some time.

5.3 Dynamical behavior of population for \(\mathbb {R}_0>1\)

In this subsection, for second set of data (\(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.1\), \(b=0.01\)) which is for reproduction no greater than one, is considered. The responses in dynamical behaviour of population under the effects of the vaccination rates, efficacy rate of vaccines and transferring rate of home isolation to susceptible are computed through Figs. 7,  8 and  9, respectively.

The impacts of the vaccination rate, i.e., \(a=0, 0.12, 0.10, 0.08, 0.06\), 0.04, 0.02 on the dynamical behaviour of all population at fixed values of other parameters \(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(b=0.01\) are shown in Fig. 7. Figure 7a examines that with the increase in time and vaccination rate, the susceptible populations are slightly changing. In the Fig. 7b, the infected populations are diminishing more slowly as compared to the Fig. 6b with the increase in time and vaccination rate. Figure 7c reveals that the vaccinated populations are increasing with the increase in time and vaccination rate. Figure 7d inferred that the home-isolation population are reducing very less with the increase in time and vaccination rate. From Fig. 7e, it is noted that with the increase in time and vaccination rate, the hospitalization populations are declining slowly. Figure 7f investigates that the recovered populations are also decreasing with the increase in time and vaccination rate because of less infected susceptible and hospital quarantine populations. From Fig. 7a–f, it is interesting to note that all populations are approaching to infected equilibrium point (\(\bar{E_1}\)) after some time.

The effects of efficacy rate of vaccines, i.e., \(b=0.05, 0.10, 0.15, 0.20\), 0.25, 0.30 on dynamical behaviour of all populations at fixed values of other parameters \(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(\epsilon _1=0.2\), \(a=0.1\) are depicted in Fig. 8a–f. Figure 8a shows that with the increase in time and efficacy rate of vaccines, the susceptible populations are changing very less. Figure 8b noted that the infected populations are decreasing slowly with the increase in time and efficacy rate of vaccines. From Fig. 8c, it is reported that the vaccinated populations are increasing with the increase in time and efficacy rate of vaccines, which clearly indicates that if the more efficient vaccine is being used to the susceptible populations then the society is safer as compared to less efficient vaccines. Figure 8d describes that the home-isolation populations are not changing much with the increase in time and efficacy rate of vaccines. Figure 8e divulges that with the increase in time and efficacy rate of vaccines, the hospitalization populations are declining more rapidly than the home isolation. Figure 8f infers that the recovered populations are also reducing with the increase in time and efficacy rate of vaccines because of less infected and susceptible populations. From Fig. 8a–f, it is remarkable to point out that all populations are approaching at \(\bar{E_1}\) after some time.

The changes in the dynamical behaviour of all population classes with transferring rate of home isolation to susceptible, i.e., \(\epsilon _1=0, 0.05, 0.10, 0.15, 0.20\), 0.25, 0.30 for fixed values of other parameters \(B_1=0.04\), \(\beta _1=0.85\), \(\lambda _1=0.4\), \(\mu =0.03\), \(\mu _1=0.035\), \(\delta _1=0.4\), \(\eta _1=0.12\), \(\gamma _1=0.02\), \(a=0.1\), \(b=0.01\) are seen in Fig. 9a–f. Figure 9a determines that with the increase in time and rate of transferring of home isolation to susceptible population in the presence of vaccination, the susceptible populations are not changing very much. Figure 9b inspects that the infected populations are decreasing less with the increase in time and the rate of transferring of home isolation to susceptible population in the presence of vaccination. Figure 9c studies that the vaccinated populations are increasing with the increase in time and \(\epsilon _1\). Figure 9d reported that the home-isolation populations are decreasing slowly with the increase in time and \(\epsilon _1\). Figure 9e explains that with the increase in time and \(\epsilon _1\), the hospitalization populations are declining slowly. Figure 9f computes that the recovered populations are decreasing with the increase in time and \(\epsilon _1\) because of less infected, susceptible and hospital quarantine populations. From Fig. 9a–f, it is curious to record that all population are approaching at \(\bar{E_1}\) after some time.

6 Conclusion

A dynamical approach is employed to examine the response of vaccination in terms of vaccination rate, efficacy rate of vaccines and transfer rate of home isolation to susceptible, on the spread of corona virus during community transmission for two cases \(\mathbb {R}_0>1\) and \(\mathbb {R}_0<1\) at infected and non-infected equilibrium points. These equilibrium points clearly indicate that the disease persists however the infections could be reduced if awareness and immunization campaigns shall be more. For both the cases of reproduction number (\(\mathbb {R}_0>1\) and \(\mathbb {R}_0<1\)), it is verified that all equilibrium points are stable under certain conditions. Moreover, the vaccinated population compartment has a great impact on the dynamical model. This compartment clearly shows that infections of the corona virus could be controlled if the vaccination rate will increase. If the infection will be controlled then less isolation at home and hospitalizations will be required. If less hospitalization is there then less pressure will be there on medical infrastructure and health warriors. From this dynamical model, it can be recommended that governments/medical agencies must focus on the vaccination campaigns/drives to reduce the spread of COVID-19 infection, and safe the human beings and economy which definitely reduce the stress of persons. Authors also suggest that more awareness among the people is an important factor regarding the preventive measures and vaccinations. Many more factors may affect the spread of COVID-19 infection and could be addressed in future by the dynamical model with incorporating the additional parameters.