Unveiling the effects of azimuthal angle and superimposed magnetic bias fields on the nonlinear magnetization dynamics of superparamagnetic nanoparticles

Abstract

Superparamagnetic nanoparticles provide an efficient way of magnetic recording media based on their magnetization dynamics. This process is predominately governed by the nonlinear magnetic susceptibility. The most accurate approach for performing the calculation of the nonlinear magnetic susceptibility requires the determination of the nonlinear magnetization’ response in thermal agitation subsistence. The recently developed procedure is rationalized by the equation of Langevin that is the equation of Gilbert preserved by an increased random field h (t) as well as processed by Gaussian white noise properties. Moreover, the procedure is predominantly considering the thermal fluctuations of the individual particle magnetization M (t). Nevertheless, this prediction relied on representing the nonlinear magnetic susceptibility and dynamic magnetic hysteresis (DMH) for any direction of AC field strengths. Herein, an illustration of the effect of the azimuthal angle $\left( \phi \right)$ on the DMH and the nonlinear AC susceptibility of nanoparticles is elucidated. A set of linear differential equations describing the statistical moments with infinite hierarchy-recurrence proprieties and susceptible to elucidate the dynamics governing the magnetization of a peculiar single superparamagnetic nanoparticle is established. The method has demonstrated low computational cost and high accuracy by considering the average of the fundamental stochastic Landau–Lifshitz–Gilbert equation in the course of its achievements. It has been found that a strong reliance of the nonlinear AC susceptibility and the DMH on the azimuthal angle $\phi$ is observed

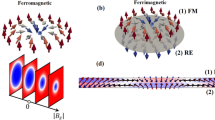
Graphical abstract

Appendix: Matrix continued fraction solution of Eq. 7

The AC stationary response of the system could be simply evaluated from the solution of the formally exact matrix continued fraction [61]:

$$\begin{aligned} C_{1}=\left( \begin{array}{c} \vdots \\ {\textbf{c}}_{1}^{-2}\left( \omega \right) \\ {\textbf{c}}_{1}^{-1}\left( \omega \right) \\ {\textbf{c}}_{1}^{-0}\left( \omega \right) \\ {\textbf{c}}_{1}^{1}\left( \omega \right) \\ {\textbf{c}}_{1}^{2}\left( \omega \right) \\ \vdots \end{array} \right) =\frac{-1}{\sqrt{4\pi }}{\textbf{S}}_{1}\cdot \left( \begin{array}{c} \vdots \\ {\textbf{0}} \\ \overline{{\textbf{p}}}_{{\textbf{1}}} \\ \overline{{\textbf{q}}}_{{\textbf{1}}} \\ \overline{{\textbf{p}}}_{{\textbf{1}}} \\ {\textbf{0}} \\ \vdots \end{array} \right) \end{aligned}$$

(10)

where ${\textbf{S}}_{1}$ is the infinite matrix continued fraction that can be easily extracted from the following recurrence equation:

$$\begin{aligned} {\textbf{S}}_{n}=-\left[ {\textbf{Q}}_{n}+{\textbf{Q}}_{n}^{+}{\textbf{S}}_{n} {\textbf{Q}}_{n+1}^{-}\right] \end{aligned}$$

(11)

herein ${\textbf{Q}}_{n}$ and ${\textbf{Q}}_{n}^{\pm }$ which design three-diagonal supermatrices and their corresponding matrix elements are provided by the following equations:

$$\begin{aligned} \left[ {\textbf{Q}}_{n}\right] _{l.m}=\delta _{l-1.m}\left( \begin{array}{cc} {\textbf{a}}_{2n} & {\textbf{b}}_{2n} \\ {\textbf{d}}_{2n} & {\textbf{a}}_{2n-1} \end{array} \right) +\delta _{l.m}\left( \begin{array}{cc} {\textbf{X}}_{2n} & {\textbf{W}}_{2n} \\ {\textbf{Y}}_{2n} & {\textbf{X}}_{2n-1} \end{array} \right) +\delta _{l+1.m}\left( \begin{array}{cc} {\textbf{a}}_{2n} & {\textbf{b}}_{2n} \\ {\textbf{d}}_{2n} & {\textbf{a}}_{2n-1} \end{array} \right) \end{aligned}$$

(12)

$$\begin{aligned} \left[ {\textbf{Q}}_{n}^{+}\right] _{l.m}=\delta _{l-1.m}\left( \begin{array}{cc} {\textbf{0}} & {\textbf{d}}_{2n} \\ {\textbf{0}} & {\textbf{0}} \end{array} \right) +\delta _{l.m}\left( \begin{array}{cc} {\textbf{Z}}_{2n} & {\textbf{Y}}_{2n} \\ {\textbf{0}} & {\textbf{Z}}_{2n-1} \end{array} \right) +\delta _{l+1.m}\left( \begin{array}{cc} {\textbf{0}} & {\textbf{d}}_{2n} \\ 0 & {\textbf{0}} \end{array} \right) \end{aligned}$$

(13)

$$\begin{aligned} \left[ {\textbf{Q}}_{n}^{-}\right] _{l.m}=\delta _{l-1.m}\left( \begin{array}{cc} {\textbf{0}} & {\textbf{0}} \\ {\textbf{b}}_{2n-1} & {\textbf{0}} \end{array} \right) +\delta _{l.m}\left( \begin{array}{cc} {\textbf{V}}_{2n} & {\textbf{0}} \\ {\textbf{W}}_{2n} & {\textbf{V}}_{2n-1} \end{array} \right) +\delta _{l+1.m}\left( \begin{array}{cc} {\textbf{0}} & {\textbf{0}} \\ {\textbf{b}}_{2n-1} & {\textbf{0}} \end{array} \right) \end{aligned}$$

(14)

In previous equations $\delta _{l.m}$ denotes the Kronecker’s delta, whereas vectors ${\textbf{c}}_{1}^{k}\left( \omega \right)$ , $\overline{{\textbf{p}}}_{{\textbf{1}}}$, and $\overline{ {\textbf{q}}}_{{\textbf{1}}}$ are given as follows:

$$\begin{aligned} {\textbf{c}}_{1}^{k}\left( \omega \right) =\left( \begin{array}{c} c_{2,-2}^{k}\left( \omega \right) \\ c_{2,-1}^{k}\left( \omega \right) \\ c_{2,0}^{k}\left( \omega \right) \\ c_{2,-1}^{k}\left( \omega \right) \\ c_{2,2}^{k}\left( \omega \right) \\ c_{1,-1}^{k}\left( \omega \right) \\ c_{1,0}^{k}\left( \omega \right) \\ c_{1,1}^{k}\left( \omega \right) \end{array} \right) \text { };\text { }\overline{{\textbf{q}}}_{{\textbf{1}}}=\left( \begin{array}{c} -\sqrt{\frac{3}{10}}\Delta \\ 0 \\ \frac{2\sigma +\Delta }{\sqrt{5}} \\ 0 \\ \sqrt{\frac{3}{10}}\Delta \\ \frac{\left( \gamma _{1}-i\gamma _{2}\right) \xi _{0}}{\sqrt{6}} \\ \frac{\gamma _{3}\xi _{0}}{\sqrt{3}} \\ -\frac{\left( \gamma _{1}+i\gamma _{2}\right) \xi _{0}}{\sqrt{6}} \end{array} \right) \text { };\text { }\overline{{\textbf{p}}}_{{\textbf{1}}}=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \frac{\left( \gamma _{1}-i\gamma _{2}\right) \xi _{0}}{2\sqrt{6}} \\ \frac{\gamma _{3}\xi _{0}}{2\sqrt{3}} \\ -\frac{\left( \gamma _{1}+i\gamma _{2}\right) \xi _{0}}{2\sqrt{6}} \end{array} \right) \end{aligned}$$

(15)

The matrices denoted ${\textbf{0}}$ represent zero matrices. Furthermore, we consider herein the five submatrices, namely ${\textbf{V}}_{l}$ , ${\textbf{W}}_{l}$ , ${\textbf{X}}_{l}$ , ${\textbf{Y}} _{l}$ and ${\textbf{Z}}_{l}$ , which play a important role in the biaxial particles’ linear response. These five submatrices are explicitly defined in reference [61]. For $\Delta =0$ , the obtained solution is simply equivalent to that found in cases of uniaxial particles. The Fourier coefficients $\left( {\textbf{c}}_{l,m}^{k}\left( \omega \right) \right)$ are considered as key parameters in the Fourier time series equation characterizing the nonlinear stationary response. Eq. 10 holds the ensemble of Fourier amplitudes requisite for the nonlinear stationary behavior. From Eq. 10, the determination of amplitude ${\textbf{c}}_{1,0}^{k}\left( \omega \right)$ and ${\textbf{c}}_{1,\pm 1}^{k}\left( \omega \right)$ allows the evaluation of the magnetization parameter provided by Eq. 7. Moreover, the determination of the amplitudes and their inclusion via equation Eq.7 permit a rigorous determination of the magnetization.

Therefore, in case we treat a nanoparticles system subjected to a strong AC field and sloping at a certain angle to the particle’s easy axis, we can calculate the matrix continued fractions necessary for the description of the nonlinear AC stationary biaxial superparamagnetic particles’ response. Surprisingly, these calculations continue to be valid for AC fields of different strengths, supporting thereby a rigorous theoretical foundation susceptible to allow a reliable comparison with experimental findings especially in case the theory of perturbation is no longer appropriate.