Impact of EMC effect on D meson modification factor in equilibrating QGP

Abstract

In this article we employ the nuclear EMC effect to extract the parton distribution functions (PDFs) inside the Lead (Pb) and Gold (Au) nuclei. Extracted PDFs are utilized to obtain the transverse momentum dependent (TMD) ones, using the computing codes like Pythia 8 or MCFM-10. Through this procedure TMDPDFs for charm and bottom quarks in Au at $\sqrt{s_{NN}}=200\;GeV$, Pb at $\sqrt{s_{NN}}=2.76\;TeV$ and $\sqrt{s_{NN}}=5.02\;TeV$ are calculated. To evaluate the validity of results and investigate the influence of nuclear EMC effect, the numerated TMDs are used as input to estimate heavy quark modification factor $R_{AA}$ at transverse plane $P_T$. This observable is calculated through numerical solution of the Fokker-Planck equation. For this purpose we need to extract the drag and diffusion coefficients, using the hard thermal loop correction. It is done in the frame work of the relativistic hydrodynamics up to the third order approximation of gradient expansion. The results are compared with same solutions when the input PFDs are considered inside the unbounded protons where the nuclear effect is not included. The comparison indicates a significant improvement of computed $R_{AA}$ with available experimental data when the EMC effect is considered.

Appendix

We have used a fully theoretical procedure, avoiding pure Monte Carlo simulations to find physical sense about the concerned parameters in our analysis. It is the reason to follow the presented methods in references [38] and [45] to put effects of all phenomena on the table. Through these methods we can prepare a very controllable comparison between different results.

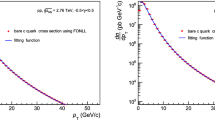
To calculate the heavy quark distribution as a function of transverse momentum after traveling through the QGP, we have solved the Fokker-Planck equation, Eq. (6). Initial conditions for numerical solution of this equation are: Heavy quark initial distribution function $f(P_T, \tau =\tau _0)$ as well as drag ($A(P_T, \tau )$) and diffusion coefficients ($D(P_T, \tau )$). Initial distribution function of heavy quark at transverse plane with and without including the EMC effect have been calculated numerically as explained in Sect. 2 where the TMDPDFs, plotted in Fig. 2, are including the EMC effect. To calculate the drag coefficient by $A(P, \tau )=-\frac{{\rm d}E}{{\rm d}x}$ we need to energy loss of heavy quark while traveling into the QGP bath. Collisional energy loss for heavy quark in equilibrating QGP are given by Eqs. (3,4). We have examined several proposed relations to calculate the radiative energy loss. According to our numerical simulations, the best applicable relation for radiative energy loss is as following [71, 72]:

$$\begin{aligned} \frac{{\rm d}E_{\rm rad}}{{\rm d}x}&= 24 \alpha _s^3(T) \rho _{QGP} \frac{1}{\mu _g} \left( 1-\beta _1 \right) \nonumber \\&\quad \times \left( \sqrt{\frac{1}{1-\beta _1}\ln \left( \frac{1}{\beta _1}\right) }-1 \right) F(\delta )\;, \nonumber \\ \end{aligned}$$

(9)

where

$$\begin{aligned} F(\delta )&= 2\delta -\frac{1}{2}\ln \left( \frac{1+\frac{M^2}{s}e^{2\delta }}{1+\frac{M^2}{s}e^{-2\delta }} \right) \nonumber \\&\quad- \left( \frac{\frac{M^2}{s}\sinh (2 \delta )}{1+2\frac{M^2}{s}\cosh (2\delta )+\frac{M^4}{s^2}} \right) \;, \nonumber \\ \delta&= \frac{1}{2}\ln \left[ \frac{1}{1-\beta _1} \left( 1+\sqrt{1-\frac{1-\beta _1}{\ln \frac{1}{\beta _1}}} \right) ^2 \right] \;, \nonumber \\ s&= 2E^2+2E\sqrt{E^2-M^2}-M^2, \beta _1=\mu _g^2/({\rm C E T})\;, \nonumber \\ C&= \frac{3}{2}-\frac{M^2}{4{ ET}}+\frac{M^4}{48 E^2 T^2 \beta _0}\nonumber \\&\quad\times \ln \left[ \frac{M^2+6{ET}(1+\beta _0)}{M^2+6{ET}(1-\beta _0} \right] \;, \nonumber \\ \beta _0&= \sqrt{1-\frac{M^2}{E^2}}, \rho _{QGP}=\lambda _q \rho _q+\lambda _g \frac{9}{4}\rho _g\;, \nonumber \\ \rho _q&= 16T^3\frac{1.202}{\pi ^2}, \rho _g=9N_fT^3\frac{1.202}{\pi ^2}\;,\nonumber \\ \mu _g&= \sqrt{4 \pi \alpha _s \left( \lambda _q+\lambda _g N_f/6 \right) }T\;. \end{aligned}$$

(10)

Here M is the HQ mass, T is the QGP temperature. In above relations, the Landau-Pomeronchuk-Migdal (LPM) effects have been taken into account trough proper definition of the Debye screening for gluon. The LPM effects cause a reduction in scattering process between HQs and the QGP by adding a limit on the formation-time on the phase space of the emitted gluon in a way that the formation time, should be smaller than the interaction time [38].

Another important phenomenon is related to the namely dead-cone effect. The rate of radiative energy loss is proportional to the mean energy of the emitted gluons [38]. The dead-cone effect includes the radiative energy loss by adding a relation between mean energy of emitted gluon and gluon emission angle (for more details please see Sect. 4 in [45]).

The effective drag coefficient should be obtained by adjusting the contribution rate of the collisional and the radiative energy loss, by fitting the theoretical calculations on the experimental data. The collisional energy loss due to interaction of HQs with light quarks is starting from the onset of fire-ball formation [15, 38]. For evaluating the contribution of collisional energy loss due to HQ-gluon interaction we have taken the $\lambda _g$ as fitting parameter. Thus, we need another fitting parameter to adjust the contribution of radiative energy loss. In this regard effective drag coefficient is taken as $A(P_T, T)=\frac{{\rm d}E_{coll}}{{\rm d}x}+K\frac{{\rm d}E_{rad}}{{\rm d}x}$ where K is free parameter that should be fixed in numerical calculations.

We can consider the QGP as an ideal noninteracting fluid, that HQs are moving while interacting with plasma constituents. On the other hand, we assume that HQs do not interact with each other too. According to the Einstein relation, the diffusion coefficient is defined as $D \propto \bar{\varDelta }^2$, where $\bar{\varDelta }^2$ is the mean square of the deviation between HQ and plasma particles velocities, in a given direction (at interaction interval $\tau$). In this situation, particles may move with a large velocity, but mean square deviation is considerably small and we can employ the nonrelativistic version of the Einstein relation [73, 74]. Thus, we have used the relation $D(P_T,T)=MTA(P_T,T)$ to calculate the diffusion coefficient [44]. The relations in Eq. (10) show that drag and diffusion coefficients are function of QGP temperature T, while they are in fact function of local time $\tau$ i.e., $T(\tau )$. This means that we need to some proper equations to calculate time evolution of QGP temperature.

Time evolution of QGP parameters is derived from the conservation of the stress-energy tensor which is written in the gradient expansion of the velocity and temperature of fields. Time evolution of the QGP temperature at the zero-order approximation of gradient expansion is given by [75, 76]:

$$\begin{aligned} T(\tau )=T_0 \left( \frac{\tau _0}{\tau }\right) ^{\frac{1}{3}}\;, \end{aligned}$$

in which $T_0$ and $\tau _0$ are initial temperature and initial local time, respectively. We have taken reported value in published papers for initial time $\tau _0$ [39], while initial temperature has been taken as a free parameter which is found by doing a fit over the experimental data.

Based on the consideration in [75, 76] the first order relation for time evolution is given given by:

$$\begin{aligned} T(\tau )= T_0 \left( \frac{\tau _0}{\tau }\right) ^{\frac{1}{3}}\left[ 1+\frac{2}{3 T_0 \tau _0}\frac{\eta }{s}\left( 1-\left( \frac{\tau _0}{\tau }\right) ^{\frac{2}{3}}\right) \right] \;, \end{aligned}$$

where $\frac{\eta }{s}$ is the viscosity to entropy ratio. In most of numerical simulations, this quantity has been taken as a free parameter which will be fixed through fitting the model on the experimental data. Implementing the viscous hydrodynamics for describing the heavy-ion collisions, leads to a surprisingly small value of the shear viscosity to entropy density ratio, $\frac{\eta }{s}$. Proposed expressions for the time evolution of $\eta /s$ through the hydrodynamic modelling which is containing high-energy heavy-ion collisions, is very different and fraught with many uncertainties. We have examined several presented expressions for QGP $\eta /s$ in different papers [77, 78]. Below equation, provides acceptable values for this quantity:

$$\begin{aligned} \frac{\eta }{s}=\frac{3T^4}{4\epsilon }\frac{27.126}{g(T)^4 \ln \left( 2.765g(T)^{-1}\right) }\;. \end{aligned}$$

Here $g(T)^2=4 \pi \alpha _s(T)$ and $\alpha _s$ is the strong coupling, given by Eq.(2).

We have also used the presented expansion $\frac{\eta }{s}= 0.097+ 0.4955 (t-1)^2- 0.1781 (t-1)^3+ 0.01738(t-1)^4$, with $t=T/T_C$ [79]. This relation is valid up to $t=4.5$ Sec , with quality of approximation $\chi ^2/dof.=0.0228$, which is acceptable for our calculations.

We have setup our calculations in radial coordinates in the transverse plane $r^2=x^2+y^2$ and $\tan \phi =y/x$, with proper time $\tau =\sqrt{t^2-z^2}$ and space-time rapidity $\varLambda =arctanh\frac{z}{t}$. By considering some conditions on the local equilibrium distribution, expanding the stress-energy tensor up to the third order term of expansion and using the fluid equation of state, the temperature T relates to the fluid energy density $\epsilon$ and pressure p, as $\epsilon =3p=3T^4/\pi ^2$ where $\pi$, that is different from conventional mathematical symbol, can be found through fluid equations of motion [75]. It may be noted that our main aim is to demonstrate the importance of adding the EMC effect in which the initial condition is affected by it. Therefore it is not harm for our results to use the ideal fluid equation of state.

Following the set of equations which describes time evolution of the QGP variables up to the third order of expansions, one can write [75, 80, 81]:

$$\begin{aligned} \frac{{\rm d}\epsilon }{{\rm d} \tau }= & -\frac{1}{\tau }\left( \frac{4}{3}\epsilon -\pi \right) \;, \\ \frac{{\rm d} \pi }{{\rm d}\tau }= & -\frac{\pi }{\tau _ {\pi }}+\frac{1}{\tau }\left( \frac{4}{3}\beta _{\pi }-\lambda \pi -\kappa \frac{\pi ^2}{\beta _{\pi }}\right) \;, \end{aligned}$$

where $\beta _{\pi }=\frac{4\epsilon }{15}$. The terms proportional to $\lambda =\frac{38}{21}$ and $\kappa =\frac{72}{245}$ are second- and third-order parts of approximation in the gradient expansion of the stress-energy tensor, respectively. The shear relaxation time $\tau _\pi$ is equal to the Boltzmann relaxation time $\tau _r$ [75] so that: $\tau _{\pi }=\tau _{r}=5\frac{\eta }{s}\frac{1}{T}=\frac{\eta }{\beta _\pi }$, while $\eta = 187.129\frac{T^3}{g^4\ln g^{-1}}$ . Another relation to calculate the shear relaxation time is $\tau _{\pi }=\frac{2-\ln {2}}{2\pi }$ [82]. As an acceptable approximation, we calculated the fireball temperature from energy density (calculated up to third order of approximation) using second order hydrodynamics relation [76]. Both results are very near to each other.

Now we have all needed equations to calculate time evolution of the fluid temperature at zero, to third order approximation of dissipative hydrodynamics. The bulk viscous pressure vanishes by applying some conditions due to symmetries, and the shear stress tensor is fully specified by the difference between the longitudinal and transverse pressures. We have numerically solved equations using the $4^{th}$ order Runge-Kutta method. Time spacing grids should be chosen very carefully. At earlier time of evolution (which starts from initial time ($\tau _0$)), gradient terms find their maximum values. This means that, initial values of variables will reveal stronger deviations from ideal fluid dynamics. Therefore, we have to choose smaller time steps to solve the dissipative fluid dynamics equations at the beginning of numerical solution procedure. We have used the adaptive step-size method to control the numerical errors. Our calculations clearly show that, without such treatment, numerical errors become so large and results are meaningful.