A variational approach for the ground-state profile of a trapped spinor-BEC: a detailed study of phase transition in spin-1 condensate at zero magnetic field

Abstract

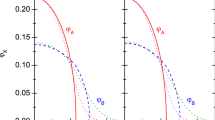
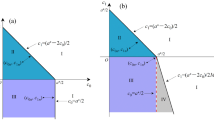
In this article, we introduce a multi-modal variational method to analytically estimate the full number- and corresponding energy-density profile of a spin-1 Bose-Einstein condensate (BEC) for a number of particles as low as 500 under harmonic confinement. To apply this method, we consider a system of spin-1 BEC under three-dimensional isotropic and effective one-dimensional harmonic confinement in the absence (negligible presence) of the magnetic field which has ground-state candidates of comparable energy. It should be noted that in such circumstances kinetic energy contribution to the ground state cannot be neglected which puts the applicability of Thomas–Fermi (T-F) approximation to question. For anti-ferromagnetic condensates, the T-F approximated energy difference between the competing stationary states (ground state and the first excited state) is approximately 0.5%. As T-F approximation is only good for condensates with a large number of particles, T-F approximated predictions can completely go wrong especially for small condensates. This is where comes the role of a detailed analysis using our variational method, which incorporates the kinetic energy contribution and accurately estimates the number- and energy-density profile even for condensates having a small number of particles. Results of our analytical method are supported by numerical simulation. This variational method is general and can be extended to other similar/higher-dimensional problems to get results beyond the accuracy of the T-F approximation.

Appendices

Variational approach for 1-D condensate

For a quasi-one-dimensional condensate the interaction parameter and the number densities can be scaled as,

$$\begin{aligned} c_0= & {} 2 \pi l^2_{yz} l_x\lambda ^{1D}_0\hbar \omega _x, \quad c_1=2 \pi l^2_{yz} l_x\lambda ^{1D}_1\hbar \omega _x, \end{aligned}$$

(65)

$$\begin{aligned} u_m= & {} 2 \pi l^2_{yz} l_x \lambda ^{1D}_0 n_m, \quad r=l_x\zeta ; \end{aligned}$$

(66)

where, $l_x^2=\hbar /(m\omega _x)$, $l_{yz}^2=\hbar /(m\omega _{yz})$, $\omega _{yz}=\sqrt{\omega _y\omega _z}$ and N is the total number of particles in the condensate. As a result, the parameters $\lambda ^{1D}_0$, $\lambda ^{1D}_1$, $\zeta$ and $u_m$ become all dimensionless. Note that we are considering the condensate to be elongated in x direction as the harmonic trapping is far lesser than the geometric mean of the trapping frequencies along the other two direction, i.e., $\omega _x<<\sqrt{\omega _{xy}}$

Thus, the phase-stationary GP equation can be rewritten in dimensionless form as,

$$\begin{aligned}&\bigg \{ -\dfrac{1}{2}\dfrac{d^2}{d\zeta ^2}+\dfrac{1}{2}\zeta ^2+ u-\mu ' +\lambda '_1\left( u_1+u_{-1}+2 \sqrt{u_{-1}u_1}\cos \theta _r\right) \bigg \} \sqrt{u_0}=0, \end{aligned}$$

(67)

$$\begin{aligned}&\bigg \{ -\dfrac{1}{2}\dfrac{d^2}{d\zeta ^2}+\dfrac{1}{2}\zeta ^2+ u-\mu ' \pm \lambda '_1\left( u_1-u_{-1}\right) \bigg \}\sqrt{u_{\pm 1}} +\lambda '_1u_0\left( \sqrt{u_{\pm 1}} +\sqrt{u_{\mp 1}}\cos \theta _r\right) =0. \end{aligned}$$

(68)

where, $\lambda _1''=\lambda ^{1D}_1/\lambda ^{1D}_0$ and $\mu '=\mu /(\hbar \omega _x)$. The total number density u is the sum of all the sub-component density, i.e., $u=u_1+u_0+u_{-1}$.

Note that the equations have similar form with those for 3-D except for the kinetic term and interaction parameters due to different scaling.

1.1 Method of variational approach for 1D:

Following the similar approach as of 3D condensate we assume the number densities,

• $u^{in}(\zeta )=f(\mu ',\zeta )$ for $|\zeta |<|\zeta _0|$,

• $u^{out}(\zeta )=(a+c|\zeta |+d\zeta ^2) \exp (-\dfrac{\zeta ^2}{b})$ for $|\zeta |\ge |\zeta _0|$;

given, the number density and its derivatives on both sides should be equal at $\zeta =\zeta _0$. As discussed, the exact functional form $f(\mu ',\zeta )$ is different for different stationary states and can be found from the solution of Eq. (67-68) by neglecting the kinetic energy term. Considering the symmetry of the problem, only the positive values for $\zeta$ and $\zeta _0$ are taken in the subsequent analysis to simplify notations.

1.1.1 Polar state:

Following the same procedure as in 3D condensate for polar state, the number density for the high density region is found out,

• $u^{in}_{pol}(\zeta )=\mu '-\zeta ^2/2$ for $\zeta <\zeta _0$.

From the smooth matching condition at $\zeta =\zeta _0$ we find all the coefficients a, b, c, d,

• $d =\exp {\Big (\dfrac{12 \zeta _0^2}{k}}\Big ) \dfrac{(k-12\mu ')\mu '-(k-20\mu ')\zeta _0^2-13 \zeta _0^4 }{2 \zeta _0^2 (-2 \mu ' + \zeta _0^2)},$

• $b = \dfrac{k}{12}$,

• $c = 48 \zeta _0^3\exp {\Big (\dfrac{12 \zeta _0^2}{k}}\Big ) \dfrac{k-12(\mu '-\zeta _0^2/2)}{k^2},$

• $a = \exp {\Big (\dfrac{12 \zeta _0^2}{k}}\Big )\dfrac{ 42\zeta _0^4-4(k-14 \mu '+22\zeta _0^2)\mu '+3k\zeta _0^2}{4 (2 \mu ' - \zeta _0^2)},$

where, $k = 6 \mu ' - 9 \zeta _0^2 + \sqrt{36 \mu '^2 - 12 \mu ' \zeta _0^2 + 33 \zeta _0^4}$. To determine $\mu '$, we use the total number conservation condition,

$$\begin{aligned} \int ^{\zeta _0}_0 u^{in}_{pol} d\zeta +\int ^{\infty }_{\zeta _0} u^{out}_{pol} d\zeta =\lambda ^{1D}_0 N. \end{aligned}$$

(69)

Following the integration and simplifying further we get the equation,

$$\begin{aligned} \begin{aligned} \dfrac{1}{16 \sqrt{3}k^2}&\Bigg [4 \sqrt{3}\zeta _0 \bigg (12 k \mu '^2 + 4 \mu ' (-5 k + 24 \mu ') \zeta _0^2- 216 \zeta _0^6 + (-53 k + 384 \mu ') \zeta _0^4 \bigg ) - \exp {\Bigg (\dfrac{12 \eta _0^2}{k1}}\Bigg ) \sqrt{k\pi }\bigg (-60 k \mu '^2 \\&\quad + 20 (7 k - 24 \mu ') \mu ' \zeta _0^2 + (29 k - 576 \mu ') \zeta _0^4 + 408 \zeta _0^6\bigg ) Erfc\Big (\dfrac{2 \sqrt{3} \zeta _0}{\sqrt{k}}\Big )\Bigg ] + \mu ' \zeta _0 - \zeta _0^3/6=\lambda ^{1D}_0N, \end{aligned} \end{aligned}$$

(70)

where, $Erfc((2 \sqrt{3} \zeta _0)/\sqrt{k})$ is the complementary error function and k is defined earlier. Here $\lambda ^{1D}_0$ is different from the 3D condensate due to scaling factor. Thus, $\mu '$ can be estimated numerically for different values of $\zeta _0$ and N. Though the procedure is same but the equation for determining $\mu '$ is different from the 3D condensate.

The polar-state energy density can be written in these dimensionless parameters as (using Eqs. (65-66) in Eq. 9),

$$\begin{aligned} e_{pol}(u(\zeta ))=\dfrac{\hbar \omega _x }{2\lambda ^{1D}_0}\Big (-\sqrt{u(\zeta )}\dfrac{d^2}{d\zeta ^2}\sqrt{u(\zeta )}+\zeta ^2u(\zeta )+u^2(\zeta )\Big ). \end{aligned}$$

(71)

The total energy for polar state can be found out by integrating the energy density,

$$\begin{aligned} E_{pol}(\zeta _0)=\int _{0}^{\zeta _0}d\zeta e_{pol}(u^{in}(\zeta ))+\int _{\zeta _0}^{\infty }d\zeta e_{pol}(u^{out}(\zeta )). \end{aligned}$$

(72)

Now from the minima of the total energy with respect to $\zeta _0$ fixes the total energy corresponding to the stationary state as well as the corresponding $\mu '$.

1.1.2 Phase-matched state

Following a similar approach, the total density in the high density region ($\zeta <\zeta _0$) is written as,

$$\begin{aligned} u^{in}= \dfrac{\mu '-\zeta ^2/2}{(1+\lambda _1'')}, \end{aligned}$$

(73)

where the sub-component densities are

$$\begin{aligned} u^{in}_{\pm 1}=u^{in}/4, \qquad u^{in}_{0}=u^{in}/2. \end{aligned}$$

(74)

In the low density region where the kinetic term plays significant role, the sub-component densities are,

$$\begin{aligned}&u_{\pm 1}^{out}(\zeta )=\dfrac{(a+c\zeta +d\zeta ^2)}{4(1+\lambda _1'')} \exp \left( -\dfrac{\zeta ^2}{b}\right) , \end{aligned}$$

(75)

$$\begin{aligned}&u_{0}^{out}(\zeta )=\dfrac{(a+c\zeta +d\zeta ^2)}{2(1+\lambda _1'')} \exp \left( -\dfrac{\zeta ^2}{b}\right) , \end{aligned}$$

(76)

for $\zeta \ge \zeta _0$, which follows from the same smooth matching condition. The parameters a, b, c and d has the same expressions as shown in case of polar state, but the $\mu '$ and the matching point $\zeta _0$ would be different for the PM state. Total number conservation for this stationary state in 1D leads to,

$$\begin{aligned} \begin{aligned} \dfrac{1}{16 \sqrt{3}k^2}&\Bigg [4 \sqrt{3}\zeta _0 \bigg (12 k \mu '^2 + 4 \mu ' (-5 k + 24 \mu ') \zeta _0^2- 216 \zeta _0^6 + (-53 k + 384 \mu ') \zeta _0^4 \bigg ) - \exp {\Bigg (\dfrac{12 \eta _0^2}{k1}}\Bigg ) \sqrt{k\pi }\bigg (-60 k \mu '^2 \\&\quad + 20 (7 k - 24 \mu ') \mu ' \zeta _0^2 + (29 k - 576 \mu ') \zeta _0^4 + 408 \zeta _0^6\bigg ) Erfc\Big (\dfrac{2 \sqrt{3} \zeta _0}{\sqrt{k}}\Big )\Bigg ] + \mu ' \zeta _0 - \zeta _0^3/6=(1+\lambda _1'')\lambda _0^{1D}N. \end{aligned}\nonumber \\ \end{aligned}$$

(77)

The parameter $\mu '$ of the PM state can be computed from this equation for different values of N and $\zeta _0$.

The energy density for PM state for 1-D harmonic confinement is,

$$\begin{aligned} e_{PM}=\dfrac{\hbar \omega _x}{2\lambda ^{1D}_0}\Big [-\sqrt{u(\zeta )}\dfrac{d^2}{d\zeta ^2}\sqrt{u(\zeta )}+\zeta ^2u(\zeta )+(1+\lambda _1'')u^2(\zeta )\Big ]. \end{aligned}$$

(78)

Now the minimization of the total energy (integrating the energy density) with respect to $\zeta _0$ helps to fix the parameter $\zeta _0$ and the total energy of the PM state.

Energy calculation using T-F approximation in dimensionless form

For an isotropic harmonic 3-D confinement, its easy to see from Eq. (51-52) that the polar state the number density varies as,

$$\begin{aligned} u^{TF}_{pol}=\mu ^{TF}_{pol}-\eta ^2/2. \end{aligned}$$

(79)

Similarly, for PM state, the total number density can be written as,

$$\begin{aligned} u^{TF}_{PM}=\dfrac{\mu ^{TF}_{PM}-\eta ^2/2}{(1+\lambda _1')}. \end{aligned}$$

(80)

Where, the T-F chemical potential can be written in terms of the corresponding T-F radius,

$$\begin{aligned} \mu ^{TF}_{PM(pol)}=\dfrac{1}{2}(\eta ^{TF}_{PM(pol)})^2. \end{aligned}$$

(81)

Now from the conservation of total number of condensate particles,

$$\begin{aligned} \int ^{\eta _{PM(pol)}^{TF}}_0 u^{TF}_{PM(pol)}\eta ^2 d\eta =\lambda _0 N/3, \end{aligned}$$

(82)

it is easy to get to the T-F radius. Thus the T-F energy can be calculated easily.

Similarly for 1D condensate,

$$\begin{aligned}&u^{TF}_{pol}=\mu ^{TF}_{pol}-\zeta ^2/2, \end{aligned}$$

(83)

$$\begin{aligned}&u^{TF}_{PM}=\dfrac{\mu ^{TF}_{PM}-\zeta ^2/2}{(1+\lambda _1'')}, \end{aligned}$$

(84)

$$\begin{aligned}&\mu ^{TF}_{PM(pol)}=\dfrac{1}{2}(\zeta ^{TF}_{PM(pol)})^2. \end{aligned}$$

(85)

To get the 1-D T-F radius we can use the total number conservation equation which for 1-D can be written as,

$$\begin{aligned} \int ^{\zeta _{PM(pol)}^{TF}}_0 u^{TF}_{PM(pol)} d\zeta =\lambda _0 N. \end{aligned}$$

(86)

The total energy in dimensionless form 1-D in polar state,

$$\begin{aligned} E^{TF}_{pol}=\int ^{\zeta ^{TF}_{pol}}_0\left[ \zeta ^2u(\zeta )+u^2(\zeta )\right] d\zeta , \end{aligned}$$

(87)

and the energy for PM state in T-F limit,

$$\begin{aligned} E^{TF}_{PM}=\int ^{\zeta ^{TF}_{PM}}_0\left[ \zeta ^2u(\zeta )+(1+\lambda _1'')u^2(\zeta )\right] d\zeta . \end{aligned}$$

(88)