1 Introduction

Coronavirus constitute a broad category of virus linked to disease spanning from the typical cold to extremely serious conditions, including such Middle East respiratory syndrome (MERS) as well as severe acute respiratory syndrome (SARS). During 2019, a new coronavirus was discovered from Wuhan, China. That represents a novel coronavirus that has never been seen among humans. Most governments throughout the globe are putting forth a lot of effort and taking important steps to stop the spread of coronavirus [1]. This is a unique descendant of the coronavirus based SARS-CoV-2, which was found near Wuhan, China [2, 3]. The number of people suffering from it climbed dramatically in the months following its discovery. The COVID-19-fighting measures implemented till around on the time of composing these words did not halt the spread of infected patients throughout the world. World Health Organization (WHO) update upon that circumstances, issued on May 25, 2020, said that there were 5,304,772 cumulative cases as well as 342,029 fatalities worldwide [4]. COVID-19 has shattered cultures and drastically impacted daily life throughout the world. While our current conditions are exceptional, they have been significantly molded by persisting social facts including such entrenched racial as well as economic inequalities, the spread of disinformation, and concerns regarding the world’s democracies’ ability to tackle severe crises.

Scientists realize that such infection is caused by the SARS-CoV-2 virus, which transmits in a variety of manners among individuals. According to current data, the virus transmits mostly between persons who are in close contact with each other, whether at a conversational length. Whenever infected individual coughs, sneezes, speaks, sings, or breathe, the virus can spread in microscopic liquid particles from their mouth or nose. Whenever infected cells throughout the atmosphere are breathed at a close approach (this is sometimes referred to as short-range aerosol or short-range airborne transmission) or come to directly interface to the eyes, nose, as well as mouth, some other human might receive the virus (droplet transmission). This virus might further transmit under inadequately ventilated and/or congested interior environments, whereby individuals prefer to invest more time. This is since aerosols may linger within the atmosphere as well as travel beyond just a conversing range (this is often called long-range aerosol or long-range airborne transmission). Individuals can get infected via contacting either eyes, nose, or mouth while contacting materials or things affected by the virus.

Employing differential systems to anticipate epidemics is particularly important in understanding the nature of the epidemic and designing effective control methods [5,6,7]. SIR or SEIR models are commonly used to examine the humanitarian spread of epidemics [8,9,10]. To simulate and investigate the COVID-19 pandemic, many models had already been presented. Lin et al. analyzed the COVID-19 pandemic by expanding the SEIR model [11], bringing under consideration risk knowledge and the accumulative problem of cases, while S symbolizes the susceptible, E represents the exposed, I signifies the infected, and R illustrates the removed cases. Anastassopoulou et al. proposed the SIR system through discrete time mode, keeping under consideration dead instances, in [12]. Casella’s SIR system is developed in [13] to study the effect for delays and to assess containment measures. The COVID-19 severity was evaluated utilizing the dynamics of transition by Wu and colleagues [14,15,16]. For modeling COVID-19 spread in such a diverse population, the wide SEIRA system was built and statistically tested in [17]. Differential formulations have different forms that can be considered as a basic differential tool to characterize multiple epidemics [18]. Artificial intelligence-based climatic exogenous variables are exploited for the forecasting of American and Brazilian COVID-19 pandemic [19]. Spatiotemporal COVID-19 modeling involving prevalence and mortality using neural networks [20], Short term prediction of COVID-19 cased for the Brazilian prospectives [21]. An analytical model for COVID-19 pandemic with the help of artificial neural networks [22].

Several research attempts were being made to suppress epidemic outbreaks by optimal control [23,24,25]. The optimal control approach appears to be to pursue the most powerful technique that reduces the rate for infections to a very potential bare minimum while circulating a therapy or prophylactic inoculation at the lowest feasible cost [24,25,26,27]. These strategies may include medications, vaccinations, social distancing, and educational initiatives [28, 29]. Differential studies of epidemic disorders have been more significant [28, 30,31,32]. Numerous trials have been conducted to control HIV [33], dengue fever [34], TB [35], delayed SIR [36], including delayed SIRS [18, 37]. With in exploration of the dynamics of epidemiological models, fractional- order differential equations introduce a new dimension. For a consequence, the fractional form of various epidemical models has been studied, as shown in [38,39,40].

Any investigation on fractional-order differential equations (FDEs) is highly essential in practically all fields, including mathematics, physics, control systems, and especially engineering. Various modalities have been used to study fractional calculus and FDEs throughout the previous three decades, including the Erdelyi–Kober operator [41], the Riemann–Liouville operator [42], the Caputo operator [43], the Weyl–Riesz operator [44], and the Grunwald–Letnikov operator [45]. In this paper, we present a novel epidemiological FO COVID-19 pandemic either a generalization of such traditional differential formulation, comparable to the one published with Gumel et al. based SARS via [46, 47]. As mentioned in the third section, infected patients are categorized into five separate groups in the SIDARTHE model based on the detection and presentation of symptoms [47].

We investigate the FO-SIDARTHE system in current paper and afterward establish the FO required conditions for the occurrence of stable outcomes. Moreover, we develop a stochastic template for solving the FO differential model relying on the COVID-19 pandemic SIDARTHE model employing four control mechanisms that take into account the availability of vaccination as well as availability of therapies across the diseased population revealed three population fraction stages. FO-SIDARTHE system is analyzed using stochastic solvers based on the Levenberg–Marquardt backpropagation approach (L-MB) and neural networks (NNs), especially L-MBNNs. Three cases containing varying values within of FO are provided in order to solve FO-SIDARTHE system through simulation software.

The remaining portions of the paper are given in regards: We devise a framework of SIDARTHE fractional differential model for the COVID-19 epidemic is presented in Sect. 2. The innovative topographies including an overview of stochastic solvers along with important innovative aspects of the L-MBNNs for such differential FO system employing a COVID-19 SIDARTHE model are provided in Sect. 3. The L-MBNNs structure is explained in Sect. 4. The results and simulations obtained employing the planned method for the FO SIDARTHE model are provided in Sect. 5. Section 6 illustrates the conclusion.

2 FO-SIDARTHE differential system

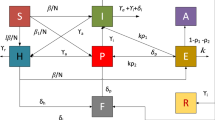
Giulia Giordano et al. [47] used the SIDARTHE model to simulate the COVID-19 outbreak, then match its findings to genuine statistics from Italy. The SIDARTHE model distinguishes between definite and indeterminate infected patients, as well as between different degrees of sickness (DOI). The whole population is divided into eight disease stages in the SIDARTHE COVID-19 epidemic model, as shown in Table 1. Figure 1 depicts the interaction \((\vec {\Psi })\) of eight-stage-based disease. In Fig. 1, the susceptible population partition S is separated into four subclasses to illustrate the concealed subclasses of the susceptible population partition S called SA,  SD,  SI,  , and SR. The entire interaction Fig. 1 has been found, and it may be investigated further to understand about the system.

Table 1 Population modeling of the COVID-19 pandemic in eight stages
Full size table

The COVID-19 pandemic SIDARTHE system is formally defined by eight dynamics [47].

A causal feature seems critical for modeling epidemic transition phenomena, because fractional derivative is highly beneficial in modeling epidemic transition systems because it considers either memory impact as well as the general features of the system, both of which are primary in the deterministic feature. The population dynamics in each category with time is represented below by eight fractional-order \((\alpha )\) differential equations, as shown in system of Eqs. (1):

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}({\mathcal {D}})^{\alpha }S(\tau )=-a_1 SI -a_2 SD -a_3 SA -a_4 SR,\\ &{}({\mathcal {D}})^{\alpha }I(\tau )=a_1 SI +a_2 SD +a_3 SA +a_4 SR -b_1I -b_2I -b_3I,\\ &{}({\mathcal {D}})^{\alpha }D(\tau )=b_1I -c_1D -c_2D,\\ &{}({\mathcal {D}})^{\alpha }A(\tau )=b_2I-\theta A -d_1A -d_2A,\\ &{}({\mathcal {D}})^{\alpha }R(\tau )=c_1D +\theta A -\chi R -\nu R,\\ &{}({\mathcal {D}})^{\alpha }T(\tau )=d_1A +\nu R -\zeta T -\mu T,\\ &{}({\mathcal {D}})^{\alpha }H(\tau )=b_3I +rD + d_2A + \chi R + \zeta T,\\ &{}({\mathcal {D}})^{\alpha }E(\tau )=\mu T. \end{aligned} \end{array}\right. } \end{aligned}$$
(1)

Parameters of FO-SIDARTHE system (1) are represented by little Greek and English characters. Each of the model parameters have positive values, and they were computed using real data in [47]. Figure 1 depicts the impact of each stage of the pandemic visually. The following are the true meanings of the SIDARTHE COVID-19 model parameters:

Fig. 1
figure 1

L-MBNNs workflow mechanism to solve the COVID-19 FO-SIDARTHE-associated model

Full size image

3 Innovative topographies including an overview of stochastic solvers

To solve either FO-SIDARTHE system, numerical stochastic operators via L-MBNNs are presented. The performance of local but also global operators using stochastic computer solvers is being used to solve a wide variety of nonlinear, complex, stiff, and singular systems [48,49,50]. The nonlinear third sort of singular model [50], fractional-order singular models [51,52,53,54]. For the fractional nonlinear-singular Lane–Emden (FNSLE) model, a revolutionary stochastic computational strategy built upon Meyer fractional wavelet neural network (MFWNN) is devised. To design a merit function for FNSLE differential equations, the modeling strength of MFWNN is employed to adapt the differential NS-FLE system to difference equations, and approximation theory is applied in mean squared error sense. We primarily explored the functional order system in this article [55]. The construction of a unique model relying upon nonlinear third-order Emden–Fowler delay differential (EFDD) equations, as well as two kinds employing the perception of delay differential with standard format of such second-order EF equation, is provided within this manuscript. The construction of a unique model relying upon nonlinear third-order Emden–Fowler delay differential (EFDD) equations, as well as two kinds employing the perception of delay differential with standard format of such second-order EF equation, is provided within this study, i.e., delayed differential model [56], as well as periodic differential system [51] represent just handful well implementations of such solvers. The goal of this work is to use the stochastic methods of the L-MBNNs to generate numerical representations of the FO derivatives of a COVID-19 SIDARTHE differential system found upon SIDARTHE phenomena. This is discovered how time-fractional-order derivatives may be used to specify system conditions in such a variety of ways. The memory function represents the derivative of fractional order, whereas the derivative order structure conveys remembrance. Real and genuine implementations are shown by more such fractional derivatives [57,58,59].

The following seem to be important innovative aspects of the L-MBNNs for such differential FO system employing a COVID-19 FO-SIDARTHE system:

  • A novel design for its FO derivatives underlying the COVID-19 FO-SIDARTHE system is addressed relying on certain SIDARTHE impacts.

  • Stochastic measures were never employed to solve basic FO derivatives of such a COVID-19 FO-SIDARTHE system that relied on SIDARTHE effects.

  • The numerical studies employing stochastic paradigms are shown effectively using the FO derivatives of the COVID-19 FO-SIDARTHE system based on the SIDARTHE effects.

  • AI is used to solve the nonlinear FO derivatives of the COVID-19 FO-SIDARTHE system relying upon that SIDARTHE impacts employing the structure of L-MBNNs.

  • Three appropriate FO variants depending upon that COVID-19 FO-SIDARTHE system have been numerically solved to validate the suggested scheme’s reliability.

  • The brilliance of stochastic computing solver-based L-MBNNs is demonstrated by comparing the produced and reference (Adams–Bashforth–Moulton) solutions.

  • The correctness of the scheme is measured by the absolute error (AE) performances obtained while solving the COVID-19 FO-SIDARTHE system.

  • The regression, STs, MSE, EHs, and correlation performances validate the developed L-MBNNs’ dependability and consistency in solving the COVID-19 FO-SIDARTHE system.

4 Suggested methodology: L-MBNNs

This section explains the suggested L-MBNNs structure for solving the fractional-order immune-chemotherapeutic treatment treating COVID-19 FO-SIDARTHE system-linked model. The approach is divided into two sections. First, the fundamental L-MBNNs operator performances are presented. Meanwhile, the L-MBNNs execution approach is used to solve the COVID-19 FO-SIDARTHE system.

Figure 1 depicts multi-layer optimization procedure employing numerical stochastic L-MBNNs, whereas Fig. 2 depicts the single-layer neuron layout. The L-MBNNs processes are supplied in MATLAB using the ‘nftool’ command, having data selected like 72% for training, 18% for testing as well as 10% authorization. The layer structure of neural networks, i.e., a single input, output and hidden layer, is exploited with 10 number of hidden neurons, one input vector and 8 target vector. The learning of the networks is performed with the help of Levenberg–Marquardt (L-M) algorithms with default setting of the parameters. The premature convergence is more probably by introduction a slight variation of the parameter of proposed L-MBNNs such as change in training, testing, validation dataset samples, layer structure, hidden neurons, and backpropagation algorithm.

Fig. 2
figure 2

The formation of a single neuron

Full size image
Fig. 3
figure 3

L-MBNNs developed for addressing FO COVID-19 SIDARTHE-related model

Full size image
Fig. 4
figure 4

STs along with MSE performances for solving the FO-SIDARTHE system

Full size image

5 Results obtained employing the planned method

Numerical performances with three possible FO modifications to address the nonlinear COVID-19 FO-SIDARTHE system through using suggested L-MBNNs are shown in this phase. In the accompanying cases, the differential description of each variant is given as follows:

Case 1:

Adopt the following FO COVID-19 SIDARTHE-related model with the designated values \(\alpha =0.3,~a_1=0.1,~a_4=0.1, ~b_1=0.05,~a_2=0.3,~b_2=0.07,~a_3=0.2,~b_3=0.09,~a_4=0.1,~c_1=0.2,~c_2=0.5,~\theta =0.7,~d_1=0.1,~d_2=0.3,~\chi =0.05,~\nu =0.07,~\zeta =0.2,~\mu =0.5,~r=0.6\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}({\mathcal {D}})^{0.3}S(\tau )=-0.1 S(\tau )I(\tau ) -0.3 S(\tau )D(\tau ) -0.2 S(\tau )A(\tau ) -0.1 S(\tau )R(\tau ), &{}S_0=0.1,\\ &{}({\mathcal {D}})^{0.3}I(\tau )=0.1 S(\tau )I(\tau ) +0.3 S(\tau )D(\tau ) +0.2 S(\tau )A(\tau ) +0.1 S(\tau )R(\tau ) -0.21I(\tau ), &{}I_0=0.1,\\ &{}({\mathcal {D}})^{0.3}D(\tau )=0.05I(\tau ) -0.7D(\tau ), &{}D_0=0.2,\\ &{}({\mathcal {D}})^{0.3}A(\tau )=0.07I(\tau )-1.1 A(\tau ), &{}A_0=0.1,\\ &{}({\mathcal {D}})^{0.3}R(\tau )=0.2D(\tau ) +0.7 A(\tau ) -0.12R(\tau ), &{}R_0=0.2,\\ &{}({\mathcal {D}})^{0.3}T(\tau )=0.1A(\tau ) +0.07 R(\tau ) -0.7 T(\tau ), &{}T_0=0.2,\\ &{}({\mathcal {D}})^{0.3}H(\tau )=0.09I(\tau ) +0.6D(\tau ) + 0.3A(\tau ) + 0.05 R(\tau ) + 0.2 T(\tau ), &{}H_0=0.1,\\ &{}({\mathcal {D}})^{0.3}E(\tau )=0.5 T(\tau ), &{}E_0=0.2. \end{aligned} \end{array}\right. } \end{aligned}$$
(2)
Fig. 5
figure 5

Results valuations and EHs for FO-SIDARTHE system

Full size image
Fig. 6
figure 6

Regression plots to solve a FO-SIDARTHE system

Full size image

Case 2:

Adopt the following FO COVID-19 SIDARTHE-related model with the designated values \(\alpha =0.3,~a_1=0.1,~a_4=0.1, ~b_1=0.05,~a_2=0.3,~b_2=0.07,~a_3=0.2,~b_3=0.09,~a_4=0.1,~c_1=0.2,~c_2=0.5,~\theta =0.7,~d_1=0.1,~d_2=0.3,~\chi =0.05,~\nu =0.07,~\zeta =0.2,~\mu =0.5,~r=0.6\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}({\mathcal {D}})^{0.5}S(\tau )=-0.1 S(\tau )I(\tau ) -0.3 S(\tau )D(\tau ) -0.2 S(\tau )A(\tau ) -0.1 S(\tau )R(\tau ), &{}S_0=0.1,\\ &{}({\mathcal {D}})^{0.5}I(\tau )=0.1 S(\tau )I(\tau ) +0.3 S(\tau )D(\tau ) +0.2 S(\tau )A(\tau ) +0.1 S(\tau )R(\tau ) -0.21I(\tau ), &{}I_0=0.1,\\ &{}({\mathcal {D}})^{0.5}D(\tau )=0.05I(\tau ) -0.7D(\tau ), &{}D_0=0.2,\\ &{}({\mathcal {D}})^{0.5}A(\tau )=0.07I(\tau )-1.1 A(\tau ), &{}A_0=0.1,\\ &{}({\mathcal {D}})^{0.5}R(\tau )=0.2D(\tau ) +0.7 A(\tau ) -0.12R(\tau ), &{}R_0=0.2,\\ &{}({\mathcal {D}})^{0.5}T(\tau )=0.1A(\tau ) +0.07 R(\tau ) -0.7 T(\tau ), &{}T_0=0.2,\\ &{}({\mathcal {D}})^{0.5}H(\tau )=0.09I(\tau ) +0.6D(\tau ) + 0.3A(\tau ) + 0.05 R(\tau ) + 0.2 T(\tau ), &{}H_0=0.1,\\ &{}({\mathcal {D}})^{0.5}E(\tau )=0.5 T(\tau ), &{}E_0=0.2. \end{aligned} \end{array}\right. } \end{aligned}$$
(3)

Case 3:

Adopt the following FO COVID-19 SIDARTHE-related model with the designated values \(\alpha =0.3,~a_1=0.1,~a_4=0.1, ~b_1=0.05,~a_2=0.3,~b_2=0.07,~a_3=0.2,~b_3=0.09,~a_4=0.1,~c_1=0.2,~c_2=0.5,~\theta =0.7,~d_1=0.1,~d_2=0.3,~\chi =0.05,~\nu =0.07,~\zeta =0.2,~\mu =0.5,~r=0.6\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}({\mathcal {D}})^{0.7}S(\tau )=-0.1 S(\tau )I(\tau ) -0.3 S(\tau )D(\tau ) -0.2 S(\tau )A(\tau ) -0.1 S(\tau )R(\tau ), &{}S_0=0.1,\\ &{}({\mathcal {D}})^{0.7}I(\tau )=0.1 S(\tau )I(\tau ) +0.3 S(\tau )D(\tau ) +0.2 S(\tau )A(\tau ) +0.1 S(\tau )R(\tau ) -0.21I(\tau ), &{}I_0=0.1,\\ &{}({\mathcal {D}})^{0.7}D(\tau )=0.05I(\tau ) -0.7D(\tau ), &{}D_0=0.2,\\ &{}({\mathcal {D}})^{0.7}A(\tau )=0.07I(\tau )-1.1 A(\tau ), &{}A_0=0.1,\\ &{}({\mathcal {D}})^{0.7}R(\tau )=0.2D(\tau ) +0.7 A(\tau ) -0.12R(\tau ), &{}R_0=0.2,\\ &{}({\mathcal {D}})^{0.7}T(\tau )=0.1A(\tau ) +0.07 R(\tau ) -0.7 T(\tau ), &{}T_0=0.2,\\ &{}({\mathcal {D}})^{0.7}H(\tau )=0.09I(\tau ) +0.6D(\tau ) + 0.3A(\tau ) + 0.05 R(\tau ) + 0.2 T(\tau ), &{}H_0=0.1,\\ &{}({\mathcal {D}})^{0.7}E(\tau )=0.5 T(\tau ), &{}E_0=0.2. \end{aligned} \end{array}\right. } \end{aligned}$$
(4)

Numerical presentations of the simulations of FO COVID-19 SIDARTHE-associated model are shown via implementing as stochastic L-MBNNs processes involving 10 neurons including data selection comprising 72% for training, 18% for testing as well as 10% authorization. Figure 3 depicts the structure of a hidden, output, and input neuron.

Table 2 For further information on the model selections, read [47] and the sources listed there
Full size table
Table 3 The L-MBNNs procedure is adopted to solve the FO differential model of COVID-19 SIDARTHE
Full size table
Fig. 7
figure 7

Result founded upon a COVID-19 FO-SIDARTHE-based system

Full size image
Fig. 8
figure 8

AE founded upon a COVID-19 FO-SIDARTHE-based system

Full size image

Figures 4, 5, and 6 show the graphical visualizations used to analyze the FO COVID-19 SIDARTHE-associated system employing the L-MBNNs processes. The graphical representations in Figs. 4 and 5 are presented to examine the best performances with STs. To solve the FO-SIDARTHE system, the MSE and STs values of training, best curves, as well as authentication are produced in Fig. 4. The derived values are \(8.1037 \times 10^{-09}\), \(1.4194 \times 10^{-08}\), and \(8.3204 \times 10^{-09}\), respectively, based on the best performances of the FO-SIDARTHE system at epochs 33, 26, and 19.

In Fig. 4, overall gradient measurements are also plotted to solve the FO COVID-19 SIDARTHE-related differential model employing L-MBNNs. For cases 1, 2, and 3, these gradient performances were determined to be \(9.2726 \times 10^{-08}\), \(9.3207 \times 10^{-08}\), and \(9.641 \times 10^{-08}\), respectively. These graphical visualizations illustrate the convergence of suggested L-MBNNs to solve the FO COVID-19 SIDARTHE differential model employing L-MBNNs. Figures 68 show the values of the fitting curves used to address every case for the proposed FO COVID-19 SIDARTHE differential model.

Those visualizations compare the performance of the reference and achieved findings. Error plots are representing the substantiation, testing, as well as training to address all scenarios of the FO COVID-19 SIDARTHE-associated differential model. Relying on the FO COVID-19 SIDARTHE-associated differential model, various EHs are displayed through Fig. 5d–f, as well as corresponding regression measures, are supplied by Fig. 5a–c. For cases 1, 2, and 3, the EHs are estimated as \(-3.3 \times 10^{-06}\), \(1.5 \times 10^{-05}\), and \(2.2 \times 10^{-06}\), respectively.

In Fig. 6, the correlation has been demonstrated to confirm the regression performance. Such correlation plots for the FO COVID-19 SIDARTHE-linked differential model are calculated as 1. The training, testing, and authentication expressions indicate the correctness of the stochastic L-MBNNs procedure for solving the fractional-order COVID-19 SIDARTHE differential model. Table 2 displays the convergence of the FO COVID-19 SIDARTHE-related differential model employing MSE, complexity, training, authentication, iterations, testing, as well as backpropagation (Table 3).

Figures 7, 8 exhibit the plotting for their result comparisons as well as AE values. To address the FO-SIDARTHE system employing stochastic L-MBNNs, numerical expressions are presented. The overlapping findings of the reference and derived numerical performances are presented in Fig. 7. The overlapping result validates the L-MBNNs’ exactness in solving the FO COVID-19 SIDARTHE-associated differential model.

Figure 8 depicts the AE parameters employed to solve the COVID-19 FO-SIDARTHE system. Regarding cases 1 to 3, in the dynamics of \(S(\tau )\), the AE values are found around \(10^{-04}-10^{-06}\), \(10^{-04}-10^{-06}\), and \(10^{-04}-10^{-07}\). Regarding cases 1 to 3, the AE values for \(I(\tau )\) are estimated in the range of \(10^{-05}-10^{-06}\), \(10^{-04}-10^{-05}\), and \(10^{-05}-10^{-07}\). Regarding cases 1 to 3, the AE for \(D(\tau )\) has been calculated as \(10^{-04}-10^{-07}\), \(10^{-04}-10^{-05}\), and \(10^{-04}-10^{-05}\). Likewise, for cases 1 to 3, the AE for \(A(\tau )\) was computed as \(10^{-04}-10^{-05}\), \(10^{-04}-10^{-06}\), and \(10^{-04}-10^{-05}\). Additionally, for cases 1 to 3, the AE for \(R(\tau )\) was estimated accordingly \(10^{-04}-10^{-05}\), \(10^{-04}-10^{-06}\), and \(10^{-04}-10^{-05}\).For cases 1 to 3, the AE for \(T(\tau )\) was determined accordingly \(10^{-04}-10^{-06}\), \(10^{-04}-10^{-05}\), and \(10^{-04}-10^{-06}\). In cases 1 to 3, the AE for \(H(\tau )\) was obtained simply \(10^{-04}-10^{-06}\), \(10^{-04}-10^{-05}\), and \(10^{-04}-10^{-05}\). Consequently, for cases 1 to 3, the AE for \(E(\tau )\) was approximated by \(10^{-04}-10^{-06}\), \(10^{-04}-10^{-05}\), and \(10^{-04}-10^{-07}\).

These AE values show how well the recommended L-MBNNs addressed the COVID-19 FO-SIDARTHE system.

6 Conclusion

The numerical representations of the COVID-19 FO-SIDARTHE-based differential model are described throughout this paper. The goal of this research is to give a FO assessment employing a differential model focused on dynamics of COVID-19 FO-SIDARTHE-based system to offer better accurate system performances. That whole investigation also included an integer, nonlinear differential system with COVID-19 pandemic effects. The FO COVID-19 SIDARTHE differential model underlying four suggested control measures, namely SI, SD, SA, and SR. The numerical performances of either the SIDARTHE differential model built on FO COVID-19 SIDARTHE have never been published or solved via stochastic Levenberg–Marquardt backpropagation neural networks. To solve the COVID-19 FO-SIDARTHE differential model, three cases with varying values of the FO have been supplied. The data used to offer the numerical solutions of the COVID-19 FO-SIDARTHE-based system are divided as follows: 72% for training, 18% for testing as well as 10% authorization. The numerical performances of the COVID-19 FO-SIDARTHE-based system were shown using ten neurons. The numerical findings of the COVID-19 FO-SIDARTHE-based system were compared with the Adams–Bashforth–Moulton differential system. The reported numerical findings were produced using L-MBNNs to decrease the MSE. The STs, regression, correlation, EHs, as well as MSE are being used to demonstrate the reliability as well as the competency of L-MBNNs, as well as their numerical performances. The matching of reference and actual findings demonstrate the accuracy of the L-MBNNs based on the COVID-19 FO-SIDARTHE-based differential model. The scheme’s performance is validated by the consistency and reliability of the suggested L-MBNNs. L-MBNNs may be exploited in the upcoming investigation to offer numerical measurement results of the Lonngren wave, fluid dynamics, information security, and bioinformatics [60,61,62,63,64,65,66,67].