1 Introduction

After the emergence of Einstein’s revolutionary conception of gravitation, known as general relativity (GR), the quest for analytical solutions to the Einstein gravitational equations (EFEs) has become a fascinating and challenging area of research. The solutions to the EFEs unlock many mysteries of the universe by providing a pathway for understanding the physical consequences of gravitational interactions. However, due to the non-linear nature of the EFEs, obtaining analytical solutions with physical significance is challenging, except in specific scenarios. Several approaches have been proposed to address this problem, with the goal of constructing feasible solutions. In this direction, Schwarzschild did the pioneering work in constructing the exact solutions to the EFEs exhibiting the exterior of static, spherically symmetric self-gravitational configurations [2]. Afterward, Tolman explored different analytical solutions by considering stellar structures coupled with perfect fluid distribution [3]. However, in the context of GR, Lemaître [4] emphasized that the stellar structures may possess anisotropic matter distributions. According to his findings, spherical symmetry does not require the presence of an isotropic pressure condition (\(p_{r}= p_{t}\)). Bowers and Liang [5] pointed out that considering anisotropy as the fluid approximation describing the matter distribution of self-gravitational systems leads to a deeper understanding of these relativistic stellar configurations. Furthermore, Ruderman investigated that the existence of nuclear matter with extreme-density regimes (\(\rho >10^{15} g/cm ^{3}\)) inside the self-gravitational compact configuration may give rise to pressure anisotropy [6].

In high-density stellar systems, the pressure manifests in two distinct components: the pressure along the radial direction (denoted as \(p_{r}\)) and the pressure along the tangential direction (denoted as \(p_{t}\)). This phenomenon results in an anisotropic pressure condition, where the radial pressure is not equal to the tangential pressure (\(p_{r}\ne p_{t}\)). This partitioning of the fluid’s pressure produces anisotropy within the interior of self-gravitational fluid spheres, which can be calculated through the anisotropic factor \(\Pi \equiv p_{t}-p_{r}\). The influence of pressure anisotropy within charged self-gravitational fluid spheres was initially studied by Bonner [7] and subsequently investigated by Herrera and Ponce de León [8]. On the other hand, Ram and Pandey explored the significance of local anisotropy within the context of alternative theories of gravitation [9]. Numerous physical phenomena occurring in high as well in low-density regimes are responsible for the departures from local isotropy. In highly dense relativistic structures, local anisotropy can arise due to phase transitions during gravitational collapse, the presence of P-type super-fluids, solid cores, viscosity, rotation, and the pion condensed phase configuration [6, 10, 11]. Furthermore, the appearance of local anisotropy within the structures of self-gravitational sources has been comprehensively studied by [12]. It is worth mentioning that despite assuming an initially isotropic matter distribution in the relativistic regime, the system tends to generate pressure anisotropy as a result of the internal physical processes within the system [13]. In this respect, various researchers [14,15,16,17,18,19] discussed the importance and implications of anisotropy, as well as the mechanisms that give rise to anisotropies within charged and uncharged self-gravitational fluid spheres, considering Einstein-Gauss-Bonnet gravities.

Apart from recognizing anisotropy as a crucial factor in comprehending the complex arrangement of self-gravitating compact sources, we can explore its connection with another physical parameter, the complexity factor, which encompasses both density gradient and pressure anisotropy. The term “complexity” comprises all the ingredients that produce intricacies in a system. Numerous efforts in developing a fundamental definition of complexity across various scientific domains have been made during the last few decades. However, an exact and all-inclusive concept of complexity that applies uniformly across all fields has yet to be achieved. Within the domain of physics, the notion of complexity emerges from examining two contrasting examples: a perfect crystal, which represents complete order and thus possesses low information content, and an isolated ideal gas, which embodies complete disorder, leading to maximum information. These serve as the simplest models and are regarded as systems with zero complexity. Additional efforts have been made to include other factors in the concept of complexity for a more comprehensive and representative definition. In this direction, Lopez–Ruiz proposed the notion of “disequilibrium” based on the statistical point of view [20]. In this context, the term “disequilibrium” reaches its maximum value for a perfect crystal, as it significantly deviates from equi-distribution among accessible states, while it remains at zero for an ideal gas. Afterward, equilibrium is achieved by defining a quantity as the product of the concepts of “disequilibrium” and information. This approach eliminates complexity for both the isolated ideal gas and the perfect crystal.

Furthermore, substantial attempts have been made to outline the concept of complexity within the framework of self-gravitational fluid spheres, such as white dwarf and neutron stars, using Einstein’s gravity and modified theories of gravitation [21,22,23]. A few years ago, Herrera [1] proposed an alternative characterization of complexity concerning static, self-gravitational perfect fluid spheres, derived from the scalar function emerging in the orthogonal decomposition of the Riemann–Christoffel curvature tensor. This novel concept is based on the assumption that relativistic systems with homogeneous density and isotropic pressure are the simplest. Moreover, this natural definition of complexity allows for the formulation of multiple solutions corresponding to anisotropic self-gravitational fluid configurations with zero complexity. Therefore, it would be intriguing to explore the impact of the complexity factor on anisotropic self-gravitational stellar configurations

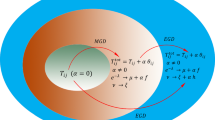
The gravitational decoupling scheme for constructing analytical solutions to EFEs of general relativity was initially proposed by Ovalle [24]. This systematic approach studies time-independent, self-gravitating stellar sources that exhibit spherical symmetry using EFEs

$$\begin{aligned} R^{\alpha }_{~\beta }-\frac{1}{2}R\delta ^{\alpha }_{~\beta } =\kappa ^{2}[T^{\alpha }_{~\beta }]^{\textrm{tot}}, \end{aligned}$$
(1)

having two sources that interact gravitationally. It is notable that in the extended form (so-called extended geometric deformation scheme) the above system affects both the radial and the temporal metric components, and these entities can interact, exchanging energy and momentum in order to decouple the EFEs [25]. Thus, the total energy-momentum tensor (EMT) can be written as

$$\begin{aligned}{}[T^{\alpha }_{~\beta }]^{\textrm{tot}} ={T}^{\alpha }_{~\beta }+\varphi \Theta ^{\alpha }_{~\beta }. \end{aligned}$$
(2)

Here, \(\Theta ^{\alpha }_{~\beta }\) is an additional gravitational source and \(\varphi \) represents a constant that is responsible for observing the effects of \(\theta ^{\alpha }_{~\beta }\) with respect to \({T}^{\alpha }_{~\beta }\). The appearance of this new gravitational source makes it very difficult to formulate analytical solutions to the EFEs. In this regard, the scheme of minimal geometric deformation emerges as a novel and beneficial technique for investigating and analyzing stellar solutions. This method is especially valuable in scenarios that go beyond trivial cases, such as when we need to approximate the interiors of self-gravitational structures with more realistic fluid distributions, as opposed to ideal perfect fluids [26, 27]. Furthermore, it is also captivating in the framework of modified gravitational theories that often introduce new and challenging characteristics due to their complex mechanisms. The MGD-scheme was primarily established [28, 29] to study the spherically symmetric, self-gravitational structures in Randall–Sundrum brane-world framework [30, 31]. Subsequently, its application extended to studying the newfound black hole solutions and hypothesized dark matter [25, 32, 33].

The MGD scheme exhibits several interesting characteristics, making it a powerful tool for exploring new analytical solutions to the EFEs. This approach includes two key features: (i) it enables the possible extension of fundamental solutions to the EFEs into more intricate domains by introducing an additional gravitational source into the seed source \(T_{~\beta }^{\alpha }\) as

$$\begin{aligned} {T}^{\alpha }_{~\beta }\mapsto [T^{\alpha }_{~\beta }]^{\textrm{tot}} ={T}^{\alpha }_{~\beta }+{T}^{(1) \alpha }_{~\beta }, \end{aligned}$$
(3)

similarly, for another gravitational source \({T}^{(2) \alpha }_{~\beta }\), we get

$$\begin{aligned} {T}^{\alpha }_{~\beta }\mapsto [T^{\alpha }_{~\beta }]^{\textrm{tot}} ={T}^{\alpha }_{~\beta }+{T}^{(2) \alpha }_{~\beta }. \end{aligned}$$
(4)

The above procedure can be repeated by introducing further gravitational sources \({T}^{(n)\alpha }_{~\beta }\) to obtain the extended form of the simple solutions to the EFEs associated with \({T}^{\alpha }_{~\beta }\). (ii) it also enables us to construct the solutions to the EFEs associated with \([T^{\alpha }_{~\beta }]^{\textrm{tot}}\) by splitting it into more simple terms as

$$\begin{aligned}{}[T^{\alpha }_{~\beta }]^{\textrm{tot}}\rightarrow \left\{ {T}^{\alpha }_{~\beta },{T}^{(i)\alpha }_{~\beta }\right\} , \end{aligned}$$
(5)

which can be solved independently.

Starting with the pioneering work of Rosseland and Eddington, the study of self-gravitational, charged fluid spheres has a long history [34, 35]. Afterward, understanding the influence of electrical charge on the evolution and mechanism of compact self-gravitational fluids has been emerged as a captivating topic for cosmologists. An analysis of the established Reissner–Nordström (RN) spacetime geometry shows that spherical, compact self-gravitating fluids possessing charged dust distributions could potentially hinder relativistic gravitational collapse, which seems to be an inherent aspect of Schwarzschild’s geometry [2, 36]. Hence, the introduction of an electric field within the matter distribution allows us to evade singularities. Bonnor investigated the electromagnetic effects on the gravitational collapse of a spherical dust fluid distribution and pointed out that the collapse process decelerates as a result of electrical repulsion. In recent times, several investigations have been carried out to find the analytical stellar solutions to the EFEs. These solutions may be used in the modeling of self-gravitational stellar configurations such as charged black holes, neutron stars, strange quark stars, and other stellar structures [37,38,39,40,41]. Varela et al. examined the self-gravitational spherical structures with a charged fluid distribution by deriving solutions to the charged EFEs subject to the Karori and Barua metric potentials. Arbanil et al. [42] analyzed several self-gravitational, charged polytropic spheres satisfying the equation of state. They examined certain physical features of the system by constructing the hydrostatic equilibrium condition. They also analyzed the Buchdahl limit and concluded that this limit is maximum and the corresponding structure is a quasi-black hole. Consequently, the modeling of charged compact stellar configuration by developing the analytical stellar solutions to charged EFEs may be proved very intriguing. In this respect, many researchers have explored analytical solutions to the charged EFEs exhibiting charged anisotropic stellar configurations [43,44,45,46,47,48,49]. Motivated by this scenario, we develop a model of spherical stellar fluids endowed with electrical charge by considering conditions that involve minimal complexity factors and isotropization.

In this article, we are mainly interested in investigating the role of the gravitational decoupling scheme in controlling certain physical features of the charged, self-gravitational compact configuration satisfying the conditions of zero complexity factor and isotropization. We will employ the MGD scheme, which is based on deforming only the radial metric component and allows no energy exchange between the two gravitational sources in Eq. (2). check grammar Next, we will need to ensure that the entire gravitational system, with \(\varphi =1\), exhibits certain features that may be different from those observed for \(\varphi =0\). More specifically, our initial requirement will be that the anisotropic pressure turns out to be isotropic for \(\varphi =1\). The subsequent sections of the article are structured in the following manner: In Sect. 2, we will review the Einstein–Maxwell formalism for a gravitationally decoupled system with spherical symmetry and derive the corresponding field equations. We present the basic ingredients of gravitational decoupling through MGD-scheme in order to generate anisotropic stellar structure solutions in Sect. 3. Section 4 is dedicated to the comprehensive study of isoropization of the self-gravitational spherical sources through graphical representation. Then, in Sect. 4, we formulate the complexity factor under MGD-scheme and generate different stellar structure models by imposing the zero complexity factor condition for Tolman IV solutions. Finally, Sect. 5 provides the main findings and the concluding remarks.

2 Einstein–Maxwell formalism of gravitationally decoupled structures

The standard action for gravitationally decoupled stellar structure may be expressed by inserting an addition lagrangian density for the additional gravitational source as

$$\begin{aligned} A=\mathbb {S}_{\textrm{EH}}+\varphi \mathbb {S}_{\Theta }=\frac{1}{2\kappa ^{2}}\int \sqrt{-\textit{g}}\left( \textrm{R}+\mathscr {L}_{m}+\mathscr {L}_{e} +\varphi \mathscr {L}_{\Theta }\right) d^{4}x, \end{aligned}$$
(6)

where \(\textrm{R}=R^{\alpha }_{~\alpha }=\textit{g}^{\alpha \beta }R_{\alpha \beta }\), with \(R_{\alpha \beta }\) being the Ricci tensor and \(\textit{g}=det(\textit{g}_{\alpha \beta })\), while \(\kappa ^{2}\) is the usual gravitational coupling constant. In addition, \(\mathscr {L}_{m}\), \(\mathscr {L}_{e}\) and \(\mathscr {L}_{\Theta }\) represent the lagrangian densities corresponding to matter, charge and extra gravitational sources, respectively. To describe the density of matter fields \(\mathscr {L}_{m}\) associated with the seed source, the corresponding energy–momentum tensor (EMT) can be encoded as

$$\begin{aligned} T_{\alpha \beta }=-\frac{2}{\sqrt{-\textit{g}}}\frac{\delta (\sqrt{-\textit{g}}\mathscr {L}_{m})}{\delta \textit{g}^{\alpha \beta }}. \end{aligned}$$
(7)

Since \(\mathscr {L}_{m}\) is a function of \(\textit{g}_{\alpha \beta }\) only, therefore the above expression implies

$$\begin{aligned} T_{\alpha \beta }=-2\frac{\delta (\mathscr {L}_{m})}{\delta \textit{g}_{\alpha \beta }}+\textit{g}^{\alpha \beta }\mathscr {L}_{m}, \end{aligned}$$
(8)

On the other hand, we denote the EMTs associated with the electromagnetic and additional gravitational fields as \(E_{\alpha \beta }\) and \(\Theta _{\alpha \beta }\), respectively, which can be defined in terms of the Lagrangian densities \(\mathscr {L}_{e}\) and \(\mathscr {L}_{\Theta }\) as

$$\begin{aligned} E_{\alpha \beta }&=-\textit{g}_{\alpha \beta }\mathscr {L}_{e}+2\frac{\delta (\mathscr {L}_{e})}{\delta \textit{g}^{\alpha \beta }}, \end{aligned}$$
(9)
$$\begin{aligned} \Theta _{\alpha \beta }&=2\frac{\delta (\mathscr {L}_{\theta })}{\delta \textit{g}^{\alpha \beta }}-\textit{g}_{\alpha \beta }\mathscr {L}_{\Theta }, \end{aligned}$$
(10)

Finally, the variation of the modified Einstein–Hilbert action (6) with respect to \(\textit{g}_{\alpha \beta }\) provides the gravitational equations of motion for the charged decoupled anisotropic system as

$$\begin{aligned} R^{\alpha }_{~\beta }-\frac{1}{2}R\delta ^{\alpha }_{~\beta }=\kappa ^{2}\left( [T^{\alpha }_{~\beta }] ^{\textrm{tot}}+E^{\alpha }_{~\beta }\right) , \end{aligned}$$
(11)

where \([T^{\alpha }_{~\beta }]^{\textrm{tot}}\) EMT describing the distribution of anisotropic fluid configuration radial pressure \(P_{r}\), tangential pressure \(P_{t}\) and energy density \(\epsilon \) is given by

$$\begin{aligned}{}[T^{\alpha }_{~\beta }]^{\textrm{tot}}=(\epsilon +P_{t})U^{\alpha }U_{\beta }-P_{t}\delta ^{\alpha }_{~\beta }+ (P_{r}-P_{t})\xi ^{\alpha }\xi _{\beta }, \end{aligned}$$
(12)

where \(\xi ^{\alpha }\) denotes the unit four-vector and \(U^{\alpha }\) symbolizes the four-velocity of the fluid configuration, defined as

$$\begin{aligned} U^{\alpha }=e^{-\nu /2}\delta ^{\alpha }_{~0} \quad and \quad \xi ^{\alpha }=e^{-\lambda /2}\delta ^{\alpha }_{~1}, \end{aligned}$$
(13)

for which \(U^{\alpha }U_{\alpha }=-\xi ^{\alpha }\xi _{\alpha }=1\) and \(\xi ^{\alpha }U_{\alpha }=0\). On the other hand, the quantity \(\Theta ^{\alpha }_{~\beta }\) stands as an additional gravitational source term that interacts with the anisotropic fluid through the constant \(\varphi \). Furthermore, the divergence-free property of the Einstein tensor enables the EMT to comply with the conservation relation

$$\begin{aligned} \nabla _{\alpha }\left( [T^{\alpha }_{~\beta }] ^{\textrm{tot}}+E^{\alpha }_{~\beta }\right) =0. \end{aligned}$$
(14)

The line element to model the interior region of spherically symmetric stellar distribution in the standard Schwarzschild-like coordinates \(x^{\alpha }=(t,r,\theta ,\vartheta )\) reads

$$\begin{aligned} ds^{2}&=\textit{g}_{\alpha \beta }dx^{\alpha }dx^{\beta }\nonumber \\&=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^{2}d\theta ^{2}-r^{2} \sin ^{2}\theta d\vartheta ^{2}, \end{aligned}$$
(15)

where the variables \(\nu \equiv \nu (r)\) and \(\lambda \equiv \lambda (r)\). In addition, the EMT describing the electromagnetic interactions on self-gravitational fluid spheres, is defined as follows

$$\begin{aligned} E^{\alpha }_{~\beta }=\frac{2}{\kappa ^{2}}\left[ \frac{1}{4}{\delta }^{\alpha }_{~\beta } F_{\sigma \varsigma }F^{\sigma \varsigma }-F^{\alpha }_{~\sigma }F^{\sigma }_{~\beta }\right] , \end{aligned}$$
(16)

where the anti-symmetric tensorial term \(F_{\alpha \beta }=\partial _{\beta }\phi _{\alpha }-\partial _{\alpha }\phi _{\beta }\) is known as Maxwell-tensor where \(\phi _{\alpha }=\phi (r)\delta ^{0}_{~\alpha }\) encodes the four-potential. Furthermore, the anti-symmetric tensor \(F_{\alpha \beta }\) satisfies the Maxwell’s equations of electromagnetic fields as

$$\begin{aligned} \nabla _{\beta }\left[ (-\textit{g})^{1/2}F^{\alpha \beta }\right] =\mu _{m}(-\textit{g})^{1/2}\textrm{J}^{\alpha },\quad \partial _{[\sigma }F_{\alpha \beta ]}=0. \end{aligned}$$
(17)

Here, \(\mu _{m}=4\pi \) is the magnetic permeability, while \(\textrm{J}^{\alpha }\) represents the current density defined as

$$\begin{aligned} \textrm{J}^{\alpha }=\varrho _{e}(r)U^{\alpha }, \quad with \quad U^{\alpha }=\frac{\delta ^{\alpha }_{~0}}{\sqrt{\textit{g}_{\alpha \alpha }}}, \end{aligned}$$
(18)

where \(\varrho _{e}\) is the electric charge density. Then, the combination of the above expressions with Maxwell’s equations produces the following \(2^{nd }\) order linear differential equation in the variable \(\phi \) as

$$\begin{aligned} \frac{d^{2}\phi }{dr^{2}}+\frac{1}{2r}\left[ 4-r(\nu '+\lambda ')\right] \frac{d\phi }{dr}= \mu _{m}\varrho _{e}(r)e^{{\nu }+\lambda /2}, \end{aligned}$$
(19)

whose solution is given as

$$\begin{aligned} \frac{d\phi }{dr}=\frac{Q(r)}{r^{2}}e^{(\nu +\lambda )/2}. \end{aligned}$$
(20)

Here, \(Q(r)=\mu _{m}\int ^{r}_{0}\varrho _{e}(r)e^{\lambda /2}y^{2}dy\) represents the total charge contained within the interior of the self-gravitating stellar configuration. Consequently, the non-null constituents of \(E^{\alpha }_{\beta }\) reads

$$\begin{aligned}&E^{0}_{~0}=E^{1}_{~1}=-E^{2}_{~2}=-E^{3}_{~3}=\frac{Q^{2}(r)}{\kappa ^{2}r^{4}}, \end{aligned}$$
(21)
$$\begin{aligned}&\kappa ^{2}([T^{0}_{~0}]^{\textrm{tot}}+E^{0}_{~0})=e^{-\lambda }\left( \frac{e^{\lambda }}{r^{2}} +\frac{\lambda '}{r}-\frac{1}{r^{2}}\right) , \end{aligned}$$
(22)
$$\begin{aligned}&\kappa ^{2}([T^{1}_{~1}]^{\textrm{tot}}+E^{1}_{~1})=e^{-\lambda }\left( \frac{e^{\lambda }}{r^{2}} -\frac{\nu '}{r}-\frac{1}{r^{2}}\right) , \end{aligned}$$
(23)
$$\begin{aligned}&\kappa ^{2}([T^{2}_{~2}]^{\textrm{tot}}+E^{2}_{~2})=e^{-\lambda }\left( \frac{\lambda '\nu '}{4}-\frac{\nu ''}{2}- \frac{\nu '^{2}}{4}-\frac{\nu '}{2r}+\frac{\lambda '}{2r}\right) , \end{aligned}$$
(24)

where \([T^{3}_{~3}]^{\textrm{tot}}+E^{3}_{~3}=[T^{2}_{~2}]^{\textrm{tot}}+E^{2}_{~2}\) as a consequence of spherically symmetric case and \(f'\equiv \partial _{r}f\). Also, from the above set of differential equations, we have

$$\begin{aligned}&[T^{0}_{~0}]^{\textrm{tot}}=T^{0}_{~0}+\varphi \Theta ^{0}_{~0}, \end{aligned}$$
(25)
$$\begin{aligned}&[T^{1}_{~1}]^{\textrm{tot}}=T^{1}_{~1}+\varphi \Theta ^{1}_{~1}, \end{aligned}$$
(26)
$$\begin{aligned}&[T^{2}_{~2}]^{\textrm{tot}}=T^{2}_{~2}+\varphi \Theta ^{2}_{~2}. \end{aligned}$$
(27)

The linear combination of the Eqs. (14)–(16) produces the generalized hydrostatic equilibrium equation for the anisotropic fluid and reads

$$\begin{aligned} 0&=\left( [T^{1}_{~1}]^{\textrm{tot}}+E^{1}_{~1}\right) '-\frac{\nu '}{2}\left( [T^{0}_{~0}]^{\textrm{tot}} +E^{0}_{~0}-[T^{1}_{~1}] ^{\textrm{tot}}-E^{1}_{~1}\right) \nonumber \\&\quad -\frac{2}{r}\left( [T^{2}_{~2}]^{\textrm{tot}}+E^{2}_{~2} -[T^{1}_{~1}]^{\textrm{tot}}-E^{1}_{~1}\right) ,\nonumber \\ 0&=\left( T^{1}_{~1}+E^{1}_{~1}\right) '-\frac{\nu '}{2}\left( T^{0}_{~0}+E^{0}_{~0}-T^{1}_{~1}-E^{1}_{~1}\right) \nonumber \\&\quad -\frac{2}{r}\left( T^{2}_{~2}+E^{2}_{~2} -T^{1}_{~1}-E^{1}_{~1}\right) +\varphi L\left( \Theta ^{\alpha }_{\alpha }\right) , \end{aligned}$$
(28)

where

$$\begin{aligned} L\left( \Theta ^{\alpha }_{\alpha }\right) \equiv \left[ \left( \Theta ^{1}_{~1}\right) '-\frac{\nu '}{2} \left( \Theta ^{0}_{~0}-\Theta ^{1}_{~1}\right) -\frac{2}{r}\left( \Theta ^{2}_{~2} -\Theta ^{1}_{~1}\right) \right] . \end{aligned}$$
(29)

The expression (28) is commonly known as the conservation equation for the charged anisotropic fluid distribution endowed with spherical symmetry. Now, we characterize the \(\Theta \)-components in terms of new variables as

$$\begin{aligned} \rho ^{\Theta }=\varphi \Theta ^{0}_{~0},\quad p_{r}^{\Theta }=-\varphi \Theta ^{1}_{~1},\quad p_{t}^{\Theta }= -\varphi \Theta ^{2}_{~2}, \end{aligned}$$
(30)

Then, we have

$$\begin{aligned} \epsilon =\rho +\rho ^{\Theta },\quad P_{r}=p_{r}+p_{r}^{\Theta }, \quad P_{t}=p_{t}+p_{t}^{\Theta }, \end{aligned}$$
(31)

where \(\epsilon \) encode the effective energy density, while \(P_{r}\) and \(P_{t}\) symbolize the effective radial and tangential pressures, respectively. By considering the above definitions, the pressure anisotropy may be expressed as

$$\begin{aligned} {[}\Pi ]^{\textrm{tot}}\equiv P_{t}-P_{r}=\Pi +\varphi \Pi _{\Theta }, \end{aligned}$$
(32)

with

$$\begin{aligned}&{[}\Pi ]^{\textrm{tot}}=p_{\bot }-p_{r} \quad and \nonumber \\&\Pi _{\Theta }=p_{\bot }^{\Theta }-p_{r}^{\Theta } =\varphi \left( \Theta ^{1}_{~1}-\Theta ^{2}_{~2}\right) . \end{aligned}$$
(33)

where \(\Pi \) and \(i_{\Theta }\) measure the pressure anisotropy caused by the seed source \(T^{\alpha }_{\beta }\) and the additional gravitational source \(\Theta ^{\alpha }_{\beta }\), respectively.

3 Gravitational decoupling by complete geometric deformation

The MGD-scheme is concerned with a certain transformation of the inverse radial-component of \(\textit{g}_{\alpha \beta }\) as

$$\begin{aligned} \left[ \tilde{\textit{g}}_{rr}(r)\right] ^{-1}\mapsto \left[ \textit{g}_{rr}(r)\right] ^{-1} =\left[ \tilde{\textit{g}}_{rr}(r)\right] ^{-1}+\varphi \mathcal {F}(r), \end{aligned}$$
(34)

where the arbitrary function \(\mathcal {F}(r)\) signifies the geometric deformation experienced by metric \(\tilde{\textit{g}}_{\alpha \beta }\). The decoupling of gravitational configurations via the above-stated transformation has been effectively utilized in various contexts, including:

  • Deriving physically viable and exact solutions for self-gravitational compact sources endowed with spherical symmetry [50,51,52,53,54,55].

  • Constructing mini black hole solutions [56].

  • Understanding the phenomena of gravitational lensing beyond the framework of Einstein’s gravity [57].

  • Establishing the uniformity of the standard Schwarzschild exterior solution for self-gravitational fluid spheres, composed of usual matter within the realm of brane-world [58].

  • Analyzing the corrections to observable parameters of dark SU(N) stars as a result of variable tension fluid branes [59].

Next, we will employ the MGD-scheme to solve the gravitational system (25)–(28). The MGD-scheme is based on the solving the EFEs for each component \(\{{T}^{\alpha }_{~\beta }, \Theta ^{\alpha }_{~\beta }\}\), independently. Then, the complete solution of the system corresponding to the gravitational source \([T^{\alpha }_{~\beta }]^{\textrm{tot}}\) is obtained by the principle of superposition. Later on, we will see that this scheme transforms the gravitational system so that the gravitational equations of motion corresponding to the \(\Theta \)-sector will satisfy the quasi-Einstein system. Now, we continue by examining a solution to the system (25)–(28) with \(\varphi =0\), given by

$$\begin{aligned} ds^{2}&=\textit{g}_{\alpha \beta }dx^{\alpha }dx^{\beta } =e^{\eta (r)}dt^{2}\nonumber \\&\quad -e^{\mu (r)}dr^{2}-r^{2}d\theta ^{2}-r^{2} \sin ^{2}\theta d\vartheta ^{2}, \end{aligned}$$
(35)

with

$$\begin{aligned} \frac{2m_{s}}{r}&\equiv 1-e^{-\mu (r)}+\frac{Q^{2}}{r^{2}}\nonumber \\&\equiv \frac{\kappa ^{2}}{2}\int ^{r}_{0}\left[ \rho (y)+\frac{Q^{2}}{8\pi y^{2}}\right] y^{2}dr+\frac{Q^{2}}{r^{2}}. \end{aligned}$$
(36)

is the mass function associated with the standard Einstein–Maxwell Now, we employ the GD by using the MGD-scheme to investigate the cumulative impact of the extra gravitational source on the seed source. To achieve this, we transform the metric variables \(e^{\lambda }\) and \(e^{\nu }\) as suggested by Ovalle [24] in the following manner

$$\begin{aligned}&\eta (r)\mapsto \nu (r)=\eta (r)+\varphi f(r), \end{aligned}$$
(37)
$$\begin{aligned}&e^{-\mu (r)}\mapsto e^{-\lambda (r)}=e^{-\mu (r)}+\varphi \mathcal {F}(r), \end{aligned}$$
(38)

where the functions f(r) and \(\mathcal {F}(r)\) represent the deformations experienced by temporal and radial metric components. one specific possibility stands out, referred to as the MGD-scheme, which reads

$$\begin{aligned}&f(r)\rightarrow 0, \end{aligned}$$
(39)
$$\begin{aligned}&\mathcal {F}(r)\rightarrow \mathcal {F}^{*}(r), \end{aligned}$$
(40)

Consequently, the line element (35) undergoes minimal deformation due to the source \(\Theta ^{\alpha }_{~\beta }\), whose radial metric component turns out to be

$$\begin{aligned} e^{-\mu (r)}\mapsto e^{-\lambda (r)}=e^{-\mu (r)}+\varphi \mathcal {F}^{*}(r), \end{aligned}$$
(41)

however, the temporal metric component remains the same. Now, by plugging the above-stated deformed metric functions into the gravitational system (22)–(24), we obtain the following sets of differential equations:

(i) The Charged EFEs equations of motion for the seed source corresponding to \(\varphi =0\), are given as

$$\begin{aligned} \kappa ^{2}\left( \rho +\frac{Q^{2}}{\kappa ^{2}r^{4}}\right)&=e^{-\mu }\left( \frac{e^{\mu }}{r^{2}} +\frac{\mu '}{r}-\frac{1}{r^{2}}\right) , \end{aligned}$$
(42)
$$\begin{aligned} \kappa ^{2}\left( p_{r}-\frac{Q^{2}}{\kappa ^{2}r^{4}}\right)&=e^{-\mu }\left( \frac{e^{\mu }}{r^{2}} -\frac{\eta '}{r}-\frac{1}{r^{2}}\right) , \end{aligned}$$
(43)
$$\begin{aligned} \kappa ^{2}\left( p_{t}+\frac{Q^{2}}{\kappa ^{2}r^{4}}\right)&=e^{-\mu }\left( \frac{\mu '\eta '}{4}-\frac{\eta ''}{2}- \frac{\eta '^{2}}{4}-\frac{\eta '}{2r}+\frac{\mu '}{2r}\right) . \end{aligned}$$
(44)

By definition, the EMT associated with the charged anisotropic seed source is divergence-free, i.e, it obeys the standard conservation relation, which can be expressed as follows

$$\begin{aligned} \frac{dp_{r}}{dr}=-\frac{\eta '}{2}(\rho +p_{r})+\frac{2}{r}\left[ (p_{t}-p_{r})+\frac{Q^{2}}{\kappa ^{2} r^{3}}\frac{dQ}{dr}\right] , \end{aligned}$$
(45)

where

$$\begin{aligned} \frac{\eta '}{2}=\frac{p_{r}\kappa ^{2}r^{4}+2rm_{s}-2Q^{2}}{2r(r^{2}-2rm_{s}+Q^{2})}. \end{aligned}$$
(46)

Here, it is notable that the above system of differential equations is equivalent to the system of Eqs. (22)–(24) if we set the coupling parameter \(\Theta =0\), between the two sectors.

(ii) Now, we proceed to the term \(\Theta ^{\alpha }_{~\beta }\) to investigate the gravitational consequences corresponding to additional source on the electrically charged anisotropic fluid solution \(\left\{ \eta , \mu , \rho , p_{r}, p_{t}\right\} \). In this respect, the quasi-Einstein gravitational system associated with \(\Theta \)-sector can be expressed by the following expressions

$$\begin{aligned} \kappa ^{2}\rho ^{\Theta }&=-\varphi \mathcal {F}^{*}\left( \frac{1}{r^{2}} +\frac{\mathcal {F}^{*'}}{r\mathcal {F}^{*}}\right) , \end{aligned}$$
(47)
$$\begin{aligned} \kappa ^{2}p_{r}^{\Theta }&=\varphi \mathcal {F}^{*}\left( \frac{1}{r^{2}}+\frac{\eta '}{r}\right) , \end{aligned}$$
(48)
$$\begin{aligned} \kappa ^{2}p_{t}^{\Theta }&=\varphi \mathcal {F}^{*}\left( \frac{\eta ''}{2}+\frac{\eta '2}{4} +\frac{\eta '}{2r}\right) +\varphi \mathcal {F}^{*}\left( \eta '+\frac{2}{r}\right) . \end{aligned}$$
(49)

Once again, the corresponding conservation relation or the hydrostatic equilibrium equation satisfying the divergence-free relation

$$\begin{aligned} \nabla _{\alpha }\Theta _{~\beta }^{\alpha }=0, \end{aligned}$$
(50)

can be explicitly written as

$$\begin{aligned} \frac{dp_{r}^{\Theta }}{dr}=-\frac{\eta '}{2}(\rho ^{\Theta }+p_{r}^{\Theta }) +\frac{2}{r}(p_{t}^{\Theta }-p_{r}^{\Theta }), \end{aligned}$$
(51)

where

$$\begin{aligned} \frac{\eta '}{2}=\frac{p_{r}\kappa ^{2}r^{4}+2rm_{s}}{2r(r^{2}-2rm_{s})}. \end{aligned}$$
(52)

From the above expression, we get

$$\begin{aligned} m=m_{s}-\frac{\varphi }{2}r\mathcal {F}^{*}. \end{aligned}$$
(53)

According to Herrera’s definition [1], the mass function m(r) for the decoupled gravitational may be expressed as

$$\begin{aligned} m(r)=\frac{\kappa ^{2} r^{3}}{6}\epsilon -\frac{\kappa ^{2}}{6}\int ^{r}_{0} \left( \epsilon 'y^{3}-\frac{6QQ'}{\kappa ^{2}y}\right) dy. \end{aligned}$$
(54)

Now, utilizing the relation (22), we get

$$\begin{aligned} m(r)=m_{s}(r)+m_{\Theta }(r), \end{aligned}$$
(55)

with

$$\begin{aligned} m_{s}(r)=\frac{\kappa ^{2} r^{3}}{6}\epsilon -\frac{\kappa ^{2}}{6}\int ^{r}_{0}\left( [\epsilon (y)]'y^{3}-\frac{6QQ'}{\kappa ^{2}y}\right) dy, \end{aligned}$$
(56)

and

$$\begin{aligned} m_{\Theta }(r)=\frac{\kappa ^{2} r^{3}}{6}\rho ^{\Theta }-\frac{\kappa ^{2}}{6}\int ^{r}_{0}[\rho ^{\Theta }(y)]'y^{3}dy, \end{aligned}$$
(57)

where \(m_{s}(r)\) and \(m_{\Theta }(r)\) encode the mass function associated with the seed source \(T^{\alpha }_{~\beta }\) and the extra gravitational source \(\Theta ^{\alpha }_{~\beta }\).

4 Isotropization of self-gravitational sources

This section explains the formulation of Casadio’s systematic method for isotropizing the decoupled gravitational system (22)–(24) using the MGD-scheme [60]. As discussed earlier in expression (32), the total anisotropy \([\Pi ]^{\textrm{tot}}\) corresponding to the decoupled gravitational system could possibly be distinct from the anisotropy caused by the extra gravitational interaction \(\varphi \Pi _{\Theta }\). Our primary objective here is to achieve isotropization. This can be accomplished by considering an anisotropic gravitational system with \(\Pi \ne 0\), leading to the transformation of the system into the isotropic regime with \([\Pi ]^{\textrm{tot}}=0\), as a result of including the additional source \(\Theta ^{\alpha }_{~\beta }\). This isotropic gravitational system is characterized by relations (22)–(24). This modification can be precisely controlled by the coupling parameter \(\varphi \). The case \(\varphi =0\) corresponds to the anisotropic configuration, while the case \(\varphi =1\) represents the isotropic gravitational system. Therefore, \([\Pi ]^{\textrm{tot}}=\Pi +\varphi \Pi _{\Theta }=0\), with \(\varphi =1\) reads

$$\begin{aligned} \Pi =-\Pi _{\Theta }\Longrightarrow \Pi =-(\Theta ^{1}_{~1}-\Theta ^{2}_{~2})=-(p_{r}^{\Theta }-p_{\bot }^{\Theta }). \end{aligned}$$
(58)

Then, the combination of the Eqs. (48) and (49) with Eq. (57) produces an ODE, defined as

$$\begin{aligned} \frac{\mathcal {F}^{*}}{4\kappa ^{2}}\left( 2\eta ''+\eta '^{2}-\frac{2\eta '}{r}-\frac{4}{r^{2}}\right) +\frac{\mathcal {F}'^{*}}{4\kappa ^{2}}\left( \eta '+\frac{2}{r}\right) +\Pi =0, \end{aligned}$$
(59)

which encode a first-order linear ODE in the deformation function \(\mathcal {F}^{*}(r)\), while it is a second-order nonlinear equation in the metric variable \(\eta (r)\). Later on, we will solve this differential equation for the function \(\mathcal {F}^{*}(r)\). The solution to this relation describes the effects of the extra gravitational source \(\Theta ^{\alpha }_{~\beta }\), which can calculated by using any well-established solution of the stellar system (42)–(44) expressed by the functions \(\eta (r)\) and \(\mu (r)\) along with assuming any feasible form of \(\mathcal {F}^{*}(r)\). As an illustrative example, we will apply the above-mentioned scheme to achieve isotropy in the self-gravitational stellar structure regulated only by the tangential pressure, as expressed by

$$\begin{aligned}&\eta (r)=\ln \left[ Y^{2}\left( 1+\frac{r^{2}}{X^{2}}\right) \right] , \end{aligned}$$
(60)
$$\begin{aligned}&e^{-\mu (r)}=\frac{X^{2}+r^{2}}{X^{2}+3r^{2}}, \end{aligned}$$
(61)
$$\begin{aligned}&\rho (r)=\frac{6r^{4}(X^{2}+r^{2})-Q^{2}(X^{2}+3r^{2})^{2}}{\kappa ^{2}r^{4}(X^{2}+3r^{2})^{2}}, \end{aligned}$$
(62)
$$\begin{aligned}&p_{t}(r)=\frac{3r^{6}-Q^{2}(X^{2}+3r^{2})^{2}}{\kappa ^{2}r^{4}(X^{2}+3r^{2})^{2}}, \end{aligned}$$
(63)
$$\begin{aligned}&p_{r}(r)-\frac{Q^{2}}{\kappa ^{2}r^{4}}=0, \quad with \quad 0\le r \le R. \end{aligned}$$
(64)

Here, R specifies the surface of the self-gravitational stellar configuration. Prospective applications of this class of solutions in finding the spherical anisotropic fluid distributions have been studied by many researchers [12, 50, 61,62,63,64]. The values of the constant parameters X and Y can be calculated via smooth matching of the inner seed metric with the outer RN metric at surface \(r>R\). In the context of gravitational decoupling, Ovalle [25] considered the following form of the well-established RN metric

$$\begin{aligned} ds^{2}&=\textit{g}_{\alpha \beta }dx^{\alpha }dx^{\beta }=\left( 1-\frac{2M}{r}+\frac{\hat{Q}^{2}}{r^{2}}\right) dt^{2}\nonumber \\&\quad -\left( 1-\frac{2M}{r}+\frac{\hat{Q}^{2}}{r^{2}}\right) ^{-1}dr^{2}-r^{2}d\theta ^{2}-r^{2} \sin ^{2}\theta d\vartheta ^{2}. \end{aligned}$$
(65)

In this expression, \(m_{s}(R)=M\) and \(Q(R)=\hat{Q}\) encode the overall mass and charge inside the self-gravitational compact structure corresponding to source \(T^{\alpha }_{~\beta }\), respectively. By expressing the first and second fundamental form explicitly, we obtain the following expressions

$$\begin{aligned}&e^{\eta (R)}=1-\frac{2M}{R}+\frac{\hat{Q}^{2}}{R^{2}}, \end{aligned}$$
(66)
$$\begin{aligned}&e^{-\mu (R)}=1-\frac{2M}{R}+\frac{\hat{Q}^{2}}{R^{2}}, \end{aligned}$$
(67)
$$\begin{aligned}&p_{r}(R)-\frac{\hat{Q}^{2}}{R^{2}}=0. \end{aligned}$$
(68)

Using the matching conditions (66), (67) and (68), we obtain

$$\begin{aligned} Y^{2}=1-\frac{3M}{R}, \quad \frac{X^{2}}{R^{2}}=\frac{R^{2}-3M}{M}, \end{aligned}$$
(69)

where, we must have \(M/R<1/3\) or \(R>3M\) for \(X^{2}>0\) and \(Y^{2}>0\). The solution of the ODE (59) can be defined as

$$\begin{aligned} \mathcal {F}^{*}(r)=\frac{r^{2}(r^{2}+X^{2})}{2r^{2}+X^{2}} \left[ \frac{1}{3r^{2}+X^{2}}-\frac{1}{\mathcal {K}^{2}}\right] . \end{aligned}$$
(70)

Here, the term \(\mathcal {K}\) denotes an arbitrary constant of integration with dimensions of length. Next, we find the value of \(P_{r}\) can be determined by plugging the metric variables (41) and (66) in the Einstein–Maxwell equation of motion (23) as

$$\begin{aligned} P_{r}=\frac{\varphi r^{2}\mathcal {F}^{*}(r)(3r^{2}+X^{2}) +Q^{2}(r^{2}+X^{2})}{\kappa ^{2}r^{4}(r^{2}+X^{2})}. \end{aligned}$$
(71)

Consequently, the matching sonstraint (68) for the outer RN metric provides

$$\begin{aligned} \mathcal {F}^{*}(R)=0\Longrightarrow \mathcal {K}^{2}=3R^{2}+X^{2}. \end{aligned}$$
(72)

This relation shows that the value of M remains same in both the cases, i.e.,

$$\begin{aligned} m(R)=m_{s}(R)=M, \end{aligned}$$
(73)

Consequently, the constant parameters X and Y retain their values, as defined in Eq. (69). Now, the corresponding deformation function turn out to be

$$\begin{aligned} \mathcal {F}^{*}(r)=\frac{3r^{2}(R^{2}-r^{2})(r^{2}+X^{2})}{(2r^{2}+X^{2})(3r^{2}+A^{2})(3R^{2}+A^{2})}. \end{aligned}$$
(74)

The expression for effective energy density \(\epsilon \) takes the form

$$\begin{aligned} \epsilon (r,\varphi )&=\rho (r)+\frac{Q^{2}(3r^{2}+X^{2})^{2}(3r^{2}+X^{2})^{2}(2R^{2}+X^{2})-\varphi r^{2}[18r^{8}-6r^{6}R^{2}+(5r^{2}-3R^{2})X^{6}]}{\kappa ^{2}(2r^{2}+X^{2})^{2}(3r^{2}+X^{2})^{2}(2R^{2} +X^{2})}\nonumber \\&\quad -\frac{\varphi r^{2}[2(11r^{4}-5r^{2}R^{2})X^{2}+(31r^{6}-9r^{4}R^{2})]}{\kappa ^{2}(2r^{2}+X^{2})^{2}(3r^{2}+X^{2})^{2} (2R^{2}+X^{2})}, \end{aligned}$$
(75)

whereas the effective radial pressure takes the following form

$$\begin{aligned} P_{r}(r,\varphi )=\frac{3\varphi r^{2}(R^{2}-r^{2})-Q^{2}(2r^{2}+X^{2})(3R^{2}+X^{2})}{\kappa ^{2}(2r^{2}+X^{2})(3R^{2}+X^{2})}. \end{aligned}$$
(76)

Finally, the effective tangential pressure can be calculated through the relation \(P_{t}=P_{r}+\Pi \), where the total anisotropy of the gravitational system is

$$\begin{aligned}{}[\Pi ]^{\textrm{tot}}(r,\varphi )=\frac{3(1-\alpha )r^{2}}{\kappa ^{2}(3r^{2}+X^{2})^{2}}. \end{aligned}$$
(77)

The above expression shows that the total anisotropy of the system vanishes for \(\varphi =1\). Notably, the relations (75)–(77) are the analytical stellar solutions to the charged EFEs of motion (22)–(24) for all values of the parameter \(\varphi \). Additionally, we can easily conclude that the case \(\varphi =0\) corresponds to the anisotropic gravitational model. However, as the value of \(\varphi \) gradually increases, it undergoes continuous deformation towards the isotropic case, characterized by \(\varphi =1\). in Eqs. (60)–(64). Therefore, we can closely observe the process of isotropization by continually varying the parameter a within the range (0, 1). In this context, the plots of total anisotropy \(\Pi \) and the radial pressure \(P_{r}\) for different values of the parameter \(\varphi \) is shown in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Diagrammatic scheme of the radial component of pressure \([P_{r}\times 10^{3}]\) versus radial coordinate r for various values of the coupling parameter \(\varphi \) with compactness factor \(\frac{M}{R}=0.2\)

Full size image

5 Complexity of gravitationally decoupled sources

This section deals with constructing a solution to the charged gravitational system of Eqs. (22)–(24) under the MGD-scheme and obeying the zero-complexity condition. The definition of complexity factor in terms of a scalar function for static, anisotropic spherical self-gravitational sources was initially suggested by Herrera [1], and then generalized to the case of dynamical sources in [65] (for further applications, see [16, 66,67,68,69]). The scalar function representing the complexity factor is denoted as \(Y_{TF}\). It can be evaluated by considering two fundamental fluid variables: the anisotropy-exhibiting factor \(\Pi \) and the density gradient \([\rho (r)]'\). According to Herrera’s newly developed definition, we define the quantity \(Y_{T F}\) as the complexity-measuring factor for time-independent, compact anisotropic fluid spheres. This factor is defined as

Fig. 2
figure 2

Diagrammatic scheme of the total pressure anisotropy \(\Pi \) versus r for various values of the coupling parameter \(\varphi \) with compactness factor \(\frac{M}{R}=0.2\)

Full size image
$$\begin{aligned} Y_{TF}=\kappa ^{2}\Pi (r)+\frac{2Q^{2}}{r^{4}}-\frac{\kappa ^{2}}{2r^{3}}\int ^{r}_{0}\left[ \rho (y)+\frac{Q^{2}}{\kappa ^{2} r^{4}}\right] 'y^{3}dy. \end{aligned}$$
(78)

As pointed out in [1], the structure scalar \(Y_{TF}\) signifies the influence of both anisotropy and density variation on the Tolman mass \((m_{T})\). More specifically, it describes how the physical parameters defined in \(Y_{TF}\) lead to variations in \(m_{T}\). The Tolman mass is can be encoded as

$$\begin{aligned} m_{T}&=\frac{\kappa ^{2}}{2}\int ^{r}_{0}e^{(\eta +\lambda )/2}\Big (T^{0}_{~0}+E^{0}_{~0}-T^{1}_{~1}-E^{1}_{~1} \nonumber \\&\quad -2T^{2}_{~2}-2E^{2}_{~2}\Big )y^{2}dy, \end{aligned}$$
(79)

Then, using Eqs. (22)–(24) in the above expression, we get

$$\begin{aligned} m_{T}=\frac{\eta '}{2}r^{2}e^{(\eta -\lambda )/2}+\int ^{r}_{0}\frac{Q^{2}}{y^{2}}e^{(\nu +\lambda )/2}dy. \end{aligned}$$
(80)

Next, we consider the four-acceleration \(a_{\alpha }\), defined by

$$\begin{aligned} a_{\alpha }=V_{\alpha ;\beta }V^{\beta }. \end{aligned}$$
(81)

For time-independent gravitational field (15), the above expression adopts a specific form

$$\begin{aligned} a_{\alpha }=a K_{\alpha }, \quad where \quad a=-\frac{m_{T}}{r^{2}}e^{-\eta /2}. \end{aligned}$$
(82)

Thus, \(m_{T}\) represent the active gravitational mass [12, 70]. To examine the impact of \(Y_{TF}\) on the mass function \(m_{T}\), we reformulate Eq. (79) in the context of the complexity-measuring factor as

$$\begin{aligned} m_{T}=\left( \frac{r}{R}\right) ^{3}M_{T}+r^{3}\int ^{R}_{r}\frac{e^{(\eta +\lambda )/2}}{y}Y_{TF}dy. \end{aligned}$$
(83)

Here, the term \(M_{T}\) denotes the total Tolman mass. Based on Herrera’s [12] observations, it is significant to mention that

  • The scalar function \(Y_{TF}\) appears to be zero not only for spherical stellar fluids with isotropic pressure but also for any other fluid configurations in which both terms in Eq. (83) vanish identically.

  • Based on the above-mentioned criteria, it is clear that there may exist various stellar configurations satisfying zero complexity factor condition.

  • It is important to emphasize that while pressure anisotropy influences \(Y_{TF}\) locally, the same does not apply to energy density inhomogeneity.

Thus, \(Y_{TF}\) measures the deviation of the Tolman mass for a specific stellar system with an isotropic fluid configuration when pressure anisotropy and energy density gradients are non-zero. Casadio and his coworkers [60] proposed that the scalar function \(Y_{TF}\) satisfies an additional property within the framework of the MGD-scheme. Hence, the overall complexity of the stellar structure will be determined by the combined contributions of two existing complexity-measuring scalar functions originating from the gravitational sources \(T^{\alpha }_{~\beta }\) and \(\Theta ^{\alpha }_{~\beta }\). Hence, based on the above-mentioned information, the complexity factor \(Y_{TF}\), as described in Eq. (78), can also be expressed as the combination of two scalar factors contributing to the complexity associated with the gravitational sources \(T^{\alpha }_{~\beta }\) and \(\Theta ^{\alpha }_{~\beta }\) as

$$\begin{aligned}{}[Y_{TF}]^{\textrm{tot}}&=\kappa ^{2}[\Pi ]^{\textrm{tot}}+\frac{2Q^{2}}{r^{4}}-\frac{\kappa ^{2}}{2r^{3}}\int ^{r}_{0} \left[ \epsilon (y)+\frac{Q^{2}}{\kappa ^{2} r^{4}}\right] 'y^{3}dy\nonumber \\&=\kappa ^{2}\Pi +\frac{2Q^{2}}{r^{4}}-\frac{\kappa ^{2}}{2r^{3}}\int ^{r}_{0}\left[ \rho (y)+\frac{Q^{2}}{\kappa ^{2} r^{4}}\right] 'y^{3}dy\nonumber \\&\quad +\kappa ^{2}\Pi _{\Theta }-\frac{\kappa ^{2}}{2r^{3}}\int ^{r}_{0} [\rho ^{\Theta }(y)]'y^{3}dy, \end{aligned}$$
(84)

which an be defined as

$$\begin{aligned}{}[Y_{TF}]^{\textrm{tot}}=Y_{TF}+Y_{TF}^{\Theta }. \end{aligned}$$
(85)

In this context, we define \(Y_{TF}\) as the complexity factor corresponding to the primary source \(T^{\alpha }_{~\beta }\), while \(Y_{TF}^{\Theta }\) represents the complexity factor linked to the additional gravitational source \(\Theta ^{\alpha }_{~\beta }\). Here, we want to emphasize that this outcome is independent of the MGD-scheme discussed in Sect. 2. Nonetheless, it implies the possibility of employing gravitational decoupling to develop a link between two distinct stellar structures, regardless of whether they possess identical or differing complexity factors.

5.1 Two stellar structures with same complexity factor

In this subsection, we impose a particular constraint on an extra gravitational source to model another spherical stellar configuration and assess its physical relevance. To achieve this, we assume that the additional fluid source is free from complexity. Consequently, we have \([Y_{TF}]^{\textrm{tot}}=Y_{TF}\), which implies \(Y^{\Theta }_{TF}=0\) or

$$\begin{aligned} \Pi _{\Theta }=\frac{1}{2r^{3}}\int ^{r}_{0}[\rho ^{\Theta }(y)]'y^{3}dy, \end{aligned}$$
(86)

where

$$\begin{aligned} \int ^{r}_{0}[\rho ^{\Theta }(y)]'y^{3}dy=\frac{2\varphi }{\kappa ^{2}}\left( \frac{\mathcal {F}'^{*}}{r^{2}}-\frac{\mathcal {F}^{*}}{2r}\right) r^{3}. \end{aligned}$$
(87)

Next, using Eqs. (47)–(49) in Eq. (86), we get

$$\begin{aligned} \mathcal {F}^{*}\left( 2\eta ''+\eta '^{2}-\frac{2\eta '}{r}-\frac{8}{r^{2}}\right) +\mathcal {F}'^{*}\left( \eta '+ \frac{4}{r}\right) =0. \end{aligned}$$
(88)

Any solution to the above differential equation can be employed to measure the additional fluid source \(\Theta ^{\alpha }_{~\beta }\). More precisely, for any solution involving metric variables \(\eta \) and \(\mu \) for the Einstein–Maxwell gravitational equations (42)–(44), the condition \([Y_{TF}]^{\textrm{tot}}=Y_{TF}\) allows us to construct another stellar solution to the system (22)–(24) satisfying same complexity factor condition. This process can be followed by continuously varying the constant parameter \(\varphi \) as in the previous section, where the initial solution corresponds to \(\varphi =0\), and the ultimate solution corresponds to \(\varphi =1\). However, since the expression (88) is independent of the parameter \(\varphi \), the complexity factor stays constant regardless of the value of \(\varphi \). This approach also indicates that matching constraints (66)–(68) have a substantial impact on defining the final outcome.. Specifically, the condition \([Y_{TF}]^{\textrm{tot}}=Y_{TF}\) can only be fulfilled by adjusting the compactness of the stellar structure. For this purpose, we consider the well-established Tolman IV metric components as a solution to the gravitational system (42)–(44), which is defined as

$$\begin{aligned} e^{\eta }&=Y^{2}\left( 1+\frac{r^{2}}{X^{2}}\right) , \end{aligned}$$
(89)
$$\begin{aligned} e^{-\mu }&=\frac{(Z^{2}-r^{2})(X^{2}+r^{2})}{Z^{2}(X^{2}+2r^{2})}, \end{aligned}$$
(90)

exhibiting the isotropic fluid configuration arises from the energy density

$$\begin{aligned} \rho (r)=\frac{3X^{4}+X^{2}(7r^{2}+3C^{2})+2r^{2}(3r^{2}+Z^{2})}{\kappa ^{2}Z^{2}(2r^{2}+X^{2})^{2}}, \end{aligned}$$
(91)

and the isotropic pressure

$$\begin{aligned} p(r)=\frac{Z^{2}-X^{2}-3r^{2}}{\kappa ^{2}Z^{2}(2r^{2}+X^{2})}, \end{aligned}$$
(92)

where the values of the constants X, Y, and Z within the mentioned solution are established through matching constraints (66)–(68). These conditions provides the same values (69) as in the previous section, along with an additional value

$$\begin{aligned} \frac{Z^{2}}{R^{2}}=\frac{R}{M}. \end{aligned}$$
(93)

Then, using the definition of complexity factor (78), we obtain the value of \(Y_{TF}\) as

$$\begin{aligned}{}[Y_{TF}]^{\textrm{tot}}=Y_{TF}=\frac{r^{2}(X^{2}+2Z^{2})}{Z^{2}(2r^{2}+X^{2})^{2}}. \end{aligned}$$
(94)

The substitution of the metric variable (89) in the differential equation (88) provides the the expression for \(\mathcal {F}^{*}(r)\) as

$$\begin{aligned} \mathcal {F}^{*}(r)=\frac{r^{2}(r^{2}+X^{2})}{\mathcal {K}^{2}(3r^{2}+2X^{2})}. \end{aligned}$$
(95)

Here, \(\mathcal {K}\) denotes an arbitrary constant of integration with dimensions of \(len\textit{g}th\). From the geometric deformation expression (38), the new form of the metric function can be cast as

$$\begin{aligned} e^{-\lambda (r)}=\frac{(Z^{2}-r^{2})(r^{2}+X^{2})}{Z^{2}(2r^{2}+X^{2})}+\varphi \frac{r^{2}(r^{2}+X^{2})}{\mathcal {K}^{2}(3r^{2}+2X^{2})}, \end{aligned}$$
(96)

which produces an effective energy density \(\epsilon \) as

$$\begin{aligned} \epsilon \left( r,\varphi ,\mathcal {K}\right) =\rho (r)+\frac{Q^{2}}{\kappa ^{2}r^{4}}-\varphi \frac{(9r^{2} +13r^{2}X^{2}+6X^{2})}{\kappa ^{2}(3r^{2}+2X^{2})^{2}\mathcal {K}^{2}}, \end{aligned}$$
(97)

and effective radial pressure component \(P_{r}\) as

$$\begin{aligned} P_{r}\left( r,\varphi ,\mathcal {K}\right) =p(r)-\frac{Q^{2}}{\kappa ^{2}r^{4}}-\varphi \frac{(3r^{2}+2X^{2})}{\kappa ^{2}(3r^{2}+2X^{2})\mathcal {K}^{2}}. \end{aligned}$$
(98)

The effective tangential pressure component is obtained through the relation \(P_{t}=P_{r}+[\Pi ]^{\textrm{tot}}\), with the pressure anisotropy

$$\begin{aligned}{}[\Pi ]^{\textrm{tot}}\left( r,\varphi ,\mathcal {K}\right) =\varphi \frac{r^{2}X^{2}}{\kappa ^{2}(3r^{2}+2X^{2}) ^{2}\mathcal {K}^{2}}. \end{aligned}$$
(99)
Fig. 3
figure 3

The behavior of the complexity factor \([Y_{TF}\times 10]\) versus radial coordinate for various values of the parameter \(\varphi \) with compactness factor \(\frac{M}{R}=0.2\)

Full size image

It is worth mentioning that the relations (89) and (96)–(99) represent complete exact solution to the charged EFEs (22)–(24). This represents a novel anisotropic form of the Tolman IV solution (89)–(92), wherein the total complexity factor \([Y_{TF}]^{\textrm{tot}}\) formally aligns with the complexity factor defined in expression (94). On the other hand, after employing the matching constraints (66)–(68) to find the constant parameters X, Y, and Z in the metric functions (89) and (96)–(99), it becomes evident that the values of X and Y remain unchanged (as in the expression (69)), while the parameter Z transforms into a function of the length \(\mathcal {K}\) and the anisotropic parameter \(\varphi \).

$$\begin{aligned} Z_{\varphi \mathcal {K}}^{2}=\frac{R^{3}}{M}-\frac{\varphi (X^{2}+2R^{2})(X^{2}+3R^{2})^{2}}{\mathcal {K}^{2}(2X^{2}+3R^{2})+\varphi (X^{4}+5X^{2}R^{2}+6R^{4})}, \end{aligned}$$
(100)

whereas the total complexity factor takes the form

$$\begin{aligned}{}[Y_{TF}]^{\textrm{tot}}\left( r,\varphi ,\mathcal {K}\right) =\frac{r^{2}(X^{2}+2Z_{\varphi \mathcal {K}}^{2})}{Z_{\varphi \mathcal {K}}^{2}(2r^{2}+X^{2})^{2}}. \end{aligned}$$
(101)

A comparison between Eqs. (94) and (101) reveals a crucial observation: the complexity factor changes (as shown in Fig. 3) as we vary the parameter \(\varphi \) until we perform a transformation on the radius \(R\rightarrow R_{\varphi \mathcal {K}}\) and the mass \(M\rightarrow M_{\varphi \mathcal {K}}\) in a manner such that

$$\begin{aligned} Z_{\varphi \mathcal {K}}(M_{\varphi \mathcal {K}},R_{\varphi \mathcal {K}})=\frac{R^{3}}{M}=Z(M,R). \end{aligned}$$
(102)

In this expression, we may consider \(\varphi =1\) for \(R_{\varphi \mathcal {K}}\) and \(M_{\varphi \mathcal {K}}\), without any loss of generality. Nevertheless, we maintain the freedom to define the arbitrary length scale \(\mathcal {K}\). This implies that the criterion \([Y_{TF}]^{\textrm{tot}}=Y_{TF}\) can be applicable across a continuous range of systems with varying radius R and mass M.

5.2 New charged stellar solutions under zero complexity factor condition

In this section, we discuss the possibility of constructing novel self-gravitational stellar models satisfying the condition \([Y_{TF}]^{\textrm{tot}}=0\) based on an initial solution where \(Y_{TF}\ne 0\). In this case, the expression \([Y_{TF}]^{\textrm{tot}}=Y_{TF}+Y_{TF}^{\Theta }\) reads

$$\begin{aligned}{}[Y_{TF}]^{\textrm{tot}}=Y_{TF}+\kappa ^{2}\Pi _{\Theta }-\frac{\kappa ^{2}}{2r^{3}}\int ^{r}_{0} [\rho ^{\Theta }(y)]'y^{3}dy, \end{aligned}$$
(103)

with \(\varphi =1\). Next, the substitution of the expressions (47)–(49) in the above expression yield the first-order ODE as

$$\begin{aligned} \frac{\mathcal {F}^{*}}{4}\left( 2\eta ''+\eta '^{2}-\frac{2\eta '}{r-\frac{8}{r^{2}}}\right) +\frac{\mathcal {F}'^{*}}{4}\left( \eta '+\frac{4}{r}\right) +Y_{TF}=0. \end{aligned}$$
(104)

Then, again using the Tolman IV solution (90), we obtain the following expression

$$\begin{aligned} \mathcal {F}^{*}(r)=\frac{r^{2}(X^{2}+r^{2})}{\mathcal {K}^{2}(3r^{2}+2X^{2})}\left[ 1 +\frac{r^{2}(X^{2}+2Z^{2})}{2Z^{2}(2r^{2}+X^{2})}\right] . \end{aligned}$$
(105)

Here, \(\mathcal {K}\) symbolize an arbitrary constant of integration (with dimensions of \(len\textit{g}th\)). Hence, the modified version of the complexity factor, derived from the transformed radial metric function (96), takes the form

$$\begin{aligned}{}[Y_{TF}]^{\textrm{tot}}(r,\varphi )=(1-\varphi )\frac{r^{2}(X^{2}+2Z^{2})}{Z^{2}(2r^{2}+X^{2})^{2}}. \end{aligned}$$
(106)

Note that the above-mentioned expression becomes zero for \(\varphi =1\), and the corresponding stellar solution emerges as complexity-free. Hence, this solution smoothly interpolates between \(\varphi =0\) (initial value) and \(\varphi =1\) (zero complexity factor). For \(\varphi =1\), the matching constraints (66)–(68) yield the same values for the constants X and Y as presented in (69). However, the value of Z turns out to be

$$\begin{aligned} Z^{2}=\frac{3\mathcal {K}^{2}(X^{2}+3R^{2})}{2(X^{2}+3R^{2}+3\mathcal {K}^{2})}. \end{aligned}$$
(107)

Finally, the new radial component can be cast as

$$\begin{aligned} e^{-\lambda (r)}=\frac{(r^{2}+X^{2})(2X^{2}-3r^{2}+6R^{2})}{(3r^{2}+2X^{2})(3R^{2}+X^{2})}, \end{aligned}$$
(108)

whereas the effective radial competent of pressure becomes

$$\begin{aligned} P_{r}=\frac{Q^{2}}{\kappa ^{2}r^{4}}+\frac{9(R^{2}-r^{2})}{\kappa ^{2}(X^{2}+3R^{2})(3r^{2}+2X^{2})}, \end{aligned}$$
(109)
$$\begin{aligned} \epsilon (r)=-\frac{Q^{2}}{\kappa ^{2}r^{4}}+\frac{3[8X^{2}+2X^{2}(7r^{2}+3R^{2})+3r^{2}(3r^{2}+R^{2})]}{\kappa ^{2}(X^{2}+3R^{2})(3r^{2}+2X^{2})^{2}}, \end{aligned}$$
(110)

The effective tangential component of pressure is \(P_{t}(r)=P_{r}(r)+[\Pi ]^{\textrm{tot}}(r)\), where pressure anisotropy is defined as

$$\begin{aligned}{}[\Pi ]^{\textrm{tot}}(r)=-\frac{3r^{2}(2X^{2}+3R^{2})}{\kappa ^{2}(X^{2}+3R^{2})(3r^{2}+2X^{2})^{2}}. \end{aligned}$$
(111)

This self-gravitational stellar model differs from the previous one in that the complexity factor vanishes for \(\varphi =1\) regardless of R and M. Hence, we have transformed the Tolman IV fluid, characterized by a given radius R, mass M, and the complexity factor (94), into an entire family of self-gravitational systems for arbitrary values of the length scale \(\mathcal {K}\). These systems share the same radius R and mass M but exhibit zero complexity, which is parameterized by \(\mathcal {K}\).

6 Summary and discussions

The gravitational decoupling scheme is an innovative and highly effective approach for modeling self-gravitating, anisotropic fluid systems with multiple energy–momentum tensors. By providing an exact solution from one of these gravitational sources, this approach allows for the construction of exact solutions involving additional sources. In this study, we investigated how both pressure anisotropy and the complexity factor of the gravitational structure play a significant role in constructing Einstein–Maxwell self-gravitational models by applying gravitational decoupling via the MGD-scheme. To obtain a gravitationally decoupled solution using the MGD scheme for the self-gravitational compact structure, we start by specifying the modified action for the decoupled system. In this manner, we obtain the charged EFEs for the decoupled gravitational system, which corresponds to the total EMT within the framework of spherically symmetric geometry. Then, for the corresponding Einstein–Maxwell system of gravitational equations, we employ the MGD-scheme, in which only the inverse-radial metric component is modified, as suggested by Ovalle [25]. This scheme divides the original system into two time-independent, spherical charged compact sources \(\{T^{\alpha }_{~\beta },\Theta ^{\alpha }_{~\beta }\}\). The gravitational source \(T^{\alpha }_{~\beta }\) describes the distribution of charged anisotropic fluid, while \(\Theta ^{\alpha }_{~\beta }\) corresponds to the quasi-Einstein system. The MGD-scheme uniquely arises from gravitational interactions between the two sectors, devoid of any exchange of energy and momentum between them.

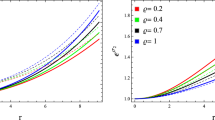
This investigation is different in a way that it focuses on employing the MGD-scheme to impose specific physical features satisfied by the entire gravitational structure. The uniqueness of this study lies in the significance of gravitational decoupling, which imparts specific physical features to the entire spherically symmetric, self-gravitational charged fluid sphere. To ensure the physical acceptability and proper behavior of any stellar structure model, it is essential to examine its fundamental thermodynamic characteristics, including density, pressure, and anisotropy. We have plotted the figures by assuming the values of the constant parameter \(\varphi =0.0,~0.2,~0.3,~0.5,~0.7,~and ~1.0\).

In Fig. 1, the effective radial pressure \(P_{r}\) profile displays a monotonically decreasing behavior with respect to r. We observed that \(P_{r}\) has attained its maximum value at the center of the self-gravitational compact system for some fixed value of \(\varphi \). The radial pressure \(P_{r}\) gradually decreases until it disappears at the boundary, as expected, due to the absence of energy flux to the surrounding spacetime. The impact resulting from the deformation parameter \(\varphi \) describes that the radial pressure increases as \(\varphi \) increases.

Due to unequal principle stresses, i.e., \(P_{r}\ne P_{t}\), pressure anisotropy arises, which is expressed through the anisotropic factor \([\Pi ]^{\textrm{total}}\), as displayed in Fig. 2. In this context, it can be easily observed that the anisotropic factor is zero at the core of the stellar system for all values of coupling parameter \(\varphi \) and then gradually increases with the increase in r. Additionally, it is observed that the anisotropic factor rises with an increase in the value of r, implying that gravitational decoupling leads to a more anisotropic nature in the fluid distribution. The positive anisotropy grows as it approaches the boundary of the stellar object.

Fig. 4
figure 4

The behavior of radial component of pressure \(P_{r}\times 10^{3}\) versus radial coordinate r for the Tolman IV solution (\(Y_{TF}\ne 0\)) and its anisotropic form with \([Y_{TF}]^{\textrm{tot}}=0\) for compactification factor \(\frac{M}{R}=0.2\)

Full size image

The behavior of the total complexity factor for first case for different values of the deformation constant is displayed in Fig. 3. The complexity factor starts at zero at the center of the configuration, gradually increases, peaks at a certain point, and then decreases towards the surface. Finally, the behavior of the radial pressure \(P_{r}\) with zero complexity factor in the last case is displayed in Fig. 4. Hence, it can be asserted that the charged complexity factor is pivotal for improving the stability of the system.