Monte-carlo simulation of the effective lunar aperture for detection of ultra-high energy neutrinos with LOFAR

Abstract

Ultra-high-energy (UHE) cosmic neutrinos interacting with the Moon’s regolith generate particle showers that emit Askaryan radiation. This radiation can be observed from the Earth using ground-based radio telescopes like LOFAR. We simulate the effective detection aperture for UHE neutrinos hitting the Moon. Under the same assumptions, results from this work are in good agreement with previous analytic parameterizations and Monte Carlo codes. The dependence of the effective detection aperture on the observing parameters, such as observing frequency and minimum detection threshold, and lunar characteristics like surface topography have been studied. Using a Monte Carlo simulation, we find that the detectable neutrino energy threshold is lowered when we include a realistic treatment of the inelasticity, transmission coefficient, and surface roughness. Lunar surface roughness at large scales enhances the total aperture for higher observation frequencies ($\nu \ge 1~\textrm{GHz}$) but has no significant effect on the LOFAR aperture. However, roughness at scales small compared to the wavelength reduces the aperture at all frequencies.

1 Introduction

The observation of ultra-high energy cosmic rays (UHECRs) suggests the existence of UHE cosmic neutrinos which are produced via the interaction of UHECRs with photons of the ubiquitous $2.73~\textrm{K}$ cosmic background radiation, either through photo-pion production for cosmic-ray protons, e.g., ($p + \gamma \rightarrow \pi ^+ + n$) or photo-disintegration for cosmic-ray nuclei, resulting in the well-known GZK cutoff [1, 2]. It has also been suggested that UHE neutrinos can be produced from topological defects, the so-called top-down models [3,4,5,6,7,8,9]. These models predict the existence of super-heavy particles as produced by cosmic strings or relics from the early universe. Due to their high mass, these particles can undergo annihilation, decay, or interaction to create a range of high-energy particles. Due to the extremely low flux and small interaction cross-section of UHE neutrinos, searches so far have only been able to place upper limits on their flux. Detecting a significant number of these particles requires building giant detectors or remotely monitoring large naturally occurring detection targets such as the Moon (with a near-surface area of $1.9 \times 10^{7}~\textrm{km}^{2}$). One effort to detect these particles involves observing a burst of Askaryan radio emission [10] with Earth-based radio telescopes. Dagkesamanskii and Zheleznykh suggested this method [11]. Several experiments [12,13,14,15,16,17,18,19] have used this technique but have so far not managed to detect the emission. The non-detection of the Askaryan radio emission from the interacting neutrinos can place an upper limit on the UHE neutrino flux. This requires an accurate knowledge of the effective lunar aperture – the aperture (i.e., area times solid angle) of the near-surface of the Moon, multiplied by the detection probability of UHE neutrinos interacting with it – which is the subject of this paper.

Different experiments have done several independent Monte Carlo calculations to determine the effective lunar aperture for UHE neutrinos interacting with the Moon. The initial lunar observations occurred in 1996 at Parkes, Australia [12]. Since simulations were unavailable then, the absence of detection did not yield an upper limit on the UHE neutrino flux. Subsequent lunar observations were carried out, accompanied by the development of separate Monte Carlo simulations [20,21,22,23]. Later, a Monte Carlo simulation was developed for the Parkes experiment [24, 25]. This simulation drew upon the previous works of the Goldstone Lunar Ultrahigh Energy Neutrino Experiment (GLUE) at NASA’s Goldstone Deep Space Communications Complex, USA [22] and the Kalyazin experiment at the Kalyazin Radio Astronomical Observatory, Russia [23]. In the NuMoon experiment, which was the pioneering low-frequency lunar experiment [26], a semi-analytic calculation of effective aperture was carried out. The present study incorporates parameterizations derived from these earlier Monte Carlo and semi-analytic calculations. In the previous NuMoon semi-analytic aperture calculation [26], the impact of surface roughness was not taken into account. In the simulation conducted by James and Protheroe [25], only the large-scale roughness of the lunar surface was considered. However, in this study, we have considered both the small-scale roughness (based on [27]) and the large-scale roughness of the lunar surface, which will be discussed in detail later. Another important aspect is the relevance of the lunar density profile. The refractive index varies with the density profile of the Moon, which, in turn, affects the hadronic shower length and the resulting Askaryan Cherenkov radiation. Scholten investigated this effect and demonstrated that calculations considering pure rock or pure regolith yielded similar limits at $100~\textrm{MHz}$ while differing at $2.2~\textrm{GHz}$ [26]. In their calculations, the regolith was modeled as a uniform layer with a constant index of refraction and a depth of $500~\textrm{m}$. In the simulation by James and Protheroe, the Moon was divided into two layers: regolith and sub-regolith [25]. However, in this current work, we have modeled the Moon as a single uniform layer with a constant index of refraction based on the arguments presented in [26]. Furthermore, James and Protheroe included secondary showers from secondary particles in their simulation. However, in this study, secondary showers were not simulated because they do not significantly contribute at low frequencies (i.e. for LOFAR observations), as the signal is dominated by downgoing showers dominate us. Because the showers are downgoing, the secondary showers occur at great depths within the Moon and are not detectable, as was also assumed in [24].

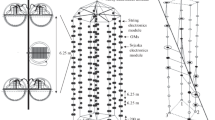
A standard simulation, calculation, or analytic parameterization of the effective aperture with similar underlying assumptions or physics is necessary to compare experimental results. A parameterization has been created by Gayley et al. [28] (see also [29, App. B]) taking into account all the known experimental effects, including surface roughness. Several approximations were used to derive this analytic expression. In this work, we study the validity of these approximations in different frequency ranges using a full Monte Carlo simulation we have developed. This work is part of the NuMoon experiment [26], a low frequency ($\sim 150~\textrm{MHz}$) search for UHE neutrinos hitting the Moon. At this frequency, the lunar regolith is relatively transparent to the emission and has a more extensive angular acceptance, giving a higher potential event rate [30]. The previous observations for the NuMoon experiment were carried out using the Westerbork Synthesis Radio Telescope array [17]. In this work, we use the LOFAR telescope. LOFAR, the LOw Frequency ARray, is a radio observatory with stations scattered all over Europe [31]. The core stations of the observatory are located in the Netherlands. The core comprises 24 stations, each containing 2 sub-fields. Each sub-field consists of 24 tiles. Each of these tiles comprises 16 high band antennas (HBA) on $4\times 4$ grid (i.e., a total of 18,432 HBA dipole antennas at the LOFAR core). The frequency range for the HBAs we are interested in is 110–$190~\textrm{MHz}$ (other frequency bands were not considered for this work). The observations are carried out in a beam-formed mode by applying geometrical delays or weights to each antenna to cancel out sensitivity in some (undesirable) directions and enhance it towards a user-defined direction.

This paper is organized as follows. In Sect. 2, we discuss the physics of particle interactions within the Moon, the radio emission process and the parameterization of the roughness of the lunar surface as well as the effects of propagation on the radio signal and the signal detection threshold for LOFAR. In Sect. 3, we describe the Monte Carlo simulation set-up for computing the effective aperture in detail. In Sect. 4, we present the entire simulation, and the results are compared to those of the analytic parameterization [28]. We replicate some of the assumptions made in the analytic parameterizations in the simulation to validate the simulation. We also study and present the results of including surface roughness on the effective lunar aperture for different frequencies. We discuss the advantages of low-frequency observations in Sect. 4.3. In Sect. 5, we summarize the main result of this paper.

2 Physics of UHE neutrino interactions and radio Askaryan Cherenkov emission in the lunar regolith

A UHE neutrino interacting with the Moon produces a particle cascade in the lunar regolith. An excess of electrons develops in the cascade, resulting in radio emission that is strongest at the Cherenkov angle. The radio waves are attenuated as they propagate through the Moon and are refracted at the lunar surface. Depending on the shower geometry, lunar surface topography, and trigger threshold, some emissions can be detected on Earth. A detailed discussion of these processes will be given in the subsequent subsections.

2.1 UHE neutrino interaction with the regolith

Lunar regolith, which is the upper layer of the lunar surface, consists of an aggregation of small rocks and fine particles made of iron and titanium compounds, believed to be ejecta from meteor impacts with the Lunar surface [32]. Our current best knowledge of the lunar regolith is based on [32]. Here we adopt the values of $\rho \approx 1.7~\textrm{g}~\textrm{cm}^{-3}$ for density and $n_{i} = 1.73$ for an index of refraction. UHE neutrinos interact with baryons in the lunar regolith with an energy-dependent mean-free path given as [30]:

$$\begin{aligned} L_{\nu } = 130 \left[ \frac{10^{20}}{E_{\nu }}\right] ^{\frac{1}{3}} [~\textrm{km}], \end{aligned}$$

(1)

which comes from summing the cross-sections for both charged- and neutral-current interactions, as both processes generate similar hadronic showers at ultra-high energies [30]. The particle showers initiated by UHE neutrinos depend on the interaction type: either charged-current (with a branching ratio of $\sim 2/3$) or neutral-current (with a branching ratio of $\sim 1/3$) interaction. In both cases, $\sim 20\%$ of the initial neutrino energy goes into creating a hadronic shower. In the charged-current interaction, $\sim 80\%$ of the primary neutrino energy produces a charged lepton (electron, muon, or tau). These charged leptons may contribute to the cascade depending on their flavor. Muons produced in the charged-current interaction travel long distances before decaying and losing much of their energy. The produced taus also travel large distances from the initial hadronic shower before decaying, producing a second distinct cascade [33]. Due to its high mass, the tau can decay into a lighter-charged lepton or a hadron, producing either an electromagnetic or a hadronic shower. These secondary showers are ignored in the simulation as they are assumed to develop deep inside the Moon and, therefore, cannot be detected. On the other hand, the electrons initiate electromagnetic showers, which are elongated by the Landau–Pomeranchuk–Migdal (LPM) effect [34]. This narrows the shower emission cone width, making a negligible contribution to the total emission as the emission cone scales inversely with the shower length. In the neutral-current interaction, on the other hand, the remaining $80\%$ of the neutrino energy is retained in a highly forward-scattered neutrino. The scattered neutrinos interact infrequently, losing their energy to the cascade.

Due to the high multiplicity of initial collisions in hadronic showers, the initial energy is divided quickly, mitigating against any LPM effects (i.e., $\pi ^0$ interactions dominate over decay). The LPM effect is caused by the increasing interaction distance with energy to orders of the typical separation distance between atoms. At very high energies, the screen field of all nuclei in the nearby region comes into play in reducing the cross-section, which falls as $\sqrt{E}$ above $E_{\textrm{LPM}}$, for both bremsstrahlung and pair production [35], thereby affecting the static electric field responsible for the interaction. The LPM effect only affects the early stages of shower development. For this work, we consider only the hadronic showers and neglect the small LPM effect on them. It should be noted that by ignoring emissions from secondary showers and electromagnetic showers, we only obtain conservative values for the effective aperture; hence, a slightly higher aperture may be expected when including this in future simulations.

The hadronic shower produced by the initial interaction takes $\sim 20\%$ of the initial neutrino energy. Askaryan pointed out that a developing hadronic shower in a dielectric medium acquires about $20\%$ to $30\%$ negative charge excess of the total charged particles N, due to electron entrainment (e.g., $\gamma + e^{-}_{\text {atoms}} \rightarrow \gamma + e^{-}$) and positron annihilation into photons ($e^{+} + e^{-}_{\text {atoms}} \rightarrow \gamma \gamma$) [10]. Thus, the shower evolves into a short transient current source, which produces coherent radio Askaryan radiation. Note that changing current always radiates independently of a medium. The radiation is emitted in a cone of half opening angle (i.e., Cherenkov angle or opening angle of the Cherenkov cone):

$$\begin{aligned} \theta _c = \arccos \Big ( \frac{1}{\beta n_{i}} \Big ) \approx 55^{\circ }. \end{aligned}$$

(2)

The radiation is strongest at $\theta _c$ due to the time compression of emissions from the entire cascade (more on this in Sect. 4.3). Askaryan’s predictions were later verified at the Stanford Linear Accelerator by shooting electron beams at ice, salt, and silica sand targets [36, 37].

Additionally, Askaryan pointed out that at wavelengths comparable to the shower dimensions, the emitted radiation from particles in the cascade is coherent, and hence the power of the radiation scales as:

$$\begin{aligned} P \propto (\varDelta q \, N \, q)^2, \end{aligned}$$

(3)

where $\varDelta q$ is the fractional charge excess (20–30% as above), N the total number of particles in the shower and q the particle charge. Due to the radio emission’s coherency, the power in the radio waves scales quadratically with N and hence with the shower energy. This makes radio detection of UHE neutrinos an attractive option. The density of a medium constrains the dimensions of a developing shower and, hence, the possible range of frequencies for which the radiation is coherent. In a dense medium like the regolith, the total width of a shower is of the order of a few centimeters, so coherency extends to $\textrm{GHz}$ frequencies. This is where most of the power is available because the coherency of the radiated wave is proportional to frequency. At lower frequencies, the emission is still detectable due to the Askaryan (or coherence) effect and its wider Cherenkov cone width.

It should be noted that Askaryan and Cherenkov emissions are not the same mechanisms. Cherenkov emission is usually defined as the radiation of a constant charge moving at a constant velocity that exceeds the speed of light in the medium. It comes from the near-field term of the Lienard–Wiechert potential. For Askaryan emission, the moving charge is time-dependent, and the emission is derived from the far-field term of the Lienard–Wiechert potential as described in [35]. Both mechanisms emit most strongly at the Cherenkov angle; hence, it is adequate to refer to this radiation as either the Askaryan radiation or the Askaryan Cherenkov radiation [38] and not as a Cherenkov radiation.

2.2 Parameterization of the spectral electric field from hadronic showers in the regolith

The peak spectral electric field and angular width of the Askaryan Cherenkov radiation produced by a hadronic shower depend on the primary neutrino energy, E, and the observation frequency, $\nu$. The $e^{-1}$ half width of the Cherenkov cone (i.e., describing the thickness of the spread of the radiation around the Cherenkov angle, $\theta _c$), $\varDelta _c$ for radio emission from hadronic showers in the regolith and valid for energies above $10~\textrm{EeV}$ is [28]:

$$\begin{aligned} \varDelta _c = 0.05\left[ \frac{\textrm{GHz}}{\nu }\right] \left[ 1+0.075\log \left( \frac{E_s}{10^{19}~\textrm{eV}}\right) \right] ^{-1} [\text {rad}], \end{aligned}$$

(4)

where $E_s$ is the hadronic shower energy (i.e. $\approx 20\%$ of the primary energy, E). This equation is obtained by multiplying the angular width constant, $C_H=2.4^{\circ }$ from [25] by $1/\sqrt{\log 2} = 1.2$, which converts $\varDelta _c$ to $e^{-1}$ half width instead of the half width at half maximum. As stated in [25], Eqs. 4 and 5 were built by scaling the parameterization of [39], which is a parameterization based on an in-ice simulation of hadronic showers valid up to $10~\textrm{EeV}$. This scaling was done to extend the validity of their parameterization for hadronic showers in the regolith with energies above $10~\textrm{EeV}$. At frequencies as low as $100~\textrm{MHz}$, the cone width from Eq. 4 ranges between $30^{\circ }$ and $25^{\circ }$ for energies between $10^{19}~\textrm{eV}$ and $10^{24}~\textrm{eV}$.

The electric field (assuming no attenuation losses in the regolith), ${\mathcal {E}}_{c} (\equiv {\mathcal {E}}_c (E_s, \nu ))$ at Earth along the Cherenkov angle from a hadronic shower in the regolith is parameterized by [25]:

$$\begin{aligned} {\mathcal {E}}_c = 0.0845\frac{\textrm{V}}{\textrm{mMHz}}\left[ \frac{\textrm{m}}{d}\right] \left[ \frac{E_s}{\textrm{EeV}}\right] \left[ \frac{\nu }{\textrm{GHz}}\right] \nonumber \\ \left[ 1+ \left( \frac{\nu }{2.32~\textrm{GHz}}\right) ^{1.23}\right] ^{-1}, \end{aligned}$$

(5)

where d is the average Earth–Moon distance (i.e., distance from the shower), and $2.32 \textrm{GHz}$ is the decoherence frequency determined by the lateral dimensions of the shower. The radio emission from a particle cascade is the coherent sum of the radiation of all charges in the shower. Due to multiple scattering – the dominant interaction process responsible for the transverse spread of particles in a shower – particles spread transversely or laterally with respect to the shower axis [35]. The transverse spread increases as the shower develops and more interactions occur. For observers at the Cherenkov angle, radiation from all points along the longitudinal extent of the shower arrives simultaneously. In this case, the decoherence frequency is determined by the lateral size of the shower. However, further away from the Cherenkov angle, the turnover frequency is determined by the longitudinal dimension of the shower [20].

A parameterization for the angular spread of the emission around the Cherenkov angle, $\theta _c$ from a hadronic shower is given by equation 12 in [40]:

$$\begin{aligned} {\mathcal {E}} (E_s, \theta , \nu ) = {\mathcal {E}}_c \exp \Big [-\Big (\frac{\theta - \theta _c }{\varDelta _c}\Big )^{2}\Big ] \Big (\frac{\sin {\theta }}{\sin {\theta _c}}\Big ) \end{aligned}$$

(6)

where ${\mathcal {E}}_c$ and $\varDelta _c$ are given in Eqs. 5 and 4 respectively. $\theta$ is the ray path angle with respect to the hadronic shower axis. The angular distribution for the spectral electric field for frequencies: $150~\textrm{MHz}$ and $1.5~\textrm{GHz}$ are shown in Fig. 1 (top) for a neutrino of primary energy, $10^{24}~\textrm{eV}$. As shown in the figure, the angular spread of the spectral electric field scales inversely with frequency. In Fig. 1 (bottom), the spectra of the electric field as a function of angular distance from the Cherenkov angle are shown. On the Cherenkov angle, $\theta _c = \theta = 54.7^{\circ }$, the emission is coherent up to $\approx 5~\textrm{GHz}$ when it departs from its linear frequency dependence. Away from the Cherenkov angle (i.e., $\theta > 54.7^{\circ }$), decoherence sets in at lower frequencies, as shown.

Fig. 1

Top: angular distribution or behavior of the emitted electric field by a hadronic shower relative to the shower axis in the regolith by a neutrino of primary energy, $10^{24}~\textrm{eV}$ and for frequencies: $150~\textrm{MHz}$ and $1.5~\textrm{GHz}$. Bottom: frequency spectrum of the emitted electric field as a function of observation angle with $\theta _c = \theta = 54.7^{\circ }$ being the Cherenkov angle

2.3 Electric field attenuation in the regolith

The attenuation of a radio signal can be understood as a loss in its amplitude or intensity as it propagates through a medium. The attenuation loss varies between different materials and is both frequency and range-dependent. Radio signals propagating in the regolith are attenuated. To model the attenuation loss, we use the mean value of the radio attenuation length, $L_\textrm{r}$ from [32], which is given by:

$$\begin{aligned} L_\textrm{r} = 9 \cdot \Big [\frac{1\textrm{GHz}}{\nu }\Big ] [\textrm{m}]. \end{aligned}$$

(7)

The radio attenuation length describes the distance in the regolith where the intensity or amplitude of the emitted radio signal has decreased to $e^{-1}$ of its initial value. This relation comes from the loss tangent measurements carried out on samples from the Moon during the Apollo mission. It can vary widely depending on the iron and titanium content of the material [32]. The distance-corrected field strength, ${\mathcal {E}} (E_s, \theta , \nu , r)$ due to attenuation losses is given by:

$$\begin{aligned} {\mathcal {E}} \equiv {\mathcal {E}} (E_s, \theta , \nu , r) = {\mathcal {E}} (E_s, \theta , \nu )e^{-r/ L_\textrm{r}(\nu )}, \end{aligned}$$

(8)

where r is the distance an emitted electric field traversed from its emission point up to the lunar-vacuum interface.

2.4 Total internal reflection (TIR) and transmission coefficient at the lunar-vacuum interface

Radio waves arriving at the lunar-vacuum interface from within the regolith are either internally reflected or refracted out of the regolith, depending on whether the angle of incidence is greater or less than the critical angle, respectively. The relationship between the angle of incidence and the refraction at the lunar-vacuum boundary is given by Snell’s law (assuming an idealized smooth lunar surface):

$$\begin{aligned} n_i \sin (i) = n_t \sin (t), \end{aligned}$$

(9)

where $n_i$ is the refractive index of regolith, $n_t (= 1)$ is the refractive index of vacuum, t is the angle of refraction to the local surface normal in vacuum (outside the regolith) for a transmitted ray, and i is the angle of incidence in the regolith to the local surface normal. To avoid total internal reflection, the radio waves must satisfy the condition:

$$\begin{aligned} \frac{n_i}{n_t} \sin (i) < 1. \end{aligned}$$

(10)

Due to the divergence of rays after refraction, the observed spherical waves emanating from within the regolith in the far field are weaker than expected from the $R^{-2}$ law, where R is the distance to the observer point. This requires modifying the standard Fresnel transmission coefficients to obtain the transmission coefficient for radiation polarized parallel to the plane of incidence [3, 41]:

$$\begin{aligned} t_{\parallel } = \frac{n_t \cos (t)}{n_i \cos (i)}\frac{2\sin (t) \cos (i)}{\sin (i +t) \cos (i-t)} = \frac{2 n_t \cos (t)}{n_i\cos (t) + n_t\cos (i)} \end{aligned}$$

(11)

and the transmission coefficient for radiation polarized perpendicular to the plane of incidence [3, 41]:

$$\begin{aligned} t_{\perp } = \frac{n_t \cos (t)}{n_i \cos (i)}\frac{2\sin (t) \cos (t)}{\sin (i + t)} = \frac{2 n_t \cos (t)}{n_i\cos (i) + n_t \cos (t)}. \end{aligned}$$

(12)

Figure 2 displays the transmission coefficients $t_{\parallel }$ and $t_{\perp }$ as a function of angle of incidence, i. Following from Eqs. 11 and 12, the transmitted electric field, ${\mathcal {E}}_{\textrm{transmitted}}$ on which we trigger is given as:

$$\begin{aligned} {\mathcal {E}}_\textrm{transmitted} = \sqrt{ ({\mathcal {E}}_{\perp } \cdot t_{\perp })^2 + ({\mathcal {E}}_{\parallel } \cdot t_{\parallel })^2}, \end{aligned}$$

(13)

where ${\mathcal {E}}_{\perp }$ and ${\mathcal {E}}_{\parallel }$ are the perpendicular and parallel components of the incident spectral electric field strength inside the regolith. They both depend on $(E_s, \theta , \nu , \theta _r, r)$.

Fig. 2

A plot of the modified transmission coefficient, $t_{\parallel }, t_{\perp }$ versus angle of incidence, i. The critical angle of the lunar surface is indicated in a black dot. Parallel and perpendicular components of the transmission coefficient are indicated with red and blue lines, respectively

2.5 Minimum detectable spectral electric field

The coherent Cherenkov radiation from a shower in the regolith is expressed in terms of spectral electric field strength, $\varUpsilon _{\textrm{rms}}$ in units of $\textrm{V}/\textrm{m}/\textrm{Hz}$ where rms stands for the root-mean-square. The sensitivity of a radio telescope is characterized by the system equivalent flux density $\big <F\big>$ in units of $\textrm{Jy}$. The rms spectral electric field for a specific signal bandwidth is related to the system equivalent flux density via [29]:

$$\begin{aligned} \big <F\big > = \frac{\varUpsilon _\textrm{rms}^2 \varDelta \nu }{Z_0} , \end{aligned}$$

(14)

where $\varDelta \nu = 80~\textrm{MHz}$ is the bandwidth of the LOFAR HBA. The relation for $\varUpsilon _\textrm{rms}$ is given by:

$$\begin{aligned} \varUpsilon _\textrm{rms} = \sqrt{\frac{\kappa T_\textrm{sys}Z_0}{\eta A_\textrm{eff} \varDelta \nu }}, \end{aligned}$$

(15)

where $\kappa$, $T_\textrm{sys}$ (comprising the instrumental noise of $200~\textrm{K}$ and the thermal emission from the Moon at the central frequency of the LOFAR HBA band, $270~\textrm{K}$ [29]), $Z_0$, $A_\textrm{eff}$ are Boltzmann’s constant, system thermal noise temperature, impedance of free space ($377~\varOmega$) and effective aperture of a telescope. $A_{\textrm{eff}}$ of an HBA dipole is limited by the available area in a tile and is given by [42]:

$$\begin{aligned} A_\textrm{eff} = \textrm{min} \Big (\frac{\lambda ^2}{3}, 1.5625 \Big )~[\textrm{m}^2], \end{aligned}$$

(16)

where $\lambda$ is calculated using the center frequency, $166~\textrm{MHz}$ of the LOFAR HBA. $A_{\textrm{eff}} = 20,063~\textrm{m}^2$ for all the 24 LOFAR core stations. Since LOFAR HBA has no movable parts, it maintains a fixed orientation on the ground. As a result, it will have a reduced projected area, $A_\textrm{eff} = 16,636~\textrm{m}^2$ for the Moon at a maximum elevation of $56^{\circ }$ from the LOFAR site. The threshold spectral electric field strength, $\varUpsilon _\textrm{min}$ above which a signal is triggered is given by equation 8 in [29]:

$$\begin{aligned} \varUpsilon _\textrm{min} (\theta ) = f_C \frac{n_{\sigma }}{\alpha } \sqrt{\frac{\eta }{\beta (\theta )}} \varUpsilon _\textrm{rms}, \end{aligned}$$

(17)

where $\eta$ is the ratio between the total pulse power and the power in the chosen polarisation channel, $\alpha$ is the fraction of the original pulse amplitude recovered after inefficiencies in pulse reconstruction, (and it simulates the phase as a phase of an Askaryan pulse is close to $\pi /2$ leading to a loss in the pulse amplitude by a factor of $\sqrt{2}$, dispersion, for which the pulse is smeared out in time in the ionosphere reducing its amplitude and sampling of the coherent Askaryan pulse such that the peak amplitude in the analog signal is missed due to finite sampling as described in [29]), $\beta (\theta )$ is the beam power at an angle $\theta$ from its axis, normalized to $\beta (0) = 1$ and $f_C$ accounts for the improvement in sensitivity from combining C independent channels with a threshold of $n_{\sigma }$ in each. $\varUpsilon _\textrm{min}$, was calculated in Sect. 3.9 of [29] for LOFAR using the following values: $T_\textrm{sys}=470~\textrm{K}$, $\alpha = 1$, $\eta = 2$, $f_C=1$, $\varDelta \nu =80~\textrm{MHz}$, $n_{\sigma } = 12.6$ and $A_\textrm{eff} = 16636~\textrm{m}^2$. Using these values $\varUpsilon _\textrm{min} = 0.024~\mu \textrm{V}/\textrm{m}/\textrm{MHz}$.

2.6 Parameterization of lunar surface roughness

Surface roughness is significant for detecting UHE neutrinos and must be included in our simulation. Signals from showers created by downward-directed interacting neutrinos (i.e., neutrinos incident at angles between $0^{\circ }$ and $90^{\circ }$ to the local lunar surface normal) which might otherwise be totally internally reflected over a smooth surface as shown in Fig. 3 are transmitted due to surface roughness as shown in Fig. 4.

Fig. 3

A figure showing the transmission of signals for downward interacting neutrinos, $\nu$, over a smooth lunar surface at high and low frequencies. a Neutrino interacting parallel to the lunar surface (i.e. $90^{\circ }$ to the lunar surface) at $1~\textrm{GHz}$. b Downward neutrino at $1~\textrm{GHz}$, c downward neutrino at $100~\textrm{MHz}$

Fig. 4

A figure showing the different scales of the Lunar surface roughness

Surface roughness in the scope of this simulation characterizes the shape and features of the lunar surface variability (i.e., topographic expression of the lunar surface) at horizontal scales from a few centimeters to a few meters. The most commonly used roughness parameters are rms height, rms deviation, rms slope, auto-correlation length, effective slope, median and absolute slope, and power spectrum. A detailed discussion of these methods can be found in [43]. With a backscattered radar experiment, Shepard et al. [44] showed that self-affine (or fractal model of) rough surfaces manifests a wavelength-dependent radar reflection and proposed the dependence of rms slope, s$_\textrm{rms}$ on the wavelength as a power-law via:

$$\begin{aligned} \begin{aligned} \tan s_\textrm{rms}&= s(\varDelta x_0) \Big ( \frac{\varDelta x}{\varDelta x_0} \Big )^{H-1} \\&\approx s_0 \Big ( \frac{\varDelta x}{\varDelta x_0} \Big )^{H-1} \\&\approx 0.29(\lambda [\textrm{cm}])^{-0.22} \\&\approx 0.14(\nu [\textrm{GHz}])^{0.22}. \end{aligned} \end{aligned}$$

(18)

Their method depends on the Hurst exponent, H ($\approx 0.78$ for the Moon [44] with typical values between 0 and 1), which relates the rms slope to the horizontal scale variation with respect to some reference value, $s_0$. Here $s_0$ is the rms slope at one reference step size, $\varDelta x_0$ ($1~\textrm{cm}$ in this case), $\lambda$ is wavelength in $\textrm{cm}$ and $\nu$ is frequency in $\textrm{GHz}$. A surface for which a change, L, along the x and y axes, must be compensated for along the z axis by a factor, $L^H$, for the surface to remain statistically identical is referred to as a self-affine surface. From Eq. 18, the Lunar surface is rougher on smaller length scales (i.e., at higher frequencies, e.g., s$_\textrm{rms} = 8.7^{\circ }$ at $1.5~\textrm{GHz}$) than on larger length scales (i.e. lower frequencies, e.g. s$_\textrm{rms} = 5.3^{\circ }$ at $150~\textrm{MHz}$). In general, surface roughness (in the context of general simulations) can be characterized in three ways: large-scale roughness (left), medium-scale roughness (middle), and small-scale roughness (right), as shown in Fig. 4. Here, we considered only the large-scale (left) and the small-scale (right) roughness (i.e., the two extremes that accurately inculcate surface effects in the simulation).

2.6.1 Large scale roughness

The large-scale roughness is simulated by randomly tilting the shower axis with respect to the local surface normal such that the transmitted part of the emission cone is different from what it originally was without any roughness. (i.e., the angular deviation of the shower axis with respect to the horizontal local surface). This produces the same effect as randomly tilting the local surface normal from the perpendicular (i.e., perpendicular here refers to the z-axis), which leads to a change in the angle of incidence the rays make with the local surface normal as is shown in Fig. 4 (left). For large-scale roughness, the slope or tilt remains constant across the entire shower emission cone or region length. As pointed out in [44], the tangent of the slope ($\tan s$) is normally distributed, not the slope s itself. We, therefore, sampled the slope tangents $\tan s$ from a Gaussian distribution. From this, we obtain the slope, s, for simulating the large-scale roughness.

2.6.2 Small scale roughness

Small-scale roughness – features that are smaller than the wavelength of the radio signal – destroys the coherence of the Askaryan Cherenkov pulse due to scatter, making the signal difficult to detect because of the loss of signal power. This can potentially reduce the effective lunar aperture and increase the energy threshold for detection. Small-scale surface roughness is typically treated with a fractal model. For a stationary dielectric surface with roughness given by a Gaussian distribution, the reflected electric field, ${\mathcal {E}}_\textrm{reflected}$ is [45]:

$$\begin{aligned} {\mathcal {E}}_\textrm{reflected} = {\mathcal {E}} \times e^{-2\kappa ^2 \xi ^2 \cos ^2 i}, \end{aligned}$$

(19)

where $\xi$ is the height deviation from the smooth local lunar surface and $2\kappa \xi \cos i$ is a phase retardation or variation factor (also called the Rayleigh roughness parameter) of the reflected electric field. It is usually called the Kirchhoff Approximation or sometimes the physical optics approximation. $\kappa$ is a wave number ($\approx \lambda ^{-1}$), and i is the angle of incidence to the surface normal. An extension of the Rayleigh roughness parameter is needed to accommodate transmitted rays across a rough Lunar surface and is given as [27]:

$$\begin{aligned} {\mathcal {E}}_\textrm{transmitted} = {\mathcal {E}} \times e^{-2\kappa ^2 \xi ^2 (n_i\cos i - n_t\cos t)^2}, \end{aligned}$$

(20)

where t is the angle of transmission of the incident ray to the surface normal. $2\kappa \xi (n_i\cos i - n_t\cos t)$ is the Rayleigh roughness parameter for a transmitted electric field, ${\mathcal {E}}_\textrm{transmitted}$. This parameter considers the refractive index, $n_i$ in the regolith and $n_t$ in a vacuum, via the products $n_i \cos i$ and $n_t\cos t$. The rms height, $\xi _\textrm{rms}$ is defined here as the square root of the variance of all points on the lunar surface about the mean value and is given by [43]:

$$\begin{aligned} \xi _\textrm{rms} = \Big [ \frac{1}{n-1}\sum _{i=1}^{n} (z(x_i) -\bar{z})^2 \Big ]^{-\frac{1}{2}}. \end{aligned}$$

(21)

Here, $z(x_i)$ represents the height of the lunar surface at point $x_i$, $\bar{z}$ is the mean height, and n represents the total number of points. As shown in [43] (equation 6), the best-fit power law to data gives the relation:

$$\begin{aligned} \xi (L) = \xi _{0} L^H, \end{aligned}$$

(22)

where L is the profile length, H the Hurst exponent (a scaling parameter) and $\xi _{0}$ is rms height of the reference profile. For the Moon, the rms height is taken as:

$$\begin{aligned} \xi _\textrm{rms} = \xi _{0} L^H= \varDelta x \cdot \tan s_\textrm{rms} = 0.29(\lambda [\textrm{cm}]) ^{0.78} \end{aligned}$$

(23)

where $\tan s_\textrm{rms}$ ($\approx \frac{\varDelta z}{\varDelta x}$) is taken from Eq. 18. $\lambda$ is wavelength and is taken as the profile length. This equation is derived by using a simple trigonometric identity. Height deviations, $\xi$, are sampled from a Gaussian distribution with mean 0 and standard deviation $\xi _\textrm{rms}$ and used in Eq. 20.

3 Monte-Carlo simulation of the effective aperture for UHE neutrinos

Sketches illustrating the geometry of the simulation setup are shown in Fig. 5 for the ‘global’ geometry and Fig. 6 for the ‘local’ geometry. Simulated neutrinos arriving from the same direction ($\varTheta = 0^\circ , \varPhi = 0^\circ$) in the ‘global’ geometry while integrating over the locations of Earth in the ‘local’ geometry. Thus, we calculate which part of the lunar sky receives a detectable signal. This effectively means that we can simulate many neutrino arrival directions simultaneously. We adopted this setup because it gives a non-zero chance for an emitted ray from the regolith to hit a detector at Earth (e.g., LOFAR) despite the latter’s relatively small projected solid angle. The Monte Carlo code for this simulation is wholly written with Python. The various parts of the simulation setup are discussed sequentially in the subsections below.

Fig. 5

A sketch illustrating this simulation’s ‘global’ geometry. Point A is the neutrino entry point in the Moon, point B is the center of the spherical Moon, point C is the interaction point with impact parameter defined as $|\overrightarrow{BC}|$, point D is the penetration point and radio emission point of the neutrino inside the Moon with penetration depth defined as $|\overrightarrow{AD}|$ and point E is the point on the surface directly above the penetration point. Top: when D lies between A and C, the neutrino direction is tilted downwards with respect to the local surface point E. Bottom: when D lies past point C, the neutrino direction is pointed upwards with respect to the local surface. Because radio waves are attenuated inside the Moon, neutrinos are only observable if the distance, $|\overrightarrow{DE}|$, is small (of the order of tens of meters)

3.1 Event generator

In the first stage of the simulation, all the event parameters are determined. These parameters include the primary neutrino energy, inelasticity, the impact parameter on the Moon, the penetration depth inside the Moon, the calculated depth below the local lunar surface, and the shower propagation direction. Note that over extra-galactic distance scales, a complete neutrino flavor mixing is expected due to oscillations; hence, equal proportions of $\nu _e, \nu _{\mu },$ and $\nu _{\tau }$ are assumed throughout the simulation [46]. Also, the simulation treats neutrinos and anti-neutrinos equally as they produce similar hadronic showers and signals. The generated neutrino event parameters are discussed in detail as follows:

• Neutrino energy: The primary neutrino energy is specified for each simulation run.

• Inelasticity: An essential parameter in determining the electric field strength of the Askaryan emission in the regolith is the energy of the induced hadronic shower. The fraction of the primary neutrino energy that goes into the hadronic shower is the inelasticity y. The induced hadronic shower will have energy $E_\textrm{sh} = yE_{\nu }$ where the average inelasticity $y_\textrm{avg} \approx 0.2$. The inelasticity distribution is taken from [47,48,49] and is shown in Fig. 7 (top). Since the maximum spectral electric field strength of the Askaryan Cherenkov radiation depends on the energy of the hadronic shower, the inelasticity plays a crucial role in determining the minimum energy threshold for detecting neutrinos.

• Impact parameter, $|\overrightarrow{BC}|$: Here, radial points, C are sampled randomly along the lunar radius as illustrated in Fig. 5. The radial distance between points, B (lunar center) and C, is the impact parameter, $|\overrightarrow{BC}|$. A sampled distribution of the impact parameters is shown in Fig. 7 (bottom). As expected, the distribution is right-skewed towards increasing radial distance (since the circular area grows with radial distance).

• Penetration depth, $|\overrightarrow{AD}|$:D is the interaction point of the neutrino inside the regolith. It is the point where the shower develops, and the radio emission is emitted. Therefore, the penetration depth is the vector’s magnitude, $\overrightarrow{AD}$ shown in Fig. 5. Depending on the energy and arrival direction of a neutrino in the ‘global geometry,’ it has a certain weight or probability $w_{\nu } (E, \varTheta ^{\prime }, {\textbf {D}})$. In this simulation, instead of calculating this weight $w_{\nu } (E, \varTheta ^{\prime }, {\textbf {D}})$, we rather sample D from an exponential distribution:

  $$\begin{aligned} {\textbf {D}} \equiv D(z) = 1/L_{\nu }(E)\exp {-z/L_{\nu }(E)} \end{aligned}$$

  (24)

  which depends on an energy-dependent neutrino mean-free-path $L_{\nu }(E)$. $L_{\nu }^{-1}$ is the scale parameter and $z > 0$ along the Z-axis as shown in Fig. 5. Neutrinos with penetration depths greater than the lunar radius are designated upward-directed neutrinos with arrival directions in the ‘local’ geometry $\varTheta > 90^{\circ }$.

• Depth below ‘local’ lunar surface, $|\overrightarrow{DE}|$: This is the neutrino depth below the ‘local’ lunar surface (see Fig. 6) calculated using simple trigonometric identities. To do this, we move to a different reference frame (i.e., from ‘global’ to ‘local’ geometry). Secondly, the impact parameter, $|\overrightarrow{BC}|$, the penetration depth, $|\vec {AD}|$ and the magnitude of the vector, $\overrightarrow{BD}$ must be known. We discard events found to “interact” outside the Moon. The depth distribution is energy-dependent, with the lower energy neutrinos penetrating deeper into the regolith and having a wider distribution.

• Shower propagation direction, $\varTheta$: All neutrinos are assumed to be coming from the single direction, $(0^{\circ }, 0^{\circ })$ (in the ‘global’ geometry). To calculate the shower propagation direction, we move to a different reference frame (i.e., from the ‘global’ geometry in Fig. 5 to the ‘local’ geometry in Fig. 6). In the ‘local’ geometry, the shower propagates in the same direction as the neutrino’s travel direction. The distribution of the calculated $\varTheta$ in the ‘local’ geometry is energy dependent, with an angular spread of this distribution scaling inversely with the primary neutrino energy. Events with $\varTheta > 90^{\circ }$ are designated as upward-directed neutrinos and downward-directed if $\varTheta \le 90^{\circ }$. Figure 8 shows the distribution of calculated $\varTheta$ (this angle is illustrated in Fig. 6) as a function of primary neutrino energy before detection. From Fig. 8, it can be seen that as the neutrino energy increases, the contribution from the upward-directed neutrinos decreases due to the increasing cross-section with energy (i.e., corresponds to a shortening of the neutrino mean-free-path which scales inversely as the cubic root of the primary neutrino energy; see Eq. 1).

Fig. 6

A sketch illustrating the ‘local’ geometry of the neutrino shower with respect to the ‘local’ lunar surface. $\overrightarrow{DE}$ is the depth below the ‘local’ lunar surface when we move from the ‘global geometry.’ Points D and E are the same points shown in Fig. 5 for the ‘global geometry.’ $\varTheta$ is the angle between the vectors, $\overrightarrow{AD}$ and $\overrightarrow{DE}$ and denotes the direction of the incoming neutrino

Fig. 7

Top: probability distribution for the inelasticity y. The average inelasticity is $\sim 21\%$. Bottom: distribution of randomly sampled impact parameters, $|\overrightarrow{BC}|$ for simulated neutrino events

Fig. 8

A histogram of calculated $\varTheta$ as a function of the primary neutrino energy before detection. The threshold line separates the downward and upward-directed neutrinos

3.2 Signal generation, propagation and triggering

A $4\pi$ emission (or solid angle) is associated with a neutrino interacting with the regolith. The emission is concentrated at the Cherenkov cone at high frequencies (above $1\textrm{GHz}$) but much more isotropic at low frequencies. The Askaryan Cherenkov emission is represented as bundles of rays (after a million rays were used in the simulation, there was no change in the final result; hence, a safe choice of five million rays was used in the final work), with each ray having associated with it a direction, solid angle ($d\varOmega _i$), spectral electric field strength, and polarization. At the neutrino penetration point D, which is assumed to be where both the shower develops, and the emission emanates (see Fig. 6), rays are generated randomly into the upper hemisphere (i.e. $2\pi$ sr emission). The remaining $2\pi$ sr emission in the lower hemisphere is discarded as it does not escape the Moon. The associated spectral electric field strength (calculated from Eq. 6) and polarization are calculated for each of the simulated rays. We assume that the refractive index, $n_i$, is constant throughout the regolith. Thus, all inhomogeneities introduced by varying $n_i$ are ignored. This means the ray path remains rectilinear between the neutrino radio emission point and the vacuum-regolith interface. At the lunar-vacuum interface, the angles of incidence, i, and refraction, t, are calculated using Snell’s law. We then account for the total internal reflection of the rays with i greater than the critical angle (refer to Sect. 2.4 for detailed discussion). Due to the divergence of the rays after refraction, we modify each ray’s standard Fresnel transmission coefficient before applying it to the emerging ray. Knowing how far the ray has traversed between the emission point, D and the lunar-vacuum interface, we account for the radio attenuation losses as explained in Sect. 2.3. At this point, we also take into account the lunar surface topography. For the surface roughness, we consider the large and small-scale roughness. For small-scale roughness, for each interacting neutrino, a height deviation, $\xi$, is taken from the Gaussian distribution and used in Eq. 20 for all transmitted rays. For the large-scale roughness, a different local surface slope s is taken from a distribution and applied as a deviation of the surface normal for each interacting neutrino. After accounting for all these factors, we trigger on the transmitted rays for which the spectral electric field strength is greater than a threshold spectral electric field (i.e. ${\mathcal {E}} > \varUpsilon _\textrm{min}$).

3.3 Solid angle of rays and their magnification factor after refraction

The associated solid angle, $\textrm{d}\varOmega _\textrm{regolith}$ for each simulated ray inside the regolith is given by:

$$\begin{aligned} \textrm{d}\varOmega _{\textrm{regolith}}=\frac{4\pi }{\mathrm {number\ of\ simulated\ rays}}. \end{aligned}$$

(25)

Note that Eq. 25 considers simulated rays distributed over all possible directions. However, after refraction, the solid angle for each ray changes as a function of the angle of incidence, i, to the surface normal. Thus, the solid angle for each ray stretches or is magnified upon refraction due to the divergence of the ray after moving into a less dense medium (vacuum). The modification or stretching factor, $\xi (i, t)$ given as [23]:

$$\begin{aligned} \xi (i, t)&= \frac{d\varOmega ^{\prime }}{d\varOmega _\textrm{regolith}} \end{aligned}$$

(26)

$$\begin{aligned}&= \big (n_i\big )^2\frac{\cos (i)}{\cos (t)} \end{aligned}$$

(27)

$$\begin{aligned}&= \big (n_i\big )^2\frac{\cos (i)}{\sqrt{1 - n_i^2 \sin ^2 (i)}}, \end{aligned}$$

(28)

where i is the angle of incidence inside the regolith, t is the angle of refraction outside the regolith and $d\varOmega ^{\prime }$ is the modified solid angle outside. In Fig. 9, the variation of the emerging modified solid angle, $d\varOmega ^{\prime }$ with i for emanating rays from the regolith is shown. $d\varOmega ^{\prime }$ grows with increasing i up to the critical angle. Therefore, the magnification of the solid angle increases the acceptance of Earth-based detection.

To test the accuracy of the magnification factor, $\xi (i, t)$ for the emerging solid angle of the rays, the detection threshold was set to 0, and all the emerging solid angles summed up to $2\pi$ as expected. Close to the critical angle, the magnification factor, $\xi (i, t)$ is very large, but the power in the signal reduces significantly due to the smaller transmission coefficient (to conserve energy) at these angles as shown in Fig. 2. Hence, the total emerging solid angle (that goes into computing the effective aperture) is not dominated by the magnified solid angles close to the critical angle, particularly at lower energies.

Fig. 9

A plot of the modified solid angle, $d\varOmega ^{\prime }$ and magnification factor as function of incidence angle, i. The solid angle of each ray inside the regolith, $d\varOmega _{i} = 2.5\times 10^{-6}$ and TIR condition given by Eq. 10 is imposed, hence the angle incidence, i lower than the critical angle of $35^{\circ }$

3.4 Computation of effective lunar aperture

From the fraction of triggered rays, an effective aperture (i.e. product of the effective area ($\pi R^2$) and solid angle ($4\pi$) with units of $\textrm{km}^2 \textrm{sr}$) of the Moon for neutrino detection can be calculated. Accurate knowledge of an effective aperture – fraction of the maximum lunar aperture, $A_\textrm{ max }( E )$ that constitutes our detectable aperture – is necessary for establishing an upper limit on the flux of UHE neutrinos in the instance of null detection or to calculate the flux if neutrinos are detected. If we assume the Moon is a perfect sphere, then the maximum possible aperture for which neutrinos can be detected is given by:

$$\begin{aligned} A_\textrm{ max }( E ) = 4\pi ^2 R^2, \end{aligned}$$

(29)

where R is the lunar radius. This is just a product of the geometric cross-section, $\pi R^2$, and the entire $4\pi$ steradians of illumination. In determining the probability, $P_{1}( E, \varTheta , |\overrightarrow{DE}| )$ of detecting a neutrino of energy, E interacting in the Moon at a penetration point D, we sum the emergent modified solid angles, $d\varOmega ^{\prime }_{k}$ of all the triggered rays, k and normalized by $4\pi$ as given by:

$$\begin{aligned} \begin{aligned} P_{1}( E, \varTheta , |\overrightarrow{DE}| )&= \frac{1}{4\pi }\sum _{{\text {triggered rays}}} d\varOmega _\textrm{regolith} \xi _{k}(i, t), \\&= \frac{1}{4\pi }\sum _{{\text {triggered rays}}} d\varOmega ^{\prime }_{k}(i, t) \end{aligned} \end{aligned}$$

(30)

By summing all $d\varOmega ^{\prime }_{k}$, we are, in effect, fixing the location of a shower in the Moon while randomizing the orientation of the observer and asking what is the probability that a randomly located observer at some Earth–Moon distance over the solid angle of the lunar sky could detect the radio signal, without specifying the viewing angle. The detection probability $P_N(E)$ per energy, E is now found by averaging over N neutrino events generated by the Monte Carlo code and is given by:

$$\begin{aligned} P_{ N }( E ) = \frac{1}{N}\sum _{j=1}^{N} P_{ 1 }( E, \varTheta _{ j }, |\overrightarrow{DE}|_{ j } ). \end{aligned}$$

(31)

The effective aperture, $A_\textrm{e }$ for N events is therefore given as:

$$\begin{aligned} \begin{aligned} A_{ e }^{N}( E )&= A_\textrm{ max }( E ) \times P_{ N }( E ) \\&= 4 \pi ^2 R^2 \times P_{ N }( E ), \end{aligned} \end{aligned}$$

(32)

In our simulation, lowering the detection threshold to zero results in $P_N(E)$ being exactly 0.5, as we exclude downward-facing rays with respect to the ‘local’ lunar surface. Consequently, Eq. 32 becomes exactly half of $A_\textrm{max}$ as shown in Eq. 29.

4 Results of simulation

4.1 Reproduction of analytical calculations

To check for consistency with previous efforts, we first try to reproduce the results of the analytical parameterization of Gayley et al. [28] as implemented by [29] (App. B). To do this, we assume a smooth lunar surface and fix several stochastic parameters to the values used in the analytical equations. These fixed parameters are: transmission coefficient $t_{\parallel } = 0.6$ (over reasonable conditions Gayley et al. [28] chose to model $t_{\parallel }$ as a constant), inelasticity $y=20\%$ and refractive index $n_i =1.73$. The analytical parameterization is given by [28]:

$$\begin{aligned} A(E) \cong A_\textrm{max}\frac{(n_i^2 -1)}{8n_i}\frac{L_r}{L_\nu }f_0^3 \varDelta _c(\varPsi _{ds} + \varPsi _{dr} + \varPsi _u), \end{aligned}$$

(33)

where $\varPsi _{ds}, \varPsi _{dr}$ and $\varPsi _u$ respectively account for downward-directed neutrino detection without roughness, downward-directed neutrino detection with roughness, and upward-directed neutrino detection without roughness. These three parameters are taken from Eqs. 55–57 in [28]. Equation 33 is called ‘analytic rough’ (AR) in this paper. A second equation is defined as:

$$\begin{aligned} A(E) \cong A_\textrm{max}\frac{(n_i^2 -1)}{8n_i}\frac{L_r}{L_\nu }f_0^3 \varDelta _c(\varPsi _{ds} + \varPsi _u), \end{aligned}$$

(34)

is what is referred to as ‘analytic smooth’ (AS) in this paper (i.e. Eq. 33 without $\varPsi _\textrm{dr}$ term). A dimensionless parameter, $f_0 = \sqrt{\log \left[ \frac{{\mathcal {E}}_c t_{\parallel }}{\varUpsilon _\textrm{min}}\right] }$ is used as trigger parameter [28]. The effective lunar aperture as a function of primary neutrino energy calculated using Eqs. 33 and 34 is shown in Fig. 10.

Fig. 10

Neutrino effective lunar apertures as a function of primary neutrino energies made using the analytic model stated in Eq. 33 (legend: total AR) and Eq. 34 (legend: total AS) for frequencies: Top: $0.15~\textrm{GHz}$, bottom: $1.50~\textrm{GHz}$. Also plotted are the three individual contributions to the total effective aperture. This plot is made using a threshold radio pulse strength of $0.024~\upmu \textrm{V}/\textrm{m}/\textrm{MHz}$

We used the same fixed values for these parameters in our simulation to validate our code before including a more realistic treatment of the transmission coefficient and inelasticity. At this point, surface roughness effects are ignored in the analytical parameterization and the simulation. In Fig. 11, the simulated and analytic effective lunar aperture for UHE neutrinos, assuming a smooth lunar surface, is shown.

Fig. 11

Plot of effective lunar aperture (for both simulation and analytic smooth) versus primary neutrino energy for a smooth lunar surface, a constant transmission coefficient, 0.6 and inelasticity, $20\%$. Top: $150~\textrm{MHz}$ bottom: $1.50~\textrm{GHz}$

Both simulation and analytic expression predict a larger effective lunar aperture at $150~\textrm{MHz}$ than $1.50~\textrm{GHz}$ since the Cherenkov cone width scales inversely with frequency. In general, there is a good agreement between the simulation and the analytic parameterization [28]. The neutrino energy threshold, which coincided with the point of most significant difference between the two results occurs at $E=6.74\times 10^{21}~\textrm{eV}$ and $1.06\times 10^{21}~\textrm{eV}$ where their ratios, $r_{\text {analytic}}^{\text {sim}}$ are 2.0 and 1.4 at $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$ respectively.

As explained in Sect. 3.1, neutrinos are classified as either downward-directed or upward-directed depending on the shower propagation direction $\varTheta$ (in the ‘local’ geometry). We simulated the relative contributions of these two classes of neutrinos to the overall aperture for frequencies of $150~\textrm{MHz}$ and $1.5~\textrm{GHz}$. Results are compared with the analytic expression and shown in Fig. 12. The following observations are made for both the simulation and the analytical expression:

• At $150~\textrm{MHz}$, the downward-directed neutrinos dominate over the upward-directed neutrinos across all energies.

• At $1.50~\textrm{GHz}$, the upward-directed neutrinos become increasingly important at lower energies.

Fig. 12

Plot of the effective lunar aperture as a function of primary neutrino energy for upward-directed ($\varPsi _{u}$ for analytic) and downward-directed ($\varPsi _{ds}$ for analytic) neutrinos, assuming a smooth lunar surface, a constant transmission coefficient, 0.6 and inelasticity, $20\%$. Top: $150~\textrm{MHz}$. Bottom: $1.50~\textrm{GHz}$

There is an excellent agreement between the downward-directed contribution from the simulation and analytic expression as shown in Fig. 8. As shown in the same figure, the contribution of upward-directed showers decreases with increasing energy. This implies that increasing primary neutrino energy should reduce the fraction of upward-directed neutrinos contributing to the total effective aperture. In the analytical solution (see Fig. 12), upward-directed showers’ relative contribution decreases with energy, but their absolute contribution rises monotonously. In the Monte Carlo results, however, we find a decrease even in the absolute contribution (see the turnover of the curve at an energy of $E \sim 10^{23}~\textrm{eV}$). The reason for this difference lies in the ‘near surface approximation’ made for the analytical result, which assumes that neutrinos creating horizontal showers (i.e. parallel to the smooth surface) do not suffer attenuation. This approximation becomes unreliable at low frequencies, for which the radio attenuation length is larger, so larger depths are probed. The error the approximation introduces will grow with energy, mainly because the neutrino cross-section grows and because observable radio waves could emerge from even larger depths. Gayley et al. [28] were aware of this and stated that their results are reliable as long as $L_r/R \ll (L_{\nu }/R)^2$ (see Eq. (24) in [28] and shown in Fig. 13. This is the threshold above which the analytic and Monte Carlo results in Fig. 12 start to diverge.

Fig. 13

A plot showing the condition for the near-surface approximation, $L_r/R \ll (L_{\nu }/R)^2$ as a function of primary neutrino energy

4.1.1 Large scale roughness with constant transmission coefficient and inelasticity

Again, we validate our simulation against the analytic model by including large-scale surface roughness. To do this, we account for large-scale surface roughness in our simulation and keep the transmission coefficient, 0.6, and the inelasticity $20\%$ constant. We simulate two scenarios here:

• 1. take the same constant slope s$_\textrm{rms}$ that was used in Gayley et al. [28] to compare results.

• 2. uses a distribution of slopes s sampled from a normal distribution.

Figure 14 shows a plot of the effective lunar aperture as a function of the primary neutrino energy for the two scenarios where we keep the transmission coefficient and inelasticity constant. We can see that the large-scale roughness in both the simulation and the analytic parameterization [28] enhances detection and, consequently, the effective lunar aperture for UHE neutrinos hitting the Moon. The large-scale surface roughness did not change the neutrino energy threshold in both the simulation and the analytic parameterization. By sampling slopes from a normal distribution in the simulation, we see a good agreement between the simulation and the analytic expression. The neutrino energy threshold occurs at $E=6.74\times 10^{21}~\textrm{eV}$ and $1.06\times 10^{21}~\textrm{eV}$ for the frequencies $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$ respectively. At these threshold energies, the ratio $r_{\text {analytic}}^{\text {sim}}$ are 1.47 and 1.5 at $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$ respectively.

By incorporating an rms slope, denoted as $s_\textrm{rms}$, in the simulation, we can compare the results with the analytic expression at the neutrino threshold energy. This threshold energy is observed at $E = 6.74\times 10^{21}\textrm{eV}$ and $1.06\times 10^{21}\textrm{eV}$ at $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$ respectively. At frequencies of $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$, the ratios $r_{\text {analytic}}^{\text {sim}}$ are found to be 2.30 and 2.33 respectively for the threshold energies.

In summary, there is a good agreement between the simulation and the analytic expression with large-scale surface roughness when surface slopes in the simulation are sampled from a realistic normal distribution. Note that when using a single rms slope, $s_\textrm{rms}$ in the simulation, the rotation of the shower axis about a rotation axis is varied randomly between clockwise and anti-clockwise directions.

Fig. 14

Plot of the effective lunar aperture as a function of primary neutrino energy with a constant inelasticity, $20\%$ and transmission coefficient, 0.6 and taking into account large scale surface roughness sampled from a distribution (rough distribution)) or a single rms slope, s$_\textrm{rms}$ (rough s$_\textrm{rms}=7.5^{\circ }$ at $150~\textrm{MHz}$, $12.3^{\circ }$ at $1.5~\textrm{GHz}$). Top: $150~\textrm{MHz}$. Bottom: $1.50~\textrm{GHz}$. Smooth in the legend implies surface roughness was not taken into account

Figure 15 shows a histogram of surface slopes, s of the triggered neutrinos. The rms of these slopes are $5.47^{\circ }$ and $11.23^{\circ }$ at $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$ respectively, which are smaller than the single rms slope $s_\textrm{rms}$. This, therefore, explains why the aperture calculation using a distribution of slopes is relatively smaller.

Fig. 15

A histogram of surface slopes of triggered neutrinos of energy, $10^{22}~\textrm{eV}$ for frequencies: $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$

4.2 Effect of transmission coefficient and inelasticity

Transmission coefficient and inelasticity are crucial in determining the minimum detectable neutrino energy. Choosing to model the transmission coefficient as a constant, as was done in the analytic parameterization via the relation: $f_0 = \sqrt{\log \left[ \frac{{\mathcal {E}}_c t_{\parallel }}{\varUpsilon _\textrm{min}}\right] }$, leads to a loss in accuracy of the aperture calculation since it influences the detectable spectral electric field and consequently the minimum detectable neutrino energy. This necessitates a proper treatment of the transmission coefficient. A realistic treatment for the inelasticity is implemented by sampling the inelasticity from a distribution as shown in Fig. 7 (right). Four scenarios are considered for this study:

• A constant inelasticity $y = 20\%$ and a constant transmission coefficient, $t =0.6$.

• A realistic inelasticity sampled from a distribution and realistic transmission coefficient correctly calculated.

• A constant inelasticity, $y=20\%$ and realistic transmission coefficient correctly calculated.

• A realistic inelasticity sampled from a distribution and constant transmission coefficient, $t=0.6$.

In all four scenarios, we assume a smooth lunar surface. Shown in Fig. 16 is a plot of effective lunar aperture versus primary neutrino energy considering the effect of transmission coefficient and inelasticity. From this Fig. 16, it is clear that the energy threshold varies for the different scenarios. This explains why it is necessary to model these parameters correctly properly. At $1.5~\textrm{GHz}$, the results from using a constant transmission coefficient and inelasticity are in good agreement with the case of a realistic transmission coefficient and inelasticity at higher energies. Thus, the values taken for the constant inelasticity and the transmission coefficient have been chosen so that the results agree with the complete calculation at the highest energies in the analytic expression.

Fig. 16

Plot of effective lunar aperture versus primary neutrino energy over a smooth lunar surface for different treatments of transmission coefficient t and inelasticity y. Top: $150~\textrm{MHz}$. Bottom: $1.50~\textrm{GHz}$

4.2.1 Large scale roughness with realistic transmission coefficient and inelasticity

Figure 17 is similar to Fig. 14 except that the transmission coefficient has appropriately been calculated and the inelasticity sampled from a realistic distribution in the simulation. Aside from an enhancement in the effective aperture due to the large-scale surface roughness, the energy threshold has changed. The cumulative effect of these three factors, surface roughness, transmission coefficient, and inelasticity, when appropriately modeled in the simulation, improves the detection probability of lower energy neutrinos.

Fig. 17

Plot of effective lunar aperture versus primary neutrino energy with realistic inelasticity, transmission coefficient, and large-scale surface roughness. Top: $150~\textrm{MHz}$. Bottom: $1.50~\textrm{GHz}$. The analytic parameterization includes only the large-scale roughness

When the transmission coefficients and inelasticities are modeled adequately for a smooth lunar surface, we observed that the energy threshold in the simulation is lower than in the analytic parameterization (see Fig. 17). The energy threshold is further lowered with the inclusion of large surface roughness. Thus, surface roughness increases the effective aperture and significantly determines (i.e. lowers) the energy threshold when the transmission coefficient and inelasticity are correctly modeled.

4.2.2 Small scale roughness with realistic transmission coefficient and inelasticity

The effect of both small and large-scale roughness has been included in the simulation and plotted out in Fig. 18. Also, the transmission coefficients and inelasticities have been appropriately modeled in the simulation. As seen in this figure, the small-scale surface roughness reduces the effective aperture due to the loss in the coherency of the signal. Like large-scale roughness, the effect of the small-scale roughness is more pronounced at $1.50~\textrm{GHz}$, consequently leading to a change in the energy threshold. In our report, we have highlighted the statistical errors associated with the simulation conducted for both large and small-scale roughness in Fig. 18. These errors have been calculated by taking the inverse square root of the number of events that were detected or contributed to the effective aperture. It is important to note that the lowest energy at $1.50~\textrm{GHz}$ in Fig. 18 is most affected by the low statistics.

Fig. 18

Plot of effective lunar aperture versus primary neutrino energy considering both the small and large scale surface roughness, calculated transmission coefficient, and inelasticity sampled from a realistic distribution. Top: $150~\textrm{MHz}$. Bottom: $1.50~\textrm{GHz}$. The analytic parameterization includes only the large-scale roughness

4.3 Merits of low- and high-frequency observations

There are advantages to both low and high frequencies, trading off between effective aperture and energy threshold, and other pros and cons on the experimental side as depicted in Fig. 19 for different radio detection thresholds.

Fig. 19

Plot of effective lunar aperture versus primary neutrino energy considering both the small and large scale surface roughness, calculated transmission coefficient, and inelasticity sampled from a realistic distribution. Results for two frequencies: $150~\textrm{MHz}$ and $1.50~\textrm{GHz}$ and two different radio sensitivity thresholds: $0.024~\upmu \textrm{V}/\textrm{m}/\textrm{MHz}$ and $0.24~\upmu \textrm{V}/\textrm{m}/\textrm{MHz}$

The Cherenkov cone width $\varDelta _c$ (Eq. 4) scales inversely with frequency, implying that at lower frequencies, there is a wider angular spread around the Cherenkov angle. Given that the refractive index of the regolith is quite large, 1.73, the Cherenkov angle – which occurs at $55^{\circ }$ – is consequently large too. Interestingly, the Cherenkov angle is the complement of the critical angle, $\sin ^{-1} \Big ( \frac{1}{n_{i}} \Big ) \approx 35^{\circ }$. Radiation is only transmitted from the regolith if it is incident at an angle less than or equal to the critical angle. This means that showers developing parallel to the flat lunar surface will produce little to no emission that escapes into free space with a signal strength above a detection threshold such that they can be observed on Earth. This is particularly true at high frequencies where the Cherenkov cone is narrow. This requirement imposes stringent restrictions on only specific shower geometries for detecting an emitted signal. Most radiation close to the Cherenkov angle suffers total internal reflection, particularly for the downward-directed neutrinos. This situation is even worse at higher frequencies where the width of the Cherenkov cone is narrower. The significant advantage of a lower frequency observation is the larger Cherenkov cone width and, hence, the broader emission spread around the Cherenkov angle – where the signals remain coherent – allowing for detectable radiation (above a trigger threshold) outside the Moon. It is worth noting that reducing the frequency also results in a decrease in the peak spectral electric field strength, as demonstrated in Eq. 5. It’s important to remember that the peak spectral electric field strength is directly proportional to the hadronic shower energy. Therefore, this implies that the larger angular spread around the Cherenkov angle is much more crucial at sufficiently high shower energies. The larger Cherenkov cone width, together with the low attenuation loss at lower frequencies, implies the following:

• A larger fraction of the lunar surface falls within our detection area, which in this work translates into having a wider range of impact parameters, $|\overrightarrow{BC}|$ as shown in Fig. 20 (top). This is a histogram of the distribution of impact parameters for neutrinos with signals above the detection threshold. It should be noted that $|\overrightarrow{BC}| = 1$ corresponds to the rim of the Moon, and $|\overrightarrow{BC}| =0$ is the lunar center. At $1.5~\textrm{GHz}$, only the narrow rim of the Moon contributes to the detectable aperture.

• As demonstrated in Fig. 20 (middle), a broader Cherenkov cone width indicates a larger angular acceptance. This means we can detect neutrinos arriving from a wider range of angles, especially at lower frequencies, allowing us to identify more shower geometries with varying $\varTheta$. At $1.5~\textrm{GHz}$, we are most sensitive to skimming neutrinos (i.e. arriving with $\varTheta$ nearly greater or less than $90^{\circ }$ ). It’s important to note that we are referring to the calculated shower propagation direction, $\varTheta$, in the ‘local’ geometry.

• Based on the data presented in Fig. 20 (bottom), we have increased sensitivity to neutrinos that interact at greater depths in the regolith due to lower radio attenuation loss. The figure illustrates that our capability to detect neutrinos is limited to depths of approximately $20~\textrm{m}$ at $1.5~\textrm{GHz}$ and around $100~\textrm{m}$ at $150~\textrm{MHz}$ for a neutrino with an energy level of roughly $10^{22}~\textrm{eV}$.

Fig. 20

A histogram of Top: impact parameters, $|\overrightarrow{BC}|$ where 1 corresponds to the rim of the Moon and 0 to the Moon center. Middle: shower propagation direction $\varTheta$ and Bottom: depth below the local lunar surface, $|\overrightarrow{DE}|$ for detected neutrinos of energy, $10^{22}~\textrm{eV}$. Realistic inelasticity and the transmission coefficient used and both small and large-scale surface roughness are factored in

When observing neutrinos, there is a trade-off between low- and high-frequency observations. The benefit of low-frequency observations is that they can detect high-energy neutrinos through a larger aperture. On the other hand, high-frequency observations can detect lower-energy neutrinos. The specific outcome of this trade-off for an experiment is dependent on the instrument’s characteristics, such as its observing frequency and radio detection threshold, as demonstrated in Fig. 19.

5 Summary and conclusion

We used a Monte Carlo simulation to determine the effective aperture for ultra-high energy (UHE) neutrinos hitting the Moon. This is crucial for low-frequency observations ($\sim 150~\textrm{MHz}$) like those conducted by LOFAR, where the small angle approximations in the analytic expression [28] fail. We explored the various assumptions that went into the analytic expressions [28] and studied their impact on the effective aperture. Assuming a smooth lunar surface, a constant transmission coefficient of 0.6, and an inelasticity of $20\%$, our simulation results agreed with the analytic parameterization indicated in Fig. 11. However, the largest difference between the two apertures occurred at an energy of $E=6.7\times 10^{21}~\textrm{eV}$ at $150~\textrm{MHz}$, with a ratio of $r_{\text {analytic}}^{\text {sim}} = 2.0$. At $1.50~\textrm{GHz}$, the energy corresponding to the largest difference was $1.1\times 10^{21}~\textrm{eV}$, with $r_{\text {analytic}}^{\text {sim}} = 1.4$. These two energies corresponded with the neutrino threshold energy for the two frequencies we considered. Additionally, we simulated the effective aperture for downward and upward-directed neutrinos to understand the slight difference between the simulation and the analytic expression [28]. We observed good agreement with the analytic expression for downward-directed neutrinos, while upward-directed neutrinos from the simulation diverged from the analytic expression with increasing energy, as shown in Fig. 12. We attribute this to the near-surface approximations in the analytic expression (see Fig. 13). It has been demonstrated that assuming a constant transmission coefficient and inelasticity can result in inaccuracies in aperture calculations since they impact the minimum energy needed for detectable neutrinos, as shown in Fig. 16. By modeling the transmission coefficient and inelasticity more accurately in the simulation for a smooth lunar surface, we lowered the energy threshold for the same trigger and reduced inaccuracies in the aperture calculations, as depicted in Fig. 17.

In this study, we have modeled the lunar surface topography at both small and large scales, as discussed in Fig. 4, and examined its impact on the effective aperture. Our simulated results have been validated against the analytic expression from [28], using a constant transmission coefficient of 0.6 and an inelasticity value of $20\%$ for large-scale roughness. We have observed a good correlation between the simulated and analytic results in Fig. 14. Our findings demonstrate that both low and high frequencies are affected by large-scale roughness, which increases the effective aperture, as shown in Figs. 14, 17, and 18. When the large-scale roughness is sampled from a realistic Gaussian distribution, the maximum ratio of simulated to analytic apertures $r_{\text {analytic}}^{\text {sim}}$ is approximately 1.47 at $150~\textrm{MHz}$ and 1.50 at $1.5~\textrm{GHz}$. In contrast, using a single rms slope as in the analytic expression yields a ratio $r_{\text {analytic}}^{\text {sim}}$ $\sim 2.30$ at $150~\textrm{MHz}$ and 2.44 at $1.5~\textrm{GHz}$. Taking into account the large-scale roughness, adequately modeled transmission coefficient, and inelasticity, we have seen that the effective aperture is heightened, and the energy threshold is lowered, as compared to the analytic expression’s prediction, as shown in Fig. 17. Furthermore, we have incorporated small-scale roughness in our simulation and found that it reduces the effective aperture enhancement caused by large-scale roughness, as seen in Fig. 18. Despite this, the overall effect of both large and small-scale roughness still enhances the effective aperture and decreases the energy threshold.

We have demonstrated that one of the merits of a lower frequency observation is to increase the detection probability by having a larger effective aperture, as shown in Fig. 11 with a trade-off on lowering the detectable energy threshold. It has also been shown that because the Cherenkov cone width scales inversely with frequency, observing at a lower frequency translates to having a more significant fraction of the lunar surface forming part of the detection area instead of the narrow lunar rim at higher frequencies (see Fig. 20 (top)). For a lower frequency observation, we have shown that the angular range over which we are sensitive to UHE neutrinos is wider (i.e., a more extensive range of geometries for UHE neutrino showers) in comparison to when observing at a higher frequency as is shown in Fig. 20 (middle). We have also demonstrated that since radio attenuation loss is inversely proportional to frequency, we are sensitive to deeper penetrating neutrinos at a lower frequency (see Fig. 20 (bottom)).

To optimize the designs of our experiments for detecting neutrinos with specific energies through the radio lunar Askaryan technique, we must understand the primary factors that impact the threshold for energy detection. Our research has revealed that two main factors affect this threshold: inelasticity and transmission coefficient (as depicted in Fig. 16). By accurately modeling these factors in simulations, we have observed a significant increase in the energy threshold for lower energies (Fig. 18). While lunar surface topography does have some impact, it is not nearly as significant as the aforementioned factors (Fig. 14). Additionally, we have found that accurately modeling inelasticity and transmission coefficient, rather than treating them as constants, is especially crucial for low-frequency observations like LOFAR (Fig. 16).