Flavored axions and the flavor problem

Abstract

A Peccei-Quinn (PQ) symmetry is proposed, in order to generate in the Standard Model (SM) quark sector a realistic mass matrix ansatz with five texture-zeros. Limiting our analysis to Hermitian mass matrices we show that this requires a minimum of 4 Higgs doublets. This model allows assigning values close to 1 for several Yukawa couplings, giving insight into the origin of the mass scales in the SM. Since the PQ charges are non-universal the model features Flavor-Changing Neutral Currents (FCNC) at the tree level. From the analytical expressions for the FCNC we report the allowed region in the parameter space obtained from the measurements of branching ratios of semileptonic meson decays.

1 Introduction

The discovery of the Higgs boson by the ATLAS [1] and CMS [2] collaborations with a mass of 125 GeV is very important because it opens up the possibility of new physics in the scalar sector. So that, from a theoretical viewpoint, an extended Higgs sector is well motivated [3], the best-known extensions are: the two Higgs doublet model [4,5,6,7,8,9,10,11,12,13,14,15,16] and models with additional singlet scalar fields [17]. On the other hand, the discovery of the Higgs boson gives experimental support to the spontaneous symmetry breaking which is the mechanism that explains the origin of the masses for both, fermions and weak gauge bosons.

The Standard Model (SM) symmetry breaking mechanism [18,19,20] with Higgs-fermion couplings proportional to the fermion masses is consistent with the experimental data; however, there are various orders of magnitude between the fermion masses which cannot be explained in the context of the SM. These masses, the three mixing angles, and the complex CP-violating phase must be adjusted with experimental data.

The Two Higgs Doublet Model (THDM) was proposed in order to give masses to up-type and down-type quarks [21] where vacuum expectation values (VEV) $v_1$ and $v_2$ are related to the electroweak VEV by the relation $v^2 = v_1^2 + v_2^2$. This THDM allows new physics through an additional charged scalar field which should be looked for in colliders as a test of multi-Higgs models. On the other hand, the singlet scalar fields are useful to break the U(1) gauge symmetries in extended electroweak models or as candidates for dark matter [16, 22,23,24,25].

Due to having three quarks up and three quarks down, the mass matrices are $3\times 3$, and under a usual assumption, these can be taken as Hermitian matrices having a total of 18 free parameters against the ten physical parameters [26]. This feature reduces the number of matrix parameters, easing the textures’ analysis when comparing them with the experimental data. One method to generate zeros and reduce the quark mass matrix parameters consists of performing a Weak Basis Transformation (WBT) on the quark fields [27,28,29]. By choosing these zeros by the WBT, the mass spectrum can be obtained according to the experimental results [28]. In particular, Fristzsch proposed a quark mass matrix ansatz with six zeros [30,31,32,33] which were put in by hand [34], but this texture predicted for the ratio $|V_{ub}/V_{cb}|\approx 0.06$ a too small magnitude [35] which is in strong tension with the present-day experimental result $(|V_{ub} /V_{cb}|_{\text {exp}} \approx 0.09)$ [35]. For this reason, some authors considered four zero-textures [29, 36,37,38]. In reference [39], the matrices with five texture-zeros could also explain the mass hierarchy and the parameters of the CKM matrix.

It is common to choose textures-zeros by hand without an underlying theory relying on first principles. Another direction that has been explored in the literature is to propose discrete symmetries and a sector with multiple scalar doublets to generate the textures of the quark mass matrices [40,41,42,43,44,45,46,47,48,49]. It is also possible to consider global symmetry groups that prohibit certain Yukawa couplings and somehow generate the zeros of the mentioned textures [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]. Another way to obtain these textures is through a flavor-dependent gauge symmetry, which can break the family universality of the Standard Model [43, 68,69,70,71,72,73,74,75,76,77,78,79,80,81]. This gauge symmetry produces textures that are linked to additional flavor-changing neutral currents that, in principle, could be measured at future colliders. There are many proposed models with flavor gauge symmetries beyond the SM such as SO(12), SU(8), 331, U(1) [82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102], among others, that attempt to explain the flavor problem and the SM mass hierarchy. Alternative mechanisms for generating textures are via additional discrete global groups, i.e., $A_4$, $\varDelta _{27}$, $Z_2$, $S_3$, etc. [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. An interesting way to explain the SM mass hierarchy is to introduce exotic quarks with ordinary charges that mix with the ordinary ones in the SM, producing small masses through the seesaw mechanism [103].

An important open problem in particle physics is the strong CP violation associated with the abelian symmetry $U(1)_A$ [104,105,106,107], which is restricted by constraints on the electric dipole moment [108,109,110] of the neutron that set limits on the $\theta$ parameter of the order of $10^{-10}$ [111, 112]. By introducing a global chiral symmetry or Peccei Quinn symmetry, this fine-tuning can be explained. But breaking this global symmetry implies the existence of a Goldstone boson, This field is known as axion and there are several models in which the axion is invisible [113,114,115,116,117,118,119]. From cosmological considerations the axion decay constant $f_a$ must be of the order of $10^{7} - 10^{17}$ GeV. On the other hand, the axion acquires a non-zero mass due to mixing with the $\pi ^0$ and $\eta$ mesons, and takes a mass given by [111, 120]

$$\begin{aligned} m_a =\frac{\sqrt{m_um_d}}{m_u+m_d}\frac{m_\pi f_\pi }{f_a}, \end{aligned}$$

(1)

where $m_\pi$ , $f_\pi$ denote the mass and decay constant of the pion, and $m_u$ and $m_d$ the masses of the up and down quarks, respectively; by this mixing, the axion decays into two photons. Axion could also be a dark matter candidate for values of the decay constant $f_a$ greater than $10^{10}$ GeV, where the different axion field production mechanisms are [121,122,123]: misalignment, global string and domain wall decays, etc, generating relic densities of the order of 0.12. Experiments designed to study $K^{\pm }\rightarrow \pi ^{\pm } \nu {\bar{\nu }}$ decays are being reinterpreted to study flavor-changing decays through axions of the form $K^{\pm }\rightarrow \pi ^{\pm } a$. Similarly, flavor-changing decays in the bottom sector are studied. On the other hand, the effective coupling of the axion to photons is excluded by low energy experiments and must be less than $10^{-11}$.

The purpose of our work is to use the PQ symmetry to generate realistic mass textures that allow us to explain the quark masses and the CKM mixing matrix of the standard model and simultaneously the strong CP problem. The idea of linking the PQ symmetry with the flavor problem was proposed in [124], and in later literature [119, 125, 126]. Recently, there has been renewed interest in this direction [127,128,129,130,131,132,133,134,135,136,137,138,139,140,141]. We impose a PQ symmetry on the SM, which can generate mass textures that reproduce the masses of the Standard Model quarks for Yukawa couplings close to unity. To obtain this result, a sector of multihiggs is needed in such a way that the hierarchy problem is reduced to defining the VEVs of the neutral components of the scalar doublets.

This work is organized as follows: in Sect. 2 we will summarize some results of the literature on five-zero textures, in Sect. 3 we carry out an analysis of the PQ charges necessary to generate the textures of the quark mass matrices, in this section, we also propose a natural way to normalize the PQ charges. In Sect. 5 we will obtain the values of the vacuum expectation values VEV of the Higgs doublets to reproduce the masses of the quarks, in this section, we also determine the values of the Yukawa couplings and the minimum number of Higgs doublets necessary to generate the texture of the quark masses as shown in the Appendix A. In Sect. 4 we show the most general Lagrangian for the axion, and we calculate the masses of the scalar fields for typical values of scalar potential couplings. In Sect. 6 we show the strongest constraints on the parameter space of the model. Finally in Sect. 7 we present our the conclusions.

2 The five texture-zero mass matrices

One of the motivations to study the texture zeros in the Standard Model (SM) and its extensions, is to simplify as much as possible the number of free parameters present in these models. The Yukawa Lagrangian, which is the responsible to give mass to the SM fermions after the spontaneous breaking of the electroweak symmetry $SU (2)_L\otimes U (1)_X \rightarrow U (1)_{EM}$, has 36 free parameters in the quark sector, enough to reproduce the experimental data in the literature, i.e., the 10 physical quantities in the quark sector (6 quark masses, 3 mixing angles and the CP violation phase of the CKM matrix). Without a Model to make predictions, discrete symmetries can be used to prohibit some components in the Yukawa matrix by generating the so-called texture zeros in the mass matrix. In many works instead of proposing a discrete symmetry, texture zeros are proposed as practical alternatives. This approach has as advantage that it is possible to choose the optimal mass matrix for analytical treatment of the problem, while simultaneously manage to adjust the mixing angles and quark masses. In the literature there are many proposed five-zero textures for the SM quark mass matrices [27, 142,143,144,145,146].¹ Several of these textures successfully reproduce the experimentally measured physical quantities. We chose the following five-zero texture because it gets a good fit for the quark masses and mixing parameters [39, 147, 148]:

$$\begin{aligned} \begin{aligned} M^{U}&= \begin{pmatrix} 0&{}\quad 0&{}\quad C_u\\ 0&{}\quad A_u &{}\quad B_u\\ C_u^*&{}\quad B_u^*&{}\quad D_u \end{pmatrix}, \\ M^{D}&= \begin{pmatrix} 0&{}\quad C_d&{}\quad 0\\ C_d^*&{}\quad 0&{}\quad B_d\\ 0&{}\quad B_d^*&{}\quad A_d \end{pmatrix}, \end{aligned} \end{aligned}$$

(2)

where $M^U$ and $M^D$ are the mass matrices for the up-type and down-type quarks, respectively. Due to the mass matrices are Hermitian, the off diagonal matrix elements are not independent, hence, the number of texture zeros in both matrices sum five. The hermitian mass matrices has been widely employed by several authors [26, 29, 36, 143, 145, 149,150,151]; however, the stability of this hypothesis under radiative corrections has been poorly studied. The stability of the texture-zeros under radiative corrections is guaranteed by the PQ symmetry; however, the stability of the Hermitian hypothesis deserves a separate study as it is pointed out in reference [149]. In such a reference, the authors concluded that the studied texture zeros of $M_u$ and $M_d$ are essentially stable against the evolution of energy scales in an analytical way by using the one-loop renormalization-group equations. By using a WBT [28, 29, 39] it is possible to remove the phases in $M^{D}$ to be absorbed by $M^{U}$, i.e., the phases in $B_d$ and $C_d$ are absorbed in $B_u$ and $C_u$, so that the mass matrices (2) can be rewritten as:

$$\begin{aligned} \begin{aligned} M^{U}&= \begin{pmatrix} 0&{}\quad 0&{}\quad |C_u|e^{i\phi _{C_u}}\\ 0&{}\quad A_u &{}\quad |B_u|e^{i\phi _{B_u}}\\ |C_u|e^{-i\phi _{C_u}}&{}\quad |B_u|e^{-i\phi _{B_u}}&{}\quad D_u \end{pmatrix}, \\ M^{D}&= \begin{pmatrix} 0&{}\quad |C_d|&{}\quad 0\\ |C_d|&{}\quad 0&{}\quad |B_d|\\ 0&{}\quad |B_d|&{}\quad A_d \end{pmatrix}, \end{aligned} \end{aligned}$$

(3)

where $\phi _ {B_u}$ and $\phi _ {C_u}$ are the respective phases of the complex entries $B_u$ and $C_u$. Since the trace and the determinant of a matrix are invariant under the diagonalization process, we can compare these invariants for the mass matrices (3) with the corresponding expressions in the mass basis where these matrices are diagonal, in such a way that we can write down the free parameters of $M^{U}$ and $M^{D}$ in terms of the quark masses.

$$\begin{aligned} D_u&=m_u-m_c+m_t-A_u, \end{aligned}$$

(4a)

$$\begin{aligned} |B_u|&=\sqrt{\frac{(A_u-m_u)(A_u+m_c)(m_t-A_u)}{A_u}},\end{aligned}$$

(4b)

$$\begin{aligned} |C_u|&=\sqrt{\frac{m_u\,m_c\,m_t}{A_u}}, \end{aligned}$$

(4c)

$$\begin{aligned} A_d&=m_d-m_s+m_b,\end{aligned}$$

(4d)

$$\begin{aligned} |B_d|&=\sqrt{\frac{(m_b-m_s)(m_d+m_b)(m_s-m_d)}{m_d-m_s+m_b}},\end{aligned}$$

(4e)

$$\begin{aligned} |C_d|&=\sqrt{\frac{m_d\,m_s\,m_b}{m_d-m_s+m_b}}. \end{aligned}$$

(4f)

For reasons of convenience we have imposed that the eigenvalues of the mass matrices for the second generation take the negative values $- m_c$ and $- m_s$. $A_u$ is left as a free parameter and its value, determined by the hierarchy of the quark masses, must be in the following interval:

$$\begin{aligned} m_u\le A_u\le m_t. \end{aligned}$$

(5)

The exact analytical diagonalization mass matrices in Eq. (3) are shown in Appendix C.

3 Textures, PQ symmetry and the minimal particle content

The five-texture zeros present in the mass matrices (2) can be generated through a PQ symmetry $U(1)_{PQ}$ on the Yukawa interaction terms between the SM fermions and the scalar doublets $\varPhi ^{\alpha }$ in the model [103, 128, 152]. We also included a heavy neutral quark Q, and two scalar singlets $S_1$ and $S_2$; the heavy quark is required to avoid the FCNC constraints while keeping the QCD anomaly at a finite value, as it will be explained below. The scalar singlet $S_1$ is necessary to break the PQ symmetry down at a given high energy scale $\varLambda _{PQ}$ (In principle, $S_2$ also breaks the PQ symmetry; however; the purpose of $S_2$ is to give mass to the heavy quark, $S_1$ cannot give mass to the heavy quark due to its PQ charge). The Leading Order (LO) Lagrangian for these fields is given by [153]:

$$\begin{aligned} {\mathcal {L}}_{\text {LO}} \supset&(D_\mu \varPhi ^{\alpha })^\dagger D^\mu \varPhi ^{\alpha } +\sum _{\psi }i\bar{\psi }\gamma ^{\mu }D_\mu \psi +\sum _{i=1}^{2} (D_\mu S_i)^\dagger D^\mu S_i\nonumber \\&- \Bigg ( {\bar{q}}_{Li}y^{D\alpha }_{ij} \varPhi ^{\alpha }d_{Rj} + {\bar{q}}_{Li}y^{U\alpha }_{ij}{\tilde{\varPhi }}^{\alpha }u_{Rj} \nonumber \\&+ \bar{\ell }_{Li}y^{E\alpha }_{ij} \varPhi ^{\alpha }e_{Rj}+ \bar{\ell }_{Li}y^{N\alpha }_{ij}{\tilde{\varPhi }}^{\alpha }\nu _{Rj} +\text {h.c} \Bigg )\nonumber \\&+(\lambda _Q{\bar{Q}}_R Q_LS_2+\text {h.c})-V(\varPhi ,S_1,S_2), \end{aligned}$$

(6)

As it is shown in the Appendix A, the minimum number of Higgs doublets necessary to generate the texture of the quark masses is four, hence $\alpha =1,2,3,4$. In this expression i, j are family indices (there is an implicit sum over repeated indices), the superindex U refers to up-type quarks (the same is true for the super indices D, E, N which refer to down-type quark, electron-like and neutrino-like fermions, respectively) and $D_\mu =\partial _\mu +i\varGamma _\mu$ is the covariant derivative in the SM. $V(\varPhi ,S_1,S_2)$ is the scalar potential which is shown in the Appendix E. In Eq. (6) $\psi$ stands for the standard model fermion fields plus the heavy quark Q. As it is shown in Table 2 the PQ charges of the heavy quark can be chosen in such a way that only the interaction with the scalar singlet $S_2$ is allowed. In our approach we assign charges $Q_{\text {PQ}}$ to the quark sector particles for the left-handed doublets ($q_L$): $x_{q_i}$, up-type right-handed singlets ($u_R$): $x_{u_i}$ and down-type right-handed singlets ($d_R$): $x_{d_i}$ for each family ($i = 1,2,3$), for the scalar doublets, $x_{\phi _{\alpha }}$  ($\alpha =1,2,3,4$) and for the scalar singlets $x_{_{S_{1,2}}}$. For the time being we only consider the quark sector but a similar analysis can be done in the lepton sector [154]. To forbid a given entry in the quark mass matrix, the corresponding sum of the PQ charges for the Yukawa interaction terms must be different from zero, i.e., $(-x_{q_i}+x_{u_j}-x_{\phi _\alpha })\ne 0$, so that we can obtain texture-zeros by imposing the following conditions:

$$\begin{aligned}&M^{U}= \begin{pmatrix} 0&{}\quad 0&{}\quad x\\ 0&{}\quad x&{}\quad x\\ x&{}\quad x&{}\quad x \end{pmatrix} \longrightarrow \begin{pmatrix} S_{11}^{U}\ne 0 &{}\quad S_{12}^{U}\ne 0 &{}\quad S_{13}^{U}= 0\\ S_{21}^{U}\ne 0 &{}\quad S_{22}^{U} = 0 &{}\quad S_{23}^{U}= 0 \\ S_{31}^{U}= 0 &{}\quad S_{32}^{U} = 0 &{}\quad S_{33}^{U}= 0 \end{pmatrix},\nonumber \\&M^{D}= \begin{pmatrix} 0&{}\quad x&{}\quad 0\\ x&{}\quad 0&{}\quad x\\ 0&{}\quad x&{}\quad x \end{pmatrix} \longrightarrow \begin{pmatrix} S_{11}^{D}\ne 0 &{}\quad S_{12}^{D} =0 &{}\quad S_{13}^{D}\ne 0\\ S_{21}^{D} =0 &{}\quad S_{22}^{D}\ne 0 &{}\quad S_{23}^{D} =0 \\ S_{31}^{D}\ne 0 &{}\quad S_{32}^{D} =0 &{}\quad S_{33}^{D} =0 \end{pmatrix}, \end{aligned}$$

(7)

where

$$\begin{aligned} S_{ij}^{U}=&(-x_{q_i}+x_{u_j}-x_{\phi _\alpha }),\nonumber \\ S_{ij}^{D}=&(-x_{q_i}+x_{d_j}+x_{\phi _\alpha }) . \end{aligned}$$

(8)

In the matrix elements of the Eq. (7) every equality must be satisfied only by one of the Higgs doublets, so in principle, we have 11 equations. The inequalities must be satisfied by all the Higgs charges $x_{\phi _\alpha }$ therefore we have $7\times 4$ inequalities. We will use the parametrization shown in the Tables 1 and 2 . The scalar singlets, $S_{1,2}$, acquire a vacuum expectation value at very high energies, where the PQ symmetry is broken. Higgs doublets $\varPhi ^{\alpha }$ adquire VEVs around the electroweak scale. Due to the particular choice of the PQ charge for the scalar singlet $S_1$ (with a VEV of order $10^6$ GeV), trilinear terms, coupling the scalar singlet $S_1$ to the scalar doublets $\varPhi _\alpha$, are allowed in the scalar potential $V(\varPhi ,S_1,S_1)$ (see Appendix E), which are useful to have a spectrum of heavy scalar doublets above the TeVs. The scalar masses are above the searches for heavy-neutral Higgs bosons for the typical benchmark models reported by ATLAS and CMS collaborations [155].

The scalar potential $V(\phi _\alpha ,S_1,S_2)$ is invariant under the symmetry $S_2\longrightarrow S_2^{\dagger }$ (which is equivalent to a $Z_2$ symmetry), but this symmetry is broken by the interaction term $\lambda _Q {\bar{Q}}_RQ_L S_2+\text {h.c.}$. In fact, from this interaction, it is also possible to generate, at one loop, a mass term for the CP-odd field $\frac{1}{2} \left( m_{\zeta _{S_2}}\right) ^2_{\text {SB}}\zeta ^2_{S_2}$ in the effective Weinberg-Coleman potential (where $\zeta _{S_2}$ is the imaginary part of $S_2$) From this interaction, there is also a self-energy correction for CP-even fields, but it comes in with an opposite sign, so these corrections softly break the $Z_2$ symmetry. As a consequence of this, $\zeta _{S_2}$ acquires a mass in the broken phase [156,157,158,159,160,161]. From Eq. (83) of Appendix E it is possible to obtain the decay of Im$S_2=\zeta _{S_2}$ in two axions which depends on the parameter $\lambda _{S_1S_2}$, $\zeta _{S_2}$ can also decay in in two SM Higgs bosons, from the term $\sum _i \lambda _{iS_2} \varPhi _i^{\dagger } \varPhi _i S_2^{*}S_2$, therefore, their interactions are not well constrained by colliders, the impact on the parameter space of our model from the cosmological signatures of this scalar is beyond the purpose of the present work and deserves a dedicated studio.

Table 1 The columns 6-8 are the PQ ($Q_{PQ}$) charges for the SM quarks in each family. The subindex $i=1,2,3$ stands for the family number in the interaction basis. The parameters $s_1, s_2$ and $\alpha$ are reals, with $s_1\ne s_2$

Table 2 Beyond SM scalar and fermion fields and their respective PQ charges. The parameters $s_1, s_2$ are reals, with $s_1\ne s_2$

As it is usual in the PQ formalism, we are interested in those charges for which the QCD anomaly N is different from zero, where

$$\begin{aligned} N= 2\sum _{i}^3x_{q_i}-\sum _{i}^3 x_{u_i}-\sum _{i}^3 x_{d_i}+A_{Q}, \end{aligned}$$

(9)

for this reason, in the literature N is used as the normalization of the Peccei-Quinn (PQ) charges. In order to generate the proper normalization to the charges in the Tables 1 and  2, for an SM fermion $\psi$ the most general PQ charges that reproduce the texture in Ref. [39] are given by the parametrization

$$\begin{aligned} Q_{PQ}({\hat{s}}_1,\epsilon ,N,\alpha )(\psi )= & {} \frac{N}{9}\left( {\hat{s}}_1 Q^{s_1}_{PQ}(\psi )\right. + \left. (\epsilon +{\hat{s}}_1) Q^{s_2}_{PQ}(\psi )\right) \nonumber \\{} & {} +\alpha Q^{V}_{PQ}(\psi ). \end{aligned}$$

(10)

In this expression, $Q^{s_1,s_2,V}_{PQ}(\psi )$ are PQ charges, whose explicit expressions are given in the Table 3, where $N= x_{Q_L}-x_{Q_R}+s_2-s_1$, $\epsilon =(1-A_Q/N)$, ${\hat{s}}_{1,2}=\frac{9}{N}s_{1,2}$ (are arbitrary real numbers such that ${\hat{s}}_1\ne {\hat{s}}_2$) and $A_{Q}=x_{Q_{L}}-x_{Q_{R}}$ is the contribution to the anomaly of the heavy quark Q, which is a singlet under the electroweak gauge group, with left (right)-handed Peccei-Quinn charges denoted by $x_{Q_{L}}(x_{Q_{R}})$. This parametrization was obtained from Tables 1 and 2 , by normalizing the PQ charges in such a way that the anomaly of $SU(3)_C$ is N for any real value of the parameters ${\hat{s}}_1$, ${\hat{s}}_2$, $\alpha$, $x_{Q_L}$ and $x_{Q_R}$. Because $x_{Q_L}$ and $x_{Q_R}$ always appear in the combination $x_{Q_L}- x_{Q_R}=N(1-\epsilon )$ and ${\hat{s}}_2={\hat{s}}_1+\epsilon$, it is more convenient to use the set of parameters ${\hat{s}}_1$, $\epsilon$, N and $\alpha$. For the FCNC processes considered in the present work, the phenomenological couplings are proportional to differences between the PQ charges of down-type quarks, so that only $\epsilon$ and N are relevant for these observables. To solve the strong CP problem $N\ne 0$ and to generate the texture-zeros in the mass matrices it is necessary to keep $\epsilon \ne 0$. It is important to note that due to the exotic heavy quark Q, It is possible to choose small PQ charges for SM fermions with a small contribution to the QCD anomaly, while the QCD anomaly remains finite (this condition is necessary to solve the strong CP problem), small couplings are also important to avoid collider constraints.

Table 3 The three columns in each slot are the Peccei-Quinn charges $x_{\psi _i}$ in each family. PQ charges are shown for the SM left-handed quarks $x_{q_i}$, the right-handed up-type $x_{u_i}$ and down-type $x_{d_i}$ quarks for the three families $i=1,2,3$

The QCD anomaly is also given by $N=A_Q/(1-\epsilon )$, this parametrization is quite convenient since by fixing N and $f_a$ for FCNC observables (for which $\alpha$ does not matter) in Eq. (10) we can vary ${\hat{s}}_1$ and $\epsilon$ for a fixed $\varLambda _{PQ}=f_a N$, in such a way that the parameter space is naturally reduced to two dimensions.

If we want to solve the domain-wall problem is necessary to calculate the QCD anomaly in a normalization such that the minimum magnitude of the non-vanishing PQ charges of the scalar fields and the quark condensates is 1 [162]. The anomaly is given by $N=x_{Q_L}-x_{Q_R}+s_2-s_1$, by choosing $s_2=-1$, $s_1=0$ and $\alpha =0$. In this case the charge of the singlet scalar $S_1$ is $s_1-s_2=1$. In this normalization, we can identify N with $N_{DW}$ [162] in such a way that $N=N_{DW}=1$, which is equivalent to $\epsilon =(x_{Q_L}-x_{Q_R})/N=2$. There are other ways of choosing the parameters which also solve the problem. The DW problem can be disposed of by introducing an explicit breaking of the PQ symmetry so that the degeneracy between the different vacua is removed and there is a unique minimum of the potential [163].

4 The effective lagrangian

The most important phenomenological consequence of non-universal PQ charges is the presence of FCNC. To determine the restrictions coming from the FCNC we start by writing the most general effective Lagrangian as [164, 165]:

$$\begin{aligned} {\mathcal {L}}_{\text {NLO}}= & {} +c_{a\varPhi ^\alpha }O_{a\varPhi ^\alpha }+c_1\frac{\alpha _1}{8\pi }O_{B}\nonumber \\{} & {} +c_2\frac{\alpha _2}{8\pi }O_{W} +c_3\frac{\alpha _3}{8\pi }O_{G}, \end{aligned}$$

(11)

$c_{a\varPhi ^\alpha }$ and $c_{1,2,3}$ are Wilson coefficients; $\alpha _{1,2,3}= \frac{g_{1,2,3}^2}{4\pi }$ where the $g_{1,2,3}$ are the coupling strengths of the electroweak interaction in the interaction basis; $q_{Li}$, $d_{Ri}$ and $u_{Ri}$, are the left-handed quark doublet, right-handed down-type and right-handed up-type quark fields, respectively; $\ell _{Li}$, $e_{Ri}$ and $\nu _{Ri}$ are the left-handed lepton doublet, right-handed charged lepton, and right-handed neutrino fields, respectively. $\psi$ stands for the SM fermion fields and the effective operators are given by

$$\begin{aligned} O_{a\varPhi ^\alpha }&= i\frac{\partial ^\mu a}{\varLambda } \left( (D_{\mu }\varPhi ^\alpha )^{\dagger } \varPhi ^\alpha -\varPhi ^{\alpha \dagger }(D_{\mu }\varPhi ^\alpha )\right) ,\nonumber \\ O_{B}&= -\frac{ a}{\varLambda }B_{\mu \nu }{\tilde{B}}^{\mu \nu },\nonumber \\ O_{W}&= -\frac{ a}{\varLambda }W_{\mu \nu }^a{\tilde{W}}^{a\mu \nu },\nonumber \\ O_{G}&= -\frac{ a}{\varLambda }G_{\mu \nu }^a{\tilde{G}}^{a\mu \nu }, \end{aligned}$$

(12)

where B, $W^a$ and $G^a$ correspond to the gauge fields associated with the SM gauge groups $U(1)_Y$, $SU(2)_L$ and $SU(3)_C$, respectively. Redefining the fields [164]

$$\begin{aligned} \varPhi ^{\alpha }&\longrightarrow e^{i\frac{x_{_{\varPhi ^{\alpha }}}}{\varLambda }a}\varPhi ^{\alpha },\nonumber \\ \psi _L&\longrightarrow e^{i\frac{x_{\psi _L}}{\varLambda }a}\psi _L,\nonumber \\ \psi _R&\longrightarrow e^{i\frac{x_{\psi _R}}{\varLambda }a}\psi _R,\nonumber \\ S_i&\longrightarrow e^{i\frac{x_{_{S_i}}}{\varLambda }a}S_i, \end{aligned}$$

(13)

where $x_ {\varPhi ^\alpha }$ and $x_ {\psi ^\alpha _{L,R}}$ are the PQ charges for the Higgs doublets and the SM fermions, respectively. By keeping the leading order LO terms in $\varLambda ^{-1}$, the Lagrangian Eq. (11) can be written as [153, 164]:

$$\begin{aligned} {\mathcal {L}}_{\text {NLO}}\longrightarrow {\mathcal {L}}_{\text {NLO}}+\varDelta {\mathcal {L}}_{\text {NLO}}, \end{aligned}$$

(14)

where

$$\begin{aligned} \varDelta {\mathcal {L}}_{\text {NLO}}&= \varDelta {\mathcal {L}}_{K^\varPhi }+\varDelta {\mathcal {L}}_{K^\psi }+\varDelta {\mathcal {L}}_{\text {Yukawa}}\nonumber \\&\quad +\varDelta {\mathcal {L}}(F_{\mu \nu })+\varDelta {\mathcal {L}}_{K^S}, \end{aligned}$$

(15)

with

$$\begin{aligned} \varDelta {\mathcal {L}}_{K^{\varPhi }}&= ix_{\varPhi ^{\alpha }}\frac{\partial ^\mu a}{\varLambda } \left[ (D_{\mu }\varPhi ^\alpha )^{\dagger } \varPhi ^\alpha -\varPhi ^{\alpha \dagger }(D_{\mu }\varPhi ^\alpha )\right] ,\\ \varDelta {\mathcal {L}}_{K^\psi }&= \frac{\partial _\mu a}{2\varLambda }\sum _{\psi }(x_{\psi _L}-x_{\psi _R})\bar{\psi }\gamma ^{\mu }\gamma ^{5} \psi -(x_{\psi _L}\\&\quad +x_{\psi _R})\bar{\psi }\gamma ^{\mu }\psi ,\\ \varDelta {\mathcal {L}}_{\text {Yukawa}}&= \frac{ia}{\varLambda }{\bar{q}}_{Li}\bigg (y^{D\alpha }_{ij}x_{d_j}-x_{q_i}y^{D\alpha }_{ ij}+x_{\varPhi ^\alpha }y^{D\alpha }_{ij}\bigg ) \varPhi ^{\alpha }d_{Rj}\\&\quad +\frac{ia}{\varLambda }{\bar{q}}_{Li}\bigg (y^{U\alpha }_{ij}x_{u_j}-x_{q_i}y^{U\alpha }_{ij}-x_{\varPhi ^\alpha }y^{U\alpha }_{ij}\bigg ) {\tilde{\varPhi }}^{\alpha }u_{Rj} \\ \varDelta {\mathcal {L}}_{K^S}&= ix_{_{S_i}}\frac{\partial ^\mu a}{\varLambda } \left[ (D_{\mu }S_i)^{\dagger } S_i -S^{\dagger }_i (D_{\mu }S_i)\right] , \end{aligned}$$

and $x_{q_i}$, $x_{u_i}$ and $x_{d_i}$ are the PQ charges for the i-th family of the quark doublet, right-handed up-type and the right-handed down-type, respectively. From Eq. (7) we see that $\varDelta {\mathcal {L}}_{\text {Yukawa}}$ is zero, this is consistent with the axion shift symmetry which only allows derivative couplings to the SM particles. The same is true for all terms without derivatives of the fields. As it is shown in Appendix D from $\varDelta {\mathcal {L}}_{K^{\varPsi }}$ we obtain the flavour-violating derivative couplings:

$$\begin{aligned} \varDelta {\mathcal {L}}_{K^D} =&-\partial _\mu a {\bar{d}}_{i}\gamma ^{\mu }\left( g_{af_if_j}^{V} + \gamma ^{5}g_{af_if_j}^{A}\right) d_{j}, \end{aligned}$$

(16)

where;

$$\begin{aligned} g_{ad_id_j}^{V,A}= \frac{1}{2f_a c^{\text {eff}}_3}\varDelta ^{Dij}_{V,A}, \end{aligned}$$

(17)

In this expression we made the substitution $\varLambda = f_a c^{\text {eff}}_3$. As shown in Appendix D the axial and vector couplings are:

$$\begin{aligned} \varDelta ^{Dij}_{V,A}= \varDelta ^{Dij}_{RR}(d)\pm \varDelta ^{Dij}_{LL}(q), \end{aligned}$$

(18)

with $\varDelta ^{Fij}_{LL}(q)= \left( U^D_{L}x_{q}~U_L^{D\dagger }\right) ^{ij}$ and $\varDelta ^{Fij}_{RR}(d)= \left( U^D_{R}x_{d}~U_R^{D\dagger }\right) ^{ij}_.$

The field redefinitions (13) induce a modification of the measure in the functional path integral whose effects can be determined from the divergence of the axial-vector current: $J^{PQ5}_{\mu }= \sum _{\psi }(x_{\psi _L}-x_{\psi _R})\bar{\psi }\gamma _\mu \gamma ^5\psi$ [166],

$$\begin{aligned} \partial ^{\mu }J^{PQ5}_{\mu }=&\sum _{\psi }2i m_{\psi } (x_{\psi _L}-x_{\psi _R}) \bar{\psi }\gamma ^5\psi \nonumber \\&-\sum _{\psi }(x_{\psi _L}-x_{\psi _R})\frac{\alpha _1 Y^2(\psi )}{2\pi }B_{\mu \nu }{\tilde{B}}^{\mu \nu }\nonumber \\&-\sum _{ SU(2)_L\text { doublets}} x_{\psi _L} \frac{\alpha _2}{4\pi }W_{\mu \nu }^a{\tilde{W}}^{a\mu \nu }\nonumber \\&-\sum _{ SU(3)\text { triplets}} (x_{\psi _L}-x_{\psi _R}) \frac{\alpha _3}{4\pi }G_{\mu \nu }^a{\tilde{G}}^{a\mu \nu }, \end{aligned}$$

(19)

where the hypercharge is normalized by $Q=T_{3L}+Y$. The Eq. (19) is an on-shell relation; and the derivative is associated with the momentum of an on-shell axion, hence, there is internal consistency. By replacing this result in ${\mathcal {L}}_{K^{\psi }}= \frac{\partial ^{\mu }a}{2\varLambda }J^{PQ5}_{\mu }= -\frac{a}{2\varLambda }\partial ^{\mu }J^{PQ5}_{\mu }$ we obtain a modification of the leading order Wilson coefficients [167]

$$\begin{aligned} c_1&\longrightarrow c_1-\frac{1}{3}\varSigma q+\frac{8}{3}\varSigma u+\frac{2}{3}\varSigma d -\varSigma \ell + 2\varSigma e,\nonumber \\ c_2&\longrightarrow c_2-3\varSigma q-\varSigma \ell ,\nonumber \\ c_3&\longrightarrow c_3-2\varSigma q +\varSigma u+\varSigma d-A_{Q}, \end{aligned}$$

(20)

where $\varSigma q\equiv x_{q_1}+x_{q_2}+x_{q_3}$ is the sum of the PQ charges of the three families, and $A_Q$ is the contribution of the heavy quark to the color anomaly which was defined in Eqs. (10) and (9). From these expressions we obtain for the SM fermions

$$\begin{aligned} \varDelta {\mathcal {L}}(F_{\mu \nu })&= \frac{ a}{\varLambda }\frac{\alpha _1}{8\pi }B_{\mu \nu }{\tilde{B}}^{\mu \nu }\nonumber \\&\quad \times \left( \frac{1}{3}\varSigma q-\frac{8}{3}\varSigma u-\frac{2}{3}\varSigma d+\varSigma \ell -2\varSigma e\right) \nonumber \\&\quad +\frac{ a}{\varLambda }\frac{\alpha _2}{8\pi }W_{\mu \nu }^a{\tilde{W}}^{a\mu \nu } \left( 3\varSigma q+\varSigma \ell \right) \nonumber \\&\quad +\frac{ a}{\varLambda }\frac{\alpha _3}{8\pi }G_{\mu \nu }^a{\tilde{G}}^{a\mu \nu } \left( 2\varSigma q -\varSigma u-\varSigma d+A_{Q}\right) . \end{aligned}$$

(21)

We define $c_3^{\text {eff}}= c_3-2\varSigma q +\varSigma u+\varSigma d-A_{Q}=-N$. In our case, there are no operators of dimension 5 in the Lagrangian before redefining the fields, i.e., $c_i=0$. It is usual to define $\varLambda = f_a c_3^{\text {eff}}$ to absorb the factor $c_3^{\text {eff}}$ in the normalization of the PQ charges.² From now on we assume that all the PQ charges are normalized in this way, so that $x_{\psi }$ stands for $x_{\psi }/c_3^{\text {eff}}$ and the effective scale is $f_a$. For normalized charges $c_{3}^{\text {eff}}=1$, we do not lose generality despite writing the expressions in terms of $f_a$.

5 Naturalness of Yukawa couplings

The previous texture analysis guarantees that the number of free parameters in the mass matrices is enough to reproduce the CKM matrix and the quark masses; as we will show our solutions are flexible enough to set most Yukawa couplings of order 1. As shown in the appendices, in order to generate the texture of the mass matrices with a PQ symmetry, it is necessary to have at least four Higgs doublets. The chosen PQ charges are enough to generate the texture-zeros; but it does not guarantee Hermitian mass matrices, it is true that non-Hermitian mass matrices are the usual ones, however, in our approach we prefer Hermitian mass matrices to gain some analytical advantages. In order to have self-adjoint matrices we impose the following restrictions on the Yukawa couplings in Eq. (3): $y^{U1}_{31}= y^{U1^*}_{13},y^{U2}_{32}= y^{U2^*}_{23}, y^{D4}_{21}= y^{D4^*}_{12}, y^{D3}_{32}= y^{D3^*}_{23}$, in addition, we require that the diagonal elements $y^{U1}_{22},y^{U3}_{33}$ and $y^{D2}_{33}$ must be real numbers.

The up and down quark mass matrices in the interaction basis are:

$$\begin{aligned} M^{U}=&{\hat{v}}_{\alpha } y^{U\alpha }_{ij}= \begin{pmatrix} 0 &{} 0 &{} y^{U1}_{13}{\hat{v}}_1\\ 0 &{} y^{U1}_{22}{\hat{v}}_1 &{} y^{U2}_{23}{\hat{v}}_2\\ y^{U1^*}_{13}{\hat{v}}_1 &{} y^{U2^*}_{23}{\hat{v}}_2 &{} y^{U3}_{33}{\hat{v}}_3 \end{pmatrix}, \end{aligned}$$

(22)

$$\begin{aligned} M^{D}=&{\hat{v}}_{\alpha } y^{D\alpha }_{ij}= \begin{pmatrix} 0 &{} |y^{D4}_{12}|{\hat{v}}_4 &{} 0\\ |y^{D4}_{12}|{\hat{v}}_4 &{} 0 &{} |y^{D3}_{23}|{\hat{v}}_3\\ 0 &{} |y^{D3}_{23}|{\hat{v}}_3 &{} y^{D2}_{33}{\hat{v}}_2 \end{pmatrix}, \end{aligned}$$

(23)

where we define the expectation values ${\hat{v}}_i= v_i/\sqrt{2}$. Here we have implicitly defined the arrays $y^{D\alpha }_{ij}$ which will be needed in the calculation of the FCNC. Taking into account the expressions (4), it is possible to establish the following relations between the masses of the up-type quarks and the VEVs

$$\begin{aligned} {\hat{v}}_1&=\left( \frac{m_u\, m_c\, m_t}{|y_{13}^{U1}|^2\,y_{22}^{U1}}\right) ^{1/3}, \end{aligned}$$

(24)

$$\begin{aligned} {\hat{v}}_2&=\sqrt{\frac{({\hat{v}}_1\,y_{22}^{U1}-m_u)({\hat{v}}_1\,y_{22}^{U1}+m_c)(m_t-{\hat{v}}_1y_{22}^{U1})}{{\hat{v}}_1\, y_ { 22}^{U1}\,|y_{23}^{U2}|^2}}, \end{aligned}$$

(25)

$$\begin{aligned} {\hat{v}}_3&=\frac{m_u-m_c+m_t-{\hat{v}}_1\,y_{22}^{U1}}{y_{33}^{U3}}. \end{aligned}$$

(26)

In an identical way for the down sector we can set the following relations:

$$\begin{aligned} {\hat{v}}_4&=\left( \frac{m_d\, m_s\, m_b}{|y_{12}^{D4}|^2\,(m_d-m_s+m_b)}\right) ^{1/2}, \end{aligned}$$

(27)

$$\begin{aligned} {\hat{v}}_3&=\sqrt{\frac{(m_s-m_d)(m_d+m_b)(m_b-m_s)}{(m_d-m_s+m_b)\,|y_{23}^{D3}|^2}}, \end{aligned}$$

(28)

$$\begin{aligned} {\hat{v}}_2&=\frac{m_d-m_s+m_b}{y_{33}^{D2}}. \end{aligned}$$

(29)

By using current quark masses at the Z pole (Table 5), i.e., $m_u=1.27$ MeV, $m_c=0.633$ GeV and $m_t=171.3$ GeV, from Eq. (24) we find the following approximate values for the vacuum expectation in terms of the masses and the Yukawas:

$$\begin{aligned} {\hat{v}}_1 y_{22}^{U1}\sim \left|\frac{y_{22}^{U1}}{y_{13}^{U1}}\right|^{2/3} (m_u m_c m_t)^{1/3} =\left|\frac{y_{22}^{U1}}{y_{13}^{U1}}\right|^{2/3} 0.516\,\text {GeV}. \end{aligned}$$

(30)

From the bottom current mass at the Z pole we can obtain ${\hat{v}}_2$ by using the Eq. (29)

$$\begin{aligned} {\hat{v}}_2\sim \frac{m_b}{y_{33}^{D2}}=\frac{2.91\, \text {GeV}}{y_{33}^{D2}}. \end{aligned}$$

(31)

Using the constraint (5) and the numerical inputs in Table 5 in Appendix C, we can establish the more restrictive condition $m_u\ll y_{22}^{U1}\, {\hat{v}}_1 \ll m_t$. The consistency between the Eqs. (25) and  (31) requires the following relation

$$\begin{aligned} \left|\frac{y^{U2}_{23}}{y^{D2}_{33}} \right|=\sqrt{ \frac{\left( m_c+{\hat{v}}_1y^{U1}_{22}\right) m_t}{m_b^2}}\sim 6.9, \end{aligned}$$

(32)

where we are assuming that ${\hat{v}}_1y^{U1}_{22} \sim 2.7\, m_c$ (see Table 5). Under similar assumptions it is also possible to get ${\hat{v}}_3$ from the Eq. (26)

$$\begin{aligned} {\hat{v}}_3\sim \frac{m_t}{y_{33}^{U3}}. \end{aligned}$$

(33)

The consistency of this result with the value for ${\hat{v}}_3$ in Eq. (28) implies

$$\begin{aligned} \left|\frac{y^{D3}_{23}}{y^{U3}_{33}} \right|=\sqrt{\frac{m_s m_b}{m_t^2}}= 2.4\times 10^{-3}, \end{aligned}$$

(34)

where, in this case, we took $m_s =56$ MeV at the Z pole. Due to Eq. (33) all the Yukawa couplings have a strong dependency on $y^{U3}_{33}$ since ${\hat{v}}_3$ is the leading term in $v=\sqrt{(v_1^2+v_2^2+v_3^2+v_4^2)}$. So, by setting various Yukawa couplings close to 1 (except $y^{U2}_{23}$, $y^{D3}_{23}$ and $y_{13}^{U1}$) we obtain:

$$\begin{aligned} {\hat{v}}_1 =&1.71 \,\text {GeV}, {\hat{v}}_2 = 2.91 \, \text {GeV}, {\hat{v}}_3 = 174.085 \, \text {GeV}. \end{aligned}$$

(35)

Finally, we can obtain ${\hat{v}}_4$ from Eq. (27)

$$\begin{aligned} {\hat{v}}_4\sim \frac{\sqrt{m_d\, m_s}}{|y^{D4}_{12}|}. \end{aligned}$$

(36)

By setting $y_{33}^{U3}\sim 0.983818$ it is possible to adjust $y_{12}^{D4}\sim 1$ through the relation $(v_1^2+v_2^2+v_3^2+v_4^2)= (246.24\,\text {GeV})^2=v^2$, which for $m_d= 3.15$ MeV implies

$$\begin{aligned} {\hat{v}}_4 = 13.3 \,\text {MeV}. \end{aligned}$$

(37)

We will adjust the scalar potential $V(\varPhi ,S_1,S_2)$ so that, at the minimum, the VEVs of the scalar doublets are precisely those required to generate the SM quark masses. We also propose rotation matrices to implement the Georgi-Nanopoulus formalism for an arbitrary number of scalar doublets.

6 Low energy constraints

Fig. 1

Tree level diagram contribution to the FCNC processes $K^{\pm }\rightarrow \pi ^{\pm }a$ and $B^{\pm }\rightarrow K^{*\pm }a$

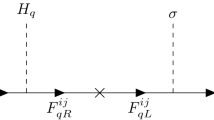
Since our model has non-universal PQ charges, in addition to the usual constraints for the axion–photon coupling, a tree level analysis of the Flavor Changing neutral currents is needed (Fig. 1). As it is mentioned in reference [163] the strongest bounds on flavor violating axion couplings to quarks come from meson decays into final states containing invisible particles. Currently, the $K^{\pm }\rightarrow \pi ^{\pm }a$ decays provide the tightest limits (E949 and E787 Experiments) for the axion mass [163]. Other important restrictions apply on axion-photon couplings [163] but require lepton couplings which we are not considering in this work, any way, in our case these bounds do not represent the strongest constraints [163]. As shown in reference [163] for the decays $K^{\pm }\rightarrow \pi ^{\pm }a$ and $B\rightarrow K^{*}a$ the tree level FCNC come from the term $\varDelta {\mathcal {L}}_{K^{\psi }}$ in the Lagrangian (15). In our approach, we assume that these terms are absent in the original Lagrangian, i.e., $c_i=0$, so these terms come from the redefinition of the fields (13) and are therefore proportional to the PQ charges. In Appendix D, it is shown that the decay widths of pseudoscalar $K^{\pm }$(B) mesons into an axion and a charged pion (vector $K^*$) are given by

$$\begin{aligned}&\varGamma (K^\pm \rightarrow \pi ^\pm a) = \frac{m_K^3}{16\pi }\left( 1-\frac{m_\pi ^2}{m_K^2}\right) ^2\lambda _{K\pi a}^{1/2} f^2_0(m_a^2) |g_{ads}^V |^2,\nonumber \\&\varGamma (B\rightarrow K^{*}a) = \frac{m_B^3}{16\pi } \lambda _{BK^{*}a}^{3/2} A_{0}^2(m^2_a)|g_{asb}^A|^2, \end{aligned}$$

(38)

where $\lambda _{Mm a}= \left( 1-\frac{(m_a+m)^2}{M^2}\right) \left( 1-\frac{(m_a-m)^2}{M^2}\right)$ and

$$\begin{aligned} g_{ad_id_j}^{V,A}= \frac{1}{2f_a c^{\text {eff}}_3}\varDelta ^{Dij}_{V,A}, \end{aligned}$$

(39)

where:

$$\begin{aligned} \varDelta ^{Dij}_{V,A}= \varDelta ^{Dij}_{RR}(d)\pm \varDelta ^{Dij}_{LL}(q), \end{aligned}$$

(40)

with $\varDelta ^{Fij}_{LL}(q)= \left( U^D_{L}x_{q}~U_L^{D\dagger }\right) ^{ij}$ and $\varDelta ^{Fij}_{RR}(d)= \left( U^D_{R}x_{d}~U_R^{D\dagger }\right) ^{ij}_.$ In the Eq. (39) we normalize the charges with $c^{\text {eff}}_3$ as it is explained in the last paragraph of Sect. 4. For $m_a \ll$ 1 MeV, the form factor is $f_0(m_a^2)\approx 1$ [172] for the decay $K^{\pm }\rightarrow \pi ^{\pm }a$. On the other side, from reference [173] we obtain: $f_0(m_a^2)\approx 0.33$ for $B^{\pm }\rightarrow K^{\pm }a$, $f_0(m_a^2)\approx 0.258$ for $B^{\pm }\rightarrow \pi ^{\pm }a$, and for decays with a vector meson in the final state $A_0(m_a^2)\approx 0.374$ for $B^{\pm }\rightarrow K^{*\pm }a$. The constraints on the axion couplings and the decay constant $f_a$ can be obtained from rare semileptonic meson decays $M\rightarrow m \bar{\nu }\nu$, where M stands for $K^{\pm },B^{\pm }$ and $m=\pi ^{\pm },K^{\pm },K^{*},\rho$. These constraints are summarized in Table 4. Figure 2 shows the decay constant $f_a$ as a function of $\epsilon$. For our PQ charges, the FCNC from the processes $B^\pm \rightarrow \pi ^{\pm }a$ and $B^\pm \rightarrow K^{*\pm }a$ are strongly suppressed, in such a way that these constraints are satisfied trivially, hence their allowed regions are not shown in Fig. 2.

Table 4 These inequalities come from the window for new physics in the branching ratio uncertainty of the meson decay in a pair $\bar{\nu }\nu$

Fig. 2

Allowed regions for semileptonic meson decays. We use the relation (1) between the axion mass and the decay constant $f_a$

In general, it is not guaranteed that the eigenstates of mass correspond to the states obtained from the Georgi Rotation, as it is argued in the reference [174] it is only necessary that the state corresponding to the Higgs of the SM coincides with one of the mass eigenstates of the neutral scalars to obtain an alignment that allows us applying the results of the formalism of Georgi [175]. In our case, we have numerically verified the alignment criteria in reference [174]. The origin of the alignment in our model is a consequence of the large suppression of the VEVs of the scalar doublets $v_i$, with $i=1,2,4$, respect to $v_3$, the VEV of $\varPhi _3$. To some extent, this alignment avoids FCNC involving the SM Higgs boson; however, after alignment, there are other sources of FCNC associated with the additional scalar doublets, which is not possible to avoid by any means.

New sources of FCNC come from the Higgs sector, as can be seen in Eq. (64) in Appendix B, where the term $-{\bar{d}}_L^{i} H_\beta ^0 Y_{ij}^{D\beta } d^{j}_{R} -{\bar{u}}_L^{i} H_\beta ^{0*} Y_{ij}^{U\beta } u^{j}_{R}$ has FCNC for $\beta =2,3,4$, however, for $\beta =1$ $Y_{ij}^{U1}$ is diagonal, $H_1^{0*}$ corresponds to the SM Higgs field, hence, there are no terms with flavor-changing neutral currents involving the SM Higgs. For $\beta =2,3,4$ the decay $B\rightarrow K^*H^{\beta }$ with a neutral scalar in the final state has no phase space, however, the FCNC process $B\rightarrow K^*H^{\beta }\rightarrow K^* \ell ^-\ell ^+$ , where the scalar is an intermediate boson, is possible, however, in this case, the scalar width is suppressed by a factor $1/M_{\beta }^4$ (for $\beta >1$ the masses are above 1TeV) and therefore this observable does not represent the strongest constraint. This justifies why in the literature the width of the FCNC process $\pi \pm \rightarrow K^\pm a$ (Eq. 39) represents the strongest constraint for a light axion. The PDG 2022 [155], set mass limits for heavy neutral Higgs bosons in the MSSM (which is a usual benchmark model for models with additional Higgs doublets) $M_{2}>389$ GeV for $\tan \beta = 10$. The constraints are stronger for larger $\tan \beta$; in our model, the $\tan \beta$ values are of order one so that in all the cases the scalar masses of our model are above these lower limits.

From astrophysical considerations are the bounds from black holes superradiance and the SN 1987A bound on the neutron electric dipole moment, which can be combined in such a way that they constrain the axion decay constant in the range [163] (see Fig. 2) : $0.8\times 10^{6}\text {GeV}\le f_a\le 2.8\times 10^{17}\text {GeV}$.

7 Summary and conclusions

In this work we have proposed a PQ symmetry that gives rise to quark mass matrices with five texture-zeros. This texture (2) can adjust in a non-trivial way the six masses of the quarks and the three CKM mixing angles and the CP violating phase. The Hermitian quark mass matrices, up-type $M^U$ and down-type $M^D$, have 18 free parameters, six of them are phases and 12 are real parameters. As it is well known in the literature, three of these real parameters can be made equal to zero through a WBT without any physical consequence [27,28,29]. Five of these phases can be reabsorbed in the fermion fields [176, 177] in such a way that we end with nine real parameters and one phase to explain the six quark masses, the three mixing angles, and the CP-violating phase, achieving parity between the number of free parameters and experimental measurements.

By imposing two texture zeros (in addition to the three zeros obtained from the  WBT) there are more experimental constraints than free parameters, this feature eliminates a large number of possible textures for the mass matrices. In Appendix A we showed that in order to generate the texture, Eq. (2), through a PQ symmetry, at least four Higgs doublets are required. In Eq. (10) we proposed a general parametrization for the PQ charges which is consistent with the texture.

Since many observables are proportional to the PQ charges normalized by the QCD anomaly, we included into the particle content a heavy quark singlet under the SM gauge electroweak gauge group $SU_L(2)\times U_Y(1)$ but with chiral charges under the PQ symmetry. The PQ charges of this heavy quark are responsible for maintaining $N\ne 0$, while we make the PQ charges of the SM quarks arbitrarily close to zero.

To generate the texture zeros of the mass matrices and simultaneously to solve the strong CP problem it is necessary to keep $\epsilon$ and N different from zero in Eq. (10). In our case, the FCNC observables do not depend on the parameters $\alpha$ and ${\hat{s}}_1$ (see Table 2 for definitions), hence, the axion decay constant $f_a$ (or the axion mass $m_a$) and $\epsilon$ were the only relevant parameters in our analysis.

In order to write down the quark mass matrices in the proper basis, in Appendix B we generalize the Georgi rotation in the two Higgs doublet formalism to rotate an arbitrary number of Higgs doublets to a basis where only one Higgs doublet acquires a vacuum expectation value.

By defining almost all the Yukawas close to 1, it was possible to determine the vacuum expectation values of the Higgs doublets from the experimental value of the quark masses and the CKM mixing matrix, this choice obeys the criteria of naturalness and is very convenient to understand the origin of the mass hierarchies in the SM.

Since in our model the PQ charges are non-universal there are FCNC at the tree level. We calculated the tree level FCNC couplings from the effective interaction Lagrangian between the kinetic term of the quarks and the axion, these couplings are well known in the literature [163]. In Appendix D we calculated the decay width for the decay of a pseudoscalar meson into a pseudoscalar (or vector) meson plus an axion. This result let us determine the region of the parameter space allowed by the experimental constraints Fig. 2.

Our model is flexible enough to accommodate possible experimental anomalies, while simultaneously is a useful approach to answer several issues in flavor physics. For future work, it is necessary to extend the PQ symmetry to leptons. Although it is true that in the literature there are textures that can adjust the parameters of the lepton sector [154, 178,179,180,181,182], these textures are different from those used with quarks [27], however, as will be shown elsewhere, it is possible to make the adjustment without additional Higgs doublets.

Appendices

Appendix A: The minimal content of Higgs doublets

The texture (42) can be obtained from a Peccei-Quinn $U(1)_{PQ}$ symmetry, incorporating in the model a minimum of 4 Higgs doublets with charges $x_\phi$.

$$\begin{aligned} M^{U}=\left( \begin{array}{ccc} 0 &{} 0 &{} x\\ 0 &{} x &{} x\\ x &{} x &{} x \end{array}\right) , M^{D}=\left( \begin{array}{ccc} 0 &{} x &{} 0\\ x &{} 0 &{} x\\ 0 &{} x &{} x \end{array}\right) . \end{aligned}$$

(42)

The idea of the demonstration is: we first observe that in terms of the charges $x_{\psi }$, each entry allowed in the array $M^{U}$ must satisfy the relation:

$$\begin{aligned} S_{ij}^{U}=-x_{q_{i}}+x_{u_{j}}-x_{\phi _{\alpha }}=0, \end{aligned}$$

(43)

where $x_{\phi _\alpha }$ represents the PQ chargue of the $\alpha$th Higgs that satisfies the equality in Eq. (43). By assuming two quarks doublets $q_{L_i}$ and $q_{L_j}$ with identical PQ charges $x_q$ and requiring $S_{ik}^{U}=-x_{q_{i}}+x_{u_{k}}-x_{\phi _{\alpha }}=0$ for any $k=1,2,3$, we also have $S_{jk}^{U}=-x_{q_{j}}+x_{u_{k}}-x_{\phi _{\alpha }}=0$, for the same k’s and the Higgs doublet $\phi _{\alpha }$ (since $x_{q_i}=x_{q_j}$). This would lead to having two rows in the matrix $M^U$ with an equivalent structure, that is to say, the allowed and forbiden terms are the same, which contradicts the structure of the matrix. Similarly, if two fields $u_{Ri}$, $u_{Rj}$ with $i\ne j$, had equal charges, it would lead to an array $M^U$ with a similar structure in two columns, which is not present in (42); the same applies to the matrix $M^D$, thus:

$$\begin{aligned} x_{q_i}\ne x_{q_j}, x_{u_i}\ne x_{u_j}, x_{d_i}\ne x_{d_j}, \text {with} i,j=1,2,3. \end{aligned}$$

(44)

From these inequalities and noting that in the third column in $M^U$ all terms are allowed, we can conclude that at least three Higgs doublets are required to reproduce the texture-zeros of the matrix $M^U$. Now it is necessary to settle if three Higgs doublets are enough to simultaneously reproduce the matrix $M^U$ and $M^D$ in 42. The third column in $M_{u}$ implies the relations

$$\begin{aligned} S^{U}_{i,3}=-x_{q_{i}}+x_{u_{3}}-x_{\phi _{\alpha }}=0, \text {for each} i=1,2,3, \end{aligned}$$

(45)

then $x_{q_{1}}=x_{u_{3}}-x_{\phi _{\alpha }}=0$ and $x_{q_{2}}=x_{u_{3}}-x_{\phi _{\alpha }}=0$. Since $x_{q_1}\ne x_{q_2}$ these equations can not be simultaneously valid for the same $x_{\phi _\alpha }$. The same is true for any pair $x_{q_{i}}$, $x_{q_{j}}$ with $i\ne j$, hence, the equalities Eq. (45) require a minimum of three higgs doublets to reproduce the texture of $M^U$. The next step is to determine if the three chosen Higgs doublets for $M^{U}$ are enough to generate the texture of $M^{D}$. For three Higgs doublets the texture (42) requires $7\times 3=21$ inequalities associated with the forbidden entries, i.e.,

$$\begin{aligned} S_{ij}^D =&-x_{q_{i}}+x_{d_{j}}+x_{\phi _\alpha }\ne 0\nonumber \\ S_{ij}^{U} =&-x_{q_{i}}+x_{u_{j}}- x_{\phi _\alpha }\ne 0, \alpha =1,2,3. \end{aligned}$$

(46)

Now, without loss of generality, we can take the charge of the singlet $x_{u_3}=0$, and from the Eq. (45) for the couplings of $u_ {R_3}$ we can identify the charges of the doublets $q_L$ with the charges of the three Higgs fields, such that: $x_ {q_i} = - x _ {\phi _i}$. With this result we can put together the Eqs. (43) and the inequalities (46), in such a way that the texture of the matrix $M^{D}$ can be written-down as 47:

$$\begin{aligned} S^D =\left( \begin{array}{ccc} x_{\phi _1}+x_{d_1}+(x_\phi )_{11}\ne 0 &{} x_{\phi _1}+x_{d_2}+(x_\phi )_{12}= 0 &{} x_{\phi _1}+x_{d_3}+(x_\phi )_{13}\ne 0\\ x_{\phi _2}+x_{d_1}+(x_\phi )_{21}= 0 &{}x_{\phi _2}+x_{d_2}+(x_\phi )_{22}\ne 0 &{} x_{\phi _2}+x_{d_3}+(x_\phi )_{23}= 0\\ x_{\phi _3}+x_{d_1}+(x_\phi )_{31}\ne 0 &{} x_{\phi _3}+x_{d_2}+(x_\phi )_{32}= 0 &{} x_{\phi _3}+x_{d_3}+(x_\phi )_{33}= 0 \end{array}\right) , \end{aligned}$$

(47)

where the inequalities must be satisfied by any $(x_\phi )_{ij}=x_{\phi _k}$, with $k=1,2,3$. For the equalities, it is enough if at least one $x_{\phi _i}$ satisfies them. In Eq. (48) we analyze each entry of $S_{21}^D$ and we obtain the following options for $(x_\phi )_{21}$:

$$\begin{aligned} (x_\phi )_{21} = {\left\{ \begin{array}{ll} x_{\phi _1} &{} \rightarrow S^{D}_{11}=0~ \text {if}~ (x_{\phi })_{11}=x_{\phi _2}~(\text {must be}\ne 0) \\ x_{\phi _2} &{} \text {is a consistent solution} \\ x_{\phi _3} &{} \rightarrow S^{D}_{13}=0~ \text {if}~ (x_{\phi })_{13}=x_{\phi _2}~(\text {must be}\ne 0), \end{array}\right. } \end{aligned}$$

(48)

By the same way, the choice $(x_\phi )_{23}=x_{\phi _1}$ in $S^D_{23}$ is not consistent with the inequality $S^D_{13}$, and the choice $(x_\phi )_{23}= x_{\phi _2}$ due to $S^D_{21}$, implies $x_{d_3}=x_{d_1}$, which is forbidden by Eq. (44), therefore the only option is $(x_\phi )_{23}=x_{\phi _3}$. The proposed analysis allows defining in a unambiguous way the fields $(x_\phi )_{ij}$ in the equalities. Proceeding in an identical way for the remaining ones, we get:

$$\begin{aligned} (x_\phi )_{21}=&x_{\phi _2}, (x_\phi )_{23}=x_{\phi _3}, (x_\phi )_{12}=x_{\phi _3},\nonumber \\ (x_\phi )_{32}=&x_{\phi _1}, (x_\phi )_{33}=x_{\phi _2}, \end{aligned}$$

(49)

By replacing these expressions in (47) $S^D$ reduces to 50:

$$\begin{aligned} S^{D} =\left( \begin{array}{ccc} x_{\phi _1}+x_{d_1}+(x_\phi )_{11}\ne 0 &{} x_{\phi _1}+x_{d_2}+x_{\phi _{3}}= 0 &{} x_{\phi _1}+x_{d_3}+(x_\phi )_{13}\ne 0\\ 2x_{\phi _2}+x_{d_1}= 0 &{} x_{\phi _2}+x_{d_2}+(x_\phi )_{22}\ne 0 &{} x_{\phi _2}+x_{d_3}+x_{\phi _{3}}= 0\\ x_{\phi _3}+x_{d_1}+(x_\phi )_{31}\ne 0 &{} x_{\phi _3}+x_{d_2}+x_{\phi _{1}}= 0 &{} x_{\phi _3}+x_{d_3}+x_{\phi _{2}}= 0 \end{array}\right) . \end{aligned}$$

(50)

From this expression we obtain the relation:

$$\begin{aligned} S^D_{21}-S^D_{11}=2x_{\phi _2}-x_{\phi _1}-(x_\phi )_{11}\ne 0, \end{aligned}$$

(51)

since this must be true for all $(x_\phi )_{11}=x_{\phi _i}$, for $i=1$ we get:

$$\begin{aligned} 2x_{\phi _2}-x_{\phi _3}-x_{\phi _{1}}\ne 0. \end{aligned}$$

(52)

We will use Eq. (52) shortly. By carrying out the same analysis for $S^{U}$ (using the same conventions $x_{u_3}=0$ and $-x_{q_i}=x_{\phi _i}$ ) there are two options for this matrix, as seen in 53:

$$\begin{aligned} S^U_{A \atopwithdelims ()B} =\left( \begin{array}{ccc} x_{\phi _1}+x_{u_1}-(x_{\phi })_{11}\ne 0 &{} x_{\phi _1}+x_{u_2}-(x_{\phi })_{12}\ne 0 &{} 0\\ x_{\phi _2}+x_{u_1}-(x_{\phi })_{21}\ne 0 &{} x_{\phi _2}+x_{u_2}-x_{\phi _{1 \atopwithdelims ()3}}=0 &{} 0\\ x_{\phi _3}+x_{u_1}-x_{\phi _{1 \atopwithdelims ()2}}=0 &{} x_{\phi _3}+x_{u_2}-x_{\phi _{2\atopwithdelims ()1}}=0 &{} 0 \end{array}\right) , \end{aligned}$$

(53)

where subscript $2\atopwithdelims ()1$ indicates that either of the two values $x_{\phi _1}$ or $x_{\phi _2}$ are possible. The subscript $A\atopwithdelims ()B$ means that all the up (down) options must be replaced simultaneously, mixing between up and down options must be avoided. From this matrix, i.e., $S^U_{A}$, we obtain $(S^U_{A})_{22}-S^U_{A})_{32}=2x_{\phi _2}-x_{\phi _3}-x_{\phi _{1}}=0$, which is forbidden by (52), then, the option $S^U_{A}$ is not possible. For the option $S^U_{B}$ we have

$$\begin{aligned} (S^U_{B})_{22}-(S^U_{B})_{32}=-2x_{\phi _3}+x_{\phi _2}+x_{\phi _{1}}=0, \end{aligned}$$

(54)

but, $(S^U_{B})_{11}-(S^U_{B})_{31}=-2x_{\phi _3}+x_{\phi _2}+x_{\phi _{1}}\ne 0$ (where we took $(x_{\phi })_{11}=x_{\phi _3}$ in $S^U_B$) that violates the inequality (54), therefore it is not possible to build the texture (42) with just three Higgs doublets. By adding a Higgs doublet, infinite solutions are presented thus demonstrating that a minimum of four Higgs doublets are required to reproduce the texture (42).

Appendix B: The mass operator matrices

The most general Lagrangian for the interaction of four Higgs doublets $\varPhi _\alpha$ with the quarks of the SM is given by

$$\begin{aligned} {\mathcal {L}}= -{\bar{q}}_L^{\prime i} \varPhi _\alpha y_{ij}^{D\alpha }d^{\prime j}_{R} -{\bar{q}}_L^{\prime i} {\tilde{\varPhi }}_\alpha y_{ij}^{U\alpha }u^{\prime j}_{R}+\text {h.c}, \end{aligned}$$

(55)

where a sum is assumed on repeated indices. Here i, j run over 1, 2, 3 and $\alpha$ over 1, 2, 3, 4. The Higgs boson doublet fields are parameterized as follows:

$$\begin{aligned} \varPhi _\alpha = \begin{pmatrix} \phi _\alpha ^{+}\\ \frac{v_\alpha +h_\alpha +i\eta _\alpha }{\sqrt{2}} \end{pmatrix}, {\tilde{\varPhi }}_\alpha =i\sigma _2 \varPhi _\alpha ^{*}. \end{aligned}$$

(56)

In a similar way as in the two Higgs doublet model [183] we rotate the Higgs fields to the (generalized) Georgi basis, i.e.,

$$\begin{aligned} \begin{pmatrix} H_1 \\ H_2 \\ H_3 \\ H_4 \end{pmatrix} = R_1(\beta _1)R_2(\beta _2)R_3(\beta _3) \begin{pmatrix} \varPhi _1\\ \varPhi _2\\ \varPhi _3\\ \varPhi _4 \end{pmatrix}=: H_{\beta } \equiv R_{\beta \alpha }\varPhi _\alpha , \end{aligned}$$

(57)

where the orthogonal matrices

$$\begin{aligned} R_1(\beta _1)= & {} \begin{pmatrix} \cos \beta _1 &{}\quad \sin \beta _1 &{}\quad 0 &{}\quad 0\\ -\sin \beta _1 &{}\quad \cos \beta _1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}, \end{aligned}$$

(58a)

$$\begin{aligned} R_2(\beta _2)= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \cos \beta _2 &{}\quad \sin \beta _2 &{}\quad 0 \\ 0 &{}\quad -\sin \beta _2 &{}\quad \cos \beta _2 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ \end{pmatrix}, \end{aligned}$$

(58b)

$$\begin{aligned} R_3(\beta _3)= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \cos \beta _3 &{}\quad \sin \beta _3 \\ 0 &{}\quad 0 &{}\quad -\sin \beta _3 &{}\quad \cos \beta _3 \\ \end{pmatrix}, \end{aligned}$$

(58c)

where $\tan \beta _1 =\frac{\sqrt{v_2^2+v_3^2+v_4^2}}{v_1}$, $\tan \beta _2 =\frac{\sqrt{v_3^2+v_4^2}}{v_2}$ and $\tan \beta _3 =\frac{v_4}{v_3}$. In these expressions $H_\beta = (H_\beta ^+,(H_\beta ^0+iH_{\beta }^{\text {odd}})/\sqrt{2})^T$. This basis is chosen in such a way that only the neutral component of $H_1$ acquires a vacuum expectation value

$$\begin{aligned}&\langle H_1^0 \rangle =\sqrt{v_1^2+v_2^2+v_3^2+v_4^2}\equiv v ,\nonumber \\&\langle H_2^0 \rangle = 0, \langle H_3^0 \rangle = 0, \langle H_4^0 \rangle = 0. \end{aligned}$$

(59)

In this way $\varPhi _\alpha y_{ij}^{F\alpha }= y_{ij}^{F\alpha }R_{\alpha \beta }^T R_{\beta \gamma } \varPhi _{\gamma }= {\mathcal {Y}}_{ij}^{F\beta } H_\beta$, and $F=U,D$; where we have defined

$$\begin{aligned} {\mathcal {Y}}^{F\beta }_{ij}=R_{\beta \alpha }y_{ij}^{F\alpha }. \end{aligned}$$

(60)

With these definitions Eq. (55) becomes

$$\begin{aligned} {\mathcal {L}} = -{\bar{q}}_L^{\prime i} H_\beta {\mathcal {Y}}_{ij}^{D\beta }d^{\prime j}_{R} -{\bar{q}}_L^{\prime i} {\tilde{H}}_\beta {\mathcal {Y}}_{ij}^{U\beta }u^{\prime j}_{R}+\text {h.c}. \end{aligned}$$

(61)

It is necessary to rotate to the mass eigenstates of the fermion mass, i.e.,

$$\begin{aligned} f_{L,R}= U^F_{L,R}f'_{L,R}, \end{aligned}$$

(62)

where the diagonalization matrices $U_{L,R}$ are defined below, in Sect. 1. From the Lagrangian for the charged currents

$$\begin{aligned} {\mathcal {L}}_{CC}=&-\frac{g}{\sqrt{2}} {\bar{u}}_{Li}'\gamma ^{\mu } d_{Li}'W^+ +\text {h.c}\nonumber \\ =&-\frac{g}{\sqrt{2}} {\bar{u}}_{Li}\gamma ^{\mu }\left( V_{_{\text {CKM}}}\right) _{ij} d_{Lj}W^+ +\text {h.c}, \end{aligned}$$

(63)

it is possible to obtain the CKM mixing matrix $V_{_{\text {CKM}}}= U^{U}_L U^{D \dagger }_L$ by rotating to the fermion mass eigenstates. In particular, we are interested in the axial neutral current coupling to the axion in the mass eigenstates

$$\begin{aligned} {\mathcal {L}}_{H^0} =&-\frac{1}{\sqrt{2}} {\bar{d}}_L^{\prime i} H_\beta ^0 {\mathcal {Y}}_{ij}^{D\beta } d^{\prime j}_{R} -\frac{1}{\sqrt{2}}{\bar{u}}_L^{\prime i} H_\beta ^0 {\mathcal {Y}}_{ij}^{U\beta } u^{\prime j}_{R} +\text {h.c},\nonumber \\ =&-\frac{1}{\sqrt{2}}{\bar{d}}_L^{i} H_\beta ^0 Y_{ij}^{D\beta } d^{j}_{R} -\frac{1}{\sqrt{2}}{\bar{u}}_L^{i} H_\beta ^0 Y_{ij}^{U\beta } u^{j}_{R} +\text {h.c}, \nonumber \\ \end{aligned}$$

(64)

where $Y_{ij}^{F\beta } = \left( U^{F}_{L} {\mathcal {Y}}^{F\beta } U^{F\dagger }_{R} \right) _{ij}$. In these expressions the mass functions in the interaction basis are:

$$\begin{aligned} M^{D}_{ij}= \frac{v}{\sqrt{2}} {\mathcal {Y}}_{ij}^{D1}, M^{U}_{ij}= \frac{v}{\sqrt{2}} {\mathcal {Y}}_{ij}^{U1}, \end{aligned}$$

(65)

where $v= \langle H_1^0 \rangle$ is the Higgs vacuum expectation value.

Appendix C: Diagonalization matrices

In order to compare with physical quantities, it is necessary to rotate fields to the mass eigenstates, i.e., $u_{L,R}=U^{U}_{L,R}u'_{L,R}$ and $d_{L,R}=U^{D}_{L,R}d'_{L,R}$, where prime means the interaction basis. In our formalism the mass matrices are Hermitian, hence the right-handed and left-handed diagonalizing matrices are identical; however, we obtain a minus sign on the quark mass eigenvalues of the second family (see comments after Eq. (4f) and references [29, 39]). To get a positive mass matrix we introduce the identity matrix written as $I_2I_2=1$ with $I_2=\text {diag}(1,-1,1)$, i.e.,

$$\begin{aligned} M^{U}_{ij}&=\left( U^{U\dagger }\lambda ^{U}U^{U}\right) _{ij}= \left( U^{U\dagger }_L m^{U}U^{U}_R\right) _{ij} =\frac{v}{\sqrt{2}}{\mathcal {Y}}^{U1}_{ij}\nonumber \\&=\frac{v}{\sqrt{2}} R_{1\alpha }y^{U\alpha }_{ij},\nonumber \\ M^{D}_{ij}&=\left( U^{D\dagger }\lambda ^{D}U^{D}\right) _{ij} = \left( U^{D\dagger }_L m^{U}U^{D}_R\right) _{ij} =\frac{v}{\sqrt{2}}{\mathcal {Y}}^{D1}_{ij}\nonumber \\&= \frac{v}{\sqrt{2}}R_{1\alpha }y^{D\alpha }_{ij}, \end{aligned}$$

(66)

where:

$$\begin{aligned} \lambda ^{U,D}&=\text {diag}(m_{u,d},-m_{c,s},m_{t,b}),\\ m^{U,D}&=\text {diag}(m_{u,d},m_{c,s},m_{t,b}), \end{aligned}$$

Table 5 Best fit point of the mass matrices parameters to the quark masses and mixing angles at the Z pole

the matrices R and ${\mathcal {Y}}$ are defined in Eqs. (57) and (60), respectively; and

$$\begin{aligned} U_L^{U,D}= U^{U,D}, U_R^{U,D}= I_2 U^{U,D}, \end{aligned}$$

(67)

where $U^{U,D}$ are the diagonalization matrices (68) and (69). In the second and fourth lines in (66) we made use of (65). It is important to stress that the texture-zeros pattern in the matrix ${\mathcal {Y}}^{F1}_{ij}$ are identical to those in the original Yukawa couplings $y^{F\alpha }_{ij}$, since the sum over $\alpha$ does not mix the i, j indices. In fact, according to Eqs. (22) and (23), $M^{U,D}= \frac{v_{\alpha }}{\sqrt{2}}y^{U,D\alpha }_{ij}=\frac{v}{\sqrt{2}} R_{1\alpha }y^{U,D\alpha }_{ij}$, therefore $R_{1\alpha }=\frac{v_{\alpha }}{v}$. The diagonalization matrices are:

$$\begin{aligned} U^{U\dagger }= & {} \begin{pmatrix} e^{i (\phi _{C_u}+ \theta _{1u})} \sqrt{\frac{m_c m_t (A_u-m_u)}{A_u (m_c+m_u) (m_t-m_u)}} &{}\quad -e^{i (\phi _{C_u}+ \theta _{2u})} \sqrt{\frac{(A_u+m_c) m_t m_u}{A_u (m_c+m_t) (m_c+m_u)}} &{}\quad e^{i (\phi _{C_u}+ \theta _{3u})} \sqrt{\frac{m_c (m_t-A_u) m_u}{A_u (m_c+m_t) (m_t-m_u)}} \\ -e^{i( \phi _{B_u}+ \theta _{1u})} \sqrt{\frac{(A_u+m_c) (m_t-A_u) m_u}{A_u (m_c+m_u) (m_t-m_u)}} &{}\quad -e^{i (\phi _{B_u}+ \theta _{2u})} \sqrt{\frac{m_c (m_t-A_u) (A_u-m_u)}{A_u (m_c+m_t) (m_c+m_u)}} &{}\quad e^{i (\phi _{B_u}+ \theta _{3u})} \sqrt{\frac{(A_u+m_c) m_t (A_u-m_u)}{A_u (m_c+m_t) (m_t-m_u)}} \\ e^{i \theta _{1u}} \sqrt{\frac{m_u (A_u-m_u)}{(m_c+m_u) (m_t-m_u)}} &{}\quad e^{i \theta _{2u}} \sqrt{\frac{m_c (A_u+m_c)}{(m_c+m_t) (m_c+m_u)}} &{}\quad e^{i \theta _{3u}}\sqrt{\frac{m_t (m_t-A_u)}{(m_c+m_t) (m_t-m_u)}} \end{pmatrix}, \end{aligned}$$

(68)

$$\begin{aligned} U^{D\dagger }= & {} \begin{pmatrix} e^{i \theta _{1d}} \sqrt{\frac{m_b (m_b-m_s) m_s}{(m_b-m_d) (m_d+m_s) (m_b+m_d-m_s)}} &{}\quad -e^{i \theta _{2d}} \sqrt{\frac{m_b (m_b+m_d) m_d}{(m_d+m_s) (m_b+m_d-m_s) (m_b+m_s)}} &{}\quad \sqrt{\frac{m_d (m_s-m_d) m_s}{(m_b-m_d) (m_b+m_d-m_s) (m_b+m_s)}} \\ e^{i \theta _{1d}} \sqrt{\frac{m_d (m_b-m_s)}{(m_b-m_d) (m_d+m_s)}} &{}\quad e^{i \theta _{2d}} \sqrt{\frac{(m_b+m_d) m_s}{(m_d+m_s) (m_b+m_s)}} &{}\quad \sqrt{\frac{m_b (m_s-m_d)}{(m_b-m_d) (m_b+m_s)}} \\ -e^{i \theta _{1d}} \sqrt{\frac{m_d (m_b+m_d) (m_s-m_d)}{(m_b-m_d) (m_d+m_s) (m_b+m_d-m_s)}} &{}\quad -e^{i \theta _{2d}} \sqrt{\frac{(m_b-m_s) m_s (m_s-m_d)}{(m_d+m_s) (m_b+m_d-m_s) (m_b+m_s)}} &{}\quad \sqrt{\frac{m_b (m_b+m_d) (m_b-m_s)}{(m_b-m_d) (m_b+m_d-m_s) (m_b+m_s)}} \end{pmatrix}, \end{aligned}$$

(69)

where $\theta _{1u},\theta _{2u},\theta _{3u},\theta _{1d}$ y $\theta _{2d}$ are arbitrary phases (a third phase for the diagonalization matrix  (69) can be absorbed by the remaining phases) which are useful to adapt to the convention of the matrix $V_{\text {CKM}}=U^{U}_{L}\,U^{D\dag }_{L}$ (Table 5). Taking as input the SM parameters at the Z pole, the best fit values are:

Appendix D: FCNC from $\varDelta {\mathcal {L}}_{K^\psi }$

The interaction term (15) between the kinetic terms of the fermions and the axion is given by:

$$\begin{aligned} \varDelta {\mathcal {L}}_{K^\psi }=&\frac{\partial _\mu a}{2f_a}\sum _{\psi }(x_{\psi _L}-x_{\psi _R})\bar{\psi }'\gamma ^{\mu }\gamma ^{5}\psi ' -(x_{\psi _L}+x_{\psi _R})\bar{\psi }\gamma ^{\mu }\psi '\\ =&-\frac{\partial _\mu a}{2f_a}\sum _{\psi }x_{\psi _L}\bar{\psi }'\gamma ^{\mu }(1-\gamma ^{5})\psi ' +x_{\psi _R}\bar{\psi }\gamma ^{\mu }(1+\gamma ^5)\psi ', \end{aligned}$$

By rotating from the interaction basis to the mass basis for the SM quarks we obtain

$$\begin{aligned} =&-\frac{\partial _\mu a}{2f_a}\Bigg ({\bar{u}}_{i}\gamma ^{\mu }\left( 1-\gamma ^{5}\right) \varDelta ^{Uij}_{LL}(q)u_{j}\nonumber \\&+ {\bar{d}}_{i}\gamma ^{\mu }\left( 1-\gamma ^{5}\right) \varDelta ^{Dij}_{LL}(q)d_{j}\nonumber + {\bar{u}}_{i}\gamma ^{\mu }\left( 1+\gamma ^{5}\right) \varDelta ^{Uij}_{RR}(u)u_{j} \nonumber \\&+ {\bar{d}}_{i}\gamma ^{\mu }\left( 1+\gamma ^{5}\right) \varDelta ^{Dij}_{RR}(d)d_{j}\Bigg ), \end{aligned}$$

(70)

where $\varDelta ^{Fij}_{LL}(q)= \left( U^D_{L}x_{q}~U_L^{D\dagger }\right) ^{ij}$ and $\varDelta ^{Fij}_{RR}(d)= \left( U^D_{R}x_{d}~U_R^{D\dagger }\right) ^{ij}_.$ From these expressions we are interested in the terms:

$$\begin{aligned} \varDelta {\mathcal {L}}_{K^D}=&-\frac{\partial _\mu a}{2f_a}\Bigg ( {\bar{d}}_{i}\gamma ^{\mu }\left( 1-\gamma ^{5}\right) \varDelta ^{Dij}_{LL}(q)d_{j}\nonumber \\&+ {\bar{d}}_{i}\gamma ^{\mu }\left( 1+\gamma ^{5}\right) \varDelta ^{Dij}_{RR}(d)d_{j}\Bigg )\end{aligned}$$

(71)

$$\begin{aligned} =&-\frac{\partial _\mu a}{2f_a} {\bar{d}}_{i}\gamma ^{\mu }\left( \varDelta ^{Dij}_{V} + \gamma ^{5}\varDelta ^{Dij}_{A}\right) d_{j},\nonumber \\ =&-\partial _\mu a {\bar{d}}_{i}\gamma ^{\mu }\left( g_{af_if_j}^{V} + \gamma ^{5}g_{af_if_j}^{A}\right) d_{j}, \end{aligned}$$

(72)

From this expression, we can infer vector and axial couplings for any type of fermions $F=U,D,E,N$

$$\begin{aligned} g_{af_if_j}^{V,A}= \frac{1}{2f_a}\varDelta ^{Fij}_{V,A}. \end{aligned}$$

(73)

These couplings (73), generate FCNC processes as those shown in Fig. 1. According to reference [184]

$$\begin{aligned} \varGamma = \frac{S|\textbf{p} |}{8\pi m_K^2} |{\mathcal {M}} |^2, \end{aligned}$$

(74)

where $|\textbf{p} |= m_K\lambda _{K\pi a}^{1/2}/2$, and $\lambda _{K\pi a}= \left( 1-\frac{(m_a+m_\pi )^2}{m_K^2}\right) \left( 1-\frac{(m_a-m_\pi )^2}{m_K^2}\right)$ and $S=1$. The leading order S matrix element for $K^-\rightarrow \pi ^-a$ is

$$\begin{aligned} {\mathcal {M}}&= \langle \pi ^-(p_{\pi }),a(p_a)|i{\mathcal {L}} (s\rightarrow d)|K^-(p_{K})\rangle \nonumber \\&= - ig_{ads}^V(p_K-p_\pi )_{\mu } \langle \pi ^-(p_{\pi })|{\bar{d}}\gamma ^\mu s|K^-(p_{K})\rangle \nonumber \\&\qquad \langle a(p_a)|a(p_a)|0\rangle \nonumber \\&= - ig_{ads}^V(m_K^2-m_\pi ^2)f_0(q^2), \end{aligned}$$

(75)

where $q^{2}=(p_K-p_\pi )^2$ and :

$$\begin{aligned}{} & {} f_{0}(q^2)=f_{+}(q^2) +\frac{q^2f_{-}(q^2)}{(m_K^2-m_\pi ^2)} ,\end{aligned}$$

(76)

$$\begin{aligned}{} & {} \langle a(p_a)|a(p_a)|0\rangle = \langle a(p_a)|a(p_a)\rangle =1 \end{aligned}$$

(77)

As the initial and final states have the same parity only the matrix elements of the vector current are different from zero [185], then

$$\begin{aligned} \varGamma (K^+\rightarrow \pi ^+a) = \frac{m_K^3}{16\pi }\left( 1-\frac{m_\pi ^2}{m_K^2}\right) ^2\lambda _{K\pi a}^{1/2} f^2_0(m_a^2) |g_{ads}^V |^2. \end{aligned}$$

(78)

To calculate the $B\rightarrow V a$ decay width, where V is a vector meson, it is necessary to consider the form factors for the quark level process $b\rightarrow q$ [186]

$$\begin{aligned}&\langle V(k,\epsilon )|{\bar{q}}\gamma ^{\mu }b|B(p)\rangle = \frac{2iV(q^2)}{m_B+m_V}\epsilon ^{\mu \nu \rho \sigma }\epsilon ^{*}_{\nu }k_{\rho }p_{\sigma }, \end{aligned}$$

(79)

$$\begin{aligned}&\langle V(k,\epsilon )|{\bar{q}}\gamma ^{\mu }\gamma ^{5}b|B(p)\rangle \nonumber \\&\quad = 2m_V A_{0}(q^2)\frac{\epsilon ^*\cdot q}{q^2}q^{\mu }+(m_B+m_V)A_{1}(q^2)\nonumber \\&\qquad \times \left( \epsilon ^{*\mu } -\frac{\epsilon ^*\cdot q}{q^2}q^{\mu }\right) -\frac{A_{2}(q^2)\epsilon ^*\cdot q}{(m_b+m_V)} \nonumber \\&\qquad \times \left[ (p+k)^{\mu }-\frac{m_B^2-m_V^2}{q^2}q^{\mu }\right] . \end{aligned}$$

(80)

There are also strong constraints from the decay $B\rightarrow K^*a$, the $K^*$ kaon is a vectorial meson, parity-even under inversion of the spatial coordinates. Due to the selection rules of the Lorentz group only the axial-vector matrix elements $\langle K^* |{\bar{s}}\gamma ^{\mu }\gamma ^5 b|B \rangle$ are different from zero

$$\begin{aligned} {\mathcal {M}}=&-ig_{asb}^Vq_{\mu } \langle K(p_{K})|{\bar{s}}\gamma ^\mu \gamma ^5 b|B(p_{P})\rangle \\ =&-ig_{asb}^V 2m_{K^*} A_{0}(q^2)\epsilon ^*\cdot q, \end{aligned}$$

where $q_{\mu }=(p_B-p_K)_{\mu }$. Summing over the final polarization states $\sum _{s}\epsilon ^{\mu *}(s)\epsilon ^{\nu *}(s)=\left( -g^{\mu \nu }+\frac{p_{K^*}^{\mu }p_{K^*}^{\nu }}{m_{K^*}^2}\right)$, we get

$$\begin{aligned} \sum _{s}|{\mathcal {M}} |^2 = |g_{asb}^A|^2 A_{0}^2(m^2_a) m_B^4\lambda _{BK^{*}a}, \end{aligned}$$

(81)

and replacing this result in Eq. (74) the width decay can be written as

$$\begin{aligned} \varGamma (B\rightarrow K^{*}a) = \frac{m_B^3}{16\pi } \lambda _{BK^{*}a}^{3/2} A_{0}^2(m^2_a)|g_{asb}^A|^2. \end{aligned}$$

(82)

Appendix E: Scalar potential

In order to explain the textures of the mass matrices of our model, four scalar doublets $\varPhi _\alpha$ were introduced in Sect. 3, additionally a scalar singlet S is required to break the PQ symmetry. For completeness it is necessary to introduce a potential $V(\varPhi ,S_1,S_2)$ with all the terms allowed by the PQ symmetry. From this potential it is possible to obtain the masses of the scalar fields allowing us to determine which of them correspond to Goldstone bosons. One of the CP odd massless scalars must correspond to the axion field associated with the breaking of PQ symmetry. The most general CP invariant scalar potential in the PQ symmetry scenario is

$$\begin{aligned} V(\varPhi ,S_i)= & {} \sum _{i=1}^4\mu _{i}^{2}\varPhi _{i}^{\dagger }\varPhi _{i} +\sum _{k=1}^2\mu _{s_k}^2 S_k^{*}S_k+\sum _{i=1}^4\lambda _{i}\left( \varPhi _{i}^{\dagger }\varPhi _{i}\right) ^{2}\nonumber \\{} & {} + \sum _{k=1}^2\lambda _{s_k}\left( S_k^{*} S_k \right) ^{2} + \sum _{i=1}^4\sum _{k=1}^2\lambda _{is_k}\left( \varPhi _{i}^{\dagger }\varPhi _{i}\right) \left( S_k^{*}S_k\right) \nonumber \\{} & {} + \sum _{\underbrace{i,j=1}_{i<j}}^4\bigg (\lambda _{ij}\left( \varPhi _{i}^{\dagger }\varPhi _{i}\right) \left( \varPhi _{j}^{\dagger }\varPhi _{j}\right) +J_{ij}\left( \varPhi _{i}^{\dagger }\varPhi _{j}\right) \left( \varPhi _{j}^{\dagger }\varPhi _{i}\right) \bigg ) \nonumber \\{} & {} + \lambda _{s_1 s_2}\left( S_1^{*}S_1\right) \left( S_2^{*}S_2\right) \nonumber \\{} & {} + K_{1}\left( \left( \varPhi _{1}^{\dagger }\varPhi _{2}\right) \left( \varPhi _{3}^{\dagger }\varPhi _{2}\right) + h.c.\right) \nonumber \\{} & {} + K_{2}\left( \left( \varPhi _{3}^{\dagger }\varPhi _{4}\right) \left( \varPhi _{3}^{\dagger }\varPhi _{1}\right) + h.c.\right) \nonumber \\{} & {} + F_1 \left( \left( \varPhi _{2}^{\dagger }\varPhi _{3}\right) S_1 +h.c.\right) \nonumber \\{} & {} + F_2 \left( \left( \varPhi _{1}^{\dagger }\varPhi _{2}\right) S_1 +h.c.\right) \nonumber \\{} & {} + \frac{1}{2} \left( m_{\zeta _{S_2}}\right) ^2_{\text {SB}}\zeta ^2_{S_2}+\frac{1}{2}\left( m_{\xi _{S_2}}\right) ^2_{\text {SB}}\xi ^2_{S_2}. \end{aligned}$$

(83)

where the terms proportional to $F_i$ are allowed by the particular choice of the PQ charges and the $F_i$ couplings have units of mass. After spontaneous symmetry breaking (SSB), the four Higgs doublets acquire a VEV that gives masses to all SM particles and the scalar doublets could be written as

$$\begin{aligned} \varPhi _\alpha =&\begin{pmatrix} \phi _\alpha ^{+}\\ \frac{v_\alpha +h_\alpha +i\eta _\alpha }{\sqrt{2}} \end{pmatrix}, {\tilde{\varPhi }}_\alpha =i\sigma _2 \varPhi _\alpha ^{*}, \nonumber \\ S_i=&\frac{v_{_{S_i}}+\xi _{S_i}+i\zeta _{S_i}}{\sqrt{2}}; i=1,2. \end{aligned}$$

(84)

The singlet scalar field $S_1$ breaks the PQ symmetry at the high energy scale given by $v_{s_1}$. The last two terms in the equation (83) correspond to soft breaking masses of the imaginary and the real part of $S_2$, which are generated at one loop in the Coleman-Weinberg potential from the interaction term $\lambda _Q S_2{\bar{Q}}_RQ_L+\text {h.c.}$ From Eqs. (35) and (37) we have the following hierarchy among VEVs, $v_4\ll v_1, v_2\ll v_3\ll v_{S_1}\sim v_{S_2}$. In the scalar sector, we have CP-even, CP-odd, and charged fields. As shown in Appendices E.1, E.2 and  E.3 by choosing the couplings close to one, as follows:

$$\begin{aligned} \lambda _{1}= & {} \lambda _{2}=\lambda _{4}=\lambda _{s_1}=\lambda _{s_2}=\lambda _{s_1 s_2}= 1,\nonumber \\ \lambda _3= & {} 0.463\nonumber \\ \lambda _{ij}= & {} 1 for any i,j, \nonumber \\ \lambda _{js_1}= & {} \lambda _{js_2}=1 for any j,\nonumber \\ J_{12}= & {} J_{13}=J_{23}=J_{24}=-1,\ \ otherwise J_{ij}=1,\nonumber \\ K_1= & {} K_2=-1,\nonumber \\ F_1= & {} F_2=-1 \text {GeV}, \end{aligned}$$

(85)

we obtain scalar masses above the TeV scale (except for the Higgs boson) allowing them to avoid LHC constraints on heavy Higgs bosons [187] and charged scalar bosons [188]. The $\lambda _{3}$ value was chosen in order to adjust the SM Higgs mass. In our approach, the $v_i$ (Eqs. (35) and (37)) are determined from the SM fermion masses and the quark mass matrix texture, $v_{s_1}$ is still a free parameter, nonetheless, this parameter is important for the axion physics due to the relation [189],

$$\begin{aligned} f_a=\frac{v_{s_1}}{2N}. \end{aligned}$$

(86)

In our calculations we took $v_{s_1}\approx v_{s_2}\approx 10^{6}$GeV. It is important to emphasize that in our model $f_a$ can take arbitrary values, however, a small $f_a$ restrict $\epsilon$ (Eq. 10) to values close to zero. Taking into account all these considerations and the Eq. (85) the scalar mass spectrum (in GeV) is:

$$\begin{aligned}&\text {CP even} =\{1.73\times 10^6,1.\times 10^6,6.54\times 10^3,1.97\times 10^3,\nonumber \\&\qquad \qquad \qquad \quad 1.09\times 10^3,125\},\nonumber \\&\text {CP odd} =\{6.54\times 10^3,1.97\times 10^3,1.09\times 10^3,0,0,m_{\zeta _{S_2}}\},\nonumber \\&\text {Charged fields} = \{6.54\times 10^3,1.97\times 10^3,1.11\times 10^3,0\}. \end{aligned}$$

(87)

The mass spectrum of the scalar fields is above the TeVs scale, except the SM Higgs which was set to 125 GeV. The pseudoscalar sector (CP odd fields) have two zero mass eigenstates, the axion field and the Goldstone boson which is absorbed by the longitudinal component of the SM Z boson. A similar result is achieved in the charged sector where it is possible to identify the two Goldstone bosons needed to give mass to the SM $W^{\pm }$ fields.

1.1 E.1: CP-even scalar sector

As shown in Eq. (56) after the SSB the four Higgs doublets and the scalar singlets acquire VEVs, yielding the squared mass matrix $M_{R}^{2}$ for CP-even scalar particles expressed in the $(h_{1},h_{2},h_{3},h_{4},\xi _{S_1}, \xi _{S_2})$ basis, with entries given by:

$$\begin{aligned} M_{R_{11}}^2= & {} -\frac{K_1v_2^2 v_3+K_2 v_3^2 v_4+\sqrt{2} F_2 v_2 v_{s_1}-4 v_1^3\lambda _1}{2 v_1},\nonumber \\ M_{R_{12}}^2= & {} \frac{F_2 v_{s_1}}{\sqrt{2}}+v_2 (K_1v_3+v_1 H_{12}),\nonumber \\ M_{R_{13}}^2= & {} \frac{K_1v_2^2}{2}+v_3 (K_2 v_4+v_1 H_{13}),\nonumber \\ M_{R_{14}}^2= & {} \frac{K_2 v_3^2}{2}+v_1 v_4 H_{14},\nonumber \\ M_{R_{15}}^2= & {} \frac{F_2 v_2}{\sqrt{2}}+v_1 v_{s_1} \lambda _{1s_1},\nonumber \\ M_{R_{22}}^2= & {} \frac{-\sqrt{2} (F_2 v_1+F_1 v_3) v_{s_1}+4 v_2^3 \lambda _2}{2 v_2},\nonumber \\ M_{R_{23}}^2= & {} K_1v_1 v_2+\frac{F_1 v_{s_1}}{\sqrt{2}}+v_2 v_3 H_{23} \nonumber \\ M_{R_{24}}^2= & {} v_2 v_4 H_{24}, \nonumber \\ M_{R_{25}}^2= & {} \frac{F_2 v_1}{\sqrt{2}}+\frac{F_1 v_3}{\sqrt{2}}+v_2 v_{s_1} \lambda _{2s_1},\nonumber \\ M_{R_{33}}^2= & {} -\frac{K_1v_1 v_2^2+\sqrt{2} F_1 v_2 v_{s_1}-4 v_3^3 \lambda _{3}}{2 v_3},\nonumber \\ M_{R_{34}}^2= & {} v_3 (K_2 v_1+v_4 H_{34}),\nonumber \\ M_{R_{35}}^2= & {} \frac{F_1 v_2}{\sqrt{2}}+v_3 v_{s_1} \lambda _{3S_1},\nonumber \\ M_{R_{44}}^2= & {} -\frac{K_2 v_1 v_3^2}{2 v_4}+2 v_4^2 \lambda _{4},\nonumber \\ M_{R_{45}}^2= & {} v_4 v_{s_1} \lambda _{4s_1},\nonumber \\ M_{R_{55}}^2= & {} \frac{-\sqrt{2} v_2 (F_2 v_1+F_1 v_3)+4 v_{s_1}^3\lambda _{S_1}}{2 v_{s_1}}\nonumber \\ M_{R_{j6}}^2= & {} \lambda _{js_2}v_jv_{s_2}\text {, for j}<5 \nonumber \\ M_{R_{56}}^2= & {} \lambda _{s_1s_2}v_{s_1}v_{s_2}\nonumber \\ M_{R_{66}}^2= & {} 2\lambda _{s_2}v_{s_2}^2+m_{\xi _{S_2}}^2. \end{aligned}$$

(88)

where $H_{ij}=\lambda _{ij}+J_{ij}$. At leading order, the eigenvalues of this matrix are approximately (in GeV):

$$\begin{aligned}&\{1.73\times 10^6,1.\times 10^6,6.54\times 10^3,1.97\times 10^3,\nonumber \\&\quad 1.09\times 10^3,125\}, \end{aligned}$$

(89)

where the value 125 GeV corresponds to the SM Higgs. Hereafter, the signs of the couplings are chosen in such a way that the eigenvalues are positive.

1.2 E.2: Charged scalar sector

The square of the mass matrix for the charged scalar sector, $M_C^2$, after SSB in the Higgs sector, can be written in the $(\phi _{1}^\pm , \phi _{2}^\pm , \phi _{3}^\pm , \phi _{4}^\pm )$ basis as

$$\begin{aligned} M_{C_{11}}^2= & {} -\frac{J_{12} v_1 v_2^2+K_1v_2^2 v_3+J_{13} v_1 v_3^2}{2 v_1}\nonumber \\{} & {} +\frac{K_2 v_3^2 v_4+J_{14} v_1 v_4^2+\sqrt{2} F_2 v_2 v_{s_1}}{2 v_1},\nonumber \\ M_{C_{12}}^2= & {} \frac{1}{2} \left( J_{12} v_1 v_2+K_1v_2 v_3+\sqrt{2} F_2 v_{s_1}\right) ,\nonumber \\ M_{C_{13}}^2= & {} \frac{1}{2} v_3 (J_{13} v_1+K_2 v_4),\nonumber \\ M_{C_{14}}^2= & {} \frac{J_{14} v_1 v_4}{2},\nonumber \\ M_{C_{22}}^2= & {} -\frac{J_{12} v_1^2 v_2+2 K_1v_1 v_2 v_3}{2 v_2}\nonumber \\{} & {} +\frac{J_{23} v_2 v_3^2+J_{24} v_2 v_4^2+\sqrt{2} F_2 v_1 v_{s_1}+\sqrt{2} F_1 v_3 v_{s_1}}{2 v_2}, \nonumber \\ M_{C_{23}}^2= & {} \frac{1}{2} \left( K_1v_1 v_2+J_{23} v_2 v_3+\sqrt{2} F_1 v_{s_1}\right) ,\nonumber \\ M_{C_{24}}^2= & {} \frac{J_{24} v_2 v_4}{2},\nonumber \\ M_{C_{33}}^2= & {} -\frac{K_1v_1 v_2^2+J_{13} v_1^2 v_3+J_{23} v_2^2 v_3}{2 v_3}\nonumber \\{} & {} +\frac{2 K_2 v_1 v_3 v_4+J_{34} v_3 v_4^2+\sqrt{2} F_1 v_2 v_{s_1}}{2 v_3},\nonumber \\ M_{C_{34}}^2= & {} \frac{1}{2} v_3 (K_2 v_1+J_{34} v_4),\nonumber \\ M_{C_{44}}^2= & {} -\frac{K_2 v_1 v_3^2+J_{14} v_1^2 v_4+J_{24} v_2^2 v_4+J_{34} v_3^2 v_4}{2 v_4}. \end{aligned}$$

(90)

For this matrix, eigenvalues numerically are close its diagonal elements, i.e., (in GeV):

$$\begin{aligned} \{6.54\times 10^3,1.97\times 10^3,1.11\times 10^3,0\}. \end{aligned}$$

(91)

The zero mass eigenvalue corresponds to the Goldstone Boson absorbed in the longitudinal component of the charged vector fields $W^\pm$.

1.3 E.3: CP-odd scalar sector

The square of the mass matrix for the CP-odd scalars in the $(\eta _{1}, \eta _{2}, \eta _{3}, \eta _{4}, \zeta _{S_1}, \zeta _{S_2})$ basis is given by

$$\begin{aligned} M_{I_{11}}^2= & {} -\frac{K_1v_2^2 v_3+K_2 v_3^2 v_4+\sqrt{2} F_2 v_2 v_{s_1}}{2 v_1}, \nonumber \\ M_{I_{12}}^2= & {} K_1v_2 v_3+\frac{F_2 v_{s_1}}{\sqrt{2}},\nonumber \\ M_{I_{13}}^2= & {} -\frac{K_1v_2^2}{2}+K_2 v_3 v_4,\nonumber \\ M_{I_{14}}^2= & {} -\frac{K_2 v_3^2}{2}, \nonumber \\ M_{I_{15}}^2= & {} \frac{F_2 v_2}{\sqrt{2}},\nonumber \\ M_{I_{22}}^2= & {} -\frac{4 K_1v_1 v_2 v_3+\sqrt{2} (F_2 v_1+F_1 v_3) v_{s_1}}{2 v_2},\nonumber \\ M_{I_{23}}^2= & {} K_1v_1 v_2+\frac{F_1 v_{s_1}}{\sqrt{2}},\nonumber \\ M_{I_{24}}^2= & {} 0,\nonumber \\ M_{I_{25}}^2= & {} \frac{-F_2 v_1+F_1 v_3}{\sqrt{2}},\nonumber \\ M_{I_{33}}^2= & {} -2 K_2 v_1 v_4-\frac{v_2 \left( K_1v_1 v_2+\sqrt{2} F_1 v_{s_1}\right) }{2 v_3},\nonumber \\ M_{I_{34}}^2= & {} K_2 v_1 v_3,\nonumber \\ M_{I_{35}}^2= & {} -\frac{F_1 v_2}{\sqrt{2}},\nonumber \\ M_{I_{44}}^2= & {} -\frac{K_2 v_1 v_3^2}{2 v_4},\nonumber \\ M_{I_{45}}^2= & {} 0,\nonumber \\ M_{I_{55}}^2= & {} -\frac{v_2 (F_2 v_1+F_1 v_3)}{\sqrt{2} v_{s_1}}\nonumber \\ M_{I_{j6}}^2= & {} 0\text {, for j}<6 \nonumber \\ M_{I_{66}}^2= & {} m_{\zeta _{S_2}}^2 \end{aligned}$$

(92)

At leading order the eigenvalues of this matrix are (in GeV):

$$\begin{aligned} \{6.54\times 10^3,1.97\times 10^3,1.09\times 10^3,0,0,m_{\zeta _2}\} \end{aligned}$$

(93)

One of the zero mass eigenvalues corresponds to the Goldstone Boson absorbed in the longitudinal component of the neutral vector field of the SM $Z^{0}$, and the other one corresponds to the axion field a.