Fully heavy dibaryons

Abstract

The existence of fully heavy dibaryons $\varOmega _{ccc}\varOmega _{bbb}$, $\varOmega _{ccb}\varOmega _{bbc}$, $\varOmega _{ccc}\varOmega _{ccc}$, and $\varOmega _{bbb}\varOmega _{bbb}$ with $J=0,~1,~2,~3$ and $P=\pm 1$ are investigated in the framework of a constituent quark model with the help of the resonating group method. The dibaryon composed of six c or b quarks with $J^{P}=0^{+}$ is able to be bound, because the requirement for antisymmetrization between the same baryon clusters introduces an attractive interaction between two fully heavy baryons. Although it is difficult for the dibaryon with the color-singlet type $\varOmega _{ccc}\varOmega _{bbb}$ to form any bound state, it is possible for the $\varOmega _{ccb}\varOmega _{bbc}$ state to be bound. The channel coupling of all channels of both $\varOmega _{ccb}\varOmega _{bbc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ structures leads to the bound conclusion of this fully heavy system composed of three c quarks and three b quarks.

1 Introduction

Understanding hadron–hadron interactions and searching for exotic hadron states are important topics in hadron physics, among which questing for dibaryons is a long-standing challenge. Among the various theoretical studies of dibaryons, the lattice quantum chromodynamics (QCD) simulations by the HAL QCD (hadrons to atomic nuclei from lattice QCD) Collaboration have investigated six-quark systems containing light or strange quarks, and have confirmed the existence of the $N\varOmega$ and $\varOmega \varOmega$ bound states with nearly physical quark masses ($m_{\pi }\simeq 146$ MeV and $m_{K}\simeq 525$ MeV) [1, 2]. Recently, Junnarkar and Mathur reported the first lattice QCD study of deuteron-like (np-like) dibaryons with heavy quark flavors, using a state-of-the-art lattice QCD calculation [3]. They suggested that dibaryons $\varOmega _{c}\varOmega _{cc} (sscscc)$, $\varOmega _{b}\varOmega _{bb} (ssbsbb)$, and $\varOmega _{ccb}\varOmega _{cbb} (ccbcbb)$ were stable under strong and electromagnetic interactions, and they also found that the binding of these dibaryons became stronger as they became heavier in mass. A dibaryon with the highest charm number $\varOmega _{ccc}\varOmega _{ccc}$ was also studied by the (2+1)-flavor lattice QCD with nearly physical light-quark masses and relativistic heavy-quark action with physical charm quark mass, and their result indicated that $\varOmega _{ccc}\varOmega _{ccc}$ was located in the unitary regime [4]. The $\varOmega _{bbb}\varOmega _{bbb}$ dibaryon was investigated in the extended one-boson exchange model, and the existence of $\varOmega _{bbb}\varOmega _{bbb}$ was proposed [5]. Moreover, the possibility of very heavy dibaryons with three charm quarks and three beauty quarks (bbbccc) was explored using a constituent model in Ref. [6], and no bound state was found below the lowest dissociation threshold.

The discovery of the doubly charmed baryon $\varXi _{cc}$ by the Large Hadron Collider beauty (LHCb) Collaboration [7] provided the crucial experimental input, the interaction between two heavy quarks, for the existence of the stable heavy tetraquark $QQ\bar{q}\bar{q}$ [8]. Eichten and Quigg also predicted the existence of the novel narrow doubly heavy tetraquark $QQ\bar{q}\bar{q}$ based on the information [9]. Inspired by the LHCb Collaboration’s observation of the hidden-charm $P_{c}$ pentaquarks [10], the work of Ref. [11] predicted the dibaryons $0^{+}$ $\varXi _{cc}\varSigma _{c}$, $1^{+}$ $\varXi _{cc}\varSigma ^{*}_{c}$, $2^{+}$ $\varXi ^{*}_{cc}\varSigma _{c}$, and $3^{+}$ $\varXi ^{*}_{cc}\varSigma ^{*}_{c}$. Recently, the LHCb Collaboration reported their results on the observations of fully charm states ($cc\bar{c}\bar{c}$). A narrow structure X(6900), matching the lineshape of a resonance, and a broad structure next to the $di-J/\psi$ mass threshold were obtained [12]. Such a breakthrough offers more information to assist the search for the tetraquark consisting of four charm quarks. It can naturally be expected that a fully heavy dibaryon cccccc will be accessible experimentally in the future.

Thus, the observation of the fully heavy dibaryons becomes more interesting. Based on the study of the strange dibaryon $N\varOmega$, we predicted the $N\varOmega$-like dibaryons $N\varOmega _{ccc}$ and $N\varOmega _{bbb}$ in the framework of the constituent quark model [13]. The study of the H particle was extended to the heavy sector states $\varLambda _{c}\varLambda _{c}$ and $\varLambda _{b}\varLambda _{b}$ [14]. In this work, we extend our study to the possibility of fully heavy dibaryon systems and investigate the interaction between two fully heavy baryons. The effective potential and binding energy, as well as the low-energy scattering phase shifts, scattering length, and effective range, are also calculated to explore the existence of fully heavy dibaryon systems.

The paper is structured as follows. Section 2 gives a brief introduction of the quark model and calculation method. The numerical results and discussion are provided in Sect. 3. A summary is presented in the last section.

2 Quark model and calculation method

We study the fully heavy dibaryon systems within the constituent quark model, which is similar to what was used in our previous work on dibaryons $d^{*}$, $N\varOmega$, and $\varOmega \varOmega$ [15,16,17], and is extended to the heavy dibaryons $N\varOmega _{ccc}$ [13]. When applied to the fully heavy systems, neither the SU(3) scalar octet meson exchange nor the Goldstone boson exchange works. Additionally, although the one-gluon-exchange interaction ($V^\mathrm{{OGE}}_{ij}$) has a tensor part in Ref. [13], it works in the coupling calculation between the S-wave and D-wave channels. We calculated the threshold energies of the S-wave states in both Ref. [13] and this work, and the coupling calculation between the S-wave and D-wave channels are tentatively not included in this work, as we are interested in the ground states of fully heavy dibaryons, and the spin-orbit and tensor interactions have very small contributions. For example, the tensor force reduced the energy of deuterons 1 or 2 MeV. For the fully heavy dibaryon, the mass shifts will be smaller, because the tensor force is inversely proportional to the masses of interacting quarks. In fact, we performed a calculation of the cccccc system including the tensor force, and the mass shift was less than 0.1 MeV, so it is safe to neglect the spin-orbit and tensor forces in the calculation of low-lying fully heavy dibaryons. To reduce the computational burden, the spin-orbit and tensor part of $V^\mathrm{{OGE}}_{ij}$ is not taken into account here. Here, we list the interaction Hamiltonian we used in this work:

Table 1 Model parameters. The mass of the u/d quark is fixed to $m_{u/d}=313~\mathrm{MeV}$

$$\begin{aligned} H=\sum _{i=1}^6\left( m_i+\frac{p_i^2}{2m_i}\right) -T_\mathrm{{CM}} +\sum _{j>i=1}^6 \left( V^\mathrm{{CON}}_{ij}+V^\mathrm{{OGE}}_{ij}\right) , \end{aligned}$$

(1)

where $T_\mathrm{{CM}}$ is the kinetic energy of the center of mass. $V^\mathrm{{CON}}_{ij}$ is the phenomenological confinement potential:

$$\begin{aligned} V_{ij}^{CON}=\left\{ \begin{array}{ll} -a_{c}{\varvec{\lambda }}^c_{i}\cdot {\varvec{\lambda }}^c_{j}~(r_{ij}^2+ v_0), &{} \text{ if } i,j \text{ in } \text{ the } \text{ same } \\ &{} \text{ cluster } \\ -a_{c}{\varvec{\lambda }}^c_{i}\cdot {\varvec{\lambda }}^c_{j}~\left( \frac{1-e^{-\mu _{q_{i}q_{j}}r_{ij}^2}}{\mu _{q_{i}q_{j}}}+ v_0\right) , &{} \text{ otherwise }. \end{array} \right. \end{aligned}$$

(2)

It is well known that confinement is a nonperturbative QCD effect. There may be important nonperturbative features missed in every two-body confinement potential model. For example, three-gluon exchange between three quarks and three-body instanton interactions do not contribute within a colorless meson or baryon, but do contribute to a multiquark system [18]. There are many other types of quark interactions resulting from multi-gluon exchanges which cannot be included in a two-body confinement potential. The QCD condensates within a nucleon and between two nucleons might be different. These arguments show that a direct extension of the two-body confinement to the multiquark system has not been justified even though it might be a good approximation in the single hadron case. The absence of an experimentally observed color van der Waals force has long been a problem for the two-body confinement potential model. Multiquark systems provide greater variation in the low-energy behavior of QCD and allow for further testing of the phenomenology built into quark models, especially the nature of confinement.

We assume the following recipe to determine the two-body matrix element of confinement: the interaction takes the normal, unscreened form (quadratic in r) when the interacting quarks always remain in the same baryon orbit, both before and after interaction; otherwise the interaction takes the screening form (second form shown in Eq. (2)). Although this has not been demonstrated to be correct, it is more sophisticated than the usual simple two-body confining interaction, and it is a physically reasonable model of nonlocal, nonperturbative effects. Even though we use a two-body interaction form to evaluate the matrix elements, our model is not a potential model. It is an effective matrix element approach extended from bound states to scattering states. It does reduce to the usual two-body confinement interaction within a single hadron. It also has the usual meaning of a two-body interaction in the asymptotic regime, although not in intermediate regions. The main physics introduced is the recognition that the confining interaction between two nucleons might differ from that within a nucleon. In particular, we represent the nonlocal, nonperturbative backflow of color (and pair creation, as seen in lattice studies  [19, 20]) by screening of the confining potential.

In Eq. (2), $\mu _{q_{i}q_{j}}$ is the color screening parameter, which is related to the flavor of the i-th quark $q_{i}$ and the j-th quark $q_{j}$. For the light quark systems, $\mu _{uu}$, $\mu _{us}$, and $\mu _{ss}$ are determined by fitting the deuteron properties, nucleon–nucleon scattering phase shifts, and hyperon–nucleon scattering phase shifts, respectively [21]. We also found that the heavier the quark, the smaller the parameter $\mu _{q_{i}q_{j}}$. When extending to the heavy quark system, the hidden-charm pentaquark system, we took $\mu _{cc}$ as an adjustable parameter from 0.01 to 0.001 fm$^{-2}$, and found that the results were insensitive to the value of $\mu _{cc}$ [22], and the $P_{c}$ states were well described in the work of Refs. [22, 23]. In fact, if the value of the $\mu _{q_{i}q_{j}}$ is very small, the exponential function can be approximated to

$$\begin{aligned} e^{-\mu _{q_{i}q_{j}}r_{i j}^{2}}=1-\mu _{q_{i}q_{j}}r_{i j}^{2}+\cdots \end{aligned}$$

(3)

Then, the confinement expression in Eq. (2) (when two quarks are in different clusters) is

$$\begin{aligned} V_{ij}^{CON}= & {} -a_{c}{\varvec{\lambda }}^c_{i}\cdot {\varvec{\lambda }}^c_{j} \left( \frac{1-e^{-\mu _{q_{i}q_{j}} r_{i j}^{2}}}{\mu _{q_{i}q_{j}}}+v_{0}\right) \nonumber \\\approx & {} -a_{c}{\varvec{\lambda }}^c_{i}\cdot {\varvec{\lambda }}^c_{j} \left( r_{i j}^{2}+v_{0}\right) , \end{aligned}$$

(4)

which is the same as the expression for two quarks in the same cluster. Thus, when the value of the $\mu _{q_{i}q_{j}}$ is very small, the screened confinement will return to the quadratic form. This is why the results are insensitive to the value of $\mu _{cc}$ and $\mu _{bb}$. Therefore, we can use the quadratic form of the confinement expression for the fully heavy dibaryon systems.

$V^\mathrm{{OGE}}_{ij}$ is the one-gluon-exchange interaction:

$$\begin{aligned} V^\mathrm{{OGE}}_{ij}&= \frac{\alpha _s(\mu ) }{4}{\varvec{\lambda }}^{c}_i \cdot {\varvec{\lambda }}^{c}_j \nonumber \\&\quad \times \left[ \frac{1}{r_{ij}}-\frac{\pi }{2}\delta ({\varvec{r}}_{ij})\left( \frac{1}{m^2_i}+\frac{1}{m^2_j} +\frac{4{\varvec{\sigma }}_i\cdot {\varvec{\sigma }}_j}{3m_im_j}\right) \right] ,\nonumber \\ \end{aligned}$$

(5)

where $\alpha _{s}(\mu )$ is the quark–gluon coupling constant. In Ref. [24], it is written as

$$\begin{aligned} \alpha _{s}(\mu )= & {} \frac{\alpha _{0}}{\ln \left( \frac{\mu ^2+\mu _{0}^2}{\varLambda _{0}^2}\right) }, \end{aligned}$$

(6)

where $\mu$ is the reduced mass of the interacting quark pair. The other symbols in the above expressions have their usual meanings. All parameters are fixed by fitting to the masses of baryons with light flavors and heavy flavors, and the MINUIT program is employed for the fitting. The model parameters and the masses of the fitted baryons with errors are shown in Tables 1 and 2.

Table 2 The masses (in MeV) of the light, charmed, and bottomed baryons. Experimental values are taken from the Particle Data Group (PDG) [32]

The resonating group method (RGM) [25, 26] and generator coordinates method [27, 28] are used to carry out a dynamical calculation. The main feature of the RGM for two-cluster systems is that it assumes that two clusters are frozen inside, and only considers the relative motion between the two clusters. Thus, the conventional ansatz for the two-cluster wavefunctions is

$$\begin{aligned} \psi _{6q} = \mathcal{A}\left[ [\phi _{B_{1}}\phi _{B_{2}}]^{[\sigma ]IS}\otimes \chi _{L}(\varvec{R})\right] ^{J}, \end{aligned}$$

(7)

where the symbol $\mathcal{A}$ is the antisymmetrization operator. For the dibaryon $\varOmega _{ccc}\varOmega _{ccc}$ or $\varOmega _{bbb}\varOmega _{bbb}$, $\mathcal{A} = 1-9P_{36}$; $\varOmega _{ccb}\varOmega _{bbc}$, $\mathcal{A} = 1-P_{16}-P_{26}-P_{34}-P_{35}+P_{16}P_{34}+P_{16}P_{35}+P_{26}P_{34}+P_{26}P_{35}$; and $\varOmega _{ccc}\varOmega _{bbb}$, $\mathcal{A} = 1$. $[\sigma ]=[222]$ gives the total color symmetry, and all other symbols have their usual meanings. $\phi _{B_{i}}$ is the three-quark cluster wavefunction, and $\chi _{L}(\varvec{R})$ is the relative motion wavefunction, which is expanded by a set of Gaussians with different centers [29],

$$\begin{aligned} \chi _{L}(\varvec{R})= & {} \frac{1}{\sqrt{4\pi }}\left( \frac{3}{2\pi b^2}\right) ^{3/4} \sum _{i=1}^{n} C_{i} \nonumber \\&\times \int \exp \left[ -\frac{3}{4b^2}(\varvec{R}-\varvec{S}_{i})^{2}\right] Y_{LM}(\hat{\varvec{S}_{i}})d\hat{\varvec{S}_{i}},~~~~~ \end{aligned}$$

(8)

where L is the orbital angular momentum between two clusters. n is the number of Gaussians used in the expansion, which is fixed by the requirement that the results are stable against the increasing of n. By including the center-of-mass motion

$$\begin{aligned} \phi _{C} (\varvec{R}_{C}) = \left( \frac{6}{\pi b^{2}}\right) ^{3/4}e^{-\frac{3\varvec{R}^{2}_{C}}{b^{2}}}, \end{aligned}$$

(9)

the ansatz Eq. (7) can be rewritten as

$$\begin{aligned} \psi _{6q}= & {} \mathcal{A} \sum _{i=1}^{n} C_{i} \int \frac{d\hat{\varvec{S}_{i}}}{\sqrt{4\pi }} \prod _{\alpha =1}^{3}\phi _{\alpha }(\varvec{S}_{i}) \prod _{\beta =4}^{6}\phi _{\beta }(-\varvec{S}_{i}) \nonumber \\&\times \left[ [\eta _{I_{1}S_{1}}(B_{1})\eta _{I_{2}S_{2}}(B_{2})]^{IS}Y_{LM}(\hat{\varvec{S}_{i}})\right] ^{J} \nonumber \\&\times [\chi _{c}(B_{1})\chi _{c}(B_{2})]^{[\sigma ]}, \end{aligned}$$

(10)

where $\phi _{\alpha }(\varvec{S}_{i})$ and $\phi _{\beta }(-\varvec{S}_{i})$ are the single-particle orbital wavefunctions with different reference centers:

$$\begin{aligned} \phi _\alpha (\varvec{S_{i}})= & {} \left( \frac{1}{\pi b^2}\right) ^{\frac{3}{4}}e^ {-\frac{(\varvec{r}_{\alpha }-\varvec{S_i}/2)^2}{2b^2}}, \nonumber \\ \phi _\beta (-\varvec{S_{i}})= & {} \left( \frac{1}{\pi b^2}\right) ^{\frac{3}{4}}e^ {-\frac{(\varvec{r}_{\beta }+\varvec{S_i}/2)^2}{2b^2}} . \end{aligned}$$

(11)

In the present work, to reduce the computational burden, perturbation theory is employed, and the zeroth-order wavefunctions are used to obtain the energy of the system in first order. The relative motion and center-of-mass motion with different masses of quarks are calculated, taking proper care. We used this method to study the dibaryon $N\varOmega$ [16], and the result was consistent with the lattice QCD [30]. The experimental result from the STAR Collaboration also supported our prediction of $N\varOmega$ resonance [31].

From the variational principle, we obtain the generalized eigenvalue equation

$$\begin{aligned} \sum _{j} C_{j}H_{i,j}= E \sum _{j} C_{j}N_{i,j}, \end{aligned}$$

(12)

where $H_{i,j}$ and $N_{i,j}$ are the Hamiltonian matrix elements and overlaps, respectively. By solving the generalized eigen problem, we can obtain the energy and the corresponding wavefunctions of the dibaryon system.

3 Results and discussion

As the first step, we calculate the energy of the color-singlet states (two clusters with color singlet) with the quantum numbers $J=0,~1,~2$, and 3. The results are listed in Table 3. Here, we should mention that in the RGM, the internal motions of clusters are frozen, and the relative motion wavefunction is expanded by a set of Gaussians (see Eq. (8)). So, in this method, the orbital angular momentum between two clusters is also the total orbital angular momentum of the system. For the $\varOmega _{ccc}\varOmega _{ccc}$ or $\varOmega _{bbb}\varOmega _{bbb}$ system, which includes six identical quarks, totally antisymmetric wavefunctions must be used. The total symmetry is determined by the symmetry of four degrees of freedom (color, isospin, spin, and orbital). Here, the symmetry of both color and isospin is symmetrical; the spin (S) is symmetrical for $S=1$ or 3, and antisymmetric for $S=0$ or 2. To obtain the totally antisymmetric wavefunction, the orbital angular momentum L should be odd for the $S=1$ or 3, and even for $S=0$ or 2. If we consider the lower partial wave, we can take $L=1$ for $S=1$ or 3, and $L=0$ for $S=0$ or 2. Then, we can obtain the total angular momentum $J=0,~1,~2,~3,~4$ with negative parity and $J=0,~2$ with positive parity. Also, the spin-orbit interaction is not included in the present calculation. So, for the case of $L=1, S=1$, the results of $J^P=0^-$ are the same with $J^P=1^-$ and $2^-$, and for the case of $L,=1, S=3$, the results of $J^P=2^-$ are the same with $J^P=3^-$ and $4^-$. Therefore, we only show the results of $J^P=1^-$ and $J^P=3^-$ in Table 3. However, nonidentical quarks in two subclusters of the system $\varOmega _{ccc}\varOmega _{bbb}$ leading to both positive and negative parity are possible for this system with $J=0,~1,~2$, and 3.

Table 3 The energy (in MeV) of the color-singlet channel for the fully heavy dibaryons

From Table 3, one can see that the energies of all states are above the corresponding theoretical threshold, except the states $\varOmega _{ccc}\varOmega _{ccc}$, $\varOmega _{bbb}\varOmega _{bbb}$, and $\varOmega _{ccb}\varOmega _{bbc}$ with $J^{P}=0^{+}$, whose energy is $-2.5$ MeV, $-0.9$ MeV, and $-1.1$ MeV lower than the corresponding thresholds, respectively. Therefore, for the $J^{P}=0^{+}$ systems, the dibaryon with six c quarks or six b quarks, or with the $ccb-bbc$ structure, can form bound states, while the one with the $ccc-bbb$ structure is unbound. This is due to the different symmetry requirements for the different dibaryon structures. An antisymmetrization operator is required for the systems $\varOmega _{ccc}\varOmega _{ccc}$, $\varOmega _{bbb}\varOmega _{bbb}$, and $\varOmega _{ccb}\varOmega _{bbc}$, while there is no symmetry requirement between the clusters $\varOmega _{ccc}$ and $\varOmega _{bbb}$. We also note that the energies of the states $\varOmega _{ccc}\varOmega _{bbb}$ with different quantum numbers are the same. This is mainly because there is no interaction between two color-singlet subclusters because there is no exchange term. In this case, the color-related interaction does not work between (ccc) and (bbb), so the energies with different total angular momenta are the same. Besides, the spin-orbit interaction is not included in present calculation, and the states with $J^P=0^+$ ($S=0, L=0$) and $J^P=0^-$ ($S=1, L=1$) have the same energy, because the two clusters are well separated to minimize the kinetic energy. However, for the hidden-color channels (two clusters with a color octet), the color-related interaction works between (ccc) and (bbb), so the results will be different for these states. The results of the hidden-color channels and the channel-coupling calculation will be shown later.

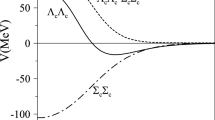
The effective potentials are also calculated to understand the interaction between two fully heavy baryons, which are shown in Figs. 1 and 2. The effective potential between two colorless clusters is defined as $V(S)=E(S)-E(\infty )$, where E(S) is the diagonal matrix element of the Hamiltonian of the system in the generating coordinate. It is clear that the potentials for the $\varOmega _{ccc}\varOmega _{ccc}$, $\varOmega _{bbb}\varOmega _{bbb}$, and $\varOmega _{ccb}\varOmega _{bbc}$ with $J^{P}=0^{+}$ are attractive, which leads to the possibility for these three channels to form bound states. However, the potentials for other channels are all repulsive, and therefore the other states are unbound.

Fig. 1

The effective potential of the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ systems

Fig. 2

The effective potential of the $\varOmega _{ccb}\varOmega _{bbc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ systems

Fig. 3

The contributions to the effective potential from the kinetic energy ($V_{vk}$), the confinement ($V_{con}$), and the one-gluon exchange ($V_{oge}$) of the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ systems with $J^{P}=0^{+}$

To investigate the interactions between two fully heavy baryons in detail, we calculate the contributions to the effective potential from the kinetic energy ($V_{vk}$), the confinement ($V_{con}$), and the one-gluon exchange ($V_{oge}$) of the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ systems with $J^{P}=0^{+}$, which are shown in Fig. 3. One can see that there is no contribution of color confinement interaction between two color-singlet clusters. For the $\varOmega _{ccc}\varOmega _{bbb}$ system, the contribution of the one-gluon exchange interaction between $\varOmega _{ccc}$ and $\varOmega _{bbb}$ is also zero, because there is no quark exchange between these two baryons. Although the one-gluon exchange interaction works for the $\varOmega _{ccc}\varOmega _{ccc}$, it is very small due to the small quark–gluon coupling constant $\alpha _s(\mu )$ used for the fully heavy system. Besides, the effective potential of the kinetic energy shows that the kinetic energy term provides attractive interactions for the $\varOmega _{ccc}\varOmega _{ccc}$ system, while it provides repulsive interactions for the $\varOmega _{ccc}\varOmega _{bbb}$ system. This is due to the different symmetry requirement for the different dibaryon structures. At finite separation, the kinetic energy of the relative motion between two clusters generally makes a positive contribution. However, the antisymmetrization operator for the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ systems causes the exchange of quarks between two clusters, which increases the motion space of each quark for the six identical quarks systems, and the internal kinetic energy of each cluster is reduced. Thus, the total kinetic energy of the six-quark system may be smaller than the sum of the internal kinetic energies of two free three-quark systems, although there is relative kinetic energy between the two clusters. Therefore, it is possible that the contribution of the kinetic energy term for the $\varOmega _{ccc}\varOmega _{ccc}$ system will be negative. For the $\varOmega _{ccc}\varOmega _{bbb}$ system, there is no quark exchange between $\varOmega _{ccc}$ and $\varOmega _{bbb}$, so the contribution of the kinetic energy term for the $\varOmega _{ccc}\varOmega _{bbb}$ system is positive.

In the above calculation, we only consider the color-singlet channels of the systems. However, the hidden-color channels and the channel-coupling effect are important in multiquark systems. Therefore, we calculate the hidden-color channels and the channel coupling of the systems. The results are presented in Tables 4 and 5, in which the binding energy is obtained by subtracting the threshold of the corresponding channel from the energy of the system. $E_{sc1}$/$B_{sc1}$ and $E_{sc2}$/$B_{sc2}$ represent the energies/binding energies of the color-singlet channels and hidden-color channels, respectively; $E_{cc}$/$B_{cc}$ represents the energies/binding energies of the channel coupling of both the color-singlet and hidden-color channels; $E^{\prime }_{cc}$/$B^{\prime }_{cc}$ represents the energies/binding energies of the channel coupling of all channels of the $\varOmega _{ccb}\varOmega _{bbc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ systems; and ub means that the energy is above the threshold of the corresponding channel.

Table 4 The energies and binding energies (in MeV) of every single channel and the channel-coupling calculation of the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ systems with $J^{P}=0^{+}$

Table 5 The energies and binding energies (in MeV) of every single channel and the channel-coupling calculation of the $\varOmega _{ccb}\varOmega _{bbc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ systems with $J^{P}=0^{+}$. $E^{\prime }_{cc}$ and $B^{\prime }_{cc}$ are the results by coupling all channels of both $\varOmega _{ccb}\varOmega _{bbc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ systems

We can see from Tables 4 and 5 that the hidden-color channels have lower energies than the corresponding color-singlet channels, and the channel coupling of the color-singlet and hidden-color channels will increase the binding energy of the systems considerably. For the cccccc system with $J^P=0^+$, the binding energy in the single-channel calculation is $-2.5$ MeV for the color-singlet channel and $-14.7$ MeV for the hidden-color channel, and it will reach $-30.1$ MeV in the channel-coupling calculation. For the bbbbbb system, the results are similar to those for the cccccc system, $-0.9$ MeV for the color-singlet channel, $-1.3$ MeV for the hidden-color channel, and $-7.6$ MeV in the channel-coupling calculation. For the cccbbb system, the state with the $\varOmega _{ccc}\varOmega _{bbb}$ structure is unbound, but the state with $\varOmega _{ccb}\varOmega _{bbc}$ is bound, and the binding energies have similar behavior as that of the cccccc system, $-1.1$ MeV for the color-singlet channel, $-11.6$ MeV for the hidden-color channel, and $-35.6$ MeV in the channel-coupling calculation. These two structures have the same quark content, and they can be coupled. The structure-coupling calculation obtains binding energy of $-80.1$ MeV for the cccbbb system with $J^P=0^+$. Thus, the fully heavy dibaryons with $J^P=0^+$ are bound states.

In determining the model parameters, the same b, which relates to the size of baryon, is used for all baryons. This is not reasonable, because the light baryons and the fully heavy baryons differ in size. A value of $b=0.518$ is good for describing the properties of the proton, while smaller b is expected to describe the fully heavy baryons. To test the dependence of the result on the baryon size parameter b, we calculate the fully heavy six-quark systems with $b=0.3$ fm. The results are as follows. The binding energy for the cccccc system with $J^P=0^+$ is $-56$ MeV; it is $-8.0$ MeV for the bbbbbb system, and $-15.4$ MeV for the cccbbb system. Therefore, the existence of fully heavy dibaryons is weakly dependent on the model parameters.

To further check the possibility of the bound state, we can also study the low-energy scattering phase shifts of the state. Here, we calculate the low-energy scattering phase shifts of the color-singlet channel of the $S-$wave $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ states, which are shown in Fig. 4. The well-developed Kohn–Hulthen–Kato (KHK) variational method is used here, the details of which can be found in Ref. [26]. It is obvious that the scattering phase shifts of the two systems reach 180 degrees at $E_{c.m.}\sim 0$ and rapidly decrease as $E_{c.m.}$ increases, suggesting the presence of a bound state.

Fig. 4

The phase shifts of the S-wave $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ systems with $J^{P}=0^{+}$

Then, we can extract the low-energy scattering parameters, scattering length $a_{0}$, and the effective range $r_{0}$ for both $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ systems using the formula

$$\begin{aligned} k\cot \delta= & {} -\frac{1}{a_{0}}+\frac{1}{2}r_{0}k^{2}+\mathcal{O}(k^{4}) \end{aligned}$$

(13)

where $\delta$ is the low-energy phase shifts obtained above, k is the momentum of relative motion with $k=\sqrt{2\mu E_{c.m.}}$, in which $\mu$ is the reduced mass of two baryons, and $E_{c.m.}$ is the incident energy. The binding energy $B^{\prime }$ can be calculated according to the relation

$$\begin{aligned} B^{\prime }= & {} \frac{\hbar ^2\alpha ^2}{2\mu } \end{aligned}$$

(14)

where $\alpha$ is the wave number which can be obtained from the relation [33]

$$\begin{aligned} r_{0}= & {} \frac{2}{\alpha }\left( 1-\frac{1}{\alpha a_{0}}\right) . \end{aligned}$$

(15)

For the bound state, the wave number $\alpha$ is the inverse of the spatial dimension of the system [34], and the required solution of Eq. (15) can be fixed accordingly. Please note that we use another method to calculate the binding energy here, so we label it $B^{\prime }$. The results are listed in Table 6, from which we can see that the scattering length is positive for both dibaryons $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$, which implies the existence of a bound state of these two fully heavy dibaryons. The binding energies obtained here are coincident with those calculated from Table 3.

Table 6 The scattering length $a_{0}$, effective range $r_{0}$, and binding energy $B^{\prime }$ of the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$ systems with $J^{P}=0^{+}$

4 Summary

The main conclusion of our dynamical investigation of fully heavy dibaryons is that the dibaryons composed of six c quarks, six b quarks, or three c quarks and three b quarks can form bound states, and the quantum number is $J^{P}=0^{+}$. However, the nature of these systems differs. For the $\varOmega _{ccc}\varOmega _{ccc}$ or $\varOmega _{bbb}\varOmega _{bbb}$, the requirement of antisymmetrization between the same baryon clusters introduces attractive interaction between two fully heavy baryons, which leads to a super-heavy bound dibaryon $\varOmega _{ccc}\varOmega _{ccc}$ or $\varOmega _{bbb}\varOmega _{bbb}$. The channel coupling between the color-singlet and hidden-color channels causes the binding energy to increase.

For the system with three c quarks and three b quarks, there is no evidence for any stable dibaryon with the structure of color-singlet $\varOmega _{ccc}\varOmega _{bbb}$. This outcome is based on the concept of “QCD-inspired” constituent quark model calculation, where the interactions among quarks are color-related. The principal reason for the instability of the $\varOmega _{ccc}\varOmega _{bbb}$ system is that there is no symmetry requirement between the subclusters $\varOmega _{ccc}$ and $\varOmega _{bbb}$ because quark c and quark b are not identical quarks. Therefore, the interaction between two subclusters is zero. In contrast, for the $\varOmega _{ccb}\varOmega _{bbc}$, the exchange of identical quarks can occur between two subclusters, resulting in nonzero exchange terms of the interaction, and thus the formation of a bound state is possible. The channel coupling of all channels of both $\varOmega _{ccb}\varOmega _{bbc}$ and $\varOmega _{ccc}\varOmega _{bbb}$ structures leads to the bound state of this fully heavy system, which is composed of three c quarks and three b quarks.

Table 7 The matrix elements in spin-flavor-color-isospin spaces of the color-singlet channel for the $\varOmega _{ccc}\varOmega _{ccc}$ system with $J^{P}=0^{+}$

The study of the interaction between two fully heavy baryons supports this conclusion, because the effective potentials are attractive. The behavior of low-energy scattering phase shifts and the scattering length also confirm the existence of stable fully heavy dibaryons $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{bbb}\varOmega _{bbb}$. The lattice QCD was used to study the highest charm dibaryon $\varOmega _{ccc}\varOmega _{ccc}$, and indicated the existence of this state [4]. We suggest that the lattice QCD indicates the existence of the fully heavy dibaryon with six b quarks, and the one with three c quarks and three b quarks.

Appendix

Table 8 The matrix elements in spin-flavor-color-isospin spaces of the hidden-color channel for the $\varOmega _{ccc}\varOmega _{ccc}$ system with $J^{P}=0^{+}$

Table 9 The cross matrix elements in spin-flavor-color-isospin spaces of the color-singlet and hidden-color channels for the $\varOmega _{ccc}\varOmega _{ccc}$ system with $J^{P}=0^{+}$

Table 10 The matrix elements in spin-flavor-color-isospin spaces of the color-singlet channel for the $\varOmega _{ccb}\varOmega _{bbc}$ system with $J^{P}=0^{+}$

Table 11 The matrix elements in spin-flavor-color-isospin spaces of the hidden-color channel for the $\varOmega _{ccb}\varOmega _{bbc}$ system with $J^{P}=0^{+}$

Table 12 The cross matrix elements in spin-flavor-color-isospin spaces of the color-singlet and hidden-color channels for the $\varOmega _{ccb}\varOmega _{bbc}$ system with $J^{P}=0^{+}$

To provide more information for the six-quark system calculation, the matrix elements in spin-flavor-color space are listed in the appendix. To save space, only the results for the $\varOmega _{ccc}\varOmega _{ccc}$ and $\varOmega _{ccb}\varOmega _{bbc}$ systems are shown in (Tables 7, 8, 9, 10, 11, 12). The definition of the matrix elements are as follows.

$$\begin{aligned} N_{D}= & {} \langle \psi |\psi \rangle , \end{aligned}$$

(A1)

$$\begin{aligned} N_{E}= & {} \langle \psi |\mathcal{A^{\prime } }\psi \rangle , \end{aligned}$$

(A2)

$$\begin{aligned} \langle H^{c}_{ij}\rangle _{D}= & {} \langle \psi |\varvec{\lambda }^c_{i}\cdot \varvec{ \lambda }^c_{j}|\psi \rangle , \end{aligned}$$

(A3)

$$\begin{aligned} \langle H^{c}_{ij}\rangle _{E}= & {} \langle \psi |\varvec{\lambda }^c_{i}\cdot \varvec{ \lambda }^c_{j}|\mathcal{A^{\prime } }\psi \rangle , \end{aligned}$$

(A4)

$$\begin{aligned} \langle H^{cs}_{ij}\rangle _{D}= & {} \langle \psi |\varvec{\lambda }^c_{i}\cdot \varvec{ \lambda }^c_{j}\varvec{\sigma }_i\cdot \varvec{\sigma }_j|\psi \rangle , \end{aligned}$$

(A5)

$$\begin{aligned} \langle H^{cs}_{ij}\rangle _{E}= & {} \langle \psi |\varvec{\lambda }^c_{i}\cdot \varvec{ \lambda }^c_{j}\varvec{\sigma }_i\cdot \varvec{\sigma }_j|\mathcal{A^{\prime } }\psi \rangle . \end{aligned}$$

(A6)

The wavefunction $\psi$ is the six-quark one in Eq.(10) without the antisymmetrization operator. The antisymmetrization operator $\mathcal{A}=1-\mathcal{A^{\prime } }$, where $\mathcal{A^{\prime } } = 9P_{36}$ for $\varOmega _{ccc}\varOmega _{ccc}$ and $\mathcal{A^{\prime } } = P_{16}+P_{26}+P_{34}+P_{35}-P_{16}P_{34}-P_{16}P_{35}-P_{26}P_{34}-P_{26}P_{35}$ for $\varOmega _{ccb}\varOmega _{bbc}$.

For the $\varOmega _{ccc}\varOmega _{ccc}$ system, the direct and exchange terms of overlap for the color-singlet channel are $N_D=1$, $N_E=-1$; for the hidden-color channel they are $N_D=1$, $N_E=-7$; and the cross ones between color-singlet and hidden-color channels are $N_D=0$, $N_E=-4$. For the $\varOmega _{ccb}\varOmega _{bbc}$ system, the direct and exchange terms of overlap for the color-singlet channel are $N_D=1$, $N_E=-8/9$; for the hidden-color channel they are $N_D=1$, $N_E=-56/9$; and the cross ones between the color-singlet and hidden-color channels are $N_D=0$, $N_E=-32/9$.