Correlation redistribution by causal horizons

Abstract

The Minkowski vacuum $|0\rangle _M$, which for an inertial observer is devoid of particles, is perceived as a thermal bath by Rindler observers living in a single Rindler wedge (Unruh in Phys Rev D 14:870, 1976) as a result of the discrepancy in the definition of positive frequency between the two classes of observers and a strong entanglement between degrees of freedom in the left and right Rindler wedges. We revisit the problem of quantification of the correlations in a two-mode state of a free neutral scalar field which is observed by an inertial observer Alice and left/right Rindler observers Rob/AntiRob, a problem that pertains to the field of relativistic quantum information and has been previously studied in Martin-Martinez et al. (Phys Rev D 82:064006, 2010) and Datta (Phys Rev A 80:052304, 2009). We focus on the analysis of informational quantities like the locally accessible and locally inaccessible information (Koashi and Winter in Phys Rev A 69:022309, 2004; Fanchini et al. in Phys Rev A 84:012313, 2011; Fanchini et al. in New J Phys 14:013027, 2012) and a closely associated entanglement measure, the entanglement of formation. We conclude that, with respect to the correlation structure probed by inertial observers alone, the introduction of a Rindler observer gives rise to a correlation redistribution which can be quantified by the entanglement of formation. Given the informational meaning of the derived correlations, we discuss on the capacity of a quantum channel to communicate classical information between accelerated parties.

1 Introduction

The black hole information problem is one of the most outstanding problems related to quantum gravity. While it may be true that in a semiclassical analysis of quantum field theory in curved spacetimes, in which gravity is treated in the purely classical framework of general relativity, some may give good arguments that information is really lost in the process of black hole formation and evaporation [1], admitting that this remains the case in the quantum theory seems really disturbing, see e.g. [2] and references therein. One important aspect related to this problem is the calculation of the detailed information flow out of black holes [3]. In that case it could prove useful to understand how informational quantities like the locally accessible information (LAI) and locally inaccessible information (LII) behave in the presence of causal horizons and revisit the study of entanglement employing one entanglement monotone which is connected to these informational quantities. We study these quantities in a far simpler scenario than that of the black hole information problem, in which a causal horizon analogous to that of the black hole is present: we consider two modes of a scalar field in the context of the Unruh effect in Minkowski spacetime. In doing so we evade the complications introduced by the true black hole, we have a system in hand for which we can evaluate the informational quantities of interest or bounds thereof, and we still retain a causal horizon, the Rindler horizon.

The Unruh effect is one of the most important predictions of Quantum Field Theory in Curved Spacetime, showing very clearly that the idea of particle is not really a fundamental concept, being observer-dependent [4] – the Minkowski vacuum $|0\rangle _M$ which, by definition, is devoid of particles for an inertial observer, is experienced as a thermal bath by one uniformly accelerated observer. The reason for that is twofold: first, such uniformly accelerated observer has a definition of energy, and hence of positive-frequency, inequivalent to that of the inertial observer. Second, such observer experiences a causal horizon which implies an information loss that renders the pure state $|0\rangle _M$ a mixed thermal state.

The setting to study the Unruh effect is to consider a D-dimensional Minkowski spacetime with coordinates $(t,x,y_i)$, where $i=1,\ldots , D-2$, and to consider observers which uniformly accelerate either towards the positive x direction or towards the negative x direction. The ones accelerating towards $x > 0$ are restricted to the so-called right Rindler wedge, ${\mathcal {U}}_\mathrm{I}$, defined by $x > |t|$ whereas the ones accelerating towards $x < 0$ are restricted to the so-called left Rindler wedge, ${\mathcal {U}}_\mathrm{II}$, defined by $x < -|t|$. Both classes of observers are called Rindler observers and some of their worldlines are shown in Fig. 1, where it is clear that the right and left Rindler wedges are causally disconnected from each other.¹

Fig. 1

Worldlines of Rindler observers on the right and left wedges, shown in gray (solid) lines. The Rindler horizons separating the wedges are shown as the red (dashed) lines

The origin of the Unruh effect lies in a strong entanglement between degrees of freedom in ${\mathcal {U}}_\mathrm{I}$ and ${\mathcal {U}}_\mathrm{II}$. In fact, it can be shown that the Minkowski vacuum can be written in a basis appropriate to the Rindler observers as [5]

$$\begin{aligned} |0\rangle _M = \prod _{\omega }\dfrac{1}{\cosh \alpha _\omega }\sum _{n_\omega =0}^{\infty }\tanh ^{n_\omega }\alpha _\omega |n_\omega \rangle ^I |n_\omega \rangle ^{II}, \end{aligned}$$

(1)

where one has introduced the so-called squeezing parameter $\alpha _\omega$ for each frequency by the relation

$$\begin{aligned} \tanh \alpha _\omega = e^{-\pi \omega /a}, \end{aligned}$$

(2)

being a the acceleration parameter of the Rindler observers. In that case, the Rindler observer is restricted to the right Rindler wedge, and thus is causally forbidden to have knowledge about the degrees of freedom in the left Rindler wedge. Due to the strong entanglement between both regions, this lack of knowledge manifests as a high degree of mixedness for the state locally probed. There are already many relevant discussions on this subject in the literature, in the field of Relativistic Quantum Information, for example Refs. [6,7,8,9,10] and references therein, to quote a few. Nonetheless, in most of these references the entanglement monotone that has been employed was the negativity, which is not directly related to informational quantities like the LAI and LII. In that case, it would be particularly interesting that the entanglement monotone employed not only have an informational meaning behind its definition, but also, allow the understanding and actual quantification on how the quantum correlation initially established between Alice and Bob is redistributed in non-inertial reference frames. In a practical setting it would allow, for example, to quantify the capacity of the established communication channels between accelerated parties. This could allow to further understand open problems related to the description of the physics of strongly accelerated bodies.

In this paper we give our first step in this program, by computing both the classical and quantum correlation distribution as locally probed by Alice, who is in an inertial reference frame, and by Rob in the right Rindler wedge, or when probed by Alice and AntiRob, in the left Rindler wedge, and interpret these results in terms of locally accessible and locally inaccessible information [11, 12]. This contrasts with [7] which analyzed just quantum discord for the Alice and Rob bipartition, aiming at answering whether or not there are quantum correlations in the near-horizon limit. We further combine the results to the methods of [11,12,13] which enables the computation of the entanglement of formation for the subsystem probed by Rob and AntiRob. The ideas of [11,12,13] allow for an interpretation of this entanglement of formation in terms of correlation redistribution. For each measure we have analyzed (mutual information, classical correlations, quantum discord and entanglement of formation) we review its definition and significance and give the plots against acceleration together with the way we interpret it. The paper is organized as follows. In Sect. 2 we introduce the problem appropriately and review the previous treatments. In Sect. 3 we develop the basic canonical quantization rules in a curved spacetime. In Sect. 4 we review the relevant modes for the analysis we wish to develop, mainly the Minkowski, Unruh and Rindler Modes. In Sect. 5 we review the transformation of the states we wish to study to the Rindler basis. In Sect. 6 we present and discuss the mutual information, a result already known from [6]. In Sect. 7 we discuss locally accessible and locally inaccessible informations and plot all such correlation measures together to show the correlation redistribution. In Sect. 8 we present the entanglement of formation and its role as a quantifier of correlation redistribution. In Sect. 9, we employ the entanglement of formation for quantification of several quantities, including a discussion on channel capacity. Finally in Sect. 10 we give the final remarks and conclusions. For completeness, in Appendix A, we describe the numerical method we have employed to evaluate the locally accessible and locally inaccessible information and in Appendix B we describe how the same numeric method allows, for a class of states, a numeric evaluation of the entanglement of formation by an optimization over two angles.

2 Basic canonical quantization in curved spacetime

We shall review the most basic approach to the canonical quantization of a Klein–Gordon field in a globally hyperbolic spacetime. We just give the basic definitions and results, referring the reader to [14, 15] for a complete account of the subject.

Let (M, g) be a globally hyperbolic spacetime, and $\phi$ be a real, minimally coupled Klein–Gordon field on said background [16]. The dynamics of $\phi$ can be encoded in the Lagrangian density

$$\begin{aligned} {\mathcal {L}}=\frac{1}{2}\left( \nabla _\mu \phi \nabla ^\mu \phi -m^2 \phi ^2\right) \sqrt{|g|}. \end{aligned}$$

(3)

The equation of motion deriving from this Lagrangian is the well-known Klein–Gordon equation

$$\begin{aligned} (\Box - m^2)\phi = 0. \end{aligned}$$

(4)

Given a Cauchy surface $\Sigma \subset M$, with normal vector field $n^\mu$ and induced metric h, we can describe this system in the canonical formalism [15]. In particular, the $\phi (x)$, for $x\in \Sigma$, act as the coordinates, and the conjugate momenta are $\pi (x)$, given by [15]:

$$\begin{aligned} \pi (x) = (n^\mu (x)\nabla _\mu \phi (x))\sqrt{h}. \end{aligned}$$

(5)

Canonical quantization therefore amounts to finding a Hilbert space on which operators $\phi (x),\pi (x)$ act satisfying the equal-time canonical commutation relations

$$\begin{aligned} {[}\phi (x),\pi (y)]=i\delta (x,y),\quad x,y\in \Sigma . \end{aligned}$$

(6)

A manner of doing so is to expand the field into modes. In particular, recall that we can define, on the space of solutions to the Klein–Gordon equation, the bilinear form

$$\begin{aligned} (\phi ,\psi )=i\int _{\Sigma }(\phi ^*\nabla _\mu \psi -\psi \nabla _\mu \phi ^*)n^\mu d\Sigma , \end{aligned}$$

(7)

which satisfies all axioms of an inner product except that it is not positive-definite. One then introduces a set of the so-called mode functions $\{u_i,u_i^*\}$ such that

$$\begin{aligned} (u_i,u_j)=\delta _{ij},\quad (u_i,u_j^*)=0,\quad (u_i^*,u_j^*)=-\delta _{ij}, \end{aligned}$$

(8)

and such that any real solution $\phi$ to Eq. (4) can be uniquely expanded as

$$\begin{aligned} \phi = \sum _i a_i u_i + a_i^*u_i^*. \end{aligned}$$

(9)

Turning $\phi (x)$ to operators would then be equivalent to turning $a_i$ to operators. One may further argue [14] that the canonical commutation relations (6) are equivalent to the commutation relations

$$\begin{aligned}{}[a_i,a_j^\dagger ]=\delta _{ij},\quad [a_i,a_j]=[a_i^\dagger ,a_j^\dagger ]=0. \end{aligned}$$

(10)

This justifies a Fock space picture on which we have a vacuum state $|0\rangle$ defined by

$$\begin{aligned} a_i|0\rangle = 0. \end{aligned}$$

(11)

Being more explicit, the one-particle space is taken as the Hilbert space completion of the space of solutions spanned by just the $\{u_i\}$, without the complex conjugates, with inner product being the restriction of the Klein–Gordon form (, ) to that subspace. The Hilbert space of the theory is the bosonic Fock space construct, based on said one-particle Hilbert space [15, 16]. The interpretation of the construction lies in the observation that if the $u_i$ are positive-frequency with respect to a family of observers following the integral lines of a timelike future-directed normalized vector field Z, by which we mean that there are $\omega _i\in [0,+\infty )$ satisfying

$$\begin{aligned} {\mathfrak {L}}_Z u_i = -i\omega _i u_i,\quad \omega _i > 0, \end{aligned}$$

(12)

then the states $|1\rangle _i = a_i^\dagger |0\rangle$ are states containing just one particle in mode $u_i$ with energy $\omega _i$ and, more generally, we shall denote by $|n\rangle _i$ the state with n particles the mode $u_i$.

In general there is not a preferred choice of mode functions $\{u_i,u_i^*\}$ as there is no privileged notion of time in an arbitrary spacetime. It is important therefore to relate the constructions obtained by two distinct choices of mode functions $\{u_i,u_i^*\}$ and $\{\bar{u}_i,\bar{u}_i^*\}$. This may be accomplished by expanding one set in terms of the other set:

$$\begin{aligned} \bar{u}_i = \sum _j \alpha _{ij}u_j + \beta _{ij}u_j^*, \end{aligned}$$

(13)

in terms of the Bogolyubov coefficients $\alpha _{ij},\beta _{ij}$ [14]. These coefficients, which can be straightforwardly computed using Eq. (8) to be

$$\begin{aligned} \alpha _{ij}=(u_j,\bar{u}_i),\quad \beta _{ij}=-(u_j^*,\bar{u}_i), \end{aligned}$$

(14)

allows us to establish a relation between the annihilation and creation operators $a_i,a_i^\dagger$ of the $\{u_i,u_i^*\}$ quantization and $\bar{a}_i,\bar{a}_i^\dagger$ of the $\{\bar{u}_i,\bar{u}_i^*\}$ quantization. The relation, which, in this approach, is the central aspect of the comparison of the two quantizations, is given by

$$\begin{aligned} \bar{a}_i = \sum _j \alpha _{ij}a_i-\beta _{ij}a_i^\dagger ,\quad \bar{a}_i^\dagger = \sum _j \alpha _{ij}^*a_i^\dagger - \beta _{ij}^*a_i. \end{aligned}$$

(15)

It immediately follows from Eq. (15) that if $|0\rangle$ is the vacuum of the $\{u_i,u_i^*\}$ quantization then, in general, $\bar{a}_i|0\rangle \ne 0$, so that it does not coincide with the vacuum $|\bar{0}\rangle$ of the $\{\bar{u}_i,\bar{u}_i^*\}$ quantization. The two vacua coincide if and only if $\beta _{ij}=0$, which in turn happens when each $\bar{u}_i$ is a combination of only positive frequency modes of the first quantization. This is the straightforward treatment taken in many references, for instance in [14]. A more rigorous treatment is presented in [15].

3 Minkowski, Unruh and Rindler modes

We now briefly review the modes of importance for the analysis we wish to develop. Consider now the two-dimensional Minkowski spacetime $(M,\eta )$ with the flat metric $(\eta _{\mu \nu })={\text {diag}}(-1,1)$. Let a real massless Klein–Gordon field $\phi$ be given. We wish to quantize the field according to the ideas of the previous section. Minkowski spacetime, however, has a timelike Killing vector field, and hence has a class of distinguished observers whose four-velocity is proportional to the Killing field, namely the inertial observers. To quantize the field in appropriate manner to this class of observers one chooses modes which are positive frequency with respect to the inertial observers. A natural family of such modes are the plane waves

$$\begin{aligned} u^M_k(t,x) = \frac{1}{\sqrt{4\pi \omega _k}}e^{-i\omega _k t + ikx},\quad \omega _k=|k|, k\in {\mathbb {R}}, \end{aligned}$$

(16)

where the superscript M indicates these are Minkowski modes. These modes define the usual Minkowski quantization used in most flat-spacetime Quantum Field Theory textbooks [17,18,19,20]. They are labelled by a real number $k\in {\mathbb {R}}$ and divide in two classes: the left-moving solutions with $k < 0$ and the right-moving solutions with $k > 0$. Employing these modes, the field expands as

$$\begin{aligned} \phi (t,x)=\int _{{\mathbb {R}}} \bigg (u_k^M(t,x)a(k)+{u_k^M}^*(t,x)a^\dagger (k) \bigg )dk, \end{aligned}$$

(17)

and it is evident that decomposing the integral on the regions $k < 0$ and $k > 0$ we may write

$$\begin{aligned} \phi (t,x) = \phi _-(t,x)+\phi _+(t,x), \end{aligned}$$

(18)

where $\phi _-$ and $\phi _+$ are, respectively, the parts of the integral with $k < 0$ and $k > 0$. This equation tells that in the quantum theory the two sectors decouple and can be studied independently [21].

Now let us consider one eternally uniformly accelerating observer, also known as a Rindler observer, living in the right Rindler wedge ${\mathcal {U}}_I$ defined in the introduction. We can choose coordinates $(\eta ,\xi )$ on ${\mathcal {U}}_I$ adapted to the worldlines of such observers, given by

$$\begin{aligned} t = \frac{1}{a}e^{a\xi }\sinh (a\eta ), \quad z = \frac{1}{a}e^{a\xi }\cosh (a\eta ). \end{aligned}$$

(19)

In terms of these coordinates the appropriate modes for the right Rindler observer are the modes

$$\begin{aligned} u^{I}_k(\eta ,\xi )=\dfrac{1}{\sqrt{4\pi \omega _k}}e^{-i\omega _k \eta +ik\xi },\quad \omega _k = |k|,k \in {\mathbb {R}}. \end{aligned}$$

(20)

where now the superscript I indicates these are Rindler modes on the right Rindler wedge.

We wish to compare the two quantizations, but the Minkowski observer also probes degrees of freedom in the left Rindler wedge. Because of that, we also need to consider Rindler modes for a Rindler observer supported in that region. We similarly introduce in region ${\mathcal {U}}_{II}$ coordinates $(\eta ,\xi )$, denoted by the same symbols as those in region ${\mathcal {U}}_I$, which relate to the Minkowski coordinates by

$$\begin{aligned} t = -\frac{1}{a}e^{a\xi }\sinh (a\eta ), \quad z = -\frac{1}{a}e^{a\xi }\cosh (a\eta ). \end{aligned}$$

(21)

Using these coordinates the appropriate mode functions for the left Rindler observer are the modes

$$\begin{aligned} u_k^{II}(\eta ,\xi )=\dfrac{1}{\sqrt{4\pi \omega _k}}e^{i\omega _k \eta +ik\xi },\quad \omega _k=|k|,k\in {\mathbb {R}}. \end{aligned}$$

(22)

The modes $u_k^I$ and $u_k^{II}$ are at first defined just on ${\mathcal {U}}_I$ and ${\mathcal {U}}_{II}$, but if we set $u_k^I$ to be zero on ${\mathcal {U}}_{II}$ and $u_k^{II}$ to be zero on ${\mathcal {U}}_{I}$, then the set of modes $\{u_k^{I},{u_k^{I}}^*,u_k^{II},{u_k^{II}}^*\}$ taken together allow us to expand the general solution to the Klein–Gordon equation as

$$\begin{aligned} \phi (\eta ,\xi ) = \sum _{A=I,II}\int _{\mathbb {R}} \bigg (\!b^A(k)u_k^A(\eta ,\xi )+{b^A}^\dagger (k){u_k^A}^*(\eta ,\xi )\!\bigg )dk.\!\!\nonumber \\ \end{aligned}$$

(23)

If we consider the space of solutions spanned by just the positive-frequency modes $\{u_k^I,u_k^{II}\}$ then it is clear that its Hilbert space completion is a direct sum ${\mathfrak {H}}_I\oplus {\mathfrak {H}}_{II}$ where ${\mathfrak {H}}_I$ is the space spanned by just the $\{u_k^I\}$ and ${\mathfrak {H}}_{II}$ is the space spanned by just the $\{u_k^{II}\}$. It follows immediately that, for the Rindler quantization, the Fock space is a tensor product

$$\begin{aligned} {\mathcal {F}}({\mathfrak {H}}_I\oplus {\mathfrak {H}}_{II})={\mathcal {F}}({\mathfrak {H}}_I)\otimes {\mathcal {F}}({\mathfrak {H}}_{II}). \end{aligned}$$

(24)

In particular the Rindler vacuum $|0\rangle ^R$ decomposes as a product

$$\begin{aligned} |0\rangle ^R = |0\rangle ^I\otimes |0\rangle ^{II}. \end{aligned}$$

(25)

We wish to compare the quantizations, which would entail the computation of the Bogolyubov coefficients relating the Rindler modes and Minkowski modes. There is, however, a workaround, which will be further relevant for the informational analysis. The idea, due to Unruh [4], is to find a new set of modes which reproduces the Minkowski quantization, but which have a simpler expression in terms of the Rindler modes [6]. The appropriate modes are the so-called Unruh modes, defined by

$$\begin{aligned} h_k^{R}&=\cosh \alpha _\omega u_k^{I}+\sinh \alpha _\omega {u_{-k}^{II}}^*, \end{aligned}$$

(26a)

$$\begin{aligned} h_{k}^{L}&=\cosh \alpha _\omega u_k^{II}+\sinh \alpha _\omega {u_{-k}^{I}}^*, \end{aligned}$$

(26b)

where the squeezing parameter $\alpha _{\omega }$ is defined by $\tanh \alpha _\omega =e^{-\pi \omega /a}$ and where $\omega = |k|$ as already explained.

These modes allow for an expansion of the general solution to the Klein–Gordon equation, which in the quantum theory gives rise to the annihilation and creation operators

$$\begin{aligned} \phi (t,x)=\sum _{A=R,L}\int \bigg (c_k^A h_k^A(t,x)+{c_k^A}^\dagger {h_k^A}^*(t,x)\bigg ) dk. \end{aligned}$$

(27)

The Unruh modes are defined explicitly in terms of Rindler modes in Eq. (26a) and so the Bogolyubov coefficients relating $h_k^R,{h_k^{R}}^*$ with the Rindler modes can be obtained by inspection [21], being simply:

$$\begin{aligned} \alpha _{kk'}^{(I)}&=\cosh \alpha _\omega \delta (k-k'),\quad \alpha _{kk'}^{(II)}=0, \end{aligned}$$

(28a)

$$\begin{aligned} \beta _{kk'}^{(I)}&=0,\quad \beta _{kk'}^{(II)}=\sinh \alpha _\omega \delta (k-k'). \end{aligned}$$

(28b)

Since the Unruh quantization agrees with the Minkowski one, they share the same vacuum $|0\rangle ^M$ and the Minkowski vacuum may be defined by the equation

$$\begin{aligned} c_k^R |0\rangle ^M = c_k^{L}|0\rangle ^M = 0, \end{aligned}$$

(29)

for $k\in {\mathbb {R}}$. Using Eqs. (28) to express $c_k^R,c_k^{L}$ in terms of $b_k^I,{b_k^I}^\dagger ,b_k^{II},{b_k^{II}}^\dagger$, one is able to solve Eq. (29) on the Rindler basis and express the Minkowski vacuum in a basis meaningful for the Rindler observers. When this is done one obtains Eq. (1) [5]. To find out what a Rindler observer living in the right Rindler wedge ${\mathcal {U}}_I$ perceives one would trace out the modes supported in the region ${\mathcal {U}}_{II}$. If this is done one obtains the density operator

$$\begin{aligned} \rho _I = \prod _\omega \frac{1}{\cosh ^2\alpha _\omega }\sum _{n_\omega =0}^\infty \tanh ^{2n}\alpha _\omega |n\rangle ^I_\omega \langle n|. \end{aligned}$$

(30)

Upon recalling the definition of the squeezing parameter, Eq. (2), one is able to find out that this is, in fact, a thermal density operator with temperature, in natural units, $T = \frac{a}{2\pi }$. This result is the Unruh effect, stating that the Minkowski vacuum is perceived as a thermal mixed state for Rindler observers living in either the right or left Rindler wedges.

4 Observers and reference frames

Two inertial observers, Alice and Bob, observe two Unruh modes $h_k^R$ and $h_{k'}^R$ of a massless Klein–Gordon field. Alice is supposed to carry a detector sensitive only to the frequency $\omega$ of mode $h_k^R$ whereas Bob is supposed to carry a detector sensitive only to frequency $\omega '$ of mode $h_{k'}^R$. The state of the system is supposed to be a maximally entangled state

$$\begin{aligned} |\psi \rangle = \frac{1}{\sqrt{2}}\bigg (|0\rangle ^R_k|0\rangle ^R_{k'} + |1\rangle ^R_k |1\rangle ^R_{k'}\bigg ). \end{aligned}$$

(31)

It is fundamental to understand here that this is a bipartition with respect to modes. The fact that Alice’s detector can only detect frequency $\omega$ and not $\omega '$ implies that she has no access to the subsystem that Bob has access and vice-versa. In particular, any information Alice is able to gather about the mode $h_{k'}^R$ is through correlations.

One now introduces a Rindler observer, living on the right Rindler wedge ${\mathcal {U}}_I$, Rob, which also carries a detector sensitive only to frequency $\omega '$. It is fundamental here that one is working with Unruh modes. In that case, a mode which for the inertial observer has some specified frequency has the same frequency for the Rindler observer [6]. In that setting, inasmuch as Bob, Rob only observes mode $h_{k'}^R$. But since we have the two disconnected Rindler wedges, ${\mathcal {U}}_I$ and ${\mathcal {U}}_{II}$, isolated from each other by causal horizons, the transformation from the inertial basis to the Rindler basis introduces one additional bipartition between the two regions, c.f. Eq. (1). While Rob can only access the part of the state of mode $h_{k'}^R$ associated to ${\mathcal {U}}_I$ a symmetric Rindler observer on the left Rindler wedge ${\mathcal {U}}_{II}$ can only observe the complementary part. The introduction of said observer has been done in Ref. [6], where he is conventionally called AntiRob. Hence the setup is that of a tripartite quantum state observed by three observers: Alice, Rob and AntiRob, the first being inertial, and the other two being uniformly accelerated, living respectively on regions I and II. Alice carries a detector sensitive only to mode $h_k^R$ whereas Rob and AntiRob carry detectors sensitive only to mode $h_{k'}^R$. In that sense, the state, which when probed by Alice and Bob was naturally bipartite – a bipartition between modes $h_k^R$ and $h_{k'}^R$ – when probed by Alice, Rob and AntiRob is naturally tripartite – a bipartition between modes $h_k^R$ and $h_{k'}^R$ with a second bipartition between regions ${\mathcal {U}}_I$ and ${\mathcal {U}}_{II}$ affecting the mode $h_{k'}^R$ subsystem. That is the setup of Refs. [6, 7] which we consider.

In [6], the author considered the evaluation of the mutual information of the three possible bipartite subsystems and the negativity as a measure of entanglement. The negativity of the bipartitions between Alice–Rob and Alice–AntiRob was observed to decrease to zero in the infinite acceleration limit, which corresponds to the near-horizon limit. The authors concluded that an entanglement degradation existed due to the horizon and supposed that there remain no quantum correlations on the near-horizon limit, since the negativity vanishes in said situation. Moreover, the authors found that the negativity for the bipartition between Rob–AntiRob, i.e., between the observers separated by the causal horizon, increased in the near-horizon limit. They noticed, however, that this entanglement is not useful as a resource because these two observers are forbidden classical communication. In [7], the author evaluated the quantum discord of the state probed by Alice and Rob. The main conclusion was a comparison to the negativity and the observation that even though the negativity vanishes on the near-horizon limit, the quantum discord does not, signaling that there are still quantum correlations in that limit, which are not captured by the negativity.

5 States in the Rindler basis

Following previous works on the subject [6, 7], the first step to perform the analysis is to expand the mode $h_{k'}^R$ part of the state in Eq. (31) into a basis appropriate for the Rindler observers. This can be done employing the transformation of the Minkowski vacuum, Eq. (1), together with the transformation of the creation and annihilation operators of Unruh modes to creation and annihilation operators of Rindler modes, which can be done with the general transformation, Eq. (15), together with the concrete Bogolyubov coefficients, Eq. (28). This last step gives the one-particle Unruh state:

$$\begin{aligned} |1\rangle ^R_{k'} = \dfrac{1}{\cosh ^2 \alpha }\sum _{n=0}^\infty \tanh ^{n}\alpha \sqrt{n+1}|n+1\rangle _{k'}^{I} |n\rangle ^{II}_{k'}, \end{aligned}$$

(32)

where $\alpha ={\text {arctanh}}(e^{-\pi \omega '/a})$ is the squeezing parameter associated to the frequency $\omega '$ of mode $h_{k'}^R$. The fact that the transformation does not change the frequency, but only the occupation numbers, leading a monochromatic state to another monochromatic state, is the reason to use Unruh modes for this analysis. With this data, let $\rho _{M,I},\rho _{M,II},\rho _{I,II}$ be the bipartite states of the subsystems probed by Alice–Rob, Alice–AntiRob and Rob–AntiRob where the subscript M means that Alice is an inertial observer and therefore measures particles according to the Minkowski quantization, Rob is a Rindler observer in the right Rindler wedge ${\mathcal {U}}_I$ and AntiRob is a Rindler observer in the left Rindler wedge ${\mathcal {U}}_{II}$, both of which measure particles according to the Rindler quantization in their respective wedges. Employing the above transformations, the states in the Rindler basis are

$$\begin{aligned}&\rho _{M,I} = \dfrac{1}{2\cosh ^2\alpha }\sum _{n=0}^\infty \tanh ^{2n}\alpha \nonumber \\&\quad \bigg [|0n\rangle _{kk'}^{M,I}\langle 0n|+\dfrac{(n+1)}{\cosh ^2\alpha }|1n+1\rangle _{kk'}^{M,I}\langle 1n+1|\nonumber \\&\quad +\dfrac{\sqrt{n+1}}{\cosh \alpha } \bigg (|0n\rangle _{kk'}^{M,I}\langle 1n+1|+|1n+1\rangle _{kk'}^{M,I}\langle 0n|\bigg )\bigg ], \end{aligned}$$

(33)

$$\begin{aligned}&\rho _{M,II}=\dfrac{1}{2\cosh ^2\alpha }\sum _{n=0}^\infty \tanh ^{2n}\alpha \nonumber \\&\quad \bigg [|0n\rangle _{kk'}^{M,II}\langle 0n|+\dfrac{n+1}{\cosh ^2\alpha }|1n\rangle _{kk'}^{M,II}\langle 1n|+\dfrac{\sqrt{n+1}\tanh \alpha }{\cosh \alpha } \nonumber \\&\quad \bigg (|0n+1\rangle _{kk'}^{M,II}\langle 1n|+|1n\rangle _{kk'}^{M,II}\langle 0n+1|\bigg )\bigg ],\nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned}&\rho _{I,II}=\dfrac{1}{2\cosh ^2\alpha }\sum _{n,m=0}^\infty \tanh ^{n+m}\alpha \nonumber \\&\quad \times \bigg (|nn\rangle _{k'}^{I,II}\langle mm|\!+\!\dfrac{\sqrt{n+1}\sqrt{m+1}}{\cosh ^2\alpha }|n+1n\rangle _{k'}^{I,II}\langle m\!+\!1 m|\bigg ). \nonumber \\ \end{aligned}$$

(35)

In that same way, one may further obtain the states of the three subsystems probed individually by Alice, Rob and AntiRob. It gives

$$\begin{aligned}&\rho _M = \frac{1}{2}\left( |0\rangle _k^M\langle 0|+|1\rangle _k^M\langle 1|\right) , \end{aligned}$$

(36)

$$\begin{aligned}&\rho _I = \sum _{n=0}^\infty \dfrac{\tanh ^{2(n-1)}\alpha }{2\cosh ^2\alpha }\bigg (\tanh ^2\alpha +\frac{n}{\cosh ^2\alpha }\bigg )|n\rangle _{k'}^I\langle n|,\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned}&\rho _{II}= \dfrac{1}{2\cosh ^2\alpha }\sum _{n=0}^\infty \tanh ^{2n}\alpha \bigg (1+\frac{n+1}{\cosh ^2\alpha }\bigg )|n\rangle _{k'}^{II}\langle n|.\nonumber \\ \end{aligned}$$

(38)

6 Mutual information

Let $\rho _{AB}$ be a bipartite state and let $\rho _A = {\text {Tr}}_B\rho _{AB}$ and $\rho _B = {\text {Tr}}_A \rho _{AB}$ be the marginal states of the two subsystems, A and B, respectively. The mutual information is defined to be

$$\begin{aligned} I(\rho _{AB})=S(\rho _{A})+S(\rho _{B})-S(\rho _{AB}), \end{aligned}$$

(39)

where $S(\rho )$ is the von Neumann entropy of the density operator $\rho$. The mutual information quantifies the total correlations between the two parts. If we have a tripartite pure state $\rho _{ABC} = |\psi \rangle \langle \psi |$ then we can extract three marginal bipartite states from it, $\rho _{AB}={\text {Tr}}_C \rho _{ABC}$, $\rho _{AC}={\text {Tr}}_B \rho _{ABC}$, and $\rho _{BC}={\text {Tr}}_A \rho _{ABC}$. In that case, the fact that $\rho _{ABC}$ is pure implies the equalities

$$\begin{aligned} S(\rho _{AB})&=S(\rho _{C}), \end{aligned}$$

(40a)

$$\begin{aligned} S(\rho _{AC})&=S(\rho _{B}),\end{aligned}$$

(40b)

$$\begin{aligned} S(\rho _{BC})&=S(\rho _{A}), \end{aligned}$$

(40c)

and this implies that the evaluation of the mutual information for such bipartite states reduces to the problem of evaluating the von Neumann entropies $S(\rho _A)$, $S(\rho _B)$, $S(\rho _C)$.

Fig. 2

von Neumann entropies of the states $\rho _M,\rho _I,\rho _{II}$. The state $\rho _M$ is shown by the black (dotted) line, $\rho _I$ by the blue (solid) line and $\rho _{II}$ by the red (dashed) line

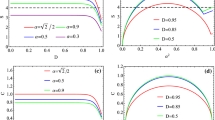
For the concrete problem we considered, all the states $\rho _M,\rho _I,\rho _{II}$ of the individual subsystems are diagonal in the Rindler occupation number basis. This means that evaluating the von Neumann entropies can be done straightforwardly. The results are shown in Fig. 2. From these entropies the mutual information can be straightforwardly obtained as well. The result is shown in Fig. 3.

Fig. 3

Mutual information – The state $\rho _{M,I}$ is the blue solid line, $\rho _{M,II}$ is the red dashed line and $\rho _{I,II}$ is the black dotted line

In Fig. 3 we see that the higher the squeezing parameter the more the correlations of the bipartition between the Minkowski and Rindler observer on the right Rindler wedge decrease and the more the correlations between the Minkowski and Rindler observer on the left Rindler wedge increase. Moreover, this follows a conservation law [6]. In fact, we have from Eqs. (39) and (40a),

$$\begin{aligned} I(\rho _{M,I})+I(\rho _{M,II})=2S(\rho _M), \end{aligned}$$

(41)

but it follows immediately from Eq. (36) that $S(\rho _A)=1$ and we find

$$\begin{aligned} I(\rho _{M,I})+I(\rho _{M,II})=2, \end{aligned}$$

(42)

which works as a conservation law, which is obeyed as a correlation transfer from the bipartition $\rho _{M,I}$ to the bipartition $\rho _{M,II}$. The meaning of this redistribution of correlation will become clear as we discuss the distinction of classical and quantum correlation in what follows.

7 Locally accessible and inaccessible information

Let again $\rho _{AB}$ be a bipartite state. The mutual information quantifies the total amount of information contained in the correlations between the two parts. One may ask how much of such information is locally accessible to each part by local measurements. This is quantified by the Locally Accessible Information (LAI) [12], also known as Classical Correlation [22]. To define it, suppose we wish to find how much information is accessible locally to B by local measurements. In that case the LAI is defined to be

$$\begin{aligned} J^\leftarrow (\rho _{AB})=\max _{{\mathbf {1}}\otimes \Pi } \bigg [S(\rho _A)-\sum _\lambda p_\lambda S(\rho _A^\lambda )\bigg ], \end{aligned}$$

(43)

where the maximum is taken over all possible projective measurements on the B subsystem. For each measurement $\Pi$, the probabilities are $p_\lambda$ and the post-selected states of the A subsystem are $\rho _A^\lambda$ (in other words, one takes the post-selected state of the composite system and traces B out). In the notation, the arrow points away from the system being measured. This quantity measures the maximum decrease in the uncertainty of the state of A that a measurement in B might impart, that being the reason why it is called Locally Accessible Information. The reason for the name Classical Correlations lies in the fact that $J^\leftarrow (\rho _{AB})$ satisfies properties that a quantifier of exclusively classical correlations should satisfy.

Associated to the LAI there is the Locally Inaccessible Information (LII). The idea is that it should quantify the amount of information contained in the correlations which cannot be accessed locally through measurements. Since the mutual information, $I(\rho _{AB})$ quantifies the total correlations, this can be defined straightforwardly as

$$\begin{aligned} {\mathcal {D}}^\leftarrow (\rho _{AB})=I(\rho _{AB})-J^\leftarrow (\rho _{AB}). \end{aligned}$$

(44)

This quantity is also known as the quantum discord and, inasmuch as $J^\leftarrow (\rho _{AB})$ quantifies the classical part of the correlations, it quantifies the quantum part of the correlations. We see from the definitions Eqs. (43) and (44) that both quantities can be very hard to compute due to the optimization they require. For a special case there is a simplification, that being the central idea of the method employed in [7], which allows the optimization to be carried out numerically as one optimization over $S^2$. We present the details of the method in Appendix A and here just give a brief overview.

The idea is that if a bipartite state $\rho _{AB}$ has one part which is effectively two-level, by which we mean it is written as

$$\begin{aligned} \rho _{AB}=\sum _{a,b=0,1}M_{ab}\otimes |a\rangle \langle b|, \end{aligned}$$

(45)

then one may focus on the measurements in B which lie in the subspace spanned by the basis operators $|a\rangle \langle b|$ for $a,b=0,1$. In that case, the measurements are represented by $2\times 2$ projectors and this enables to parameterize them by points on a sphere. Concretely, every measurement of interest consists of two projectors $\Pi _\pm ({\mathbf {x}})$ for ${\mathbf {x}}\in S^2$ given by

$$\begin{aligned} \Pi _{\pm }({\mathbf {x}}) = \frac{1}{2}\left[ {\mathbf {1}}\pm {\mathbf {x}}\cdot \sigma \right] ,\quad {\mathbf {x}}\in S^2, \end{aligned}$$

(46)

where $\sigma =(\sigma _1,\sigma _2,\sigma _3)$ is a vector whose components are three operators whose matrix representations are the Pauli matrices. In that case, $J^\leftarrow (\rho _{AB})$ may be obtained by an optimization over $S^2$ and ${\mathcal {D}}^\leftarrow (\rho _{AB})$ may be obtained from it. The two angles over which we optimize are the two angles that parameterize the measurement according to Eq. (46).

Considering the concrete state we are working with, there are two bipartitions to which the method applies, namely the bipartitions between Alice–Rob and Alice–AntiRob. The subsystem which is effectively two level is that of Alice, i.e., of the inertial observer, and hence the method allows to compute the LAI and LII for measurements made on the subsystem probed by the inertial observer. In other words, we are able to plot the LAI $J^\rightarrow (\rho _{M,I})$ and $J^\rightarrow (\rho _{M,II})$, and the LII ${\mathcal {D}}^\rightarrow (\rho _{M,I})$ and ${\mathcal {D}}^\rightarrow (\rho _{M,II})$. We plot, in Fig. 4, all correlations – mutual information, LAI and LII – for the Alice–Rob bipartition, with measurements carried out by Alice as a function of the squeezing parameter. Remark that the classical and quantum correlation differ quantitatively, while showing a similar behavior. We plot the same, in Fig. 5, for the Alice–AntiRob bipartition.

Fig. 4

State $\rho _{M,I}$ – Classical Correlations is the solid blue line, quantum discord is the black (dotted) line and mutual information is the red (dashed) line

Fig. 5

State $\rho _{M,II}$ – Classical Correlations is the solid blue line, quantum discord is the black dotted line and mutual information is the red dashed line

Finally, to discuss the results, it is very instructive to plot all correlations measures (LAI, LII and mutual information) for the two bipartitions together. Doing so, using different colors for each bipartition we obtain the plot shown in Fig. 6.

Fig. 6

States $\rho _{M,I}$ and $\rho _{M,II}$ compared – The state $\rho _{M,I}$ is depicted by the blue lines and $\rho _{M,II}$ by the red lines. Classical Correlations are the solid lines, quantum discord are the dotted lines and mutual information are dashed lines

There, the blue lines correspond to the bipartition between the inertial observer and the right Rindler observer, with the classical correlations and quantum discord characterizing respectively the locally accessible and locally inaccessible information for the inertial observer. The red lines are the plots for the bipartition among the inertial observer and the left Rindler observer and now the classical correlations and quantum discord characterize respectively the locally accessible and locally inaccessible information for the inertial observer. The case of zero acceleration and hence zero squeezing parameter is obviously the case in which we are considering just inertial observers. Hence we clearly see in the plot that when there is a non-zero acceleration, compared to the situation in which there is not, a trade-off of the correlations occur.

8 Entanglement of formation

Entanglement of formation is a measure of entanglement for mixed states that satisfies the basic requirements one would expect of an entanglement measure [23]. If $\rho _{AB}$ is such a state, one defines the entanglement of formation to be

$$\begin{aligned} E_F(\rho _{AB})= & {} \inf _{\{(|\psi _i\rangle ,p_i)\}}\sum _i p_i S\bigg ({\text {Tr}}_A(|\psi _i\rangle \langle \psi _i|)\bigg )\nonumber \\= & {} \inf _{\{(|\psi _i\rangle ,p_i)\}}\sum _i p_i S\bigg ({\text {Tr}}_B(|\psi _i\rangle \langle \psi _i|)\bigg ), \end{aligned}$$

(47)

where the infimum is taken over the set of all ensembles of pure states that realize $\rho _{AB}$.

This measure has an operational interpretation that makes it valuable for applications. Still, in the present case, it is worth considering it because of its special connection to LAI and LII [11,12,13].

This connection lies in the relation that if $\rho _{ABC} = |\psi \rangle \langle \psi |$ is a tripartite pure state, then the entanglement of formation of the AB subsystem is connected to the LAI of the AC subsystem by means of the equation

$$\begin{aligned} E_F(\rho _{AB})+J^\leftarrow (\rho _{AC})=S(\rho _A). \end{aligned}$$

(48)

By varying the subsystems one obtains other equations like that [13]. This relation has been employed in [11] in order to obtain an important monogamy relation between entanglement of formation and quantum discord.

This relation has a very important impact on the interpretation of what entanglement of formation is quantifying. By rewriting the equation as

$$\begin{aligned} J^\leftarrow (\rho _{AC})=S(\rho _A)-E_F(\rho _{AB}), \end{aligned}$$

(49)

and recalling that $J^\leftarrow (\rho _{AC})$ is the information contained in the correlations between A and C locally accessible to C by measurements, and recalling that $S(\rho _A)$ is the uncertainty in the state of A, we see that when $E_F(\rho _{AB}) = 0$, all the information is locally accessible, and when $E_F(\rho _{AB}) > 0$ the locally accessible information decreases. In that setting, $E_F(\rho _{AB})$ signals a correlation redistribution by which an observer of C alone looses access to information contained in the correlations of its state with that of the A subsystem. This interpretation of $E_F(\rho _{AB})$ demands no “entanglement as a resource” argument, and is available even if the subsystems A and B are separated by a causal horizon and the corresponding observers are forbidden classical communication.

Equation (48) immediately implies that if C is effectively two-level, in the sense of Eq. (45), then the method of [7], which we have outlined in the previous section, allows for the numeric evaluation of $J^\leftarrow (\rho _{AC})$, and hence of $E_F(\rho _{AB})$. The details of how this is done are presented in Appendix B.

Fig. 7

State $\rho _{I,II}$ – Entanglement of formation

For the concrete problem we are considering, the only effectively two-level state is that of the subsystem probed by the inertial observer alone, which corresponds to the mode $h_k^R$ of the field. This allowed us the evaluation of $J^\rightarrow (\rho _{M,I})$ and $J^\rightarrow (\rho _{M,II})$. Both LAIs, on the other hand, lead to the same entanglement of formation, because the entanglement of formation is symmetric, i.e. $E_F(\rho _{I,II})=E_F(\rho _{II,I})$. The obtained entanglement of formation is shown in Fig. 7 and we notice that it matches the overall behavior of the negativity computed in [6].

We must stress that considering that the state $\rho _{I,II}$ is relatively complex (c.f. Eq. (35)) it is remarkable that we are able to compute the entanglement of formation, which is defined by a very difficult optimization, by just optimizing over two angles.

9 Bounds on the other informational quantities

The approach we presented here allowed us to evaluate the entanglement of formation $E_F(\rho _{I,II})$ of the state probed by the two Rindler observers Rob and AntiRob, the LAI and LII $J^\rightarrow (\rho _{M,I})$ and ${\mathcal {D}}^\rightarrow (\rho _{M,I})$ for the state probed by Alice and Rob and the LAI and LII $J^\rightarrow (\rho _{M,II})$ and ${\mathcal {D}}^\rightarrow (\rho _{M,II})$ for the state probed by Alice and Anti-Rob. This is not a complete characterization of the correlations of the complete system, as some of the measures cannot be evaluated by the method we have employed. These are for each subsystem:

• Alice-Rob: entanglement of formation $E_F(\rho _{M,I})$, LAI and LII with measurements in Rob’s side, $J^\leftarrow (\rho _{M,I})$ and ${\mathcal {D}}^\leftarrow (\rho _{M,I})$;

• Alice–AntiRob: entanglement of formation $E_F(\rho _{M,II})$, LAI and LII with measurements in Rob’s side, $J^\leftarrow (\rho _{M,II})$ and ${\mathcal {D}}^\leftarrow (\rho _{M,II})$;

• Rob-AntiRob: LAI and LII with measurements in both sides, $J^\leftarrow (\rho _{I,II})$, ${\mathcal {D}}^\leftarrow (\rho _{I,II})$, $J^\rightarrow (\rho _{I,II})$ and ${\mathcal {D}}^\rightarrow (\rho _{I,II})$.

It turns out, however, that even though we are not able to evaluate these quantities, we can find bounds for most of them, which gives an overall idea of their behavior. The only quantities we are not able to bound employing this method are the LAI and LII for both the Alice–Rob and Alice–AntiRob subsystems, with measurements on Rob’s side. To explain how we obtain these bounds, we start with the Rob-AntiRob bipartition and with the evaluation of bounds on $J^\leftarrow (\rho _{I,II})$. By definition, this quantity is upper bounded by $S(\rho _I)$. On the other hand it has a lower bound in terms of the entanglement of formation $E_F(\rho _{I,II})$ [24, 25]:

$$\begin{aligned} J^\leftarrow (\rho _{I,II})\ge S(\rho _I)-\sqrt{S(\rho _I)^2-E_F(\rho _{I,II})^2}. \end{aligned}$$

(50)

Therefore we have both lower and upper bounds on the classical correlations of the quantum state probed by the two Rindler observers

$$\begin{aligned} S(\rho _I)-\sqrt{S(\rho _{II})^2-E_F(\rho _{I,II})^2} \le J^\leftarrow (\rho _{I,II}) \le S(\rho _I).\nonumber \\ \end{aligned}$$

(51)

Given that employing the method we have described we were able to numerically evaluate $S(\rho _I)$ and $E_F(\rho _{I,II})$ we can plot the lower and upper bounds and describe the region where $J^\leftarrow (\rho _{I,II})$ should be. Clearly the exact same procedure can be done replacing I by II and, given that the entanglement of formation is symmetric under this exchange, the same entanglement of formation that we have already obtained is going to give us bounds for $J^\rightarrow (\rho _{I,II})$. We plot both of these in Figs. 8 and 9.

Fig. 8

Bounds on $J^\leftarrow (\rho _{I,II})$

Fig. 9

Bounds on $J^\rightarrow (\rho _{I,II})$

Likewise, we can use this to obtain lower and upper bounds on the LII ${\mathcal {D}}^\leftarrow (\rho _{I,II})$. Indeed, we just need to take the negative of inequality (51) and add the mutual information $I(\rho _{I,II})$. Once this is done we get the bounds

$$\begin{aligned}&S(\rho _{II})-S(\rho _M)\le {\mathcal {D}}^\leftarrow (\rho _{I,II})\nonumber \\&\quad \le \sqrt{S(\rho _I)^2-E_F(\rho _{I,II})^2}+S(\rho _{II})-S(\rho _M), \end{aligned}$$

(52)

and since we know how to numerically evaluate all the quantities appearing in it, we can plot both bounds and find the region in which this informational quantity lies. Again the exact same procedure can be carried out exchanging I and II and the same entanglement of formation gives us knowledge of lower and upper bounds on ${\mathcal {D}}^\rightarrow (\rho _{I,II})$. Both these LII’s are shown in Figs. 10 and 11.

Fig. 10

Bounds on $\mathcal{D }^\leftarrow (\rho _{I,II})$

Fig. 11

Bounds on $\mathcal{D }^\rightarrow (\rho _{I,II})$

Finally, we can also apply this idea to find bounds over $E_F(\rho _{M,I})=E_F(\rho _{I,M})$ and $E_F(\rho _{M,II})=E_F(\rho _{II,M})$. Specifically using Eq. (48) we find

$$\begin{aligned} E_F(\rho _{M,I})= & {} S(\rho _I)-J^\leftarrow (\rho _{I,II}), \end{aligned}$$

(53)

$$\begin{aligned} E_F(\rho _{M,II})= & {} S(\rho _{II})-J^\rightarrow (\rho _{I,II}). \end{aligned}$$

(54)

Therefore, taking the negative of inequality (51) and ad-ding $S(\rho _I)$ we obtain an upper bound on $E_F(\rho _{M,I})$ and then exchanging $I\leftrightarrow II$ we obtain also an upper bound on $E_F(\rho _{M,II})$ which are then shown in Figs. 12 and 13:

$$\begin{aligned}&0\le E_F(\rho _{M,I}) \le \sqrt{S(\rho _I)^2-E_F(\rho _{I,II})^2}, \end{aligned}$$

(55)

$$\begin{aligned}&0\le E_F(\rho _{M,II}) \le \sqrt{S(\rho _{II})^2-E_F(\rho _{I,II})^2}. \end{aligned}$$

(56)

Fig. 12

Upper bound on $E_F(\rho _{M,I})$

Fig. 13

Upper bound on $E_F(\rho _{M,II})$

We close this section with a brief interpretation of the results. By observing these bounds on the several informational quantities what we are able to see is that, concerning the Rob–AntiRob bipartition, both the LAI and LII increase with the acceleration of the these observers. The more they are accelerated the more correlated they will perceive the state and, viewing LAI as classical correlations and LII as quantum correlations, this behavior is the same for both of them. An important aspect of those results is the fact that the LAI is closely related to the capacity of the channel [26]. We observe that, in this case, the capacity of the channel to communicate classical information is given by maximizing the accessible information. Although we do not maximize it specifically in regard of the message, we note that since $J^\leftarrow (\rho _{I,II})\ne J^\rightarrow (\rho _{I,II})$ the capacities from sending classical messages from I to II and vice-versa are not necessarily symmetric. We can immediately see that by maximizing $J^\leftarrow (\rho _{I,II})$ and $J^\rightarrow (\rho _{I,II})$, the capacities $C (I\rightarrow II )$ and $C (II\rightarrow I )$ are respectively given by the red curves in Figs. 8 and 9. Therefore, while for small acceleration, there is an asymmetry in the capacities, as the acceleration is increased both capacities tend to be equal. In general, both increase as the counter-acceleration of the observers Rob and AntiRob increases.

We can extend this discussion to understand the entanglement behavior as the acceleration of the Rindler observers goes to zero and infinity. These are captured by the squeezing parameter also going to zero or infinity, respectively. If we consider Eq. (32) we see that the state $|1\rangle ^R_{k'}$ has a separable $\alpha =0$ limit

$$\begin{aligned} |1\rangle ^R_{k'}=|1\rangle ^I_{k'}|0\rangle ^{II}_{k'}. \end{aligned}$$

(57)

That is expected, as we are in the inertial situation, with two inertial observers and no causal horizon imparting a redistribution of correlations. When $\alpha$ is small, we have a small deviation of that situation. This behavior is reproduced in the plots. In Fig. 6 we see that regarding the Alice–Rob bipartition, at zero acceleration we get the results for two inertial observers, whereas all correlation measures are zero for the Alice–AntiRob bipartition. For small, but nonzero acceleration we see that the results are just slight deviations from the inertial calculations, since the curves are all seem to be continuous.

In the infinite acceleration limit, the state is

$$\begin{aligned} |1\rangle ^R_{k'} = \lim _{\alpha \rightarrow \infty }\dfrac{1}{\cosh ^2 \alpha }\sum _{n=0}^\infty \sqrt{n+1}|n+1\rangle _{k'}^{I} |n\rangle ^{II}_{k'}, \end{aligned}$$

(58)

and therefore a highly entangled state. The limit normalization implies that the summation be more relevant for n larger than $\cosh ^2 \alpha$, involving highly excited states. Together with Eq. (31) we obtain the limiting states corresponding to Eqs. (33)–(35),

$$\begin{aligned} \rho _{M,I}\approx & {} \lim _{\alpha \rightarrow \infty }\dfrac{1}{2\cosh ^2\alpha }\sum _{n=0}^\infty |0n\rangle _{kk'}^{M,I}\langle 0n|, \end{aligned}$$

(59)

$$\begin{aligned} \rho _{M,II}\approx & {} \lim _{\alpha \rightarrow \infty }\dfrac{1}{2\cosh ^2\alpha }\sum _{n=0}^\infty |0n\rangle _{kk'}^{M,II}\langle 0n|,\end{aligned}$$

(60)

$$\begin{aligned} \rho _{I,II}\approx & {} \lim _{\alpha \rightarrow \infty }\dfrac{1}{2\cosh ^2\alpha }\sum _{n,m=0}^\infty |nn\rangle _{k'}^{I,II}\langle mm|. \end{aligned}$$

(61)

The pairs Alice–Rob, and Alice–AntiRob tend to be disentangled at the limit of infinite acceleration. Therefore, although the upper-limit for the entanglement of formation show an increasing tendency in Figs. 12, and 13, the actual entanglement goes to zero. This occurs as a manifestation of the monogamy of entanglement [27], and the consequence is that the state (61), for the pair Rob–AntiRob, tends to a maximally entangled pure state in the same limit. These results agree with the findings in Ref. [6], in terms of the negativity measure of entanglement, and are reflected in the scaling of the entanglement of formation shown in Figs. 7, 12, and 13. Remark that quantum and classical correlation are significantly different in nature, and therefore, it is not surprising that they give different values at those limits of low and high accelerations, as stressed out by comparing the entanglement with the quantities plotted in Fig. 6.

10 Discussion and conclusions

We revisited the analysis of correlations of a two-mode state of a massless Klein–Gordon field which, for two inertial observers, Alice and Bob, is maximally entangled, when Bob is replaced by the Rindler observers Rob and AntiRob on respectively the right and left Rindler wedges. Our focus has been on informational quantities: the locally accessible and locally inaccessible information, and the entanglement of formation directly connected to the previous two.

We built upon the method of [7] and evaluated both LAI and LII for both the Alice–Rob and Alice–AntiRob bipartitions and found a correlation redistribution associated to both quantities. Moreover, the ideas of [11,12,13] allowed us to use these results to evaluate the entanglement of formation for the Rob–AntiRob bipartition. Given its relation to LAI and LII we are led to interpret it as a quantifier of the correlation redistribution. Our conclusion is that the causal horizon affecting the Rindler observers impart a correlation redistribution on the system when compared to the situation on which it is probed by two observers that neither perceive such causal horizon. Furthermore, the correlation redistribution imparted by the causal horizon appears to be quantified by the entanglement across the horizon. In that sense, even though such entanglement cannot be employed as a resource for any quantum computation task because the Rob–AntiRob bipartition is deprived of classical communication, the Entanglement of Formation is an important measure for quantification of the information content in accelerated frames in a consistent way.

Other than the quantities we could compute numerically, namely, the LAI and LII for the bipartitions M, I and M, II with measurements on M and the entanglement of formation of the bipartition I, II there are other informational quantities that one would like to evaluate to have a complete picture of how the correlations are distributed in the system. These would be the entanglement of formations $E_F(\rho _{M,I})$ and $E_F(\rho _{M,II})$, the LAI and LII for the bipartitions M, I and M, II with now measurements being made either in I or II and the LAI and LII for the bipartition I, II with measurements in either side. While the method we have employed does not allow for the numeric evaluation of these quantities exactly it did allow us to find bounds for most of them which gives one overall idea of their behavior as a function of the squeezing parameter. This was only possible because of the tight connection between the entanglement monotone employed, the entanglement of formation, with the aforementioned informational quantities.

The overall method employed is perhaps of general interest in quantum information. It shows that if we have a tripartite state with only one effectively two-level part, then we can evaluate by optimizations over $S^2$, the LAI and LII for the bipartitions involving the two-level part and the entanglement of formation for the complementary bipartition which does not have the two-level part, no matter how complicated their states might be. Finally, all the other EoF’s, LAI’s and LII’s can be immediately bounded.

Appendices

Appendix A: Classical correlations for system with 2-level part

Let $\rho _{AC}$ be a bipartite state. The locally accessible information by measurements in C is defined to be

$$\begin{aligned} J^\leftarrow (\rho _{AC})=\max _{\{{\mathbf {1}}\otimes \Pi _\lambda \}}\left[ S(\rho _A)-\sum _\lambda p_\lambda S(\rho _A^\lambda ) \right] \end{aligned}$$

(A.1)

where the maximum is taken over all projective measurement acting on the composite system which act trivially upon A, ${\mathbf {1}}\otimes \Pi _\lambda$ is such a measurement acting just on C with probabilities $p_\lambda$ and post-selected states $\rho _{AC}^\lambda$. Finally $\rho _A$ and $\rho _A^\lambda$ are the states of A immediately before and immediately after the measurement, the later being assumed the result was $\lambda$.

In that case one is able to interpret $J^\leftarrow (\rho _{AC})$ as the maximum mean decrease in the von Neumann entropy of the state of A when measurements are performed in C. Because of this one calls $J^\leftarrow (\rho _{AC})$ the locally accessible information by measurements in C. In this notation the arrow always points from the subsystem being measured to the subsystem which we infer the decrease in von Neumann entropy. It is worth mentioning that $J^\leftarrow (\rho _{AC})$ satisfies the properties of classical correlations [22], that being another name commonly given to this particular measure of correlations.

In general, like for the entanglement of formation, it is a hard task to compute the locally accessible information for a given states because of the optimization involved on its definition. The situation is drastically different for the case on which the state of C is a two-level state. In that case one can show the optimization is effectively over $S^2$ and that it is possible to devise an algorithm to carry it out numerically. We shall review this method now, which was successfully used in [7] in the context of relativistic quantum information.

First one notices that it is always possible to write $\rho _{AC}$ as

$$\begin{aligned} \rho _{AC} = \sum _{a,b=0,1} M_{ab}\otimes |a\rangle \langle b|, \end{aligned}$$

(A.2)

where $M_{ab}$ are operators on A. The projective measurements on C which are relevant to the optimization are the ones in the space spanned by the projectors $|a\rangle \langle b|$. Thus the $\Pi _\lambda$ are hermitian operators in this subspace of the space of operators which are projectors $\Pi _\lambda ^2 = \Pi _\lambda$ and which satisfies the resolution of identity

$$\begin{aligned} \sum _\lambda \Pi _\lambda = {\mathbf {1}}. \end{aligned}$$

(A.3)

These conditions implies that for $\lambda$ there are only two possible values, which we shall label $\lambda = \pm$. Being $2\times 2$ hermitian operators, the matrix representation of the $\Pi _\pm$ can be written as linear combinations of the Pauli matrices together with the $2\times 2$ identity. Abusing notation and denoting the matrices of $\Pi _\pm$ by $\Pi _{\pm }$ as well, one shows that the desired expression is

$$\begin{aligned} \Pi _{\pm } = \frac{1}{2}[{\mathbf {1}}\pm {\mathbf {x}}\cdot \mathbf {\sigma }],\quad {\mathbf {x}}\in S^2 \end{aligned}$$

(A.4)

This means that measurements on subsystem C are parameterized by two angles once we write

$$\begin{aligned} {\mathbf {x}} = (\cos \phi \sin \theta ,\sin \phi \sin \theta ,\cos \theta ). \end{aligned}$$

(A.5)

Now we first discuss the probabilities of the measurement. The probabilities $p_\pm ({\mathbf {x}})$ can be obtained using the standard expression

$$\begin{aligned} p_{\pm }({\mathbf {x}})= {\text {Tr}} \Pi _\pm ({\mathbf {x}}) \rho _{AC} \Pi _{\pm }({\mathbf {x}}). \end{aligned}$$

(A.6)

Performing this computation using Eq. (A.4) one is led to the result that

$$\begin{aligned} p_{\pm }= & {} \dfrac{1\pm x_3}{2}{\text {Tr}} M_{00}\pm \dfrac{x_1-ix_2}{2}{\text {Tr}} M_{10}\nonumber \\&\pm \dfrac{x_1+ix_2}{2}{\text {Tr}} M_{01}+\dfrac{1\mp x_3}{2}{\text {Tr}} M_{11}. \end{aligned}$$

(A.7)

Once the measurement is enacted, the post-selected states, $\rho _{AC}^\pm ({\mathbf {x}})$, still have a two-level part. This means that there is a new set of operators $M_{ab}^\pm ({\mathbf {x}})$ such that we can write

$$\begin{aligned} \rho _{AC}^\pm ({\mathbf {x}}) = \sum _{a,b=0,1}M_{ab}^\pm ({\mathbf {x}}) \otimes |a\rangle \langle b|. \end{aligned}$$

(A.8)

In that sense, the whole effect of the measurement on the state is to shift the operators $M_{ab}$ to new operators $M_{ab}^\pm ({\mathbf {x}})$ which depend on the obtained result as well as in the measurement through the angle dependence. These operators can also be obtained from the standard formula for the post-selected states:

$$\begin{aligned} \rho _{AC}^\pm ({\mathbf {x}}) = \dfrac{1}{p_\pm ({\mathbf {x}})} \Pi _\pm ({\mathbf {x}}) \rho _{AC} \Pi _{\pm }({\mathbf {x}}). \end{aligned}$$

(A.9)

Using this formula, one can obtain the postselected operators $M_{ab}^\pm ({\mathbf {x}})$ which are given by

$$\begin{aligned} M_{00}^\pm ({\mathbf {x}})&= \dfrac{1\pm x_3}{2}M_{00}\pm \dfrac{x_1-ix_2}{2}M_{10},\nonumber \\ M_{10}^\pm ({\mathbf {x}})&= \pm \dfrac{x_1+ix_2}{2}M_{00}+ \dfrac{1\mp x_3}{2}M_{10},\nonumber \\ M_{01}^\pm ({\mathbf {x}})&= \dfrac{1\mp x_3}{2}M_{01}\pm \dfrac{x_1-ix_2}{2}M_{11},\nonumber \\ M_{11}^\pm ({\mathbf {x}})&= \pm \dfrac{x_1+ix_2}{2}M_{01}+\dfrac{1\mp x_3}{2}M_{11}. \end{aligned}$$

(A.10)

In that case, the postselected states of A which are of interest to compute the locally accessible information ends up simply as

$$\begin{aligned} \rho _A^\pm ({\mathbf {x}}) = M_{00}^\pm ({\mathbf {x}}) + M_{11}^\pm ({\mathbf {x}}), \end{aligned}$$

(A.11)

or in terms of the initial operators $M_{ab}$ it is

$$\begin{aligned} \rho _{A}^\pm ({\mathbf {x}})= & {} \dfrac{1\pm x_3}{2}M_{00}\pm \dfrac{x_1-ix_2}{2}M_{10} \nonumber \\&\pm \dfrac{x_1+ix_2}{2}M_{01}+\dfrac{1\mp x_3}{2}M_{11}. \end{aligned}$$

(A.12)

Thus we observe that given the initial operators $M_{ab}$ specifying the state of the system prior to measurement, using the above formulae we are able to compute for an arbitrary measurement parameterized by ${\mathbf {x}}\in S^2$ the probabilities for the two possible results as well as the post-selected states of the subsystem A.

Now this reveals one algorithm for computing the locally accessible information. Considering that the operator $M_{ab}$ may live in one Hilbert space of arbitrary dimension – which could as well be infinite – we work with an upper cutoff N on the dimension of that Hilbert space which in practice one makes as large as desired to get more accurate results. The overall method one employs in practice is thus:

• 1. Define the matrices $M_{ab}$. If they are operators acting on some infinite-dimensional Hilbert space, we impose one upper cutoff N on the number of basis elements of ${\mathscr {H}}_A$ entering the definition.

• 2. Use Eq. (A.10) to define the post-selected matrices $M_{ab}^\pm ({\mathbf {x}})$ as functions of ${\mathbf {x}}\in S^2$. With them define $p_\pm ({\mathbf {x}})$ the probabilities and $\rho _{A}^\pm ({\mathbf {x}})$ the post-selected states of A.

• 3. Compute the entropies $S(\rho _A)$ and $S(\rho _A^\pm ({\mathbf {x}}))$ numerically, obviously depending on the upper cutoff N introduced on step (1). With them define the function

  $$\begin{aligned} J^\leftarrow (\rho _{AC};{\mathbf {x}})=S(\rho _A)-\sum _{\lambda =\pm }p_\lambda ({\mathbf {x}})S(\rho _A^\lambda ({\mathbf {x}})),\quad {\mathbf {x}}\in S^2. \end{aligned}$$

• 4. Express ${\mathbf {x}} = (\cos \phi \sin \theta ,\sin \phi \sin \theta ,\cos \theta )$ and maximize the classical correlation, $J^\leftarrow (\rho _{AC};{\mathbf {x}})$, in the two angles or use another more convenient parameterization of $S^2$.

• 5. Increase the upper cutoff N until getting the desired precision in the results.

The idea behind this method, which is the parameterization of the measurements by points of a sphere, was used successfully in [7] in the context of relativistic quantum information in order to compute the quantum discord of a state of this kind. The method looks like a logical implementation in a general context of the idea presented there.

Appendix B: From $J^\leftarrow (\rho _{AC})$ to $E_F(\rho _{AB})$

We now explain how we go from locally accessible information to entanglement of formation, which is the central objective. The key idea is that the entanglement of formation holds a particularly important relation to locally accessible information when we consider tripartite pure states [11,12,13]. In that case, if $\rho _{ABC}$ is pure, we have the equation

$$\begin{aligned} E_F(\rho _{AB}) + J^\leftarrow (\rho _{AC})=S(\rho _A) \end{aligned}$$

(B.13)

and other similar equations obtained by varying A, B and C. Thus knowledge of $J^\leftarrow (\rho _{AC})$ yields $E_F(\rho _{AB})$ and vice versa. One important point to mention is that, as already pointed, by varying the subsystems we also have the companion equation

$$\begin{aligned} E_F(\rho _{BA})+ J^\leftarrow (\rho _{BC})=S(\rho _B), \end{aligned}$$

(B.14)

thus, even though the two locally accessible informations $J^\leftarrow (\rho _{AC})$ and $J^\leftarrow (\rho _{BC})$ will in general differ, they can be used by employing these equations to obtain the same entanglement of formation, as $E_F(\rho _{AB})=E_F(\rho _{BA})$, since it is symmetric with respect to exchange in the two subsystems.

Of course we can use the definition of locally accessible information on Eq. (B.13) to directly obtain one new formula for entanglement of formation

$$\begin{aligned} E_F(\rho _{AB})= \min _{\{{\mathbf {1}}\otimes \Pi _\lambda \}} \sum _{\lambda } p_\lambda S(\rho _A^\lambda ). \end{aligned}$$

(B.15)

Thus, when $\rho _{ABC}$ is a tripartite pure state, we are able to get $E_F(\rho _{AB})$ by the above optimization over measurements on $\rho _{AC}$ which act just on the C subsystem.

It is now clear how the algorithm can be used for the case in which $\rho _{C}$ is a two-level state. We can use it to first numerically optimize and obtain $J^\leftarrow (\rho _{AC})$ or $J^\leftarrow (\rho _{BC})$, both of which will give the same entanglement of formation by employing Eq. (B.13) or we can adapt the algorithm directly to this new equation and optimize for the entanglement of formation directly.

When C is a two-level state, again the measurements which are relevant are those whose projectors expand in its two-dimensional basis and which can be written in terms of Pauli matrices together with the $2\times 2$ identity using Eq. (A.4). This means that the optimization defining the entanglement of formation is again an optimization over $S^2$. Being explicit, the recipe one would use in practice would then be:

• 1. Construct the state $\rho _{AC} = {\text {Tr}}_{B}\rho _{ABC}$ and write it in the form

  $$\begin{aligned} \rho _{AC} = \sum _{a,b=0,1} M_{ab} \otimes |a\rangle \langle b| \end{aligned}$$

• 2. Define the matrices $M_{ab}$. If they are operators acting on some infinite-dimensional Hilbert space, we impose one upper cutoff N on the number of basis elements of ${\mathscr {H}}_A$ entering the definition.

• 3. Use Eq. A.10 to define the post-selected matrices $M_{ab}^\pm ({\mathbf {x}})$ as functions of ${\mathbf {x}}\in S^2$. With them define $p_\pm ({\mathbf {x}})$ the probabilities and $\rho _{A}^\pm ({\mathbf {x}})$ the post-selected states of A.

• 4. Compute the entropies $S(\rho _A^\pm ({\mathbf {x}}))$ numerically, obviously depending on the upper cutoff N introduced on step (1). With them define the function

  $$\begin{aligned} E_F(\rho _{AB};{\mathbf {x}})=\sum _{\lambda =\pm }p_\lambda ({\mathbf {x}})S(\rho _A^\lambda ({\mathbf {x}})),\quad {\mathbf {x}}\in S^2. \end{aligned}$$

• 5. Express ${\mathbf {x}} = (\cos \phi \sin \theta ,\sin \phi \sin \theta ,\cos \theta )$ and minimize the entanglement of formation $E_F(\rho _{AB};{\mathbf {x}})$ in the two angles or use another more convenient parameterization of $S^2$.

• 6. Increase the upper cutoff N until getting the desired precision in the results.

Clearly, in practice one ends up needing to resort to numerical methods as such to compute the entanglement of formation, but the optimization over $S^2$ is arguably simpler than the original one which defines the entanglement of formation.