The study of doubly charmed pentaquark $c c {\bar{q}}qq$ with the SU(3) symmetry

Abstract

We study the masses and lifetimes of doubly charmed pentaquark $P_{cc{\bar{q}}qq}(q=u,d,s)$ primarily. The operation of masses carried out by the doubly heavy triquark-diquark model, whose results suggests the existence of stable states $cc{\bar{s}} ud$ with the parity $J^P=\frac{1}{2}^-$. The roughly calculation about lifetimes show the short magnitudes, $(4.65^{+0.71}_{-0.55})\times 10^{-13}s$ for the parity $J^P=\frac{1}{2}^-$ and $(0.93^{+0.14}_{-0.11})\times 10^{-12} s$ for $J^P=\frac{3}{2}^-$. Since the pentaquark $cc{\bar{s}} ud$ is interpreted as the stable bound states against strong decays, then we will focus on the production and possible decay channels of the pentaquark in the next step, the study would be fairly valuable supports for future experiments. For completeness, we systematically studied the production from $\Omega _{ccc}$ and the decay modes in the framework SU(3) flavor symmetry, including the processes of semi-leptonic and two body non-leptonic decays. Synthetically, we make a collection of the golden channels.

1 Introduction

In 2015, the LHCb collaboration announced the findings of the first pentaquark states $P_c(4380)^+$ and $P_c(4450)^+$ in the decay $\Lambda _b^0\rightarrow J/\psi pK^-$, the masses and decay widths were measured respectively, $M(P_c(4380))=(4380\pm 8\pm 29)$ MeV, $\Gamma =(205\pm 18\pm 86)$ MeV and $M(P_c(4450))=(4449.8\pm 1.7\pm 2.5)$ MeV, $\Gamma =(39\pm 5\pm 19)$ MeV [1]. Subsequently, in 2019, the LHCb collaboration reported a new pentaquark $P_c(4312)^+$ [2], in addition, the analyses revealed that $P_c(4450)^+$ observed previously actually were the average of two narrow resonances $P_c(4440)^+$ and $P_c(4457)^+$. So far, numerous theoretical interpretations of the nature of the pentaquark followed the discoveries, including hadronic molecules [3, 4], compact pentaquarks states [5, 6], hadro-charmonia [7], and cusp effects [5]. Many theoretical studies devoted to the pentaquark have achieved remarkable results, for instance, effective field theory discuss the possible configurations of pentaquark [3, 8, 9], QCD sum rules study the masses of $P_c(4380)$ pentaquark [10, 11], and quark model study the masses [12,13,14], etc. At present, the discovered pentaquarks are largely what is called hidden charmed pentaquark with charmed quarks pair $c{\bar{c}}$, the states with two heavy charmed quarks $P(cc{\bar{q}}qq)$ are similarly available in quark model. Following the research of discovered $P_c$ pentaquark states, there are many attempts to study the existence and stable of the doubly charmed pentaquark states. For instance, constituent quark model with color-magnetic [15, 16] and one boson exchange [17, 18], in which the authors discuss the mass splittings of different configuration pentaquarks and some stable pentaquarks are predicted. The study with chiral effective field theory suggest one stable pentaquark state $ccud{\bar{s}}$ [19]. The masses and pole residues of doubly charmed pentaquark are considered with QCD sum rules [20]. However, it is still an open question to distinguish the configurations of doubly charmed pentaquark, either the compact states or molecule states. In addition, the production and decays have not been discussed well by now. Therefore, we try to study the mass of doubly charmed pentaquark with the non-relativity constituent diquark model [21, 22], and forcing on the production and decay modes of the pentaquark states under a systematic SU(3) symmetry analysis in the paper. The nature of the doubly charmed pentaquark may offer the possible for the probe of strong force in greater detail and the understanding of quantum chromodynamics. Furthermore, the two charmed quarks in pentaquark mean more scales, which might be an ideal probe to study the interplay between perturbative QCD and non-perturbative QCD, eventually leading the development of multi scale physics, especially the factorization approach.

Doubly charmed pentaquark $P(cc{\bar{q}}qq)$ can be dealt with the compact pentaquark interpretation. We follow here the intuitive picture in which the heavier components form a nucleus and the lighter one is in an orbit around this nucleus, as it is energetically easier to excite light degrees of freedom. The light diquark qq is the lightest, thus to be the lighter one around the nucleus. Then the remaining part is the heavier nucleus. With that, we prefer that the doubly charmed pentaquark is the colored diquark-triquark template with the configuration $[[cc]_{{\bar{3}}}q_{{\bar{3}}}]_{3}$ in the paper. The diquark with two charmed quarks cc forms a color triplet $\bar{3}_c$ spin-1 state, as suggested by perturbative arguments and pauli exclusion principle. While the light diquark qq forms a color triplet $\bar{3}_c$ spin-0 state, as the hypothesis of “good” diquark. At this stage, we employ the triquark-diquark model [6, 21, 22], which heavy diquark $[cc]_{{\bar{3}}}$ combines with antiquark $q_{{\bar{3}}}$ to form a triquark system $[[cc]_{{\bar{3}}}q_{{\bar{3}}}]_{3}$, and then, merging with light diquark $[qq']_{{\bar{3}}}$ to form the doubly charmed pentquark state. Once applying the effective Hamiltonian of mass spectrum, the masses of pentaquark would be achieved. In addition, the lifetimes can be estimated with the implement of operator product expansion(OPE) approach [23, 24]. Upon the heavy quark expanding and optical theorem, we can directly determine the lifetimes at the next-to-leading order of $P(cc{\bar{q}}qq)$ with the different parities.

The flavor SU(3) symmetry is a convincing tool to analyze the production and decay behaviours of hadrons, which has been successfully applied to the meson or baryon system [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Though the SU(3) breaking effects in charm quark transition might be sizable, the results can still describe the experimental data well in a global viewpoint. The doubly charmed pentaquark can be produced from triply charmed baryon $\Omega _{ccc}$ with one charmed quark weak decays, $c\rightarrow q{\bar{q}}q$. Moreover, the decays of pentaquark similarly give priority to the charmed quark decays. Therefore, we will force on the charmed quark weak decays both in the production and decay processes. To be more explicit, one can write down the Hamiltonian at the hadron level with hadron fields and transition operators. Some limited amount of input parameters will be introduced to describe the non-perturbative transitions. With the SU(3) amplitudes, one can obtain relations between decay widths of different processes, which can be examined in experiment. Such an analysis is also helpful to identify the decay modes that will be mostly useful to discover the doubly charmed pentaquark state $P(c c{\bar{q}}qq)$. Since the SU(3) analysis is based on the light quark symmetry, thus the analytical results can work well in all states with $P({cc}{{\bar{q}}qq})$ flavor constituents, for instance, the states with molecular picture.

The rest of this paper is organized as follows. In Sect. 2, we discuss the mass spectrums and lifetimes of doubly charmed pentaquark. Section 3 is devoted to discuss the production and decay behaviours, which including two body production processes, mesonic semi- and non-leptonic decays. In Sect. 5, we present a collection of the golden channels. We make a short summary in the end.

2 Mass and lifetime of $P(c c{\bar{q}}qq)$ state

2.1 Mass

We study the mass spectrum of S-wave pentaquark states $P_{cc{\bar{q}}qq}(q=u,d,s)$ in the framework of non-relativity doubly heavy triquark-diquark model [6, 21, 22]. Under the picture of diquark consisting of two light quarks $qq'$ in color ${\bar{3}}$ state and triquark consisting of doubly heavy diquark cc in color ${\bar{3}}$ plus a light anti-quark ${\bar{q}}$ in color ${\bar{3}}$, which labeled as $[[cc]_{c{\bar{3}}}[{\bar{q}}]_{c{\bar{3}}}]_{c 3}[qq']_{c{\bar{3}}}$, the effective Hamiltonian of mass spectrum can then be written as

$$\begin{aligned} {\mathcal {H}}=M_0+H_{hd}+H_{ld}, \end{aligned}$$

(1)

with the constituent mass of diquark and triquark is $M_0$, in addition, the interaction of triquark $H_{hd}$ contains the coupling of spin-spin $S_c\cdot S_c$ in the heavy diquark $[cc]_{{\bar{3}}}$, and the coupling with the triquark $S_c\cdot S_{{\bar{q}}}$, the coupling coefficients are represented with ${\mathcal {K}}_{cc}, {\mathcal {K}}_{c{\bar{q}}}$. The last term $H_{ld}$ provides the interaction between two light quark q and $q'$ in diquark, and all possible spin-spin interactions among the light diquark $[qq']_{{\bar{3}}}$ and triquark $[[cc]_{{\bar{3}}}{{\bar{q}}}_{{\bar{3}}}]_{3}$. We respectively give the forms as follows.

$$\begin{aligned} M_0= & {} m_{cc}+m_{qq'}+m_{{\bar{q}}},\nonumber \\ H_{hd}= & {} 2 ({\mathcal {K}}_{cc})_{{\bar{3}}} (S_c\cdot S_c)+4 ({\mathcal {K}}_{c{\bar{q}}})(S_c\cdot S_{{\bar{q}}})\nonumber ,\\ H_{ld}= & {} 2({\mathcal {K}}_{qq'})_{{\bar{3}}} (S_{q}\cdot S_{q'})+4({\mathcal {K}}_{cq})_{{\bar{3}}}(S_c\cdot S_q)\nonumber \\&+4({\mathcal {K}}_{cq'})_{{\bar{3}}}(S_c\cdot S_{q'})+2({\mathcal {K}}_{q{\bar{q}}})(S_q\cdot S_{{\bar{q}}})\nonumber \\&+2({\mathcal {K}}_{q'{\bar{q}}})(S_{q'}\cdot S_{{\bar{q}}}). \end{aligned}$$

(2)

In the doubly heavy triquark-diquark system, the suggested spin of doubly heavy charmed diquark is $S_{cc}=1$. Similarly, the spin of “good” light diquark in the S-wave pentaquark state $P_{cc{\bar{q}} qq}$ is chosen as $S_{qq'}=0$ [41]. Accordingly, we can write directly the possible configuration of S-wave pentaquark $P_{cc{\bar{q}}qq}$, signed as $|S_{cc},S_t,L_t; S_{qq'},L_{qq'};S,L\rangle$.

$$\begin{aligned}&|1,\frac{1}{2},0;0,0;\frac{1}{2},0\rangle&\ \ J^P=\frac{1}{2}^-,\nonumber \\&|1,\frac{3}{2},0;0,0;\frac{3}{2},0\rangle&\ \ J^P=\frac{3}{2}^-. \end{aligned}$$

(3)

Here, the light diquark $qq'$ can be any one of the constituents (ud, du, us, su, ds, sd). Except for the spin of doubly heavy diquark $S_{cc}$ and light diquark $S_{qq'}$, the orbital angular momentum $L_t=L_{qq'}=L=0$, the spin of triquark ($[cc] {\bar{q}}$) $S_t$ turn out to be $\frac{1}{2}$ or $\frac{3}{2}$.

The two states with the spin-parity $J^P=\frac{1}{2}^-$ and $J^P=\frac{3}{2}^-$, sandwiching the effective mass Hamiltonian Eq. 1, then yield the mass spectrum matrix of S-wave pentaquark $P_{cc{\bar{q}}qq}$:

$$\begin{aligned}&{\mathcal {M}}^{S=0}_{J=1/2,3/2}=m_{cc}+m_{{\bar{q}}}+m_{qq'}+\frac{1}{2}({\mathcal {K}}_{cc})_{{\bar{3}}}-\frac{3}{2}({\mathcal {K}}_{qq'})_{{\bar{3}}}\nonumber \\&\quad +\left( \begin{array}{c@{\qquad }c} -2{\mathcal {K}}_{c{\bar{q}}}+\frac{1}{4}({\mathcal {K}}_{cq})_{{\bar{3}}}&{} \frac{1}{2}{\mathcal {K}}_{c{\bar{q}}}+\frac{1}{12}(1+\sqrt{10})\\ +\frac{1}{4}({\mathcal {K}}_{cq'})_{{\bar{3}}}&{}({\mathcal {K}}_{q{\bar{q}}}+{\mathcal {K}}_{q'{\bar{q}}})\\ 0&{}{\mathcal {K}}_{c{\bar{q}}} \end{array}\right) .\nonumber \\ \end{aligned}$$

(4)

In particular, the determination of spin-spin interaction between three spins inside the triquark, i.e., $S_c\cdot S_{{\bar{q}}}$, can be drawn by the Wigner 6j-symbols. Further more, for the interaction between triquark and light diquark, such as, $S_{c}\cdot S_{q}$ and $S_{q}\cdot S_{{\bar{q}}}$, it is convenient to utilize the Wigner 9j-symbols to describe the recouplings. The remaining step is the numerical operation. With regard to the work, we choose the values of spin-spin coupling given as [42]: $({\mathcal {K}}_{cc})_{{\bar{3}}}=57$ MeV, $({\mathcal {K}}_{qq'})_{{\bar{3}}}=98$ MeV, $({\mathcal {K}}_{su/d})_{{\bar{3}}}=59$ MeV, $({\mathcal {K}}_{cu/d})_{{\bar{3}}}=15$ MeV, $({\mathcal {K}}_{cs})_{{\bar{3}}}=50$ MeV, ${\mathcal {K}}_{c{\bar{u}}/{\bar{d}}}=72$ MeV, ${\mathcal {K}}_{u{\bar{d}}/d{\bar{u}}}=318$ MeV, ${\mathcal {K}}_{s{\bar{d}}/{\bar{u}}}=200$ MeV. We adopt the mass of quark and diquark [42], for instance, $m_{u/d}=362$ MeV, $m_s=540$ MeV, $m_c=1.667$ GeV, $m_{cc}\sim 2m_c$, $m_{ud}=576$ MeV, $m_{sq}=800$ MeV. Certainly, one should consider the uncertainty in these couplings and masses. We assign the couplings to be $10\%$ of each value, so as the mass of heavy charmed diquark.

We diagonalize the mass matrix and obtain the split mass of pentaquark $P_{cc{\bar{q}}qq}$ shown in Table 1. As a contrast, we show the results from chiral effective theory(ChEFT), quark model with color-magnetic interaction(CMI) and QCD sum rule(QCDSR). Moreover, the lowest strong thresholds are placed at the end of the table. From which we may find that the center mass of pentaquark $P_{cc{\bar{s}} ud}$ with parity $\frac{1}{2}^-$ is smaller than the lowest strong threshold $\Xi _{ccq}\bar{K}$ about 23 MeV. Therefore, it is possible a stable bound state against the strong interaction. The conclusion is consistent with the Refs. [16, 19]. Still, it is worth noting, the difference value much smaller than the uncertainties in our work, this may play an increasingly role at the final conclusion. In addition, the mass of P($\frac{1}{2}^-$) with the constituents $cc{\bar{u}} su, cc{\bar{u}} sd, cc{\bar{d}} s u$ and $cc{\bar{d}} s d$ are higher slightly than the lowest strong thresholds about 10 MeV, which may lead the final options open for the considerable uncertainties from couplings ${\mathcal {K}}_{cc}$ and diquark mass $m_{cc}$. Nevertheless, the work have suggested the potential stable state $P_{cc{\bar{s}} ud}(\frac{1}{2}^-)$, which should be further confirmed in experimental sides. In the following, we will intimately discuss the production and decay modes of pentaquark $cc{\bar{q}}qq$ under the SU(3) symmetry analysis.

Table 1 The split mass of pentaquark $P_{cc{\bar{q}}qq}$ with the S-wave in the parity of $J^P=\frac{1}{2}^-,\frac{3}{2}^-$, in the unit of GeV. n represent the light quark u, d. I is the isospin of pentaquark

2.2 Lifetimes

In the part, we roughly study the lifetimes of pentaquark $P_{cc{\bar{q}}qq}$ with the parity $J^P=\frac{1}{2}^-,\frac{3}{2}^-$, under the framework of operator product expansion(OPE) technique. As always, the decay widths can be expressed as

$$\begin{aligned} \Gamma (P_{cc{\bar{q}}qq}\rightarrow X)= & {} \frac{1}{2m_P} \sum _X \int \prod _i \Bigg [ \frac{d^3 \overrightarrow{p}_i}{(2\pi )^3 2E_i}\Bigg ] (2\pi )^4 \delta ^4\nonumber \\&\times \left( p_P-\sum _i p_i\right) N\sum _{\lambda }|\langle X|{\mathcal {H}}| P_{cc{\bar{q}}qq}\rangle |^2,\nonumber \\ \end{aligned}$$

(5)

therein, $m_P$, $\lambda$ and $p_P^{\mu }$ are the mass, spin and four-momentum of pentaquark $P_{cc{\bar{q}}qq}$ respectively. ${\mathcal {H}}$ can match with that of electro-weak effective Hamiltonian ${\mathcal {H}}_{eff}^{ew}$. The coefficient $N=(\frac{1}{2},\frac{1}{4})$, accordingly corresponds with spin parity $J^P=(\frac{1}{2}^-, \frac{3}{2}^-)$ of pentaquark. Based on the optical theorem and the heavy quark expanding(HQE), the decay widths from leading dimension contribution can be deduced as

$$\begin{aligned}&\Gamma (P_{cc{\bar{q}}qq} \rightarrow X)= \frac{G_F^2m_c^5}{192\pi ^3} |V_{CKM}|^2 N \sum _{\lambda } c_{3,c} \frac{\langle P_{cc{\bar{q}}qq}|{\bar{c}} c|P_{cc{\bar{q}}qq}\rangle }{2m_P},\nonumber \\ \end{aligned}$$

(6)

where $G_F$ is the Fermi constant, $V_{CKM}$ is the CKM element, the coefficients $c_{3,c}$ is the perturbative coefficient of HQE. Further more, the heavy quark matrix element is corresponding with charm number of pentaquark state.

$$\begin{aligned} \sum _{\lambda } \frac{\langle P_{cc{\bar{q}}qq}|{\bar{c}} c|P_{cc{\bar{q}}qq}\rangle }{2m_P}=2+{\mathcal {O}}(1/m_c). \end{aligned}$$

(7)

Consequently, we reach the decay widths and lifetimes under the leading and next-to-leading order,

$$\begin{aligned}&\Gamma \left( P\left( \frac{1}{2}^-\right) \right) =\left\{ \begin{array}{l} (7.68^{+0.88}_{-0.88})\times 10^{-13} \mathrm{GeV} , \;\text {LO} \\ (1.42^{+0.19}_{-0.19})\times 10^{-12} \ \mathrm{GeV} ,\; \text {NLO} \end{array}\right. ,&\Gamma \left( P\left( \frac{3}{2}^-\right) \right) =\left\{ \begin{array}{l} (3.84^{+0.44}_{-0.44})\times 10^{-13} \mathrm{GeV} , \;\text {LO} \\ (7.08^{+0.95}_{-0.95})\times 10^{-13} \ \mathrm{GeV} ,\; \text {NLO} \end{array}\right. ,\nonumber \\&\tau \left( P\left( \frac{1}{2}^-\right) \right) =\left\{ \begin{array}{l} (8.58^{+1.11}_{- 0.88})\times 10^{-13} s , \;\text {LO} \\ (4.65^{+0.71}_{-0.55})\times 10^{-13 } s ,\; \text {NLO} \end{array}\right. ,&\tau \left( P\left( \frac{3}{2}^-\right) \right) =\left\{ \begin{array}{l} (1.72^{+0.22}_{-0.18})\times 10^{-12} s , \;\text {LO} \\ (0.93^{+0.14}_{-0.11})\times 10^{-12} s ,\; \text {NLO} \end{array}\right. . \end{aligned}$$

(8)

In this work, the heavy quark mass $m_c=1.4\ \mathrm{GeV}$, the perturbative short-distance coefficient have been determined as $c_{3,c}=6.29\pm 0.72$ at the leading order(LO), and $c_{3,c}=11.61\pm 1.55$ at the next-to-leading order(NLO) [23].

3 SU(3) analysis

We will discuss the possible production and decay modes of pentaquark with the quark constituent of $cc{\bar{q}}qq$ in this section. The production can be achieved by the study about weak decays of triply heavy baryon $\Omega _{ccc}$. At the stage of decay modes, we focus on the explores of stable pentaquark candidates, which give priority to the weak decays similarly.

The weak interaction of production and decays for the pentaquark states, with the transition $c\rightarrow q{\bar{q}}q$, can be classified by the quantities of CKM matrix elements.

• For the case of c quark semi-leptonic decays,

  $$\begin{aligned} c\rightarrow d/ s \ell ^+ \nu _{\ell }. \end{aligned}$$

  (9)

  The general electro-weak Hamiltonian can be expressed as

  $$\begin{aligned} {{{\mathcal {H}}}}_{eff}= & {} \frac{G_F}{\sqrt{2}} \left[ V_{cq}^* {\bar{q}} \gamma ^\mu (1-\gamma _5)c {\bar{\nu }}_{\ell } \gamma _\mu (1-\gamma _5) \ell \right] +h.c.,\nonumber \\ \end{aligned}$$

  (10)

  with $q=(d,s)$, in which the transition operator of $c\rightarrow q \ell ^+ \nu _{\ell }$ forms a SU(3) triplet $H_{ 3}$, and $(H_{ 3})_1=0,~(H_{ 3})_2=V_{cd}^*,~(H_{ 3})_3=V_{cs}^*$.

• For the case of c quark non-leptonic decays, we classify the transitions into three groups.

  $$\begin{aligned} c\rightarrow s {\bar{d}} u, \; c\rightarrow u {\bar{d}} d/{\bar{s}} s, \; c\rightarrow d {\bar{s}} u, \; \end{aligned}$$

  (11)

  which are Cabibbo allowed, singly Cabibbo suppressed, and doubly Cabibbo suppressed transitions respectively. The transition $c \rightarrow q_1 {\bar{q}}_2 q_3$ can be decomposed as . Here, we offer the nonzero SU(3) tensor components of Cabibbo allowed transition given as

  $$\begin{aligned} (H_{ 6})_{31}^2=-(H_{6})_{13}^2=1,\;\;\; (H_{\overline{15}})_{31}^2= (H_{\overline{15}})_{13}^2=1.\nonumber \\ \end{aligned}$$

  (12)

  As the transition of ${\bar{c}}\rightarrow {\bar{u}} d{\bar{d}}$ and ${\bar{c}}\rightarrow {\bar{u}} s{\bar{s}}$ with singly Cabibbo suppressed, the combination of tensor components are corresponding with the overall CKM factor, which defined as $V_{cs}^* V_{us}=sin(\theta _C)$.

  $$\begin{aligned} (H_{6})_{31}^3= & {} -(H_{6})_{13}^3 =(H_{ 6})_{12}^2 =-(H_{ 6})_{21}^2 =\sin (\theta _C),\nonumber \\ (H_{\overline{15}})_{31}^3= & {} (H_{\overline{15}})_{13}^3=-(H_{\overline{15}})_{12}^2 =-(H_{\overline{15}})_{21}^2= \sin (\theta _C).\nonumber \\ \end{aligned}$$

  (13)

  For the doubly Cabibbo suppressed transition ${\bar{c}}\rightarrow {\bar{d}} s {\bar{u}}$, we have

  $$\begin{aligned} (H_{ 6})_{21}^3= & {} -(H_{ 6})_{12}^3=-\sin ^2\theta _C,\nonumber \\ (H_{\overline{15}})_{21}^3= & {} (H_{\overline{15}})_{12}^3 =-\sin ^2\theta _C. \end{aligned}$$

  (14)

3.1 Particle multiplets in SU(3)

The pentaquark with the quark constituents ${c c}{{\bar{q}}qq}$ contain three light quark and thus can form an SU(3) ${\bar{\mathbf{6}}}$ and an SU(3) $\mathbf{15}$, labeled as $P_6$ and $P_{15}$ respectively. We give the SU(3) representations $P_6$ as follows.

$$\begin{aligned} (P_{6})^{[2,3]}_1= & {} \frac{1}{\sqrt{2}} P_{{\bar{u}}ds}^0,\; (P_{6})^{[3,1]}_2= \frac{1}{\sqrt{2}} P_{{\bar{d}}su}^{++},\nonumber \\ (P_{6})^{[1,2]}_3= & {} \frac{1}{\sqrt{2}} P_{{\bar{s}}ud}^{++},\nonumber \\ (P_{6})^{[1,2]}_1= & {} (P_{6})^{[2,3]}_3= \frac{1}{2} P_{({\bar{u}}u,\bar{s}s)d}^+,\nonumber \\ (P_{6})^{[3,1]}_1= & {} (P_{6})^{[2,3]}_2= \frac{1}{2} P_{(\bar{u}u,\bar{d}d)s}^{+},\nonumber \\ (P_{6})^{[1,2]}_2= & {} (P_{6})^{[3,1]}_3= \frac{1}{2} P_{(\bar{d}d,\bar{s}s)u}^{++}. \end{aligned}$$

(15)

It should be noted that the tensor representation, for instance, $(P_{6})^{[2,3]}_1$ with two antisymmetry upper indices [2, 3], can be reformulated by the SU(3) invariant tensor $\varepsilon ^{ijk}$ written as $(P_{6})^{[2,3]}_1=(P_6)_{\{1,1\}} \varepsilon ^{123}$. The component fields in 15 states are

$$\begin{aligned} (P_{15})^{\{2,3\}}_1= & {} \frac{1}{\sqrt{2}} {P'}_{ds{\bar{u}}}^0,\nonumber \\ (P_{15})^{\{3,1\}}_2= & {} \frac{1}{\sqrt{2}} {P'}_{su{\bar{d}}}^{++},\quad (P_{15})^{\{1,2\}}_3= \frac{1}{\sqrt{2}} P_{ud{\bar{s}}}^{++}, \nonumber \\ (P_{15})^{\{1,1\}}_1= & {} \frac{{P'}_{\pi u}^{++}}{\sqrt{2}}+\frac{{P'}_{\eta u}^{++}}{\sqrt{6}} \nonumber \\ (P_{15})^{\{1,2\}}_1= & {} \frac{1}{\sqrt{2}}(\frac{{P'}_{\pi d}^{+}}{\sqrt{2}}+\frac{{P'}_{\eta d}^{+}}{\sqrt{6}}),\nonumber \\ (P_{15})^{\{1,3\}}_1= & {} \frac{1}{\sqrt{2}}\left( \frac{{P'}^{+}_{\pi s}}{\sqrt{2}}+\frac{{P'}^{+}_{\eta s}}{\sqrt{6}}\right) ,\nonumber \\ (P_{15})^{\{2,1\}}_2= & {} \frac{1}{\sqrt{2}}(-\frac{{P'}^{++}_{\pi u}}{\sqrt{2}}+\frac{{P'}^{++}_{\eta u}}{\sqrt{6}}),\nonumber \\ (P_{15})^{\{2,2\}}_2= & {} \left( -\frac{{P'}^{+}_{\pi d}}{\sqrt{2}}+\frac{{P'}^{+}_{\eta d}}{\sqrt{6}}\right) ,\nonumber \\ (P_{15})^{\{2,3\}}_2= & {} \frac{1}{\sqrt{2}}\left( -\frac{{P'}^{+}_{\pi s}}{\sqrt{2}}+\frac{{P'}^{+}_{\eta s}}{\sqrt{6}}\right) , \nonumber \\ (P_{15})^{\{3,1\}}_3= & {} -\frac{1}{\sqrt{3}}{P'}^{++}_{\eta u},\nonumber \\ (P_{15})^{\{3,2\}}_3= & {} -\frac{1}{\sqrt{3}}{P'}^{+}_{\eta d}, \; (P_{15})^{\{3,3\}}_3=-\frac{1}{\sqrt{3}}{P'}^{+}_{\eta s}, \nonumber \\ (P_{15})^{\{2,2\}}_1= & {} {P'}^{0}_{dd{\bar{u}}},\; (P_{15})^{\{3,3\}}_1={P'}^{0}_{ss{\bar{u}}},\; (P_{15})^{\{1,1\}}_2={P'}^{+++}_{uu{\bar{d}}}, \nonumber \\ (P_{15})^{\{3,3\}}_2= & {} {P'}^{+}_{ss{\bar{d}}},\; (P_{15})^{\{1,1\}}_3={P'}^{+++}_{uu{\bar{s}}},\; (P_{15})^{\{2,2\}}_3={P'}^{+}_{dd{\bar{s}}}.\nonumber \\ \end{aligned}$$

(16)

In addition, the baryons with the components qqq, can form an SU(3) octet $T_8$ and an SU(3) decuplet $T_{10}$. The octet has the expression

$$\begin{aligned} T_8= \left( \begin{array}{ccc} \frac{1}{\sqrt{2}} \Sigma ^0+\frac{1}{\sqrt{6}} \Lambda ^0 &{} \Sigma ^+ &{} p \\ \Sigma ^- &{} -\frac{1}{\sqrt{2}} \Sigma ^0+\frac{1}{\sqrt{6}} \Lambda ^0&{} n \\ \Xi ^- &{} \Xi ^0 &{} -\sqrt{\frac{2}{3}} \Lambda ^0 \end{array} \right) ,\nonumber \\ \end{aligned}$$

(17)

and the light decuplet is given as

$$\begin{aligned} (T_{10})^{111}= & {} \Delta ^{++},\;\;\; (T_{10})^{112}= (T_{10})^{121}=(T_{10})^{211}= \frac{1}{\sqrt{3}} \Delta ^{+},\nonumber \\ (T_{10})^{222}= & {} \Delta ^{-},\;\;\; (T_{10})^{122}= (T_{10})^{212}=(T_{10})^{221}= \frac{1}{\sqrt{3}} \Delta ^0, \nonumber \\ (T_{10})^{113}= & {} (T_{10})^{131}=(T_{10})^{311}= \frac{1}{\sqrt{3}} \Sigma ^{\prime +},\nonumber \\ (T_{10})^{223}= & {} (T_{10})^{232}=(T_{10})^{322}= \frac{1}{\sqrt{3}} \Sigma ^{\prime -},\nonumber \\ (T_{10})^{123}= & {} (T_{10})^{132}=(T_{10})^{213}=(T_{10})^{231}\nonumber \\= & {} (T_{10})^{312}=(T_{10})^{321}= \frac{1}{\sqrt{6}} \Sigma ^{\prime 0},\nonumber \\ (T_{10})^{133}= & {} (T_{10})^{313}=(T_{10})^{331}= \frac{1}{\sqrt{3}} \Xi ^{\prime 0},\nonumber \\ (T_{10})^{233}= & {} (T_{10})^{323}=(T_{10})^{332}= \frac{1}{\sqrt{3}} \Xi ^{\prime -}, \nonumber \\ (T_{10})^{333}= & {} \Omega ^-. \end{aligned}$$

(18)

Consistently, the singly charmed baryons cqq are expected to form a anti-triplet and a sextet, respectively as [43, 44]

(19)

In the meson sector, singly charmed mesons form an SU(3) triplet or anti-triplet, light mesons form an octet plus singlet, all multiplets are collected as

$$\begin{aligned}&M_{8}=\begin{pmatrix} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{}\pi ^+ &{} K^+\\ \pi ^-&{}-\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}&{}{K^0}\\ K^-&{}{\bar{K}}^0 &{}-2\frac{\eta }{\sqrt{6}} \end{pmatrix},\;\; D_i^T = \left( \begin{array}{c} D^0 \\ D^+ \\ D^+_s \end{array}\right) \,,\;\;\nonumber \\&\quad {\overline{D}}^i= \left( \begin{array}{c} {\overline{D}}^0 \\ D^- \\ D^-_s \end{array}\right) . \end{aligned}$$

(20)

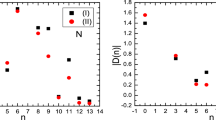
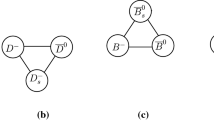
For completeness, we also draw the weight diagrams of multiplets, shown in Figs. 1 and 2.

Fig. 1

The weight diagram for the pentaquark sextet $P_6$ is given in (a). Besides, The weight diagrams of mesons, provided in (b–d), charmed mesons anti-triplet and triplet to be (b, c), light meson octet to be (d)

Fig. 2

The weight diagrams for the singly charmed baryons are given in (a, b), which triplet $T_{c{\bar{3}}}$ to be (a), sextet $T_{c6}$ to be (b). The light baryon multiplets are $T_8, T_{10}$ shown in (c, d) respectively

Fig. 3

Two typical Feynman diagrams for the production of doubly heavy pentaquark $P_{cc{\bar{q}}qq}$ from the triply charmed baryon $\Omega _{ccc}$. The production depends on the transition $c\rightarrow q{\bar{q}}q$ in quark level, which leads to similar topologies (a, b) including one light meson and doubly heavy pentaquark in final states

Table 2 The production of pentaquark $P_{6}(cc\bar{q}qq)$ from triply heavy baryon $\Omega _{ccc}$, sC represents the overall CKM factor $\sin (\theta _ C)$

Table 3 The production of pentaquark $P_{15}(cc\bar{q}qq)$ from triply heavy baryon $\Omega _{ccc}$

3.2 Production of $P_{c c{\bar{q}}qq}$ from $\Omega _{ccc}$

The pentaquark $P_{cc{\bar{q}}qq}$ can be produced by the weak decays of triply charmed baryon $\Omega _{ccc}$, once one charmed quark decays $c\rightarrow q{\bar{q}}q$ in baryon. The typical Feynman diagrams with two final states are shown in Fig. 3. In particular, the final states include the pentaquark we wanted and a light meson. Within the framework of SU(3) symmetry analysis, we then construct the Hamiltonians at the hadronic level, which straightly written as

$$\begin{aligned} {\mathcal {H}}= & {} a_1 \Omega _{ccc} (H_6)^{[ij]}_{l} (P_6)_{[ij]}^k (M)_k^l+a_2 \Omega _{ccc} (H_6)^{[ij]}_{k} \\&\times (P_6)_{[il]}^k (M)_j^l+a_3 \Omega _{ccc} (H_{15})^{[ij]}_{k} (P_6)_{[il]}^k (M)_j^l,\\ {\mathcal {H}}= & {} b_1 \Omega _{ccc} (H_{6})^{[ij]}_{k} (P_{15})_{\{il\}}^k (M)_j^l+b_2 \Omega _{ccc} \\&\times (H_{15})^{\{ij\}}_{l} (P_{15})_{\{ij\}}^k (M)_k^l+b_3 \Omega _{ccc} (H_{15})^{[ij]}_{k} (P_{15})_{\{il\}}^k (M)_j^l. \end{aligned}$$

where the coefficients, such as $a_1,a_2,b_1,b_2,\ldots$, represent the non-perturbative parameters. The SU(3) representations of the corresponding hadrons and transitions above, permit us to expand the Hamiltonians into diverse decay channels, revealed with combinations of non-perturbative coefficients. We forward and collect the possible production channels of $P_6(cc\bar{q}qq)$ states in Table 2. Especially, the Cabibbo allowed, singly Cabibbo suppressed and doubly Cabibbo suppressed are displayed respectively. In addition, the channels corresponding with $P_{15}(cc\bar{q}qq)$ states are placed into Table 3. Referring to the amplitudes of production channels above, we reduce the relations between different channels.

$$\begin{aligned} \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\bar{d}su}^{++} \pi ^0 )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+} \pi ^+ ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\bar{d}su}^{++} K^0 )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\bar{s}ud}^{++} {\overline{K}}^0 ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{ud\bar{s}}^{++} {\overline{K}}^0 )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{su\bar{d}}^{++} K^0 ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{su\bar{d}}^{++} \pi ^0 )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{\pi s}^{+} \pi ^+ ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{\pi u}^{++} \pi ^0 )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{\eta u}^{++} \eta _q ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{\pi u}^{++} K^0 )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow {P'}_{\pi d}^{+} K^+ ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+} \pi ^+ )= & {} \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+} K^+ ),\\ \Gamma (\Omega _{ccc}^{++}\rightarrow P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++} \pi ^0 )= & {} 3\Gamma (\Omega _{ccc}^{++}\rightarrow P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++} \eta _q ). \end{aligned}$$

The Cabibbo allowed production channel of $P_6(cc\bar{q}qq)$ and $P_{15}(cc\bar{q}qq)$ states $\Omega _{ccc}^{++}\rightarrow P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+} \pi ^+$, $\Omega _{ccc}^{++}\rightarrow {P'}_{\eta s}^{+} \pi ^+$, $\Omega _{ccc}^{++}\rightarrow {P'}_{\pi s}^{+} \pi ^+$ and $\Omega _{ccc}^{++}\rightarrow {P'}_{ss\bar{d}}^{+} K^+$, receive the largest contribution, meanwhile, the charged final light mesons possess high detection efficiency. Consequently, we suggest that these channels can be the preference choices for the studying in the future experiment.

Table 4 Pentaquark $P_{6}(cc\bar{q}qq)$ decays into charmed mesons and octet light baryons with the Cabibbo allowed, singly Cabibbo suppressed and doubly Cabibbo suppressed. sC represents the overall CKM factor $\sin (\theta _ C)$

Table 5 Pentaquark $P_{6}(cc\bar{q}qq)$ decays into charmed mesons and decuplet light baryons with Cabibbo allowed, the singly Cabibbo suppressed and doubly Cabibbo suppressed

3.3 Decay modes of pentaquark $P_6(cc{\bar{q}}qq)$

In this part, we will study the possible decays of pentaquark $P_{c c{\bar{q}}qq}$ states. Generally, the excited states $P_{15}$ can primarily decays into $P_6$ states. In that case, we need only to discuss the decay modes of $P_6$ states individually in the paper. As first step, we consider the semileptonic decays of $P_6(cc{\bar{q}}qq)$ with the transition of $c \rightarrow d/s \ell ^+ \nu$. Following the SU(3) analysis, the construction of the corresponding Hamiltonian is forward, which can be constructed as

$$\begin{aligned} {\mathcal {H}}= & {} a_1' (P_6)^{[ij]}_{k} (H_3)^k (\overline{T}_{c{\bar{3}}})_{[ij]} \ell \bar{\nu }. \end{aligned}$$

(21)

The Hamiltonian including sextet pentaquark $P_6$ with two antisymmetry upper indices in initial state, and triplet singly charmed baryon $T_{c{\bar{3}}}$ with two antisymmetry lower indices in final states, can then be represented into a compact form: $a_1 (P_6)_{\{ij\}} (H_3)^i (\overline{T}_{c{\bar{3}}})^j \ell \bar{\nu }$. We expand the new Hamiltonian and obtain six channels, ${\mathcal {M}}(P_{\bar{d}su}^{++}\rightarrow \Xi _c^+ l^+\nu )= -\sqrt{2} {\mathcal {M}}(P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow \Xi _c^0 l^+\nu )=-\sqrt{2}{\mathcal {M}}(P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \Lambda _c^+ l^+\nu )=-\frac{a_1 \left( V_{\text {cd}}\right) {}^*}{\sqrt{2}}$, and ${\mathcal {M}}(P_{\bar{s}ud}^{++}\rightarrow \Lambda _c^+ l^+\nu )=\sqrt{2} {\mathcal {M}}(P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow \Xi _c^0 l^+\nu )=-\sqrt{2}{\mathcal {M}}(_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \Xi _c^+ l^+\nu )=\frac{a_1 \left( V_{\text {cs}}\right) {}^*}{\sqrt{2}}$. Accordingly, the relations of decay width between six channels can be deduced directly, with the effect of phase spaces ignored, given as

$$\begin{aligned} \Gamma (P_{\bar{d}su}^{++}\rightarrow \Xi _c^+ l^+\nu )= & {} 2 \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow \Xi _c^0 l^+\nu )\\= & {} 2\Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \Lambda _c^+ l^+\nu ),\\ \Gamma (P_{\bar{s}ud}^{++}\rightarrow \Lambda _c^+ l^+\nu )= & {} 2 \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow \Xi _c^0 l^+\nu )\\= & {} 2\Gamma (_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \Xi _c^+ l^+\nu ). \end{aligned}$$

The transition of charmed quark decay $c \rightarrow q\bar{q}q$ can lead to non-leptonic decays of pentaquark $c c{\bar{q}}qq$ states $P_6$. Immediately, it is straightforward to construct the Hamiltonian in the hadronic level under the SU(3) light quark symmetry. We raise the possible Hamiltonians of sextet pentaquark $P_6$ decay into the charmed mesons and light baryon $T_8$, $T_{10}$ as follows.

$$\begin{aligned} H= & {} a_1 (P_{6})_{\{ij\}} (H_{\overline{6}})_{k}^{[il]}({\bar{D}})^{j}(\overline{T}_{8})_{l}^{k}\nonumber \\&+a_2 (P_{6})_{\{ij\}}(H_{\overline{6}})_{k}^{[il]}({\bar{D}})^{k}(\overline{T}_{8})_{l}^{j}\nonumber \\&+a_3 (P_{6})_{\{ij\}} (H_{15})_{k}^{\{il\}}({\bar{D}})^{j}(\overline{T}_{8})_{l}^{k}\nonumber \\&+a_4 (P_{6})_{\{ij\}} (H_{15})_{k}^{\{il\}}({\bar{D}})^{k}(\overline{T}_{8})_{l}^{j}\nonumber \\&+a_5 (P_{6})_{\{ij\}} (H_{15})_{k}^{\{ij\}}({\bar{D}})^{l}(\overline{T}_{8})_{l}^{k},\nonumber \\ H= & {} b_1 (P_{6})_{\{ij\}} (H_{\overline{6}})_{k}^{[jl]}({\bar{D}})^{k}(\overline{T}_{10})_{\{l\alpha \beta \}}\varepsilon ^{i\alpha \beta }\nonumber \\&+b_2 (P_{6})_{\{ij\}} (H_{\overline{6}})_{k}^{[jl]}({\bar{D}})^{\alpha }(\overline{T}_{10})_{\{l\alpha \beta \}}\varepsilon ^{ik\beta }\nonumber \\&+b_3 (P_{6})_{\{ij\}} (H_{15})_{k}^{\{jl\}}({\bar{D}})^{k}(\overline{T}_{10})_{\{l\alpha \beta \}}\varepsilon ^{i\alpha \beta }\nonumber \\&+b_4 (P_{6})_{\{ij\}} (H_{15})_{k}^{\{jl\}}({\bar{D}})^{\alpha }(\overline{T}_{10})_{\{l\alpha \beta \}}\varepsilon ^{ik\beta }\nonumber \\&+b_5 (P_{6})_{\{ij\}} (H_{15})_{k}^{\{l\alpha \}}({\bar{D}})^{j}(\overline{T}_{10})_{\{l\alpha \beta \}}\varepsilon ^{ik\beta }. \end{aligned}$$

(22)

We expand the Hamiltonians and collect the possible processes, entrying into Tables 4 and 5. Meanwhile, it is ready to reduce the relations of decay width between different channels. We deduced the relations as follows.

$$\begin{aligned}&\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^0 \Lambda ^0)= 3\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^0 \Sigma ^0),\\&\Gamma (P_{\bar{d}su}^{++}\rightarrow D^+ \Sigma ^+) = \Gamma (P_{\bar{s}ud}^{++}\rightarrow D^+_s p),\\&\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^+ \Delta ^{-})= 3\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^+_s \Sigma ^{\prime -}),\\&\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^+ \Sigma ^{\prime -})= \Gamma (P_{\bar{u}ds}^{0}\rightarrow D^+_s \Xi ^{\prime -}),\\&\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^+ \Xi ^{\prime -})= \frac{1}{3}\Gamma (P_{\bar{u}ds}^{0}\rightarrow D^+_s \Omega ^-),\\&\Gamma (P_{\bar{d}su}^{++}\rightarrow D^0 \Delta ^{++}) = 3\Gamma (P_{\bar{d}su}^{++}\rightarrow D^+_s \Sigma ^{\prime +}),\\&\Gamma (P_{\bar{d}su}^{++}\rightarrow D^+ \Sigma ^{\prime +})= \Gamma (P_{\bar{s}ud}^{++}\rightarrow D^+_s \Delta ^{+}),\\&\Gamma (P_{\bar{s}ud}^{++}\rightarrow D^0 \Delta ^{++}) = 3\Gamma (P_{\bar{s}ud}^{++}\rightarrow D^+ \Delta ^{+}),\\&\Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow D^0 p)= \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow D^0 \Sigma ^+),\\&\Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow D^+ p) = \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow D^+_s \Sigma ^+),\\&\Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow D^0 \Delta ^{+})= \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow D^0 \Sigma ^{\prime +}),\\&\Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow D^+ \Delta ^{0}) = \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow D^+_s \Xi ^{\prime 0}),\\&\Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow D^+_s \Delta ^{0})= \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow D^+_s \Delta ^{+}),\\&\Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow D^+_s \Sigma ^{\prime 0}) = \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow D^+ \Sigma ^{\prime 0}),\\&\Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow D^+ \Xi ^{\prime 0})= \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow D^+ \Sigma ^{\prime +}),\\&\Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow D^+ \Delta ^{+}) = \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow D^+_s \Sigma ^{\prime +}). \end{aligned}$$

Table 6 Pentaquark $P_{6}(cc\bar{q}qq)$ decays into light mesons and singly charmed baryons triplet with Cabibbo allowed, the singly Cabibbo suppressed and doubly Cabibbo suppressed

Table 7 Pentaquark $P_{6}(cc\bar{q}qq)$ decays into light mesons and singly charmed baryons sextet with Cabibbo allowed, the singly Cabibbo suppressed and doubly Cabibbo suppressed

More technically, the Hamiltonians of the sextet state $P_{6}$ decay into light mesons and singly charmed baryons can be constructed below.

$$\begin{aligned} H= & {} c_1 (P_{6})_{\{ij\}}(H_{{\bar{6}}})_k^{[il]}(M)_{l}^j(\overline{T}_{c{\bar{3}}})^{k}\nonumber \\&+c_2 (P_{6})_{\{ij\}}(H_{{\bar{6}}})_k^{[il]}(M)_{l}^k(\overline{T}_{c{\bar{3}}})^{j}\nonumber \\&+c_3 (P_{6})_{\{ij\}}(H_{15})_k^{\{il\}}(M)_{l}^j(\overline{T}_{c{\bar{3}}})^{k}\nonumber \\&+c_4 (P_{6})_{\{ij\}}(H_{15})_k^{\{il\}}(M)_{l}^k(\overline{T}_{c{\bar{3}}})^{j}\nonumber \\&+c_5 (P_{6})_{\{ij\}}(H_{15})_k^{\{ij\}}(M)_{l}^k(\overline{T}_{c{\bar{3}}})^{l},\nonumber \\ H= & {} d_1 (P_{6})_{\{ij\}}(H_{{\bar{6}}})_k^{[jl]}(M)_{l}^{\alpha }(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{ik\beta }\nonumber \\&+d_2 (P_{6})_{\{ij\}}(H_{{\bar{6}}})_k^{[j\alpha ]}(M)_{l}^{k}(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{il\beta }\nonumber \\&+d_3 (P_{6})_{\{ij\}}(H_{{\bar{6}}})_k^{[j\alpha ]}(M)_{l}^{\beta }(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{ikl}\nonumber \\&+d_4 (P_{6})_{\{ij\}}(H_{15})_k^{\{jl\}}(M)_{l}^{\alpha }(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{ik\beta }\nonumber \\&+d_5 (P_{6})_{\{ij\}}(H_{15})_k^{\{j\alpha \}}(M)_{l}^{k}(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{il\beta }\nonumber \\&+d_6 (P_{6})_{\{ij\}}(H_{15})_k^{\{j\alpha \}}(M)_{l}^{\beta }(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{ikl}\nonumber \\&+d_7 (P_{6})_{\{ij\}}(H_{15})_k^{\{\alpha \beta \}}(M)_{l}^{j}(\overline{T}_{c6})_{\{\alpha \beta \}}\varepsilon ^{ikl}. \end{aligned}$$

(23)

Fig. 4

The weak decay diagrams of the doubly heavy pentaquark $P_{6}$ are given in (a–d), which semi-leptonic decays to be (a), non-leptonic decays to be (b–d)

We expand the decay channels of pentaquark octet $P_{10}$ turning into anti-charmed mesons and light baryon, whose decay amplitudes collected in Tables 6 and 7. The relations between different channels are given as follows.

$$\begin{aligned} \Gamma (P_{\bar{u}ds}^{0}\rightarrow \pi ^0 \Omega _{c}^{0})= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow \pi ^+ \Omega _{c}^{0})\\= & {} 2\Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow {\overline{K}}^0 \Xi _{c}^{\prime +}),\\ \Gamma (P_{\bar{u}ds}^{0}\rightarrow \pi ^0 \Xi _c^0)= & {} \frac{1}{3}\Gamma (P_{\bar{u}ds}^{0}\rightarrow \eta _q \Xi _c^0),\\ \Gamma (P_{\bar{u}ds}^{0}\rightarrow \pi ^- \Xi _c^+)= & {} \Gamma (P_{\bar{u}ds}^{0}\rightarrow K^- \Lambda _c^+),\\ \Gamma (P_{\bar{u}ds}^{0}\rightarrow \pi ^- \Xi _{c}^{\prime +})= & {} \Gamma (P_{\bar{u}ds}^{0}\rightarrow K^- \Sigma _{c}^{+}),\\ \Gamma (P_{\bar{u}ds}^{0}\rightarrow K^0 \Omega _{c}^{0})= & {} \Gamma (P_{\bar{u}ds}^{0}\rightarrow {\overline{K}}^0 \Sigma _{c}^{0}),\\ \Gamma (P_{\bar{u}ds}^{0}\rightarrow \pi ^0 \Xi _{c}^{\prime 0})= & {} 3\Gamma (P_{\bar{u}ds}^{0}\rightarrow \eta _q \Xi _{c}^{\prime 0}),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow \pi ^+ \Sigma _{c}^{0})= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow K^+ \Omega _{c}^{0}),\\ \Gamma (P_{\bar{d}su}^{++}\rightarrow \pi ^+ \Xi _c^+)= & {} \Gamma (P_{\bar{s}ud}^{++}\rightarrow K^+ \Lambda _c^+),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow K^+ \Xi _c^0)= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow \pi ^+ \Xi _c^0),\\ \Gamma (P_{\bar{d}su}^{++}\rightarrow \pi ^+ \Xi _{c}^{\prime +})= & {} \frac{1}{2}\Gamma (P_{\bar{d}su}^{++}\rightarrow {\overline{K}}^0 \Sigma _{c}^{++})\\= & {} \Gamma (P_{\bar{s}ud}^{++}\rightarrow K^+ \Sigma _{c}^{+})\\= & {} \frac{1}{2}\Gamma (P_{\bar{s}ud}^{++}\rightarrow K^0 \Sigma _{c}^{++}),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow K^0 \Xi _c^+)= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow {\overline{K}}^0 \Lambda _c^+),\\ \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \pi ^+ \Lambda _c^+)= & {} \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow K^+ \Xi _c^+),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow K^+ \Xi _{c}^{\prime 0})= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow \pi ^+ \Xi _{c}^{\prime 0}),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow K^0 \Xi _{c}^{\prime +})= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow {\overline{K}}^0 \Sigma _{c}^{+}),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow \pi ^- \Sigma _{c}^{++})= & {} \Gamma (P_{\{\bar{u}u,\bar{d}d\}\bar{s}}^{+}\rightarrow K^- \Sigma _{c}^{++}),\\ \Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow K^+ \Sigma _{c}^{0})= & {} 2\Gamma (P_{\{\bar{u}u,\bar{s}s\}\bar{d}}^{+}\rightarrow K^0 \Sigma _{c}^{+}),\\ \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \pi ^+ \Sigma _{c}^{+})= & {} \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow K^+ \Xi _{c}^{\prime +})\\= & {} 3\Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \eta _q \Sigma _{c}^{++})\\= & {} \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \pi ^0 \Sigma _{c}^{++}),\\ \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow \pi ^+ \Xi _{c}^{\prime +})= & {} \frac{1}{2}\Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow {\overline{K}}^0 \Sigma _{c}^{++}),\\ \Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow K^+ \Sigma _{c}^{+})= & {} \frac{1}{2}\Gamma (P_{\{\bar{d}d,\bar{s}s\}\bar{u}}^{++}\rightarrow K^0 \Sigma _{c}^{++}). \end{aligned}$$

Table 8 The golden channels of decays with Cabibbo allowed $P(cc{\bar{q}}qq)$

4 Golden channels

As a collection, we will screen out some golden channels to reconstruct the pentaquark $P_{cc{\bar{q}}qq}$ in the section. In principle, the main considerations are the CKM elements in the transition (Fig. 4). The amplitudes of c-quark decay transitions such as $c\rightarrow s{\bar{d}} u$ and $c\rightarrow s\ell ^+ \nu _{\ell }$ will receive the largest contribution as $V_{cs}^*\sim 1$. Beyond that, the detection efficiency is also a serviceable factor, generally speaking, charged particles have higher rates to be detected than neutral particles. According to the selection schemes, one use the following criteria [44], finally, we can obtain the golden decay channels in Table 8.

• Branching fractions: one chooses the corresponding channels with the quark transition of ${\bar{c}}\rightarrow {\bar{s}}d {\bar{u}}$ or ${\bar{c}}\rightarrow {\bar{s}}\ell ^- {\bar{\nu }}_{\ell }$.

• Detection efficiency: one removes all channels with the hadrons $\pi ^0$, $K^0$, $\overline{K}^0$, n, $\Sigma ^{+}(\rightarrow p \pi ^0)$ and $\Sigma ^-(\rightarrow n \pi ^-)$ in final states, but keep the processes with $\pi ^\pm$, $\Sigma ^{0}(\rightarrow N \pi \gamma )$, $\Lambda ^0(\rightarrow p \pi ^-)$ and $\Delta ^0(\rightarrow N \pi )$.

5 Conclusions

In the paper, we discussed the mass spectrums of doubly charmed pentaquarks $P_{cc{\bar{q}}qq}$ primarily under the doubly heavy triquark-diquark model. Moreover, the lifetimes were considered at the next-to-leading order with the approach of OPE. The calculation suggested some potential stable pentaquark states against strong interaction, for instance, $cc{\bar{s}} ud$ with the parity $J^P=\frac{1}{2}^-$. Further more, the lifetimes obtained as $\tau (P_{cc{\bar{q}}qq}(\frac{1}{2}^-))=(4.65^{+0.71}_{-0.55})\times 10^{-13}s$ and $\tau (P_{cc{\bar{q}}qq}(\frac{3}{2}^-))=(0.93^{+0.14}_{-0.11})\times 10^{-12} s$. Subsequently, we systematically discussed the production and decay behaviors of $P(cc{\bar{q}}qq)$, such as semi- or non-leptonic processes. Finally, we collected the golden channels of decay processes, which with the largest branching fraction and experimental detector efficiency. Inspired by the fact that theoretical predictions for doubly charmed baryon give good consistency with the experimental side [45,46,47], in which the suggested channels of theoretical studies are extracted from the weak decays of charmed quark, ultimately prompting the discovery of doubly charmed baryon [48]. Our study of pentaquark $P(cc{\bar{q}}qq)$ which are similar with doubly charmed baryon, therefore, are helpful to search for the doubly charmed pentaquark in future experiments.