1 Introduction

Following Bekenstein’s [1, 2] and Hawking’s [3,4,5] pioneering work on black holes (BHs), their thermodynamic properties have attracted an enormous interest, ever since. On the other hand, in recent years, an alternative theory of gravity, known as Conformal Gravity (CG) (see, e.g., the review [6]), has been proposed as a viable solution of the dark matter/dark energy puzzle. According to this theory, dark matter and dark energy can be understood as an artefact, due to the attempt to describe global physical effect in purely local galactic terms.

Here we study BH thermodynamics in CG. We do so by employing various methods, as, e.g., Thermodynamic Geometry (TG) [7,8,9,10,11], that is also a very active area of research by itself. Below we show that such approach can fruitfully be applied also in CG, an interesting result in its own right.

Our focus here is on stability and phase transitions. Hawking first suggested [3,4,5] that the Schwarzschild BH is thermodynamically unstable, due to its negative specific heat, for which the more the BH emits, the hotter becomes. Subsequent work shows that other BHs in 3+1 dimensions, such as Kerr, Reissner-Nordström and Kerr-Newmann, are unstable, i.e. the entropy is a concave function. As we shall see, it is not clear whether this condition is sufficient to characterize the stability of non-extensive systems, like BHs.

Currently, two are the main approaches to have BHs with positive specific heat. The first is to lower dimensions to 2+1, hence to consider the Bañados–Teitelboim–Zanelli (BTZ) solution there [12]. The other way is to include a negative cosmological constant, \(\varLambda < 0\), that is to have asymptotically Anti de Sitter (AdS) spacetimes rather than flat Minkowski [13].

Relation between stability and positive values of the specific heat holds only for extensive systems [14]. However, BH are not extensive objects, their entropy scales as the area, not the volume, hence stability is not related to the concavity of the entropy function. Stability of this kind of systems need be studied with a different criteria, named Poincaré (or turning point) method [15], that holds for a generic out-of-equilibrium entropy, and requires only that equilibrium is reached in an extreme point [16,17,18,19,20,21,22]. The peculiarity of gravitating systems, in this respect, is that the algebraic sign (±) of the thermodynamic quantities is not an indicator of stability. On the other hand, a change of sign is correlated to a change of stability. This analysis is not always compatible with the conclusions based on the concavity of the entropy. For example, the Poincaré method does not predict instability for the Schwarzschild or Kerr BHs [22].

In addition to stability, phase transitions in BHs are of great interest. Important examples are the Hawking-Page phase transition [13], the AdS/CFT correspondence and its relation to deconfinement at finite temperature in gauge theories. A simple way to study BH phase transitions is to employ the TG proposed by Ruppeiner. TG is based on the definition of a metric in the thermodynamic space [7,8,9,10,11]

$$\begin{aligned} g^{\mathrm{TG}}_{\mu \nu } \equiv -\frac{\partial ^2 S}{\partial X^\mu \partial X^\nu } \;. \end{aligned}$$
(1)

where S is the entropy, while \(X^\mu \in (E,P,N,\,\ldots )\), with E energy, P pressure, N number of particles, etc.. This way, critical phenomena are related to distinctive signs of the scalar curvature, \(R^{\mathrm{TG}}\), obtained from such metric: \(R^{\mathrm{TG}} = 0\) means a system made of noninteracting components, while for \(R^{\mathrm{TG}} < 0\) such components attract each other, and for \(R^{\mathrm{TG}} > 0\) repel each other. Moreover, \(R^{\mathrm{TG}}\) diverges in a second order phase transition as the correlation volume, while it appears to have a local maximum at a crossover, as happens in quantum chromodynamics [23,24,25,26,27].

TG has been tested in many different systems: phase coexistence for helium, hydrogen, neon and argon [28], for the Lennard Jones fluids [29, 30], for ferromagnetic systems and liquid liquid phase transitions [31]; in the liquid gas like first order phase transition in dyonic charged AdS BH [32]; in quantum chromodynamics (QCD) to describe crossover from Hadron gas and Quark Gluon Plasma [23,24,25,26,27]; in the Hawking Page transitions in Gauss Bonnet AdS [33], Reissner Nordstrom AdS and the Kerr AdS [34]. A list of results have been obtained by applying TG to BHs [35,36,37,38,39,40,41,42,43,44,45].

Our paper is organized as follows. We shall first briefly review the basic ideas of CG and of BHs in CG in Sect. 2. We shall then introduce Ruppeiner’s TG in Sect. 3, while Sect. 4 offers a discussion about stability in extensive and non-extensive systems. Section 5 is devoted to the main results of this paper, that is the study of the stability and phase transitions of the (A)dS Schwarzschild BH in CG. Our comments and conclusions are in Sect. 6. The paper is closed by two Appendices, devoted to the details of some computations.

2 BH thermodynamics in CG

Let us start by recalling what is Weyl symmetry, as this will help us to clarify the general set-up, and to identify the theory of gravity we are actually investigating. A scaling of the distance

$$\begin{aligned} \Vert x\Vert ^2 \equiv g_{\mu \nu } x^\mu x^\nu \, \rightarrow \, \varOmega ^2 \Vert x\Vert ^2 \end{aligned}$$
(2)

can be obtained in two ways

$$\begin{aligned} x^\mu \rightarrow \varOmega \; x^\mu \quad \mathrm{and} \quad g_{\mu \nu } \rightarrow g_{\mu \nu } \, \end{aligned}$$
(3)

or

$$\begin{aligned} x^\mu \rightarrow x^\mu \quad \mathrm{and} \quad g_{\mu \nu } \rightarrow \varOmega ^2 g_{\mu \nu } \,. \end{aligned}$$
(4)

In both cases the matter fields \(\varPhi _i\), when present, transform as

$$\begin{aligned} \varPhi _i (x) \rightarrow \varOmega ^{d_\varPhi } \varPhi _i (x) \,, \end{aligned}$$
(5)

where \(d_\varPhi \) is their scale dimension.

The two scalings are equivalent in practise, but not in spirit. The second way to transform are the Weyl transformations. They turn a spatiotemporal transformation (acting on \(x^\mu \)) into a field/internal transformation (acting on \(g_{\mu \nu }\)), hence something that, when \(\varOmega (x)\), one could gauge in the usual way, i.e., by improving standard derivatives (e.g., \(\partial _\mu \phi \), for \(\varPhi _i \equiv \phi \), a scalar field) to covariant derivatives (e.g., \(\partial _\mu \rightarrow \partial _\mu + d_\phi W_\mu \)) with the Weyl-gauge field transforming as \(W_\mu \rightarrow W_\mu - \partial _\mu \ln \varOmega \). On this see [46], and also [47].

The latter reference tells the history of this idea, that actually is the first historical example of what we nowadays call gauge theory. As recalled there, Weyl’s first attempt to propose a theory of gravity based on this symmetry was not taken seriously by Einstein (nor other scientists of that time). Over the years, though, the role of Weyl symmetry in gravity had a resurgence, starting from the work of Deser, Jackiw and Templeton in 2+1 dimensions in [48, 49], implicitly as part of a larger theory, then more explicitly as a separate subject, again in 2+1 dimensions in [50] (where the term “conformal gravity” is first used), and later in 1+1 dimensions in [51]. On the other hand, a dilaton-improved Einstein–Hilbert action in 3+1 dimensions, that enjoys Weyl symmetry, is employed in [52] to study the thermodynamics of BHs. There too such theory is called conformal gravity.

For us, CG (which we may as well call Weyl gravity) is a theory of gravity in 3+1 dimensions, enjoying Weyl symmetry, whose action is [6, 53,54,55,56,57,58,59]

$$\begin{aligned} I_{W} = \alpha _{W} \;\int d^4x \sqrt{|g|}\;C^{\mu \nu \rho \sigma } C_{\mu \nu \rho \sigma } \;, \end{aligned}$$
(6)

where

$$\begin{aligned} C^\lambda _{\mu \nu \rho }= & {} \displaystyle R^\lambda _{\mu \nu \rho } + \frac{1}{6}\;R \left( g^\lambda _{\nu }R_{\mu \rho }-g^\lambda _{\rho }R_{\mu \nu }\right) \nonumber \\&\displaystyle - \frac{1}{2}\left( g^\lambda _{\nu }R_{\mu \rho } - g^\lambda _{\rho }R_{\mu \nu } - g_{\mu \nu }R^\lambda _{\rho } + g_{\mu \rho }R^\lambda _{\nu } \right) \end{aligned}$$
(7)

is the Weyl tensor, expressed in terms of the Riemann tensor, \(R^\lambda _{\mu \nu \rho }\), and its contractions, the Ricci tensor, \(R_{\mu \nu }\) and the scalar curvature, R.

In dimensions \(n>3\), under Weyl transformations: \(C^\lambda _{\mu \nu \rho } \rightarrow C^\lambda _{\mu \nu \rho }\) (that, from \(C^\lambda _{\mu \nu \rho } (\eta ) = 0\), gives \(C^\lambda _{\mu \nu \rho } (\varOmega ^2 \eta ) = 0\)), which, together with \(g_{\mu \nu } \rightarrow \varOmega ^2 g_{\mu \nu }\), and \(g^{\mu \nu } \rightarrow \varOmega ^{-2} g^{\mu \nu }\), gives \(C^{\lambda \mu \nu \rho } \rightarrow \varOmega ^{-6} C^{\lambda \mu \nu \rho }\) and \(C_{\lambda \mu \nu \rho } \rightarrow \varOmega ^{2} C_{\lambda \mu \nu \rho }\), while \(\sqrt{|g|} \rightarrow \varOmega ^n \sqrt{|g|}\). With these

$$\begin{aligned} I_W \rightarrow \varOmega ^{d_\alpha + n - 4} I_W \,, \end{aligned}$$
(8)

where \(\alpha _W \rightarrow \varOmega ^{d_\alpha } \alpha _W\) (recall that \(d^n x\) does not scaleFootnote 1). This means that \(d_\alpha = 4 - n\), i.e., for \(n=4\), our case, \(\alpha _W\) is dimensionless. From a different perspective, since \([C^\lambda _{\mu \nu \rho }] = [L]^{-2}\) (recall that \([g_{\mu \nu }] = 1\)), then, in units \(c = 1 = \hbar \), \([\alpha _W] = [L]^{(4 - n)}\), that is again the same result.

Variation of the action in Eq. (6) with respect to \(g_{\mu \nu }\) gives the Euler-Lagrange equations for the theory, called Bach equations in vacuum (no matter)

$$\begin{aligned} \frac{g_{\mu \alpha }g_{\nu \beta }}{\sqrt{|g|}}\;\frac{\delta I_W}{\delta g_{\alpha \beta }} = 2\;\alpha _{W}\;W_{\mu \nu } = 0 , \end{aligned}$$
(9)

where the Bach tensor is defined as

$$\begin{aligned} W_{\mu \nu } = W^{(2)}_{\mu \nu } - \frac{1}{3}\;W^{(1)}_{\mu \nu } \;, \end{aligned}$$
(10)

with

$$\begin{aligned} W_{\mu \nu }^{(1)}= & {} 2\;g_{\mu \nu } R^{;\beta }_{\;;\beta } - 2\; R_{;\mu \;;\nu } -2\; R R_{\mu \nu } + \frac{1}{2} \; g_{\mu \nu } R^2 \;,\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} W_{\mu \nu }^{(2)}= & {} \frac{1}{2}\;g_{\mu \nu } R^{;\beta }_{\;;\beta } + R_{\mu \nu \;;\beta }^{\;\;\;;\beta } - R_{\mu \;;\nu ;\beta }^{\;\;\beta } - R_{\nu \;;\mu ;\beta }^{\;\;\beta } \nonumber \\&- 2\;R_{\mu \beta }R_{\nu }^{\;\beta } +\frac{1}{2}\;g_{\mu \nu } R_{\alpha \beta }R^{\alpha \beta } \,, \end{aligned}$$
(12)

where, as usual, \(\bullet ;_\mu \equiv \nabla _{\mu } \bullet \), indicates the covariant derivative.

The complete and exact vacuum solution is a static, spherically symmetric geometry given by [55]

$$\begin{aligned} ds^2 = -f(r)\;dt^2 + \frac{dr^2}{f(r)} + r^2\;d\omega ^2_{S^2} \;, \end{aligned}$$
(13)

where r is the radial coordinate, and \(d\omega ^2_{S^2}\) is the line element of the 2-sphere \(S^2\). All other static, spherically symmetric line elements are conformal to Eq. (13). The function f(r) takes the form known as the Mannheim–Kazanas (MK) solution [55, 56]

$$\begin{aligned} f(r) = c_1 + c_2 \; r + \frac{c_3}{r} +c_4\;r^2 \;, \end{aligned}$$
(14)

where \(c_1\), \(c_2\), \(c_3\) and \(c_4\) are four integration constants, of which only three are independent, due to the constraint

$$\begin{aligned} c_1^2 = 3\;c_2\;c_3+1 \;, \end{aligned}$$
(15)

imposed by Bach equations. Indeed, since all information is contained in \(W^{rr}\), which only involves derivatives up to third order. In a static geometry \(W^{0r}\) is identically zero, while other terms are obtained through the Bianchi and trace identities [55].

The event horizon is found in the usual way, by solving \(f(r_{\mathrm{h}}) = 0\). We do not deem useful to show the complicated general solution here, but we shall discuss the particular cases of interest, when they appear.

2.1 Comparison with standard gravity

We need now to understand which aspects of interests change, and which do not change in this picture, as compared to standard gravity of the Einstein kind, including a cosmological constant (for a general discussion on CG and Einstein gravity see, e.g. [60]).

To start, let us look at the question of the asymptotic behavior of (14). In standard Einstein gravity, in most cases one requires the solutions to asymptote to flat space, as is the case of Schwarzschild solution (sometimes one might require more sophisticated asymptotics too). Clearly, given the Weyl symmetry at work in CG, the flat spacetimes can be mapped into conformally flat, and the theory will not appreciate the difference. Henceforth, what in standard gravity is the request that the solution asymptotes to Minkowsky, corresponds in CG to the request that the solution asymptotes to conformally flat spaces.

Let us then look at MK solution (14). The mentioned Schwarzschild solution is also a solution here, when \(c_1=1\), \(c_3=-M\), in the proper units (see the following discussion in point (a) below) and \(c_2 = 0 = c_4\). Therefore, as just said the spacetime is actually flat when \(r \rightarrow \infty \).

As for the other coefficients, \(c_2\) and \(c_4\), things are more involved, as for comparing with standard gravity, but still one needs to impose the necessary boundary conditions. For instance, if only \(c_4\) is nonzero, this would solve the problem because both dS and AdS spacetimes, being maximally symmetric, are conformally flat. Of course, just like in Einstein gravity, it could be of interest that the solutions do not asymptote to flat space.

In this paper we take the above duly into account, and the solutions we are going to consider are always either flat or conformally flat. For instance, we shall be requiring \(c_2\) (related to \(\varXi \) in the thermodynamics correspondence set below, see later), but should retain \(c_4\), related to the cosmological “constant” \(\varLambda \). Henceforth, we shall be dealing with spaces that asymptote to either dS or AdS, depending on the sign of \(c_4\). These, being maximally symmetric spaces, are conformally flat.

Let us now turn our attention to (a) how the integration constants \(c_1, ..., c_4\), need be associated to BH thermodynamic variables, such as mass, volume, pressure, etc.; (b) the BH temperature; (c) the BH entropy, that plays a crucial role in TG.

  1. (a)

    First, notice that four scales have appeared in Eq. (14), and we are soon going to identify them with scales known from Einstein gravity, such as, e.g., the cosmological constant. This is quite a different story, tough. In the non-conformal case, one starts off with an action that indeed has the scale. Hence, clearly, this scale is found in the solutions. Here such scales are dynamically generated, i.e., they only appear when the Euler–Lagrange equations are solved. Since such equations identify the field configurations that minimize the action functional (Hamilton principle), this amount to fix a specific minimum, identified by a specific set of constants. On the other hand, conformal/Weyl symmetry is at work also on-shell. Therefore, the scale fixing is only apparent, and, in a way reminiscent of the spontaneous breaking of symmetry: all configurations obtained Weyl-transforming the solution in Eq. (14) are solutions too. Notice that this is an entirely classical phenomenon. Enthalpy, evaluated as the Noether charge corresponding to the time-like Killing vector for Eq. (13), is [61]

    $$\begin{aligned} H = \alpha _W \left[ \frac{c_2\;(c_1 - 1)}{6} - c_3\;c_4 \right] \;. \end{aligned}$$
    (16)

    We observe that, if in Eq. (14) one sets

    $$\begin{aligned} c_1 \equiv 1 \; \;, \; c_2 \equiv 0 \; \;, \; c_3 \equiv -\eta \; \;, \; \displaystyle c_4 \equiv -\frac{\varLambda }{3} \;, \end{aligned}$$
    (17)

    the line element in Eq. (13) is an (A)dS line element, with [13],

    $$\begin{aligned} f(r) = 1 -\frac{\eta }{r} - \frac{\varLambda }{3}\;r^2\;, \end{aligned}$$
    (18)

    where \(\eta \) in Einstein gravity is 2MG, while \(\varLambda \) plays the role of the cosmological constant. Immediately, one sees that the dimensions are not the same here, as compared to Einstein gravity, essentially due to the lack of the Newton constant G here, with \([G] = [L]^2\). In fact, while here \([\eta ] = [L]\) matches \([M G] = [L]\) of Einstein gravity, the same cannot be said of M itself, for which \([M] = [L]^{-1} \ne [\eta ] = [L]\) (mismatch of \([L]^2\)). Similarly, here \([\varLambda ] = [L]^{-2}\), just like in Einstein gravity, nonetheless, when one computes the associated pressure, say it P, according to Einstein gravity one finds \(P \sim \varLambda /G\), hence \([P] = [L]^{-4}\) (again a mismatch of \([L]^2\)). Nonetheless, if one considers that, as we shall see, the variable playing the role of the volume here (we call it \(\varGamma \) below) is such that \([\varGamma ] = [L]\), rather than \([V] = [L]^3\) of Einstein gravity (mismatch of \([L]^2\)), we see that a proper “PdV” can be included in our thermodynamic analysis as “\((-\varLambda ) d\varGamma \)” (on the sign, see below).

  2. (b)

    As for the Hawking temperature, although its relation with the “mass” is clearly modified by the new settings, as explained above, its structure is insensitive to conformal/Weyl transformations. This is an old, and quite general result proved in [62], based on the fact that a conformal/Weyl invariant surface gravity, \(\kappa _W\), of a conformal Killing horizon can be found to agree with the surface gravity, \(\kappa \), of the Killing horizon. The latter is proportional to the Hawking temperature in the usual way, \(T = \kappa / 2 \pi = \kappa _W / 2 \pi \), where the last equality is the result. More recently, this was applied to certain (2+1)-dimensional systems, to show how an ultra-static metric can still have interesting conformal Killing horizons, hence, an associated Hawking phenomenon [63, 64]. Let us then evaluate the Hawking temperature according to

    $$\begin{aligned} T = \frac{1}{4\pi }\; \left[ \frac{df(r)}{dr}\right] _{r = r_{\mathrm{h}}} = \frac{r^2_h-\left( 3\;c_3+c_1\;r_{\mathrm{h}}\right) ^2}{12\;\pi \;c_3\;r^2_h} \;, \end{aligned}$$
    (19)

    and stress that this expression is invariant under Weyl transformations, \(T \rightarrow T\).

  3. (c)

    The last, and most important point to discuss is the BH entropy, that is central to the analysis we want to perform, based on TG. One could be tempted to use the Bekenstein formula for it

    $$\begin{aligned} S_B = \frac{1}{4 G} {{\mathcal {A}}}_\varSigma \;, \end{aligned}$$
    (20)

    as sometimes done in the literature for similar theories that are different from the one we deal with here, as explained earlier here. There \({{\mathcal {A}}}_\varSigma \) is the area of the event horizon \(\varSigma \).

If this entropy is used, we have immediately two issues. First, we have no scale G in our theory here. Second, the area must respond to Weyl transformations, hence, recalling that out of this entropy we need to construct a metric in the thermodynamic space of TG, such metric would scale too.

Both problems are solved at once if one considers that this is not Einstenin gravity, and a generalization of Bekenstein entropy to gravity theories other than Einstein’s is indeed available. Such generalization was discovered by Wald in [65], and it is based on the Noether charge associated to diffeomorphisms, that are generic translations. In this approach, the expression for the entropy is the integral of the Noether potential over the BH’s bifurcation surface [65], or any arbitrary slice of a Killing horizon [66] (so that the formula applies to BHs other than the eternal stationary, including those formed through a dynamical process in the past). For a recent discussion see, e.g., [67].

The explicit formula is [65, 67]

$$\begin{aligned} S = - 2 \pi \int _\varSigma d^2 x \; \sqrt{h} \; \epsilon _{\mu \nu } \epsilon _{\rho \sigma } \; \displaystyle \frac{\delta {{\mathcal {L}}}}{\delta R_{\mu \nu \rho \sigma }} \;, \end{aligned}$$
(21)

where \(\epsilon _{\mu \nu } = 1/\Vert x\Vert ^2 (x_\mu x_\nu - x_\nu x_\mu )\) is the normal bivector to the arbitrary slice of the Killing horizon \(\varSigma \), identified by (\(r=r_{\mathrm{h}}\), and \(t=\mathrm{const.}\)) (note that \(\epsilon ^{\mu \nu }\epsilon _{\mu \nu }=-2\)), with induced metric \(h_{\alpha \beta }\), whose determinant is h. The formula applies to theories with Lagrangian density \({{\mathcal {L}}} (R_{\mu \nu \rho \sigma }, \nabla _\lambda R_{\mu \nu \rho \sigma }, \nabla _{(\lambda \kappa \ldots )} R_{\mu \nu \rho \sigma }, \varPhi _i, \nabla _\lambda \varPhi _i, \nabla _{(\lambda \kappa \ldots )} \varPhi _i)\), that, in general, includes the matter fields, \(\varPhi _i\), that also may contribute to the entropy.

When \({{\mathcal {L}}} = \displaystyle \frac{1}{16 \pi G} R\), then

$$\begin{aligned} \delta {{\mathcal {L}}}/ \delta R_{\mu \nu \rho \sigma } = \displaystyle \frac{1}{32 \pi G} (g^{\mu \rho } g^{\nu \sigma } - g^{\nu \rho } g^{\mu \sigma })\;, \end{aligned}$$
(22)

hence

$$\begin{aligned} S= & {} - \displaystyle \frac{1}{16 G} \int _\varSigma d^2 x \; \sqrt{h} \; \epsilon _{\mu \nu } \epsilon _{\rho \sigma } (g^{\mu \rho } g^{\nu \sigma } - g^{\nu \rho } g^{\mu \sigma }) \nonumber \\= & {} \frac{1}{4 G} \int _\varSigma d^2 x \; \sqrt{h} = \frac{1}{4 G} {{\mathcal {A}}}_\varSigma = S_B \;. \end{aligned}$$
(23)

That is, for Einstein theory the two entropies coincide (due to \(\delta \varLambda / \delta R_{\mu \nu \rho \sigma } = 0\), this is true also in the case of a nonzero cosmological constant).

In our case, though, the two entropies differ, and the Wald entropy is clearly

$$\begin{aligned} S = -4\,\pi \alpha _W \; \int _\varSigma \sqrt{h}\; d\varSigma C^{\mu \nu \lambda \rho } \; \epsilon _{\mu \nu }\epsilon _{\lambda \rho } \;, \end{aligned}$$
(24)

where we have used \(\delta {{\mathcal {L}}}_W/ \delta R_{\mu \nu \lambda \rho } = 2 C^{\mu \nu \lambda \rho }\) (see the action in (6) and the definition of the the Weyl tensor in terms of the Riemann tensor (7)).

The first thing we notice is that this entropy is invariant under Weyl scaling, as it must be. Indeed, \(C^{\mu \nu \lambda \rho } \rightarrow \varOmega ^{-6} C^{\mu \nu \lambda \rho }\), whereas \(\sqrt{h} \rightarrow \varOmega ^2 \sqrt{h}\), and \(\epsilon _{\mu \nu } \rightarrow \varOmega ^2 \epsilon _{\mu \nu }\) (recall that \(x_\mu \rightarrow \varOmega ^2 x_\mu \) and \(\Vert x \Vert \rightarrow \varOmega \Vert x \Vert \)). Altogether, \(S \rightarrow \varOmega ^{2} \varOmega ^{2}\varOmega ^{2} \varOmega ^{-6} S = S\).

Writing in explicitly the Weyl tensor evaluated for the geometry in Eq. (13) with Eq. (14), one obtains [61, 68]

$$\begin{aligned} S = \frac{4 \pi \alpha _W }{6} \left( 1 - c_1 - \frac{3\;c_3}{r_{\mathrm{h}}} \right) \;, \end{aligned}$$
(25)

where \(\varSigma \equiv S^2\), is the two sphere, so that we have the factor \(4 \pi \).

A note on the coupling \(\alpha _W\) is now in order. Putting the choice of Eq. (17) into Eq. (25), one finds that the entropy is positive only if

$$\begin{aligned} \alpha _W\;c_3<0 \;. \end{aligned}$$
(26)

Since in Einstein gravity \(\eta = 2 M G^2>0\), the Einstein Schwarzschild limit (\(c_1=1\) and \(c_2=0\)) also requires \(c_3<0\). Therefore, to have a positive entropy in the Schwarzschild limit, the coupling constant \(\alpha _W\) must be positive. Moreover, from Eq. (16) the entalphy of a Schwarzschild BH is positive if \(\alpha _W c_3\, c_4<0\), that is \(c_4>0\) (i.e \(\varLambda <0\)), and negative otherwise.

2.2 Thermodynamics

The enthalpy, the temperature, and the entropy in Eqs. (16), (19), and (25) are evaluated geometrically. However, they have a clear thermodynamic meaning. Moreover, in Weyl gravity the cosmological constant arises as a parameter of the solution, \(\varLambda = - 3\,c_4\), rather than as a fixed parameter of the theory. It is then natural to treat it as a potential.

In Einstein gravity, where the entropy is simply proportional to the horizon area, such potential is the pressure, \(P=-\varLambda /(8\,\pi \,G)\), whose conjugate thermodynamic variable is an effective volume inside the horizon. Therefore, the first law of thermodynamics, including changes in the cosmological constant, contains a work term of the form \(V\, dP = \varGamma \,d(-\varLambda )\) (\(\varGamma \) being the conjugate variable of \(\varLambda \)). For a general, charged and rotating black holes, with angular momenta \(J_i\) (whose conjugate variables are the angular velocities \(\varOmega _i\)) and charges \(Q_\alpha \) (whose conjugate variables are the potential \(\varPhi _\alpha \)), the first law reads [69, 70]

$$\begin{aligned} dH = TdS+\sum _i\varOmega _idJ_i+\sum _\alpha \varPhi _\alpha dQ_\alpha + VdP \;, \end{aligned}$$
(27)

where H is the total gravitational enthalpy.

In conformal gravity, on the other hand, the entropy has a manifest dependence on \(\varLambda \) [61]. Hence, the quantity \(\varGamma \) is not simply proportional to the volume. Nevertheless, \(\varGamma \) and \(\varLambda \), and thus \(c_3\) and \(c_4\) in Eq. (14), are conjugate variables (the relationship between \(c_4\) and \(\varGamma \) is in Eq. (31) below). Therefore the work term can be simply written as \(\varGamma \,d(-\varLambda )\) again. As for \(c_3\) and \(c_4\), by defining \(\varXi \equiv c_2\) and \(\varPsi = \partial H / \partial \varXi \big |_{S,\varLambda }\) [61], the other two integrations constants in Eq. (14), \(c_1\) and \(c_2\), can be promoted to two conjugated variables. Notice, though, that this lacks an interpretation in the Einstein gravity terms of the “charge” \(\varXi \) and of the “potential” \(\varPsi \) (the relationship between \(c_1\) and \(\varPsi \) is in Eq. (31) below).

According to the previous discussions, the enthalpy depends on three independent functions, \(H=H(S,\varGamma \),\(\varXi )\), and three different conjugate variables [61]

$$\begin{aligned} \displaystyle T=\frac{\partial H}{\partial S}\big |_{\varLambda ,\varXi } \;, \quad \varPsi = \frac{\partial H}{\partial \varXi }\big |_{S,\varLambda } \;, \quad \varGamma = \frac{\partial H}{\partial (-\varLambda )}\big |_{S,\varXi } \;,\nonumber \\ \end{aligned}$$
(28)

where the sign “−” in the last identity holds because in Einstein gravity one identifies the pressure as \(P\propto -\varLambda \). Therefore, the first law of BH thermodynamics is given by [61]

$$\begin{aligned} dH = T\;dS + \varPsi \;d\varXi + \varGamma \;d(-\varLambda ) \;, \end{aligned}$$
(29)

where the variables [61]

$$\begin{aligned} \varXi \equiv c_2 \;, \quad \varLambda = - 3\,c_4\;, \end{aligned}$$
(30)

and

$$\begin{aligned} \displaystyle \varPsi = \frac{\alpha _W}{6} \; (c_1-1) \;, \quad \displaystyle \varGamma = - \frac{\alpha _W}{6} \;c_3 \;, \end{aligned}$$
(31)

have been defined.

Without loss of generality, we set \(\alpha _W = 1/(2\,\pi )\) (for \(\alpha _W<0\) one has to change the sign of the rescaling also, \(S\rightarrow - 2 \pi \, \alpha _W\, S\), in the next equations in order to have a positive entropy, but in this case one can study dS BHs only, see “Appendix B”).

By writing Eqs. (19) and (25) in terms of the thermodynamic variables, one finds that the entropy depends only on the temperature, T, and on \(\varGamma \),

$$\begin{aligned} (3\;S-1)^2 = 1+\left( 12\pi \right) ^2\;\varGamma \;T \;, \end{aligned}$$
(32)

and the two solutions, \(S_+\) and \(S_-\), are

$$\begin{aligned} S_{\pm } = \frac{1\pm \sqrt{1+\left( 12\pi \right) ^2\varGamma T}}{3} = -4\;\pi \;\varPsi + \frac{12\;\pi \;\varGamma }{r_\pm } \;,\nonumber \\ \end{aligned}$$
(33)

where the last equality is due to the Wald formula of Eq. (25), with \(1/r_\pm \) solutions of Eq. (19), i.e.

$$\begin{aligned} \frac{1}{r_{\pm }} = \frac{1+12\;\pi \;\varPsi \pm \sqrt{1+\left( 12\pi \right) ^2\varGamma \;T}}{36\;\pi \;\varGamma } \;. \end{aligned}$$
(34)

Therefore, the event horizon, \(r_{\mathrm{h}}\), is given by

$$\begin{aligned} r_{\mathrm{h}} = {\left\{ \begin{array}{ll} r_- \qquad \text {for}\; S_-\\ r_+ \qquad \text {for}\; S_+ \end{array}\right. } \;. \end{aligned}$$
(35)

Note that \(S_- < 1/3\), while \(S_+ > 1/3\) \(\;\forall \,\varGamma \,T\).

It is useful to stress that the two branches, (\(S_+,r_+\)) and (\(S_-,r_-\)), should be considered completely independent. From now on, the sign + or - indicates the specific branch. The expressions of \(\varLambda \), H and \(\varXi \) as a function of T, \(\varGamma \) and \(\varPsi \) are in “Appendix A”.

However, the entropy as a function of H, \(\varLambda \) and \(\varXi \) (both for \((S_-,H_-,\varLambda _-,\varXi _-)\) or \((S_+,H_+,\varLambda _+,\varXi _+)\)) is solution of the some equation

$$\begin{aligned} \begin{aligned}&\varLambda _\pm \left[ (1-S_\pm )\;S_\pm ^2+32\;\pi ^3\;\varPsi (H_\pm , \varLambda _\pm ,\varXi _\pm )^3\right] ^2\\&\quad =- 12\;\pi ^2\;H_\pm ^2\;\Bigg [(S_\pm -1)\;S_\pm ^2 \\&\qquad + 16\;\pi ^2\;\varPsi (H_\pm , \varLambda _\pm ,\varXi _\pm )^2\;(1+4\;\pi \;\varPsi (H_\pm , \varLambda _\pm ,\varXi _\pm ))\Bigg ] \;, \end{aligned} \end{aligned}$$
(36)

where \(\varPsi (H_\pm , \varLambda _\pm ,\varXi _\pm ) \) can be evaluated by reversing the Smarr relation [61],

$$\begin{aligned} H_\pm = \varPsi \;\varXi _\pm - 2\;\varLambda _\pm \;\varGamma \;, \end{aligned}$$
(37)

together with

$$\begin{aligned} \varXi _\pm = -\frac{2\;\varPsi \;(1+6\;\pi \;\varPsi )}{3\;\varGamma } \;. \end{aligned}$$
(38)

From now on, the subscript “±” is not shown when the expression is valid for both sets \((S_-, H_-, \varLambda _-, \varXi _-)\) and \((S_+, H_+, \varLambda _+, \varXi _+)\). Moreover, when \(S < 1/3\), what follows refers to the branch \(S=S_-\), whereas when \(S>1/3\), the results are for \(S=S_+\).

We study the Schwarzschild (A)dS BH limit, i.e. the solution with \((c_1,c_2)=(1,0)\), or equivalently, with \((\varPsi ,\varXi )=(0,0)\), for which Eq. (36) becomes

$$\begin{aligned} \varLambda \;S^2\;(S-1)+12\;\pi ^2\;H^2=0 \;. \end{aligned}$$
(39)

According to Eq. (39), \(\varLambda <0\) when \(S>1\) and \(\varLambda >0\) if \(0<S<1\). Therefore, AdS BHs have entropy larger than 1 and positive H, the dS BHs have entropy \(0<S<1\), and \(H<0\).

On physical grounds, one can only consider the solution \(S_+\) with \(\varGamma T\) positive.

Fig. 1
figure 1

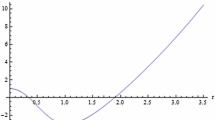
S as a function of \(\varGamma T\) from Eq. (32): if the entropy is greater than 1/3 the solution is given by \(S_+\) and \(r_+\), otherwise by \(S_-\) and \(r_-\). In bold we indicate the only physically acceptable values with \(\varGamma T > 0\)

Full size image

Indeed, looking at the Schwarzschild limit, \(\varPsi =0\), of Eq. (34) one finds that \(\varGamma \) must be always positive in order to have a positive event horizon \(r_\pm \). Thus for entropy \(0<S<2/3\) the temperature is negative for positive “volume” \(\varGamma \). The solutions are plotted in Fig. 1.

Let us summarize the previous results for the (A)dS Schwarzschild BHs as follows:

  • BHs with entropy \(0<S<2/3\) have negative temperature T, and we do not study them, as we see no physical reason for \(T<0\) in a classical scenario;

  • excluding the branch \(T<0\) means, at once, that a) at \(T=0\) the BH has a relic entropy, \(S=2/3\), and b) no value of the allowed T corresponds to several values of S (see [71]);

  • BHs with entropy \(2/3<S<1\) have positive \(\varGamma \), T and \(\varLambda \) (they are dS BHs), but have negative enthalpy, \(H<0\), because \(sg(H)=-sg(\alpha _W\,\varGamma \,\varLambda )\);

  • BHs with entropy \(S>1\) have positive \(\varGamma \), T and H, but have \(\varLambda <0\) (they are AdS BHs).

3 Ruppeiner metric

In the Gaussian thermodynamic fluctuation theory (see Sect. 4), the probability of fluctuations away from the equilibrium configurations of a given system turns out to be [8,9,10,11]

$$\begin{aligned} dP\propto \exp \left\{ -\frac{\varDelta \ell ^2}{2}\right\} \;\;dX^1\ldots dX^n \;, \end{aligned}$$
(40)

where \(X^\mu \) are the usual variables describing the state of the system, i.e. \(X^\mu \in (E,P,N,\,\ldots )\), where E is the energy, P is the pressure, N is the number of particles, etc. and

$$\begin{aligned} \varDelta \ell ^2 = g^{\mathrm{TG}}_{\mu \nu }\;\varDelta X^\mu \;\varDelta X^\nu \;, \end{aligned}$$
(41)

with

$$\begin{aligned} g^{\mathrm{TG}}_{\mu \nu } \equiv -\frac{\partial ^2 S}{\partial X^\mu \partial X^\nu } \;. \end{aligned}$$
(42)

Here \(\varDelta X^\mu = X^\mu - X^\mu _0\), represent fluctuations of the state variables from an equilibrium configuration, \(X^\mu _0\). Consequently, the thermodynamic space can be equipped with a metric, \(g^{\mathrm{TG}}_{\mu \nu }\), with a clear physical meaning: it measures the distance between two states of the system and, through Eq. (40), it quantifies the probability of fluctuation between them. The farther the states are, the less likely they are to fluctuate.

In Ruppeiner theory \(\varDelta \ell ^2\) is an invariant quantity and can be evaluated by different coordinates. Indeed, the inverse metric, \(g_{\mathrm{TG}}^{\mu \nu }\), can be written as [44]

$$\begin{aligned} g_{\mathrm{TG}}^{\mu \nu } = \frac{\partial ^2 \varPhi }{\partial \theta _\mu \partial \theta _\nu } \;, \end{aligned}$$
(43)

where the Massieu function \(\varPhi \) is the Legendre transform of the entropy with respect to the variables \(\theta _\mu \):

$$\begin{aligned} \varPhi = S - \theta \mu X^\mu \;. \end{aligned}$$
(44)

\(X^\mu \) and \(\theta _\mu \) are conjugate variables defined as

$$\begin{aligned} \theta _\mu = \frac{\partial S}{\partial X^\mu } \;,\qquad X^\mu = -\frac{\partial \varPhi }{\partial \theta _\mu } \;. \end{aligned}$$
(45)

For example, if \(X^\mu =(E,\,P,\,N,\ldots )\), then

$$\begin{aligned} \theta _\mu = \left( 1/T,-V/T,-\mu /T,\ldots \right) \;, \end{aligned}$$

where V is the volume, \(\mu \) the chemical potential, etc.

Once we have a metric, the next natural step is to evaluate the Riemann tensor and its contractions, and to ask for their physical relevance.

For systems depending only on two variables, \((X^1,X^2)\), the scalar curvature takes the simple form

$$\begin{aligned} R^{\mathrm{TG}} = \frac{1}{2\;g_{\mathrm{TG}}^2}\;\left| \begin{array}{ccc} S_{,11} &{} S_{,12} &{} S_{,22}\\ S_{,111} &{} S_{,112} &{} S_{,122}\\ S_{,112} &{} S_{,122} &{} S_{,222}\\ \end{array} \right| \;, \end{aligned}$$
(46)

where \(g^{\mathrm{TG}}\) is the determinant of the metric, and the commas indicate standard derivatives, as usual.

One of the most important, widely checked, results of Ruppeiner geometry concerns the sign of the scalar curvature which is related with the nature of the interaction occurring in the system.

According to the conventions of Eq. (42) (notice that one could define the metric as \(g^{\mathrm{TG}}_{\mu \nu } \equiv +\partial ^2S/\partial X^\mu \partial X^\nu \), thus reversing the sign of \(R^{\mathrm{TG}}\)), the properties of \(R^{\mathrm{TG}}\) are summarized as

  • \(R^{\mathrm{TG}} = 0\), no interaction;

  • \(R^{\mathrm{TG}} > 0\), repulsive interaction dominates;

  • \(R^{\mathrm{TG}} < 0\), attractive interaction dominates.

The magnitude of \(R^{\mathrm{TG}}\) also bears useful information. Since this curvature scalar here has units of volume, Ruppeiner suggested that, at the critical points, it diverges as the correlation volume, \(\xi ^d\). This is the so-called “interaction hypothesis”. In general, one can show that \(R^{\mathrm{TG}}\) is a measure of the smallest volume where one can describe the given subsystem, surrounded by a uniform environment [11].

Therefore, the scalar curvature is a very useful tool to study phase transitions, especially when there is no knowledge of the underlying degrees of freedom, as is the case of BHs.

4 Stability

4.1 Extensive thermodynamics

In extensive thermodynamics, stability is defined through the Hessian of the entropy. Indeed, by considering for simplicity two systems in thermal contact with entropy S(M, J) (where M is the mass and J is some other extensive parameter), a transfer of some mass dM from the first to the second subsystem, would produce a new configuration with total entropy given by [14, 22]:

$$\begin{aligned} S(M+dM,J)+S(M-dM,J)\le 2\;S(M,J) \;. \end{aligned}$$
(47)

The differential form of Eq. (47) is

$$\begin{aligned} H_{,MM} = \frac{\partial ^2 S}{\partial M^2} \le 0 \;. \end{aligned}$$
(48)

Similarly, if one transfers dJ, at fixed mass, from one subsystem to the other, one gets

$$\begin{aligned} H_{,JJ} = \frac{\partial ^2 S}{\partial J^2} \le 0 \;, \end{aligned}$$
(49)

and in the case of transfer of dM and dJ

$$\begin{aligned} \det H = \frac{\partial ^2 S}{\partial J^2}\;\frac{\partial ^2 S}{\partial M^2} - \left( \frac{\partial ^2 S}{\partial M\;\partial J}\right) ^2 \ge 0 \;. \end{aligned}$$
(50)

Only two of Eqs. (48–50) are independent and the entropy extensivity is a crucial hypothesis to obtain Eq. (47). Thus, in ordinary thermodynamics the stability can be achieved by requiring two of Eqs. (48–50). This is not the case for non-extensive systems, such as BHs. However, before discussing how to infer stability indications in non-extensive systems, it is useful to recall the connection between stability and Ruppeiner metric.

Ruppeiner metric, defined in Eq. (42), is essentially the opposite of the Hessian of the entropy and a generalization of the condition of Eqs. (48–50) for systems with more extensive variables can be done as follows. Let us consider a system with entropy S, in thermal contact and in equilibrium with an environment, of entropy \(S_e\). The total entropy is

$$\begin{aligned} S_{tot} = S + S_e \;. \end{aligned}$$
(51)

Due to a small fluctuation \(\left( \varDelta X^\alpha ,\;\varDelta X_e^\alpha \right) \) away from the equilibrium values and since for isolated systems energy conservation requires \(\varDelta X=-\varDelta X_e\), the maximum entropy condition is equivalent to

$$\begin{aligned} \frac{\partial S}{\partial X^\mu } = \frac{\partial S_e}{\partial X_e^\mu } \;, \end{aligned}$$
(52)

and for large environments, the total entropy changes according to [38]

$$\begin{aligned} \varDelta S_{tot}\simeq & {} \frac{1}{2}\;\left( \frac{\partial ^2 S}{\partial X^\mu \;\partial X^\nu } \right) \;\varDelta X^\mu \varDelta X^\nu \nonumber \\= & {} - \frac{1}{2}\;g^{\mathrm{TG}}_{\mu \nu }\; \varDelta X^\mu \varDelta X^\nu . \end{aligned}$$
(53)

Therefore, the Gaussian probability to find the state at \(X^\mu +\varDelta X^\mu \), starting from \(X^\mu \), is

$$\begin{aligned} dP\propto & {} \;\displaystyle \exp \left\{ -\frac{g^{\mathrm{TG}}_{\mu \nu }}{2}\;\varDelta X^\mu \;\varDelta X^\nu \right\} \;\;dX^1\ldots dX^\mu \nonumber \\= & {} \displaystyle \exp \left\{ -\frac{\varDelta \ell ^2}{2}\right\} \;\;dX^1\ldots dX^\mu \;, \end{aligned}$$
(54)

where \(\varDelta \ell ^2 = g^{\mathrm{TG}}_{\mu \nu }\;\varDelta X^\mu \;\varDelta X^\nu \) is the distance between \(X^\mu \) and \(X^\mu +\varDelta X^\mu \) in the thermodynamic manifold.

Equation (53) allows to easily generalize the conditions of Eqs. (47–49) to systems with more variables. After the fluctuations \(\varDelta X^\mu \) have taken place, the new state is less stable than the previous one, if and only if its entropy is smaller than, or equal to, the entropy of the initial one, so that \(\varDelta S_{tot}\le 0\). This implies that \(g^{\mathrm{TG}}_{\mu \nu }\) must be a positive definite matrix, that can be studied, e.g., through the Sylvester criteria.

4.2 Stability in non extensive thermodynamics

Without requiring extensiveness of the potentials, the system stability can be studied by the Poincaré method [15, 22] which is constructed in analogy with ordinary thermodynamics.

Let us consider a system out of equilibrium with entropy \({\widehat{S}}(Y^\mu ,X^\mu )\), being \(X^\mu =\{E,\;N\;,\ldots \}\) the usual equilibrium variables (with conjugate variables, \(\theta _\mu \), as discussed in the previous section) and \(Y^\mu \) other variables characterizing the non equilibrium condition.

Clearly, equilibrium takes place when the system depends only on \(X^\mu \), i.e., when [17, 18, 22]

$$\begin{aligned} Y^\mu = Y^\mu (X^\nu ) \;. \end{aligned}$$
(55)

These can be regarded as solution of the equilibrium equations

$$\begin{aligned} \frac{\partial {\widehat{S}}}{\partial Y^\mu }\Bigg |_{eq}=0 \;. \end{aligned}$$
(56)

Let us define now some non-equilibrium functions (in the same way as in Eq. (45))

$$\begin{aligned} {\widehat{\theta }}_\mu (Y^\nu ,X^\nu ) \equiv \frac{\partial \widehat{S}}{\partial X^\mu } \;, \end{aligned}$$
(57)

and such that at the equilibrium

$$\begin{aligned} {\widehat{\theta }}_\mu (Y^\nu ,X^\nu )\Bigg |_{eq}=\theta _\mu (X^\nu ) \;. \end{aligned}$$
(58)

If one assumes that \(Y^\mu \) can be chosen in such a way the Hessian of \({\widehat{S}}\) is diagonal, the “Poincaré” coefficients of stability” are defined through the equations

$$\begin{aligned} \lambda _\rho (X^\mu ) \equiv \partial ^2_{\rho }{\widehat{S}}(Y^\nu (X^\mu ),X^\mu )\Bigg |_{eq} \;. \end{aligned}$$
(59)

where \(\lambda _\rho (X^\mu )\) are the Hessian eigenvalues and an instability appears if some \(\lambda _\rho > 0\).

Without any knowledge about the out of equilibrium function, \({\widehat{S}}\), due to Eqs. (56) and (57), one can link the equilibrium variables \(\theta _\mu \) and \(X^\mu \), with the non equilibrium ones by [22]

$$\begin{aligned} \frac{\partial \theta _\mu }{\partial X^\mu } = \left( \frac{\partial ^2 {\widehat{S}}}{\partial {Y^\mu }^2} \right) _{eq} - \sum _\rho \;\frac{1}{\lambda _\rho }\; \left( \frac{\partial {\widehat{\theta }}_\mu }{\partial Y^{\rho }} \right) _{eq}^2 \;. \end{aligned}$$
(60)

The left-hand side involves only equilibrium variables, while the right-and side contains only the non equilibrium ones. Therefore, by previous equation, one obtains informations on the non equilibrium states if the properties of the system at equilibrium are known. For example, if the function \(\theta _\mu = \theta _\mu (X^\mu )\) has an inflection point (point P in Fig. 2) and \(\partial \theta _\mu /\partial X^\mu \) changes sign, also the right-hand side of Eq. (60) changes its sign. This could be due to an eigenvalue turning from negative to positive value (or vice versa), describing a new phase in the stability of the system.

In fact, when at least one of the eigenvalues \(\lambda _\rho \) changes sign, the Hessian has a zero, and \(\partial \theta _\mu /\partial X^\mu \) diverges. This implies that the plot of \(\theta ^\mu (X^\nu )\) along the equilibrium points has a vertical tangent and one can study a change in stability by inspection of the plot of the equilibrium functions \(\theta ^\mu (X^\nu )\).

Moreover, one has to verify which branch is stable and in [20,21,22] the following criteria have been suggested:

  1. 1.

    if one can prove the stability of even a single point, then all the other ones in the same stability sequence are stable, until the first turning point is reached. After the turning point the system is unstable;

  2. 2.

    if a stable point is unknown, one can never say anything about the branch with positive slope. Instead, the branch with negative slope, near the turning point, is always unstable;

  3. 3.

    changes of stability can only occur at turning points or bifurcations. Indeed, according to Eq. (60), there are other stability points besides the turning points, since it is possible that \((\partial _\rho {\widehat{\theta }}_\nu )_{eq}=0\) when the sign of \(\lambda _\rho \) changes, but \(\partial _\mu \theta _\nu \) does not diverge. It can be shown that this can only happen at a bifurcation point [20,21,22];

  4. 4.

    a vertical asymptote signals the endpoints (boundary) of the (non)equilibrium sequence and it is not related to stability.

Finally, there are points where the slope of \(\theta _\mu \) changes, but \(\partial \theta _\mu /\partial X^\mu =0\) (see points Q in Fig. 2), but they do not correspond to system instability. These points could indicate a sign variation in the specific heat, as in the case of the four dimensional Kerr BH in the microcanonical ensemble [22]. Therefore, they are stable according to the Poincaré method, but unstable if one considers the sign of the specific heat only.

Fig. 2
figure 2

Generic plot of a conjugate variable \(\theta _\mu \) against \(X^\mu \), along an equilibrium sequence. The point P is a turning point. The upper branch is unstable, while the lower branch can be either fully stable, or simply more stable than the upper branch. The sign of the slope also changes at the horizontal tangent at \(Q'\), but this has no relation with a change of stability, even if the slope changes sign there

Full size image

5 Stability of the Schwarzschild (A)dS BH in CG

5.1 Stability analysis: specific heat and TG

Usual stability analysis is based on the specific heat at constant V. Since for (A)dS BH the volume arises as the conjugate variable of the cosmological constant, we analogously define the specific heat at constant \(\varGamma \) as

$$\begin{aligned} C_\varGamma = T\;\left( \frac{\partial S}{\partial T}\right) _\varGamma = \frac{S\,(3\;S-2)}{2\;(3\;S-1)} \;. \end{aligned}$$
(61)

Stability can be studied also by the metric \(g^{\mathrm{TG}}_{\mu \nu }\), requiring that \(g^{\mathrm{TG}}_{\mu \nu }\) is a definite positive tensor. For a \(2\times 2\) matrix, necessary and sufficient condition is that both the determinant, \(g^{\mathrm{TG}}\), and the first element, \(g^{\mathrm{TG}}_{HH}\) are positive. For Schwarzschild BH in CG, one has:

$$\begin{aligned} g^{\mathrm{TG}} = \frac{S^6\;(1-S)^5 (3\,S-1)}{36\;\pi ^4\;H^6\;(2-3\;S)^4}\;, \end{aligned}$$
(62)

and

$$\begin{aligned} g^{\mathrm{TG}}_{HH} = \frac{2\;(S-1)\;S^2\;(3\,S-4)}{H^2\;(3 S-2)^3}\,. \end{aligned}$$
(63)

Figure 3 shows the specific heat \(C_\varGamma \) (red line), \(g^{\mathrm{TG}}\) (continuous black line) and \(g^{\mathrm{TG}}_{,HH}\) (dotted line) for Schwarzschild BHs.

Let us recall (see Sect. 2.2) that Schwarzschild (A)dS BHs have entropy (greater)smaller than 1 and (positive)negative H:

  • Schwarzschild dS BHs  Both methods, the sign of \(C_\varGamma \) in Eq. (61), and the request that \(g^{\mathrm{TG}}_{\mu \nu }\) is definite positive, give stable BHs for all values of the entropy;

  • Schwarzschild AdS BHs  The two methods give opposite outcomes, as according to the sign of \(C_\varGamma \), they are always stable, while looking at \(g^{\mathrm{TG}}\) and \(g^{\mathrm{TG}}_{HH}\), they are never stable.

Thus the two methods are in agreement for dS BHs in the range \(2/3< S < 1\), i.e. in a small interval of the possible values of S. The disagreement in other ranges of S is not unexpected, though, as discussed in the “Introduction” [22]. Indeed, non-extensivity plays a central role in BH thermodynamics and, in the next section, the Poincaré method will be applied for both dS and AdS BHs, in order to overcome these difficulties.

Fig. 3
figure 3

The specific heat (red line), \(g^{\mathrm{TG}}\) (continuous black line) and \(g^{\mathrm{TG}}_{,HH}\) (dotted line) for Schwarzschild BH

Full size image

The other information coming from TG are contained in the Ruppeiner scalar curvature of Schwarzschild (A)dS BH, which turns out to be

$$\begin{aligned} R^{\mathrm{TG}} = \frac{5\;(4-3\;S)\;S-6}{2\;(3\;S-2)\;(S-1)^2\; (3\;S-1)^2} \; \end{aligned}$$
(64)

and is shown in Fig. 4.

Fig. 4
figure 4

\(R^{\mathrm{TG}}\) as a function of S. The dotted line refers to the range where gravitational interaction has a repulsive behavior, according to TG, hence we exclude it

Full size image

  • dS BHs  For dS BHs (that have \(S<1\)) \(R^{\mathrm{TG}}\) diverges at \(S=2/3\) and 1, as expected according to the stability analysis and defines the range of stability where both methods agree. For \(S=2/3\) one gets

    $$\begin{aligned} \varGamma T= & {} 0\;, \;\; H =-\frac{1}{2(9\;\pi )^2\,\varGamma } \;, \end{aligned}$$
    (65)
    $$\begin{aligned} \varLambda= & {} \frac{1}{(18\;\pi )^2\,\varGamma ^2} \;,\;\; r_{\mathrm{h}} = 18\;\pi \;\varGamma \;. \end{aligned}$$
    (66)

    For \(S=1\) one has

    $$\begin{aligned} \varGamma T= & {} \frac{1}{(48\;\pi )^2} \;,\qquad H=\varLambda =0 \;, \end{aligned}$$
    (67)
    $$\begin{aligned} r_{\mathrm{h}}= & {} 12\;\pi \;\varGamma \;. \end{aligned}$$
    (68)

    Moreover R changes sign at

    $$\begin{aligned} S_{\mathrm{0}} = \frac{2}{3}\left( 1+\sqrt{\frac{1}{10}}\right) \;, \end{aligned}$$
    (69)

    with

    $$\begin{aligned} \varGamma _{\mathrm{0}}= & {} \sqrt{\frac{35 - \sqrt{10}}{2\,\left( 90\,\pi \right) ^2}}\,\frac{1}{\sqrt{\varLambda _0}} \;, \end{aligned}$$
    (70)
    $$\begin{aligned} H_{\mathrm{0}}= & {} -\sqrt{\frac{35 - \sqrt{10}}{2}}\,\frac{\sqrt{\varLambda _0}}{45\;\pi } \;, \end{aligned}$$
    (71)
    $$\begin{aligned} T_{\mathrm{0}}= & {} \sqrt{\frac{5 + \sqrt{10}}{60\;\pi ^2}}\,\sqrt{\varLambda _0} \;, \end{aligned}$$
    (72)

    and \(\varLambda _0>0\).

  • AdS BHs  (\(S>1\)) \(R^{\mathrm{TG}}\) diverges at \(S=1\) and is always negative.

According to the usual interpretation of the sign of \(R^{\mathrm{TG}}\), one might conclude that for dS BHs there is a change in the nature of the interaction of the fundamental degrees of freedom: repulsive for \(2/3< S < S_0\), attractive for \(S_0< S < 1\), where \(S_0\) is given in Eq. (69). On the other hand, for AdS BHs, \(R^{\mathrm{TG}}\) always points to attractive interaction. Although, in other systems, changes of sign of \(R^{\mathrm{TG}}\) have been seen [23,24,25] near the critical point (and, although recent general results, on the fundamental quantum gravitational interaction, indicate a fermionic nature of such degrees of freedom [72]), we take here the view that the physical region for Schwarzschild BHs in conformal gravity requires an entropy greater than the \(S_0\) in Eq. (69), in order to have a consistent interpretation with the attractive nature of the gravitational interaction.

Moreover, \(R^{\mathrm{TG}}\) diverges at \(S=1\), indicating a phase transition from a dS BH (\(S_0< S < 1\)) to an AdS BH (\(S > 1\)). Assuming that the usual “interaction hypothesis” of TG also holds true for non-extensive systems (i.e. \(R^{TG}\propto \xi ^d\) at the transition), this is a second-order phase transition, because the correlation length, \(\xi \), diverges.

5.2 Stability studied with Poincaré method

Isolated BHs, i.e. those with H as a control parameter, and \(\varLambda \) and \(\varXi \) fixed, are all either stable or unstable. In fact, in this case, the linear series that corresponds to H is \(\theta _1(H)\) and there are no vertical tangents.

Change of stability occurs only in two cases (both related to AdS BHs):

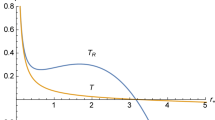
  • For BHs in the canonical ensemble, with enthalpy fluctuations at constant \(\varLambda \) (see Fig. 5). Indeed, the linear series of \(H(\theta _1)\) with fixed \(\varLambda \) has a vertical tangent when \(S_{\mathrm{c}}=4/3\).

  • For BHs with \(\varLambda \) as a control parameter, and fluctuation of \(\theta _2=-\varGamma /T\) at fixed \(\theta _1=1/T\) (see Fig. 6). The critical point occurs always at \(S_{\mathrm{c}}=4/3\).

In both cases, the critical point corresponds to a BH whose enthalpy is (\(\varLambda <0\))

$$\begin{aligned} H_{\mathrm{c}}=\frac{2\;\sqrt{-\varLambda }}{9\;\pi } \;, \end{aligned}$$
(73)

and with a temperature and \(\varGamma \) variable given by

$$\begin{aligned} T_{\mathrm{c}} = \frac{\sqrt{-\varLambda }}{2\;\pi } \;,\qquad \varGamma _{\mathrm{c}} = \frac{1}{9\;\pi \sqrt{-\varLambda }} \;. \end{aligned}$$
(74)

Thus they are BHs with surface gravity and radius given by

$$\begin{aligned} \kappa _{\mathrm{c}} = \frac{1}{r_{\mathrm{c}}}=\sqrt{-\varLambda } \;. \end{aligned}$$
(75)

At this point stability changes from an unstable phase to a more stable one. According to the Poincaré criteria, the branch with negative slope (\(S>4/3\)) is always unstable, but we can say nothing about the cases with positive slope, except that it is more stable than the previous one.

Fig. 5
figure 5

Plot of H as a function of \(\theta _1=1/T\) at \(\varGamma =\)const

Full size image
Fig. 6
figure 6

Plot of \(\theta _2\) as a function of P at fixed \(\theta _1\)

Full size image

6 Comments and conclusions

We studied the thermodynamics of spherically symmetric, neutral and non-rotating black holes in Conformal Gravity. We did so by means of different approaches, trying this way to test the reliability of the methods themselves, in a context still largely unexplored.

In fact, one such methods is Thermodynamic Geometry, an important area of research by itself. We showed here that it can be applied to Conformal Gravity too, because all the key thermodynamic variables are insensitive to Weyl scaling. This method focuses on the study of the concavity of the entropy, with the evaluation of the corresponding thermodynamic curvature \(R^{\mathrm{TG}}\).

The other methods used here are the evaluation of the specific heat, and the Poincaré method (that is a method relating equilibrium and out-of-equilibrium thermodynamics).

The two stability analyses based on the specific heat, and on the entropy concavity, agree for dS black holes in the range of entropy, \(2/3< S < 1\), where the Thermodynamic Geometry scalar curvature, \(R^{\mathrm{TG}}\), diverges at the boundary. Moreover, Thermodynamic Geometry predicts a second order phase transition, from a dS black hole to an AdS black hole, at \(S=1\), but according to Poincaré criteria, black holes in Conformal Gravity are stable or in saddle point for \(S < 4/3\) (and unstable for \(S > 4/3\)). Hence there is no definite answer on whether such transition takes place.

Non-extensivity of the entropy can have a crucial role in determining the black holes stability in the parametric space, hence the Poincaré method might be considered more reliable than other methods. Nonetheless, it is important to show here the results based on the extensive point of view, followed by many authors [33,34,35,36,37,38,39,40,41,42,43,44,45]. Therefore, we have presented here both analyses, because we wanted to show how the two approaches, differing for the way the entropy is seen, work. Thermodynamics Geometry takes the view that the entropy is an extensive quantity, while the Poincaré method does not require extensiveness.