Resonance contributions $\phi (1020, 1680)\rightarrow K\bar{K}$ for the three-body decays $B\rightarrow K\bar{K} h$

Abstract

We study the contributions for the $K^+K^-$ and $K^0\bar{K}^0$ originating from the intermediate states $\phi (1020)$ and $\phi (1680)$ in the charmless three-body decays $B\rightarrow K\bar{K} h$, with $h=(\pi , K)$, in the perturbative QCD approach. The subprocesses $\phi (1020,1680)\rightarrow K\bar{K}$ are introduced into the distribution amplitudes of $K\bar{K}$ system via the kaon electromagnetic form factors with the coefficients taken from the fitted results. The predictions of the branching fractions for the decays $B\rightarrow \phi (1680)h$ with the intermediate state $\phi (1680)$ decays into $K^+K^-$ or $K^0\bar{K}^0$ are about $6{-}8\%$ of the corresponding results for the quasi-two-body decays $B\rightarrow \phi (1020)h \rightarrow K^+ K^- h$ in this work.

1 Introduction

Charmless three-body hadronic B meson decays are very important for us to test the Standard Model and to explore Quantum Chromodynamics (QCD). The decay amplitudes of these three-body processes are always described as the coherent sum of the resonant and nonresonant contributions in the isobar formalism [1,2,3], although the isobar model violates unitarity and needs improvement [4]. The resonance contributions, which are related to the low energy scalar, vector and tensor intermediate states and are associated with the various subprocesses of the three-body decays, could be isolated from the total decay amplitudes and studied in the quasi-two-body framework [5,6,7]. The studies of the quasi-two-body decays could also help us to investigate the properties of different resonances and will lead us to understand the relationship among the different three-body processes with the same intermediate state.

In addition to the contributions from the S-wave intermediate state $f_0(980)$ and the D-wave resonance $f^\prime _2(1525)$, etc., the $K\bar{K}$ in the charmless three-body decays $B\rightarrow K\bar{K} h$, with h is pion or kaon, have contributions from the P-wave resonances $\rho (770)$, $\omega (782)$, $\phi (1020)$ and their excited states [7]. The contributions from the resonance $\rho (1450)^0$ and from the tails of the Breit–Wigner (BW) formula [8] for the intermediate states $\rho (770)$ and $\omega (782)$ for $K^+K^-$ in the three-body decays $B^\pm \rightarrow K^+K^-\pi ^\pm$ have been discussed in Ref. [9]. In this work, we shall focus on the quasi-two-body decays $B\rightarrow \phi (1020,1680)h \rightarrow K\bar{K} h$ within the perturbative QCD (PQCD) approach [10,11,12,13], with $K\bar{K}$ is the $K^+K^-$ or $K^0\bar{K}^0$ in the final state. One should note that the $K^0\bar{K}^0$ which comes from the P-wave intermediate states could form the $K^0_S$ plus $K^0_L$ but cannot generate the $K^0_S$ pair in the final state because of Bose–Einstein statistics. We need to stress that the rescattering effects [14,15,16] in the final states were found to have important contributions for the three-body B decays [17], which will be investigated in a subsequent work.

The parameters, such as mass and decay width for $\phi (1020)$ the ground state of $s\bar{s}$, have been measured quite well with the processes $e^+e^-\rightarrow K^+K^-(\gamma )$ and $e^+e^-\rightarrow K^0_SK^0_L$ [18,19,20,21,22,23,24]. The $K^+K^-$ and $K^0\bar{K}^0$ branching fractions for $\phi (1020)$ are consistent with the mass dependence in the two-body breakup momentum for the charged and neutral kaon as expected from P-wave decay [25]. The structure-dependent radiative corrections to the $\phi (1020)$ decays into $K^+K^-$ and $K^0_SK^0_L$ can be found in [26]. The $2^3S_1$ $s\bar{s}$ state $\phi (1680)$ was discovered in the processes of $e^+e^-\rightarrow K^0_SK^\pm \pi ^\mp$ [27], with the decay dominant into $KK^*(892)$ [28, 29]. The $K\bar{K}$ channel for $\phi (1680)$ was found to be about $7\%$ of the $KK^*(892)$ for the branching fraction [28]. In Ref. [30], the contribution from the subprocess $\phi (1680) \rightarrow K^+ K^-$ for the three-body decay $B^0_s\rightarrow J/\psi K^+K^-$ was found to be $(4.0\pm 0.3\pm 0.3)\%$ of the total branching fraction by LHCb Collaboration recently, which is about $6\%$ of the contribution from $\phi (1020) \rightarrow K^+ K^-$ in the same decay channel. The detailed discussions of the general aspects for $\phi (1680)$ can be found in Ref. [31]. The $1^{--}$ resonance $\phi (2175)$ was found by the BaBar Collaboration [32] and confirmed by different experiments [33,34,35,36,37,38]. In view of its ambiguous nature [39], we shall leave the possible subprocess $\phi (2175)\rightarrow K\bar{K}$ to future studies.

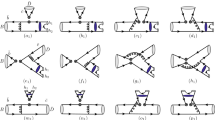
The intermediate states of the quasi-two-body decays $B\rightarrow \phi (1020,1680)h \rightarrow K\bar{K} h$ are generated in the hadronization of the quark–antiquark pair $s\bar{s}$ as demonstrated in Fig. 1, in which the factorizable and nonfactorizable diagrams have been merged for the sake of simplicity, the symbol B in the diagrams stands for the mesons $B^+, B^0$ and $B^0_s$, and the inclusion of charge-conjugate processes throughout this work is implied. The subprocesses $\phi (1020,1680)\rightarrow K\bar{K}$, which cannot be calculated in the PQCD approach, will be introduced into the distribution amplitudes of the $K\bar{K}$ system by the vector meson dominance kaon electromagnetic form factor. The PQCD approach has been adopted in Refs. [40,41,42,43] for the tree-body B decays, and the quasi-two-body framework based on PQCD has been discussed in detail in [5], followed by Refs. [44,45,46,47,48,49] for the charmless quasi-two-body B meson decays recently. Parallel analyses of the three-body B decays with the QCD factorization (QCDF) can be found in Refs. [50,51,52,53,54,55,56,57,58,59,60,61], and for relevant work within the symmetries one is referred to Refs. [62,63,64,65,66,67,68,69,70,71].

This paper is organized as follows. In Sect. 2, we give a brief review of the vector time-like form factors for the kaon, we present the P-wave $K\bar{K}$ system distribution amplitudes and the differential branching fractions. In Sect. 3, we provide numerical results for the concerned decay processes and give some necessary discussions. Summary of this work is presented in Sect. 4. The relevant quasi-two-body decay amplitudes are collected in the appendix.

Fig. 1

Typical Feynman diagrams for $B\rightarrow \phi (1020, 1680)h\rightarrow KK h$ decays. The symbol $\times$ denotes the possible attachments for hard gluons, the symbol $\phi$ and the rectangle represent the resonances $\phi (1020)$ and $\phi (1680)$. The symbol $\otimes$ is the weak vertex, B, K and h stand for $B^+, B^0, B^0_s$, the final states $K^\pm , K^0, \bar{K}^0$ and the bachelor state of the pion or kaon, respectively, and $k_B, k$ and $k_3$ are the momenta for the spectator quarks

2 Framework

In light-cone coordinates, with the mass $m_B$, the momenta $p_B$ for the B meson and $k_B$ for its light spectator quark are written as

$$\begin{aligned} p_B=\frac{m_B}{\sqrt{2}}(1,1,0_\mathrm{T}),\quad k_B=\left( \frac{m_B}{\sqrt{2}}x_B, 0, k_{B\mathrm{T}}\right) \end{aligned}$$

(1)

in the rest frame of the B meson. For the kaon pair generated from the intermediate states $\phi (1020)$ or $\phi (1680)$ by the strong interaction, we have momentum $p=\frac{m_B}{\sqrt{2}}(\zeta , 1, 0_\mathrm{T})$ and the longitudinal polarization vector $\epsilon _L=\frac{1}{\sqrt{2}}(-\sqrt{\zeta }, 1/\sqrt{\zeta }, 0_\mathrm{T})$, with the variable $\zeta =s/m^2_B$ and the invariant mass square $s=m^2_{KK}\equiv p^2$. The spectator quark comes from the B meson and goes into resonance in the hadronization as shown in Fig. 1a having momentum $k=(0, \frac{m_B}{\sqrt{2}}z, k_\mathrm{T})$. For the bachelor final state of the pion or kaon and its spectator quark, we define the momenta $p_3$ and $k_3$ as

$$\begin{aligned} p_3=\frac{m_B}{\sqrt{2}}(1-\zeta , 0, 0_\mathrm{T}),\quad k_3=\left( \frac{m_B}{\sqrt{2}}(1-\zeta )x_3, 0, k_{3\mathrm{T}}\right) \!.\nonumber \\ \end{aligned}$$

(2)

The $x_B$, z and $x_3$ above, which run from zero to one in the numerical calculation, are the momentum fractions for B meson, intermediate state and the bachelor final state, respectively.

The vector time-like form factors $F_{K^+}(s)$ and $F_{K^0}(s)$ for the charged and neutral kaons are related to the electromagnetic form factors for $K^+$ and $K^0$, respectively, which are defined as [72]

$$\begin{aligned} \langle K^+(p_1) K^-(p_2) | j^{em}_\mu | 0 \rangle= & {} (p_1-p_2)_\mu \,F_{K^+}(s), \end{aligned}$$

(3)

$$\begin{aligned} \langle K^0(p_1)\bar{K}^0(p_2) | j^{em}_\mu | 0 \rangle= & {} (p_1-p_2)_\mu \,F_{K^0}(s), \end{aligned}$$

(4)

with the squared invariant mass $s=(p_1+p_2)^2$, the constraints $F_{K^+}(0)=1$ and $F_{K^0}(0)=0$, and the electromagnetic current $j^{em}_\mu =\frac{2}{3}\bar{u}\gamma _\mu u-\frac{1}{3}\bar{d}\gamma _\mu d -\frac{1}{3}\bar{s}\gamma _\mu s$ carried by the light quarks u, d and s [73]. The form factors $F_{K^+}$ and $F_{K^0}$ can be separated into the isospin $I=1$ and $I=0$ components as $F_{K^{+(0)}}=F_{K^{+(0)}}^{I=1} + F_{K^{+(0)}}^{I=0}$, with the $F_{K^+}^{I=0}=F_{K^0}^{I=0}$ and $F_{K^+}^{I=1}=-F_{K^0}^{I=1}$, and $\langle K^+(p_1) \bar{K}^0(p_2) | \bar{u} \gamma _\mu d | 0 \rangle =(p_1-p_2)_\mu 2F_{K^+}^{I=1}(s)$ [7, 72].

With the BW formula for the resonances $\omega$ and $\phi$ and the Gounaris–Sakurai (GS) model [74] for $\rho$, we have the electromagnetic form factors [72, 75, 76]

$$\begin{aligned} F_{K^+}(s)= & {} +\frac{1}{2}\sum _{i=\rho ,\rho ^\prime ,\ldots } c^K_i \mathrm{GS}_i(s) +\frac{1}{6}\sum _{i=\omega ,\omega ^\prime ,\ldots } c^K_i \mathrm{BW}_i(s)\nonumber \\&+\frac{1}{3}\sum _{i=\phi ,\phi ^\prime ,\ldots } c^K_i \mathrm{BW}_i(s), \end{aligned}$$

(5)

$$\begin{aligned} F_{K^0}(s)= & {} -\frac{1}{2}\sum _{i=\rho ,\rho ^\prime ,\ldots } c^K_i \mathrm{GS}_i(s) +\frac{1}{6}\sum _{i=\omega ,\omega ^\prime ,\ldots } c^K_i \mathrm{BW}_i(s)\nonumber \\&+\frac{1}{3}\sum _{i=\phi ,\phi ^\prime ,\ldots } c^K_i \mathrm{BW}_i(s), \end{aligned}$$

(6)

where $\sum$ means the summation for the resonances $\rho , \omega$ or $\phi$ and their corresponding excited states, $c^K_i$ is proportional to the coupling constant $g_{iK\bar{K}}$, and the coefficients have the constraints [76]

$$\begin{aligned} \sum _{i=\rho ,\rho ^\prime ,\ldots } c^K_i =1, \qquad \frac{1}{3}\sum _{i=\omega ,\omega ^\prime ,\ldots } c^K_i +\frac{2}{3}\sum _{i=\phi ,\phi ^\prime ,\ldots } c^K_i =1\nonumber \\ \end{aligned}$$

(7)

to provide the proper normalizations of the form factors $F_{K^+}(0)=1$ and $F_{K^0}(0)=0$. One should note that the possibility of SU(3) violations is allowed, which could and indeed will become manifest in the differences between the fitted normalization coefficients [72]. For the explicit expressions and auxiliary functions for BW and GS one is referred to Refs. [74, 77].

Phenomenologically, the vector time-like form factor for the kaon can also be defined by [56]

$$\begin{aligned} \langle K^+(p_1) K^-(p_2) |\bar{q}\gamma _\mu q | 0 \rangle= & {} (p_1-p_2)_\mu \,F_{K^+K^-}^{q}(s), \end{aligned}$$

(8)

$$\begin{aligned} \langle K^0(p_1)\bar{K}^0(p_2) |\bar{q}\gamma _\mu q | 0 \rangle= & {} (p_1-p_2)_\mu \,F_{K^0\bar{K}^0}^{q}(s). \end{aligned}$$

(9)

When considering only the resonance contributions, we have

$$\begin{aligned} F_{K^+K^-}^{u}= & {} F_{K^0\bar{K}^0}^{d}= F_\rho +3 F_\omega , \end{aligned}$$

(10)

$$\begin{aligned} F_{K^+K^-}^{d}= & {} F_{K^0\bar{K}^0}^{u}=-F_\rho +3 F_\omega , \end{aligned}$$

(11)

$$\begin{aligned} F_{K^+K^-}^{s}= & {} F_{K^0\bar{K}^0}^{s}=-3 F_\phi . \end{aligned}$$

(12)

Then the electromagnetic form factors can also be expressed by $F_{K^+}=F_\rho +F_\omega +F_\phi$ and $F_{K^0}=-F_\rho +F_\omega +F_\phi$ [56] for the resonance components. The expressions for $F_\rho , F_\omega$ and $F_\phi$ can be found in [56, 78]. It is easy to check that

$$\begin{aligned}&F_\phi =\frac{1}{3}\sum _\phi c^K_\phi \mathrm{BW}_\phi (s), \nonumber \\&F_{K^+K^-}^{s}=F_{K^0\bar{K}^0}^{s}=-\sum _\phi c^K_\phi \mathrm{BW}_\phi (s). \end{aligned}$$

(13)

We are concerned only with the $\phi$ component of the vector kaon time-like form factors in this work. For simplicity, we employ $F_K$ to stand for $F_{K^+K^-}^{s}$ and $F_{K^0\bar{K}^0}^{s}$ in the following discussions.

For the subprocesses $\phi (1020,1680)\rightarrow K\bar{K}$, the P-wave $K\bar{K}$ system distribution amplitudes are organized into [9, 79]

$$\begin{aligned} \phi ^{P\text {-wave}}_{K\bar{K}}(z,s)= & {} \frac{-1}{\sqrt{2N_c}} \left[ \sqrt{s}\,{\epsilon /}\!_L\phi ^0(z,s) \right. \nonumber \\&\left. +{\epsilon /}\!_L {p/} \phi ^t(z,s) +\sqrt{s} \phi ^s(z,s) \right] , \end{aligned}$$

(14)

with the momentum $p=p_1+p_2$. We have the distribution amplitudes

$$\begin{aligned} \phi ^{0}(z,s)= & {} \frac{3F_K(s)}{\sqrt{2N_c}} z(1-z)\left[ 1+a_2^{\phi } C^{3/2}_2(1-2z) \right] , \end{aligned}$$

(15)

$$\begin{aligned} \phi ^{s}(z,s)= & {} \frac{3F^s_K(s)}{2\sqrt{2N_c}}(1-2z), \end{aligned}$$

(16)

$$\begin{aligned} \phi ^{t}(z,s)= & {} \frac{3F^t_K(s)}{2\sqrt{2N_c}}(1-2z)^2, \end{aligned}$$

(17)

with the Gegenbauer polynomial $C^{3/2}_2(\chi )=3\left( 5\chi ^2-1\right) /2$ and $F^{s,t}_K(s)\approx (f^T_{\phi }/f_{\phi })F_K(s)$ [5] with the ratio $f^T_{\phi }/f_{\phi }=0.75$ at the scale $\mu =2$ GeV [80]. The Gegenbauer moment $a_2^{\phi }$ for $\phi ^{0}(z,s)$ is the same as in the distribution amplitudes of the light vector meson $\phi$ in [79] for the two-body B meson decays.

The CP averaged differential branching fractions (${{\mathcal {B}}}$) for the quasi-two-body decays $B\rightarrow \phi (1020,1680)h \rightarrow K\bar{K} h$ are written as [9, 52, 81]

$$\begin{aligned} \frac{\mathrm{d}{{{\mathcal {B}}}}}{\mathrm{d}\zeta }=\tau _B\frac{q^3_h q^3}{12\pi ^3m^5_B}\overline{|{\mathcal {A}}|^2}, \end{aligned}$$

(18)

where $\tau _B$ is the B meson mean lifetime. The magnitudes of the momenta q and $q_h$ for the kaon and the bachelor h in the rest frame of the resonances $\phi (1020,1680)$ are written as

$$\begin{aligned} q= & {} \frac{1}{2}\sqrt{s-4m^2_K}, \end{aligned}$$

(19)

$$\begin{aligned} q_h= & {} \frac{1}{2\sqrt{s}}\sqrt{\left( m^2_{B}-m_{h}^2\right) ^2 -2\left( m^2_{B}+m_{h}^2\right) s+s^2}, \end{aligned}$$

(20)

with the mass $m_h$ for the bachelor meson pion or kaon. The direct CP asymmetry ${\mathcal {A}}_{CP}$ is defined as

$$\begin{aligned} {\mathcal {A}}_{CP}=\frac{{{{\mathcal {B}}}}(\bar{B}\rightarrow \bar{f})-{{{\mathcal {B}}}}(B\rightarrow f)}{{{{\mathcal {B}}}}(\bar{B}\rightarrow \bar{f})+{{{\mathcal {B}}}}(B\rightarrow f)}. \end{aligned}$$

(21)

The Lorentz invariant decay amplitudes for the quasi-two-body decays $B\rightarrow \phi (1020,1680)h \rightarrow K\bar{K} h$ are collected in the appendix.

3 Results

In the numerical calculation, we employ the decay constants $f_B=0.189$ GeV and $f_{B_s}=0.231$ GeV [82], the mean lives $\tau _{B^0}=(1.520\pm 0.004)\times 10^{-12}$ s, $\tau _{B^+}=(1.638\pm 0.004)\times 10^{-12}$ s and $\tau _{B^0_s}=(1.509\pm 0.004)\times 10^{-12}$ s [29] for the $B^0, B^+$ and $B^0_s$ mesons, respectively. The masses and the decay constants for the relevant particles in this work, the full widths for $\phi (1020)$ and $\phi (1680)$, and the Wolfenstein parameters of the Cabibbo–Kobayashi–Maskawa (CKM) matrix are presented in Table 1.

Table 1 Masses, decay constants, full widths of $\phi (1020)$ and $\phi (1680)$ (in units of GeV) and Wolfenstein parameters [29]

The coefficients $c^K_{\phi (1020)}$ and $c^K_{\phi (1680)}$ in the electromagnetic form factors $F_{K^+}$ and $F_{K^0}$, see Eqs. (5) and (6), have been fitted to the data in Refs. [72, 75, 76]. The results of the constrained and unconstrained fits in [72, 75] and the results of Model I and Model II in [76] for $c^K_{\phi (1020)}$ agree. But the fit results for $c^K_{\phi (1680)}$ are quite different in Refs. [72, 75, 76], with the results $-0.018\mp 0.006$ $(0.001\mp 0.007)$ and $0.0042\pm 0.0015$ $(0.0136\pm 0.0024)$ of the constrained (unconstrained) fits in [72] and [75], respectively, and $-0.117\pm 0.020$ $(-0.150\pm 0.009)$ for Model I (II) in [76]. While one can find that the coefficient $c_{\rho (1450)}$ for the pion electromagnetic form factor $F_\pi$ in Refs. [77, 83,84,85,86] by different collaborations are consistent with each other. By refer to the discussions in [72] for hadronic invariant amplitudes for $\rho \rightarrow \pi ^+\pi ^-$ and $\phi \rightarrow K^+K^-$, one could obtain the relation $|g_{\phi (1680)KK}|\approx |g_{\rho (1450)\pi \pi }|/\sqrt{2}$ within SU(3) symmetry. With the relations

$$\begin{aligned}&|c_{\rho (1450)}|\approx \frac{f_{\rho (1450)}|g_{\rho (1450)\pi \pi }|}{\sqrt{2} m_{\rho (1450)}}, \nonumber \\&|c^K_{\phi (1680)}|\approx \frac{f_{\phi (1680)}|g_{\phi (1680)KK}|}{ m_{\phi (1680)}}, \end{aligned}$$

(22)

and the result $|c_{\rho (1450)}|=0.178$¹ from [77], it is easy to get $|c^K_{\phi (1680)}|\approx 0.160$ assuming the decay constants $f_{\rho (1450)}/f_{\phi (1680)}\approx f_{\rho (770)}/f_{\phi (1020)}$. With the partial width ratio [28]

$$\begin{aligned} \frac{\Gamma {(KK)}}{\Gamma {(KK^*(892))}}\approx 0.073, \end{aligned}$$

(23)

and the rough branching ratio ${{{\mathcal {B}}}}_{KK^*(892)}\approx 0.7$ [37, 87] for the resonance $\phi (1680)$, one could estimate $|c^K_{\phi (1680)}|\approx 0.092$. Meanwhile, with the decay widths $19.8\pm 4.3$ MeV in [88] and 17 MeV in [89] for $\phi (1680)\rightarrow K\bar{K}$, we estimate the coefficient $|c^K_{\phi (1680)}|$ to be about 0.130–0.162. In view of our estimated values, we employ the fitted result $c^K_{\phi (1680)}=-0.150\pm 0.009$ [76] in our numerical calculation in this work. As for the coefficient $c^K_{\phi (1020)}$ of the electromagnetic form factors $F_{K^+}$ and $F_{K^0}$, we adopt its fitted value 1.038 in Model II in Ref. [76].

Utilizing the differential branching fraction Eq. (18) and the decay amplitudes collected in Appendix A, we obtain the concerned direct CP asymmetries and the CP averaged branching fractions for the quasi-two-body decays $B\rightarrow \phi (1020)h \rightarrow K\bar{K} h$ in Table 2 and $B\rightarrow \phi (1680)h \rightarrow K^+ K^- h$ in Table 3. Only the modes $B^+\rightarrow \phi (1020,1680) K^+$ and $B_s^0 \rightarrow \phi (1020,1680) \pi ^0$ with $\phi (1020,1680)$ decay into $K^+K^-$ or $K^0\bar{K}^0$, which contain the contributions from the current–current operators of the weak effective Hamiltonian [90], have the direct CP asymmetries in Tables 2 and 3. The first error of these results in Tables 2 and 3 comes from the uncertainty of the shape parameters $\omega _B=0.40\pm 0.04$ for $B^+$ and $B^{0}$ and $\omega _{B}=0.50\pm 0.05$ for $B^0_s$; the second error is induced by the chiral scale parameters $m^\pi _0=1.40\pm 0.10$ GeV and $m^K_0=1.60\pm 0.10$ GeV, which are defined using the meson masses and the component quark masses as $m^{\pi (K)}_0=\frac{m_{\pi (K)}}{m_q+m_{q^\prime }}$, and the Gegenbauer moment $a^{\pi ,K}_2=0.25\pm 0.15$ for $\pi$ and K as in [91]. The third one is contributed by the Gegenbauer moment $a_2^{\phi }=0.18\pm 0.08$ [79] and the fourth error in Table 3 comes from the variation of the coefficient $c^K_{\phi (1680)}$ of the form factor $F_K$, which will not change the direct CP asymmetries. There are other errors coming from the uncertainties of the masses and the decay constants of the initial and final states, the other parameters in the distribution amplitudes of the bachelor pion or kaon, the Wolfenstein parameters of the CKM matrix, etc., which are small and have been neglected.

Table 2 PQCD predictions of the CP averaged branching fractions and the direct CP asymmetries for the $B\rightarrow \phi (1020)h \rightarrow K\bar{K} h$ decays

Table 3 PQCD predictions of the CP averaged branching fractions and the direct CP asymmetries for the $B\rightarrow \phi (1680)h \rightarrow K^+ K^- h$ decays. The decay mode with the subprocess $\phi (1680)\rightarrow K^0\bar{K}^0$ has the same branching fraction and direct CP asymmetry of its corresponding decay with $\phi (1680)\rightarrow K^+K^-$

Table 4 Comparison of the extracted predictions with the experimental measurements for the relevant two-body branching fractions. The errors for the predictions have been added in quadrature

The two-body branching fractions for $B\rightarrow \phi h$ can be extracted from the quasi-two-body predictions with the relation

$$\begin{aligned} \Gamma (B\rightarrow \phi h\rightarrow K\bar{K} h)\approx \Gamma (B\rightarrow \phi h)\cdot {{{\mathcal {B}}}}(\phi \rightarrow K\bar{K}). \end{aligned}$$

(24)

In Ref. [46], the parameter $\eta$ was defined to measure the violation of the factorization relation the Eq. (24) for the $B\rightarrow K_0^{*}(1430) h$ and $B\rightarrow K_0^{*}(1430) h\rightarrow K\pi h$ decays. For the decays $B\rightarrow \phi (1020) h$ and $B\rightarrow \phi (1020) h\rightarrow K\bar{K} h$ in this work, we have the definition

$$\begin{aligned} \eta= & {} \frac{\Gamma (B\rightarrow \phi (1020)h\rightarrow K\bar{K} h)}{\Gamma (B\rightarrow \phi (1020)h)\cdot {{{\mathcal {B}}}}(\phi (1020)\rightarrow K\bar{K})}\nonumber \\\approx & {} \frac{m^4_{\phi (1020)}}{384\pi ^2 m^3_{B} f^2_\phi {\hat{q}}^3_h } \frac{1}{{{{\mathcal {B}}}}(\phi (1020)\rightarrow K\bar{K}) }\nonumber \\&\times \int ^{(m_{B}-m_h)^2}_{4 m_K^2}\frac{\mathrm{d}s}{s^3}\frac{\lambda ^{3/2}(m^2_B,s,m^2_h)\lambda ^{3/2}(s,m^2_K,m^2_K) }{(s-m^2_{\phi (1020)})^2+(m_{\phi (1020)}\Gamma _{\phi (1020)}(s))^2}, \nonumber \\ \end{aligned}$$

(25)

where $\lambda (a,b,c)=a^2+b^2+c^2-2ab-2ac-2bc$, the ${\hat{q}}_h$ is the expression of Eq. (20) in the rest frame of the B meson and fixed at $s=m^2_{\phi }$. As an example, we have $\eta \approx 1.07$ for the decays $B^0\rightarrow \phi (1020) K^0$ and $B^0\rightarrow \phi (1020) K^0\rightarrow K^+K^- K^0$ with the branching fraction ${{{\mathcal {B}}}}(\phi (1020)\rightarrow K^+K^-)=0.492$ [29]. It means that the violation of Eq. (24) is small when neglecting the effect of the squared invariant mass s in the decay amplitudes of the quasi-two-body decays. As regards the verification of Eq. (25), we calculate the decay $B^0\rightarrow \phi (1020) K^0$ in the two-body framework of the PQCD approach with the same parameters and obtain its branching fraction ${{{\mathcal {B}}}}(B^0\rightarrow \phi (1020) K^0)\approx 7.21\times 10^{-6}$, which is about $98.0\%$ of the result $7.36\times 10^{-6}$ in Table 4, extracted with the corresponding quasi-two-body result in Table 2 with the factorization relation.

The comparison of the extracted PQCD predictions with the experimental measurements for the relevant two-body branching fractions is shown in Table 4. The branching ratio $8.8^{+0.7}_{-0.6}\times 10^{-6}$ for the two-body decay $B^+\rightarrow \phi (1020) K^+$, which was averaged from the results in Refs. [92,93,94,95], presented by the BaBar, CDF, Belle and CLEO Collaborations, is consistent with the prediction $(8.19\pm 1.71)\times 10^{-6}$ in this work. The data ${{{\mathcal {B}}}}=(7.3\pm 0.7)\times 10^{-6}$ in [29] averaged from the results in [92, 96,97,98] for the decay $B^0\rightarrow \phi (1020) K^0$ agree well with our prediction $(7.36\pm 1.81)\times 10^{-6}$ in Table 4. In [99], an upper limit of $1.5\times 10^{-7}$ was set by LHCb at $90\%$ confidence level for the branching fraction of the decay $B^{\pm }\rightarrow \phi \pi ^{\pm }$. Very recently, the LHCb Collaboration presented the fit fraction $(0.3\pm 0.1\pm 0.1)\%$ of the total branching fraction of $B^\pm \rightarrow \pi ^\pm K^+K^-$ for the subprocess $\phi (1020)\rightarrow K^+K^-$ in Ref. [17], meaning the two-body branching ratio ${{{\mathcal {B}}}}(B^{\pm }\rightarrow \phi (1020) \pi ^{\pm })=(3.2\pm 1.5)\times 10^{-8}$ [100], which is larger than the corresponding prediction in 4 but both with large uncertainty.

The $B^+\rightarrow \phi (1020) \pi ^+$ was studied in [101] with its branching ratio at about $5\times 10^{-9}$ within QCDF, which agree with our prediction $(7.28\pm 4.54)\times 10^{-9}$ within errors. The predicted results in Table 2 for the decays $B_s^0\rightarrow \phi (1020) \bar{K}^0$ and $B_s^0 \rightarrow \phi (1020) \pi ^0$ are consistent with the theoretical results in Refs. [79, 101,102,103] within errors by considering ${{{\mathcal {B}}}}(\phi (1020)\rightarrow K^+K^-)=0.492$ [29]. The branching ratios for the two-body decays $B\rightarrow \phi \pi$ were found to be enhanced by the $\omega$–$\phi$ mixing effect in [104]. The $\omega$–$\phi$ mixing effect for the quasi-two-body decays $B\rightarrow \phi (1020,1680)h \rightarrow K\bar{K} h$ is out of the scope of this work and will be left to future studies. The penguin-dominated two-body decays $B^\pm \rightarrow K^\pm \phi (1020)$ and $B^0\rightarrow K^0 \phi (1020)$ have been studied in Refs. [105,106,107] within the PQCD approach with the consistent results with the values predicted in Table 4.

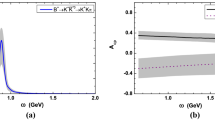
The predictions for the branching fractions of the decays $B\rightarrow \phi (1680)h \rightarrow K^+ K^- h$ in Table 3 are about $6{-}8\%$ of the corresponding results for $B\rightarrow \phi (1020)h \rightarrow K^+ K^- h$ in Table 2. The main portion of these branching fractions for $B\rightarrow \phi (1020,1680)h \rightarrow K^+ K^- h$ lies in the region around the pole masses of the intermediate states $\phi (1020)$ and $\phi (1680)$, which could be concluded from the differential branching fractions for the decays $B^0\rightarrow \phi (1020) K^0\rightarrow K^+K^- K^0$ and $B^0\rightarrow \phi (1680) K^0\rightarrow K^+K^- K^0$ shown in Fig. 2. In Ref. [30], the contributions from the subprocesses $\phi (1020) \rightarrow K^+ K^-$ and $\phi (1680) \rightarrow K^+ K^-$ were fitted by LHCb to be $(70.5\pm 0.6\pm 1.2)\%$ and $(4.0\pm 0.3\pm 0.3)\%$, respectively, of the total branching fraction for the three-body decay $B^0_s\rightarrow J/\psi K^+K^-$, implying a ratio of about 0.06 between the branching fractions of the quasi-two-body decays $B^0_s\rightarrow J/\psi \phi (1680)\rightarrow J/\psi K^+K^-$ and $B^0_s\rightarrow J/\psi \phi (1020) \rightarrow J/\psi K^+K^-$, which is consistent with the results $6\%$-$8\%$ in this work for $B\rightarrow \phi (1680,1020)h \rightarrow K^+ K^- h$. We need to stress that there will be interference between the contributions from $\phi (1020)$ and $\phi (1680)$, which could increase or decrease the total contributions from these two resonances dependent on the phase difference between them. According to Fig. 2, the contribution for $K^+K^-$ from the resonance $\phi (1020)$ is down by a factor of 10 at the peak of $\phi (1680)$ compared with the contribution from $\phi (1680)$, which means that the amplitudes are different by a factor about 3 and the interference allows for a variation between $(1+1/3)^2\approx 1.8$ and $(1-1/3)^2\approx 0.4$ in the region around the pole mass of $\phi (1680)$.

Fig. 2

Differential branching fractions from the threshold of $K^+K^-$ to 3 GeV for the $B^0\rightarrow \phi (1020) K^0\rightarrow K^+K^- K^0$ and $B^0\rightarrow \phi (1680) K^0\rightarrow K^+K^- K^0$ decays

The ratio between the branching fractions of the decays $\phi (1680) \rightarrow K^0 \bar{K}^0$ and $\phi (1680) \rightarrow K^+ K^-$ is close to one because of the coupling constants $g_{\phi (1680) K^0 \bar{K}^0}=g_{\phi (1680) K^+ K^-}$ [72] and $m^2_{\phi (1680)}-4m^2_{K^0} \approx m^2_{\phi (1680)}-4m^2_{K^+}$. This means that the decay mode with the subprocess $\phi (1680)\rightarrow K^0\bar{K}^0$ has the same branching fraction as its corresponding process with $\phi (1680)\rightarrow K^+K^-$ for $B\rightarrow \phi (1680)h \rightarrow K\bar{K} h$. Meanwhile, for the decays $\phi (1020) \rightarrow K^0 \bar{K}^0$ and $\phi (1020) \rightarrow K^+ K^-$, one has a ratio 0.66 between their branching fractions, which is consistent with the ratio 0.69 between the branching fractions in [29] for these two decays, with the coupling constants $g_{\phi (1020) K^0 \bar{K}^0}=g_{\phi (1020) K^+ K^-}$ [18, 72]. The results in Table 2 for the subprocess $\phi (1020) \rightarrow K^0 \bar{K}^0$ are deduced from ${{{\mathcal {B}}}}(\phi (1020) \rightarrow K^0 \bar{K}^0)=34.0\%$ [29] along with the results in the same table for the decays with the subprocess $\phi (1020) \rightarrow K^+ K^-$. With the decay amplitude for $B^+\rightarrow \phi (1020) K^+ \rightarrow K^+K^- K^+$, we calculate the branching fraction and direct CP asymmetry for the decay $B^+\rightarrow \phi (1020) K^+ \rightarrow K^0\bar{K}^0 K^+$, and obtain the central values ${{{\mathcal {B}}}}=2.83\times 10^{-6}$ and ${\mathcal {A}}_{CP}=-1.25\%$ for it, which are well in agreement with the results in Table 2 for this process.

4 Summary

In this work, we studied the contributions for the $K^+K^-$ and $K^0\bar{K}^0$ which originated from the intermediate states $\phi (1020)$ and $\phi (1680)$ in the charmless three-body decays $B\rightarrow K\bar{K} h$ in PQCD approach. The subprocesses $\phi (1020,1680)\rightarrow K\bar{K}$ were introduced into the distribution amplitudes of $K\bar{K}$ system via the kaon electromagnetic form factor with the coefficients $c^K_{\phi (1020)}$ and $c^K_{\phi (1680)}$ adopted from the fitted results. With $c^K_{\phi (1020)}=1.038$ and $c^K_{\phi (1680)}=-0.150\pm 0.009$ we predicted the branching fractions for the quasi-two-body decays $B\rightarrow \phi (1020)h \rightarrow K\bar{K} h$ and $B\rightarrow \phi (1680)h \rightarrow K^+ K^- h$ and the direct CP asymmetries for the decay modes $B^+\rightarrow \phi (1020,1680) K^+$ and $B_s^0 \rightarrow \phi (1020,1680) \pi ^0$ with $\phi (1020,1680)$ decay into $K^+K^-$ or $K^0\bar{K}^0$.

The predictions for the branching fractions of the decays $B\rightarrow \phi (1680)h \rightarrow K^+ K^- h$ are about $6\%$–$8\%$ of the corresponding results for $B\rightarrow \phi (1020)h \rightarrow K^+ K^- h$ in this work. The branching fraction for the decay $\phi (1680) \rightarrow K^0 \bar{K}^0$ is equal to that for $\phi (1680) \rightarrow K^+ K^-$, and the decay mode with the subprocess $\phi (1680)\rightarrow K^0\bar{K}^0$ has the same branching fraction as the corresponding mode with $\phi (1680)\rightarrow K^+K^-$ for $B\rightarrow \phi (1680)h \rightarrow K\bar{K} h$. We defined the parameter $\eta$ to measure the violation of the factorization relation for the decays $B\rightarrow \phi h$ and $B\rightarrow \phi h \rightarrow K\bar{K} h$ and found the violation to be quite small. With the factorization relation, we extracted the branching fractions for the two-body decays $B^{0,+}\rightarrow \phi (1020) K^{0,+}$ and $B^{0,+}\rightarrow \phi (1020) \pi ^{0,+}$. The predictions for the decays $B^0\rightarrow \phi (1020) K^0$ and $B^{+}\rightarrow \phi (1020) K^{+}$ are in agreement with the existing data. Our results for $B^{0,+}\rightarrow \phi (1020) \pi ^{0,+}$ are consistent with the theoretical results in the literature.

Appendix A: Decay amplitudes

The Lorentz invariant decay amplitude ${\mathcal {A}}$ for the quasi-two-body processes $B\rightarrow \phi (1020, 1680)h\rightarrow KK h$ is given by ${\mathcal {A}}=\Phi _B\otimes H\otimes \Phi _{h}\otimes \Phi _{KK}$ [5, 40] in the PQCD approach, according to the Feynman diagrams of Fig. 1. The hard kernel H contains one hard gluon exchange at the leading order in the strong coupling $\alpha _s$. The distribution amplitudes $\Phi _B, \Phi _{h}$ and $\Phi _{KK}$ absorb the nonperturbative dynamics in the relevant processes. $\Phi _B$ and $\Phi _{h}$ for the B meson and the bachelor final state h in this work are the same as those widely employed in the studies of the hadronic B meson decays in the PQCD approach, for which one can find the expressions and parameters in the appendix of [46] and the references therein.

With the subprocesses $\phi \rightarrow {K^+ K^-, \bar{K}^0 K^0}$, and $\phi$ being $\phi (1020)$ or $\phi (1680)$, the concerned quasi-two-body decay amplitudes are given as follows:

$$\begin{aligned}&\mathcal{A}(B^+ \rightarrow \phi K^+) = \frac{G_F}{\sqrt{2}} \left\{ V_{ub}^*V_{us}[a_1F^{LL}_{Ah}+C_1M^{LL}_{Ah}] \right. \nonumber \\&\qquad -V_{tb}^*V_{ts}\left[ \left( a_3+a_4+a_5-\frac{a_7+a_9+a_{10}}{2}\right) F^{LL}_{Th}\right. \nonumber \\&\qquad +(a_4+a_{10})F^{LL}_{Ah}+(a_6+a_8)F^{SP}_{Ah}\nonumber \\&\qquad +\left( C_3+C_4-\frac{C_9}{2}-\frac{C_{10}}{2}\right) M^{LL}_{Th}\nonumber \\&\qquad +\left( C_5-\frac{C_7}{2}\right) M^{LR}_{Th} +\left( C_6-\frac{C_8}{2}\right) M^{SP}_{Th}\nonumber \\&\qquad \left. \left. +(C_3+C_9) M^{LL}_{Ah}+(C_5+C_7) M^{LR}_{Ah}\right] \right\} , \end{aligned}$$

(A1)

$$\begin{aligned}&\mathcal{A}(B^+ \rightarrow \phi \pi ^+) =\frac{G_F}{\sqrt{2}}\left\{ -V_{tb}^*V_{td} \right. \nonumber \\&\qquad \times \left[ \left( a_3+a_5-\frac{a_7+a_9}{2}\right) F^{LL}_{Th}\right. \nonumber \\&\qquad +\left( C_4-\frac{C_{10}}{2}\right) M^{LL}_{Th}\nonumber \\&\qquad \left. \left. +\left( C_6-\frac{C_8}{2}\right) M^{SP}_{Th}\right] \right\} , \end{aligned}$$

(A2)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow \phi K^0) =\frac{G_F}{\sqrt{2}} \big \{-V_{tb}^*V_{td}\nonumber \\&\qquad \times \left[ \left( a_3+a_5-\frac{a_7+a_9}{2}\right) F^{LL}_{Th}\right. \nonumber \\&\qquad +\left( a_4-\frac{a_{10}}{2}\right) (F^{LL}_{Th}+F^{LL}_{Ah})\nonumber \\&\qquad +\left( a_6-\frac{a_8}{2}\right) F^{SP}_{Ah}+\left( C_4 -\frac{C_{10}}{2}\right) M^{LL}_{Th}\nonumber \\&\qquad +\left( C_3-\frac{C_9}{2}\right) (M^{LL}_{Th}+M^{LL}_{Ah})\nonumber \\&\qquad +\left( C_5-\frac{C_7}{2}\right) (M^{LR}_{Th}+M^{LR}_{Ah})\nonumber \\&\qquad \left. \left. +\left( C_6-\frac{C_8}{2}\right) M^{SP}_{Th}\right] \right\} , \end{aligned}$$

(A3)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow \phi \pi ^0) = \frac{-1}{\sqrt{2}} \mathcal{A}(B^ +\rightarrow \phi \pi ^+), \end{aligned}$$

(A4)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow \phi \bar{K}^0) = \frac{G_F}{\sqrt{2}} \left\{ -V_{tb}^*V_{ts}\left[ \left( a_4-\frac{a_{10}}{2}\right) \right. \right. (F^{LL}_{T\phi }\nonumber \\&\qquad +F^{LL}_{A\phi })+\left( a_6-\frac{a_8}{2}\right) (F^{SP}_{T\phi }+F^{SP}_{A\phi })\nonumber \\&\qquad +\left( a_3+a_5-\frac{a_7+a_9}{2}\right) F^{LL}_{Th}\nonumber \\&\qquad +\left( C_4-\frac{C_{10}}{2}\right) M^{LL}_{Th}\nonumber \\&\qquad +\left( C_6-\frac{C_8}{2}\right) M^{SP}_{Th}\nonumber \\&\qquad +\left( C_3-\frac{C_9}{2}\right) (M^{LL}_{T\phi }+M^{LL}_{A\phi })\nonumber \\&\qquad \left. \left. +\left( C_5-\frac{C_7}{2}\right) (M^{LR}_{T\phi }+M^{LR}_{A\phi })\right] \right\} , \end{aligned}$$

(A5)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow \phi \pi ^0) = \frac{G_F}{2} \left\{ V_{ub}^*V_{us}[a_2 F^{LL}_{T\phi }+C_2 M^{LL}_{T\phi }] \right. \nonumber \\&\qquad -V_{tb}^*V_{ts}\left[ \frac{3}{2}(a_9-a_7)F^{LL}_{T\phi } +\frac{3}{2}C_{10}M^{LL}_{T\phi }\right. \nonumber \\&\qquad \left. \left. +\frac{3}{2}C_8 M^{SP}_{T\phi }\right] \right\} , \end{aligned}$$

(A6)

where $G_F$ is the Fermi coupling constant, the V are the CKM matrix elements. The combinations $a_i$ for the Wilson coefficients are defined as

$$\begin{aligned}&a_1=C_2+\frac{C_1}{3},\quad a_2= C_1+\frac{C_2}{3},\quad a_3= C_3+\frac{C_4}{3},\nonumber \\&\quad a_4=C_4+\frac{C_3}{3}, \quad a_5= C_5+\frac{C_6}{3}, \end{aligned}$$

(A7)

$$\begin{aligned}&a_6= C_6+\frac{C_5}{3},\quad a_7=C_7+\frac{C_8}{3},\quad a_8= C_8+\frac{C_7}{3},\nonumber \\&\quad a_9= C_9+\frac{C_{10}}{3},\quad a_{10}= C_{10}+\frac{C_{9}}{3}. \end{aligned}$$

(A8)

It should be understood that the Wilson coefficients $C_i$, the amplitudes F and M for the factorizable and nonfactorizable Feynman diagrams, respectively, appear in convolutions in the momentum fractions and the impact parameters b.

The amplitudes from Fig. 1a are written as

$$\begin{aligned} F^{LL}_{T\phi }= & {} 8\pi C_F m^4_B f_h (\zeta -1) \int \mathrm{d}x_B \mathrm{d}z\int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [(1+z)\phi ^0 +\sqrt{\zeta }(1-2z)(\phi ^s+\phi ^t)\big ]\nonumber \\&\times E_{a12}(t_{a1})h_{a1}(x_B,z,b_B,b)\nonumber \\&+[\zeta \phi ^0+2 \sqrt{\zeta } \phi ^s]E_{a12}(t_{a2})h_{a2}(x_B,z,b_B,b) \big \}, \end{aligned}$$

(A9)

$$\begin{aligned} F^{LR}_{T\phi }= & {} -F^{LL}_{T\phi }, \end{aligned}$$

(A10)

$$\begin{aligned} F^{SP}_{T\phi }= & {} 16\pi C_F m^4_B r f_h \int \mathrm{d}x_B \mathrm{d}z\int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [(\zeta (2z-1)+1)\phi ^0 +\sqrt{\zeta }((2+z)\phi ^s-z\phi ^t)\big ]\nonumber \\&\times E_{a12}(t_{a1})h_{a1}(x_B,z,b_B,b)\nonumber \\&+\big [x_B\phi ^0+2\sqrt{\zeta }(\zeta -x_B+1)\phi ^s\big ]\nonumber \\&\times E_{a12}(t_{a2})h_{a2}(x_B,z,b_B,b)\big \}, \end{aligned}$$

(A11)

$$\begin{aligned} M^{LL}_{T\phi }= & {} 32\pi C_F m^4_B/\sqrt{2N_c} (\zeta -1) \int \mathrm{d}x_B \mathrm{d}z\mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b_3 \mathrm{d}b_3\phi _B(x_B,b_B)\phi ^A\nonumber \\&\times \big \{\big [((1-\zeta )(1-x_3)-x_B -z\zeta )\phi ^0-\sqrt{\zeta }z(\phi ^s-\phi ^t)\big ]\nonumber \\&\times E_{a34}(t_{a3})h_{a3}(x_B,z,x_3,b_B,b_3)\nonumber \\&+\big [(x_3(\zeta -1)+x_B-z)\phi ^0+z\sqrt{\zeta }(\phi ^s +\phi ^t)\big ]\nonumber \\&\times E_{a34}(t_{a4})h_{a4}(x_B,z,x_3,b_B,b_3) \big \}, \end{aligned}$$

(A12)

$$\begin{aligned} M^{LR}_{T\phi }= & {} 32\pi C_F r m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b_3 \mathrm{d}b_3\phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [((1-x_3)(1-\zeta )-x_B)(\phi ^P+\phi ^T)\nonumber \\&\times (\phi ^0+\sqrt{\zeta }(\phi ^s-\phi ^t))\nonumber \\&-\sqrt{\zeta } z(\phi ^P-\phi ^T)(\sqrt{\zeta }\phi ^0 -\phi ^s-\phi ^t)E_{a34}(t_{a3})\nonumber \\&\times h_{a3}(x_B,z,x_3,b_B,b_3)\nonumber \\&+\big [\sqrt{\zeta }z(\phi ^P +\phi ^T)(\sqrt{\zeta }\phi ^0-\phi ^s-\phi ^t)\nonumber \\&+(x_B-x_3(1-\zeta ))(\phi ^P-\phi ^T)(\phi ^0 +\sqrt{\zeta }(\phi ^s-\phi ^t))\big ]\nonumber \\&\times E_{a34}(t_{a4})h_{a4}(x_B,z,x_3,b_B,b_3)\big \}, \end{aligned}$$

(A13)

$$\begin{aligned} M^{SP}_{T\phi }= & {} 32\pi C_F m^4_B/\sqrt{2N_c} (\zeta -1) \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b_3 \mathrm{d}b_3\phi _B(x_B,b_B)\nonumber \\&\times \phi ^A\big \{\big [((1-\zeta )(x_3-1)+x_B -z)\phi ^0+\sqrt{\zeta }z(\phi ^s\nonumber \\&+\phi ^t)\big ]E_{a34}(t_{a3})h_{a3}(x_B,z,x_3,b_B,b_3)\nonumber \\&+\big [(x_3(1-\zeta )-x_B-z\zeta )\phi ^0-z\sqrt{\zeta }(\phi ^s -\phi ^t) \big ]\nonumber \\&\times E_{a34}(t_{a4})h_{a4}(x_B,z,x_3,b_B,b_3) \big \}, \end{aligned}$$

(A14)

where the color factor $C_F=4/3$ and the ratio $r=m^h_0/m_B$. The amplitudes from Fig. 1b are written as

$$\begin{aligned} F^{LL}_{A\phi }= & {} 8\pi C_F m^4_B f_B \int \mathrm{d}z \mathrm{d}x_3\int b \mathrm{d}b b_3 \mathrm{d}b_3\nonumber \\&\times \big \{\big [(1-\zeta )(1-z)\phi ^A\phi ^0\nonumber \\&+2r\sqrt{\zeta }\phi ^P((z-2)\phi ^s-z\phi ^t)\big ]E_{b12}(t_{b1})\nonumber \\&\times h_{b1}(z,x_3,b,b_3)\nonumber \\&+\big [[(1-x_3)\zeta ^2+(2x_3-1)\zeta -x_3]\phi ^A\phi ^0\nonumber \\&+2r\sqrt{\zeta }[((1-x_3)\zeta +x_3)(\phi ^P+\phi ^T)\nonumber \\&+(\phi ^P-\phi ^T)]\phi ^s\big ]E_{b12}(t_{b2})h_{b2}(z,x_3,b,b_3) \big \},\nonumber \\ \end{aligned}$$

(A15)

$$\begin{aligned} F^{LR}_{A\phi }= & {} -F^{LL}_{A\phi }, \end{aligned}$$

(A16)

$$\begin{aligned} F^{SP}_{A\phi }= & {} 16\pi C_F m^4_B f_B \int \mathrm{d}z \mathrm{d}x_3\int b \mathrm{d}b b_3 \mathrm{d}b_3\nonumber \\&\times \big \{\big [2r(1+(z-1)\zeta )\phi ^P\phi ^0\nonumber \\&-\sqrt{\zeta }(1-\zeta )(1-z)\phi ^A(\phi ^s+\phi ^t)\big ]\nonumber \\&\times E_{b12}(t_{b1})h_{b1}(z,x_3,b,b_3)\nonumber \\&+\big [r\left( x_3(1-\zeta )(\phi ^P -\phi ^T)-2\zeta \phi ^T\right) \phi ^0\nonumber \\&+2\sqrt{\zeta }(\zeta -1)\phi ^A\phi ^s \big ]E_{b12}(t_{b2})\nonumber \\&\times h_{b2}(z,x_3,b,b_3)\big \}, \end{aligned}$$

(A17)

$$\begin{aligned} M^{LL}_{A\phi }= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b \mathrm{d}b\phi _B(x_B,b_B)\nonumber \\&\big \{\big [[(x_3-z-1)\zeta ^2+(1+z-2 x_3-x_B)\zeta \nonumber \\&+x_3+x_B]\phi ^A\phi ^0\nonumber \\&+r\sqrt{\zeta }[z(\phi ^P-\phi ^T)(\phi ^s+\phi ^t)\nonumber \\&+((1-x_3)(1-\zeta )-x_B)\nonumber \\&(\phi ^P+\phi ^T)(\phi ^s -\phi ^t)-4\phi ^P\phi ^s]\big ]\nonumber \\&\times E_{b34}(t_{b3})h_{b3}(x_B,z,x_3,b_B,b)\nonumber \\&+\big [(1-\zeta )^2(z-1)\phi ^A\phi ^0\nonumber \\&+ r\sqrt{\zeta }[(\zeta (1-x_3)+x_3 -x_B)\nonumber \\&\times (\phi ^P-\phi ^T)(\phi ^s+\phi ^t)\nonumber \\&+(1-z)(\phi ^P+\phi ^T)(\phi ^s-\phi ^t)]\big ]\nonumber \\&\times E_{b34}(t_{b4})h_{b4}(x_B,z,x_3,b_B,b)\big \}, \end{aligned}$$

(A18)

$$\begin{aligned} M^{LR}_{A\phi }= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [r [(2+\zeta x_3-x_3-x_B)(\phi ^P+\phi ^T)\nonumber \\&-\zeta z(\phi ^P-\phi ^T)-2 \zeta \phi ^P]\phi ^0\nonumber \\&+\sqrt{\zeta }(1-\zeta )(1+z)\phi ^A(\phi ^s-\phi ^t)\big ]\nonumber \\&\times E_{b34}(t_{b3})h_{b3}(x_B,z,x_3,b_B,b)\nonumber \\&+ \big [r[(x_3(1-\zeta )-x_B)(\phi ^P+\phi ^T)\nonumber \\&+\zeta z(\phi ^P-\phi ^T)+2\zeta \phi ^T]\phi ^0\nonumber \\&+\sqrt{\zeta }(1-\zeta )(1-z)\phi ^A(\phi ^s-\phi ^t) \big ]\nonumber \\&\times E_{b34}(t_{b4})h_{b4}(x_B,z,x_3,b_B,b)\big \}, \end{aligned}$$

(A19)

$$\begin{aligned} M^{SP}_{A\phi }= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b \mathrm{d}b\phi _B(x_B,b_B)\nonumber \\&\big \{\big [(\zeta -1)[(\zeta -1)z+1]\phi ^A\phi ^0\nonumber \\&+r\sqrt{\zeta }\times [((1-\zeta )(x_3-1)+x_B)\nonumber \\&(\phi ^P-\phi ^T)(\phi ^s+\phi ^t)\nonumber \\&-z(\phi ^P+\phi ^T)(\phi ^s-\phi ^t)+4\phi ^P\phi ^s]\big ]\nonumber \\&\times E_{b34}(t_{b3})h_{b3}(x_B,z,x_3,b_B,b)\nonumber \\&+\big [[(\zeta -1)(x_3(\zeta -1)+x_B)\nonumber \\&+\zeta z(1-\zeta )]\phi ^A\phi ^0+r\sqrt{\zeta }[(z-1)\nonumber \\&\times (\phi ^P-\phi ^T)(\phi ^s+\phi ^t)\nonumber \\&+((\zeta -1)x_3+x_B-\zeta )(\phi ^P +\phi ^T)(\phi ^s-\phi ^t)]\big ]\nonumber \\&\times E_{b34}(t_{b4})h_{b4}(x_B,z,x_3,b_B,b)\big \}. \end{aligned}$$

(A20)

The amplitudes from Fig. 1c are written as

$$\begin{aligned} F^{LL}_{Th}= & {} 8\pi C_F m^4_B F_K\int \mathrm{d}x_B \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b_3 \mathrm{d}b_3 \phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [(1-\zeta )[(x_3(\zeta -1)-1)\phi ^A\nonumber \\&+r(2x_3-1)\phi ^P]-r(1 +\zeta -2x_3(1-\zeta ))\phi ^T\big ]\nonumber \\&\times E_{c12}(t_{c1})h_{c1}(x_B,x_3,b_B,b_3)\nonumber \\&+\left[ x_B(1-\zeta )\zeta \phi ^A -2r(1-\zeta (1-x_B))\phi ^P\right] \nonumber \\&\times E_{c12}(t_{c2}) h_{c2}(x_B,x_3,b_B,b_3)\big \}, \end{aligned}$$

(A21)

$$\begin{aligned} F^{LR}_{Th}= & {} F^{LL}_{Th}, \end{aligned}$$

(A22)

$$\begin{aligned} M^{LL}_{Th}= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\phi ^0 \nonumber \\&\times \big \{\big [(x_B+z-1)(1-\zeta )^2\phi ^A\nonumber \\&+r[\zeta (x_B+z)\times (\phi ^P+\phi ^T) \nonumber \\&+x_3(1-\zeta )(\phi ^P-\phi ^T)\nonumber \\&-2\zeta \phi ^T]\big ] E_{c34}(t_{c3})h_{c3}(x_B,z,x_3,b_B,b)\nonumber \\&+\big [(\zeta -1)[x_3(\zeta -1)+x_B -z]\phi ^A\nonumber \\&+r[x_3(\zeta -1)(\phi ^P+\phi ^T)\nonumber \\&-(x_B-z)\zeta (\phi ^P_K -\phi ^T_K)]\big ]\nonumber \\&\times E_{c34}(t_{c4})h_{c4}(x_B,z,x_3,b_B,b)\big \}, \end{aligned}$$

(A23)

$$\begin{aligned} M^{LR}_{Th}= & {} 32\pi C_F m^4_B\sqrt{\zeta }/\sqrt{2N_c}\nonumber \\&\times \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [(1-x_B-z)(\zeta -1)(\phi ^s+\phi ^t)\phi ^A-r\nonumber \\&\times (x_3(1-\zeta )+\zeta )(\phi ^s-\phi ^t)(\phi ^P+\phi ^T)\nonumber \\&-r(1-x_B-z)(\phi ^s +\phi ^t)(\phi ^P-\phi ^T)\big ]\nonumber \\&\times E_{c34}(t_{c3})h_{c3}(x_B,z,x_3,b_B,b)\nonumber \\&+\big [(z-x_B)(1-\zeta )(\phi ^s-\phi ^t)\phi ^A\nonumber \\&+rx_3(1-\zeta )(\phi ^s+\phi ^t)(\phi ^P+\phi ^T)\nonumber \\&+r(z-x_B)(\phi ^s-\phi ^t)(\phi ^P-\phi ^T)\big ]\nonumber \\&\times E_{c34}(t_{c4})h_{c4}(x_B,z,x_3,b_B,b)\big \}, \end{aligned}$$

(A24)

$$\begin{aligned} M^{SP}_{Th}= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\phi ^0\nonumber \\&\times \big \{\big [(\zeta (x_3-1)-x_3+x_B +z-1)(1-\zeta )\phi ^A\nonumber \\&+ r x_3(1-\zeta )(\phi ^P+\phi ^T) + r\zeta (x_B+z)(\phi ^P-\phi ^T)\nonumber \\&+2r\zeta \phi ^T\big ] E_{c34}(t_{c3})h_{c3}(x_B,z,x_3,b_B,b)+\big [(z-x_B) \nonumber \\&\times (1-\zeta )^2\phi ^A+r\zeta (z-x_B)(\phi ^P+\phi ^T)\nonumber \\&-rx_3(1-\zeta )(\phi ^P-\phi ^T)\big ]\nonumber \\&\times E_{c34}(t_{c4})h_{c4}(x_B,z,x_3,b_B,b)\big \}. \end{aligned}$$

(A25)

The amplitudes from Fig. 1d are written as

$$\begin{aligned} F^{LL}_{Ah}= & {} 8\pi C_F m^4_B f_B \int \mathrm{d}z \mathrm{d}x_3\int b \mathrm{d}b b_3 \mathrm{d}b_3\nonumber \\&\times \big \{\big [(x_3(1-\zeta )-1)(\zeta -1)\phi ^0\phi ^A\nonumber \\&+2r\sqrt{\zeta }\phi ^s[x_3(\zeta -1)(\phi ^P-\phi ^T) +2\phi ^P]\big ]\nonumber \\&\times E_{d12}(t_{d1})h_{d1}(z,x_3,b,b_3)+\big [z(\zeta -1)\phi ^0\phi ^A\nonumber \\&-2r\sqrt{\zeta }[z(\phi ^s+\phi ^t)\nonumber \\&+(1-\zeta )(\phi ^s-\phi ^t)]\phi ^P\big ] E_{d12}(t_{d2})\nonumber \\&\times h_{d2}(z,x_3,b,b_3) \big \}, \end{aligned}$$

(A26)

$$\begin{aligned} F^{LR}_{Ah}= & {} -F^{LL}_{Ah}, \end{aligned}$$

(A27)

$$\begin{aligned} F^{SP}_{Ah}= & {} 16\pi C_F m^4_B f_B \int \mathrm{d}z \mathrm{d}x_3\int b \mathrm{d}b b_3 \mathrm{d}b_3\nonumber \\&\times \big \{\big [(\zeta -1)[2\sqrt{\zeta }\phi ^s\phi ^A\nonumber \\&+r(1-x_3)\phi ^0 \phi ^P]- r[\zeta +x_3(\zeta -1)+1]\phi ^0\phi ^T\big ]\nonumber \\&\times E_{d12}(t_{d1})h_{d1}(z,x_3,b,b_3)\nonumber \\&+ \big [z\sqrt{\zeta }(\zeta -1)(\phi ^s-\phi ^t)\phi ^A\nonumber \\&+2r(z \zeta +\zeta -1)\phi ^0\phi ^P \big ]E_{d12}(t_{d2})h_{d2}(z,x_3,b,b_3)\big \},\nonumber \\ \end{aligned}$$

(A28)

$$\begin{aligned} M^{LL}_{Ah}= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \nonumber \\&\times \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\int b_B \mathrm{d}b_B b \mathrm{d}b\phi _B(x_B,b_B) \nonumber \\&\times \big \{\big [[(x_B+z-1)\zeta ^2+ (1-2x_B- 2z)\zeta \nonumber \\&+x_B+z]\phi ^0\phi ^A\nonumber \\&-r\sqrt{\zeta }[(\eta (1-x_3)+x_3)(\phi ^s-\phi ^t)(\phi ^P+\phi ^T)\nonumber \\&+(1-x_B-z)(\phi ^s+\phi ^t)(\phi ^P-\phi ^T)- 4\phi ^s\phi ^P]\big ]\nonumber \\&\times E_{d34}(t_{d3})h_{d3}(x_B,z,x_3,b_B,b)\nonumber \\&+\big [(\zeta -1)((1-x_3)(1-\zeta )+\zeta (x_B-z))\phi ^0\phi ^A\nonumber \\&+r\sqrt{\zeta }[(x_B-z)(\phi ^s-\phi ^t)\nonumber \\&\times (\phi ^P+\phi ^T)+(1-\zeta )(x_3-1)\nonumber \\&(\phi ^s +\phi ^t)(\phi ^P-\phi ^T)]\big ]\nonumber \\&\times E_{d34}(t_{d4})h_{d4}(x_B,z,x_3,b_B,b) \big \}, \end{aligned}$$

(A29)

$$\begin{aligned} M^{LR}_{Ah}= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\int b_B \mathrm{d}b_B b \mathrm{d}b \phi _B(x_B,b_B)\nonumber \\&\times \big \{\big [\sqrt{\zeta }(1-\zeta )(x_B+z-2)(\phi ^s +\phi ^t)\phi ^A\nonumber \\&+ r\phi ^0[\zeta (x_B+z-1)(\phi ^P+\phi ^T)\nonumber \\&+ (1+x_3-\zeta x_3)(\phi ^P-\phi ^T)\nonumber \\&-2\zeta \phi ^T]\big ]E_{d34}(t_{d3})h_{d3}(x_B,z,x_3,b_B,b)\nonumber \\&+\big [\sqrt{\zeta }(1-\zeta )(x_B-z)(\phi ^s+\phi ^t)\phi ^A\nonumber \\&+r\phi ^0[\zeta (x_B-z)(\phi ^P +\phi ^T)\nonumber \\&+(1-\zeta )(1-x_3)(\phi ^P-\phi ^T)]\big ]\nonumber \\&\times E_{d34}(t_{d4})h_{d4}(x_B,z,x_3,b_B,b)\big \}, \end{aligned}$$

(A30)

$$\begin{aligned} M^{SP}_{Ah}= & {} 32\pi C_F m^4_B/\sqrt{2N_c} \int \mathrm{d}x_B \mathrm{d}z \mathrm{d}x_3\nonumber \\&\times \int b_B \mathrm{d}b_B b \mathrm{d}b\phi _B(x_B,b_B)\big \{\big [(\zeta -1)[x_3(\zeta -1)\nonumber \\&-\zeta (x_B+z)+1]\phi ^0\phi ^A\nonumber \\&- r\sqrt{\zeta }[(x_B+z-1)(\phi ^s-\phi ^t)(\phi ^P+\phi ^T)\nonumber \\&+ (\zeta x_3-\zeta -x_3)(\phi ^s+\phi ^t)(\phi ^P-\phi ^T)\nonumber \\&+4\phi ^s\phi ^P]\big ]E_{d34}(t_{d3})\nonumber \\&\times h_{d3}(x_B,z,x_3,b_B,b)+ \big [(\zeta -1)^2(z-x_B)\phi ^0\phi ^A\nonumber \\&-r\sqrt{\zeta }[(1-\zeta )(x_3-1)(\phi ^s-\phi ^t)(\phi ^P +\phi ^T)\nonumber \\&+(x_B-z)(\phi ^s+\phi ^t)\nonumber \\&\times (\phi ^P-\phi ^T) \big ] E_{d34}(t_{d4})h_{d4}(x_B,z,x_3,b_B,b) \big \}. \nonumber \\ \end{aligned}$$

(A31)

For the errors induced by the parameter ${\mathcal {P}}\pm \Delta {\mathcal {P}}$ for the ${\mathcal {B}}$ and ${\mathcal {A}}_{CP}$ in the numerical calculation of this work, we employ the formulas [46]

$$\begin{aligned}&\Delta {\mathcal {B}}=\left| \frac{\partial {\mathcal {B}}}{\partial {\mathcal {P}}}\right| \Delta {\mathcal {P}},\nonumber \\&\Delta {\mathcal {A}}_{CP}=\frac{2({\mathcal {B}}\Delta \overline{{\mathcal {B}}}-\overline{{\mathcal {B}}}\Delta {\mathcal {B}})}{(\overline{{\mathcal {B}}}+{\mathcal {B}})^2}. \end{aligned}$$

(A32)

The PQCD functions which appear in the factorization formulas, Eqs. (A9)–(A31), can be found in Appendix B of [46].