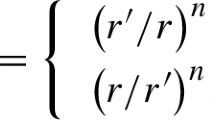Effect of rotation and magnetic field in the gyroscopic precession around a neutron star

Abstract

General relativistic effects are essential in defining the spacetime around massive astrophysical objects. The effects can be captured using a test gyro. If the gyro rotates at some fixed orbit around the star, then the gyro precession frequency captures all the general relativistic effects. In this article, we calculate the overall precession frequency of a test gyro orbiting a rotating neutron star or a rotating magnetar. We find that the gyro precession frequency diverges as it approaches a black hole, whereas, for a neutron star, it always remains finite. For a rotating neutron star, a prograde motion of the gyro gives a single minimum, whereas a retrograde motion gives a double minimum. We also find that the gyroscope precession frequency depends on the star’s mass and rotation rate. Depending on the magnetic field configuration, we find that of the precession frequency of the gyro differs significantly inside the star; however, outside the star, the effect is not very prominent. Also, the gyro precession frequency depends more significantly on the star’s rotation rate than its magnetic field strength.

1 Introduction

Local inertial frames are dragged along the central object due to their rotation, and this effect is known as the Lense-Thirring (LT) effect [1]. The general relativistic (GR) effect of a spacetime (ST) can be well studied if we place a gyro near the central object and study the gyro precession (GP). From its advent general Relativity faced many challenges, some of which have been solved and some are yet to be solved: One such case is the geodetic precession (also known as de Sitter precession). Geodetic precession was measured in the field of the Sun by accurately tracking the orbit of the Earth-Moon system with the Lunar Laser Ranging technique, and also in the field of the Earth itself with the dedicated Gravity Probe B (GP-B)space-based experiment and its spaceborne gyroscopes [2, 3]. Still some challenges remain, and the recent overview of such challenges can be found in [4, 5] and references therein.

In this article, we try to calculate the spin precession frequency of a gyro orbiting around a compact object. A gyro is a spinning test particle whose mass does not affect the spacetime around the central object. If the gyro itself rotates around the central object with some angular velocity, some other effects become essential along with the LT effect. The gyro precession frequency (GPF) then includes LT precession, geodetic precession, and other kinematic effects. We call this as overall precession. The GPF has all the information about the GR effect of the ST near the central object. The test gyro can be any spinning test particle whose mass is negligible compared to the mass of the central object, such that it does not affect the ST of the central object. The test particle can be some spinning object like a pulsar in case of a supermassive black hole or some planets in case of neutron stars (NSs) (PSR B1620–26 [6], PSR B1257+12 [7]). It can even be some spinning object created in the circumstellar disk of a NS (4U 0142+61 [8]). The recent exciting scenario of the GR spin precessions of rogue planets orbiting supermassive Black Holes was studied, which surprisingly could sustain life depending on the GR spin precessions [9]. Very recently LT effect would have been allegedly detected in an NS-WD binary system [10, 11].

For a weak gravitational field, the gravitational potential created by the rotation of the central object takes a similar form as that of the electromagnetic potential created by the motion of charges. From this analogy, the effect is known as the “Gravitomagnetic (GM) effect”. The word “gravitomagnetism” was introduced by Thorne [12,13,14]. Oliver Heaviside investigated the analogy between gravitation and electromagnetism [15]. In 1918, Thirring [16] pointed out that the geodesic equation may be written in terms of a Lorentz force, acted by a gravitoelectric and gravitomagnetic field. Later this led to the concept of the LT effect [1]. As a massive NS drags the ST, the axis itself about which the GPF is measured is dragged along some killing trajectory. The GPF coincides with the vorticity field of the killing congruence, and the vorticity vector is analogous to the magnetic field.

However, in addition, there can be a real ultra-strong magnetic field in NSs, especially in the case of magnetars. Magnetars are NSs with an ultra-strong magnetic field at their surface [17, 18]. Some anomalous X-ray pulsars [19,20,21] and some soft gamma repeaters [22,23,24] falls under such magnetars. Moreover, from the virial theorem, it is inferred that the magnetic field’s central value can be 3 orders higher than the surface value. The magnetic field configuration outside the star is known to be poloidal. However, the magnetic field inside the star can be much complex, and recent studies have shown that it can be anything from poloidal, toroidal to TT. Moreover, the stability of the magnetic configuration hints towards TT configuration. The recent discovery of several magnetars shows that the surface field as high as $10^{15}$ G, which infers the center field to be of the order of $10^{18}$ G.

In such ST, we study not only the GM effect but also the effect of the magnetic field on the GM effect. The magnetic field also distorts the ST as it also contributes to energy-momentum tensor. The GPF is affected by the mass, rotation, and magnetic field of the central object. In our study, the central object we focus on is a rotating NS or a magnetar. The information on the mass, angular momentum, and magnetic field are embedded in the ST, and the GPF catches this information and relays them to us. In this article, initially we study mostly NSs, stars whose surface magnetic field are of the order of $10^{12}$ G and so the magnetic effect on GPF can be neglected. However, later when we study magnetars (surface field is about $10^{15}$ G) we include magnetic effect while studying GPF.

Previously in the literature, there had been studies regarding gyroscopic precession. Lense and Thirring [1] studied frame-dragging in great detail, and therefore the frame-dragging effect is also known as LT effect. They investigated the field of a rotating (concerning the asymptotic Minkowski space) solid mass sphere. Pugh proposed a technique to use the gyroscopic stability of a spinning artificial satellite to measure the LT effect [25]. Furthermore, Schiff derived the spin precession frequency of a gyro revolving around the Earth. He showed that the spin precession frequency has three different effects, namely Thomas precession, geodetic precession, and LT precession [26]. The LT spin precession was measured with the Gravity Probe-B spacecraft [2, 27]. More insight to the experiments involving the gyroscopic effect of the satellites like Gravity Probe-B and LAGEOS was given by Ciufolini and Wheeler [28]. Several performed or proposed attempts to detect the LT effect affecting the orbital motions of natural and artificial bodies in the gravitational fields of the Sun, Earth, Mars, and Jupiter have also been reviewed [29]. The relativistic LT precession was measured with a $0.5\%$ precision by LAGEOS and LARES satellites [30,31,32]. The details on many other experimental tests of general relativity was given by Will [33]. Hartle [34] did the first calculation involving the frame-dragging effect in NS. Using perturbative approximation for slowly rotating stars, he calculated the structural changes in the star. Glendenning and Weber [35] showed that the LT effect could alter the Keplerian frequency and the moment of inertia of the star [36]. Morsink and Stella [37] studied the frame-dragging effect in and around a rotating NS, and they found that the quasi-periodic oscillation frequency is related to the oscillation frequency of the star along the $\theta$ and $\phi$ direction. Chakraborty et al. [38] calculated the frame-dragging rate inside a rotating NS and found that the frame-dragging rate differs with the azimuthal angle of the star. Chatterjee et al. [39] subsequently studied the effect of the magnetic field on the LT precession frequency. In this paper, we are not restricted to the LT precession frequency, but we calculate the overall precession of the gyro around a rotating NS or a rotating magnetar. The overall precession frequency includes effects from frame-dragging, geodetic, and other kinematic effects. If the angular velocity of the gyro is zero, we only have a frame-dragging effect. The geodetic effect is exclusively added to it when the angular velocity of the gyro is equal to that of Kepler frequency. For an arbitrary angular velocity of the gyro, we have overall frequency (which also includes kinematic effects).

In this paper, we first give the detail formalism to calculate the overall precession frequency of a test gyro for an axisymmetric ST in Sect. 2. Our results are given in Sect. 3, and finally, in Sect. 4, we summarize our findings and discuss them.

2 Formalism

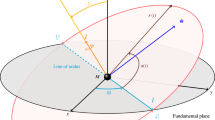
Our main objective is to obtain complete information about the geometry of ST near a central object by studying the GPF of a test gyro moving in a circular path around an NS or a magnetar with constant nonzero angular velocity. By allowing such motion of gyro around NS, we can calculate the overall precession frequency. The overall precession frequency includes frame-dragging, geodetic, and other kinematic effects. The frame-dragging precession or the LT precession provides information about the rotation rate of the NS. The geodetic effect has information about the curvature of ST. Figure 1 shows the sketch of the gyro orbiting ($\varOmega$) and precessing ($\varOmega _P$) around an NS rotating with angular velocity $\omega$. Studying the nature of $\varOmega _P$, we can deduce the information about the spacetime around the compact object. If the gyro’s orbital angular velocity is equal to that of the angular velocity of the circular geodesic at a distance from the star, it gets trapped in an orbit around an NS. Most of the astrophysical objects which revolve around another object move along a geodesic (circular or elliptical). Practically, the test gyro can only lie outside the star surface. However, theoretically, we can study the effect on test gyro even at the star’s interior [38, 39]. However, this is only to get some idea of the GR effect of ST inside a star. In this article, we have provided the variation of $\varOmega _P$ with respect to distance from the center both in the interior and exterior region of the NS.

Fig. 1

Sketch of a test gyro orbiting with orbital velocity $\varOmega$ around a rotating NS whose angular velocity is $\omega$. The precession frequency of gyro is $\varOmega _{P}$

2.1 Rotating and magnetic NS model

To model a NS (or a magnetar) in the GR framework, we start with a metric describing the ST of an NS. The formalism that will follow in this subsection is used in the xns code [40, 41]. Restricting ourselves within a stationary and axisymmetric configuration and assuming that the rotation and magnetic axis are aligned, the general line element in spherical coordinates is given by,

$$\begin{aligned} ds^2 = -\alpha ^{2}dt^2 + \psi ^{4}\left( dr^2 + r^{2}d\theta ^2 + r^{2}\sin ^{2}{\theta }\left( d\phi + \beta dt\right) ^2\right) \end{aligned}$$

(1)

where $\alpha$ is the lapse function, $\beta$ is the shift vector and $\psi$ is the spatial conformal factor. The conformal factors, $\alpha (r,\theta )$ and $\psi (r,\theta )$ are now a function of r and $\theta$.

For the equilibrium configuration, the stress-energy tensor is of the form,

$$\begin{aligned} T^{\mu \nu } = \left( e + p + b^{2}\right) u^{\mu }u^{\nu } - b^{\mu }b^{\nu } + \left( p + \frac{1}{2}b^2\right) g^{\mu \nu } \end{aligned}$$

(2)

where e is the total energy density, p is the pressure, $u^\mu$ is the four-velocity of the fluid, $b^\mu$ is the magnetic field in comoving frame and is given by,

$$\begin{aligned} b^\mu = \tilde{F}^{\mu \nu }u_\nu . \end{aligned}$$

(3)

Here, $\tilde{F}^{\mu \nu }$ is the dual of electro-magnetic tensor ${F}^{\mu \nu }$.

2.1.1 Rotational configuration

For an ideal hydrodynamic condition, the electromagnetic tensor is zero. Assuming an axisymmetric star, Eq. 1 is almost the form of axisymmetric metric with the identification of shift vector as the negative of intrinsic angular velocity about the symmetry axis ($\omega _i=-\beta$). The modulus of the four-vector is given by

$$\begin{aligned} u=\frac{\psi ^2r\sin \theta (\omega -\omega _i)}{\alpha } \end{aligned}$$

(4)

where, $\omega =\frac{d\phi }{dt}$, the angular velocity of the fluid seen by an observer at rest at infinity. With given values of $\omega$ and central density and assuming a barotropic EoS, the code starts with given initial guess values of $\alpha , \psi$, and $\omega _i$ (obtained from the spherical solution of TOV [43]) and solves them till desired converges is achieved.

2.1.2 Magnetic field configuration

Starting with the divergence-free condition for the magnetic field, which is,

$$\begin{aligned} D_iB^i=\frac{1}{\sqrt{\gamma }}\partial _i(\sqrt{\gamma }B^i)=0 , \end{aligned}$$

(5)

gives us the components of poloidal magnetic field,

$$\begin{aligned} B^r=\frac{1}{\sqrt{\gamma }}\partial _\theta A^\phi , \quad B^\theta =\frac{1}{\sqrt{\gamma }}\partial _r A^\phi , \end{aligned}$$

(6)

where,

$$\begin{aligned} \sqrt{\gamma }=\sqrt{{\text {det}}|{\gamma _{ij}}|}=\psi ^6r^2\sin {\theta } . \end{aligned}$$

(7)

The components of the magnetic field are obtained in terms of the partial derivatives of components of vector potential $A_i$, which is given by $B^i=\epsilon ^{ijk}\partial _j A_k$. $A_\phi$ are called magnetic flux functions and $A_\phi =const$ are magnetic surfaces containing poloidal field lines.

In presence of external electro-magnetic field, the Euler equation takes the form,

$$\begin{aligned} \partial _ip+(e+p)\partial _i\ln {\alpha }=L_i=\epsilon _{ijk}J^iB^k, \end{aligned}$$

(8)

where $L_i$ is the Lorentz force, $J^i$ is the conduction current which is given as,

$$\begin{aligned} J^i=\alpha ^{-1}\epsilon ^{ijk}\partial _i(\alpha B_k). \end{aligned}$$

(9)

Lorentz force can be obtained from a freely specifiable function of potential, which is here coined as the magnetisation function $\mathcal {M}(A_\phi )$, given by,

$$\begin{aligned} L_i=\sigma h \partial _i\mathcal {M}=\sigma h \frac{d\mathcal {M}}{dA_\phi }\partial _iA_\phi . \end{aligned}$$

(10)

Due to the presence of axisymmetry, the $\phi$ component of the Lorentz force disappears. So we have

$$\begin{aligned} L_\phi&=\alpha ^{-1}B^i\partial _i(\alpha B_\phi )=0 \end{aligned}$$

(11)

$$\begin{aligned} \implies B_\phi&=\alpha ^{-1}\mathcal {I}(A_\phi ), \end{aligned}$$

(12)

where $\mathcal {I}(A_\phi )$ is again a freely specifiable function, and is related to poloidal current as,

$$\begin{aligned} {} J^r&=\alpha ^{-1}B^r\frac{d\mathcal {I}}{dA_\phi } \end{aligned}$$

(13)

$$\begin{aligned} J^\theta&=\alpha ^{-1}B^\theta \frac{d\mathcal {I}}{dA_\phi }. \end{aligned}$$

(14)

Using the definition of Lorentz force the toroidal current can be expressed as,

$$\begin{aligned} J^\phi =\sigma h \frac{d\mathcal {M}}{dA_\phi }+\frac{\mathcal {I}}{\varpi ^2} \frac{d\mathcal {I}}{dA_\phi }, \end{aligned}$$

(15)

where $\varpi ^2=\alpha ^2\psi ^4r^2\sin ^2{\theta }$.

2.1.3 Choices for poloidal and twisted-torus configurations

In this case, $A_\phi \ne 0$, and hence the groundwork mentioned above works well. The freely specifiable functions $\mathcal {M}$ and $\mathcal {I}$ are chosen for these particular types of magnetic fields, which are as follows,

$$\begin{aligned} \mathcal {M}(A_\phi )=k_{pol}\left( A_\phi +\xi \frac{1}{2}A^2_\phi \right) \end{aligned}$$

(16)

where, $k_{pol}$ is the poloidal magnetization constant, $\xi$ is the non-linear poloidal term, and

$$\begin{aligned} \mathcal {I}(A_\phi )= \frac{a}{\zeta +1}\varTheta [A_\phi - A^{max}_\phi ](A_\phi - A^{max}_\phi )^{\zeta +1} \end{aligned}$$

(17)

where, $\varTheta [.]$ is the Heaviside function, $A^{max}_\phi$ is the maximum value of the $\phi$ component of the vector potential that reaches on the stellar surface, a is the twisted torus magnetization constant and $\zeta$ is the twisted torus magnetization index.

Using Eqs. (13–15), we get,

$$\begin{aligned} J^r= & {} \alpha ^{-1}B^ra\varTheta [A_\phi - A^{max}_\phi ](A_\phi - A^{max}_\phi )^\zeta \end{aligned}$$

(18)

$$\begin{aligned} J^\theta= & {} \alpha ^{-1}B^{\theta }a\varTheta [A_\phi - A^{max}_\phi ](A_\phi - A^{max}_\phi )^{\zeta } \end{aligned}$$

(19)

$$\begin{aligned} J^\phi= & {} \sigma h k_{pol}(1+\xi A_\phi )\nonumber \\&\quad +\frac{a^2}{(\zeta +1)\varpi ^2}\varTheta [A_\phi - A^{max}_\phi ](A_\phi - A^{max}_\phi )^{2\zeta +1}\nonumber \\ \end{aligned}$$

(20)

where Eqs. (18) and (19) are the poloidal components and Eq. (20) is the toroidal component. To enable purely poloidal case, one needs to set $a=0$, which will switch off the poloidal currents and only toroidal current survives, producing poloidal magnetic field.

2.1.4 Choices for purely toroidal configurations

For $A_\phi =0$ the free functions and magnetic surfaces, cannot be defined. Nonetheless, Eq. (8) is unaffected and can be used here. The scalar function $\mathcal {M}$ can still be comprehended because Eq. (10) still holds, except that $\mathcal {M}$ can’t be written in terms of $A_\phi$ anymore.

Defining a new variable,

$$\begin{aligned} G=\sigma h\varpi ^2=\sigma h \alpha ^2\psi ^4r^2\sin ^2{\theta }, \end{aligned}$$

(21)

and expressing the old variables in terms of G,

$$\begin{aligned} B_\phi&=\frac{1}{\alpha }\mathcal {I}(G) \end{aligned}$$

(22)

$$\begin{aligned} \mathcal {M}(G)&=-\int \frac{\mathcal {I}}{G} \frac{\text {d}\mathcal {I}}{\text {d}G}dG \end{aligned}$$

(23)

Assuming a barotropic-type expression for $\mathcal {I}$, which is given as,

$$\begin{aligned} \mathcal {I}(G)=K_mG^m \end{aligned}$$

(24)

where, $K_m$ is the toroidal magnetisation constant, and $m\ge 1$ is the toroidal magnetisation index, we get,

$$\begin{aligned} \mathcal {M}(G)=-\frac{mK^2_m}{2m-1}G^{2m-1} \end{aligned}$$

(25)

and the magnetic field is given by,

$$\begin{aligned} B_\phi =\alpha ^{-1}K_m(\sigma h \varpi ^2)^m \end{aligned}$$

(26)

Here also, the free function $\mathcal {I}$ is smartly chosen such that the field is confined within the star as well as it is symmetric with respect to equatorial plane. The configuration of ST and the magnetic field configuration stated above (Eqs. 1–26) are explained in much more detail in [40, 41].

Fig. 2

Pressure, as a function of energy density, plotted for four different EoS. The black solid curve describes the stiff polytropic EoS. The red short dashed curve is for the polytrope with moderate stiffness. The blue dashed curve is for soft polytope, and the green dot-dashed curve is for the Glendenning EoS. The value of $\delta$ for the polytropes is the same ($\delta =2$) only the value of k differs

2.2 EoS

The central object, the NS, is obtained by solving the XNS code. The code needs the EoS of matter to solve for a stable NS configuration. In this calculation, we have used Polytropic EoS described by the relation

$$\begin{aligned} P=k\rho ^{\delta }, \end{aligned}$$

(27)

where P is the pressure, $\rho$ is the mass density, $\delta$ is the polytropic index, and k is the proportionality constant. In this calculation, we have kept the value of $\delta =2$. For comparison, we have also used a tabulated EoS with Glendenning parameter setting [42] (modelling it with piecewise polytrope). The XNS code is challenging to solve with tabulated EoS, and therefore, we use mainly polytropes. For some EoS (like the Glendenning), it is easier to mimic them with piecewise polytrope; however, for many tabulated EoS, it leads to numerical errors. Therefore, in this work, we use single polytope to do our calculation which does not change our findings qualitatively.

Figure 2 shows the plot of four different EoS curves obtained from the Glendenning EoS and Polytropic EoS. We have plotted three curves with different values of k to have quantitatively three different EoS, one soft, one standard, and one stiff. The value of $\delta$ for the curve remains the same, but we have changed the value of k to obtain different slopes. $k=2.2\times 10^5$ gives a stiff curve, whereas $k=8.7\times 10^4$ gives a soft curve. The Glendenning EoS and $k=1.5\times 10^5$ lie in between the two. Most of our calculation is done with the polytropic EoS at $k=1.5\times 10^5$. The other polytropes with different k values are to discuss the effect EoS has in the GP.

2.3 Numerical scheme

The Einstein equations are solved by providing proper initial guess values (obtained from the TOV solution [43]). XNS uses a self-consistent method and searches for axisymmetric equilibrium solutions of the compact stars in the presence of magnetic field and rotation. The metric terms and fluid parameters are derived at the same time. For the magnetic field, some free functions are defined (Sect. 2.1), and the appropriate value of these functions are chosen to obtain the desired value of the magnetic field and configuration.

A starting guess for the metric terms $(\alpha ,\psi ,-\beta )$ is provided from the previous step. For the first step, the spherically symmetric Tolman-Oppenheimer-Volkoff

(TOV) solution in isotropic coordinates, for the metric of a static and non-magnetized NS with a central density value $\rho _c$ is computed through a shooting method for Ordinary Differential Equations. On top of these metric terms and for each grid point, the angular velocity $\omega$ is derived, then three velocities v, Lorentz factor and the conserved quantities are determined. The set of XCFC (Extended Conformally Flat Condition) equations is solved for this set of conserved variables, and a new metric is computed. Solutions are searched in terms of spherical harmonics $Y_l(\theta )$ as,

$$\begin{aligned} u\left( r,\theta \right) =\sum ^\infty _{l=0}\left( A_l(r)Y_l(\theta )\right) \end{aligned}$$

(28)

Thus the values of $\beta$, $\psi$ and $\alpha$ are found so that we can calculate values of metric coefficients. These steps are repeated until convergence to the desired tolerance is achieved.

Using the same approach, here, the variable $\tilde{A}_\phi (r,\theta )$ is searched in terms of series of vector-spherical harmonics. Proceeding similarly, the vector spherical harmonics are decomposed into the angular part and radial part. The solutions are achieved by iteration until convergence because here, the source terms are non-linear.

For purely poloidal or toroidal field configurations, solutions are searched for 20 harmonics. For twisted-torus (TT) configuration, 40 harmonics are used. This is enough to achieve satisfying results, as the conclusions are consistent with the theory.

Figure 3a shows the variation of the poloidal magnetic field inside a star. The maximum central value of the magnetic field is assumed to be $1.0 \times 10^{18}$ G, whereas, at the surface, its value decreases by four orders of magnitude. Figure 2b shows the variation of the toroidal magnetic field inside a star. The maximum value of field strength is taken $8\times 10^{17}$ G. Figure 4 shows a TT type magnetic field with a different combination of poloidal and toroidal parameters. The black solid curve has a higher toroidal component (a) while the blue dashed curve has a higher poloidal component ($k_{pol}$).

Fig. 3

The magnetic field configuration of the star is shown. Variation of the magnitude of the magnetic field with distance along the equatorial plane is shown for the poloidal (a) and toroidal (b) field. Curves are drawn for three different magnetic field strength, the black solid curve for the maximum strength and blue dashed curve for the minimal strength. The logarithmic value of the magnetic field is plotted along the y-axis as the field strength varies from $10^{14}$ G to $10^{18}$ G. The central energy density of star is taken to be $1.0\times 10^{15}$ g $cm^{-3}$

Fig. 4

Variation of the magnitude of the magnetic field with distance along the equatorial plane is shown for the TT magnetic field configuration. Nomenclature of the curve remains the same as Fig. 3

2.4 Calculation of overall frequency

Having defined our model and finding the metric coefficient with some polytropic EoS, we can proceed to calculate the overall frequency. As stated before, the overall frequency is the total effect arising from frame-dragging, geodetic effect and kinematic effects. We start with defining a stationary observer rotating around the central object with their four velocity given by [44]:

$$\begin{aligned} u^\mu = u^t(1,0,0,\varOmega ) \end{aligned}$$

(29)

where $\varOmega$ is the angular velocity of the observer. The test gyro is attached to the stationary observer which moves along a Killing trajectory in a stationary ST. The spin of the gyro does Fermi-Walker transport [45] along

$$\begin{aligned} u = (-K^2)^{-\frac{1}{2}}K \end{aligned}$$

(30)

where K is the timelike killing vector field. In this case the GPF coincides with the vorticity field associated with the killing congruence. The gyro rotates with an angular velocity with respect to the co-rotating spatial frame which is Fermi-Walker transported and this angular velocity is termed as “gravitomagnetic precession”, because the vorticity vector takes the role of magnetic field (and thus the analogy with electromagnetism) in the 3+1 splitting of the ST [46]. Therefore the general spin precession frequency of a test gyro is the rescaled vorticity field of the observer congruence and can be expressed in the form [45]:

$$\begin{aligned} \tilde{\varOmega }_P = \frac{1}{2K^2}*(\tilde{K} \wedge d\tilde{K})\ \end{aligned}$$

(31)

where $\varOmega _P$ is the spin precession frequency in coordinate basis, $*$ represents the Hodge star operator or Hodge dual, $\wedge$ is the wedge product, $\tilde{K}$, $\tilde{\varOmega }_P$ are the one-forms of K and $\varOmega _P$ respectively.

With the choice of axisymmetric metric, the metric ST is independent of t and $\phi$. Therefore, it has two Killing vector, time translation killing vector $\partial _t$, and azimuthal Killing vector $\partial _\phi$. In any stationary ST, there exists a timelike killing vector. For a general stationary ST which also possesses a space-like Killing vector, we can write the general timelike Killing vector as a linear combination of the timelike killing vector $\partial _t$ and spacelike killing vector $\partial _\phi$ as follows:

$$\begin{aligned} K=\partial _t+\varOmega \partial _\phi , \end{aligned}$$

(32)

where $\varOmega$ represents the angular velocity for an observer moving along integral curves of K. The timelike killing vector approaches a timelike unit vector at spatial infinity, giving the coefficient of $\partial _t$ to be 1.

In a stationary and axisymmetric ST with coordinates $t, r, \theta , \phi$, expression (31) becomes [44]:

$$\begin{aligned} {\varvec{\Omega }}_P= & {} \frac{1}{2\sqrt{-g}\left( 1+2\varOmega \frac{g_{t\phi }}{g_{tt}}+\varOmega ^2\frac{g_{\phi \phi }}{g_{tt}}\right) }. \nonumber \\&\quad \left[ -\sqrt{g_{rr}}\left[ \left( g_{t\phi ,\theta } -\frac{g_{t\phi }}{g_{tt}} g_{tt,\theta }\right) +\varOmega \left( g_{\phi \phi ,\theta } -\frac{g_{\phi \phi }}{g_{tt}} g_{tt,\theta }\right) \right. \right. \nonumber \\&\quad \left. \left. + \varOmega ^2 \left( \frac{g_{t\phi }}{g_{tt}}g_{\phi \phi ,\theta } -\frac{g_{\phi \phi }}{g_{tt}} g_{t\phi ,\theta }\right) \right] \hat{r} \right. \nonumber \\&\quad \left. +\sqrt{g_{\theta \theta }}\left[ \left( g_{t\phi ,r} -\frac{g_{t\phi }}{g_{tt}} g_{tt,r}\right) +\varOmega \left( g_{\phi \phi ,r} -\frac{g_{\phi \phi }}{g_{tt}} g_{tt,r}\right) \right. \right. \nonumber \\&\quad \left. \left. + \varOmega ^2 \left( \frac{g_{t\phi }}{g_{tt}}g_{\phi \phi ,r} -\frac{g_{\phi \phi }}{g_{tt}} g_{t\phi ,r}\right) \right] \hat{\theta } \right] . \end{aligned}$$

(33)

Once we find the metric coefficients of the given astrophysical ST, we use the above formula to find the overall precession frequency of the test gyro.

For $\varOmega =0$, the above equation reduces to LT precession frequency of the test gyro due to the rotation in any stationary and axisymmetric ST [38, 45].

$$\begin{aligned} {\varvec{{\Omega }}}_P|_{\varOmega =0}= & {} \frac{1}{2\sqrt{-g}}\left[ -\sqrt{g_{rr}}\left( g_{t\phi ,\theta } -\frac{g_{t\phi }}{g_{tt}} g_{tt,\theta }\right) \hat{r}\right. \nonumber \\&\quad \left. +\sqrt{g_{\theta \theta }}\left( g_{t\phi ,r}-\frac{g_{t\phi }}{g_{tt}} g_{tt,r}\right) \hat{\theta }\right] . \end{aligned}$$

(34)

Using the metric coefficients, the GPF is calculated for any spherically symmetric objects (non-rotating NS) or axisymmetric objects (rotating or magnetized NS).

2.4.1 GP in a symmetric ST

The spherically symmetric metric is a good starting point for describing a non-rotating non-magnetic star using the XNS code.

If the NS is spherically symmetric, then the shift vector $\beta$ = 0. So $\varOmega _{P}$ takes the form:

$$\begin{aligned} {\varvec{{\Omega }}}_P = \frac{\varOmega \left( \alpha \frac{d \psi }{d \theta } -\psi \frac{d \alpha }{d \theta }\right) }{\alpha ^2 \psi - r^2 \psi ^3 \varOmega ^2} \hat{r} + \frac{\varOmega \left( \alpha \left( r \frac{d \psi }{d r}+\psi \right) -r \psi \frac{d \alpha }{d r}\right) }{\alpha ^2 \psi - r^2 \psi ^3 \varOmega ^2} \hat{\theta } . \end{aligned}$$

(35)

The magnitude of $\varOmega _P$ is:

$$\begin{aligned} \frac{\varOmega \sqrt{\left( \left( \psi \frac{d \alpha }{d \theta }-\alpha \frac{d \psi }{d \theta }\right) ^2+\left( r \psi \frac{d \alpha }{d r}-\alpha \left( r \frac{d \psi }{d r} + \psi \right) \right) ^2\right) }}{\left( \alpha ^2 \psi - r^2 \psi ^3 \varOmega ^2\right) } \end{aligned}$$

(36)

Fig. 5

Variation of $\varOmega _{P}$ with distance from centre along the equatorial plane orbiting around spherically symmetric star with central energy density of $1.0\times 10^{15}$ g cm$^{-3}$. Curve for three value of $\varOmega$ are shown in the figure, starting from lower (black solid curve) to as high as 500 rad s$^{-1}$ (blue dashed curve). The frequency in Hz can be calculated as: $f=\frac{Z}{2 \pi }$, where Z cab be $\varOmega$, $\varOmega _{P}$ or $\omega$ in rad s$^{-1}$

Figure 5 shows the GPF obtained by solving the XNS code for a non-rotating NS. The variation of $\varOmega _P$ with distance along the equatorial plane is shown. Here a polytropic EoS with $K = 1.5\times 10^5$ is used to build a static NS. The curves show that the precession frequency is maximum at the center, decreases to a local minimum near the surface of the star, and later increases and saturates to the value of the orbital angular velocity of the gyro at a significant distance. Increasing the orbital angular velocity of the gyro increases $\varOmega _P$ at the center, and also, the curve shift to higher frequencies.

2.4.2 GP in a axisymmetric ST

For a axisymmetric metric, we calculate $\varOmega _P$ by inserting the values of the metric coefficient in Eq. 33. In the equatorial plane $\varOmega _P$ takes the simple form given by

$$\begin{aligned} {\varvec{{\Omega }}}_P=\omega _r \hat{r}+\omega _{\theta } \hat{\theta } \end{aligned}$$

(37)

where

$$\begin{aligned} \omega _r= & {} \frac{\psi A -2 \alpha ^2 (\beta +\varOmega ) \frac{\partial \psi }{\partial \theta }}{2 \alpha ^3 \psi -2 \alpha r^2 \psi ^3 (\beta +\varOmega )^2}\nonumber \\ \omega _{\theta }= & {} \frac{\psi B+2 \alpha ^2 r (\beta +\varOmega ) \frac{\partial \psi }{\partial r}}{2 \alpha ^3 \psi -2 \alpha r^2 \psi ^3 (\beta +\varOmega )^2} \end{aligned}$$

(38)

and

$A = \left( 2 \alpha (\beta +\varOmega )\frac{\partial \alpha }{\partial \theta }-\frac{\partial \beta }{\partial \theta } \left( \alpha ^2+r^2 \psi ^2 (\beta +\varOmega )^2\right) \right)$

$B=\left( r \frac{\partial \beta }{\partial r} \left( \alpha ^2+r^2 \psi ^2 (\beta +\varOmega )^2\right) +2 \alpha (\beta +\varOmega ) \left( \alpha -r \frac{\partial \alpha }{\partial r}\right) \right)$

The magnitude of the precession vector is given by

$$\begin{aligned}&|{{\varvec{{\Omega }}}_P}|= \sqrt{\frac{C^2+\left( \psi D+2 \alpha ^2 r (\beta +\varOmega ) \frac{\partial \psi }{\partial r}\right) ^2}{\left( 2 \alpha ^3 \psi -2 \alpha r^2 \psi ^3 (\beta +\varOmega )^2\right) ^2}},\nonumber \\ C= & {} \left( \psi \left( 2 \alpha (\beta +\varOmega ) \frac{\partial \alpha }{\partial \theta }-\frac{\partial \beta }{\partial \theta } \left( \alpha ^2+r^2 \psi ^2 (\beta +\varOmega )^2\right) \right) \right. \nonumber \\&\quad \left. -2 \alpha ^2 (\beta +\varOmega ) \frac{\partial \psi }{\partial \theta }\right) . \end{aligned}$$

(39)

$D=\left( r \frac{\partial \beta }{\partial r} \left( \alpha ^2+r^2 \psi ^2 (\beta +\varOmega )^2\right) +2 \alpha (\beta +\varOmega ) \left( \alpha -r \frac{\partial \alpha }{\partial r}\right) \right)$

In Sect. 4, we discuss the nature of GPF for rotating and magnetized stars in great detail. Analytically, we can find the value of $\varOmega$ for which the central value of $\varOmega _P$ is minimized.

$$\begin{aligned} {\frac{\partial \varOmega _P}{\partial \varOmega }}{|}_{r = 0}^{\theta =\frac{\pi }{2}} = 0 \end{aligned}$$

(40)

The analytical equation is given by

$$\begin{aligned}&2\left( 2 \alpha \psi \frac{\partial \alpha }{\partial \theta }-2 \alpha ^2 \frac{\partial \psi }{\partial \theta }\right) \left( \psi \left( 2 \alpha \frac{\partial \alpha }{\partial \theta } (\beta +\varOmega )-\alpha ^2 \frac{\partial \beta }{\partial \theta }\right) \right. \nonumber \\&\quad -\left. 2 \alpha ^2 \frac{\partial \psi }{\partial \theta } (\beta +\varOmega )\right) +8 \alpha ^4 \psi ^2 (\beta +\varOmega ) = 0 \end{aligned}$$

(41)

and the solution for $\varOmega$ comes out to be

$$\begin{aligned} {{\varOmega }_*} = \frac{E-\alpha ^2 \psi \frac{\partial \beta }{\partial \theta } \frac{\partial \psi }{\partial \theta }-2 \alpha ^2 \beta (\frac{\partial \psi }{\partial \theta })^2-2 \alpha ^2 \beta \psi ^2}{2 \left( -2 \alpha \psi \frac{\partial \alpha }{\partial \theta } \frac{\partial \psi }{\partial \theta }+\psi ^2 (\frac{\partial \alpha }{\partial \theta })^2+\alpha ^2 (\frac{\partial \psi }{\partial \theta })^2+\alpha ^2 \psi ^2\right) } \end{aligned}$$

(42)

where $E = \alpha \psi ^2 \frac{\partial \alpha }{\partial \theta } \frac{\partial \beta }{\partial \theta } + 4 \alpha \beta \psi \frac{\partial \alpha }{\partial \theta } \frac{\partial \psi }{\partial \theta }-2\beta \psi ^2 (\frac{\partial \alpha }{\partial \theta })^2$

Numerically, the value of $\varOmega _*\sim \beta _c$ where $\beta _c$ is the value of $\beta$ at the center of the NS. This is because of the minimization of frame-dragging at the center. But $\varOmega _*$ is not exactly equal to $\beta _c$ as other effects like geodetic effects are non-zero even if they are small relative to dragging effect at the center of the star (effect of drag on $\varOmega _P$ is higher if the magnitude of $[\varOmega -\beta _c]$ is higher).

3 Results

In this section, we calculate the precession frequency of the test gyro around a rotating or a magnetized NS. However, before doing that, we want to calculate the acceleration of the test gyro around the central object. Also, the orbital angular velocity of the gyro cannot be arbitrary. The time-like boundary condition limits it. Brief nomenclature: $M_\circ$ is solar mass, M is the mass of that particular central object around which gyro is orbiting.

3.1 Acceleration of the test gyroscope

In the first case, we consider gyroscopes with constant orbital angular velocity along all the distances from the central object. Here the gyro will experience a non-zero acceleration as they are not along the geodesics. This is because of the spin-gravity coupling [47]. The gyro follows a helical path tangent to the killing trajectory and, therefore, is accelerated. The reason for the four acceleration can be understood by looking into the GR analog of inertial forces present. In static spacetime where $\omega =0$, the objects following circular path experience only gravitational and centrifugal forces [48, 49]. In stationary cases ($\omega \ne 0$), Coriolis force also comes into play [50], because of the inherent rotation of spacetime.

We calculate the components of acceleration using the expression [51] (Fig. 6),

$$\begin{aligned} \alpha _{\mu }=\frac{1}{2}\nabla _{\mu }\mathrm{ln}~|K^2|. \end{aligned}$$

(43)

The magnitude of the acceleration (acceleration scalar) is :

$$\begin{aligned} \alpha =\sqrt{\alpha ^{\mu }\alpha _{\mu }}. \end{aligned}$$

(44)

Fig. 6

a Magnitude of acceleration with distance from centre along the equitorial plane around NSs with varying central density. The blue dashed line is for central density of $1.2\times 10^{15}$ g cm$^{-3}$, the red short dashed line is for $1.0\times 10^{15}$ g cm$^{-3}$ and the black solid line is for $7.8\times 10^{14}$ g cm$^{-3}$. Here the value of $\varOmega$ is taken to be 2000 rad s$^{-1}$. The NS’s angular velocity is 3000 rad s$^{-1}$. The plotting format (bold, thick lines for star exterior and thin lines for the star interior) is done to show the distinction between the interior and exterior regions clearly. b Variation of acceleration with respect to distance at the exterior region of NS. The texture and color of plots follow same nomenclature as a

3.2 Circular geodesics

In the second case we consider gyroscopes revolving along circular geodesics. The angular velocity (denoted as $\varOmega =\varOmega _g$) of a particle moving on a circular equatorial geodesic is obtained from geodesic equation:

$$\begin{aligned} \partial _{r}g_{tt} (\frac{dt}{d\tau })^2 + 2 \partial _{r}g_{t\phi } \frac{dt}{d\tau } \frac{d\phi }{d\tau } + \partial _{r}g_{\varphi \phi }(\frac{d\phi }{d\tau })^2=0 . \end{aligned}$$

(45)

Solving for angular velocity, we get:

$$\begin{aligned} \varOmega _g = \frac{d\phi }{dt} = \frac{-\partial _{r} g_{t\phi } \pm \sqrt{(\partial _{r}g_{t\phi })^2 - \partial _{r}g_{tt}\partial _{r}g_{\phi \phi }}}{\partial _{r}g_{rr}}. \end{aligned}$$

(46)

In this study we have mostly considered gyros with non-zero acceleration whereas the geodesic cases are examined for some important scenarios.

3.3 Range of $\varOmega$

Determining the values of the metric coefficients, we proceed further to study the properties of ST and behavior of test gyro. For four-velocity u to be time-like, $K^2$ must be negative and is given by [44, 45]:

$$\begin{aligned} K^2 = g_{\phi \phi }\varOmega ^2+2g_{t\phi }\varOmega +g_{tt} < 0, \end{aligned}$$

(47)

Solving the above equation one obtains the allowed range of $\varOmega$ at any fixed $(r,\theta )$,

$$\begin{aligned} \varOmega _-(r,\theta )< \varOmega (r,\theta ) < \varOmega _+(r,\theta ). \end{aligned}$$

(48)

Figure 7 gives a range of $\varOmega$, which satisfies the time-like limit. The range of $\varOmega$ gets narrower as we move away from the center of the star. The range gets more restricted with the increase in the mass of the NS. The value of $\varOmega$, which we choose for our calculation lies within this range. Figure 8 shows how the magnetic field affects the timelike limit of $\varOmega$ around the NS. The magnetic field narrows the limit by a small amount.

Fig. 7

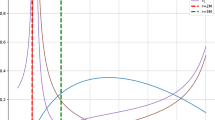
Plots of the limiting values of the orbital velocity of the gyro with distance from the center of the NS. The black solid curve for prograde motion and red short dashed curve for retrograde motion are for central energy density $5.1\times 10^{14} g cm^{-3}$ and the blue dashed curve for prograde motion and green dot dashed curve for prograde motion for central energy density of $1.2\times 10^{15}$ g cm$^{-3}$. The NS’s rotation rate ($\omega$) is taken to be 700 rad s$^{-1}$. a Shows the range close to the centre of the star and b shows the range further outwards

Fig. 8

Plots of the limiting values of $\varOmega$ with distance from the center of a magnetized NS. The black solid curve and red short dashed curve are respectively for prograde and retrograde motion for non-magnetic case. The blue dashed curve and green dot dashed curve are repectively for prograde and retrograde motion around a magnetar with poloidal magnetic field with central magnetic field of $1.0\times 10^{18} G$. $\omega$ is zero for this case as we have considered a static star here. a Curves are from center to 2 km. b Curves are from 2 to 16 km

Fig. 9

Plots of the limiting values of the angular velocity of the gyro with distance from the center of a 8 $M_\circ$ Kerr BH ($a = 0.7$ M). The black solid curve is for prograde motion, and the red short dashed curve is for retrograde motion. The event horizon of the BH is around 20.3 km

As discussed earlier that for BH, the orbit of the gyro motion is restricted only outside the event horizon, which is also depicted in Fig. 9. This is because the inertial frame itself is dragged close to the timelike limit near the horizon. Therefore near the event horizon the curve has a boundary. However, in the allowed region the range of $\varOmega$ is maximum near the event horizon and becomes narrow as we move further away from the horizon of the BH.

Our main aim is to study the GPF, and from it, we analyze the properties of the central object. First, we analyze if the GPF can distinguish central objects (whether an NS or a BH). Further, we analyze the nature of GPF for a rotating NS having different mass, frequency, and EoS. Next, we analyze the GPF for a magnetar having different field strength and magnetic configuration. Finally, we analyze the GPF for a rotating magnetar. The results and the figures are plotted mostly along the equatorial plane unless and otherwise stated. The results are shown for polytrope with $K=1.5\times 10^5$ unless stated otherwise.

3.4 BH or NS

In this section, we study the GPF and obtain the difference the gyro frequency would suffer depending on the central object. The Kerr metric is used for describing a spinning BH of mass M and angular momentum J, and in Boyer-Lindquist coordinates it is written as

$$\begin{aligned} ds^2&=-\left( 1-\frac{2Mr}{\rho ^2}\right) dt^2 - \frac{4Mar\sin ^2\theta }{\rho ^2}d\phi dt + \frac{\rho ^2}{\varDelta }dr^2\nonumber \\&\quad + \rho ^2 d\theta ^2 + \left( r^2+a^2+\frac{2Mra^2 \sin ^2\theta }{\rho ^2}\right) \sin ^2\theta d\phi ^2, \end{aligned}$$

(49)

where a is the Kerr parameter, defined as $a=\frac{J}{M}$, the angular momentum per unit mass and $\rho$ and $\varDelta$ as

$$\begin{aligned} \rho ^2=r^2+a^2 \cos ^2\theta , \varDelta =r^2-2Mr+a^2. \end{aligned}$$

(50)

Fig. 10

a Variation of the GPF along the equatorial plane around a 8 $M_\circ$ ($M_\circ$ being the solar mass and M being the mass of the BH in this case) Kerr BH ($a = 0.7 M$) with $\varOmega = 2000$ rad s$^{-1}$, 3000 rad s$^{-1}$, $\varOmega _{BH}$ and 3700 rad s$^{-1}$ is indicated by black-solid curve, red-short dashed curve, blue dashed curve and green-long dashed curve respectively. b PF along the equatorial plane around a $1.5 M_\circ$ NS ($\omega = 700$ rad s$^{-1}$) of radius $\sim 11$ km with $\varOmega = 100$ rad s$^{-1}$. The black solid curve and the red short dashed curve are for interior and exterior regions of the star respectively

We calculate the magnitude of the overall GPF by substituting the metric coefficients in Eq. 33, and it comes out to be

$$\begin{aligned} |{\varvec{{\Omega }}}_P| = {\frac{a M \varOmega ^2 \left( a^2+3 r^2\right) +\varOmega G + a M}{r^2 [r \left( \varOmega ^2 \left( a^2+r^2\right) -1\right) +2 M (a \varOmega -1)^2]}} \end{aligned}$$

(51)

where $G = [r^2 (r-3 M)-2 a^2 M]$

In Fig. 10a, we plot the curves for the central object being a Kerr BH, and in Fig. 10b, the curve is plotted with the central object being a rotating NS. In case of BHs starting with smaller values of $\varOmega$, the GPF gradually increases as we approach the BH, and it diverges before the event horizon is reached. As we increase the value of $\varOmega$, the divergence happens more and more close to the event horizon. This continues till the gyro orbital velocity becomes equal to that of BH rotational velocity.

The angular velocity of Kerr Black hole is given by:

$$\begin{aligned} \varOmega _{BH} = \frac{a}{2 M r_h}, \quad r_h = M + \sqrt{M^2 - a^2}. \end{aligned}$$

(52)

So, when $\varOmega = \varOmega _{BH}$, we get null point when

$$\begin{aligned}&a^4+a^2 \left( 3 r^2-4 M \left( \sqrt{M^2-a^2}+2 M\right) \right) \nonumber \\&\quad +2 \left( \sqrt{M^2-a^2}+M\right) (r-2 M)^2 (M+r) = 0 \end{aligned}$$

(53)

For a given BH (fixed mass) and for a chosen a, we solve for the value of r when the GPF becomes zero. We find that for $a=0.7 M$ (for a 8 solar mass BH), the null point tends to coincide with the event horizon. With our choice of M and a this happens at $\varOmega = \varOmega _{BH}=3520$ rad s$^{-1}$ . Further increasing $\varOmega$ the null point shifts away from the event horizon but the curve again diverges near the horizon.

In the case of NS, $\varOmega _P$ is finite for all the values $\varOmega$ within the timelike limit as we approach the NS. The qualitative behavior of $\varOmega _P$ (increasing or decreasing as we approach the surface of NS) depends on the value of $\varOmega$ and is discussed in the subsequent section. However, the GPF does not diverge at all as we approach an NS, whereas for BH, either it diverges or becomes zero as we approach the event horizon. Thus seeing the behavior of spinning test gyro approaching a compact object, the central object can be identified whether it is a rotating BH or a rotating NS.

3.5 Rotating NS

Once the difference between the NS and BH has been established, we proceed to analyze the ST near a rotating NS. The mass and the angular momentum of the NS will deform and drag the ST which would reveal itself in the overall precession of the gyro.

3.5.1 Dependence of GPF on the orbital angular velocity of gyro

In this article, we calculate the overall frequency of the gyro. The overall frequency of the gyro depends on the value of the orbital velocity of the gyro.

To analyze the overall frequency we look back at Eq. 33. Let us assume

$$\begin{aligned} \xi = \frac{1}{2\sqrt{-g}\left( 1+2\varOmega \frac{g_{t\phi }}{g_{tt}} +\varOmega ^2\frac{g_{\phi \phi }}{g_{tt}}\right) }\sqrt{g_{\theta \theta }}. \end{aligned}$$

(54)

Near the center, the change in frame-dragging is negative. This is clear when we look into the terms in Eq. (33). The two dominating terms competing with each other are $\xi \frac{dg_{t\phi }}{dr}$ (negative sign) and $\xi \varOmega \frac{dg_{\phi \phi }}{dr}$ (positive sign). They compete with each other to determine the overall precession rate of the gyro. Initially, the first term dominates, and we have an overall negative value. However, with an increase in radial distance, the positive term starts to increase. This makes the overall negative value to decrease and thus decreasing the magnitude (we are plotting the magnitude of GPF) as shown in Fig. 11. At some distance from the center, the two terms cancel out each other, giving a null point. Starting with LT precession, the null point is obtained at a distance of around 6.7 km from the star center. As $\varOmega$ becomes non-zero (GPF is now the overall frequency) and increases, the GPF at the center of the star diminishes, and the null point shifts close to the center. For a particular value of $\varOmega$, say $\varOmega =\varOmega _{*}$ the central value of $\varOmega _P$ is minimized (shown in Sect. 2.4.2). In our calculation, for a NS with $\omega = 700$ rad s$^{-1}$, the value of $\varOmega _{*} = 325$ rad s$^{-1}$. For $\varOmega$ > $\varOmega _{*}$, the null point does not exist. $\varOmega _P$ starts with a finite value and increases after that.

In Fig. 11, the angular velocity of the gyroscope is positive with respect to the angular velocity of the star (prograde motion). Therefore, the initial value of the overall precession frequency of the gyroscope decreases with increasing $\varOmega$ as both dominating terms have opposite sign. If the sense of revolution of the gyro is opposite to that of the angular velocity of the star (retrograde motion), the precession rate becomes more negative. This is because both the terms mentioned above have the same sign. Therefore the initial values of the overall precession frequency of the gyroscope increase with increasing the magnitude of $\varOmega$. This is the reason why the value of $\varOmega _P$ can become more significant than $\omega$ and $\varOmega$. In Fig. 12, we plot the GPF for retrograde motion of the gyro. In this case, as we move outwards towards the surface of the NS, the net value of two terms changes sign twice, which results in the occurrence of two null points for a given range of $\varOmega$. This is a unique case for NS with gyro having retrograde motion where two null points appear. Eventually, the GPF value settles to a negative value as we move outside the star. When the value of retrograde $\varOmega$ is sufficiently large, the net value of both terms doesn’t change sign at all, and we do not have any null point.

Fig. 11

LT precession frequency and overall precession rate along the equatorial plane around a $1.5 M_0$ NS ($\omega = 700$ rad s$^{-1}$) of radius 11 km with varying the orbital angular velocity of the gyro. The black solid curve denotes the LT precession rate (magnitude of $\varOmega _P$ with $\varOmega =0$), the red short dashed curve, blue dashed curve and the green dot dashed curve denote overall precession rate for $\varOmega = 100$ rad s$^{-1}$, $\varOmega _{*}$ and 500 rad s$^{-1}$ respectively

Fig. 12

Overall precession frequency along the equator for a $1.5 M_0$ NS ($\omega = 700$ rad s$^{-1}$) with a sense of orbital angular velocity of the gyro opposite to that of star’s rotation. The black solid curve is for $\varOmega =50$ rad s$^{-1}$, the red short dashed curve is for $\varOmega =100$ rad s$^{-1}$, and the blue dashed curve is for $\varOmega =200$ rad s$^{-1}$

As mentioned earlier, a spinning planet revolving around a pulsar can be considered as a spinning gyro orbiting around that pulsar. Considering the example of planet Draugr orbiting around PSR B1257+12 (spinning at the rate of $\sim$ 1010 rad s$^{-1}$) at a distance of 0.19 AU (Astronomical unit), with orbital frequency ($\varOmega$) $\sim 2.88\times 10^{-6}$ $rads^{-1}$. Neglecting the orbit inclination (which is small) and using Eq. 33 we obtain the value of $\varOmega _P$ to be $\sim$ $2.89\times 10^{-6}$ $rads^{-1}$. At this distance from the star, the term involving frame-dragging ($\xi \frac{dg_{t\phi }}{dr}$) and the gravitational effect due to the magnetic field becomes negligible, and the geodetic effect dictates the $\varOmega _P$. An advanced astrophysical observation in the future should be able to detect the value of the overall precession frequency of the planets revolving around a compact object.

Fig. 13

$\varOmega _P$ of gyro along different azimuthal planes around a $1.5 M_\circ$ NS ($\omega =700$ rad s$^{-1}$) with positive orbital angular velocity $\varOmega =100$ rad s$^{-1}$. The black solid curve, red short dashed curve and blue dashed curve are for $\theta = 90^{\circ },45^{\circ },0^{\circ }$ respectively

3.5.2 Dependence on azimuthal position

The GPF also varies as we change the azimuthal position; that is, the precession frequency of the gyro depends on the position of the orbit. However, the plane remains the same, and only the orbit shifts to lower azimuth. In Fig. 13, the azimuthal dependence of the GPF is plotted. As expected for a prograde motion along the equator, there is one null point (consistent with Fig. 11). As we move to a smaller azimuthal angle first, the null point disappears, and then the minima is lost at around $\theta =40^{\circ }$, where we reach a saddle point. Moving to much smaller azimuthal angles, the minima again reappears, and finally, a null point in the GPF is generated for the pole. The position of the polar null point of the GP occurs at the larger radial distance than that of the equatorial null point.

Fig. 14

Effect of the angular velocity of the star on $\varOmega _P$ around a $1.5 M_\circ$ NS with central energy density $1.0\times 10^{15}$ g cm$^{-3}$. The solid black line, red short dashed line, and blue dashed line are for $\omega = 215$ rad s$^{-1}$, 300 rad s$^{-1}$, 500 rad s$^{-1}$ respectively. Here $\varOmega$ is taken to be 100 rad s$^{-1}$

3.5.3 Dependence on the angular velocity of the NS

Keeping the angular velocity of the gyro to be $\varOmega =100$ rad s$^{-1}$, we find that the GP goes close to zero at the center of the star rotating at 215 rad s$^{-1}$, thus $\varOmega _{*} = 100$ rad s$^{-1}$ for $\omega = 215$ rad s$^{-1}$. Whenever $\omega$ is about twice the orbital angular velocity of the gyro, the GPF at the center of the star becomes a minimum (close to zero). As we move outwards, $\varOmega _P$ starts to grow and asymptotically attains the value of $\varOmega$. Increasing the angular velocity of the star increases the drag in and around the central object. This frame-dragging rate increases the overall precession rate proportionally, as shown in Fig. 14. Also, the null point appears for higher $\omega$, and it shifts outward with an increase in $\omega$.

Fig. 15

Effect of the angular velocity of the star on $\varOmega _P$ of a gyro moving in a stable circular geodesic around a $1.5 M_\circ$ NS. The central energy density is taken to be $7.4\times 10^{14}$ g cm$^{-3}$. The solid black line, red short dashed line, and blue dashed line are for $\omega = 4000$ rad s$^{-1}$, 2000 rad s$^{-1}$, 0 rad s$^{-1}$ respectively. The thicker line indicates exterior region. Here $\varOmega$ is equal to $\varOmega _g$

When the gyro is allowed to move along circular geodesic, the variation of gyro-precession frequency with respect to the distance from star’s surface is monotonic and decreasing. Figure 15 shows the effect of NS’s rotation on the GPF of gyro moving in a circular geodesic orbit around the star. We can see that as increase in rotation increases the drag in spacetime around the NS, this also increases the value of $\varOmega _P$ along the geodesic orbit at all distances outside the star. In such cases of geodesic motion of gyro around compact objects like NS, the values of $\varOmega _g$ is very high and completely dictates the values of $\varOmega _P$ in the exterior region of the star.

3.5.4 Dependence on Mass and EoS

Fig. 16

a $\varOmega _P$ of the gyro orbiting with $\varOmega =100$ rad s$^{-1}$ around NS ($\omega = 700$ rad s$^{-1}$) of different mass is shown in the figure. The black solid line shows variation of $\varOmega _P$ for a $1.6 M_\circ$ star, the red short dashed and blue dashed line are for $1.4 M_\circ$ and $1.25 M_\circ$ respectively. b $\varOmega _P$ of the gyro in the exterior region of the star. The nomenclature of curves are same as that of a

Fig. 17

$\varOmega _P$ of the gyro orbiting along circular geodesic around NS ($\omega = 700$ rad s$^{-1}$) of different mass. The black solid line shows variation of $\varOmega _P$ for a $1.6 M_\circ$ star, the red short dashed and blue dashed line are for $1.4 M_\circ$ and $1.25 M_\circ$ respectively. The thicker part of each curve denotes exterior region

The GPF shows different natures for the different central object. Therefore, it is reasonable to think that the mass of the NS would have some effect on the GPF. The three different curves in Fig. 16a, shows the nature of GPF for three different masses having $\omega =700$ rad s$^{-1}$ and $\varOmega =100$ rad s$^{-1}$. For an NS having higher mass, the precession frequency of the gyro revolving around it is higher. Keeping all rotation effects constant, increasing the mass increases the change in temporal and radial metric coefficients. This increases the value of initial precession frequency and the maxima. In Fig. 16b, we have plotted GPF beyond the surface of the NS. The nature of the precession frequency remains the same; however, there is some difference in the overall value. Therefore, if the GPF near an NS can be measured accurately, then one can get some idea about the mass of an NS around which it is precessing.

Figure 17 shows how the mass of an NS affects the variation of GPF orbiting along circular geodesic. The case here is different from that of the accelerating case of Fig. 16. In Fig. 16b, the value of $\varOmega _P$ in the exterior region (but not too far from the surface) for the most massive NS is least, while in the case of circular geodesic (Fig. 17) the GPF around the most massive star is the highest. The orbital velocities of the gyro $\varOmega _g$ has to be higher around a more massive star for a stable circular orbit to exist at a certain distance from the star. This increases the value of $\varOmega _{P}$.

Fig. 18

$\varOmega _P$ of the gyro around NSs ($\omega = 700$ rad s$^{-1}$) of four different EoS is shown. The gyro’s orbital frequency is taken as $\varOmega = 100$ rad s$^{-1}$. The black solid line is for a stiff polytropic star. The red short dashed curve is for a standard polytropic star. The blue dashed line is for a softer polytropic EoS and the green dot dashed curve is for Glendenning EoS

The maximum mass and the compactness of an NS depends on the EoS describing the star. Stiff EoS gives rise to more compact and massive stars, whereas soft EoS offers less massive stars. If the EoS of the star is stiff, it rapidly changes the values of metric coefficients, which leads to the shift in the gyroscopic precession frequencies. Figure 18 shows that the stiffer the EoS, the more the value of GPF at the center of the star. However, the behavior of the curves beyond the star radius is more or less identical. Therefore, it is challenging to differentiate stars of the same mass having different EoS using a gyro.

3.6 Static magnetar

The effects discussed till now are due to the distortion in ST caused by the mass and angular velocity of the star. Till now, we have studied NSs (stars whose surface magnetic field is about $10^{12}$ G), and so the magnetic field effect on the GPF is negligible. However, for NSs whose surface magnetic field strength is around $10^{15}$ G (the magnetars), the magnetic field effect cannot be neglected. In this section, we study the GPF around magnetars.

Fig. 19

We have plotted the effect of a poloidal magnetic field on $\varOmega _P$ along the equatorial plane (a) and polar plane (b). The black solid curve, the red short dashed curve and the blue dashed curve are for central magnetic field of $1.0\times 10^{18} G, 3.5\times 10^{17} G, 7.5\times 10^{16} G$ respectively. $\varOmega$ is taken to be 100 rad s$^{-1}$. The central energy density of the NS is taken to be $1.0\times 10^{15}$ g cm$^{-3}$

For a non-rotating magnetar, the GPF has no local maxima inside the star, unlike most of the previous cases with frame-dragging effect. The initial value of the precession frequency is higher for the higher values of the central magnetic field for the poloidal field, as can be seen from Fig. 19a. There is a local minima near the surface of the star and higher the magnetic field the more shallower the minima gets. Outside the star, the difference in the GPF for different field strength is minimal, and therefore it is difficult to test the magnetic field strength of a star using a gyro.

In Fig. 19b, we have plotted the GPF along the polar plane. Along the equatorial direction, the curves are stiffer than along the polar plane as the variation of the poloidal field along the equator is much stiffer. Along the equatorial plane, the curves have a local minimum, whereas, for the polar plane, the curves decrease monotonically. The change in metric coefficients is most considerable along the equator thus explaining the plots in Fig. 19a. The effect of the magnetic field becomes significant only after the central value of the field is a few times $10^{17}$ G. The result for $\varOmega =0$ is similar to that obtained earlier [39], and is not discussed here where the frame-dragging frequency has a null point along the equator.

Fig. 20

We have plotted the effect of poloidal magnetic field on $\varOmega _P$ along the equatorial plane. Here we have $\varOmega = \varOmega _g$. The black solid curve, the red short dashed curve and the blue dashed curve are for central magnetic field of $8.0\times 10^{17} G, 5.0\times 10^{17} G, 4.5\times 10^{16} G$ respectively. The central energy density of the NS is taken to be $1.0\times 10^{15}$ g cm$^{-3}$

Figure 20 shows the poloidal case where the gyro is revoloving along circular geodesic. Unlike the previous case shown in Fig. 19, the higher magnetic field case will have greater value of GPF because the $\varOmega _g$ completely dominates the behaviour of $\varOmega _P$ for circulat geodesic orbit.

Fig. 21

We have plotted the effect of a toroidal magnetic field on $\varOmega _P$ along the equatorial plane (a) and along the polar plane (b). The black solid curve, the red short dashed curve and the blue dashed curve are for central magnetic field of $8.0\times 10^{17} G, 5.0\times 10^{17} G, 4.5\times 10^{16} G$ respectively. $\varOmega$ is taken to be 100 rad s$^{-1}$. The central energy density of the NS is taken to be $1.0\times 10^{15} g cm^{-3}$

In case of the toroidal field, the star becomes prolate and the curves become drastically different. The GPF at the star centre decreases with increase in field strength (along the equatorial direction), as can be seen from Fig. 21. The curve with the larger magnetic field strength is flatter than the curve with lesser field strength. The GPF outside the star for three different magnetic field strength is also not much different. Along the polar direction, the curves become even flatter with an increase in the magnetic field without any local minima.

For the poloidal case, the magnetic field makes the GP curve stiffer, and the maximum of the gyro frequency increases at the center. As the curves become stiff, the local minima become more prominent. However, for the toroidal field, the magnetic field makes the gyro frequency curve flatter, and the maxima of the gyro frequency at the center goes down. As the field strength grows, the curves become flatter, and the local minima also disappear. This is more prominent inside the star, but also have some effect near the surface. The change in the magnetic field distribution changes the radial and azimuthal distribution of mass in the star. The term $\xi \varOmega \frac{dg_{\phi \phi }}{dr}$ dictates the value of GPF, where $\xi$ is defined in Eq. 54. And the coefficient of $\varOmega$ in this dominating term can be greater than unity. Due to the absence of the other dominating term $\xi \frac{dg_{t\phi }}{dr}$, the overall magnitude of the GPF doesn’t decrease, unlike the case of rotating NS with positive $\varOmega$ around it. Thus the value of $\varOmega _P$ can become larger than $\varOmega$. Looking at the nature of the GPF, we can get some idea about the magnetic field distribution inside the star.

Fig. 22

We have plotted the effect of toroidal magnetic field on $\varOmega _P$ along the equatorial plane. Here we have $\varOmega = \varOmega _g$. The black solid curve, the red short dashed curve and the blue dashed curve are for central magnetic field of $8.0\times 10^{17} G, 5.0\times 10^{17} G, 4.5\times 10^{16} G$ respectively. The central energy density of the NS is taken to be $1.0\times 10^{15}$ g cm$^{-3}$

Fig. 23

We have plotted the effect of a TT type of magnetic field on the variation of $\varOmega _P$ with distance from center along the equatorial plane a from center to 4 km, b from 4 to 16 km. The radius of the star is around 11 km. The black solid curve, the red short dashed curve and the blue dashed curve are for central magnetic field of $6.6\times 10^{17} G, 4.7\times 10^{17} G, 3.6\times 10^{16} G$ respectively. $\varOmega$ is taken to be 100 rad s$^{-1}$. The central energy density of the NS is taken to be $1.0\times 10^{15}$ g cm$^{-3}$

In Fig. 22 we have shown the variation of GPF with distance from star’s surface for a gyro following circular geodesic. Here the value of GPF is maximum for the minimum magnetic field case while in the previous case of poloidal field, the GPF was maximum for maximum value of magnetic field (Fig. 20). In this case we can see that the oblateness caused by poloidal field can increase the value of geodesic angular velocity $\varOmega _g$ at a particular distance which increases the value of $\varOmega _{P}$ at that distance.

For the case of TT magnetic field configuration, the GPF does not vary much with the change in field strength, as the configuration is constructed by including both poloidal and toroidal effects (Fig. 23). Both cancel each other’s effect, thus subsequently affecting GPF slightly (poloidal term makes NS oblate, and toroidal makes it prolate). The $\varOmega _P$ at the centre decreases with decrease in field strength, however, the change is very small. This is beacuse the poloidal deformation dominates over the toroidal deformation. The effect of TT can be made higher only if one of the parameters (poloidal or toroidal) completely dominates over the other. However, that is effectively going over to either poloidal or toroidal field configuration.

Fig. 24

a $\varOmega _P$ of the gyro around a rotating and magnetized NS with different values of $\omega$ and with a fixed value of B. The black solid line is for a extreme rotating magnetized NS. The red short dashed curve is for a highly rotating and magnetized NS. The blue dashed line is for a moderately rapidly rotating NS. The green dot dashed curve is for a slowly rotating NS. The value of $\varOmega$ is taken to be 100 rad s$^{-1}$. b Nature of $\varOmega _P$ for different values of $\varOmega$ around a rotating and magnetized star ($\omega = 700$ rad s$^{-1}$ and $B_{max} = 6\times 10^{17} G$). The black solid line, red short dashed line and blue dashed line are for $\varOmega = 100$ rad s$^{-1}$, 300 rad s$^{-1}$ and 350 rad s$^{-1}$ respectively

3.7 Rotating magnetar

In Fig. 24, we have included both rotation and poloidal magnetic field in constructing the NS models. The poloidal field is chosen as this has the maximum effect on the GPF. We start with a figure where we keep the magnetic field fixed ($B_{max} = 6 \times 10^{17} G$) and vary the rotational velocity of the star (also $\varOmega$ is also kept constant). This is shown in Fig. 24a. For $\omega =200$ rad s$^{-1}$ the central value of GPF is minimum (almost zero). Increasing the value of $\omega$ further, the central value of $\varOmega _P$ starts to increase. The local minima shifts away from the centre and the value of local maxima also increases.

Next, we see the variation of GPF keeping the magnetic field and $\omega$ fixed and varying $\varOmega$ (Fig. 24b). For the lower value of $\varOmega$, the GPF is maximum at the star center, and the curve is similar to that of the rotational curve. However, as we increase $\varOmega$, the central value GPF decreases, and the maximum occurs at some distance inside the star. Again increasing $\varOmega$ to 350 rad s$^{-1}$, the null point occurs at the center of the star.

Finally, keeping the star rotational velocity and orbital angular velocity of the gyro fixed ($\varOmega =100$ rad s$^{-1}$), we vary the magnetic field to see the change in GPF. In Fig. 25a, we keep the $\omega$ to a higher value and see that for higher magnetic field strength, the central value of GPF is higher as well as the second maximum. However, the location of the null point does not change much with magnetic field strength. Lowering the field strength to lesser values than $10^{17}$ G replicates the GPF curve obtained for rotational effect only. However, with such a high value of $\omega$, we do not get a null point at the star center. The null point of the GPF at the star centre can be obtained for lower $\omega$ value as shown in Fig. 25b. For the choice of $\omega =215$ rad s$^{-1}$ and $\varOmega =100$ rad s$^{-1}$, we get a null point at the center of the star for $B=6\times 10^{17}$ G. Null point can also be obtained for a different combination of these three values but will not add anything qualitatively. The main conclusion that we deduce from here is that the magnetic field does have some non-trivial effect on the geometry of SP near an NS; however, the effect is small compared to that of rotational effect. Also, the poloidal configuration deforms the ST near an NS the most.

Looking at all the effects, we can conclude that the magnetic field has some measurable effect near the ST of an NS; however, for a rotating magnetized star, the rotation effect dominates the magnetic effect. The effect of the orbital velocity of the gyro is also quite significant in determining the overall GPF.

Fig. 25

a $\varOmega _P$ of the gyro around a rotating and magnetized NS with different values of B. Here $\omega =700$ rad s$^{-1}$. The black solid line is for the highest magnetic field strength. The red short dashed curve is for a moderate field strength. The blue dashed line is for comparatively lesser strength. The value of $\varOmega$ is taken to be 100 rad s$^{-1}$. b Similar curve with only $\omega =215$ rad s$^{-1}$

4 Summary and conclusion

In this work, we have studied the effect of an NS on a test gyroscope when placed near it. We have looked into the overall gyro precession frequency and not only the LT precession frequency. The study is essential to track the relativistic effect that affects a spinning particle in the field of NS gravity. If the star is rotating, the relativistic effect includes the curving of ST and frame-dragging. We also studied the effect of the magnetic field in the ST near a magnetar. All the effects are studied by looking into the GPF of the test gyro.

Keeping the test gyro at a fixed orbit with non zero orbital velocity. The orbital velocity of the gyro can lie within a range of value within some $10^4$–10$^5$ rad s$^{-1}$, fixed by the time-like condition. The test gyro can be along the geodesic, or it can be given finite acceleration to stay in a circular path with constant orbital angular velocity along all distances.

The GPF behaves differently when it approaches a BH or an NS. For a given mass and angular momentum of BH, if we keep on increasing the value of the orbital angular velocity of gyro starting from zero, up to a specific range, the GPF increases monotonically and diverges as it approaches the BH. After reaching a specific value of $\varOmega$, a minimum starts to appear. For some $\varOmega$, the minima become a null point at a distance, almost coinciding with the event horizon. Whereas for an NS, the GPF is always finite and for some range of $\varOmega$ a local minimum also appears at some distance from the center. Thus, the GR effect on a spinning particle differs depending on its proximity to a BH or an NS.

The sense of the orbital angular frequency of the gyro to that of the angular velocity of NS has a significant effect in determining the nature of variation of GPF with distance. If the gyroscope has a prograde motion with the star, the central value of precession frequency is maximum for a static gyro. It decreases with an increase in gyro angular velocity. However, if the gyro is in retrograde motion, the gyro frequency increases with an increase in gyro angular velocity. Also, for a specific range of orbital frequency, there exist two null points in GPF at some distance from the centre of the star. The existence and location of the null point of the GPF also depend on the azimuthal position of the NS. This is important in determining the movement of a real spinning particle encircling an NS.

The angular velocity of the NS affects significantly towards determining the GPF. If the orbital angular velocity of gyro and the drag due to the angular velocity of the star are the same, the value of GPF at the centre is zero and increases with radial distance. Also, the null point shifts towards the surface with an increase in angular velocity of the NS for a given value of $\varOmega$. In the case of geodesic motion we showed that increasing star’s rotation increases the value of geodesic angular velocity and thus increasing the GPF. The GPF also changes with the change in mass of the star. Therefore, observing the GPF, we can get some idea about the angular velocity and the mass of an NS. The local minima of the GPF depend on the azimuthal distribution, the orbital velocity of the gyro, star’s rotation rate, mass, and EoS.

We have also studied the GPF in and around a magnetar. In the present calculation, we have used three different field configurations: Poloidal, Toroidal, and TT type of fields in the star. The position and value of the local minima in the magnitude of the precession rate depend strongly on the distribution and strength of the magnetic field. For poloidal fields, an increase in the field strength makes the GPF curve stiffer, and the local minima are much more prominent. Whereas for the toroidal fields, the growth in field strength makes the GPF curve flat, and the local minima almost disappear for very high field strength. For TT field, the variation of the GPF with the magnetic field is very less, as both poloidal and toroidal parameters cancel out each other.

In the case of circular geodesics, we showed that the effect of poloidal and toroidal field on GPF are also opposite. Increasing the field strength increases the value of GPF in case of poloidal field while in toroidal case it decreases. So we can safely conclude that looking at the GPF, we can distinguish between the magnetic field profile distribution present in the star. When both rotation and magnetic field is included for an NS, the GPF depends more firmly on the rotation than that to the magnetic field.

Finally we can conclude that outside the NS the GR effect of ST on the GPF is small compared to that in the inside. Therefore, to study the ST in and around massive objects, all such GR treatment is essential. Outside the star, the gyro can differentiate between the different compact object as it approaches. However, properties of a particular central object (like its mass, rotational speed, magnetic field) are difficult to gauge and need precise observation. We should mention here that this calculation was done with polytropic EoS. Although, this is sufficient for the current study, however, in future we hope to employ piecewise polytrope to mimic realistic NS calculation. Employing realistic EoS, if such accurate observation can be made we can deduce some of the properties of NS or BH around which it is encircling. All this effect can have critical observational signatures, and recent astrophysical observation is bound to provide such trademarks.