Abstract
We consider the imbalance of matter and antimatter by using a gravitational baryogenesis mechanism in the background of Dvali–Gabadadze–Porrati (DGP) brane cosmology. By taking into account a flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric in the DGP brane model, we find that for a radiation dominated universe, \(w=1/3\), the ratio of baryon number density to entropy from the gravitational baryogenesis is not zero, contrary to ordinary general relativity. Also, we study the ratio of baryon number density to entropy against the observational constraints in DGP cosmology.
Similar content being viewed by others
1 Introduction
The Dvali–Gabadadze–Porrati (DGP) brane world model assumes the existence of a 5-dimensional Minkowski space, within which ordinary 4-dimensional Minkowski space is embedded. The model introduces an action consisting of two terms. One term is the usual Einstein–Hilbert action, which involves only the 4-dimensional spacetime dimensions. The other term is the equivalent of the Einstein–Hilbert action, as extended to all 5-dimensions. The 4-dimensional term dominates at short distances, and the 5-dimensional term dominates at long distances [1,2,3,4]. However, there are two different approaches to embedding the 4-dimensional brane into the 5-dimensional spacetime, and the DGP model has two separate branches, indicated by \(\epsilon \), with distinct aspects. The \(\epsilon = +1\) branch can illustrate the present accelerating cosmic expansion without introducing the mysterious fluid called dark energy [5], while, for the \(\epsilon = -1\) branch, dark energy is needed in order to yield an accelerating expansion [6, 7]. Moreover, inflation in the DGP model displays some new characteristics. It must be noted that only in the \(\epsilon = -1\) case inflation can be exited spontaneously [8,9,10,11,12,13].
The gravitational baryogenesis (GB) process was proposed in 2004 by Davoudiasl et al. [14], in order to explain the observed imbalance of matter over antimatter in the observable universe. The cosmic microwave background observations [15] and also the Big Bang nucleosynthesis [16] admit this imbalance of matter (baryons) and antimatter (antibaryons). According to the Sakharov benchmark [17,18,19,20], the GB procedure is based on the presence of a CP-violating interaction term so that it can explain the fundamental conditions for the generation of the imbalance of matter and antimatter in the observed universe. In this paper we try to consider the GB process in the context of DGP brane cosmology, and the goal of the present paper is to highlight the differences of the GB process between the DGP brane cosmology and standard cosmology. However, the imbalance of the matter and antimatter GB term is given by [14]
this term may result from the higher-order interactions in the gravitational physics. In Eq. (1), \(M_*\) is the cutoff scale of the underlying effective gravitational theory, \(J^{\mu }\) stands for the baryonic matter current and, finally, g is the determinant of the metric \(g_{\mu \nu }\). R is the Ricci scalar. In the general relativity (GR) regime for flat FLRW metric the ratio of baryon number density to entropy, \(n_\mathrm{B}/s\), for a radiation dominated universe is zero, thus at early times the GB process cannot generate a baryonic matter asymmetry. However, we show that, in the context of DGP brane cosmology, the ratio of baryon number density to entropy differs from zero in the radiation dominated universe. We try to find the general expression for the ratio of baryon number density to entropy in a DGP brane world and we show that the results may be compatible with the observational constraint, \(n_\mathrm{B}/s<9 \times 10^{-11}\). The GB mechanism has been studied in various theories in f(R) gravity [21, 22], in brane world scenarios [23], in loop quantum cosmology [24], in f(T) gravity [25], in Gauss–Bonnet brane world cosmology [26], in Gauss–Bonnet gravity [27], in running vacuum models [28], and in Hořava gravity [29]; also see Refs. [30,31,32,33,34,35].
This paper is organized as follows: In Sect. 2, we consider the modified Friedmann equations in the framework of a DGP brane universe and we take the cosmological evolution of the model in the ultra-high energy limit. In Sect. 3 we study in detail the cases in which the resulting ratio of baryon number density/entropy can be compatible with the observational data. Conclusions are drawn in the last section.
2 The Friedmann equation in DGP brane world
A homogeneous and isotropic universe can be described by the FLRW line element, as follows:
One can obtain the Friedmann equations on the warped DGP brane [36, 37]:
where \(\mu \) is a parameter standing for the strength of the induced gravity on the brane, H is the Hubble parameter, k is the spatial curvature of the FLRW metric, and \(\rho \) denotes for the total energy density. For \(\epsilon =+1\), the brane tension is negative, while, for \(\epsilon =-1\), it is positive. \(\chi \) is given by
where
where \(\Lambda \) is given by
\(^{(5)}\Lambda \) is the 5-dimensional cosmological constant in the bulk, \(\lambda \) is the brane tension, \(\kappa _{_{5}}\) stands for the 5-dimensional Newton constant, and \({\mathcal {E}}_0\) is a constant related to Weyl radiation. For simplicity, we will put \(\Lambda =0\); thus Eq. (2) can be written as
To discuss the GB mechanism in the very early era of the universe in which the total energy density is very high, we will consider only the ultra-high energy limit, \(\rho \gg \rho _0\). So, for a flat FLRW universe (\(k=0\)), the Friedmann equation is given by
This equation is a modification of 4-dimensional gravity with minor corrections, where \(\mu \) must have as energy scale the Planck scale in the DGP model.
The conservation equation for the universe with the perfect fluid is given by
where w is the equation of state parameter.
Differentiating Eq. (8) with respect to cosmic time gives
3 Gravitational baryogenesis in DGP brane cosmology
From Eq. (1), the baryon number density to entropy ratio, \(\frac{n_\mathrm{B}}{s}\), for the GB term can be written as [14],
Here \(T_\mathrm{D}\) is the decoupling temperature. Thus, the derivative of the Ricci scalar plays a crucial role in the calculation of the ratio of \(\frac{n_\mathrm{B}}{s}\) in the context of GB. To proceed, we must assume that the universe is filled by a perfect fluid with pressure p and energy density \(\rho \), which are related by \(p=w\rho \). In the GR context, the Ricci scalar can easily be obtained by using the Einstein equations, as follows:
where \(\mu ^2\sim m_\mathrm{p}^2\) and \(m_\mathrm{p}\) is the 4-dimensional Planck mass. The ratio of the baryon number density to entropy is calculated by the derivative of the Ricci scalar \(\dot{R}\), which in Einstein relativity is
and from the above equation it can be seen that in the case of a radiation dominated universe, namely \(w=1/3\), the derivative of the Ricci scalar is zero, so the ratio of the baryon number density to entropy is zero.
To continue we consider the GB mechanism in a DGP brane scenario by taking \(\epsilon =-1\), so by merging Eqs. (8) and (10), the Ricci scalar, \(R=12 H^2+6\dot{H}\), can written as
To consider the differences between the DGP brane cosmology and the standard cosmology by comparing the resulting ratio of baryon number density to entropy in the DGP model, we must calculate \(\dot{R}\):
Because of the first and third terms in the DGP Ricci scalar of Eq. (14), the resulting ratio of baryon number density to entropy even for a radiation dominated universe with \(w=1/3\) is not zero, which indicates the effects of the extra dimension of the theory.
Therefore, in the DGP brane cosmology the ratio of baryon number density to entropy in the context of the GB mechanism is not zero, contrary to the GR one. In the next section we consider our results by using DGP brane cosmology and we check that our results can be compatible with the observational constraints.
In the DGP brane scenario by using the Friedmann equation (8) and taking the continuity equation (9), with \(p=w\rho \), the first order differential equation for \(\rho \) is given by
From the above equation the energy density as a function of the cosmic time is
where we have normalized the energy density to \(\rho (t)=2\rho _0\) at \(t=0\) and we have considered the integration constant to be zero. Assuming that the universe enters the states of thermal equilibrium (quasi-static thermal equilibrium), the total energy density as a function of the temperature is
We can easily obtain the decoupling times \(t_\mathrm{D1}\) and \(t_\mathrm{D2}\) as a function of the decoupling temperature \(T_\mathrm{D}\), by merging Eqs. (17) and (18), and the results are
From the above equations it can be seen that we have two decoupling times. Thus, from Eq. (19) we can see that the parameter \(\rho _0\) is constrained to satisfy the inequality \(60\rho _0<\pi ^2 g_* T_\mathrm{D}^4\), so it must be at least four orders smaller in comparison to the decoupling temperature. By using Eq. (17) and replacing in Eq. (15), we can write the derivative of \(\dot{R}\) as a function of the cosmic time as follows:
so by using the first decoupling time \(t_\mathrm{D1}\) (19), the term \(\dot{R}\) as a function of the decoupling temperature is
By replacing \(\dot{R}\) from Eq. (22) in Eq. (11), the final expression of the ratio of baryon number density to entropy in the DGP brane model is
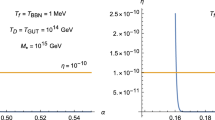
Here we discuss under which conditions the resulting ratio of baryon number density to entropy can be compatible with the theoretical bound \(n_\mathrm{B}/s\preceq 9 \times 10^{-11}\). We use Planck units for simplicity, and we choose the cutoff scale \(M_{*}\) to be equal to \(M_{*}=10^{12}\)GeV, and the decoupling temperature is chosen \(T_\mathrm{D}=M_{I}=2\times 10^{16}\) GeV, where \(M_{I}\) is the upper bound for the tensor-mode fluctuations constraints on the inflationary scale. Also we set that \(g_\mathrm{b}\simeq \mathcal{O}(1)\) and \(g_{*}=106\), which is the total number of the effectively massless particles in the early universe. Finally, we assume that \(\rho _{0}\simeq 1.56\times 10^{49}\)GeV\(^4\) and we can use the effective equation of state parameter, w, to obtain the ratio of baryon number density to entropy. For \(w=1/3\), the radiation dominated universe, the ratio of baryon number density to entropy obtained by gravitational baryogenesis (23) approximately is equal to \(n_\mathrm{B}/s\simeq 8.38193\times 10^{-11}\), which is compatible with the observational bounds. Also, by choosing \(w=0\), which corresponds to the matter dominated epoch, the ratio of baryon number density to entropy is \(n_\mathrm{B}/s\simeq -0.00123978\), which is not compatible with the observational bounds.
By repeating the above calculations for GB with the second decoupling time \(t_\mathrm{D2}\) for \(w=1/3\) we find that the ratio of baryon number density to entropy obtained by GB mechanism is \(n_\mathrm{B}/s\simeq 9.53281\times 10^{-11}\), which is compatible with the observational bounds. Also, for a matter dominated \(w=0\) universe, the resulting ratio of baryon number density to entropy is \(n_\mathrm{B}/s\simeq 5.66208\times 10^{-11}\), which is again compatible with the observational bounds. Note that in DGP brane cosmology the ratio of baryon number density to entropy sensitively depends on the parameter \(\rho _0\), which for consistency has to be roughly smaller than the fourth power of the decoupling temperature, that is, \(\rho _{0}\prec T_\mathrm{D}^4\).
4 Conclusions
In this paper we have studied the effects of brane cosmology in the context of the DGP model via the GB mechanism. Also, we have explicitly obtained the baryon number density to entropy ratio for the DGP brane in background of FLRW universe, and to do this the derivative of the Ricci scalar, \(\dot{R}\), is calculated. The crucial point of our work is the fact that even in the case of a radiation dominated epoch, the ratio of baryon number density to entropy is not zero, which is in contrast to the standard cosmology. Thus, if the GB mechanism is to be discussed as regards a viable baryon asymmetry generating mechanism, DGP brane cosmology extremely affects the amount of imbalance of matter and antimatter in the early universe. We have considered the cosmological evolutions in the context of the DGP brane model, which is consistent with the observational bounds on gravitational baryogenesis. As we have shown, by fixing the parameters of the model the observational bounds on the ratio of baryon number density to entropy can be achieved. Finally, from the expression of the decoupling time, we have found that the critical density parameter must be smaller than the fourth power of the decoupling temperature, namely \(\rho _{0}\prec T_\mathrm{D}^4\).
References
D. Dvali, G. Gabadadze, M. Porrati, Phys. Lett. B 485, 208 (2000)
C. Charmousis, R. Gregory, N. Kaloper, A. Padilla, JHEP 0610, 066 (2006)
R. Gregory, N. Kaloper, R.C. Myers, A. Padilla, JHEP 0710, 069 (2007)
D. Gorbunov, K. Koyama, S. Sibiryakov, Phys. Rev. D 73, 044016 (2006)
C. Deffayet, Phys. Lett. B 199, 502 (2001)
A. Lue, G.D. Starkman, Phys. Rev. D 70, 101501(R) (2004)
L.P. Chimento, R. Lazkoz, R. Maartens, I. Quiros, JCAP 0609, 004 (2006)
M. Bouhmadi-Lopez, R. Maartens, D. Wands, Phys. Rev. D 70, 123519 (2004)
R. Cai, H. Zhang, JCAP 0408, 017 (2004)
E. Papantonopoulos, V. Zamarias, JCAP 0410, 001 (2004)
H. Zhang, R. Cai, JCAP 0408, 017 (2004)
H. Zhang, Z. Zhu, Phys. Lett. B 641, 405 (2006)
S. del Campo, R. Herrera, Phys. Lett. B 653, 122 (2007)
H. Davoudiasl, R. Kitano, G.D. Kribs, H. Murayama, P.J. Steinhardt, Phys. Rev. Lett. 93, 201301 (2004)
C.L. Bennett et al., WMAP Collaboration. Astrophys. J. Suppl. 148, 1 (2003)
S. Burles, K.M. Nollett, M.S. Turner, Phys. Rev. D 63, 063512 (2001)
A.D. Sakharov, Pisma Zh. Eksp. Teor. Fiz. 5, 32 (1967)
A.D. Sakharov, JETP Lett. 5, 24 (1967)
A.D. Sakharov, Sov. Phys. Usp. 34, 392 (1991)
A.D. Sakharov, Usp. Fiz. Nauk 161, 61 (1991)
G. Lambiase, G. Scarpetta, Phys. Rev. D 74, 087504 (2006)
M.P.L.P. Ramos, J. Páramos, Phys. Rev. D 96, 104024 (2017)
T. Shiromizu, K. Koyama, JCAP 0407, 011 (2004)
S.D. Odintsov, V.K. Oikonomou, EPL 116, 49001 (2016). arXiv:1610.02533
V.K. Oikonomou, E.N. Saridakis, Phys. Rev. D 94, 124005 (2016)
M.C. Bento, R. Gonzalez, Felipe, N.M.C. Santos, Phys. Rev. D 71, 123517 (2005)
S.D. Odintsov, V.K. Oikonomou, Phys. Lett. B 760, 259 (2016)
V.K. Oikonomou, Supriya Pan, Rafael C. Nunes, arXiv:1610.01453
S. Maity, P. Rudra, arXiv:1802.00313
G. Lambiase, S. Mohanty, A.R. Prasanna, Int. J. Mod. Phys. D 22, 1330030 (2013)
G. Lambiase, Phys. Lett. B 642, 9 (2006)
H. Li, M.z Li, X.m Zhang, Phys. Rev. D 70, 047302 (2004)
L. Pizza, arXiv:1506.08321 [gr-qc]
J.A.S. Lima, D. Singleton, arXiv:1610.01591 [gr-qc]
V.K. Oikonomou, Int. J. Geom. Meth. Mod. Phys. 13, 1650033 (2016)
K. Maeda, S. Mizuno, T. Torii, Phys. Rev. D 68, 024033 (2003)
K. Zhang, P. Wu, H. Yu, Phys. Lett. B 690, 229 (2010)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Atazadeh, K. Gravitational baryogenesis in DGP brane cosmology. Eur. Phys. J. C 78, 455 (2018). https://doi.org/10.1140/epjc/s10052-018-5952-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5952-4