Electroweak vacuum stability in classically conformal $B-L$ extension of the standard model

Abstract

We consider the minimal U(1)$_{B-L}$ extension of the standard model (SM) with the classically conformal invariance, where an anomaly-free U(1)$_{B-L}$ gauge symmetry is introduced along with three generations of right-handed neutrinos and a U(1)$_{B-L}$ Higgs field. Because of the classically conformal symmetry, all dimensional parameters are forbidden. The $B-L$ gauge symmetry is radiatively broken through the Coleman–Weinberg mechanism, generating the mass for the $U(1)_{B-L}$ gauge boson ($Z^\prime$ boson) and the right-handed neutrinos. Through a small negative coupling between the SM Higgs doublet and the $B-L$ Higgs field, the negative mass term for the SM Higgs doublet is generated and the electroweak symmetry is broken. In this model context, we investigate the electroweak vacuum instability problem in the SM. It is well known that in the classically conformal U(1)$_{B-L}$ extension of the SM, the electroweak vacuum remains unstable in the renormalization group analysis at the one-loop level. In this paper, we extend the analysis to the two-loop level, and perform parameter scans. We identify a parameter region which not only solve the vacuum instability problem, but also satisfy the recent ATLAS and CMS bounds from search for $Z^\prime$ boson resonance at the LHC Run-2. Considering self-energy corrections to the SM Higgs doublet through the right-handed neutrinos and the $Z^\prime$ boson, we derive the naturalness bound on the model parameters to realize the electroweak scale without fine-tunings.

1 Introduction

The stability of the electroweak scale is one of the biggest mysteries in the standard model (SM), since the self-energy of the SM Higgs doublet field receives quantum corrections which are quadratically sensitive to the ultraviolet cutoff of the SM. A fine-tuning of the Higgs mass parameter is required to reproduce the correct electroweak scale if the ultraviolet cutoff scale is far above the electroweak scale (the gauge hierarchy problem). This problem can be solved if new physics beyond the SM makes the self-energy of the SM Higgs doublet insensitive (or logarithmically sensitive) to the ultraviolet cutoff. It is well known that supersymmetric extension of the SM can achieve this insensitivity. Despite lots of efforts of searching for supersymmetry at the large hadron collider (LHC) experiments, current LHC data include less indications for productions of supersymmetric particles. Hence we may seek other possibilities to solve the gauge hierarchy problem without supersymmetry.

According to the argument by Bardeen [1] once the classical conformal invariance and its minimal violation by quantum anomalies are imposed on the SM (or the general Higgs model), the model can be logarithmically sensitive to the ultraviolet cutoff. If this is the case, we introduce the classically conformal symmetry to the SM to make the model free from the quadratic corrections.¹ In this system, there is no mass parameter in the original Lagrangian, and the mass scale must be generated by quantum corrections. The massless U(1) Higgs model discussed by Coleman and Weinberg [3] nicely fits this picture, where the model is defined as a massless, conformal invariant theory, and the U(1) gauge symmetry is radiatively broken by the Coleman–Weinberg (CW) mechanism, generating a mass scale through the dimensional transmutation.

Recently, the extension of the SM with the classically conformal invariance has received a fair amount of attention, and many models in this direction have been proposed [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Among them, the classically conformal U(1)$_{B-L}$ extension of the SM [28, 29] is a very simple and well-motivated model, since the $B-L$ (baryon number minus lepton number) is a unique anomaly-free global symmetry and it can easily be gauged. Once the U(1)$_{B-L}$ is gauged, we need new chiral fermions to cancel the U(1)$_{B-L}$ gauge and the mixed gravitational anomalies. The simplest possibility is to introduce three right-handed neutrinos, which are nothing but the particles that we need to incorporate the neutrino mass in the SM. In this conformal symmetric model, the $B-L$ gauge symmetry is broken by the vacuum expectation value (VEV) of the $B-L$ Higgs field developed by the CW mechanism, and the masses for $Z^\prime$ boson and three right-handed neutrinos are generated. This radiative $B-L$ gauge symmetry breaking is the sole origin of the mass scale in this model, and the negative mass squared for the SM Higgs doublet is generated by this symmetry breaking [28].

The SM Higgs boson was finally discovered at the LHC, and the experimental confirmations of the Higgs properties in the SM have just begun. According to the SM, we can read off the value of the quartic Higgs coupling at the electroweak scale from the measured Higgs boson mass, and we can investigate the behavior of the Higgs potential toward high energies by extrapolating the quartic coupling through its renormalization group evolution. It turns out that the running quartic coupling becomes negative around $10^{10}$ GeV [30], and this fact means that the electroweak vacuum is not stable. Practically, this instability may not be a problem, since the lifetime of our electroweak vacuum is estimated to be much longer than the age of the universe [31]. However, in our context of the classically conformal extension of the SM, this electroweak vacuum instability seems to cause a theoretical inconsistency. The instability indicates that the electroweak symmetry is radiatively broken at a very high energy, which in turn generates a large mass term for the $B-L$ Higgs field. Therefore, with such a large mass, the $B-L$ symmetry breaking is no longer triggered by the CW mechanism.

In this paper, we investigate the electroweak vacuum stability in the context of the classically conformal U(1)$_{B-L}$ extension of the SM. It is well known that the electroweak vacuum is still unstable in this context in the renormalization group analysis at the one-loop level [26, 27]. We extend the analysis to the two-loop level and find that there exist parameter regions which can keep the electroweak vacuum stable. In our analysis, we use the result from the combined analysis by the ATLAS and the CMS experiments for the Higgs boson mass measurement in the range of $m_{\mathrm{h}}=$125.09 ± 0.21 (stat.) ± 0.11 (syst.) GeV [32] and the recent result of top quark mass measurement $m_{\mathrm{t}}=$ 172.38 ± 0.10 ± 0.65 [33] by the CMS experiments. We also consider the current collider bounds, namely, a lower bound on the $B-L$ gauge symmetry breaking scale from the LEP electroweak precision measurements, and a lower bound on the $Z^\prime$ boson mass from the recent ATLAS [34] and CMS [35] results at the LHC Run-2. In addition, we evaluate self-energy corrections to the SM Higgs doublet from the heavy states, the $Z^\prime$ boson and the right-handed neutrinos associated with the $B-L$ symmetry breaking, and find naturalness bounds to reproduce the electroweak scale without any fine-tunings of model parameters.

This paper is organized as follows. Our model is defined in the next section. In Sect. 3, we discuss the radiative $B-L$ symmetry breaking through the CW mechanism and the electroweak symmetry breaking triggered by it. In Sect. 4, we analyze the renormalization group evolutions of the couplings at the two-loop level, and find a parameter regions which can keep the quartic SM Higgs coupling to be positive anywhere between the electroweak scale and the Planck scale. We also consider the current collider bounds of the model parameters, in particular, the recent ATLAS and CMS results of search for $Z^\prime$ boson resonance at the LHC Run-2 are interpreted to our $B-L$ model. In Sect. 5, we evaluate self-energy corrections to the SM Higgs doublet, and we derive the naturalness bounds to reproduce the electroweak scale without fine-tunings for the model parameters. We summarize our results in Sect. 6. Formulas we used in our analysis are listed in the appendices.

Table 1 The particle contents of the $U(1)_{B-L}$ extended SM. In addition to the SM particle contents, the right-handed neutrino $N_R^i$ ($i=1,2,3$ denotes the generation index) and a complex scalar $\Phi$ are introduced

2 Classically conformal $U(1)_{B-L}$ extended SM

We investigate the minimal U(1)$_{B-L}$ extension of the SM with the classically conformal invariance, where the model is based on the gauge group SU(3)$_C \times$SU(2)$_L \times$U(1)$_Y \times$ U(1)$_{B-L}$. The particle contents of the model are listed in Table 1. In addition to the SM particle contents, we introduce the $B-L$ Higgs field with the $B-L$ charge 2 ($\Phi$) and three right-handed neutrinos ($N_\mathrm{R}^i$) for cancelation of all the gauge and gravitational anomalies. The covariant derivative relevant to U(1)$_Y \times$ U(1)$_{B-L}$ is given by

$$\begin{aligned} D_\mu = \partial _\mu - i (Q_Y~~Q_{BL}) \left( \begin{array}{cc} g_{1} &{} g_{YB} \\ g_{BY} &{} g_{BL} \end{array} \right) \left( \begin{array}{c} B_\mu \\ Z^\prime _\mu \end{array} \right) , \end{aligned}$$

(2.1)

where $Q_Y$ and $Q_{BL}$ are U(1)$_Y$ and U(1)$_{B-L}$ charges of a particle, respectively, and gs are the gauge couplings. Because of the kinetic mixing between the two U(1) gauge bosons, the off-diagonal elements ($g_{YB}$ and $g_{BY}$) are introduced. In the following analysis, we take the boundary condition, $g_{YB}=g_{BY}=0$, at the $B-L$ symmetry breaking scale, where the two U(1) gauge bosons are diagonal with each other, for simplicity.

The Yukawa sector of the SM is extended to have

$$\begin{aligned} \mathcal {L}_{\mathrm{Yukawa}} \supset -Y^{ij}_{\mathrm{D}} \overline{\ell ^i_{\mathrm{L}}} H N_\mathrm{R}^j -\frac{1}{2} Y^k_{\mathrm{N}} \Phi \overline{N_\mathrm{R}^{k C}} N_\mathrm{R}^k + \mathrm{h.c.}, \end{aligned}$$

(2.2)

where the first term is the neutrino Dirac Yukawa coupling, while the second term is the Majorana Yukawa coupling. Without loss of generality, we have already diagonalized the Majorana Yukawa coupling. The $B-L$ gauge symmetry breaking generates the Majorana neutrino mass term in the second term. The seesaw mechanism [36,37,38,39,40,41] is automatically implemented in the model after the electroweak symmetry breaking.

We apply the classically conformal invariance to the model, and the scalar potential is given by

$$\begin{aligned} V = \lambda (H^{\dagger }H)^{2} + \lambda _{2} (\Phi ^{\dagger }\Phi )^{2} + \lambda _{3} (H^{\dagger }H) (\Phi ^{\dagger }\Phi ). \end{aligned}$$

(2.3)

Note that the mass terms are all forbidden by the conformal invariance. If $\lambda _3$ is negligibly small, we can analyze the Higgs potential separately for $\Phi$ and H. This will be justified in the next section. When the Majorana Yukawa coupling $Y_\mathrm{N}^i$ is negligible compared to the U(1)$_{B-L}$ gauge coupling, the $\Phi$ sector is identical to the original Coleman–Weinberg model [3], so that the U(1)$_{B-L}$ gauge symmetry is radiatively broken. The mass term for the SM Higgs doublet is generated through $\lambda _3$ with the non-zero VEV of $\Phi$, and the electroweak symmetry is broken when we choose $\lambda _3 <0$ [28]. Therefore, the electroweak symmetry breaking is driven by the radiative $B-L$ symmetry breaking.

3 Radiative gauge symmetry breakings

Assuming a negligibly small $\lambda _3$, we first analyze the U(1)$_{B-L}$ Higgs sector. Without mass terms, the CW potential [3] at the one-loop level (in the Landau gauge) is found to be

$$\begin{aligned} V(\phi ) = \frac{\lambda _2}{4} \phi ^4 + \frac{\beta _\Phi }{8} \phi ^4 \left( \ln \left[ \frac{\phi ^2}{M^2} \right] - \frac{25}{6} \right) , \end{aligned}$$

(3.1)

where $\phi / \sqrt{2} = \mathfrak {R}[\Phi ]$, and we have chosen the renormalization scale to be the VEV of $\Phi$ ($\langle \phi \rangle =M$). Here, the coefficient of the one-loop quantum corrections is given by

$$\begin{aligned} \beta _\Phi= & {} \frac{1}{16 \pi ^2} \left[ 20\lambda _2^2 + 96 g_{BL}^4 - \sum _i(Y_N^i)^4 \right] \nonumber \\\simeq & {} \frac{1}{16 \pi ^2} \left[ 96 g_{BL}^4 - \sum _i(Y_N^i)^4 \right] , \end{aligned}$$

(3.2)

where, in the last expression, we have used $\lambda _2^2 \ll g_{BL}^4$ as usual in the CW mechanism. The stationary condition $\left. \mathrm{d}V/\mathrm{d}\phi \right| _{\phi =M} = 0$ leads to

$$\begin{aligned} \lambda _2 = \frac{11}{6} \beta _\Phi , \end{aligned}$$

(3.3)

and this $\lambda _2$ is nothing but the renormalized quartic coupling at M defined as

$$\begin{aligned} \lambda _2 = \frac{1}{3 !}\left. \frac{\mathrm{d}^4V(\phi )}{\mathrm{d} \phi ^4} \right| _{\phi =M}. \end{aligned}$$

(3.4)

For a more detailed discussion, see [26].

Associated with this radiative U(1)$_{B-L}$ symmetry breaking, the $Z^\prime$ boson and the right-handed Majorana neutrinos acquire their masses as

$$\begin{aligned} M_{Z^\prime } = 2 g_{BL} M, \quad M_\mathrm{N}^i = \frac{Y_\mathrm{N}^i}{\sqrt{2}} M. \end{aligned}$$

(3.5)

In this paper, we assume degenerate masses for the three Majorana neutrinos, $Y_\mathrm{N}^i = y_\mathrm{N}$ (equivalently, $M_\mathrm{N}^i=M_\mathrm{N}$) for all $i=1,2,3$, for simplicity. The U(1)$_{B-L}$ Higgs boson mass is given by

$$\begin{aligned} M_\phi ^2 = \left. \frac{\mathrm{d}^2 V}{\mathrm{d}\phi ^2}\right| _{\phi =M} =\beta _\Phi M^2 \simeq \frac{3}{8 \pi ^2} \frac{ M_{Z^\prime }^4 - 2 M_\mathrm{N}^4}{M^2}. \end{aligned}$$

(3.6)

When the Majorana Yukawa coupling is negligibly small, this reduces to the well-known relation derived in the radiative symmetry breaking by the CW mechanism [3]. For a sizable Majorana mass, this formula indicates that the potential minimum disappears for $M_\mathrm{N} > M_{Z^\prime }/2^{1/4}$, leading to the upper bound on the right-handed neutrino mass in order for the U(1)$_{B-L}$ symmetry to be broken radiatively.

Once the U(1)$_{B-L}$ gauge symmetry is radiatively broken by the CW mechanism, the electroweak symmetry is subsequently triggered through the coupling $\lambda _3$. With $\langle \phi \rangle =M$, the SM Higgs potential is given by

$$\begin{aligned} V(h) = \frac{\lambda }{4}h^4 + \frac{\lambda _{3}}{4} M ^2 h^2, \end{aligned}$$

(3.7)

where $H = 1/\sqrt{2}\, (0 \; \; h)^T$ in the unitary gauge. Choosing $\lambda _3 < 0$, the electroweak symmetry is broken in the same way as in the SM [28]. However, the crucial difference from the SM is that in our model the electroweak symmetry breaking originates from the radiative breaking of the U(1)$_{B-L}$ gauge symmetry. At the tree level, the stationary condition $V^\prime |_{h=v} = 0$ leads to the relation $|\lambda _3|= 2 \lambda (v/M)^2$, and the Higgs boson mass $m_\mathrm{h}$ is given by

$$\begin{aligned} m_\mathrm{h}^2 = \left. \frac{\mathrm{d}^2 V}{\mathrm{d}h^2} \right| _{h=v} = |\lambda _3| M^2 = 2 \lambda v^2. \end{aligned}$$

(3.8)

In the following renormalization group analysis, this relation, $\lambda _3=- m_\mathrm{h}^2/M^2$, is used as the boundary condition for $\lambda _3$ at the normalization scale $\mu =M$. Since $M \gtrsim 3$ TeV by the LEP constraint [42,43,44], $|\lambda _3| \lesssim 10^{-3}$. With such a small $\lambda _3$, the back reaction to the $B-L$ Higgs sector through $\lambda _3 v^2$ is negligibly small, and this fact allows us to treat the two Higgs sectors separately.²

4 Electroweak vacuum stability

In the context of the classically conformal U(1)$_{B-L}$ extended model discussed in the previous sections, we now investigate a possibility to solve the electroweak vacuum instability problem. The electroweak vacuum stability has been investigated in the minimal $B-L$ model [45, 46] (see also [47]), and the parameter regions for which the electroweak vacuum is stable have been identified. A crucial difference in our analysis from the previous one is that our model is classically conformal and the gauge symmetry breaking originates from the CW mechanism. Hence, we have constraints on the initial values of $\lambda _2$ and $\lambda _3$ at the scale M, and it is non-trivial to solve the electroweak vacuum instability problem. In the classically conformal extension of the SM the electroweak vacuum stability has been investigated though the renormalization group analysis at the one-loop level in [26, 27], it turns out that there is no parameter region to keep the electroweak vacuum stable. In the following, we extend the renormalization group analysis to the two-loop level, and examine if the vacuum instability can be resolved by the higher order corrections.

In our analysis, we employ the SM renormalization group (RG) equations at the two-loop level [30] from the top quark pole mass to the U(1)$_{B-L}$ Higgs VEV (M), and connect the RG equations to those of the minimal U(1)$_{B-L}$ extended SM at the two-loop level.³ All formulas used in our analysis are listed in the appendices. As is well known, the RG evolutions of the Higgs quartic coupling is sensitive to the input values of the Higgs boson and top quark masses. For inputs for the Higgs boson mass and top quark pole mass, we adopt the result from the combined analysis by the ATLAS and the CMS experiments for the Higgs boson mass measurement in the range of $m_{\mathrm{h}}=$125.09 ± 0.21 (stat.) ± 0.11 (syst.) GeV [32] and the recent result of top quark mass measurement by the CMS experiments [33] in the range of $m_{\mathrm{t}}=$ 172.38 ± 0.10 ± 0.65.

The RG evolutions of the Higgs quartic coupling are shown in Fig. 1 for two different values of $m_\mathrm{h}=125.09$ GeV (left panel) and 125.41 GeV (right panel) with a fixed $m_\mathrm{t}=171.63$ GeV. Here we have fixed the other parameters as $g_{BL}=0.314$, $g_{YB}=g_{BY}=0$ and $y_\mathrm{N}=0$ at $\mu =M=4$ TeV. The solid lines denote the RG evolutions of the Higgs quartic coupling in our model, while the dashed lines denote those in the SM. We can see that in our model, the Higgs quartic coupling remains positive up to the Planck scale, $M_{\mathrm{Pl}}=1.2 \times 10^{19}$ GeV, and therefore the electroweak vacuum becomes stable. As the same as in the SM [30], the situation becomes better with an increasing (decreasing) value of $m_\mathrm{h}$ ($m_\mathrm{t}$) for a fixed value of the $m_\mathrm{t}$ ($m_\mathrm{h}$).

Fig. 1

The renormalization group evolution of the Higgs quartic coupling ($\lambda$) in the $B-L$ model (solid lines), along with the one in the SM (dashed lines). We have taken $m_\mathrm{h}=125.09$ GeV (left panel) and $m_\mathrm{h}=125.41$ GeV (right panel) with the fixed values of $M= 4.0$ TeV and $m_\mathrm{t}=$ 171.63 GeV

-12pt

Fig. 2

The results of parameter scans for $M_{Z^\prime }$ and $M_\mathrm{N}$. We have used $m_\mathrm{h}=125.09$ GeV (two panels in the left column) and $m_\mathrm{h}=125.41$ GeV (two panels in the right column), for the fixed value of $m_\mathrm{t}=$ 171.63 GeV. In each panel, three regions from left to right correspond to $M=3.5$, 4.0 and 4.5 TeV, respectively

In order to identify parameter regions to keep the electroweak vacuum stable, we perform parameter scans for the free parameters $M_{Z^\prime }$ and $M_\mathrm{N}$ with fixed values of $M=3.5$, 4.0 and 4.5 TeV. Here, we have used the same values for $m_\mathrm{h}$ and $m_\mathrm{t}$ as in Fig. 1. In this analysis, we impose the following conditions for the running couplings at $M \le \mu \le M_{\mathrm{Pl}}$: the stability of the Higgs potential ($\lambda , \lambda _2 > 0$ and $|\lambda _3|^2 < 4 \lambda \lambda _2$), and the conditions that all the running couplings remain in the perturbative regime, namely, $g_i^2 (i=1,2,3), g_{BL}^2, g_{YB}^2, g_{BY}^2 <4 \pi$ and $\lambda , \lambda _{2,3} < 4 \pi$. The results are shown in Fig. 2. In this Figure, we also show the $B-L$ Higgs boson mass by using Eq. (3.6). As we expect, the allowed region becomes larger as $m_\mathrm{h}$ is increased.

We also perform parameter scan for various values of $m_\mathrm{h}$ and $m_\mathrm{t}$ in the ranges of $124.68 \le m_\mathrm{h}/\mathrm{GeV} \le 125.32$ and $171.63 \le m_\mathrm{t}/\mathrm{GeV} \le 173.13$, with fixed values of $M=2$ and 4 TeV. The results are shown in Fig. 3 for $M=2$ TeV (left panel) and $M=4$ TeV (right panel). The parameter sets inside of the triangles satisfy all constraints of the electroweak vacuum stability and the perturbativity of the running couplings. For a fixed $m_\mathrm{h}$, there is an upper bound on $m_\mathrm{t}$, or equivalently, there is a lower bound on $m_\mathrm{h}$ for a fixed $m_\mathrm{t}$. The allowed region for $M=4$ TeV is more restricted than the one for $M=2$ TeV. When we increase the M value further, the allowed region disappears (see Fig. 4).

Fig. 3

The results of parameter scans for various values of $m_\mathrm{h}$ and $m_\mathrm{t}$ in the ranges of $124.68 \le m_\mathrm{h}/\mathrm{GeV} \le 125.32$ and $171.63 \le m_\mathrm{t}/\mathrm{GeV} \le 173.13$, with the fixed values of $M=2$ TeV (left panel) and $M=4$ TeV (right panel)

Fig. 4

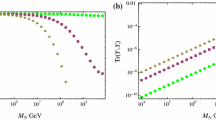
The results of parameter scans for various values of $\alpha _{BL}=g_{BL}^2/(4 \pi )$ and $M_{Z^\prime }$. We have used $m_\mathrm{h} = 124.77$ GeV (left panel) and 125.09 GeV (right panel) with $m_\mathrm{t} = 171.63$ GeV. The regions inside the shaded triangles satisfy all the constraints. The vertical solid lines from left to right correspond to the limits from the LEP, the ATLAS with the LHC Run-1, the CMS with the LHC Run-1, the CMS with the LHC Run-2 and the ATLAS with the LHC Run-2, respectively. The naturalness argument prefers the regions on the left sides of the diagonal dashed lines

Finally, we show in Fig. 4 the results of our parameter scans for various values of $g_{BL}$ and M, with $m_\mathrm{h}=124.77$ GeV (left panel) and 125.09 GeV (right panel) for $m_\mathrm{t}=171.63$ GeV. In this figure, we present the results with $\alpha _{BL}=g_{BL}^2/(4 \pi )$ and $M_{Z^\prime }$ by using the mass formula $M_{Z^\prime }=2 g_{BL} M$. Here we have considered not only the conditions of the electroweak vacuum stability and the perturbativity, but also the current collider bounds. The search for effective 4-Fermi interactions mediated by the $Z^\prime _{BL}$ boson at the LEP leads to a bound [42] (see also [43, 44])

$$\begin{aligned} \frac{M_{Z^\prime }}{g_{BL}} \ge 6.9 \; \mathrm{TeV} \end{aligned}$$

(4.1)

at 95% confidence level. The ATLAS and the CMS collaborations have searched for $Z^\prime$ boson resonance at the LHC Run-1 with $\sqrt{s}=8$ TeV. The most stringent bounds on the $Z^\prime$ boson production cross section times branching ratio have been obtained by using the dilepton final state. For the so-called sequential SM $Z^\prime$ model [50], where the $Z^\prime$ boson has exactly the same couplings with the SM fermions as those of the SM Z boson, the cross section bounds lead to lower bounds on the $Z^\prime$ boson mass as $M_{Z^\prime } \ge 2.90$ TeV from the ATALS analysis [51] and $M_{Z^\prime } \ge 2.96$ TeV from the CMS analysis [52, 53], respectively. Very recently, these bounds have been updated by the ATLAS [34] and CMS [35] analysis with the LHC Run-2 at $\sqrt{s}=13$ TeV as $M_{Z^\prime } \ge 3.4$ TeV (ATLAS) and $M_{Z^\prime } \ge 3.15$ TeV (CMS), respectively. We interpret theses ATLAS and CMS ret the $B-L$ $Z^\prime$ boson case. In our model, the U(1)$_{B-L}$ gauge coupling is a free parameter, and for a fixed gauge coupling we can read off the lower limit on the $Z^\prime$ boson mass from the ATLAS and CMS cross section bounds. In this way, we can find an upper (lower) bound on the U(1)$_{B-L}$ gauge coupling $\alpha _{BL}=g_{BL}^2/(4 \pi )$ ($Z^\prime$ boson mass $M_{Z^\prime }$) as a function of $M_{Z^\prime }$ ($\alpha _{BL}$). In interpreting the ATLAS and the CMS results to the $B-L$ model, we follow a strategy presented in detail in [54] (see also [55, 56]). In Fig. 4, the vertical solid lines correspond to the bounds from the LEP result, the ATLAS with the LHC Run-1, the CSM with the LHC Run 1, the CMS with the LHC Run-2, and the ATLAS with the LHC Run-2, from left to right. The parameters inside the shaded triangles satisfy all the constraints. Naturalness bound, which will be obtained in the next section, is also shown as the dashed lines. In, for example, Ref. [57], the search reach of the $Z^\prime$ boson at the LHC Run 2 with a 14 TeV collider energy and a 100/fb luminosity is obtained as $M_{Z^\prime } \simeq 5$ TeV for $\alpha _{BL}\simeq 0.01$. A large potion of the allowed regions presented in Fig. 4 can be tested in the near future. The (indirect) search reach of the future $e^+ e^-$ linear collider with a 1 TeV collider energy can be as large as 10 TeV (see, for example, [29]), and almost of all allowed regions presented in Fig. 4 can be covered.

5 Constraints from naturalness

Once the U(1)$_{B-L}$ gauge symmetry is radiatively broken by the CW mechanism, the masses for the $Z^\prime$ boson and the Majorana neutrinos are generated, which in general create self-energy corrections to the SM Higgs doublet. If the $B-L$ gauge symmetry breaking scale is very large, the self-energy corrections may exceed the electroweak scale and require us to fine-tune the model parameters in reproducing the correct electroweak scale. Two major corrections have been discussed in [28, 29]: one is one-loop corrections with the Majorana neutrinos, and the other is two-loop corrections involving the $Z^\prime$ boson and the top quark. In the calculations of the self-energy corrections in [29], the cutoff procedure with the Planck scale cutoff is applied to derive the naturalness bounds. Although this treatment is good for rough estimates, in order to derive more accurate naturalness bounds we will renormalize the loop corrections properly in this section.

Since the original theory is classically conformal and defined as a massless theory, the self-energy corrections to the SM Higgs doublet originates from corrections to the quartic coupling $\lambda _3$. Thus, what we calculate to derive the naturalness bounds is quantum corrections to the term $\lambda _3 h^2 \phi ^2$ in the effective Higgs potential. For the one-loop diagram involving the Majorana neutrinos (for the Feynman diagram, see Fig. 3 in [29]), we calculate the effective potential as

$$\begin{aligned} \Delta V_\mathrm{1-loop} \supset - \frac{|Y_\mathrm{D}|^2 |Y_\mathrm{N}|^2}{16 \pi ^2} h^2 \phi ^2 \left( \ln [\phi ^2] + C \right) , \end{aligned}$$

(5.1)

where the logarithmic divergence and the terms independent of $\phi$ are all encoded in C. By adding a counter term, we renormalize the coupling $\lambda _3$ with the renormalization condition,

$$\begin{aligned} \frac{\partial ^4}{\partial h^2 \partial \phi ^2} V_\mathrm{eff} \Big |_{h=0, \phi =M} = \lambda _3, \end{aligned}$$

(5.2)

where $V_\mathrm{eff}$ is the sum of the tree-level potential and $\Delta V_\mathrm{1-loop}$, and $\lambda _3$ is the renormalized coupling. As a result, we obtain

$$\begin{aligned} V_\mathrm{eff} \supset \left[ \frac{1}{4} \lambda _3 - \frac{|Y_\mathrm{D}|^2 |Y_\mathrm{N}|^2}{16 \pi ^2} \left( \ln \left[ \frac{\phi ^2}{M^2}\right] -3 \right) \right] h^2 \phi ^2. \end{aligned}$$

(5.3)

Substituting $\phi =M$, we obtain the SM Higgs self-energy correction as

$$\begin{aligned} \Delta m_\mathrm{h}^2 = \frac{3 |Y_\mathrm{D}|^2 |Y_\mathrm{N}|^2}{8 \pi ^2} M^2 \sim \frac{3 m_\nu M_\mathrm{N}^3}{4 \pi ^2 v^2} \end{aligned}$$

(5.4)

where we have used the seesaw formula, $m_\nu \sim Y_\mathrm{D}^2 v^2/M_\mathrm{N}$ [36,37,38,39,40,41]. If $\Delta m_\mathrm{h}^2$ is much larger than the electroweak scale, we need a fine-tuning of the tree-level Higgs mass ($|\lambda _3| M^2/2$) to reproduce the correct Higgs VEV, $v=246$ GeV. Here, we introduce the naturalness condition as

$$\begin{aligned} \delta = \frac{m_\mathrm{h}^2}{2 |\Delta m_\mathrm{h}^2|} \gtrsim 1. \end{aligned}$$

(5.5)

For example, when the light neutrino mass scale is around $m_\nu \simeq 0.1$ eV after the seesaw mechanism, we have an upper bound for the Majorana mass as $M_\mathrm{N} \lesssim 4 \times 10^6$ GeV.

For the two-loop diagrams involving $Z^\prime$ boson and top quark (for the Feynman diagrams, see Fig. 4 in [29]), we have

$$\begin{aligned} \Delta V_\mathrm{2-loop} \supset - \frac{2 \alpha _{BL}^2 m_\mathrm{t}^2}{\pi ^2 v^2} h^2 \phi ^2 \left( \ln [\phi ^2] + C \right) , \end{aligned}$$

(5.6)

where the logarithmic divergence and the terms independent of $\phi$ are all encoded in C. Following the same strategy as the above, we obtain

$$\begin{aligned} \Delta m_\mathrm{h}^2 = \frac{3 \alpha _{BL} m_\mathrm{t}^2}{4 \pi ^2 v^2} M_{Z^\prime }^2. \end{aligned}$$

(5.7)

The dashed lines shown in Fig. 4 are plotted by using the condition $\delta =1$ in Eq. (5.5).

6 Conclusions

We have considered the minimal $B-L$ extension of the Standard Model, where the anomaly-free global $B-L$ symmetry in the Standard Model is gauged and three right-hand neutrinos and a $B-L$ Higgs field are introduced. This model is very simple and well motivated, since the right-handed neutrinos acquire their Majorana masses associated with the $B-L$ gauge symmetry breaking, and the seesaw mechanism for the neutrino mass generation is automatically implemented. Motivated by the argument that the Higgs model can be free from the gauge hierarchy problem once the classically conformal symmetry is imposed in the model, we have introduced the classically conformal symmetry to the minimal $B-L$ model. In this context, the $B-L$ symmetry is radiatively broken by the Coleman–Weinberg mechanism and this breaking is the sole origin of all mass parameters in the model. The electroweak symmetry breaking is realized by the negative mass term for the Higgs doublet, which is subsequently generated through the $B-L$ gauge symmetry breaking. Therefore, the electroweak symmetry breaking originates from the radiative $B-L$ gauge symmetry breaking.

In the context of the classically conformal $B-L$ model, we have investigated the electroweak vacuum instability problem. With the measured Higgs boson mass around 125 GeV, it turns out that the electroweak vacuum is not the true minimum in the effective Higgs potential of the Standard Model. In other words, the electroweak symmetry is radiatively broken at some energy much higher than the electroweak scale. This ruins the theoretical consistency of our model that the radiative $B-L$ symmetry breaking is the sole origin of the mass. We have analyzed the renormalization group evolutions of the model couplings at the two-loop level with the recent results of the Higgs boson mass and top quark mass measurements at the LHC. We have identified parameter regions which satisfy the conditions of the stability of the electroweak vacuum and the perturbativity of the running couplings, as well as the current collider bounds from the search for the $B-L$ gauge boson, in particular, at the LHC Run-2.

In addition, we have considered the naturalness of the electroweak scale against self-energy corrections for the Higgs doublet. We have refined the previously obtained results in a theoretically consistent way for the Coleman–Weinberg effective potential, and derived the naturalness bounds on the $B-L$ gauge boson and the right-handed neutrino masses. The allowed regions satisfying the naturalness bounds can be tested in the future collider experiments.

Appendices

Appendix A: The beta functions for the SM couplings

1.1 A.1: The one-loop beta functions for the SM gauge couplings

We have

$$\begin{aligned} \beta _{g_{1}}^{(1)} = \frac{41}{10} g_{1}^3,\quad \beta _{g_{2}}^{(1)} = -\frac{19}{6} g_{2}^3,\quad \beta _{g_{3}}^{(1)} = -7 g_{3}^3. \end{aligned}$$

(A.1)

1.2 A.2: The one-loop beta function for the top Yukawa coupling

We have

$$\begin{aligned} \beta _{y_{\mathrm{t}}}^{(1)}= & {} y_{\mathrm{t}}\bigg (-\frac{17}{20} g_{1}^2-\frac{9 g_{2}^2}{4}- 8 g_{3}^2+\frac{9 y_{\mathrm{t}}^2}{2}\bigg ). \end{aligned}$$

(A.2)

1.3 A.3: The one-loop beta function for the quartic Higgs coupling

We have

$$\begin{aligned} \beta _{\lambda }^{(1)}= & {} -\lambda \bigg (\frac{9 g_{1}^2}{5}+9 g_{2}^2\bigg )+\frac{9}{4} \bigg (\frac{2}{5} g_{1}^2 g_{2}^2+ \frac{3 g_{1}^4}{25}+ g_{2}^{4}\bigg )\nonumber \\&+12 \lambda ^{2}+12 \lambda y_{\mathrm{t}}^{2}-12 y_{\mathrm{t}}^{4}. \end{aligned}$$

(A.3)

1.4 A.4: The two-loop beta functions for the gauge couplings

We have

$$\begin{aligned} \beta _{g_{1}}^{(2)}= & {} g_{1}^3 \Big (\frac{199 g_{1}^2}{50}+ \frac{27 g_{2}^2}{10}+ \frac{44 g_{3}^2}{5}- \frac{17 y_{\mathrm{t}}^2}{10}\Big ), \nonumber \\ \beta _{g_{2}}^{(2)}= & {} g_{2}^3 \Big (\frac{9 g_{1}^2}{10}+ \frac{35 g_{2}^2}{6}+ 12 g_{3}^2- \frac{3 y_{\mathrm{t}}^2}{2}\Big ), \nonumber \\ \beta _{g_{3}}^{(2)}= & {} g_{3}^3 \Big (\frac{11 g_{1}^2}{10}+ \frac{9 g_{2}^2}{2}-26 g_{3}^{2}- 2 y_{\mathrm{t}}^2\Big ). \end{aligned}$$

(A.4)

1.5 A.5: The two-loop beta function for the top Yukawa coupling

We have

$$\begin{aligned} \beta _{y_{\mathrm{t}}}^{(2)}= & {} y_{\mathrm{t}}\bigg (y_{\mathrm{t}}^2 \bigg (\frac{393 g_{1}^2}{80}+\frac{225 g_{2}^2}{16}+36 g_{3}^2\bigg )- \frac{9}{20} g_{1}^2 g_{2}^2\nonumber \\&+ \frac{19}{15} g_{1}^2 g_{3}^2+\frac{1187 g_{1}^4}{600}+ 9 g_{2}^2 g_{3}^2- \frac{23 g_{2}^{4}}{4}-108 g_{3}^4\nonumber \\&+ \frac{3 \lambda ^2}{2}- 6\lambda y_{\mathrm{t}}^2- 12 y_{\mathrm{t}}^{4}\bigg ). \end{aligned}$$

(A.5)

1.6 A.6: The two-loop beta function for the Higgs quartic coupling

We have

$$\begin{aligned} \beta _{\lambda }^{(2)}= & {} \bigg ( 10 \lambda y_{\mathrm{t}}^2 \bigg (\frac{17 g_{1}^2}{20}+\frac{9 g_{2}^2}{4}+8 g_{3}^2\bigg ) + 18 \lambda ^2 \bigg (\frac{3 g_{1}^2}{5}+3g_{2}^2\bigg ) \nonumber \\&- \lambda \bigg (-\frac{117}{20} g_{1}^2 g_{2}^2-\frac{1887}{200} g_{1}^4+\frac{73g_{2}^4}{8}\bigg ) -\frac{1677}{200} g_{1}^4 g_{2}^2 \nonumber \\&-\frac{289}{40} g_{1}^2 g_{2}^4- \frac{3}{5} g_{1}^2 y_{\mathrm{t}}^2 \bigg (\frac{57 g_{1}^2}{10}-21 g_{2}^2\bigg )-\frac{3411 g_{1}^6}{1000} \nonumber \\&- \frac{16}{5} g_{1}^2 y_{\mathrm{t}}^4+\frac{305 g_{2}^6}{8}- \frac{9}{2} g_{2}^4 y_{\mathrm{t}}^2-64 g_{3}^2 y_{\mathrm{t}}^4-78 \lambda ^3\nonumber \\&-72 \lambda ^2 y_{\mathrm{t}}^2 - 3\lambda y_{\mathrm{t}}^4+60 y_{\mathrm{t}}^6\bigg ). \end{aligned}$$

(A.6)

In our analysis, we numerically solve the SM RG equations with the following boundary conditions at $\mu =m_\mathrm{t}$ [30]⁴:

$$\begin{aligned} g_3(m_\mathrm{t})= & {} \sqrt{\frac{5}{3}} \left[ 1.1666 + 0.00314 \left( \frac{\alpha _3(m_\mathrm{Z}) - 0.1184}{0.0007} \right) \right. \nonumber \\&\left. - 0.00046 \left( \frac{m_\mathrm{t}}{\mathrm{GeV}} - 173.34 \right) \right] , \nonumber \\ g_2(m_\mathrm{t})= & {} 0.64779 + 0.00004 \left( \frac{m_\mathrm{t}}{\mathrm{GeV}} - 173.34 \right) \nonumber \\&+ 0.00011 \left( \frac{m_\mathrm{W} - 80.384{\mathrm{GeV}}}{0.014\mathrm{GeV}} \right) , \nonumber \\ g_1(m_\mathrm{t})= & {} 0.35830 + 0.00011 \left( \frac{m_\mathrm{t}}{\mathrm{GeV}} - 173.34 \right) \nonumber \\&- 0.00020\left( \frac{m_\mathrm{W} - 80.384{\mathrm{GeV}}}{0.014\mathrm{GeV}} \right) ,\nonumber \\ y_\mathrm{t}(m_\mathrm{t})= & {} 0.93690 + 0.00556 \left( \frac{m_\mathrm{t}}{\mathrm{GeV}} - 173.34 \right) \nonumber \\&- 0.00042 \left( \frac{\alpha _3(m_\mathrm{Z}) - 0.1184}{0.0007} \right) , \nonumber \\ \lambda (m_\mathrm{t})= & {} 0.12604 + 0.00206 \left( \frac{m_\mathrm{h}}{\mathrm{GeV}} - 125.15 \right) \nonumber \\&- 0.00004 \left( \frac{m_\mathrm{t}}{\mathrm{GeV}} - 173.34\right) . \end{aligned}$$

(A.7)

We have used the inputs, $\alpha _3(m_\mathrm{Z}) = 0.1184$ and $m_\mathrm{W}=80.384$ GeV.

Appendix B: The beta functions for the couplings in the U(1)$_{B-L}$ extended SM

1.1 B.1: The one-loop beta functions for the gauge couplings

We have

$$\begin{aligned} \beta _{g_{1}}^{(1)}= & {} \frac{1}{10} \left( g_{1} \Bigg (32 \sqrt{\frac{5}{3}} g_{BL} g_{BY}+41 g_{BY}^2+180 g_{YB}^2 \right) \nonumber \\&+ 32 \sqrt{10} g_{1}^2 g_{YB}+41 g_{1}^3\nonumber \\&+4 g_{BY} g_{YB} \Bigg (15 \sqrt{6} g_{BL}+ 4 \sqrt{10} g_{BY}\Bigg )\Bigg ), \nonumber \\ \beta _{g_{2}}^{(1)}= & {} -\frac{19}{6} g_{2}^3, \nonumber \\ \beta _{g_{3}}^{(1)}= & {} -7 g_{3}^3, \nonumber \\ \beta _{g_{BY}}^{(1)}= & {} \frac{1}{10} \Bigg (4 g_{1} g_{YB} \Big (15 \sqrt{6} g_{BL}+4 \sqrt{10} g_{BY} \Bigg )\nonumber \\&+ g_{1}^2 \Bigg (32 \sqrt{\frac{5}{3}} g_{BL}+41 g_{BY}\Bigg ) \nonumber \\&+ g_{BY} \Bigg (64 \sqrt{\frac{5}{3}} g_{BL} g_{BY}+120 g_{BL}^2+41 g_{BY}^2\Bigg )\Bigg ), \nonumber \\ \beta _{g_{YB}}^{(1)}= & {} \frac{1}{10} \Bigg ( g_{1} \Bigg (41 \sqrt{\frac{2}{3}} g_{BL} g_{BY} {+}16 \sqrt{10} \Bigg (\frac{2 g_{BL}^2}{3}+2 g_{YB}^2\Bigg )\Bigg ) \nonumber \\&+ 41 g_{1}^2 g_{YB}+4 g_{YB} \Bigg (8 \sqrt{\frac{5}{3}} g_{BL} g_{BY} \nonumber \\&+45 \Bigg (\frac{2 g_{BL}^2}{3}+ g_{YB}^2\Bigg )\Bigg )\Bigg ), \nonumber \\ \beta _{g_{BL}}^{(1)}= & {} \sqrt{\frac{3}{2}}\Bigg (\frac{1}{10} \Big (4 \sqrt{\frac{2}{3}} g_{BL} \Bigg (g_{YB} \Bigg (4 \sqrt{10} g_{1} +45 g_{YB}\Bigg ) \nonumber \\&+30 g_{BL}^2\Bigg ) + g{BY} \Bigg ( g_{YB} \Bigg (41 g_{1}^2+16 \sqrt{10} g_{YB}\Bigg ) \nonumber \\&+ 32 \sqrt{10} g_{YB}^2\Bigg )+41 \sqrt{\frac{2}{3}} g_{BL} g_{BY}^2\Bigg ) \Bigg ). \end{aligned}$$

(B.1)

1.2 B.2: The one-loop beta function for the top Yukawa coupling

We have

$$\begin{aligned} \beta _{y_{\mathrm{t}}}^{(1)}= & {} \frac{9 y_{\mathrm{t}}^3}{2}- y_{\mathrm{t}} \Bigg (\sqrt{\frac{5}{3}} g_{BY} g_{BL}+\frac{2}{3} g_{BL}^2 + \sqrt{\frac{5}{2}} g_{1} g_{YB}\nonumber \\&+ \frac{17 g_{1}^2}{20}+\frac{9 g_{2}^2}{4}+8 g_{3}^2+\frac{17 g_{BY}^2}{20}+g_{YB}^2\Bigg ). \end{aligned}$$

(B.2)

1.3 B.3: The one-loop beta function for the Majorana Yukawa coupling

We have

$$\begin{aligned} \beta _{Y_{\mathrm{N}}}^{(1)}= & {} 2 \Bigg (10 \Bigg (\frac{Y_{\mathrm{N}}}{2}\Bigg )^3-9 \frac{Y_{\mathrm{N}}}{2}\Bigg (\frac{2}{3} g_{BL}^2+g_{YB}^2\Bigg )\Bigg ). \end{aligned}$$

(B.3)

1.4 B.4: The one-loop beta function for the scalar quartic couplings

We have

$$\begin{aligned} \beta _{\lambda }^{(1)}= & {} 2\Big ( \frac{\lambda }{2} \Big (-\frac{9}{5} g_{1}^2-9 g_{2}^2-\frac{9 g_{BY}^2}{5}+12 y_{\mathrm{t}}^2\Big ) \nonumber \\&+ 24 \Big (\frac{\lambda }{2}\Big )^2+\frac{9}{20} g_{1}^2 g_{2}^2+\frac{27}{100} g_{1}^2 g_{BY}^2 \nonumber \\&+ \frac{27}{200} g_{1}^4 {+}\frac{9}{20} g_{2}^2 g_{BY}^2+\frac{9 g_{2}^4}{8}+\frac{27 g_{BY}^4}{200} {+} \lambda _{3}^2-6 y_{\mathrm{t}}^4 \Big ), \nonumber \\ \beta _{\lambda _{2}}^{(1)}= & {} 2 \Big (-36 \lambda _{2} \Big (\frac{2}{3} g_{BL}^2+ g_{YB}^2\Big )+ 144 g_{YB}^2 g_{BL}^2 \nonumber \\&+ 48 g_{BL}^4+108 g_{YB}^4+ 10 \lambda _{2}^2+\lambda _{3}^2+3 \lambda _{2} Y_{\mathrm{N}}^2-\frac{3}{2} Y_{\mathrm{N}}^4\Big ), \nonumber \\ \beta _{\lambda _{3}}^{(1)}= & {} -\lambda _3 \Big (24 g_{BL}^2+\frac{9}{10} g_1^2+\frac{9}{2} g_2^2 +\frac{9 g_{BY}^2}{10}+36 g_{YB}^2\Big ) \nonumber \\&+ \frac{36}{5} \sqrt{6} g_1 g_{BY} g_{YB} g_{BL}+\frac{36}{5} g_{BY}^2 g_{BL}^2 + \frac{54}{5} g_1^2 g_{YB}^2 \nonumber \\&+ 4 \lambda _2^2+6 \lambda \lambda _3+8 \lambda _2 \lambda _3 + \lambda _3 \Big (3 Y_{\mathrm{N}}^2+6 y_{\mathrm{t}}^2\Big ). \end{aligned}$$

(B.4)

1.5 B.5: The two-loop beta functions for the gauge couplings

We have

$$\begin{aligned} \beta _{g_{1}}^{(2)}= & {} \frac{1}{100} \Bigg (398 g_{1}^5+328 \sqrt{10} g_{BY} g_{1}^4+398 g_{BY} g_{1}^4 \\&+328 \sqrt{10} g_{YB} g_{1}^4\\&+270 g_{2}^2 g_{1}^3+ 880 g_{3}^2 g_{1}^3 + 328 \sqrt{10} g_{BY}^2 g_{1}^3\\&+1318 g_{BY}^2 g_{1}^3 + 920 g_{YB}^2 g_{1}^3-170 y_{\mathrm{t}}^2 g_{1}^3\\&+ \frac{1840}{3} g_{BL}{}^2 g_{1}^3+ 328 \sqrt{10} g_{BY} g_{YB} g_{1}^3 \\&+ 3680 g_{BY} g_{YB} g_{1}^3+656 \sqrt{\frac{5}{3}} g_{BY} g_{BL} g_{1}^3 \\&+ 328 \sqrt{10} g_{BY}^3 g_{1}^2 + 1318 g_{BY}^3 g_{1}^2\\&+1120 \sqrt{10} g_{BY} g_{YB}^2 g_{1}^2 + 920 g_{BY} g_{YB}^2 g_{1}^2 \\&-200 g_{BY} y_{\mathrm{t}}^2 g_{1}^2+ \frac{2240}{3} \sqrt{10} g_{BY} g_{BL}^2 g_{1}^2 \\&+\frac{1840}{3} g_{BY} g_{BL}^2 g_{1}^2+360 \sqrt{10} g_{2}^2 g_{BY} g_{1}^2 \\&+ 270 g_{2}^2 g_{BY} g_{1}^2+320 \sqrt{10} g_{3}^2 g_{BY} g_{1}^2\\&+880 g_{3}^2 g_{BY} g_{1}^2 + 1120 \sqrt{10} g_{BY}^2 g_{YB} g_{1}^2 \\&+3680 g_{BY}^2 g_{YB} g_{1}^2+656 \sqrt{\frac{5}{3}} g_{BY}^2 g_{BL} g_{1}^2 \\&+ 3680 \sqrt{\frac{2}{3}} g_{BY}^2 g_{BL} g_{1}^2 + 328 \sqrt{10} g_{BY}^4 g_{1} \\&+920 g_{BY}^4 g_{1}+14400 g_{YB}^4 g_{1} \\&+ 360 \sqrt{10} g_{2}^2 g_{BY}^2 g_{1} +1800 g_{2}^2 g_{BY}^2 g_{1} \\&+ 320 \sqrt{10} g_{3}^2 g_{BY}^2 g_{1}+ 1600 g_{3}^2 g_{BY}^2 g_{1} \\&+ 1120 \sqrt{10} g_{BY}^2 g_{YB}^2 g_{1}+ 5600 g_{BY}^2 g_{YB}^2 g_{1} \\&- 80 g_{BY}^2 y_{\mathrm{t}}^2 g_{1} - 85 \sqrt{10} g_{BY} g_{YB} y_{\mathrm{t}}^2 g_{1} \end{aligned}$$

$$\begin{aligned}&+\frac{2240}{3} \sqrt{10} g_{BY}^2 g_{BL}^2 g_{1} \\&+\frac{11200}{3} g_{BY}^2 g_{BL}^2 g_{1}+9600 g_{YB}^2 g_{BL}^2 g_{1} \\&- 45 g_{BY}^2 Y_{\mathrm{N}}^2 g_{1}+1120 \sqrt{10} g_{BY}^3 g_{YB} g_{1} \\&+ 2240 \sqrt{\frac{5}{3}}g_{BY}^3 g_{BL} g_{1} +3680 \sqrt{\frac{2}{3}} g_{BY}^3 g_{BL} g_{1} \\&-100 \sqrt{\frac{5}{3}} g_{BY} y_{\mathrm{t}}^2 g_{BL} g_{1} \\&+ 920 g_{BY}^5+ 14400 g_{BY} g_{YB}^4+1800 g_{2}^2 g_{BY}^3\\&+1600 g_{3}^2 g_{BY}^3+5600 g_{BY}^3 g_{YB}^2 \\&- 50 \sqrt{10} g_{BY}^2 g_{YB} y_{\mathrm{t}}^2+\frac{11200}{3} g_{BY}^3 g_{BL}^2\\&+ 9600 g_{BY} g_{YB}^2 g_{BL}^2 \\&- 15 \sqrt{15} g_{BY}^2 g_{BL} Y_{\mathrm{N}}^2+ 2240 \sqrt{ \frac{5}{3} } g_{BY}^4 g_{BL} \\&- 80 \sqrt{\frac{5}{3}} g_{BY}^2 y_{\mathrm{t}}^2 g_{BL}\Bigg ), \\ \beta _{g_{2}}^{(2)}= & {} \frac{1}{30} g_{2}^3 \Bigg (4 \sqrt{10} g_{1} g_{YB}+11 g_{1}^2\\&+45 g_{2}^2-260 g_{3}^2 \\&+ 8\sqrt{\frac{5}{3}} g_{BL} g_{BY}+\frac{40 g_{BL}^2}{3}+11 g_{BY}^2\\&+20 g_{YB}^2-20 y_{\mathrm{t}}^2\Bigg ), \\ \beta _{g_{3}}^{(2)}= & {} \frac{1}{10} g_{3}^3 \Big (36 \sqrt{10} g_{1} g_{YB}+27 g_{1}^2\\&+175 g_{2}^2+360 g_{3}^2 \\&+ 24\sqrt{15} g_{BL} g_{BY}+120 g_{BL}^2\\&+27 g_{BY}^2+180 g_{YB}^2-45 y_{\mathrm{t}}^2\Big ), \end{aligned}$$

$$\begin{aligned} \beta _{g_{BY}}^{(2)}= & {} \frac{1}{100} \Big (18 g_{BY} g_{1}^4+380 g_{YB} g_{1}^4+328 \sqrt{\frac{5}{3}} g_{BL} g_{1}^4\\&+18 g_{BY}^2 g_{1}^3+328 \sqrt{10} g_{YB}^2 g_{1}^3 \\&+ 164 \sqrt{10} g_{BY} g_{YB} g_{1}^3 + 380 g_{BY} g_{YB} g_{1}^3\\&+328 \sqrt{\frac{5}{3}} g_{BY} g_{BL} g_{1}^3+ 920 \sqrt{\frac{2}{3}} g_{BY} g_{BL} g_{1}^3 \\&+1840 \sqrt{\frac{2}{3}} g_{YB} g_{BL}g_{1}^3+ 18 g_{BY}^3 g_{1}^2+920 g_{YB}^3 g_{1}^2\\&+\frac{2240}{3} \sqrt{\frac{5}{3}} g_{BL}^3 g_{1}^2+ 328 \sqrt{10} g_{BY} g_{YB}^2 g_{1}^2 \\&+ 1840 g_{BY} g_{YB}^2 g_{1}^2+ \frac{3680}{3} g_{BY} g_{BL}^2 g_{1}^2 \\&+\frac{1840}{3} g_{YB} g_{BL}^2 g_{1}^2+ 180 g_{2}^2 g_{YB} g_{1}^2+880 g_{3}^2 g_{YB}g_{1}^2 \\&+ 380 g_{BY}^2 g_{YB} g_{1}^2-85\sqrt{10} y_{\mathrm{t}}^{*} g_{YB} y_{\mathrm{t}} g_{1}^2\\&+ 320\sqrt{\frac{5}{3}} g_{3}^2 g_{BL} g_{1}^2+328 \sqrt{\frac{5}{3}} g_{BY}^2 g_{BL} g_{1}^2 \\&+ 920 \sqrt{\frac{2}{3}} g_{BY}^2 g_{BL} g_{1}^2+1120 \sqrt{\frac{5}{3}} g_{YB}^2 g_{BL}g_{1}^2\\&+ 2896 \sqrt{\frac{5}{3}} g_{BY} g_{YB} g_{BL} g_{1}^2{+}1840 \sqrt{\frac{2}{3}} g_{BY}g_{YB} g_{BL} g_{1}^2 \\ \end{aligned}$$

$$\begin{aligned}&\quad -100 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} y_{\mathrm{t}} g_{BL} g_{1}^2+18g_{BY}^4 g_{1}+ 920 g_{BY} g_{YB}^3 g_{1}\\&\quad +\frac{2240}{3} \sqrt{\frac{5}{3}} g_{BY} g_{BL}^3 g_{1} \\&\quad + \frac{11200}{3} \sqrt{\frac{2}{3}} g_{BY}g_{BL}^3 g_{1}+3200 \sqrt{6} g_{YB} g_{BL}^3 g_{1}\\&\quad + 90 g_{2}^2 g_{BY}^2g_{1}+1840 g_{BY}^2 g_{YB}^2 g_{1} \\&\quad + \frac{2240}{3} \sqrt{10} g_{BY}^2 g_{BL}^2g_{1}+\frac{1120}{3} \sqrt{10} g_{BY} g_{YB}g_{BL}^2 g_{1}\\&\quad + \frac{1840}{3} g_{BY} g_{YB} g_{BL}^2 g_{1}-60 \sqrt{15}g_{BY} g_{BL} Y_{\mathrm{N}}^2 g_{1} \\&\quad +180 g_{2}^2 g_{BY} g_{YB} g_{1}+880 g_{3}^2 g_{BY} g_{YB} g_{1} \\&\quad - 50 \sqrt{10} y_{\mathrm{t}}^{*} g_{BY} g_{YB} y_{\mathrm{t}} g_{1}+328\sqrt{\frac{5}{3}} g_{BY}^3 g_{BL} g_{1}\\&\quad +920 \sqrt{\frac{2}{3}} g_{BY}^3 g_{BL} g_{1} \\&\quad + 1120 \sqrt{\frac{5}{3}} g_{BY} g_{YB}^2 g_{BL}g_{1}+5600 \sqrt{\frac{2}{3}} g_{BY} g_{YB}^2 g_{BL} g_{1}\\&\quad + 120 \sqrt{15} g_{2}^2 g_{BY} g_{BL} g_{1} \nonumber \\&\quad + 600 \sqrt{6} g_{2}^2 g_{BY} g_{BL} g_{1}+320\sqrt{\frac{5}{3}} g_{3}^2 g_{BY} g_{BL} g_{1}\\&\quad +1600 \sqrt{\frac{2}{3}} g_{3}^2 g_{BY}g_{BL} g_{1} \nonumber \\&\quad + 2896 \sqrt{\frac{5}{3}} g_{BY}^2 g_{YB} g_{BL} g_{1}+1840\sqrt{\frac{2}{3}} g_{BY}^2 g_{YB} g_{BL} g_{1}\\&\quad - 80 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}} g_{BL} g_{1}+560 \sqrt{10} g_{BY}^2 g_{YB}^3 \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\quad + \frac{11200}{3} \sqrt{\frac{2}{3}} g_{BY}^2 g_{BL}^3+3200 \sqrt{6} g_{BY} g_{YB} g_{BL}^3\\&\quad +1120 \sqrt{10} g_{BY}^3 g_{BL}^2-\frac{400}{3} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}} g_{BL}^2 \nonumber \\&\quad - 300 g_{BY} g_{BL}^2 Y_{\mathrm{N}}^2+180 \sqrt{10} g_{2}^2 g_{BY}^2 g_{YB}\\&\quad + 160 \sqrt{10} g_{3}^2 g_{BY}^2 g_{YB}-425 y_{\mathrm{t}}^{*} g_{BY} g_{YB}^2 y_{\mathrm{t}} \nonumber \\&\quad + 4800 \sqrt{6} g_{BY} g_{YB}^3 g_{BL}+600 \sqrt{6} g_{2}^2 g_{BY}^2 g_{BL}\\&\quad + 1600 \sqrt{\frac{2}{3}} g_{3}^2 g_{BY}^2 g_{BL}+5600 \sqrt{\frac{2}{3}} g_{BY}^2g_{YB}^2 g_{BL} \nonumber \\&\quad + 1840 \sqrt{\frac{2}{3}} g_{BY}^3 g_{YB} g_{BL}-500 \sqrt{\frac{2}{3}} y_{\mathrm{t}}^{*} g_{BY} g_{YB} y_{\mathrm{t}} g_{BL}\\&\quad +120 \sqrt{15} g_{2}^2 g_{BL} g_{1}^2+560 \sqrt{10} g_{BY} g_{YB}^3 g_{1} \nonumber \\&\quad + 160 \sqrt{10} g_{3}^2 g_{BY} g_{YB} g_{1}+4800 \sqrt{6} g_{YB}^3 g_{BL} g_{1}\\&\quad +380 g_{BY}^3 g_{YB} g_{1}+\frac{3680}{3} g_{BY}^2 g_{BL}^2 g_{1} \nonumber \\&\quad + 164 \sqrt{10} g_{BY}^4 g_{YB}+90 g_{2}^2 g_{BY} g_{1}^2\\&\quad +164 \sqrt{10} g_{BY}^2 g_{YB} g_{1}^2+920 \sqrt{\frac{2}{3}} g_{BY}^4 g_{BL} \Bigg ), \end{aligned}$$

$$\begin{aligned} \beta _{g_{YB}}^{(2)}= & {} \frac{1}{100} \Big (920 g_{1} g_{YB}^4+560 \sqrt{10} g_{BY} g_{YB}^4+4800 \sqrt{6} g_{BL} g_{YB}^4\\&+ 328 \sqrt{10} g_{1}^2 g_{YB}^3+9600 g_{BL}^2 g_{YB}^3 \\&+ 1840 g_{1} g_{BY} g_{YB}^3 + 1120 \sqrt{\frac{5}{3}} g_{1} g_{BL} g_{YB}^3\\&+920 \sqrt{\frac{2}{3}} g_{1}g_{BL} g_{YB}^3+ 1120 \sqrt{\frac{5}{3}} g_{BY} g_{BL} g_{YB}^3 \\&+5600 \sqrt{\frac{2}{3}} g_{BY} g_{BL} g_{YB}^3+ 380 g_{1}^3g_{YB}^2+164 \sqrt{10} g_{BY}^3 g_{YB}^2\\&+3200 \sqrt{6} g_{BL}^3 g_{YB}^2 \\&+ 180 g_{1} g_{2}^2 g_{YB}^2+880 g_{1} g_{3}^2 g_{YB}^2+380 g_{1} g_{BY}^2 g_{YB}^2\\&+ \frac{1120}{3} \sqrt{10} g_{1} g_{BL}^2 g_{YB}^2+\frac{1840}{3} g_{1} g_{BL}^2g_{YB}^2 \\&+ \frac{1120}{3} \sqrt{10} g_{BY} g_{BL}^2 g_{YB}^2+\frac{11200}{3} g_{BY} g_{BL}^2 g_{YB}^2\\&+ 164 \sqrt{10} g_{1}^2 g_{BY}g_{YB}^2+180 \sqrt{10} g_{2}^2 g_{BY} g_{YB}^2 \\&+ 160 \sqrt{10} g_{3}^2 g_{BY} g_{YB}^2+656 \sqrt{\frac{5}{3}} g_{1}^2 g_{BL}g_{YB}^2\\&+1840 \sqrt{\frac{2}{3}} g_{1}^2 g_{BL} g_{YB}^2+1840 \sqrt{\frac{2}{3}} g_{BY}^2 g_{BL} g_{YB}^2 \\&+ 2896 \sqrt{\frac{5}{3}} g_{1}g_{BY} g_{BL} g_{YB}^2+1840 \sqrt{\frac{2}{3}} g_{1} g_{BY} g_{BL} g_{YB}^2\\&+ 6400 g_{BL}^4 g_{YB}+18 g_{1}g_{BY}^3 g_{YB} \\&+\frac{2240}{3} \sqrt{\frac{5}{3}} g_{1} g_{BL}^3 g_{YB}+ \frac{1840}{3} \sqrt{\frac{2}{3}} g_{1} g_{BL}^3 g_{YB}\\&+\frac{2240}{3} \sqrt{\frac{5}{3}} g_{BY} g_{BL}^3 g_{YB} \\&+ \frac{2240}{3} \sqrt{10} g_{BY}^2 g_{BL}^2 g_{YB}+\frac{3680}{3} g_{BY}^2 g_{BL}^2 g_{YB} \\ \end{aligned}$$

$$\begin{aligned}&\quad + \frac{2896}{3} \sqrt{10} g_{1} g_{BY} g_{BL}^2 g_{YB}+\frac{3680}{3} g_{1} g_{BY} g_{BL}^2 g_{YB}\\&\quad + 18 g_{1}^3 g_{BY} g_{YB}+90 g_{1} g_{2}^2 g_{BY} g_{YB} \\&\quad - 80 y_{\mathrm{t}}^{*} g_{BY}^2 y_{\mathrm{t}} g_{YB}-200 y_{\mathrm{t}}^{*} g_{1} g_{BY} y_{\mathrm{t}} g_{YB}\\&\quad + 328 \sqrt{\frac{5}{3}} g_{1}^3 g_{BL} g_{YB}+380 \sqrt{\frac{2}{3}} g_{1}^3 g_{BL}g_{YB} \\&\quad + 328 \sqrt{\frac{5}{3}} g_{BY}^3 g_{BL} g_{YB}+920 \sqrt{\frac{2}{3}} g_{BY}^3 g_{BL} g_{YB}\\&\quad +120 \sqrt{15} g_{1} g_{2}^2 g_{BL} g_{YB}+60 \sqrt{6} g_{1} g_{2}^2 g_{BL} g_{YB} \\&\quad + 320 \sqrt{\frac{5}{3}} g_{1} g_{3}^2 g_{BL} g_{YB}+880\sqrt{\frac{2}{3}} g_{1} g_{3}^2 g_{BL} g_{YB}\\&\quad + 328 \sqrt{\frac{5}{3}} g_{1} g_{BY}^2 g_{BL} g_{YB}+380 \sqrt{\frac{2}{3}} g_{1} g_{BY}^2 g_{BL} g_{YB} \\&\quad + 328 \sqrt{\frac{5}{3}} g_{1}^2 g_{BY} g_{BL} g_{YB}+920 \sqrt{\frac{2}{3}} g_{1}^2 g_{BY} g_{BL}g_{YB}\\&\quad +120 \sqrt{15} g_{2}^2 g_{BY} g_{BL} g_{YB} \\&\quad +600 \sqrt{6} g_{2}^2 g_{BY} g_{BL} g_{YB}\\&\quad + 320 \sqrt{\frac{5}{3}} g_{3}^2 g_{BY} g_{BL} g_{YB}+1600 \sqrt{\frac{2}{3}} g_{3}^2 g_{BY} g_{BL} g_{YB} \\&\quad - 170 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} g_{1} y_{\mathrm{t}} g_{BL} g_{YB}\\&\quad - 100 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}} g_{BL} g_{YB}-180 Y_{\mathrm{N}} g_{BY}^2 Y_{\mathrm{N}} g_{YB} \\&\quad + \frac{2240}{9}\sqrt{10} g_{1} g_{BL}^4+\frac{22400}{9} g_{BY} g_{BL}^4\\&\quad +\frac{4480}{3} \sqrt{\frac{5}{3}} g_{BY}^2 g_{BL}^3+ \\&\quad + \frac{3680}{3} \sqrt{\frac{2}{3}} g_{1} g_{BY} g_{BL}^3+\frac{328}{3} \sqrt{10} g_{1}^3 g_{BL}^2\\&\quad + \frac{1840}{3} g_{BY}^3 g_{BL}^2+120 \sqrt{10} g_{1} g_{2}^2 g_{BL}^2 \\&\quad + \frac{320}{3} \sqrt{10} g_{1} g_{3}^2 g_{BL}^2+\frac{328}{3} \sqrt{10} g_{1} g_{BY}^2 g_{BL}^2\\&\quad + \frac{1840}{3} g_{1}^2 g_{BY} g_{BL}^2+1200 g_{2}^2 g_{BY} g_{BL}^2 \\&\quad + \frac{3200}{3} g_{3}^2 g_{BY} g_{BL}^2-\frac{100}{3} \sqrt{10} y_{\mathrm{t}}^{*} g_{1} y_{\mathrm{t}} g_{BL}^2\\&\quad - \frac{80}{3} \sqrt{10} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}} g_{BL}^2+6 \sqrt{6} g_{1} g_{BY}^3 g_{BL} \\&\quad + 6\sqrt{6} g_{1}^3 g_{BY} g_{BL}+30 \sqrt{6} g_{1} g_{2}^2 g_{BY} g_{BL}\\&\quad - 60\sqrt{10} Y_{\mathrm{N}} g_{BY} g_{BL}^2 Y_{\mathrm{N}}-170 y_{\mathrm{t}}^{*} g_{1}^2 y_{\mathrm{t}} g_{YB}\Big ), \end{aligned}$$

$$\begin{aligned} \beta _{g_{BL}}^{(2)}= & {} \sqrt{\frac{3}{2}}\frac{1}{100} \Big (920 g_{YB}^5+328 \sqrt{10} g_{1} g_{YB}^4\nonumber \\&+2240 \sqrt{\frac{5}{3}} g_{BL} g_{YB}^4 +920\sqrt{\frac{2}{3}} g_{BL} g_{YB}^4 \nonumber \\&+380 g_{1}^2 g_{YB}^3+ 380 g_{BY}^2 g_{YB}^3+\frac{2240}{3} \sqrt{10} g_{BL}^2 g_{YB}^3\nonumber \\&+\frac{41840}{3} g_{BL}^2 g_{YB}^3 + 656\sqrt{\frac{5}{3}} g_{1} g_{BL} g_{YB}^3 \nonumber \\&+3680 \sqrt{\frac{2}{3}} g_{1} g_{BL} g_{YB}^3+ 656\sqrt{\frac{5}{3}} g_{BY} g_{BL} g_{YB}^3 \nonumber \\&+\frac{4480}{3} \sqrt{\frac{5}{3}} g_{BL}^3 g_{YB}^2 + \frac{41840}{3} \sqrt{\frac{2}{3}} g_{BL}^3 g_{YB}^2 \nonumber \\&+\frac{2240}{3} \sqrt{10} g_{1} g_{BL}^2 g_{YB}^2+\frac{7360}{3} g_{1} g_{BL}^2 g_{YB}^2 \nonumber \\&+\frac{656}{3} \sqrt{10} g_{BY} g_{BL}^2 g_{YB}^2+ \frac{7360}{3} g_{BY} g_{BL}^2 g_{YB}^2 \nonumber \\&-85 \sqrt{10} y_{\mathrm{t}}^{*} g_{1} y_{\mathrm{t}} g_{YB}^2- 50 \sqrt{10} y_{\mathrm{t}}^{*} g_{BY}y_{\mathrm{t}} g_{YB}^2 \nonumber \\&+656 \sqrt{\frac{5}{3}} g_{1}^2 g_{BL} g_{YB}^2+ 380 \sqrt{\frac{2}{3}} g_{1}^2 g_{BL} g_{YB}^2 \nonumber \\&+ 240 \sqrt{15} g_{2}^2 g_{BL} g_{YB}^2+ 60 \sqrt{6} g_{2}^2 g_{BL} g_{YB}^2 \nonumber \\&+640 \sqrt{\frac{5}{3}} g_{3}^2 g_{BL} g_{YB}^2+ 880 \sqrt{\frac{2}{3}} g_{3}^2 g_{BL} g_{YB}^2 \nonumber \\&+656 \sqrt{\frac{5}{3}} g_{BY}^2 g_{BL} g_{YB}^2+ 380 \sqrt{\frac{2}{3}} g_{BY}^2 g_{BL} g_{YB}^2 \nonumber \\&-425 \sqrt{\frac{2}{3}} y_{\mathrm{t}}^{*} y_{\mathrm{t}} g_{BL} g_{YB}^2+ 18 g_{BY}^4 g_{YB} \nonumber \\&+\frac{4480}{9} \sqrt{10} g_{BL}^4 g_{YB}+\frac{80000}{9} g_{BL}^4 g_{YB} \end{aligned}$$

$$\begin{aligned}&+ \frac{4480}{3} \sqrt{\frac{5}{3}} g_{1} g_{BL}^3 g_{YB}+\frac{4480}{3} \sqrt{\frac{5}{3}} g_{BY} g_{BL}^3 g_{YB} \nonumber \\&+ \frac{7360}{3} \sqrt{\frac{2}{3}} g_{BY} g_{BL}^3 g_{YB}+18 g_{1}^2 g_{BY}^2 g_{YB} \nonumber \\&+90 g_{2}^2 g_{BY}^2 g_{YB}+\frac{656}{3} \sqrt{10} g_{1}^2 g_{BL}^2 g_{YB} \nonumber \\&+ \frac{1840}{3} g_{1}^2 g_{BL}^2 g_{YB} + 240 \sqrt{10} g_{2}^2 g_{BL}^2 g_{YB}\nonumber \\&+1200 g_{2}^2 g_{BL}^2 g_{YB} + \frac{640}{3} \sqrt{10} g_{3}^2 g_{BL}^2 g_{YB} \nonumber \\&+\frac{3200}{3} g_{3}^2 g_{BL}^2 g_{YB}+\frac{656}{3} \sqrt{10} g_{BY}^2 g_{BL}^2 g_{YB} \nonumber \\&+\frac{1840}{3} g_{BY}^2 g_{BL}^2 g_{YB}-\frac{1000}{3} y_{\mathrm{t}}^{*} y_{\mathrm{t}} g_{BL}^2 g_{YB} \nonumber \\&-100 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} g_{1} y_{\mathrm{t}} g_{BL} g_{YB}- 80 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}} g_{BL} g_{YB} \nonumber \\&-60 \sqrt{15} Y_{\mathrm{N}} g_{BY} g_{BL} Y_{\mathrm{N}} g_{YB} \nonumber \\&+\frac{80000}{9} \sqrt{\frac{2}{3}} g_{BL}^5+\frac{4480}{9} \sqrt{10} g_{BY} g_{BL}^4 \nonumber \\&+ \frac{1840}{3}\sqrt{\frac{2}{3}} g_{1}^2 g_{BL}^3+400 \sqrt{6} g_{2}^2 g_{BL}^3 \nonumber \\&+\frac{3200}{3} \sqrt{\frac{2}{3}} g_{3}^2 g_{BL}^3+\frac{1840}{3} \sqrt{\frac{2}{3}} g_{BY}^2 g_{BL}^3 \nonumber \\&-\frac{400}{3} \sqrt{\frac{2}{3}} y_{\mathrm{t}}^{*} y_{\mathrm{t}} g_{BL}^3+6 \sqrt{6} g_{BY}^4 g_{BL} +6 \sqrt{6} g_{1}^2 g_{BY}^2 g_{BL} \nonumber \\&+ 30 \sqrt{6} g_{2}^2 g_{BY}^2 g_{BL}-100 \sqrt{6} Y_{\mathrm{N}} g_{BL}^3 Y_{\mathrm{N}} \nonumber \\&+180 g_{2}^2 g_{YB}^3+880 g_{3}^2 g_{YB}^3\Big ) . \end{aligned}$$

(B.5)

1.6 B.6: The two-loop beta function for the top Yukawa coupling

We have

$$\begin{aligned} \beta _{y_{\mathrm{t}}}^{(2)}= & {} \frac{1}{600} y_{\mathrm{t}} \Big (3600 \Big (\frac{\lambda }{2}\Big )^2+500 \sqrt{15} g_{BY} y_{\mathrm{t}} g_{BL}y_{\mathrm{t}}^{*} \nonumber \\&+ 1000 y_{\mathrm{t}} g_{BL}^2 y_{\mathrm{t}}^{*}-340\sqrt{\frac{2}{3}} g_{1} g_{BY} g_{YB} g_{BL} \nonumber \\&+ 50 \sqrt{\frac{5}{3}} g_{1}^2 g_{BY} g_{BL}-\frac{100}{3} \sqrt{10} g_{1} g_{YB} g_{BL}^2 \nonumber \\&+ \frac{190}{3} g_{1}^2 g_{BL}^2+270 \sqrt{15} g_{2}^2 g_{BY} g_{BL} \nonumber \\&+450 g_{2}^2 \sqrt{\frac{5}{3}} g_{BL}^2-800g_{3}^2 g_{BY} g_{BL} -\frac{1600}{3} g_{3}^2 g_{BL}^2\nonumber \\&-100 \sqrt{\frac{5}{3}} g_{BY} g_{YB}^2 g_{BL} \nonumber \\&+\frac{26600}{3} \sqrt{\frac{5}{3}} g_{BY} g_{BL}^3+10850 g_{BY}^2 g_{BL}^2 \nonumber \\&+4016 \sqrt{\frac{5}{3}} g_{BY}^3 g_{BL}- \frac{200}{3} g_{YB}^2 g_{BL}^2 +\frac{40600}{9} g_{BL}^4 \nonumber \\&+750 \sqrt{10} g_{1} g_{YB} y_{\mathrm{t}} y_{\mathrm{t}}^{*}+1275 g_{1}^2 y_{\mathrm{t}} y_{\mathrm{t}}^{*} +3375 g_{2}^2 y_{\mathrm{t}} y_{\mathrm{t}}^{*}\nonumber \\&+12000 g_{3}^2 y_{\mathrm{t}} y_{\mathrm{t}}^{*}+1275 g_{BY}^2 y_{\mathrm{t}} y_{\mathrm{t}}^{*} \nonumber \\&+1500 g_{YB}^2 y_{\mathrm{t}} y_{\mathrm{t}}^{*}- 4050 y_{\mathrm{t}}^2 \Big (y_{\mathrm{t}}^{*}\Big )^2+405\sqrt{10} g_{1} g_{2}^2 g_{YB} \nonumber \\&-270 g_{1}^2 g_{2}^2- 400 \sqrt{10} g_{1} g_{3}^2 g_{YB} \nonumber \\&+760 g_{1}^2 g_{3}^2+25 \sqrt{10}g_{1} g_{BY}^2 g_{YB}- 106 g_{1}^2 g_{BY}^2 \nonumber \\&+2008 \sqrt{10}g_{1}^3 g_{YB}+ 16275 g_{1}^2 g_{YB}^2 \nonumber \\&+ 6650 \sqrt{10} g_{1} g_{YB}^3+1187 g_{1}^4+5400 g_{2}^2g_{3}^2-270 g_{2}^2 g_{BY}^2 \nonumber \\&+675 g_{2}^2 g_{YB}^2-3450 g_{2}^4+760 g_{3}^2 g_{BY}^2 \nonumber \\&-800 g_{3}^2 g_{YB}^2- 64800 g_{3}^4+ 95 g_{BY}^2 g_{YB}^2\nonumber \\&+1187 g_{BY}^4 +10150 g_{YB}^4+300 \lambda _{3}^2\Big ) \nonumber \\&+ \frac{320}{3} g_{BL}^2+\frac{1}{80} \Big (y_{\mathrm{t}}^2 y_{\mathrm{t}}^{*} \Big (-960 \frac{\lambda }{2} +100 \sqrt{\frac{5}{3}} g_{BY} g_{BL}\nonumber \\&+-540 y_{\mathrm{t}} y_{\mathrm{t}}^{*}+50 \sqrt{10} g_{1}g_{YB} \nonumber \\&+ 223 g_{1}^2+675 g_{2}^2+1280 g_{3}^2+223 g_{BY}^2\nonumber \\&+160 g_{YB}^2\Big ) +120 y_{\mathrm{t}}^3 \Big (y_{\mathrm{t}}^{*}\Big )^2\Big ) . \end{aligned}$$

(B.6)

1.7 B.7: The two-loop beta functions for the heavy neutrino Yukawa coupling

We have

$$\begin{aligned} \beta _{Y_{\mathrm{N}}}^{(2)}= & {} \frac{1}{20} \Big (-Y_{\mathrm{N}} \Big (-225 Y_{\mathrm{N}} \Big (\frac{2}{3} g_{BL}^2+g_{YB}^2\Big ) Y_{\mathrm{N}} \nonumber \\&+128 \sqrt{\frac{5}{3}} g_{BY} g_{BL}^3+70 g_{BY}^2 g_{BL}^2 \nonumber \\&+7380 g_{YB}^2 g_{BL}^2+ 2540 g_{BL}^4+45 Y_{\mathrm{N}}^4 \nonumber \\&+96 \sqrt{10} g_{1} g_{YB}^3 +105 g_{1}^2 g_{YB}^2+5715 g_{YB}^4 \nonumber \\&- 80 \lambda _{2}^2-20 \lambda _{3}^2\Big )+880 g_{BL}^2 Y_{\mathrm{N}}^2 Y_{\mathrm{N}} + 1320 g_{YB}^2 Y_{\mathrm{N}}^2 Y_{\mathrm{N}}\nonumber \\&-160 \lambda _{2} Y_{\mathrm{N}}^2 Y_{\mathrm{N}}- 10 Y_{\mathrm{N}}^5 . \end{aligned}$$

(B.7)

1.8 B.8: The two-loop beta functions for the scalar quartic couplings

We have

$$\begin{aligned} \beta _{\lambda }^{(2)}= & {} 2\Big (-\frac{3411 g_{1}^6}{2000}-\frac{4221 g_{BY}^2 g_{1}^4}{2000}+\frac{1887}{400} \lambda g_{1}^4 \\&-\frac{48}{5} \sqrt{\frac{2}{5}} g_{2}^2 g_{YB} g_{1}^3+12 \sqrt{\frac{2}{5}} g_{YB} \lambda g_{1}^3 \\&- \frac{10971 g_{BY}^4 g_{1}^2}{2000}-\frac{8}{5} \Big (y_{\mathrm{t}}^{*}\Big )^2 y_{\mathrm{t}}^2 g_{1}^2 \\&+ \frac{63}{10}y_{\mathrm{t}}^{*} g_{2}^2 y_{\mathrm{t}} g_{1}^2+\frac{621}{200} g_{BY}^2 \lambda g_{1}^2 \\&+ \frac{153}{10} g_{YB}^2 \lambda g_{1}^2+18 g_{YB}^2 \lambda _{3} g_{1}^2 \\&- 2 \sqrt{10} \Big (y_{\mathrm{t}}^{*}\Big )^2 g_{YB} y_{\mathrm{t}}^2 g_{1}+5 \sqrt{\frac{5}{2}} y_{\mathrm{t}}^{*} g_{YB} y_{\mathrm{t}} \lambda g_{1} \\&-\frac{12}{5} \sqrt{6} y_{\mathrm{t}}^{*} g_{BY} g_{YB} y_{\mathrm{t}} g_{BL} g_{1}\\&+12 \sqrt{6} g_{BY} g_{YB} \lambda _{3} g_{BL} g_{1}+ \frac{305 g_{2}^6}{16}- \frac{4221 g_{BY}^6}{2000} \\&-39 \lambda ^3-4 \lambda _{3}^3-32 \Big (y_{\mathrm{t}}^{*}\Big )^2 g_{3}^2 y_{\mathrm{t}}^2 -\frac{8}{5} \Big (y_{\mathrm{t}}^{*}\Big )^2 g_{BY}^2 y_{\mathrm{t}}^2\\&-4 \Big (y_{\mathrm{t}}^{*}\Big )^2 g_{YB} y_{\mathrm{t}}^2 \\&+ 27 g_{2}^2 \lambda ^2-36 y_{\mathrm{t}}^{*} y_{\mathrm{t}} \lambda ^2+g_{YB}^2 \lambda _{3}^2 - 5 \lambda \lambda _{3}^2\\&-\frac{8}{3} \Big (y_{\mathrm{t}}^{*}\Big )^2 y_{\mathrm{t}}^2 g_{BL}^2+32 \lambda _{3}^2 g_{BL}^2 \\&+ \frac{51}{5} g_{BY}^2 \lambda g_{BL}^2+12 g_{BY}^2 \lambda _{3} g_{BL}^2 \\&- \frac{289}{80} \Big (g_{1}^2 g_{2}^4+g_{BY}^2 g_{2}^4\Big )-\frac{1677}{400} \Big (g_{2}^2 g_{1}^4 + g_{2}^2 g_{BY}^4\Big ) \\&- \frac{9}{4} y_{\mathrm{t}}^{*} g_{2}^4 y_{\mathrm{t}}+\frac{63}{10}y_{\mathrm{t}}^{*} g_{2}^2 g_{BY}^2 y_{\mathrm{t}} \\ \end{aligned}$$

$$\begin{aligned}&-\frac{171}{100} y_{\mathrm{t}}^{*} \Big (g_{1}^4+2 g_{BY}^2 g_{1}^2+ g_{BY}^4\Big ) y_{\mathrm{t}}-\frac{73}{16}g_{2}^4 \lambda \\&+\frac{1887}{400} g_{BY}^4 \lambda - \frac{3}{2} \Big (y_{\mathrm{t}}^{*}\Big )^2 y_{\mathrm{t}}^2 \lambda +40 y_{\mathrm{t}}^{*} g_{3}^3 y_{\mathrm{t}} \lambda \\&+\frac{45}{4} y_{\mathrm{t}}^{*} g_{2}^2 y_{\mathrm{t}} \lambda \\&+5 y_{\mathrm{t}}^{*} g_{YB}^2 y_{\mathrm{t}} \lambda +\frac{108}{5} \Big (\frac{1}{4} g_{1}^2 \lambda ^2+\frac{1}{4} g_{BY}^2 \lambda ^2\Big ) \\&+ \frac{117}{20} \Big (\frac{1}{2} g_{1}^2 \lambda g_{2}^2+g_{BY}^2 \lambda _{3} g_{2}^2\Big ) -\frac{32}{5} \sqrt{\frac{3}{5}} g_{2}^2 g_{BY}^3 g_{BL}\\&-4 \sqrt{\frac{5}{3}} \Big (y_{\mathrm{t}}^{*}\Big )^2 g_{BY} y_{\mathrm{t}}^2 g_{BL} \\&+ 8 \sqrt{\frac{3}{5}} g_{BY}^3 \lambda g_{BL}+5 \sqrt{\frac{2}{3}} y_{\mathrm{t}}^{*} y_{\mathrm{t}} \lambda g_{BL}\\&+ 5 \sqrt{\frac{5}{3}} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}} \lambda g_{BL}\\&- 9 \sqrt{\frac{2}{5}} y_{\mathrm{t}}^{*} y_{\mathrm{t}} \Big (g_{YB} g_{1}^3 +\sqrt{\frac{2}{3}} g_{BY} g_{BL} g_{1}^2-g_{2}^2 g_{YB} g_{1}\\&+g_{BY}^2 g_{YB} g_{1} -\sqrt{\frac{2}{3}} g_{2}^2 g_{BY} g_{BL}\Big ) \\&-\frac{144}{25} \sqrt{\frac{2}{5}} \Big (g_{YB} g_{1}^5+g_{BY}^2 g_{YB} g_{1}^3 \\&+\sqrt{\frac{2}{3}} g_{BY}^3 g_{BL} g_{1}^2+\sqrt{\frac{2}{3}} g_{BY}^5 g_{BL}\Big ) \\&+ \frac{17}{4} y_{\mathrm{t}}^{*} y_{\mathrm{t}}\lambda \Big (g_{1}^2+\frac{2}{3} g_{BL}^2\Big )\\&-\frac{18}{5} y_{\mathrm{t}}^{*} y_{\mathrm{t}} \Big (g_{1}^2 g_{YB}^2+\frac{2}{3} g_{BY}^2 g_{BL}^2\Big ) \\&-\frac{117}{10} \Big (g_{1}^2 g_{2}^2 g_{YB}^2+\frac{2}{3} g_{2}^2 g_{BY}^2 g_{BL}^2\Big ) \\&- \frac{351}{50} \Big (g_{YB}^2 g_{1}^4+g_{BY}^2 g_{YB}^2 g_{1}^2+\frac{2}{3} g_{BY}^2 g_{BL}^2 g_{1}^2\\&+\frac{2}{3} g_{BY}^4 g_{BL}^2\Big )\Big ), \end{aligned}$$

$$\begin{aligned} \beta _{\lambda _{2}}^{(2)}= & {} \frac{2}{5} \Big (1440 g_{YB}^2 g_{BL}^2 Y_{\mathrm{N}} Y_{\mathrm{N}}+75 \lambda _{2} g_{BL}^2 Y_{\mathrm{N}} Y_{\mathrm{N}} \\&+90 g_{BL}^2 Y_{\mathrm{N}}^2 \Big (Y_{\mathrm{N}}\Big )^2+480 g_{BL}^4 Y_{\mathrm{N}} Y_{\mathrm{N}} \\&+ 60 \sqrt{6} g_{1} g_{BY} g_{YB} \lambda _{3} g_{BL}-6144 \sqrt{10} g_{1} g_{YB}^3 g_{BL}^2 \\&-4008 g_{1}^2 g_{YB}^2 g_{BL}^2-4008 g_{BY}^2 g_{YB}^2 g_{BL}^2 \\&+ 640 \sqrt{\frac{5}{3}} g_{BY} \lambda _{2} g_{BL}^3+422 g_{BY}^2 \lambda _{2} g_{BL}^2 + 60 g_{BY}^2 \lambda _{3} g_{BL}^2\\&-4096 \sqrt{\frac{5}{3}} g_{BY} g_{BL}^5-2672 g_{BY}^2 g_{BL}^4 \\&+ 11760 g_{YB}^2 \lambda _{2} g_{BL}^2-83520 g_{YB}^4 g_{BL}^2-55680 g_{YB}^2 g_{BL}^4 \\&+5280 \lambda _{2} g_{BL}^4+1120 \lambda _{2}^2 g_{BL}^2-17920 g_{BL}^6 \\&+ \frac{225}{2} g_{YB}^2 \lambda _{2} Y_{\mathrm{N}}^2 +1080 g_{YB}^4 Y_{\mathrm{N}}^2 + 135 g_{YB}^2 Y_{\mathrm{N}}^2 \Big (Y_{\mathrm{N}}\Big )^2\\&+\frac{45}{2} \lambda _{2} Y_{\mathrm{N}}^4 -150 \lambda _{2}^2 Y_{\mathrm{N}}^2 +270 Y_{\mathrm{N}}^6 \\&- 30 \lambda _{3}^2 y_{\mathrm{t}} y_{\mathrm{t}}^{*}+480 \sqrt{10} g_{1} g_{YB}^3 \lambda _{2} +633 g_{1}^2 g_{YB}^2 \lambda _{2}\\&+90 g_{1}^2 g_{YB}^2 \lambda _{3}-4608 \sqrt{10} g_{1} g_{YB}^5 \\&- 6012 g_{1}^2 g_{YB}^4+6 g_{1}^2 \lambda _{3}^2+30 g_{2}^2 \lambda _{3}^2 + 6 g_{BY}^2 \lambda _{3}^2\\&+11880 g_{YB}^4 \lambda _{2}+1680 g_{YB}^2 \lambda _{2}^2 \\&- 60480 g_{YB}^6-50 \lambda _{2} \lambda _{3}^2-600 \lambda _{2}^3-20 \lambda _{3}^3\Big ), \end{aligned}$$

$$\begin{aligned} \beta _{\lambda _{3}}^{(2)}= & {} -\frac{6417}{50} g_{YB}^2 g_{1}^4+\frac{1671}{400} \lambda _{3} g_{1}^4 -\frac{2304}{5} \sqrt{\frac{2}{5}} g_{YB}^3 g_{1}^3\nonumber \\&+12 \sqrt{\frac{2}{5}} g_{YB} \lambda _{3} g_{1}^3 \nonumber \\&- \frac{1137}{25} \sqrt{6} g_{BY} g_{YB} g_{BL} g_{1}^3-\frac{4428}{5} g_{YB}^4 g_{1}^2 \nonumber \\&-\frac{81}{2} g_{2}^2 g_{YB}^2 g_{1}^2-\frac{81}{10} g_{BY}^2 g_{YB}^2 g_{1}^2 \nonumber \\&+ \frac{3}{5} \lambda _{3}^2 g_{1}^2-\frac{27}{5} g_{BY}^2 g_{BL}^2 g_{1}^2 -216 g_{YB}^2 g_{BL}^2 g_{1}^2\nonumber \\&-\frac{342}{5} y_{\mathrm{t}}^{*} g_{YB}^2 y_{\mathrm{t}} g_{1}^2 +108 g_{YB}^2 \lambda g_{1}^2 \nonumber \\&+72 g_{YB}^2 \lambda _{2} g_{1}^2+\frac{9}{8} g_{2}^2 \lambda _{3} g_{1}^2 +\frac{81}{40} g_{BY}^2 \lambda _{3} g_{1}^2\nonumber \\&+\frac{1491}{10} g_{YB}^2 \lambda _{3} g_{1}^2 +\frac{36}{5} \lambda \lambda _{3} g_{1}^2 \nonumber \\&- \frac{44608 g_{BY} g_{YB}^2 g_{BL} g_{1}^2}{5\sqrt{15}}-\frac{1424}{5} \sqrt{6} g_{BY} g_{YB} g_{BL}^3 g_{1} \nonumber \\&-\frac{1536}{5} \sqrt{\frac{2}{5}} g_{BY}^2 g_{YB} g_{BL}^2 g_{1}\nonumber \\&- 48 \sqrt{10} y_{\mathrm{t}}^{*} g_{YB} y_{\mathrm{t}} g_{BL}^2 g_{1}-72 \sqrt{10} y_{\mathrm{t}}^{*} g_{YB}^3 y_{\mathrm{t}} g_{1} \nonumber \\&+ 96 \sqrt{10} g_{YB}^3 \lambda _{3} g_{1}-\frac{2016}{5} \sqrt{6} g_{BY} g_{YB}^3 g_{BL} g_{1} \nonumber \\&- \frac{1137}{25} \sqrt{6} g_{BY}^3 g_{YB} g_{BL} g_{1} -27 \sqrt{6} g_{2}^2 g_{BY} g_{YB} g_{BL} g_{1}\nonumber \\&-\frac{228}{5} \sqrt{6} y_{\mathrm{t}}^{*} g_{BY} g_{YB} y_{\mathrm{t}} g_{BL} g_{1} \nonumber \\&+72 \sqrt{6} g_{BY} g_{YB} \frac{\lambda }{2} g_{BL} g_{1}+48 \sqrt{6} g_{BY} g_{YB} \lambda _{2} g_{BL} g_{1} \nonumber \\&+\frac{24}{5} \sqrt{6} g_{BY} g_{YB} \lambda _{3} g_{BL} g_{1} \nonumber \\&- \frac{1968}{5} g_{BY}^2 g_{BL}^4-64 y_{\mathrm{t}}^{*} y_{\mathrm{t}} g_{BL}^4+672 \lambda _{3} g_{BL}^4-11 \lambda _{3}^3 \nonumber \\&- \frac{1024}{5} \sqrt{\frac{3}{5}} g_{BY}^3 g_{BL}^3-32 \sqrt{15} y_{\mathrm{t}}^{*} g_{BY} y_{\mathrm{t}}g_{BL}^3 \nonumber \\&+128 \sqrt{\frac{5}{3}} g_{BY} \lambda _{3} g_{BL}^3+3 g_{2}^2 \lambda _{3}^2 +\frac{3}{5} g_{BY}^2 \lambda _{3}^2 -36 \lambda \lambda _{3}^2\nonumber \\&-48 \lambda _{2} \lambda _{3}^2 -\frac{2139}{25} g_{BY}^4 g_{BL}^2-27 g_{2}^2 g_{BY}^2 g_{BL}^2 \nonumber \\&- 216 g_{BY}^2 g_{YB}^2 g_{BL}^2+16 \lambda _{3}^2 g_{BL}^2-\frac{228}{5} y_{\mathrm{t}}^{*} g_{BY}^2 y_{\mathrm{t}} g_{BL}^2 \end{aligned}$$

$$\begin{aligned}&-192 y_{\mathrm{t}}^{*}g_{YB}^2 y_{\mathrm{t}} g_{BL}^2+72 g_{BY}^2 \frac{\lambda }{2} g_{BL}^2 \nonumber \\&+ 48 g_{BY}^2 \lambda _{2} g_{BL}^2+\frac{497}{5} g_{BY}^2 \lambda _{3} g_{BL}^2+1200 g_{YB}^2 \lambda _{3} g_{BL}^2 \nonumber \\&+256 \lambda _{2} \lambda _{3} g_{BL}^2-\frac{3}{2} \lambda _{3} Y_{\mathrm{N}}^4 \nonumber \\&-144 y_{\mathrm{t}}^{*} g_{YB}^4 y_{\mathrm{t}} - \frac{145}{16} g_{2}^4 \lambda _{3}+\frac{1671}{400} g_{BY}^4 \lambda _{3} \nonumber \\&+1512 g_{YB}^3 \lambda _{3}+ \frac{9}{8} g_{2}^2 g_{BY}^2 \lambda _{3} -\frac{27}{2} \Big (y_{\mathrm{t}}^{*}\Big )^2 y_{\mathrm{t}}^2 \lambda _{3} \nonumber \\&- 15 \lambda ^2 \lambda _{3}-40 \lambda _{2}^2 \lambda _{3}+\frac{17}{4} y_{\mathrm{t}}^{*} \Big (g_{1}^2 +g_{BY}^2\Big ) y_{\mathrm{t}} \lambda _{3}\nonumber \\&+36 g_{2}^2\lambda \lambda _{3}+\frac{36}{5} g_{BY}^2 \lambda \lambda _{3} \nonumber \\&+ 384 g_{YB}^2 \lambda _{2} \lambda _{3}-48 \sqrt{15} y_{\mathrm{t}}^{*} g_{BY} g_{YB}^2 y_{\mathrm{t}} g_{BL} \nonumber \\&+8 \sqrt{\frac{3}{5}} g_{BY}^3 \lambda _{3} g_{BL}+24 \lambda _{3}^2 \Big (g_{YB}^2 + \frac{2}{3} g_{BL}^2\Big ) \nonumber \\&+ 5 y_{\mathrm{t}}^{*} y_{\mathrm{t}} \lambda _{3} \Big (\frac{9 g_{2}^2}{4}+8 g_{3}^2+g_{YB}^2 + \frac{2}{3} g_{BL}^2+\sqrt{\frac{5}{2}} g_{1} g_{YB}\nonumber \\&-\frac{36}{5} \lambda - \frac{12 \lambda _{3}}{5}+\sqrt{\frac{5}{3}} g_{BY} g_{BL}\Big ) \nonumber \\&+ \frac{1}{4} Y_{\mathrm{N}} \Big (\frac{72}{5} g_{1}^2 g_{YB}^2+30 \lambda _{3} g_{YB}^2 \nonumber \\&+ \frac{48}{5} \sqrt{6} g_{1} g_{BY} g_{BL} g_{YB}-8 \lambda _{3}^2+\frac{48}{5}g_{BY}^2 g_{BL}^2 \nonumber \\&+ 20 \lambda _{3} g_{BL}^2-32 \lambda _{2} \lambda _{3}\Big ) Y_{\mathrm{N}}. \end{aligned}$$

(B.8)