1 Introduction

Wormholes are non-singular space-time structures connecting two (or more) different universes or parts of the same universe [1]. However, in the conventional approaches for (traversable) wormholes, there are problems in the “naturalness”. First, the hypothetical exotic matters, which violate the energy conditions in the standard general relativity (GR) but are essential for sustaining the throats of wormholes, have never been discovered [2,3,4,5,6,7]. Second, the usual cuts and pastes of the throats and subsequent putting of the hypothetical matters to the throats by hand to satisfy the Einstein equation [8, 9] are too artificial to be considered as a natural process. Moreover, we do not know much about the formation mechanism of wormholes due to the gravitationally repulsive nature of the exotic matters.

To circumvent the obstacle by exotic matters, one may consider other extended theories of gravity so that the exotic matters are naturally generated. For example, one may consider non-minimally coupled scalar–tensor gravity theories [10,11,12,13,14,15,16,17,18], higher curvature gravities [19,20,21,22,23,24,25], higher dimensional gravities [26,27,28,29,30,31,32,33], and brane-worlds theories [34,35,36]. (For a more complete and modern review, see Ref. [37] and the references therein.) On the other hand, to cure the problem of artificiality of the conventional cuts and pastes construction of throats of wormholes, a new approach for the wormhole construction has been proposed recently [38, 39]. In the new approach, the throat is defined as the place where the solutions are smoothly joined. There, the metric and its derivatives are continuous so that the exotic matters are not introduced at the throats.

From the new definition, throats cannot be constructed arbitrarily contrary to the conventional cuts and pastes approach. For example, we consider a four dimensional spherically symmetric wormhole connecting two remote parts of the same universe (or mathematically equivalently, the reflection symmetric two universes). The metric is described by

$$\begin{aligned} \mathrm{d}s^2=-N_{\pm }(r)^2 c^2 \mathrm{d}t^2+\frac{\mathrm{d}r^2}{f_{\pm }(r)}+r^2 \left( \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2\right) \nonumber \\ \end{aligned}$$
(1)

with two coordinate patches, each one covering the range \([r_0, +\infty )\). Then the radius of throat \(r_0\) is defined as

$$\begin{aligned} \left. \frac{\mathrm{d}N_{\pm }}{\mathrm{d}r}\right| _{r_0}=\left. \frac{\mathrm{d}f_{\pm }}{\mathrm{d}r}\right| _{r_0} =0 \end{aligned}$$
(2)

with the usual matching condition

$$\begin{aligned} N_+(r_0)=N_-(r_0), ~f_+(r_0)=f_-(r_0) \end{aligned}$$
(3)

by demanding that the metric and the Schwarzschild coordinates be continuous, though not generally smooth, across the throat. If there exists a coordinate patch \(\mathcal{M}_+\) in which the singularities are absent for all values of \(r \ge r_0\), one can construct a smooth regular wormhole-like geometry, which may or may not be traversable depending on the location of \(r_0\), by joining \(\mathcal{M}_+\) and its mirror patch \(\mathcal{M}_-\) at the throat \(r_0\). Here, it is important to note that, in the new approach, \(f_\pm (r_0)\) does not need to vanish, in contrast to the Morris–Thorne approach [2,3,4,5,6,7], while the quantities \({\mathrm{d}N_{\pm }(r_0)}/{\mathrm{d}r},~ {\mathrm{d}f_{\pm }(r_0)}/{\mathrm{d}r}\) in (2) do not need to vanish in both the Morris–Thorne approach [2,3,4,5,6,7] and the cuts and pastes approach of Visser [8, 9].

So, in the new approach, we have two options for exact solutions of the same Einstein equation when the throat point \(r_0\) exists. We may consider either the usual solutions for compact objects, like the black holes which may have singularities (but usually shielded by the horizons) generally, or wormhole-like objects which do not have singularities in the whole space-time domain. We do not have a priori reason to choose only one of the two options so that we can consider both options equally. This is in contrast to the Morris–Thorne-type traversable wormholes, which cannot co-exist with the solutions of black holes with the same conserved charges. In this context, we call the new type of wormholes as “natural wormholes” and the their throats as the natural throats to distinguish these from the previously known wormholes.

Originally the new wormhole solutions [38] have been studied in Hořava (or Hořava–Lifshitz) gravity, which has been proposed as a renormalizable quantum gravity based on different scaling dimensions between the space and time coordinates [40]. But the new approach can be applied to other gravity theories as well if the natural throat exists. However, the existence of the throat for black holes with rotation would be very difficult unless some coincidences occur. For the Kerr black hole in GR, there are more metric functions and there is no solution for the throat where all the metric functions join smoothly simultaneously. This implies that the wormhole throat in the spherically symmetric configurations could easily be destroyed by adding other conserved charges. Conversely, the wormhole throat could be formed only after losing all charges except the mass [39]. It has been also argued that the situation with electromagnetic charges would be similar because there are additional gauge fields to be joined smoothly at the same throat. One can easily show that there is no solution for the throat where the electromagnetic fields \(F^{\pm }_{\mu \nu }\) join smoothly, \({\mathrm{d}F^{\pm }_{\mu \nu }(r_0)}/{\mathrm{d}r}=0,~ F^+_{\mu \nu } (r_0)=F^-_{\mu \nu }(r_0)\), in addition to the conditions for the metric (3).

The purpose of this paper is to see whether the concept of natural wormholes could also be generalized to charged cases or not. In particular, in order to see the generic role of charges for non-linear electromagnetic fields at short distances, we consider the Born–Infeld (BI) action, instead of the usual Maxwell action, without modifying the Einstein–Hilbert action at short distances.

The organization of this paper is as follows. In Sect. 2, we set up the basic equations of Einstein–Born–Infeld gravity with a cosmological constant and study the exact solutions for spherically symmetric black holes and their physical properties, including the black hole thermodynamics and phase structures. In Sect. 3, we study the natural wormhole geometry as the solution of the Einstein equation without introducing additional matters at the throat based on the construction sketched in Sect. 1. We show that the BI field equation without additional terms at the throat is still valid even with the throat from some reasonable conditions of “coordinate independent” continuity of metric tensors, the preservation of the usual gravitational Bianchi identity, and the continuity equation of the energy-momentum tensors for the BI fields. In Sect. 4, we conclude with several discussions. Throughout this paper, we use the conventional units for the speed of light c and the Boltzman constant \(k_\mathrm{B}\), \(c=k_\mathrm{B}=1\), but keep the Newton constant G and the Planck constant \(\hbar \) unless stated otherwise.

2 Black hole solutions in Einstein–Born–Infeld gravity

Born–Infeld action of non-linear electrodynamics was originally introduced to solve the infinite self-energy of a point charge in Maxwell’s linear electrodynamics [41, 42]. When this action is combined with Einstein action to study the gravity of charged objects, the short-distance behavior of the metric is modified [43, 44]. With the recent development of D-branes, the Born–Infeld-type action has attracted renewed interests as an effective action for low-energy superstring theory [45,46,47]. There have been extensive studies about black hole solutions in the Einstein gravity coupled to Born–Infeld electrodynamics [Einstein–Born–Infeld (EBI) gravity] [48,49,50,51,52,53,54,55,56,57,58]. In this section, we briefly describe EBI gravity and its black hole solutions.

Since our results do not depend much on the space-time dimensions \(D \ge 4\), we consider the EBI gravity action with a cosmological constant \(\Lambda \) in \(D=3+1\) dimensions for simplicity,

$$\begin{aligned} S = \int \mathrm{d}^{4} x \sqrt{-g} \left[ \frac{(R - 2\Lambda )}{16 \pi G} + L(F) \right] , \end{aligned}$$
(4)

where L(F) is the BI Lagrangian density given by

$$\begin{aligned} L(F) = 4 \beta ^2 \left( 1 - \sqrt{ 1 + \frac{ F_{\mu \nu } F^{\mu \nu } }{2 \beta ^2} } \right) . \end{aligned}$$
(5)

Here, the parameter \(\beta ~\) is a coupling constant with dimensions \([\mathrm{length}]^{-2}\) which needs to flow to infinity to recover the usual Maxwell electrodynamics with \(L(F)=-F_{\mu \nu } F^{\mu \nu } \equiv -{F}^2\) at low energies. The correction terms from a finite \(\beta \) represent the effect of the non-linear BI fields. This situation is similar to the Lagrangian for a relativistic free particle \(mc^2 (1-\sqrt{1-{v}^2/c^2})\), which reduces to the Newtonian Lagrangian \(\frac{1}{2} m v^2\) for \(c \rightarrow \infty \) limit. As the speed of light c gives the upper limit for the speed v of a particle, the parameter \(\beta \) gives the upper limit for the strength of fields \(\sqrt{-\frac{1}{2} {F}^2}\) if \({F}^2 <0\).

Taking \(16 \pi G = 1\) for simplicity, the equations of motion are obtained:

$$\begin{aligned} \nabla _{\mu } \left( \frac{F^{\mu \nu }}{\sqrt{ 1 + \frac{ F^2 }{2 \beta ^2} }} \right) = 0, \end{aligned}$$
(6)
$$\begin{aligned} R_{\mu \nu } - \frac{1}{2}R g_{\mu \nu } + \Lambda g_{\mu \nu }=\frac{1}{2} T_{\mu \nu }, \end{aligned}$$
(7)

where the energy-momentum tensor for BI fields is given by

$$\begin{aligned} T_{\mu \nu }=g_{\mu \nu } L(F) +\frac{4 F_{\rho \mu } F^\rho _{\nu } }{\sqrt{ 1 + \frac{ F^2 }{2 \beta ^2} }}. \end{aligned}$$
(8)

Let us now consider a static and spherically symmetric solution with the metric ansatz

$$\begin{aligned} \mathrm{d}s^2 = - N^2 (r) \mathrm{d}t^2 + \frac{1}{f(r)} \mathrm{d}r^2 + r^2 (\mathrm{d} \theta ^2 + \sin ^2 \theta \mathrm{d} \phi ^2). \end{aligned}$$
(9)

For the staticFootnote 1 electrically charged case where the only non-vanishing component of the field strength tensor is \(F_{rt} \equiv E \), one can find

$$\begin{aligned} N^2(r)=f(r). \end{aligned}$$
(10)

Then the general solution for the BI electric field is obtained from Eq. (6) as

$$\begin{aligned} E(r) = \frac{Q}{\sqrt{ r^{4} + \frac{Q^2}{\beta ^2}} }, \end{aligned}$$
(11)

where Q is the integration constant that represents the electric charge localized at the origin. Note that the electric field is finite in the limit \(r \rightarrow 0\), \(E(r) \approx \pm |\beta |\) for \(|\beta |<\infty \) due to the non-linear effect of BI fields while it reduces to the usual Coulomb field \(E \approx Q/r^2\) in the limit \(|\beta | \rightarrow \infty \) (Fig. 1).

Fig. 1
figure 1

The plots of E(r) for varying \(\beta \) with a fixed Q. In particular, we consider \(\beta =5,~1,~1/2,~1/3,\) (top to bottom) with \(Q=1\)

Full size image

Now, from (10) and (11), the Einstein equation (7) reduces to

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}r} (r f ) = 1 - \Lambda r^2 + 2 \beta ^2 \left( r^2 - \sqrt{ r^{4} + \frac{ Q^2}{ \beta ^2} } \right) , \end{aligned}$$
(12)

and a simple integration over r gives

$$\begin{aligned} f = 1 -\frac{2 C}{r}- \frac{\Lambda }{3} r^2 + \frac{2 \beta ^2}{r} \int _0^r r^{2} \left( 1 - \sqrt{ 1 + \frac{Q^2}{\beta ^2 r^{4}} } \right) dr,\nonumber \\ \end{aligned}$$
(13)

where C is an integration constant.

With a straightforward integration, one can express the solution in a compact form in terms of the incomplete elliptic integral of the first kind,

$$\begin{aligned} f= & {} 1 - \frac{2C}{r} - \frac{\Lambda }{3} r^2 + \frac{2\beta ^2}{3} r^2 \left( 1 - \sqrt{ 1+ \frac{Q^2}{ \beta ^2 r^{4} } } \right) \nonumber \\&- \frac{4 }{3 r} \sqrt{-i {\beta Q^3}}~ \mathrm{EllipticF} \left( r \sqrt{\frac{i \beta }{Q}},i \right) . \end{aligned}$$
(14)

For small r, this may be expanded as

$$\begin{aligned} f(r) = 1 - 2 \beta Q - \frac{2C}{r} + \frac{1}{3} (2 \beta ^2 - \Lambda ) r^2 -\frac{\beta ^3}{5 Q}r^4+\mathcal{O}(r^6),\nonumber \\ \end{aligned}$$
(15)

which shows a mass-like term \(-2C/r\). The parameter C is called an intrinsic mass [49] and represents the mass-like behavior near the origin. However, it is important to note that this is not the usual ADM mass defined at large r. In order to see this, it is convenient to reorganize the integral in (13) as \(\int ^r_0=\int ^\infty _0+\int ^r_\infty \) so that the integral \(\int ^r_\infty \) is convergent in the limit \(r\rightarrow \infty \). Then we have another expression for the solution

$$\begin{aligned} f(r)= & {} 1 - \frac{2 M}{r} - \frac{\Lambda }{3} r^2 + \frac{2 }{3} \beta ^2 r^2 \left( 1 - \sqrt{ 1+ \frac{Q^2}{ \beta ^2 r^{4} } } \right) \nonumber \\&+ \frac{4}{3} \frac{Q^2}{r^{2}}~ {_2 F}_1 \left( \frac{1}{2}, \frac{1}{4}; \frac{5}{4}; \frac{-Q^2}{\beta ^2 r^{4}} \right) , \end{aligned}$$
(16)

in terms of the hypergeometric function [50,51,52,53, 56]. Here, M is another mass parameter, defined by

$$\begin{aligned} M\equiv & {} C+ M_{0}, \end{aligned}$$
(17)
$$\begin{aligned} M_{0}= & {} \frac{2}{3} \sqrt{ \frac{\beta Q^3}{\pi } } \Gamma \left( \frac{1}{4} \right) \Gamma \left( \frac{5}{4} \right) , \end{aligned}$$
(18)

where \(M_{0}\) comes from the \(\int ^\infty _0\) part of the integral. One can find that the total mass M, which is the sum of the intrinsic mass C and the (finite) self-energy of a point charge \(M_0\), is the usual ADM mass defined by the asymptotic behavior of the metric at large r

$$\begin{aligned} f(r) = 1 - \frac{\Lambda }{3} r^2 - \frac{2 M }{r} + \frac{Q^2}{r^{2}} -\frac{Q^4}{20 \beta ^2 r^6} + \mathcal{O}(r^{-10}).\nonumber \\ \end{aligned}$$
(19)

This shows that the physical parameters, like the mass and the cosmological constant, are shifted at the short distances due to non-linear effects of BI fields: The fourth term on the right-hand side of (15) represents the space with an effective cosmological constant \({\Lambda }_\mathrm{eff}={\Lambda }-2 \beta ^2\), which can behave like an anti de Sitter space \(({\Lambda }_\mathrm{eff}<0)\) near the origin even though it behaves like a flat \(({\Lambda }=0)\) or a de Sitter \(({\Lambda }>0)\) space at the asymptotic infinity.

The solution (14) or (16) has a curvature singularity at the origin, \(r=0\),

$$\begin{aligned}&R=\frac{4 \beta Q}{r^2} +4 ({\Lambda }-2 \beta ^2) + \frac{6 \beta ^3}{Q}r^2+ \mathcal{O}(r^4), \nonumber \\&R^{{\mu }{\nu }}R_{{\mu }{\nu }}=\frac{8 \beta ^2 Q^2}{r^4} +\frac{8 \beta Q ({\Lambda }-2 \beta ^2)}{r^2}\nonumber \\&\qquad \qquad \qquad +\, 4 ({\Lambda }^2-4 {\Lambda }\beta ^2+6 \beta ^4) +\mathcal{O}(r^2), \nonumber \\&R^{{\mu }{\nu }{\alpha }\beta }R_{{\mu }{\nu }{\alpha }\beta }=\frac{48 C^2}{r^6} +\frac{32 \beta Q C}{r^5} +\frac{16 \beta ^2 Q^2}{r^4} +\mathcal{O}(r^{-2}).\nonumber \\ \end{aligned}$$
(20)

Note that the leading singularity near \(r=0\) is of the order \(\mathcal{O}(r^{-6})\) in the Riemann tensor square, which is the same as that of Schwarzschild (Sch) black hole. But this singularity is absent for the marginal case of \(C=0\) (\(M=M_{0}\)) due to the regular behavior of the solution near the origin (15), which is the same as that of Reissner–Nodstrom (RN) black hole.Footnote 2 On the other hand, it can be shown that there is no curvature singularity at the horizon, which is defined as the solution for \(f(r)=0\) in our case, as expected [50].

Fig. 2
figure 2

The plots of f(r) for varying M with a fixed \(\beta Q >1/2\) and cosmological constant \(\Lambda \) (\(\Lambda <0\) (left), \(\Lambda =0\) (center), \(\Lambda >0\) (right)). We consider \(M=0,~0.95,~1.2,~M_0,~1.5\) (top to bottom) with \(Q=1,\beta =1\), \(M_0=1.236\ldots \), and \(\Lambda =\pm 1/5\) for the (A)dS cases

Full size image
Fig. 3
figure 3

The plots of the ADM mass M vs. the black hole horizon radius \(r_+\) for varying \(\beta Q\) with a fixed cosmological constant \(\Lambda \). For small \(r_+\), there is no significant difference for different values of cosmological constant (left). The marginal mass \(M_0\) is given by the mass value at \(r_+=0\). The top two curves represent \(M_0>M^*,~M_0=M^*\) for \(\beta Q>1/2,~\beta Q=1/2\), respectively, with the extremal mass \(M^*\), whereas the bottom two curves represent the cases where \(M^*\) is absent for \(\beta Q<1/2\). We consider \(\beta Q={2/3,~1/2,~2/4.5,~1/3}\) (top to bottom) with \(\beta =2\). The effect of cosmological constant is important for large \(r_+\) (right): (\(\Lambda <0\) (thin curve), \(\Lambda =0\) (medium curve), \(\Lambda >0\) (thick curve)). We consider \(\Lambda =\pm 1/5\) for the (A)dS cases

Full size image

The solution can have two horizons generally and the Hawking temperature for the outer horizon \(r_+\) is given by

$$\begin{aligned} T_H\equiv & {} \frac{\hbar }{4 \pi } \left. \frac{\mathrm{d}f}{\mathrm{d}r} \right| _{r=r_+} \nonumber \\= & {} \frac{\hbar }{4 \pi } \left[ \frac{1}{r_+}-{\Lambda }r_+ +2 \beta ^2 r_+ \left( 1-\sqrt{1+\frac{Q^2}{\beta r_+^4}} \right) \right] .\nonumber \\ \end{aligned}$$
(21)

There exists an extremal black hole limit of vanishing temperature, where the outer horizon \(r_+\) meets the inner horizon \(r_-\) at

$$\begin{aligned} r^*_+=\sqrt{ \frac{{\Lambda }-2 \beta ^2 \pm 2 \sqrt{(\beta ^2-{\Lambda }/2)^2+{\Lambda }({\Lambda }-4 \beta ^2)(\beta ^2 Q^2-1/4)} }{{\Lambda }({\Lambda }-4 \beta ^2)} }\nonumber \\ \end{aligned}$$
(22)

for a non-vanishing cosmological constant \({\Lambda }\) and

$$\begin{aligned} r^*_+=\sqrt{Q^2- \frac{1}{4 \beta ^2}} \end{aligned}$$
(23)

for vanishing \({\Lambda }\). At the extremal point, the ADM mass M

$$\begin{aligned} M= & {} \frac{r_+}{2} \left[ 1 - \frac{\Lambda }{3} r_+^2 + \frac{2 }{3} \beta ^2 r_+^2 \left( 1 - \sqrt{ 1+ \frac{Q^2}{ \beta ^2 r_+^{4} } } \right) \right. \nonumber \\&\left. + \frac{4}{3} \frac{Q^2}{r_+^{2}}~ {_2 F}_1 \left( \frac{1}{2}, \frac{1}{4}; \frac{5}{4}; \frac{-Q^2}{\beta ^2 r_+^{4}} \right) \right] \end{aligned}$$
(24)

gets the minimum

$$\begin{aligned} M^*=\frac{r_+^*}{3} \left[ 1 + \frac{2 Q^2}{{r_+^*}^{2}}~ {_2 F}_1 \left( \frac{1}{2}, \frac{1}{4}; \frac{5}{4}; \frac{-Q^2}{\beta ^2 {r_+^*}^{4}} \right) \right] . \end{aligned}$$
(25)

The first law of black hole thermodynamics is found as

$$\begin{aligned} \mathrm{d}M=T_+ \mathrm{d}S_\mathrm{BH} +A_0(r_+) \mathrm{d}Q, \end{aligned}$$
(26)

with the usual Bekenstein–Hawking entropy formula by

$$\begin{aligned} S_\mathrm{BH}=\frac{\pi r_+^2}{\hbar G}, \end{aligned}$$
(27)

and the scalar potential [51]

$$\begin{aligned} A_0(r)=\frac{1}{r}~ {_2 F}_1 \left( \frac{1}{2}, \frac{1}{4}; \frac{5}{4}; \frac{-Q^2}{\beta ^2 {r}^{4}} \right) . \end{aligned}$$
(28)

Now, from the result (22), one can classify the black holes in terms of the values of \(\beta Q\) and the cosmological constant \({\Lambda }\).

  1. (i)

    \(\beta Q >1/2\): In this case, the black hole may have one non-degenerate horizon (type I), or two non-degenerate (non-extremal) horizons or one degenerate (extremal) horizons (type II), depending on the mass for the asymptotically AdS (\({\Lambda }<0\)) or flat (\({\Lambda }=0\)), i.e., the type I for \(M \ge M_0\) and the type II for \(M < M_0\) (Fig. 2a, b). There can be a phase transition from a Schwarzschild (Sch)-like type I black hole to Reissner–Nordström (RN)-like type II black hole when the mass becomes smaller than the marginal mass \(M_0\), which is the mass value at \(r_+=0\) in Fig. 3. When the mass is smaller than the extremal mass \(M^*\), which is the mass value at the extremal point in Fig. 3 (top curve), the singularity at \(r=0\) becomes naked as usual. In the limit \(\beta \rightarrow \infty \), only the RN-like type II black holes are possible as in GR. On the other hand, for asymptotically dS (\({\Lambda }>0\)) case, the situation is more complicated due to the cosmological horizon. In this case, there can exist maximally three horizons (two smaller ones for black holes and the largest one for the cosmological horizon), depending on the mass and the cosmological constant (Fig. 2c).

  1. (ii)

    \(\beta Q =1/2\): In this case, only the Sch-like type I black holes are possible (Fig. 4). It is peculiar that the horizon shrinks to zero size for the marginal case \(M=M_0\), even though its mass has still a non-vanishing value (Fig. 3). This does not mean that the metric is a flat Minkowskian. This rather means that all the gravitational energy is stored in the BI electric field as a self-energy. When the mass is smaller than the marginal mass \(M_0\), the singularity at \(r=0\) becomes naked. Note that this is the case where the GR limit \(\beta \rightarrow \infty \) does not exist.

  2. (iii)

    \(\beta Q <1/2\): This case is similar to the case (ii), except that the marginal case has no (even a point) horizon so that its singularity is naked always (Fig. 5).

Fig. 4
figure 4

The plots of f(r) for varying M with a fixed \(\beta Q=1/2\) and cosmological constant \(\Lambda \) (\(\Lambda <0\) (left), \(\Lambda =0\) (center), \(\Lambda >0\) (right)). We consider \(M=0,~0.85,~M_0,~0.9,~1.2\) (top to bottom) with \(Q=1,\beta =1/2\), \(M_0=0.874\ldots \), and \(\Lambda =\pm 1/5\) for the (A)dS cases

Full size image
Fig. 5
figure 5

The plots of f(r) for varying M with a fixed \(\beta Q<1/2\) and cosmological constant \(\Lambda \) (\(\Lambda <0\) (left), \(\Lambda =0\) (center), \(\Lambda >0\) (right)). We consider \(M=0,~0.7,~M_0,~0.75,~1.2\) (top to bottom) with \(Q=1,\beta =1/3\), \(M_0=0.714\ldots \), and \(\Lambda =\pm 1/5\) for the (A)dS cases

Full size image

3 Construction of natural wormhole solutions

The strategy to construct a natural wormhole is to find the throat radius \(r_0\) defined by (2) with the matching condition (3) [38, 39]. Based on this definition, cases (i) and (ii) in Figs. 2 and 4, respectively, and the case (iii) in Fig. 5a (AdS case) show the throats depending on the mass M for given values of \(\beta Q\) and \({\Lambda }\). More details are as follows.

For the case (i) of \(\beta Q>1/2\), there is no throat for the Sch-like type I black holes with \(M>M_0\) down to the marginal case of \(M=M_0\), where a point-like throat is generated at the origin. The zero-size (\(r_0=0\)) throat can grow as the black hole loses its mass. But, down to the extremal case of \(M=M^*~(<M_0)\), where the inner and outer horizons meet at \(r_+^*\) and Hawking temperature vanishes (Fig. 6), the throat is inside the outer horizon and non-traversable.Footnote 3 As the black hole loses its mass further, there emerges and grows a traversable throat from the extremal black hole horizon.Footnote 4

Fig. 6
figure 6

The plots of the Hawking temperature \(T_H\) vs. the black hole horizon radius \(r_+\) for varying \(\beta Q\) with a fixed cosmological constant \(\Lambda \). We consider \(\beta Q=1/3,~2/4.5,~1/2,~2/3\) (top to bottom curves) with \(\beta =2\), \(\Lambda =-1/5\) (left: AdS case), \(\Lambda =0\) (center: flat case), \(\Lambda =1/5\) (right: dS case)

Full size image

For the AdS case (Fig. 2a), the throat grows and persists until its mass M vanishes. However, for the flat (Fig. 2b) and dS (Fig. 2c) cases, the throat does not grow to an indefinitely large size. There is a maximum size at a certain mass \(\widetilde{M}\) before M vanishes, i.e., \(M^*>\widetilde{M}>0\). If we further reduce the mass below \(\widetilde{M}\), only the space-time with a naked singularity is a possible solution. So, the usual naked singularity solution for \(M<M^*\) may be replaced by the non-singular wormhole geometry until a certain (non-negative) mass \(\widetilde{M}\) is reached in flat and dS cases. This may suggest the generalized cosmic censorship [38, 39] by the existence of a wormhole-like structure around the origin, which has been thought to be a singular point of black hole solutions where all the usual physical laws could break down and might be regarded as an indication of the incompleteness of general relativity.

For the case (ii) of \(\beta Q =1/2\), a point-like throat can be generated at the origin, contrary to the generation of a finite-size throat for the case (i). But its growing process is the same as the case (i), showing the existence of a maximum size of the throat with the mass \(\widetilde{M}>0\) for flat and dS cases, and \(\widetilde{M}=0\) for AdS case (Fig. 4).

For the case (iii) of \(\beta Q <1/2\), the natural wormhole geometry exists only for AdS case (Fig. 5a) and its growing behavior is similar to the case (ii). On the other hand, for flat and dS cases (Fig. 5b, c), only the Sch-like type I black hole solution for \(M>M_0\) or the naked singularity solution for \(0<M<M_0\) can exist.

So far, we have considered geometric aspects in constructing the natural wormhole. Here, it is important to note that the right-hand side of the Einstein equation depends only on the values of the BI field strength themselves, not on their derivatives. This means that Eq. (7) is still valid even in the presence of the throat \(r_0\), where the BI fields do not join smoothly, i.e., their (spatial) derivatives are discontinuous (Fig. 1). This would be valid for any kind of matter field including gauge field if the coupling with the matter and gravity does not contain derivatives. In other words, the same solution of the Einstein equation (7) without the throat can also be the exact solution for each patch of the wormhole geometry even when considering matter coupled system.

However, the above argument would not hold for the BI field equation (6), which depends on the derivatives of BI fields. Equation (6) for the wormhole geometry with a throat can be modified due to the discontinuities of derivatives of BI fields. To find the possible modification term, let us introduce another coordinate \(\eta \) which spans the whole wormhole space-times with a geodesically complete ranges \((-\infty ,+\infty )\) by joining two coordinate patches, each one covering \([r_0, +\infty )\) with the throat at \(\eta =0\) for \(r=r_0\). For example, we may consider the Ellis-type metric ansatz for a traversable wormhole, i.e., a throat-type geometry that physical objects can propagate through,

$$\begin{aligned} \mathrm{d}s^2=-N^2(l) \mathrm{d}t^2+{\mathrm{d}l^2}+r^2({l})\left( \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2\right) , \end{aligned}$$
(29)

where l is the proper length from the throat given by

$$\begin{aligned} l(r)=\pm \int ^r_{r_0} {\mathrm{d}r}/{\sqrt{f(r)}}. \end{aligned}$$
(30)

Then, in the region close to the throat \(\eta =0\), one may expand the original coordinate \(r^{\pm }\) for each patch as

$$\begin{aligned} r^{\pm } (\eta )=r_0 +\left. \left( \frac{\mathrm{d}r}{\mathrm{d} \eta }\right) \right| ^{\pm }_{{r_0}} \eta + \frac{1}{2}\left. \left( \frac{\mathrm{d}r^2}{\mathrm{d} \eta ^2}\right) \right| ^{\pm }_{{r_0}} \eta ^2+\cdots . \end{aligned}$$
(31)

Here, we note that \( ({\mathrm{d}r}/{\mathrm{d} \eta })|^+_{{r_0}}\ge 0, ~({\mathrm{d}r}/{\mathrm{d} \eta })|^-_{{r_0}} \le 0\), and \(({\mathrm{d}r^2}/{\mathrm{d} \eta ^2})|^\pm _{{r_0}}>0\) in order that the minimum radius \(r_0\) exists.

In general, there are two options for the choice of \(\eta \) coordinate.

  1. (a)

    First, if we consider the regular coordinate transformation \(r^{\pm }(\eta )\) of (31) without singularity, we need to consider \(({\mathrm{d}r}/{\mathrm{d} \eta })|^+_{{r_0}}=({\mathrm{d}r}/{\mathrm{d} \eta })|^-_{{r_0}}=0\) but its inverse transformation \(\eta (r^{\pm })\) becomes singular at the throat, \(({\mathrm{d}\eta }/{\mathrm{d} r})|^\pm _{{r_0}} \rightarrow \pm \infty \) (top curve in Fig. 7) [2,3,4,5,6,7,8,9].

  2. (b)

    Second, if we consider the case of \(({\mathrm{d}r}/{\mathrm{d} \eta })|^\pm _{{r_0}}\ne 0\) (bottom curve in Fig. 7), we have a singularity—a delta function singularity due to the discontinuity of \(({\mathrm{d}r}/{\mathrm{d} \eta })^\pm _0\)—in the third term of (31) so that the coordinate transformation \(r^{\pm } (\eta )\) becomes singular at the throat.

Fig. 7
figure 7

The plots of possible \(r(\eta )\) functions

Full size image

The second option was not considered before [2,3,4,5,6,7,8,9] but it seems that both options are possible on the general ground. For example, if we consider the derivative of the metric tensor \(g^{\pm }_{{\mu }{\nu }}(r)\) with respect to the proper length l in the Schwarzschild coordinate (1)

$$\begin{aligned} \frac{\mathrm{d}g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}l}=\left( \frac{\mathrm{d}r^{\pm }}{\mathrm{d}l} \right) \frac{\mathrm{d}g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}r^{\pm }}=\pm \sqrt{f^{\pm }(r)} ~ \frac{\mathrm{d}g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}r^{\pm }}, \end{aligned}$$
(32)

one can join the metric smoothly, \({\mathrm{d}g^{+}_{{\mu }{\nu }}(r)}/{\mathrm{d}l}|_{r_0}={\mathrm{d}g^{-}_{{\mu }{\nu }}(r)}/{\mathrm{d}l}|_{r_0}=0\), by considering either \(f^{\pm }(r_0)=0\) (Morris–Thorne approach [2,3,4,5,6,7]) or \({\mathrm{d}g^{+}_{{\mu }{\nu }}}/{\mathrm{d}r}|_{r_0}={\mathrm{d}g^{-}_{{\mu }{\nu }}}/{\mathrm{d}r}|_{r_0}=0\) (new approach in this paper [38, 39]).

But, independently of the choice of the two options, we may generally obtain the radial component of the BI electric field and its derivative,

(33)

where we have used the continuity of the field \(E^+(r_0)=-E^-(r_0)\) and \(\mathrm{d}{\epsilon }(\pm \eta )/\mathrm{d} \eta =\pm {\delta }(\eta )\) with the step function \({\epsilon }(\eta )\) (Fig. 8).

Fig. 8
figure 8

The plots of \(E(\eta )\) and \({\mathbf{E}^{\pm }(\eta )}=E(\eta ) \hat{\eta } \) functions

Full size image

In general, singularities may enter into the BI field equation when it involves the radial derivative \(\frac{\mathrm{d}}{\mathrm{d}r}\) for the wormhole geometry with a throat, regardless of the choice of \(\eta \) coordinate unless we fine-tune the coordinate \(\eta \) [2,3,4,5,6,7,8,9] so that

$$\begin{aligned} \left. \left( \frac{\mathrm{d} \eta }{\mathrm{d} r} \right) \right| ^+_{r_0} =-\left. \left( \frac{\mathrm{d} \eta }{\mathrm{d} r} \right) \right| ^-_{r_0}. \end{aligned}$$
(34)

Note that the condition (34) has been implicitly assumed in the Morris–Thorne construction for the first option, though \((\mathrm{d} \eta /\mathrm{d}r)^{\pm }_{r_0}\) becomes infinity [2,3,4,5,6,7]. Now, in order to understand the condition (34) in our construction for the second option, let us consider the second derivatives of the metric tensor \(g^{\pm }_{{\mu }{\nu }}(r)\) with respect to \(\eta \)

$$\begin{aligned} \frac{\mathrm{d}^2g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}\eta ^2}= \left( \frac{\mathrm{d}r^{\pm }}{\mathrm{d}\eta } \right) ^2 \frac{\mathrm{d}^2g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}{r^{\pm }}^2} +\left( \frac{\mathrm{d}^2r^{\pm }}{\mathrm{d}\eta ^2} \right) \frac{\mathrm{d}g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}r^{\pm }}. \end{aligned}$$
(35)

Then the continuity of the second derivatives with respect to \(\eta \) and r at the throat [note that the second term in (35) vanishes in our case],

$$\begin{aligned}&\left. \left( \frac{\mathrm{d}^2g^{+}_{{\mu }{\nu }}}{\mathrm{d}\eta ^2}\right) \right| _{r_0} =\left. \left( \frac{\mathrm{d}^2g^{-}_{{\mu }{\nu }}}{\mathrm{d}\eta ^2}\right) \right| _{r_0},\nonumber \\&\left. \left( \frac{\mathrm{d}^2g^{+}_{{\mu }{\nu }}}{\mathrm{d}{r^+}^2}\right) \right| _{r_0} =\left. \left( \frac{\mathrm{d}^2g^{-}_{{\mu }{\nu }}}{\mathrm{d}{r^-}^2}\right) \right| _{r_0}, \end{aligned}$$
(36)

requires the condition (34) naturally. Note that, in the usual case of the first option, the first term in (35) vanishes and one can obtain another condition \(\left( \frac{\mathrm{d}^2r^{+}}{\mathrm{d}\eta ^2}\right) _{r_0} =\left( \frac{\mathrm{d}^2r^{-}}{\mathrm{d}\eta ^2}\right) _{r_0}\) from the continuity of the first derivative with respect to r, \(\left( \frac{\mathrm{d}g^{+}_{{\mu }{\nu }}}{\mathrm{d}r^+}\right) _{r_0} =\left( \frac{\mathrm{d}g^{-}_{{\mu }{\nu }}}{\mathrm{d}r^-}\right) _{r_0}\), which need not to be vanished [2,3,4,5,6,7,8,9]. On the other hand, in our case of the second option, the condition (34) is also necessary in order to have the continuity of the metric tensor and its derivatives in a “coordinate independent” way. Here, it is important to note that there is no constraint on \(\left( \frac{\mathrm{d}^2r^{\pm }}{\mathrm{d}\eta ^2}\right) \) which is crucial for the discussion of the energy condition in Sect. 4.

Another important consequence of the condition (34) is the consistency of the field equation (6) with the Einstein equation (7). In the usual equations of motion, we need the Bianchi identity for the Riemann tensors and the continuity equation for the (matter’s) energy-momentum tensors

$$\begin{aligned} \nabla _{\mu } T^{{\mu }{\nu }}= 0. \end{aligned}$$
(37)

But, instead of considering the continuity equation (37), there is an easier way to check it. It is to consider the general relation before implementing (37),

$$\begin{aligned} p_{\theta }=p_{\phi }=-{\rho }-\frac{r}{2} \frac{\mathrm{d}}{\mathrm{d}r} \rho -\frac{r}{2}\nabla _{\mu } T^{{\mu }}_r, \end{aligned}$$
(38)

for the energy-momentum tensor \( T^{{\mu }}_{ {\nu }}{(r)}= \mathrm{{diag}}(-\rho ,p_r,p_{\theta },p_{\phi })\) with

$$\begin{aligned} \rho= & {} -p_r=-4 \beta ^2 \left( 1-\frac{1}{\sqrt{1-E^2/\beta ^2}} \right) ,\nonumber \\ ~p_{\theta }= & {} p_{\phi }=4 \beta ^2 \left( 1-{\sqrt{1-E^2/\beta ^2}} \right) . \end{aligned}$$
(39)

Note that, when the usual continuity equation (37) is used, we have the conventional relation (see Ref. [60], for example),

$$\begin{aligned} p_{\theta }=p_{\phi }=-{\rho }-\frac{r}{2} \frac{\mathrm{d}}{\mathrm{d}r} \rho . \end{aligned}$$
(40)

In other words, if the usual relation (40) is violated, the continuity equation (37) is also violated exactly at the same place where (40) fails. Actually, in our case, (40) fails at the throat if the condition (34) is not considered! From Eq. (39), \((p_\theta ,p_\phi )\) of (40) depend only on the field E(r), not on its derivatives \(\mathrm{d}E(r)/\mathrm{d}r\) so that they are not affected by the presence of the throat. However, the right hand side of (40) depends on \(\mathrm{d}E(r)/\mathrm{d}r\), as well as E(r), which introduces the additional delta-function term at the throat. This means that, in order to have a “consistent” equation (40), we need a counter term on the right-hand side to cancel the singular term at the throat implying the violation of the continuity equation,

$$\begin{aligned} \nabla _{\mu } T^{{\mu }{\nu }}\sim {\delta }(\eta ). \end{aligned}$$
(41)

Because the Einstein equation (7) is not affected by the existence of the natural wormhole, this violation of the continuity equation means that the Bianchi identity for the curvature tensor fails also at the throat,

$$\begin{aligned} \nabla _{\mu } G^{{\mu }{\nu }}\sim {\delta }(\eta ), \end{aligned}$$
(42)

with the Einstein tensor \(G_{{\mu }{\nu }}=R_{{\mu }{\nu }}-\frac{1}{2} R g_{{\mu }{\nu }}.\) In electrodynamics, the Bianchi identity \({\partial }_{{\mu }}\tilde{F}^{{\mu }{\nu }}=0\), with the dual field strength \(\tilde{F}^{{\mu }{\nu }}=\frac{1}{2} {\epsilon }^{\mu {\nu }\sigma \rho } F_{\sigma \rho },\) is violated at the location of the magnetic monopole. In our case, this electromagnetic Bianchi identity works as one can easily check from the solution (11) since \(\tilde{F}^{{\mu }{\nu }}=0\). But we may have a violation of the gravitational Bianchi identity at the throat if we do not require the condition (34).Footnote 5 This can be considered as further support of the condition (34) in our new approach.

4 Energy conditions

In the usual set-up of wormholes, exotic matters violating the energy conditions are essential to sustain the throats.Footnote 6 Even when we look for wormhole solutions without the explicit introduction of exotic matters, we need some effective matter terms in the Einstein equation which play the role of exotic matters. Wormhole solutions in higher-derivative gravities is one example. In that case, higher-derivative terms act as the effective energy-momentum tensor which can violate the energy conditions generally. However, this is not the case in our construction of natural wormholes and all the energy conditions can be normal.

To see this, let us consider

$$\begin{aligned}&\rho +p_{\theta }=\rho +p_{\phi } =4 \beta ^2 \left( \frac{1}{\sqrt{1-E^2/\beta ^2}} -{\sqrt{1-E^2/\beta ^2}} \right) , \end{aligned}$$
(43)
$$\begin{aligned}&\rho -p_{\theta }=4 \beta ^2 \left( \frac{1}{\sqrt{1-E^2/\beta ^2}} +{\sqrt{1-E^2/\beta ^2}}-2 \right) , \end{aligned}$$
(44)
$$\begin{aligned}&\rho +\sum _i p_{i}=2 p_{\theta }= 4 \beta ^2 \left( 1-{\sqrt{1-E^2/\beta ^2}}\right) , \end{aligned}$$
(45)

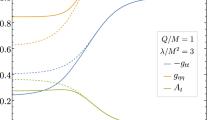
where we have used \(\rho +p_r=0\) from (39). Then it is easy to see that the quantities in (43), (45), as well as \(\rho \) in (39), are all non-negative for the whole range of \(E(r) \le \beta \). In Fig. 9, we have plotted the case for two horizons in the RN-like type II black hole but the result is the same as the Sch-like type I case. This shows that the strong energy condition (SEC: \(\rho +p_i \ge 0, ~\rho +\sum _i p_{i} \ge 0\)), which includes the null energy condition (NEC: \(\rho +p_i \ge 0\)), is satisfied as well as the weak energy condition (WEC: \(\rho \ge 0, ~\rho +p_{i} \ge 0\)) and the dominant energy condition (DEC: \(\rho \ge |p_i|\) or equivalently \(\rho \pm p_i \ge 0\)).

Fig. 9
figure 9

The plots of \(\rho -p_\theta \), \(\rho \), \(\rho +p_\theta \), (three thick curves, left to right), \(\rho +\sum _i p_{i}\) (thin dotted curve), and f(r) (thin solid curve) for \(\beta =1,~ Q=1\)

Full size image

In order to understand the physical origin of this result, which is unusual in the conventional wormhole physics, let us consider the usual Morris–Thorne ansatz instead of (1) [2,3,4,5,6,7,8,9],

$$\begin{aligned} \mathrm{d}s^2= & {} -e^{2 \phi _{\pm }(r)}\mathrm{d}t^2+\frac{\mathrm{d}r^2}{1-b_{\pm }(r)/r}\nonumber \\&+r^2 \left( \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2\right) . \end{aligned}$$
(46)

Then the energy density and pressures are given by

$$\begin{aligned} \rho= & {} {2} \left[ \frac{1}{r^2}\frac{\mathrm{d}b}{\mathrm{d}r}-\Lambda \right] ,\end{aligned}$$
(47)
$$\begin{aligned} p_r= & {} {2} \left[ -\frac{b}{r^3}+2\left( 1-\frac{b}{r}\right) {\frac{1}{r}\frac{\mathrm{d} \phi }{\mathrm{d}r}}+\Lambda \right] , \end{aligned}$$
(48)
$$\begin{aligned} p_\theta= & {} p_\phi ={2} \left\{ \left( 1-\frac{b}{r} \right) \left[ \frac{\mathrm{d}^2\phi }{\mathrm{d}r^2}+\frac{\mathrm{d}\phi }{\mathrm{d}r} \left( \frac{\mathrm{d}\phi }{\mathrm{d}r}+\frac{1}{r} \right) \right] \right. \nonumber \\&-\left. \frac{1}{2r^2}\left( r \frac{\mathrm{d}b}{\mathrm{d}r} -b \right) \left( \frac{\mathrm{d}\phi }{\mathrm{d}r}+\frac{1}{r}\right) +\Lambda \right\} , \end{aligned}$$
(49)

from the Einstein equation, \(G_{{\mu }{\nu }}+{\Lambda }g_{{\mu }{\nu }}=T_{{\mu }{\nu }}{/2}\).

An important combination of the quantities in (47)–(49), which is crucial for the violation of energy condition in the usual approach [2,3,4,5,6,7,8,9], is

$$\begin{aligned} \rho +p_r=-\frac{{2} e^{2 \phi }}{r} \frac{\mathrm{d}}{\mathrm{d}r}\left[ \frac{e^{-2 \phi }}{r} \left( 1-\frac{b}{r} \right) \right] . \end{aligned}$$
(50)

In the usual approach of the first option, the quantity in the bracket vanishes at the throat \(r=r_0\) since, when we consider the proper length l, for example, \(({\mathrm{d}r}/{\mathrm{d} l})|_{r_0}=\pm \sqrt{1-b(r_0)/r_0}=0\), i.e., \(b(r_0)=r_0\). But, in order that \(b(r)<r\) for \(r>r_0\) so that r is the space-like coordinate for an observer outside the throat, the quantity in the bracket needs to be positive, i.e., it has “positive” derivative,Footnote 7

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}r}\left[ \frac{e^{-2 \phi }}{r} \left( 1-\frac{b}{r} \right) \right] >0, \end{aligned}$$
(51)

which reduces to

$$\begin{aligned} \rho +p_r <0, \end{aligned}$$
(52)

so that all the energy conditions are violated. However, this is not the case in our approach of the second option, where the quantity in the bracket does not vanish at the throat for the traversable wormhole. The radial derivative of the quantity in the bracket, which is a positive quantity for \(r>r_0\), can have any values. Actually, in our example, we have \(\rho +p_r =0\). One can also obtain similar results for other combinations of the energy and pressures as in Fig. 9. This shows that the exoticity of the energy-momentum tensor for matters or effective matters from the modified gravities is not essential in the new approach.

5 Discussion

We have studied a new approach to construct a natural wormhole geometry in EBI gravity without introducing additional exotic matters at the throat. BI field equations are not modified at the throat for coordinate independent conditions of continuous metric tensor and its derivatives, even though BI fields have discontinuities in their derivatives generally. If we do not require the newly introduced conditions, the modification term exists and it produces the violation of the gravitational Bianchi identity. This supports the necessity of the new conditions in our construction. Remarkably, there is no violation of energy conditions and the energy-momentum tensors are normal. It is shown that this is the crucial effect of the new approach and the exoticity of the energy-momentum tensors for the matters is not essential for natural wormholes. It would be a challenging problem to see whether the non-exoticity in the energy-momentum tensors is a sign for the stability of wormholes or not. Several further remarks are in order.

First, the new approach for wormholes has been first studied in Hořava gravity [38], which has been proposed as a renormalizable quantum gravity model, where the effective energy-momentum tensors from the higher spatial derivative contributions violate the usual energy conditions in general. There, it has been argued that the Hořava gravity wormhole is the result of microscopic wormholes created by negative energy quanta which have entered the black hole horizon in Hawking radiation process.Footnote 8 In other words, the existence of wormholes may reflect the quantum gravity effect of black holes. However, we have found that the natural wormhole construction is still valid in the classically charged black holes in GR and the usual energy conditions can be satisfied too. This indicates that the formation mechanism for the natural charged wormholes has a classical origin in contrast to vacuum wormholes in Hořava gravity and other higher curvature gravities. So, there are two possible origins for wormholes, one for the classical and the other for the quantum mechanical ones, and both effects need to be considered generally. Actually, in our wormholes for EBI gravity, there is the upper bound for the electric field which may reflect the quantum mechanical pair creation of photonsFootnote 9 at short distances so that both the classical and the quantum effects are involved in the natural wormholes.

Second, we note that the new approach may have some difficulties when extending to higher-derivative gravity theories due to possible singularities at the throat. For example, when third-order spatial derivatives appear in the Einstein equation, we need to consider

$$\begin{aligned} \frac{\mathrm{d}^3g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}l^3}= & {} \left( \frac{\mathrm{d}r^{\pm }}{dl} \right) ^3 \frac{\mathrm{d}^3g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}{r^\pm }^3} \nonumber \\&+3 \left( \frac{\mathrm{d}^2r^{\pm }}{\mathrm{d}l^2} \right) \left( \frac{\mathrm{d}r^{\pm }}{\mathrm{d}l} \right) \frac{\mathrm{d}^2g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}{r^\pm }^2}\nonumber \\&+\left( \frac{\mathrm{d}^3r^{\pm }}{\mathrm{d}l^3} \right) \frac{\mathrm{d}g^{\pm }_{{\mu }{\nu }}(r)}{\mathrm{d}r^{\pm }}. \end{aligned}$$
(53)

In the usual Morris–Thorne approach, only the third term survives at the horizon due to \((\mathrm{d}r^{\pm }/\mathrm{d}l)|_{r_0}=0\) and it remains finite by the continuity condition \((\mathrm{d}^2r^{+}/\mathrm{d}l^2)|_{r_0}=(\mathrm{d}^2r^{-}/\mathrm{d}l^2)|_{r_0}\). Similarly, one may generalize this argument to arbitrarily higher-order derivatives in the Einstein equation. On the other hand, in the new approach the third term vanishes but the first two terms survive at the throat due to \((\mathrm{d}g^{\pm }_{{\mu }{\nu }}/\mathrm{d}r^{\pm })|_{r_0}=0\). However, the second term can cause a singularity due to the discontinuity of \((\mathrm{d}r^{\pm }/\mathrm{d}l)|_{r_0}\) unless we consider the case of \((\mathrm{d}^2g^{\pm }_{{\mu }{\nu }}/\mathrm{d}{r^\pm }^2)|_{r_0}=0\), which does not seem to be quite generic. This might imply that the new approach is not sufficiently complete as to describe all the generic higher-derivative gravity theories. Or this might imply that the natural wormholes are unstable for the case where the higher derivatives are involved like rotating black holes in Hořava gravity or other higher curvature gravities, as has been pointed out by one of us recently [39].

Note added: After finishing this paper, a related paper [65] appeared whose analysis of black hole in four dimensions is partly overlapping with ours.